A Combination of Docking, QM/MM Methods, and MD Simulation for Binding Affinity Estimation of Metalloprotein Ligands

Abstract

To alleviate the problems in the receptor-based design of metalloprotein ligands due to inadequacies in the force-field description of coordination bonds, a four-tier approach was devised. Representative ligand-metalloprotein interaction energies are obtained by subsequent application of (1) docking with metal-binding-guided selection of modes; (2) optimization of the ligand-metalloprotein complex geometry by combined quantum mechanics and molecular mechanics (QM/MM) methods; (3) conformational sampling of the complex with constrained metal bonds by force-field based molecular dynamics (MD); and (4) a single point QM/MM energy calculation for the time-averaged structures. The QM/MM interaction energies are, in a linear combination with the desolvation-characterizing changes in the solvent-accessible surface areas, correlated with experimental data. The approach was applied to structural correlation of published binding free energies of a diverse set of 28 hydroxamate inhibitors to zinc-dependent matrix metalloproteinase 9 (MMP-9). Inclusion of step 3 and step 4 significantly improved both correlation and prediction. The two descriptors explained 90% of variance in inhibition constants of all 28 inhibitors, ranging from 0.08 to 349 nM, with the average unassigned error of 0.318 log units. The structural and energetic information obtained from the time-averaged MD simulation results helped understand the differences in binding modes of related compounds.

Introduction

Metalloproteins play important roles in physiological processes (hemoglobin, cytochrome oxidase, catalase and superoxide dismutase), the receptor binding of potential drugs (carbonic anhydrases, matrix metalloproteinases, thermolysin, leucine aminopeptidase, phospolipase C, carboxypeptidase A and B, adenosine and cytidine deaminase), and drug metabolism (cytochromes P450 and methane monooxygenase), to give just a few examples.^1–3 In drug design, a description of the ligand interactions with transition metals poses a challenge due to the possibility of multi-dentate coordination bonding that is most appropriately treated at the quantum mechanical level.^4–11 This study presents an approach to a receptor-based estimation of binding affinities of metalloprotein ligands that is more reliable than standard ensemble-based techniques at the expense of a modest increase in the computing time.

The fastest and usually least precise descriptions of coordination bonds are obtained using molecular mechanical approaches. Several techniques are available with varying levels of sophistication. The nonbonded approach^12,13 uses optimized electrostatics and van der Waals terms,^14,15 occasionally using dummy cations placed around the metal atom^16,17 to enforce the correct coordination geometry. The geometry enforcement is more stringent in the bonded model^18–20 that utilizes the bond terms including bond stretching, angle bending, and torsional terms. These approaches require a predefined valence of the coordinating metal, in contrast to the directional force field YETI that is more flexible in selection of appropriate valence.^21,22 Further force-field enhancements include addition of polarizable bonds,^23,24 directionality based on orbital hybridization,²⁵ and ligand field stabilization energy.^26,27 Unfortunately, the more sophisticated force fields are not readily available for a routine use in modeling of ligand-metal interactions.

Combined quantum mechanical and molecular mechanical (QM/MM) methods represent an economical approach to characterization of macromolecular processes that include changes in the covalent bond status.^28–31 The atoms directly involved in the chemical steps are typically included in the QM region, whereas the rest of the system is treated at the MM level. Initially developed for gas-phase calculations,³² the QM/MM approach was first applied to enzyme systems by Warshel & Levitt.²⁸ QM/MM methods combine the efficiency of MM allowing for free energy simulations of macromolecules, with the accuracy and a systematic improvement potential provided by QM.³³ The methods have been implemented in combination with semi empirical and ab initio molecular orbital theory and with density functional theory (DFT). QM/MM-based molecular dynamics (MD) simulations have been used for modeling of enzymatic reactions,^31,34,35 but are computationally intensive and currently impractical for the prediction of binding affinities of a series of metalloprotein ligands. Alternatively, a large system as a whole can be treated at the QM level by fragmenting, linearly scaling approaches;³⁶ however, the QM/MM treatment seems to provide a better focus by applying the most sophisticated methods to the key chemical steps and the fast methods to the less important noncovalent processes.

Several categories of the methods for prediction of binding affinities to the receptors with known structures are available. Free Energy Perturbation (FEP),³⁷ Thermodynamic Integration,³⁸ and similar techniques³⁹ are the most sophisticated tools for free energy calculations. Extensive sampling resulting in extreme demands on computational resources and limitation to close homologs currently preclude their routine use in drug design. Computational costs can be reduced by partitioning of the binding energy into individual contributions and, in further simplification, by replacing the ensembles of structures generated in molecular simulations by single structures.

In ensemble-based partitioning approaches, only two states needs to be considered: complexes and free interaction partners. The approaches in this category can be classified according to the use of adjustable parameters in the final relation between the binding affinity and the calculated free energy contributions. The MM-PBSA^40,41 and MM-GBSA⁴² methods form the parameter-free category while the Linear Response (LR, a.k.a. Linear Interaction Energy) method^43–45 and its extended version (ELR)^46–48 represent the parametrized category. The contributions to the binding free energy are expressed as the differences Δ between the solvated ligand in the bound and free states in the ensemble averages (denoted by angle brackets) of respective quantities.

In ELR type methods, binding free energy ΔG_b is calculated as the linear combination of the differences Δ in the van der Waals energies, electrostatic energies,^43–45 and the solvent-accessible surface areas^46–48 (SASA) obtained from MD or Monte Carlo simulations:

$$\mathrm{\Delta }{G}_{\text{b}}=\mathrm{\alpha }\times \mathrm{\Delta }\langle {\text{E}}_{\text{vdW}}\rangle +\mathrm{\beta }\times \mathrm{\Delta }\langle {\text{E}}_{\text{el}}\rangle +\mathrm{\gamma }\times \mathrm{\Delta }\langle \text{SASA}\rangle +\mathrm{\kappa }.$$ (1)

The adjustable parameters α, β, and γ contain the protein-solvent and solvent-solvent interactions.^49–51 The van der Waals parameter α depends on the used force field, as was shown e.g. for thrombin.^47,49,52 Its magnitude was analyzed with respect to hydrophobicity of the binding site.⁴⁹ The coulombic scaling coefficient β varies with the ligand nature and ligand surroundings (protein or water),^53–55 although its equality to ½ was assumed initially based on the linear response of the surroundings to electric fields.^43–45 Similar method for treatment of hydration of more complex molecules⁵⁶ required the use H-bond donor and acceptor counts, in addition to the quantities present in Eq. 1. Continuing studies of more diverse ligands may reveal the need for further empirical corrections.

Single-structure-based partitioning approaches, represented by VALIDATE,⁵⁷ the Free Energy Force Field approach,^58,59 COMBINE analysis,⁶⁰ and a single-structure version of the LR method using continuum electrostatics,⁶¹ replace the ensemble averages by a single configuration, usually obtained by a direct geometry optimization of the receptor-ligand complex. Scoring functions are simplified single-structure-based partitioning approaches that are categorized as force field-based methods,^62,63 empirical free energy scoring functions,^64–66 and knowledge-based scoring functions.^67–69 They are mainly used in high-throughput virtual screening, in connection with fast docking procedures.

To overcome the limitations of the aforementioned methods in prediction of binding affinities to metalloproteins due to the difficulties in handling the transition metal atoms, we have combined docking, QM/MM calculations, and force-field-based MD methods into a coherent approach. The approach is tested using inhibitors of matrix metalloproteinases (MMPs),⁷⁰ which belong to the most-studied metalloenzymes. Development of MMP inhibitors is complicated by structural relatedness of the MMP family,⁷¹ in which some members assume normal physiological roles and others are pathological, depending upon given concentration or activity.

Results and Discussion

Interactions of metalloproteins with ligands are often difficult to describe effectively due to the limited availability of appropriate force fields. To predict binding affinities in these cases, we devised a four-tier procedure consisting of: (1) docking with the selection of poses based upon appropriate metal binding; (2) QM/MM optimization of the best docked geometries; (3) MD simulation with the metal binding group of the ligand confined in the geometry from Step 2; and (4) QM/MM single point interaction energy calculation based on the time-averaged structures from Step 3:

$$\mathrm{\Delta }\langle {\text{E}}_{\text{QM/MM}}\rangle =\langle {\text{E}}_{\text{QM/MM}}^{\text{complex}}\rangle -\langle {\text{E}}_{\text{QM/MM}}^{\text{ligand}}\rangle -\langle {\text{E}}_{\text{QM/MM}}^{\text{receptor}}\rangle .$$ (2)

The QM/MM interaction energies are correlated in an ELR-type approach, along with SASA crudely parametrizing desolvation, with experimental affinities. The use of the energies of the time-averaged structures in place of the ensemble averages of energies was previously shown to provide equivalent results in a parametrized partitioning approach to binding affinity correlations⁷² and in protein pK_a prediction.⁷³ The approach was tested using published data⁷⁰ on inhibition of 28 hydroxamate inhibitors of MMP-9 (Table 1).

Table 1.

Structures, inhibition constants,⁷⁰ and the simulation results of the studied MMP-9 inhibitors.

No	X	R1	R2	log(1/Ki), Ki in M		−Δ<EvdW> a (kcal/mol)	−Δ<Eel> a (kcal/mol)	−Δ<EQM/MM> b (kcal/mol)		−Δ<SASA> (Å2)
				exp.	calc. d			Min	MD	Min c	MD a
1	X1	CH2CH3		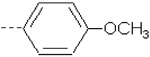8.297	8.035	111.93	189.63	1216.74	689.95	417.06	389.34
2 e	X1	CH2CH3		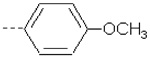6.457	6.728	86.41	192.93	1177.15	489.14	324.51	311.53
3	X1	CH3		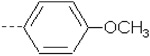8.693	8.819	107.04	174.78	1130.66	860.87	350.53	411.94
4	X1		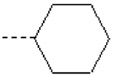	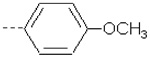8.182	7.803	106.40	169.62	1105.70	721.32	425.77	343.59
5	X1		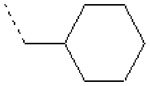	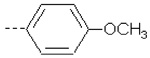8.341	8.233	95.40	155.90	1140.95	520.52	437.80	496.27
6	X1		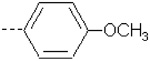	8.189	8.315	121.79	192.67	723.49	736.12	370.67	404.369
7	X1	(CH2)2N(CH2CH3)2		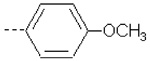7.777	7.924	72.34	148.89	1107.33	646.02	455.69	395.52
8	X1		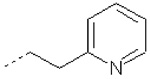	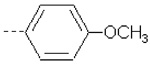8.466	8.337	127.92	239.22	1090.74	533.07	460.21	504.04
9	X1	(CH2)2OCH2CH3		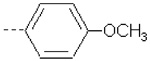8.197	8.322	120.93	190.55	980.36	746.42	381.41	400.46
10	X1	CH2CH3		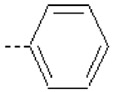7.370	7.226	88.32	159.09	874.43	639.75	320.68	305.84
11	X1	CH2CH3		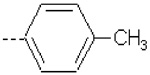7.379	7.562	103.30	179.29	1016.72	696.22	353.45	323.61
12	X1	CH2CH3		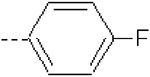7.285	7.253	88.67	192.33	879.98	614.65	303.00	321.47
13	X1	CH2CH3		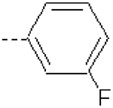7.096	7.017	90.80	182.57	868.42	589.55	316.57	302.09
14	X1	CH2CH3		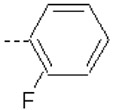7.493	7.122	98.18	176.21	879.45	595.82	322.45	312.99
15	X1	CH2CH3		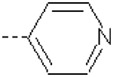6.556	7.218	87.85	156.83	887.22	608.37	348.26	319.82
16	X1	CH2CH3		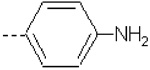7.020	7.635	95.44	183.74	982.55	696.22	334.14	333.28
17	X1	CH2CH3		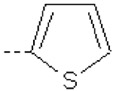7.228	7.224	94.51	159.36	949.87	595.82	319.49	326.53
18	X1	CH2CH3		7.848	8.158	123.38	183.20	1307.85	551.90	459.85	471.31
19	X1	CH2CH3		9.509	9.197	121.99	227.93	1127.44	940.95	429.04	423.94
20	X1	CH2CH3		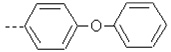10.10	10.18	123.45	206.88	1121.86	834.28	451.32	604.77
21	X1	CH2CH3		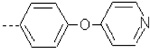9.222	8.554	124.01	195.86	1058.55	740.15	456.49	434.23
22	X1	CH2CH3		10.00	9.977	137.04	224.55	1127.20	771.52	472.26	608.05
23	X1	CH2CH3		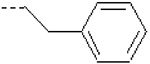7.417	7.675	111.28	197.02	1037.06	771.52	389.28	302.73
24	X2	CH2CH3		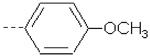7.959	8.114	0.74	0.82	1023.59	727.60	384.47	381.87
25	X3	CH2CH3		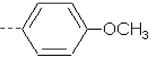8.420	8.026	103.83	203.22	1013.16	683.67	361.72	391.05
26	X4	CH2CH3		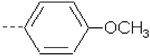8.947	9.193	110.63	189.12	1009.13	771.52	345.50	504.02
27	X5	CH2CH3		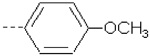8.284	8.218	132.48	237.82	879.21	740.15	428.73	389.68
28	X6	CH2CH3		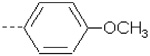6.500	6.081	95.55	180.16	549.68	464.73	253.08	237.38

^aThe LR terms for van der Waals and electrostatic energies and for the SASA change were obtained using MD simulation with explicit solvent.

^bThe QM/MM energy terms calculated for optimized structures after QM/MM minimization and for time-averaged structures after MD simulation.

^cThe SASA change for optimized structures after QM/MM minimization.

^dCalculated from Eq. 3 with optimized values of adjustable parameters for Step 4 (Table 2, last row).

^eConfiguration of C-3 (marked with an asterisk) is S in 2 while in other compounds it is R.

Step 1 - Docking

Docking of the inhibitors to the MMP-9 structure taken from the Protein Data Bank⁷⁴ (PDB file 1GKC) was performed using FlexX.^64,75 The ranking of poses was based upon the distance between catalytic zinc and both hydroxamate oxygens in the interval 1.5 – 2.5 Å as the primary criterion and the FlexX score as the secondary criterion.⁷⁶ Docking provided a greater variety of the initial binding modes than superposition of the ligands with the ligand in the PDB file of the complex.⁷⁷ Since the MD simulations routinely do not sample conformations too different from the starting conformations, this step was instrumental in selecting the binding mode explaining the experimental data for several compounds. To reduce the QM/MM convergence time, for the top complexes of each ligand, the mobile region within 5 Å of the ligand superposition was briefly optimized by the conjugate gradient minimization using OPLS-AA force field.

Step 2 - QM/MM Geometry Optimization

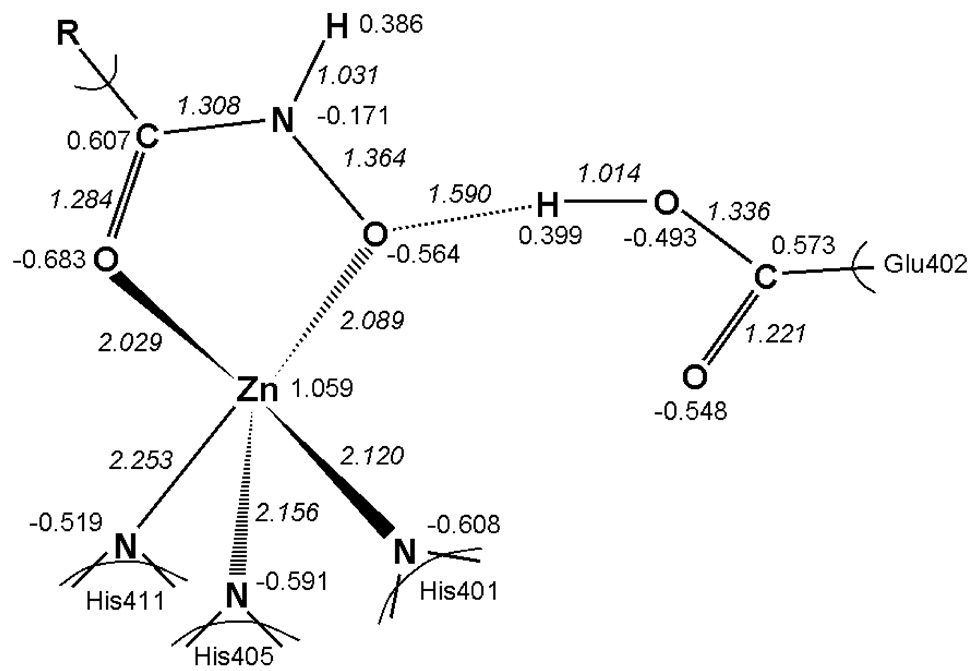
The charges and inter-atomic distances for all 28 ligands (Table 1) do not differ much; therefore we present them as average values in Figure 1. The maximum standard deviations were 8.1 % for charges and 2.5 % for distances. Charge transfer from hydroxamate group to zinc is significant, albeit very similar for all studied compounds (Figure 1). For the free/bound hydroxamates, the average bond lengths were (in Å): C=0 1.236/1.284, C-N 1.355/1.308, N–O 1.401/1.364, and O–H 0.982/1.590, respectively. In the QM/MM geometry optimization of the complex, the proton from the hydroxamate OH group was transferred to the Glu402 oxygen but remained H-bonded to the parent oxygen. The average C=0, C-N and N-O bond lengths for the bound state obtained here (1.284, 1.308 and 1.364 Å) are closer to deprotonated Zn-coordinated hydroxamate (1.294, 1.317 and 1.378 Å) than to neutral hydroxamate with respective distances of 1.279, 1.337 and 1.416 Å.⁷⁸ The distance between Glu402 oxygen and oxygen of the reverse hydroxamate (2.70 Å) in MMP-9 and hydroxamate oxygen in MMP-7⁷⁹ and MMP-8^80,81 (2.6–2.8 Å) complex are in close agreement with the distance found in Step 2 (2.604 Å). These facts suggest that bound hydroxamate structure is, in the presence of proton-accepting Glu402, closer to deprotonated state than to neutral form. Hydroxamates approach the binding site as neutral molecules (pK_a ≥ 8.9 for the studied compounds)⁸² and require ionized Glu402 for full potency.⁸³

Figure 1.

Average Mulliken charges and bond lengths (Å, in italics) for the complete set of 28 hydroxamate complexes (Table 1) after QM/MM optimization. The maximum standard deviations were 8.1 % for charges and 2.5 % for distances.

Two hydroxamate oxygens may bind to zinc in monodentate or bidentate configurations that result in four- or five-fold coordination, respectively. Among the structures of hydroxamates bound to MMPs in PDB, the bidentate zinc binding prevails, with trigonal bipyramidal (TB) configurations occurring about six times more frequently than the square-based pyramid (SP). After QM/MM optimization, the bidentate TB coordination was observed in the studied hydroxamate structures, as evidenced by the average geometries of all 28 complexes (Figure 1). The bond lengths of the two Zn-O bonds (Zn-O1 and Zn-O2) are 2.029±0.018 Å and 2.089±0.012 Å, respectively, which indicates that the two oxygens coordinate with zinc about equally. The average bond angles O1-Zn-N in His401, His405 and His411 in these complexes are 121.77±14.81°, 135.58±8.95°, and 82.06±1.65°, respectively (ideal values for TB: 120°, 120°, 90°; and for SP: 90°, 180°, 90°). The average bond angles O2-Zn-N in the same order are 101.55±1.89°, 95.07±2.13°, and 155.23±2.98°, respectively (both TB and SP: 90°, 90°, 180°). The average bond angle of O2-Zn-O1 is 79.66±0.61° , approaching the ideal value of 90° for both TB and SP configurations.

The QM/MM approach for the entire binding domain provided a more realistic picture than the studies using reduced systems^{5,10,78,84,85} that do not consider the protein surroundings of bound ligands. In this case, ionized Glu402 is crucial for a correct description of binding. The QM/MM approach handled the zinc-ligand charge transfer,³⁶ bond length changes, polarization, and ionization²⁵ upon binding to zinc, which would be difficult to describe by advanced force fields.^21–27 Albeit very similar in the studied set, the electronic phenomena can be anticipated to play a more important role in a heterogeneous series of ligands.

Step 3 - MD Simulations

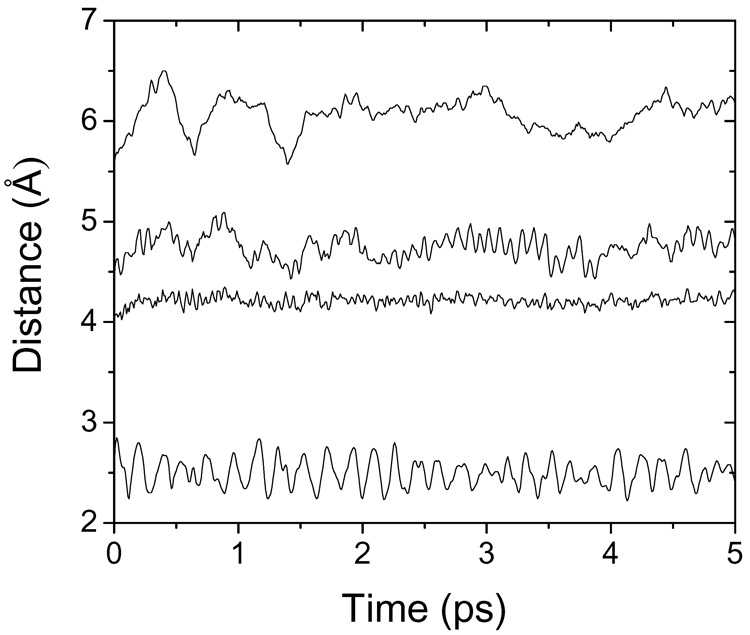
The QM/MM optimized complexes were subjected to the MD simulation with the constrained zinc-hydroxamate oxygens bond lengths and angles, to obtain conformational sampling for the rest of the complex. To reduce the computational expense, only one MD simulation, for the enzyme-inhibitor complex, was performed.⁴¹ The energy terms for the enzyme and inhibitor taken from the MD simulation for the complex were comparable to those obtained from running separate simulations for the enzyme and inhibitor, as checked for several inhibitors. Inspection of the trajectories revealed that the secondary and tertiary structure of the ligand-receptor complex remained stable during the entire 200-ps simulation period (data not shown). The influence of zinc bond constrains on movement of other ligand parts is illustrated in Figure 2. The chiral carbon (Table 1) that is only 2–3 bonds apart from the constrained hydroxamate oxygens is comparatively rigid. The ring nitrogen and phosphorus are separated by 1–2 more bonds from the constrained part and exhibit amplitudes comparable to those of distant binding site parts like the oxygen of Glu402 that is H-bonded to hydroxamate oxygen. The ensemble averages of the van der Waals and electrostatic energies that were calculated for the time-averaged structures obtained after 5 ps simulations are listed in Table 1. Longer simulation times provided similar samplings that did not improve the correlations using Eq. 1 and Eq. 3 and the results are not shown. The ΔSASA terms were lower for the time-averaged structures from Step 3 than for the minimized structures from Step 2 in 16 cases (Table 1). For 12 ligands, however, the ΔSASA terms increased, indicating that MD sampling found better binding modes than minimization. The largest increases were observed for ligands 3, 5, 6, 8, 20, 22, 25, and 26.

Figure 2.

The effect of constrained zinc binding on the MD simulation of ligand 20 (Table 1) in the MMP-9 active site. Distances between catalytic zinc and, from the top, phosphorus, ring nitrogen, and chiral carbon atoms (structures in Table 1) and between hydroxamate oxygen (O2) and Glu402 oxygen in 10 fs intervals throughout the 5-ps MD simulation.

Step 4 - Calculation of QM/MM Interaction Energies

For the time-averaged structures resulting from 5-ps MD simulations, single point QM/MM interaction energies were calculated according to Eq. 2 and are summarized in Table 1. The time-averaged structures were used to preserve conformational sampling obtained in Step 3 that should result in more realistic descriptions than using the single optimized structures.⁶¹ As can be expected, the QM/MM energy changes are much smaller for the time-averaged structures from Step 3 than for the minimized structures in Step 2. The QM/MM calculations properly treat the coordination bonds between zinc and the ligands. Therefore, the QM/MM interaction energies are expected to provide better energy estimates than the MM-based force field simulations.

Correlations with Inhibitory Activities

The QM/MM energies, along with SASA characterizing ligand desolvation, were correlated with experimental binding affinities using Eq. 3, in a way reminiscent of the ELR approach (Eq. 1):

$$\mathrm{\Delta }{G}_{\text{b}}=\mathrm{\alpha }\times \mathrm{\Delta }\langle {\text{E}}_{\text{QM/MM}}\rangle +\mathrm{\gamma }\times \mathrm{\Delta }\langle \text{SASA}\rangle +\mathrm{\kappa }$$ (3)

For a comparison, the MD results were correlated with biological data using Eq. 1. The influence of the SASA’s polar and nonpolar components, as well as that of the constant term κ were examined. The resulting equations are not listed because they improved neither correlations nor predictions.

The fits of Eq. 1 and Eq. 3, with logK_i on the left side, to the inhibition data for the 28 compounds for individual Steps are summarized in Table 2. Prediction of the MMP-9 inhibition constant based upon the linear correlation of the experimental data with the FlexX scores in Step 1 resulted in a poor correlation characterized by r² = 0.044, with r being the correlation coefficient.

Table 2.

Correlations of inhibitory potencies with the energy and SASA terms obtained by different methods for 28 MMP-9 inhibitors. The logK_i, K_i in M, values were used instead of ΔG_b in Eq. 1 and Eq. 3.

Method	Step	Eq.	a α×10−3 (mol/kcal)	b β×10−3 (mol/kcal)	c γ×10−3 (1/Å2)	κ	r2	SD	F	LOO d		LSO e
										q2	RMSE	q2	RMSE
FlexX f	1	-	69.7±63.71	-	-	−5.831±1.997	0.044	0.966	1.198	−0.079	0.989	−1.110	0.994
QM/MM Minimization	2	3	−0.420±1.190	-	12.30±3.12	−3.744±0.966	0.504	0.709	12.72	0.380	0.750	−0.457	0.808
QM/MM Minimization	2	3	-	-	11.55±2.26	−3.606±0.870	0.502	0.697	26.21	0.423	0.723	−0.278	0.751
MD	3	1	11.25±10.50	−4.090±6.010	8.380±1.240	−4.315±0.551	0.764	0.499	25.96	0.566	0.627	0.180	0.662
MD	3	1	4.630±4.060	-	8.680±1.150	−4.137±0.478	0.760	0.494	39.55	0.602	0.600	0.272	0.629
MD	3	1	-	-	9.230±1.105	4.399±0.422	0.747	0.496	76.91	0.717	0.506	0.442	0.531
QM/MM	4	3	3.592±0.580	-	7.543±0.727	−2.623±0.394	0.900	0.318	112.8	0.879	0.331	0.769	0.319

^aCharacterizes QM/MM interaction energy (Eq. 3) or van der Waals energy (Eq. 1).

^bCharacterizes electrostatic energy ( Eq. 1 only).

^cCharacterizes the solvent accessible surface area (Eq. 1 and Eq. 3).

^dLeave-one-out cross-validation.

^eLeave-several-out cross-validation: random selection of 6-member test set, repeated 200 times.

^fThe correlation between logK_i and the FlexX scores, with the slope α and the intercept κ.

The QM/MM energies of the ligand-enzyme complexes with optimized geometries, obtained in Step 2, resulted in a slightly improved statistics (r² = 0.504, Table 2). The correlation is dominated by the SASA term. Inclusion of the QM/MM energy for the optimized geometry did not improve the correlation. The pertinent regression parameter α has a negative sign and an inflated error, possibly due to a moderate cross-correlation between the QM/MM energy and the SASA term (r²=0.460).

The use of the energy terms from the MD conformational sampling in Step 3 pushed the correlation to r²=0.764 (Table 2). Compounds 3, 7, 20, 22, and 26 (Table 1) that saw the greatest description improvement in Step 3 (0.6 – 1.1 log units), exhibit a significant change in the conformation of the bound ligand upon MD sampling. The change in the binding conformation is accompanied by a large increase of ΔSASA, except compound 7. Descriptions for other compounds with ΔSASA increased upon MD sampling (5, 6, 8, and 25, Table 1) improved by 0.1 – 0.3 log units. For the van der Waals coefficient α, the error is almost equal to the parameter estimate, while for the coulombic coefficient β, the sign of the parameter estimate is negative and the error term larger than the parameter estimate. This misbehavior may be caused by the collinearity problem of the van der Waals and electrostatic terms (r²=0.712 – 0.839 for different simulation times). The low value of the van der Waals coefficient α might indicate a low hydrophobicity of the MMP 9 binding site, if the results of the original analysis⁴⁹ are also valid for correlations with the explicit SASA term. Cross-correlation of van der Waals and SASA terms was very weak (r²=0.174).

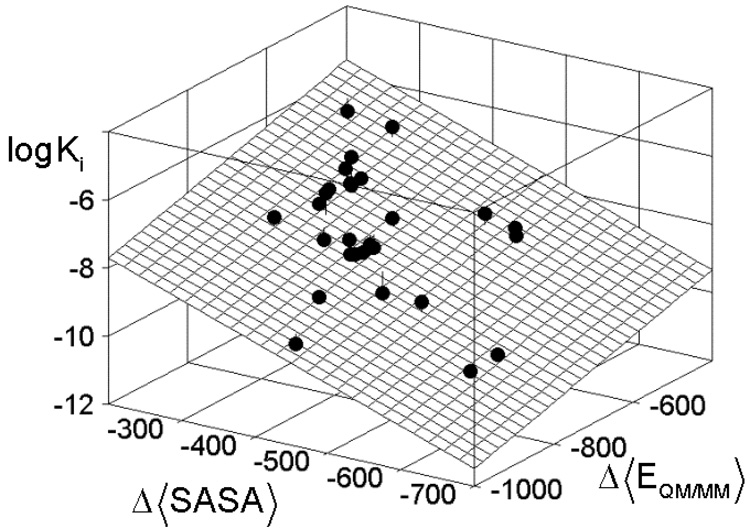
The best model for Step 4 contained just the single point QM/MM energy for the time-averaged structures and the SASA term and was obtained using the data from a 5-ps MD simulation. This treatment was most beneficial for compounds 18 and 19, the residuals of which decreased from ~1.0 in Step 3 to ~0.3 log units in Step 4, and compounds 5 and 8, with residuals improving from ~ 0.6 to ~0.1 log units. The correlation for all 28 compounds is characterized by r² = 0.900 and the standard deviation SD = 0.318 reflecting a good agreement between actual and calculated values (Table 2). For each parameter, the probability >F ratio was <0.0001, implying that the likelihood of a random occurrence of a significant parameter is negligible. The cross-correlation between the QM/MM energy and SASA is very weak as indicated by the r² value of 0.140. The dominance of the SASA terms, clearly seen in Table 2, is probably reflecting the effect of burial of the inhibitor in the binding site. This phenomenon was described previously in the analysis of binding energies of several ligand-protein complexes.⁸⁶ A plot of experimental activity as a linear combination of contributions from QM/MM energy and SASA is shown in Figure 3. The quality of correlations in Step 4 remained at about the same level with the increase in the MD simulation time for obtaining the time-averaged structures. Consequently, the simulation time of 5 ps seems to be sufficient for the binding energy analyses in the studied case, which is characteristic by constrained geometry of the zinc binding group in the complex and rigid protein structure outside the 5-Å region around the ligand superposition.

Figure 3.

Experimental inhibition constants K_i (M) of hydroxamates (Table 1) vs MMP-9 as a linear combination of the change in the SASA (Ų) caused by binding and the QM/MM interaction energy (kcal/mol) for the time-averaged structures obtained by MD simulation.

The adjustable parameter κ in Eq. 3 yields an attractive term of about −2.623 log units (Table 2), providing a base value for the inhibitors that is then modulated by the QM/MM interaction and SASA terms. The values of the QM/MM terms (Table 1) are negative and the associated positive coefficient (Table 2) implies that a strong interaction between the inhibitor and the binding site is important for inhibition. The SASA terms (Table 1) are negative, implying burial of the surface area upon binding. The associated parameter γ (Table 2) is positive so that the removal of mostly hydrophobic surface area from the contact with water upon binding promotes the binding, which simply reflects the hydrophobic effect.⁸⁷ The obtained values of γ (Table 2: 0.00754-0.011 Å⁻²; multiplied by R×T×ln10 = 1.419 kcal/mol to account for the change of the dependent variable from free energy to log K_i as described in part Methods/Data Set) are in the same range as the slopes of the linear dependencies of solvation free energies on SASA: 0.007 kcal/(mol×Ų) for alkanes,⁸⁸ and 0.016⁸⁹ or 0.020 kcal/(mol×Ų)⁴⁶ for various compounds.

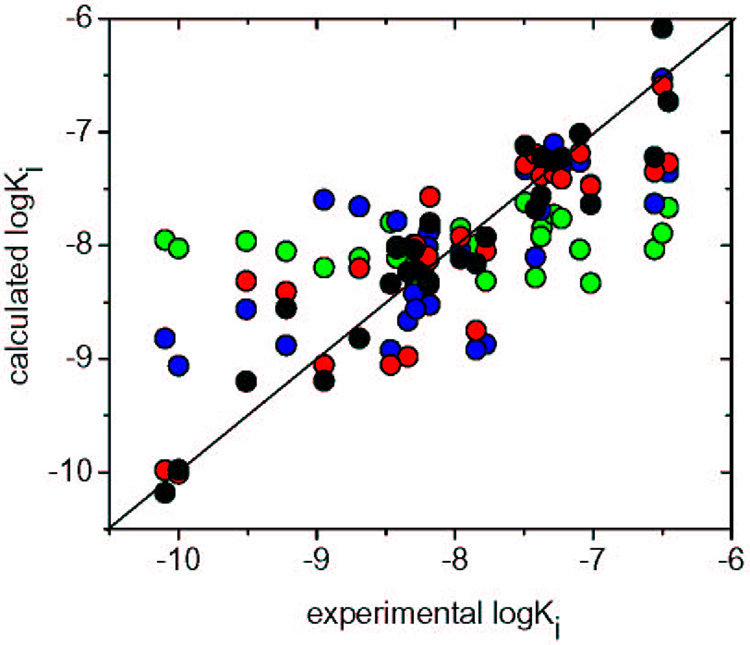
The robustness of the regression equations and their predictive abilities were probed by cross-validation. The leave-one-out (LOO) procedure and especially the leave-several-out (LSO) procedure with a random selection of 6-member test set that was repeated 200 times provided a thorough evaluation. The predictive root mean squared error (RMSE) for Eq 3 obtained for the 5 ps MD simulation time is the lowest among all correlations. The RMSE values using LOO (0.331) and LSO (0.319) were comparable to that of the RMSE of the whole data set (0.315). Inclusion of all Steps in the correlation was warranted by the improvement in descriptive and predictive ability. The quality of correlations for individual Steps is documented in Figure 4.

Figure 4.

Correlations between experimental and calculated inhibition potencies of hydroxamates vs. MMP-9 as obtained by FlexX docking with the zinc binding based selection of modes in Step 1 (green), QM/MM minimization in Step 2 (blue), MD simulation with constrained zinc bonds in Step 3 (red), and by QM/MM energy calculations for the time-averaged structures from MD simulation in Step 4 (black). All correlation results are summarized in Table 2.

The correlation described by Eq. 3 with the optimized parameters given in Table 2 is much better than our previous ELR results⁷⁷ obtained from MD simulations with nonbonded zinc-ligand interactions. The predictive ability of the ELR model for all 28 compounds was characterized by RMSE from LSO cross-validation between 0.584 and 1.173, depending upon the simulation time (Table 6, model A in ref. 77). Comparison of these values with equivalent LSO RMSE values in the right-most column of Table 2 shows that current correlations were significantly better only for Step 4 (RMSE 0.319), where single-point QM/MM energies of the time-averaged structures were used. The results from MD simulations employing the same time-averaged structures (Step 3), although run with improved starting geometries of hydroxamate groups from the QM/MM minimization in Step 2, did not show any major progress: the best RMSE was 0.531 that is only slightly better than 0.584 resulting from a less constrained MD simulation. The QM/MM energy from the minimization procedure (Step 2) ended with the best RMSE of 0.751 that is not much better than RMSE of 0.785 that was obtained previously with a force-field minimization. Apparently, conformational sampling embodied in the time-averaged structures (Step 3) and a good description of the zinc coordination bonds (Step 4) are jointly required for a good correlation with experimental inhibitory potencies and none of these procedures alone is making a major breakthrough.

Binding Trends

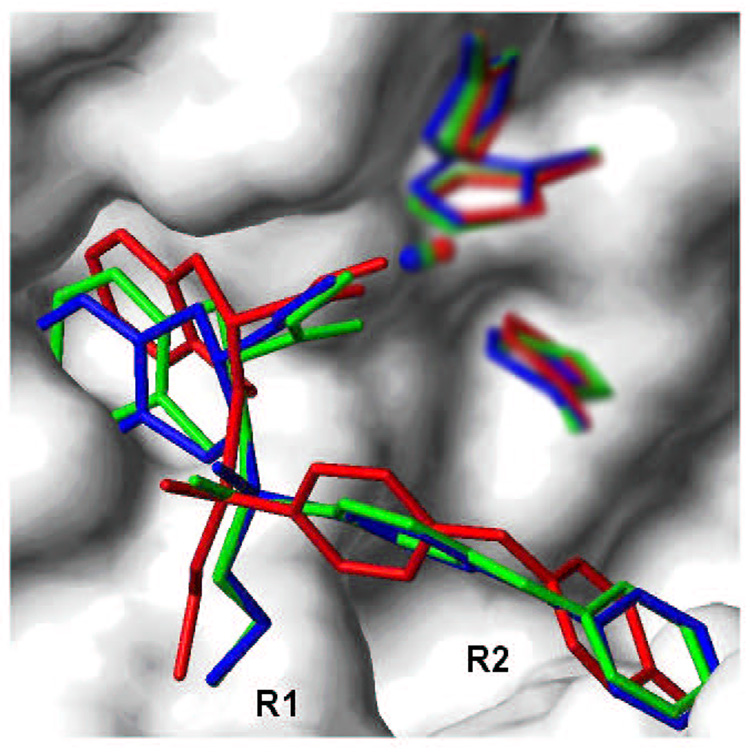
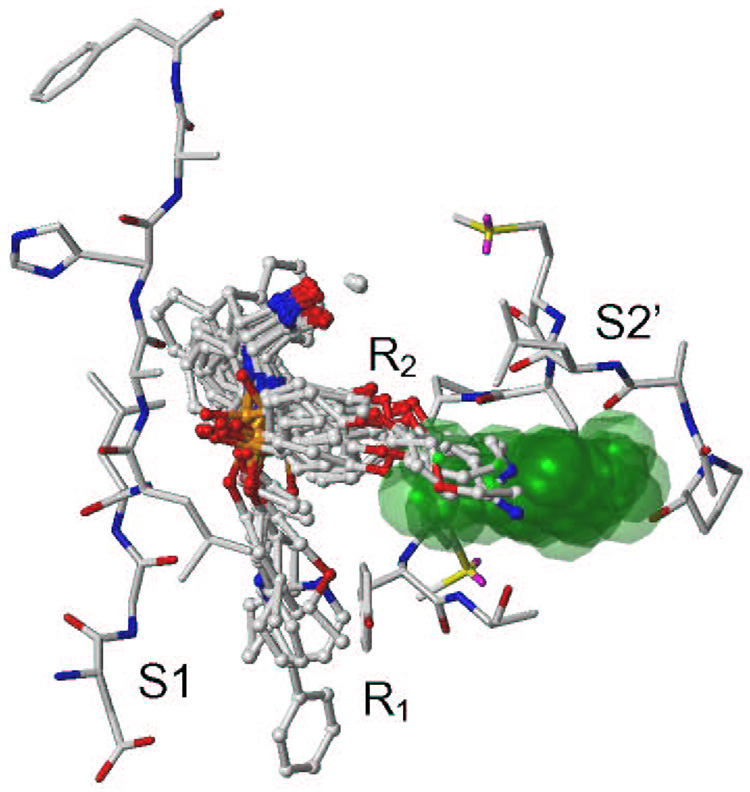
Eq. 3 and underlying structural information on bound ligands present a straightforward framework for understanding the trends in the observed activities. For a given series of hydroxamate derivatives in Table 1, the ranges for the contributions from QM/MM interactions and burial of solvent accessible surface area are 451.81 kcal/mol and 305.97 Ų, respectively. The SASA term contributes more to the computed activities than the QM/MM term. Representative binding modes of compound 22 (Table 1) obtained after FlexX docking, minimization, and MD simulation are illustrated in Figure 5. The differences between minimized structures and time-averaged structures after MD sampling in Step 3 were sometimes larger than those shown in Figure 5, especially for compounds 3, 7, 20, and 26 (Table 1). The S1 subsite is structurally defined by Asp185, Gly186, Leu187, Leu188, Ala189, His190, Ala191, and Phe192, while the S2’ subsite is defined by Ala417, Leu418, Met419, Tyr420, Pro421, Met422, and Tyr423. The P=O group of all the ligands except 2, 3, 13, 16, 20, and 25 forms hydrogen bonds with the backbone NH of Leu188. In general, the R₁ substituents occupy the pocket lined with residues of the S1 subsite while R₂ substituents occupy the S2’ subsite (Figure 6). Even compounds with longer R₂ substituents (compounds 18–22) leave an empty pocket in the S2’ subsite. Since these are the most potent compounds in the given series, further lengthening of the R₂ substituents may be helpful in designing more potent inhibitors.

Figure 5.

The binding modes of compound 22 (Table 1) in active site of MMP-9 obtained from FlexX docking (green), QM/MM optimization (blue), and MD simulation (red). The R₁ and R₂ substituents bind in S1 and S2’ subsites, respectively. The time-averaged protein surface after MD simulation (Step 3) is shown in white for clarity. The imidazole rings of His401, His405, and His411, as well as catalytic zinc were included in creating the surface but are also shown in corresponding colors. The surface of the protein was z-clipped for better view.

Figure 6.

The binding modes of compounds with longer R₁ (compounds 4 – 9) and R₂ (18 – 22) substituents (Table 1) shown in ball and stick mode. Compounds with smaller R₁ and R₂ substituents follow a similar pattern. The catalytic zinc is represented as sphere. The empty pocket of the S2’ subsite, created with the SiteID module of Sybyl,⁹⁶ is represented by transparent green space fill. The residues of the S2’ and S1 subsites as well as residues surrounding the empty pocket for compound 4 are shown in atom color in the capped stick mode. All structures are time-averaged structures from MD simulation (Step 3).

The Effect of Stereoisomerism

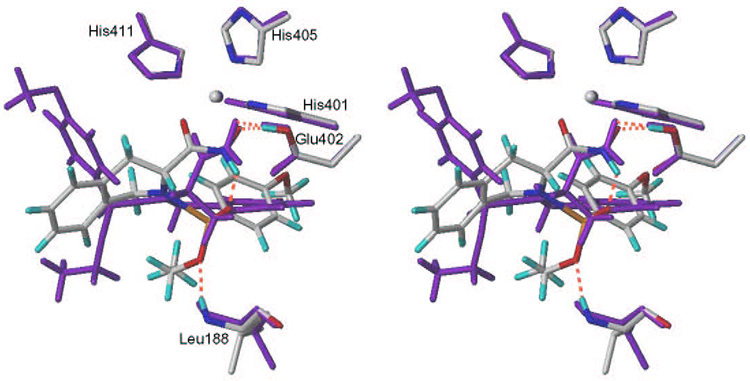
Compound 1 is a potent inhibitor (K_i = 5.05 nM) while compound 2 exhibits only moderate activity (K_i = 349 nM). The compounds are structurally similar except the configuration on C-3 where 1 exhibits the R-configuration while in 2 it is the S-configuration. The importance of the R-configuration at the α carbon is well documented.^90–94 Binding modes after MD simulation (Step 3) of the two inhibitors are shown in Figure 7. The zinc-binding group is tightly bound to zinc in both the compounds but the rest of the ligand is flipped by 180°. In case of 1, several hydrogen bonds can be discerned: between the oxygen atom of the ethyl ester group and the main chain NH of Leu188; between the hydroxamate OH and oxygen of Glu402 (and also an intramolecular H-bond with the phosphonamide oxygen). In contrast, compound 2 forms only one hydrogen bond with the Glu402 (Figure 7). The H-bond pattern is reflected in computed QM/MM interaction terms (Table 1) that are equal to −698.95 kcal/mol for 1 and −489.14 kcal/mol for 2. Additional benefit for 1 comes from the burial of more SASA (−389.34 Ų) than for 2 (−311.53 Ų).

Figure 7.

Stereo view of the binding modes and key interactions of isomers 1 (atom color) and 2 (purple) in MMP-9 active site (time-averaged structures after the Step 3). Compound 1 forms hydrogen bonds with Leu188 and Glu402, while compound 2 engages in hydrogen bond with Glu402 only. The hydrogen bonds are shown in dashed lines (magenta). Structures of isomers are shown in Table 1.

The Role of 4-Methoxyphenyl in R₂ Position

Substitution of 4-methoxyphenyl in the R₂ position in 1 with pyridine ring in 15 resulted in a severe loss of activity. The fact can be explained by the lower QM/MM energy values as well as a lower burial of SASA in 15 as compared to 1 (Table 1). Compounds 10 – 12 (K_i = 42.7, 41.8, and 51.9 nM, respectively) are structural analogs of compound 1 but exhibit lower activity as compared to 1 (K_i = 5.05 nM). The 4-methoxyphenyl group in R₂ position of 1 is replaced with phenyl (10), 4-methylphenyl (11), and 4-fluorophenyl (12) substituents. Compounds 10 – 12 exhibit less burial of SASA and similar (11) or lower QM/MM energy values (10 and 12), as compared to 1 (Table 1).

Interactions vs. SASA Burial

Compound 19 (R₂=Ph-Ph) differs from 20 (R₂=Ph-O-Ph) in the interlinking oxygen atom and exhibits a lower activity. The ether linkage in 20 is expected to be better solvated in the unbound state of the ligand than in the bound state. However, this factor is not encoded in the overall ΔSASA value: greater ΔSASA (−604.77 Ų) of 20 than 19 (−423.94 Ų) merely reflects the size difference as both ligands bind in a similar way. Although the QM/MM energy term is more favorable for 19 (−940.95 kcal/mol) than for 20 (−834.28 kcal/mol), this contribution is negated by the dominance of the SASA term and consequently higher activity for compound 20.

Compounds 20 and 21 differ in isosteric R₂ substituents (Ph-O-Ph and Ph-O-C₆H₅N, respectively). The QM/MM as well as SASA terms are more favorable for compound 20 as compared to compound 21 (Table 1). For compound 20, MD simulation in Step 3 found a new time-averaged binding mode resulting in a substantial increase in ΔSASA that explains higher activity of 20 as compared to 21. In this mode, the P=O group of 20 forms H-bond interaction with backbone NH of Ala189 that was not observed after QM/MM minimization in Step 2.

MD simulation also found a new time-averaged binding mode for compound 26, resulting in a significant increase in ΔSASA and improvement in description of activity after Step 3 as compared to Step 2. A closer look at the structural changes shows that the new mode also exhibits a different H-bonding interaction pattern: the P=0 group forms H-bond with backbone NH of Leu188, while after Step 2 the NH group in X4 was H-bonded with the backbone C=0 group of Gly186.

Methods

Data Set

Published inhibitory potencies, characterized by the inhibition constants K_i at 37 °C, of a series of 28 hydroxamate derivatives⁷⁰ towards MMP-9 were used (Table 1). The inhibition constants are the inverse values of the association constants K. The left sides of Eq. 1 and Eq. 3 are the binding free energies ΔG_b = − R×T×lnK = R×T×ln10×logK_i. The logK_i values were used as dependent variables, in order to work with the dependent variables that are most common in medicinal chemistry. The optimized values of adjustable parameters α, β, γ, and κ (Table 2) can be recalculated for the ΔG_b as independent variable by multiplication with R×T×ln10 = 1.419 kcal/mol.

Coordinates of the MMP-9 catalytic domain were taken from the recently reported x-ray crystal structure of the MMP-9 in the complex with N-formyl-N-hydroxy-2-(2-methylpropyl)-β-alanyl-N,3-dimethyl-L-valinamide, a ‘reverse hydroxamate’ inhibitor, as deposited in the PDB (file 1GKC).⁹⁵

Construction of Initial Inhibitor/Enzyme Complexes

Three-dimensional structures of ligands were constructed using the SYBYL6.9 suite of programs⁹⁶ running under Irix 6.5. Full geometry optimization and charges were calculated using DFT/B3LYP-6–31G** approach.⁹⁷ The inhibitors were docked into the active site of MMP-9 using the FlexX program that considers ligand conformational flexibility by an incremental fragment placing technique.^64,75 For each ligand, the best conformation in the active site was selected from the top 30 poses generated by FlexX using the distances in the interval 1.5 – 2.5 Å between both hydroxamate oxygens and the catalytic zinc atom as the primary criterion and the FlexX ranking as the secondary criterion.⁷⁶ Step 1 was completed by a brief MM geometry optimization using the OPLS-AA force field with a distance-dependent dielectrics and conjugate gradient algorithm with a convergence criterion of 0.001 kcal/(mol×Å).

QM/MM Calculations⁹⁸ were used for three purposes: optimization of the initial geometries of the inhibitor-enzyme complexes and estimation of their interaction energies (Step 2), as well as estimation of the interaction energies for the time-averaged structures (Step 4) obtained by MD simulation (Step 3). The QM region consisted of side chains of His405 and His411, the backbone atoms and side chains of His401 and Glu402, the entire inhibitor, and the zinc ion. The backbone atoms were included to obtain valid QM/MM cuts. The rest of the protein was treated with MM. The protein and water outside 5 Å of the ligand superposition after Step 1 were frozen.

The interface between QM and MM regions is mediated by frozen orbitals.⁹⁹ The QM and MM regions interact via two mechanisms: electrostatic interactions between MM point charges and the QM wave function, and van der Waals interactions between QM and MM atoms. For the MM and QM parts of the QM/MM calculations, OPLS-AA force field¹⁰⁰ and DFT functional B3LYP¹⁰¹ were deployed, respectively. All charges in the MM region were treated using the OPLS-AA force field. The 6–31G* basis set was used in the interface region between the QM and MM regions. The LAV3P** basis set was employed for geometry optimization: for Zn, S and P atoms, this means the Los Alamos effective core potential (ECP)^102,103 with all the s functions and the last p and d gaussian uncontracted; for the remaining atoms, it implies 6–31G** basis set. The maximum number of iterations was set to 100 cycles and all calculations converged before reaching this limit: the root mean squared change in density matrix elements was less than the criterion of 5.0×10⁻⁶. B3LYP provides as good or better geometries and energies as those from correlated ab initio methods for the first-row transition metal complexes.⁵ We therefore selected B3LYP to optimize the structures of the complexes in Step 2. In Step 4, the interaction energies were calculated by subtracting the QM/MM energy of the ligand and the receptor from the QM/MM energy of the complex for the time-averaged structures (Eq. 2).

Molecular Dynamics Simulations were performed using SYBYL 6.9 under isothermal/isobaric (NPT) conditions with Tripos force field.¹⁰⁴ The QM/MM-optimized bonds between the zinc-binding group (hydroxamate oxygens) of inhibitors, zinc and nitrogens of His401, His405, and His411, slightly different for each ligand, were restrained with a harmonic potential (the force constant 200, power 2) throughout the simulation. The Mulliken charges¹⁰⁵ resulting from the QM/MM optimization were used for the QM region (ligand, catalytic zinc, coordinating histidine and glutamate residues). For the rest of the protein and water, Gasteiger-Hückel charges¹⁰⁶ were used. For each system, only one set of simulations was performed with the ligand bound to the protein with a cap comprising two layers of water (TIP3P) molecules,¹⁰⁴ surrounding the complex. The water molecules were then minimized for 10,000 cycles using conjugate gradient minimization keeping the protein and ligand atom fixed to its initial positions. The outer portion of the water cap was farther than 5 Å from the ligand superposition after Step 2 and was assigned to the frozen region. Subsequently MD simulation was performed for 20 ps for the mobile water molecules, keeping the protein, ligand, and crystal water and frozen water fixed. This solvent equilibration phase was performed in order for the solvent molecule to readjust to the potential field of the ligand-receptor complex.

After the 15-ps heating phase, when the temperature of the system was raised from 0 to 300 K, the equilibration run was performed for 100 ps. Finally, the production phase was carried out at 300 K for 200 ps. The time step of the simulations was 1 fs with a cutoff of 12 Ǻ for nonbonded interactions. The nonbonded pairs were updated every 25 fs. All residues within 5 Ǻ of any atom in the ligand superposition after Step 2 were allowed to move freely and the remaining part of the protein and water was kept frozen. This setting was identical for all ligands. The time-averaged structures, obtained from the readings in 100 fs intervals, of the complete mobile region were collected at appropriate times. These structures were briefly minimized, to relieve the worst conflicts, using the Tripos force field with a distance-dependent dielectrics and the Powell conjugate gradient algorithm with a convergence criterion of 0.001 kcal/(mol×Å). The minimization produces structures with standard bond length and angles, with the dihedrals representing the ensemble. The time-averaged structures were shown to provide similar LIE correlations as ensemble averages.^72,73 The single-point QM/MM energy calculations on the time-averaged structures were used to estimate the zinc binding energies. The polar, non-polar and total solvent accessible surface area (SASA) terms were calculated using the ProsSat option in the Homology module of the Insight II modeling package.¹⁰⁷

Regression and Cross-Validation

The least-square fits¹⁰⁸ were based on Eq 1 and Eq 3 with the constant term. The robustness of the regression equations and their predictive abilities were probed by cross-validation. For this purpose, the fits to the potency data are generated leaving out one or more inhibitors from the calibration process. The resulting equation for each fit is used to predict the potencies of the omitted compounds. We used the leave-one-out (LOO) approach and the leave-several-out (LSO) approach, where 6 inhibitors were randomly omitted and the process was repeated 200 times. The correlations of the LOO and LSO predictions with the actual potencies were characterized by the root mean square errors (RMSE).

Conclusions

A computational approach combining docking, QM/MM calculations, and MD simulations was developed for prediction of binding affinities of ligands to metalloproteins. The use of QM/MM energies in the ELR-type correlations was facilitated by the use of time-averaged structures from MD simulations. The application of the approach to the MMP-9 inhibition by 28 hydroxamates resulted in an excellent correlation (r² = 0.900) between experimental and calculated values for all tested compounds that exhibit ~4000-fold difference in binding affinity, with the inhibition constants K_i ranging from 0.08 to 349 nM. Prediction ability of the correlation is characterized by RMSE ~ 0.3 for the logK_i values, as compared to RMSE > 0.6 if the QM/MM term is not used. The examination of the energetic and structural results provides a basis for understanding activity differences of individual inhibitors and for their rational design. The proposed approach improves the descriptive and predictive abilities for metalloprotein ligand affinity prediction as compared to the LR approach at the expense of about a four-fold increase in the computational time.