The effects of aging on the speed-accuracy compromise: Boundary optimality in the diffusion model

Abstract

We evaluated age-related differences in the optimality of decision boundary settings in a diffusion model analysis. In the model, the width of the decision boundary represents the amount of evidence that must accumulate in favor of a response alternative before a decision is made. Wide boundaries lead to slow but accurate responding, and narrow boundaries lead to fast but inaccurate responding. There is a single value of boundary separation that produces the most correct answers in a given period of time, and we will refer to this value as the reward rate optimal boundary (RROB). Across a variety of decision tasks, we consistently found that older adults used boundaries that were much wider than the RROB value. Young adults used boundaries that were closer to the RROB value, although age differences in optimality were smaller with instructions emphasizing speed than with instructions emphasizing accuracy. Young adults adjusted their boundary settings to more closely approach the RROB value when they were provided with accuracy feedback and extensive practice. Older participants showed no evidence of making boundary adjustments in response to feedback or task practice, and they consistently used boundary separation values that produced accuracy levels that were near asymptote. Our results suggest that young participants attempt to balance speed and accuracy to achieve the most correct answers per unit time, whereas older participants attempt to minimize errors even if they must respond quite slowly to do so.

To make good decisions, one must gather an appropriate amount of information before selecting an alternative. Gathering more information leads to more accurate but slower decisions, a situation referred to as the speed-accuracy tradeoff. Decision makers are faced with the dilemma of adopting a level of conservativeness that appropriately balances the speed and accuracy of their responding.

Prior research shows that young and older adults differ in terms of how they balance speed and accuracy. Older adults make decisions slowly and avoid errors, whereas young adults decide more quickly and are more accepting of errors (Baron & Matilla, 1989; Hertzog, Vernon, & Rypma, 1993; Rabbitt, 1979; Salthouse, 1979; Smith & Brewer, 1985, 1995). Perhaps older adults are influenced by a lifetime of experience in which arriving at the correct answer is well worth the necessary deliberation. In this article, we explore the difference between young and older adults by examining the optimality of boundary settings using the diffusion model. As we explain in detail below, the diffusion model is a model of two-choice decision tasks that makes choices based on evidence accumulated over time (Ratcliff, 1978; Ratcliff & McKoon, 2008). One advantage of applying the model is that it accounts for speed-accuracy tradeoffs in terms of a single parameter representing response conservativeness: boundary separation. Boundary separation determines the amount of evidence that must accumulate in favor of a response alternative before a choice is made. If a great deal of evidence must accumulate (i.e., wide boundaries), decisions are slow but accurate. If only a little evidence must accumulate (i.e., narrow boundaries), decisions are fast but error prone.

Along the boundary separation continuum, one can define the single boundary value optimizes the reward rate, which is defined as the number of correct answers per unit time (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Gold & Shadlen, 2002; Simen et al., in press; for earlier treatments of optimality issues, see Edwards, 1965 and Wald & Wolfowitz, 1948). We will refer to this boundary setting as the reward rate optimal boundary (RROB). In the current project, we performed analyses to find the RROB value for each participant in several datasets that were previously fit and interpreted with the diffusion model. Each dataset included elderly participants and college-aged participants. For each age group, we compared the boundary actually used by each participant to the RROB value. Our goal was to explore how age-related differences in boundary optimization processes contribute to aging effects in simple decision tasks. In the sections that follow, we first describe the diffusion model and our procedures for finding RROB values, and then we describe the particular experiments that we evaluated.

The Diffusion Model

The diffusion model is a member of the broad class of sequential sampling models (for a review, see Ratcliff and Smith, 2004). All of these models assume that decisions are made by sampling evidence repeatedly until the accumulated evidence in favor of a response meets a criterion. The nature of the evidence depends on the task; for example, the evidence may result from the match of a test stimulus to the contents of memory in a recognition task. Evidence accumulation begins at a starting point (z) that lies between a lower boundary at zero and an upper boundary at a (see Figure 1). The position of the starting point varies uniformly across trials with a range of s_t. Each boundary is associated with one of the two alternative responses; for example, in a recognition experiment the top boundary could be associated with an “old” (studied) response and the bottom boundary could be associated with a “new” (not studied) response. A larger boundary separation (a) indicates more caution in selecting a response, in that a great deal of evidence must accumulate before a response is made.

Figure 1.

Illustration of the diffusion model. The horizontal lines at 0 and a are the response boundaries. In this example, the boundaries are for “new” versus “old” responses in a recognition task. The line at z is the starting point, which varies from trial to trial across the range s_Z. The straight arrows show average drift rates, and the wavy lines represent the actual accumulation paths that are subject to moment-to-moment noise (s). Three average drift rates are shown to illustrate the across-trial variability in drift, which is normally distributed with a standard deviation of η. Predicted response time distributions are shown at each boundary.

Evidence drifts toward one of the boundaries with an average rate indexed by the parameter ν, and drift rates within a stimulus class are subject to Gaussian variation across trials with standard deviation η. A drift criterion (dc) defines the zero point in drift, with drift rates above the drift criterion moving toward the top boundary and drift rates below the drift criterion moving toward the bottom boundary (see Ratcliff, 1985; Ratcliff & McKoon, 2008). Drift rates are represented by the straight arrows in Figure 1. The magnitude of the drift rate reflects the quality of the stimulus – strong stimuli (e.g., words studied 10 times) have high drift rates and weak stimuli (e.g., words studied only once) have drift rates closer to zero. The evidence accumulation process fluctuates randomly from moment to moment within a trial, as displayed by the highly variable paths in Figure 1. When the evidence value reaches a boundary, the process terminates and the response associated with that boundary is made. As a result of the noise in drift, the diffusion process sometimes terminates on the boundary opposite the direction of drift, leading to errors.

Response time (RT) distributions are determined by the distributions of process termination times, which are shown outside of each boundary in Figure 1. To represent the time required for aspects of a task such as encoding the test stimulus or executing a motor response, a non-decision component is added to the decision times for every trial. Non-decision times vary uniformly across trials with a mean of T_er and a range of s_t. The models applied in the current project also contained a parameter estimating the proportion of RT contaminants (p_o). Contaminated trials include an additional response delay drawn randomly from a uniform distribution to represent lapses in attention. Including this parameter makes the model less sensitive to processing contaminants that may affect empirical data (Ratcliff & Tuerlinckx, 2002).

Many studies have applied the diffusion model to aging experiments, and these studies consistently demonstrate that older participants set substantially wider boundaries than young participants (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff, Thapar, & McKoon, 2001, 2003, 2004, 2006a, 2006b, 2007; Thapar, Ratcliff, & McKoon, 2003; Spaniol, Madden, & Voss, 2006; Spaniol, Voss, & Grady, 2008). Although this finding is consistent with the general idea that older participants are cautious in their decision making (Baron & Matilla, 1989; Botwinick, 1969; Hertzog et al., 1993; Rabbitt, 1979; Salthouse, 1979; Smith & Brewer, 1985, 1995), existing studies have gained little theoretical insight into the effects of aging on boundary adjustment processes. In the next section, we describe the optimality analyses that we used to explore this issue.

Optimality of the Boundary Parameter

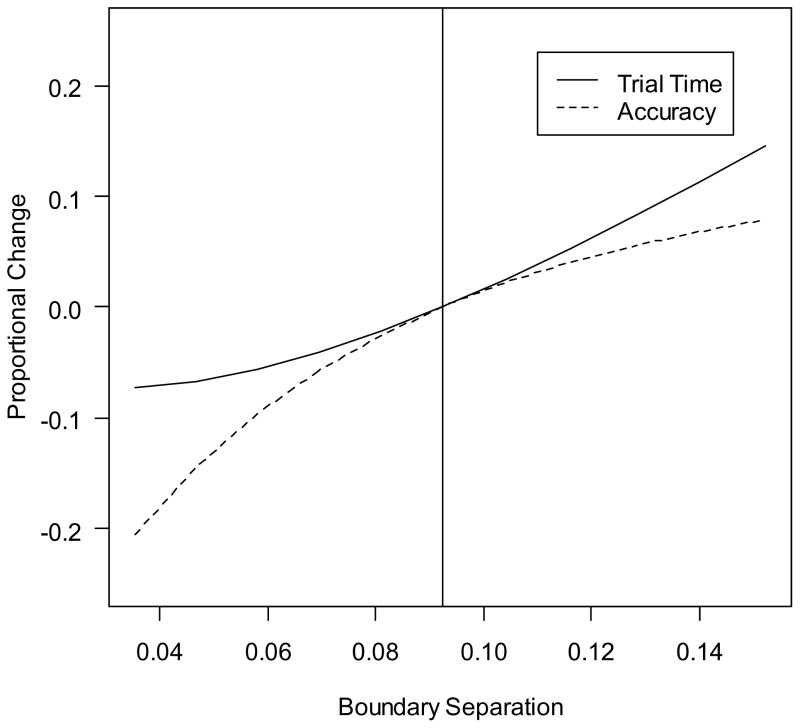
In a diffusion model analysis, one can identify the particular boundary separation that is optimal given the evidence available for the task, the characteristics of the task itself, and a definition of the reward index, i.e., the aspect of performance that is being optimized (Bogacz et al., 2006). A variety of reward indexes can be selected, and different optimal values will result based on the selected index. One popular reward index is reward rate (RR); that is, the rate at which correct answers are produced (Gold & Shadlen, 2002). When the boundary is set at a very low value, responses are made quickly but are very inaccurate. Correct trials are interspersed with many incorrect trials, leading to a low overall reward rate. When the boundary is set at a very high value, responses tend to be correct but each trial takes a long time, again leading to a low reward rate. Between these extremes lies the reward rate optimal boundary (RROB), the one value that perfectly balances the costs of inaccuracy and slowness and leads to the maximal possible rate of reward (Bogacz et al., 2006). Figure 2 shows an example of the function relating reward rate to boundary width. The RROB value is marked with the vertical line, and reward rate drops as the boundary moves below or above this optimal. Reward rate drops more steeply below than above the optimal value.

Figure 2.

Example function relating reward rate to boundary position. Reward rate is measured as the number of correct responses per second. The optimal boundary position is marked by a dashed line.

Studies of boundary optimization have focused on paradigms in which participants complete as many trials as possible in a fixed period of time; thus, achieving a higher reward rate also means achieving more total rewards (e.g., Bogacz et al., 2006; Bogacz, Hu, Holmes, & Cohen, in press; Simen et al., in press). This study examines optimality in the more typical decision making situation in which participants complete a fixed number of trials regardless of the amount of time required to complete them. Although optimizing the reward rate does not maximize the total number of correct answers in a fixed-trial paradigm, reward rate provides a useful performance criterion nevertheless. Figure 3 illustrates the significance of the optimal boundary defined by reward rate. The plot shows the proportional change in accuracy and total trial time (RT plus all delays due to the experimental procedure) across a range of boundary settings in reference to performance with RROB value, which is marked by the vertical line. Values to the right of the RROB value are proportional increases in both measures, and values to the left are proportional decreases in both measures. As the boundary moves lower than the RROB value, the proportional loss to accuracy outweighs the reduction in trial time. As the boundary moves higher than the RROB value, the proportional increase in trial time outweighs the increase in accuracy. Therefore, deviating from the RROB value means making undue sacrifices in one aspect of performance to achieve small gains in another aspect.

Figure 3.

Proportional change in total trial time (solid line) and accuracy (dashed line) as the boundary separation moves away from the reward rate optimal boundary (RROB), which is marked by the vertical line. Values below the RROB are proportional decreases and values above the RROB are proportional increases.

We chose to asses optimality defined by reward rate because of this measure’s direct link to the speed-accuracy tradeoff shown in Figure 3. We do not make the strong claim that participants are explicitly calculating reward rate as they perform a task; we only claim that deviating from the RROB value reflects insensitivity to disadvantageous speed-accuracy tradeoffs. If a participant decreases boundary width any time the gain in speed outweighs cost in accuracy and increases boundary width any time the gain in accuracy outweighs the cost in speed, then the participant’s boundary separation should closely approximate the RROB value. Therefore, the deviation from the RROB value offers a quantitative index that defines a participant’s position relative to an objectively balanced speed-accuracy compromise.

RROB values are affected by the remaining (non-boundary) diffusion model parameters and aspects of the experimental task, such as the delay from a response on one trial to the presentation of the stimulus on the next trial (RSI, or the Response Stimulus Interval) and the delay used as a penalty for incorrect responses (EP, or Error Penalty). As a result, RROB values must be calculated separately for every participant and for separate experimental tasks completed by the same participant.

Experiments and Objectives

All of the experiments we report are re-analyses of completed experiments. Experiment 1 was an analysis of two-choice decision making in college-aged, 60–74 year old, and 75–85 year old adults. Participants in each age group completed letter discrimination, brightness discrimination, and recognition memory tasks. For each task, half of the blocks were completed with an emphasis on accuracy and half of the blocks were completed with an emphasis on speed. Our primary interest was exploring how boundary settings varied with age, and how age interacted with instructions and tasks. Experiment 2 included groups of young and older adults who completed a numerosity-judgment task with or without accuracy feedback, providing the opportunity to explore potential age-related differences in the ability to strategically adjust response boundaries in response to feedback. In Experiment 3, young and older participants completed eight sessions of the numerosity task, which allowed us to explore boundary optimality in participants with extensive task practice.

Comparing the age groups in terms of deviation from the RROB value will distinguish between several possible explanations for the heightened conservativeness of older participants compared to younger participants. One possibility is that both age groups approach optimality, but that RROB values are wider for older participants. RROB values depend on parameters that can differ between young and older participants, such as the non-decision latency. Our analyses could show that young and older participants are similar in their sensitivity to disadvantageous speed-accuracy tradeoffs despite their differences in overall response conservativeness.

Another possible explanation for boundary differences is that one age group is more sensitive to asymmetries in the speed-accuracy tradeoff than the other. In our analyses, this would result in age-based differences in deviation from the RROB value. Differences of this sort could take on two forms. In one scenario, young participants may deviate from the RROB value by using boundaries that are too narrow. Instead of trying to balance speed and accuracy, young participants may be in a hurry to get out of the experiment. For example, they could set a low criterion for accuracy and go as fast as possible without going below this accuracy level. In another scenario, older participants’ may use boundaries that are wider than the RROB. Older participants’ strategy for adjusting their boundaries may focus on accuracy. For example, older participants may simply set their boundaries wide enough to ensure that they almost never make avoidable errors (i.e., they never hastily make one response only to realize that the other was required). This latter explanation would be consistent with previous research that suggests that older participants respond more slowly than is required to maintain a high level of accuracy (e.g., Hertzog et al., 1993; Smith & Brewer, 1995).

Experiment 1

In the first experiment, we explore the effects of aging on boundary optimality for several simple two-choice tasks with both speed and accuracy instructions.

Methods

Experimental Tasks

For Experiment 1, we conducted re-analyses of data reported by Ratcliff et al. (2006b). In this study, participants completed a series of simple decision making tasks, including letter discrimination, brightness discrimination, and recognition memory¹. All tasks were completed by 10 participants in each of three age groups: college-aged, 60–74 year old, and 75–85 year old participants. Participants completed four sessions of each task, and always completed all of the sessions within a task before moving on to the next task.

For the letter discrimination task, letter stimuli were briefly presented followed by a mask. The participants chose which of two alternative letters they saw. Task difficulty was manipulated by presenting letters for different durations, with six duration conditions: 10, 20, 30, 40, 80, or 120 ms. (The durations were misreported as 10, 20, 30, 40, 50, or 60 ms in Ratcliff et al., 2006b. The difference does not affect the fits reported by those authors, because the fits were done with the last three duration conditions collapsed.) Task blocks consisted of 16 trials from each of the duration conditions in a random order. Each trial consisted of a 500 ms fixation symbol, the letter stimulus, and a 10 ms mask. For accuracy blocks, the word ERROR appeared on the screen for 300 ms after each incorrect response. For speed blocks, the words TOO SLOW appeared on the screen for 700 ms after any response that took longer than 650 ms.

In the brightness discrimination task, participants saw 64 × 64 pixel squares. A proportion of the pixels were randomly selected to appear as white and the remaining pixels were black. Participants decided whether the patches as a whole were “bright” or “dark.” Difficulty was manipulated by varying the presentation duration and the proportion of white versus black pixels. Patches were presented for either 50, 100, or 150 ms. For each patch, either .65, .575, or .525 of the pixels were the color corresponding to the required response (e.g., easy “dark” stimuli were 65% black pixels and easy “bright” stimuli were 65% white pixels). An equal number of trials were allocated to each of the nine difficulty conditions created by the factorial combination of the duration and proportion variables, and each block had a random order of difficulty conditions. Each trial consisted of a 250 ms fixation symbol, presentation of the stimulus, and four successive random pattern masks that each remained on the screen for 17 ms. A 500 ms pause followed each response. In the accuracy condition, the word ERROR was displayed for 300 ms following each incorrect response. In the speed condition, a TOO SLOW message was displayed for 300 ms after each trial with an RT over 700 ms.

For the recognition memory task, participants studied lists of words then completed tests in which they had to decide whether candidate words were on the last list they studied. High, low, and very low frequency words were used for each study and test list (Kucera & Francis, 1967). Memory performance is an inverse function of frequency – participants are better able to recognize lower frequency targets and reject lower-frequency lures. As an additional difficulty manipulation, half of the words on each study list were presented once and the remaining words were presented three times. Each test included six targets and six lures from each of the three frequency conditions. Three of the targets within each frequency condition had been studied once, and the rest had been studied three times. For the accuracy blocks, there was a 250 ms pause after each response, and incorrect responses resulted in an ERROR message that was displayed for 300 ms. For the speed blocks, there was a 300 ms pause after each response and RTs above a cutoff resulted in a TOO SLOW message that was displayed for 300 ms. The too-slow cutoff was 800 ms for young participants and 900 ms for the two groups of older participants.

Diffusion Model Fits and Analysis Methods

For all diffusion model fits we report, the model was fit to the probability of each response in every experimental condition as well as the .1, .3, .5, .7, and .9 quantiles of the RT distribution associated with each response.

Bogacz et al. (2006) derived analytical solutions for optimal boundary values, but these solutions only apply to the simple diffusion model without across-trial variability in drift rate, T_er, or starting point. These additional sources of variability allow the model to fit empirical data when RT distributions differ for correct and incorrect responses (Ratcliff, Van Zandt, & McKoon, 1999). No analytical solutions for optimal boundaries are available for the full model, but optimal values can be found numerically (Bogacz et al., 2006). Accordingly, we evaluated RROB values for the full model using a search routine.² For each candidate boundary value generated by the search routine, a subroutine generated predicted mean RTs and response probabilities for every condition, and the weighted averages of the error rates and the mean RTs across conditions were used to calculate reward rate. The full reward rate equation for accuracy conditions is

$$\text{RR}=(1-\text{ER})/(\text{MRT}+\text{RSI}+\text{EP}\times \text{ER})$$

where ER is the error rate, MRT is the overall mean response time, RSI is the delay between trials, and EP is the delay incurred for errors (i.e., the duration of the “ERROR” message). The full reward rate equation for the speed conditions is

$$\text{RR}=(1-\text{ER})/(\text{MRT}+\text{RSI}+\text{SP}\times \text{PCUT})$$

where PCUT is the proportion of reaction times past the “TOO SLOW” cutoff and SP (for Slowness Penalty) is the duration of the “TOO SLOW” message.

We found RROB values for both speed and accuracy blocks for each individual participant. Because reward rate is sensitive to different factors on speed and accuracy blocks, the optimal boundaries will be different. RROB values are lower in speed conditions than in accuracy conditions, because in the former slow responding leads to time penalties and in the latter incorrect responding leads to time penalties.

Results and Discussion

Reward rate analyses

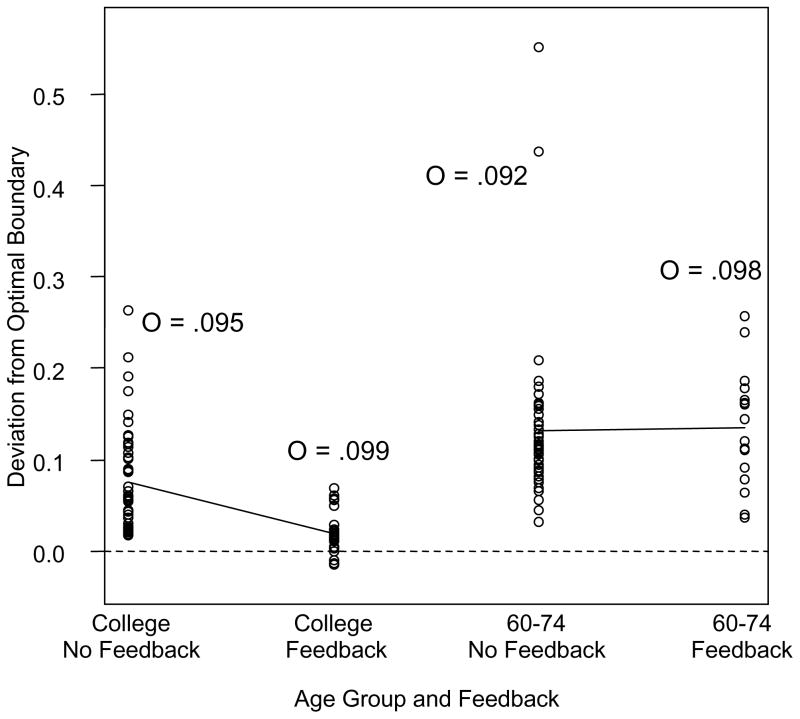
After computing the RROB value for each participant in each experimental task and instruction condition, we subtracted this value from the participants’ actual boundary separation to derive deviation scores. Positive deviation scores indicate that the actual boundary setting is wider than the RROB value, and negative scores indicate the opposite. Figure 4 displays these deviation scores for Experiment 1, and the average RROB values for each group are reported adjacent to the data points. The RROB values were fairly consistent across the age groups, but the deviation scores showed clear age effects. Young participants had relatively small deviation scores, and responded to the instruction manipulation by setting boundaries that were higher than optimal in the accuracy conditions and lower than optimal in the speed conditions (except for recognition). The 60–74 year old participants also had relatively small deviation scores, but they responded less dramatically to the speed-accuracy instructions in that their boundaries did not go below optimal when speed was emphasized. The 75–85 year old participants had much higher deviation scores than the younger groups, but their deviations were smaller in the speed conditions than the accuracy conditions.

Figure 4.

Deviation scores across age groups, tasks, and instruction conditions in Experiment 1. Deviations were measured as the actual boundary minus the corresponding RROB value. Each point represents a participant, and the lines connect the means of the age groups for each task and instruction condition. The average RROB values for each age group are reported near the corresponding data points (marked with “O =” to indicate they are optimal values).

An ANOVA showed a significant effect of age on deviation scores, F(2,27) = 23.47, p <.001, η²_p = .635, which arose because deviation scores were larger for 75–85 year old participants compared to both college aged and 60–74 year old participants. The latter two age groups did not differ significantly in follow-up contrasts. Both the task [F(2,54) = 9.18, p < .001, η²_p = .254] and instruction [F(1,27) = 131.93, p < .001, η²_p = .83] main effects were also significant. Deviation scores were larger with accuracy instructions than with speed instructions and were larger in the recognition task than in the letter or brightness tasks. Both the task and age effects ₂ significantly interacted with instructions, F(2,54) = 3.45, p < .05, η²_p = .113, and F(2,27) = 4.81, p < .05, η²_p = .263, respectively. The qualitative pattern across tasks was the same regardless of instructions, but the task effect was larger with accuracy instructions than with speed instructions. The age × instruction interaction was also a matter of degree: participants in all age groups had lower deviation scores with speed than with accuracy instructions, but this difference was larger for 75–85 year old participants than for the other two age groups.

Comparison to asymptotic accuracy levels

Figure 5 shows the function relating accuracy to boundary separation using the average parameters across participants. The actual boundary separation for each age group is marked by a solid line and the RROB value is marked by a dashed line. All of the marked boundaries are from the accuracy instruction blocks. Table 1 reports the average deviation between actual and asymptotic accuracy levels for each task. Accuracy for each task was measured as the percent correct across all conditions. In the diffusion model, asymptotic accuracy is limited by across trial variation in drift rates. That is, even if boundaries are so wide that within-trial variation has no impact on performance, errors will still be made because some trials will have drift rates in the wrong direction (i.e., negative drift rates for a stimulus requiring a top boundary response).

Figure 5.

Functions relating overall accuracy to boundary separation in college-aged (left), 60–74 year old (middle), and 75–85 year old adults (right) in Experiment 1. The first row shows results from the letter discrimination task, the second shows results from brightness discrimination, and the third shows results from recognition memory. The functions were constructed using parameter values averaged over participants. On each plot, the average actual boundary value is marked with a solid line and the average RROB value is marked with a dashed line. The marked boundaries are from the accuracy instruction blocks.

Table 1.

Difference between asymptotic accuracy and actual accuracy

	Age Group
Task and Condition	College	60–74	75–85
Letter
Accuracy	.071 (.012)	.067 (.017)	.035 (.010)
Speed	.138 (.012)	.099 (.012)	.070 (.014)
Brightness
Accuracy	.082 (.020)	.040 (.007)	.023 (.006)
Speed	.189 (.025)	.077 (.009)	.065 (.013)
Recognition
Accuracy	.023 (.002)	.025 (.002)	.018 (.001)
Speed	.081 (.005)	.054 (.003)	.048 (.002)
Numerosity (Ex. 2)
Feedback	.118 (.013)	.025 (.004)	------
No Feedback	.041 (.006)	.023 (.003)	------
Numerosity (Ex. 3)
Session 1	.068 (.012)	.028 (.003)	------
Session 2	.079 (.016)	.026 (.002)	------
Session 3	.093 (.016)	.020 (.002)	------
Session 4	.088 (.014)	.020 (.003)	------
Session 5	.101 (.017)	.015 (.002)	------
Session 6	.107 (.018)	.017 (.002)	------
Session 7	.085 (.011)	.012 (.001)	------
Session 8	.089 (.012)	.012 (.001)	------

Note: Results are based on data averaged across participants. Accuracy was defined as the overall proportion correct. Standard errors are in parentheses.

We will first discuss results from the accuracy conditions. In the letter discrimination task, young participants had a higher level of asymptotic accuracy than either group of older participants. The average deviations in Table 1 show that the oldest participants achieved very close to asymptotic accuracy levels (.035), whereas the 60–74 year old and college-aged participants were a little farther from asymptotic accuracy levels (about .07). For brightness discrimination, the accuracy functions were similar for college and 60–74 year old participants, with lower accuracy for 75–85 year old participants. Both groups of older adults came close to the maximum possible accuracy value, whereas young adults were farther from the asymptote. For recognition memory, all age groups showed similar accuracy functions and achieved very close to the maximum possible accuracy.

All age groups used lower boundary values in the speed conditions; consequently, all showed larger deviations from the asymptotic accuracy value compared to the accuracy conditions, as shown in Table 1. Other than this overall drop, the patterns among the age groups were very similar to the results from accuracy blocks. Both groups of older participants were closer to asymptotic accuracy than the young participants across all three tasks.

Summary

Experiment 1 showed that the age groups had similar RROB values, but their actual boundary values showed substantial age effects. The oldest participants were consistently further above the RROB than college-aged participants or 60–74 year old participants. Both groups of older participants were close to asymptotic accuracy levels on accuracy blocks, suggesting that older participants were generally unwilling to make avoidable errors. This aversion to errors could explain why the 75–85 year old participants used boundaries that were much wider than the RROB value. Consistent with this notion, asking participants to emphasize speed attenuated age differences in boundary optimality. In the next two experiments, we explore age differences in the effects of feedback and task practice on boundary settings.

Experiment 2

In the second experiment, we compared young and older participants with and without task feedback. Participants performed a numerosity judgment task in which an array of asterisks was presented on the screen and they had to quickly decide whether there were more or less than 50 asterisks.

If participants are attempting to find a boundary position that balances speed and accuracy, they should meet this goal more effectively when feedback is available. Without feedback, participants should be largely unaware of their accuracy. Thus, they should experience difficulty in identifying disadvantageous speed-accuracy tradeoffs. The differences between performance with and without feedback for each age group will reveal potential age-related differences in boundary adjustment processes.

Methods

Experimental Task

Experiment 2 used a numerosity discrimination task (see Ratcliff, 2008; Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, in press). For this task, participants saw a 10 × 10 grid of characters with some spaces blank and some filled by asterisks. Asterisks appeared in random positions with the number of asterisks determined by the difficulty condition. Participants decided whether there were more or less than 50 asterisks displayed (by requiring relatively quick response times we ensured that counting did not play a role in the judgments). For stimuli requiring a “small” response, the number of asterisks displayed was randomly selected from a uniform distribution with a range from 31 to 50. The range for “large” stimuli was 51 to 70. Within each category, stimuli were grouped into four bins that were treated as four difficulty conditions. Moving across difficulty levels from easy to hard, level 1 had 31–35 asterisks for “small” and 66–70 asterisks for “large,” level 2 had 36–40 and 61–65 asterisks, level 3 had 41–45 and 56–60 asterisks, and level 4 had 46–50 and 51–55 asterisks. Each trial was followed by either a CORRECT or an ERROR message for 600 ms in the feedback condition. Participants in both conditions were instructed to try and balance speed and accuracy with their responding.

The project that produced the data for Experiment 2 included college-aged and older (60–74 year old) participants, and both groups initially received accuracy feedback. The experiment was designed to serve as a baseline for a population of older adults with Alzheimer’s disease (not reported here), and these participants responded very negatively to feedback. Therefore, feedback was eliminated and a new sample of young and older participants completed the task without feedback. Although only the no-feedback results were of interest for the initial project, we included the feedback participants in the optimality analyses so we could contrast boundary adjustments with and without feedback. Data from 31 young and 16 older participants were collected with feedback. The no-feedback condition includes 45 young and 42 older participants.

Diffusion Model Fits and Analysis Methods

The model for the numerosity task used four drift rates for the four difficulty levels. Only four were needed because large and small asterisk displays in the same difficulty condition were given the same drift rates with reversed signs. For example, if arrays with 56–60 asterisks had an average drift of .2 then arrays with 41–45 asterisks had an average drift of −.2. In addition, the model freely estimated a drift criterion parameter and subtracted this value from all of the drift rates. For this task, the drift criterion reflects the number of asterisks at the cutoff dividing “small” and “large” responses. The cutoff prescribed by the task was 50, and using this value would lead to balanced drift rates corresponding to a drift criterion of zero. In practice, participants vary in terms of where they place the cutoff. For example, one participant may call any array with over 52 asterisks “large,” corresponding to a slightly positive drift criterion and a bias towards the “small” response. Starting point was also freely adjusted in fits to accommodate response biases. In all, the free parameters were a, z, s_z, ν₁ – ν₄, η, T_er, s_t, dc, and p_o.

The project that produced the data analyzed in Experiment 2 has not yet been incorporated into a manuscript. Consequently, we report the parameter values in Table 2, and we will briefly discuss some of the differences in parameter values across the age groups. As expected, older participants used wider boundaries than young participants. Young participants who did not receive accuracy feedback used wider boundaries than their counterparts in the feedback condition, but feedback had no effect on boundaries for older participants. Drift rates were similar for the two age groups and did not vary consistently with the feedback variable. The young participants appear to have higher drift rates without feedback, but this was offset by an increase in the standard deviation of drift across trials (η). T_er was about 100 ms longer for older than for young participants and was not affected by feedback for either age group. Without feedback, the drift criterion parameters for both groups showed a substantial bias in drift towards the “small” response (the bottom boundary). This indicates that participants tended to use a cutoff between “small” and “large” responses that was above 50 asterisks. Both groups were closer to the unbiased value of zero when feedback was provided, though a fairly large bias still remained for older participants. Starting points were approximately equidistant from the two boundaries in all conditions, although older participants did show a small displacement towards the lower boundary (i.e., a slight bias in favor of the “small” response).

Table 2.

Parameter values from Experiment 2

	Parameter
Age and Feedback (FB)	a	z	sz	ν1	ν2	ν3	ν4	η	Ter	st	dc	po
College
FB	.117	.057	.071	.350	.279	.177	.062	.113	375	175	.005	.002
No FB	.170	.083	.084	.451	.342	.206	.069	.191	373	165	.078	.018
60–74
FB	.232	.103	.052	.480	.357	.208	.073	.170	475	100	.038	.005
No FB	.234	.106	.071	.429	.324	.196	.065	.163	480	165	.074	.017

Note: a is boundary separation, z is starting point, s_z is the range in starting point variation, ν₁–ν₄ are the drift rates for the four difficulty conditions from easiest to hardest, η is the standard deviation in drift rates, T_er is the average non-decision component of RT, s_t is the range of variation in T_er, dc is the drift criterion, and p_o is the proportion of trials with response time contaminants; FB = feedback.

We used the same procedures for finding RROB values as in Experiment 1. Since 600 ms of feedback followed all trials regardless of accuracy, there was no time penalty for incorrect responses and the RSI was 600 ms. In the no feedback condition, both the RSI and the error penalty were zero.

Results and Discussion

Reward rate analyses

Figure 6 shows the deviation scores produced by subtracting the RROB value from the actual boundary setting for each participant in each feedback condition. As in the first experiment, RROB values were similar for young and older adults, but the age groups differed in their deviation scores. Without feedback, both older and younger participants had high deviation scores, although deviation scores were a little lower for young participants. The large deviations from the RROB are not surprising – without feedback participants did not have the information they needed to determine if boundary adjustments led to a more balanced compromise between speed and accuracy. With feedback, the deviation scores for young participants decreased substantially, whereas deviation scores for older participants remained as high as in the no feedback condition.

Figure 6.

Deviation scores for young and older participants with and without accuracy feedback in Experiment 2. Deviations were measured as the actual boundary minus the corresponding RROB value. Each point represents a participant, and the lines connect the means of the no feedback and feedback conditions for each age group. The average RROB values for each condition are reported near the corresponding data points (marked with “O =” to indicate they are optimal values).

The effects suggested by Figure 6 were confirmed with a factorial ANOVA on the ₂ deviation scores. The results showed a significant effect of age, F(1,130) = 48.69, p < .001, η²_p = .272, and a significant effect of feedback, F(1,130) = 4.85, p < .05, η²_p = .036. However, the feedback main effect was qualified by a significant interaction, F(1,130) = 5.64, p < .05, η²_p = .042, which was created because feedback affected deviation scores for young participants but not for older participants.

Comparison to asymptotic accuracy levels

Figure 7 shows the functions relating accuracy to boundary width for young and older participants both with and without feedback. The actual boundary settings and RROB values are marked with solid and dashed lines, respectively. Without feedback, both groups of participants used boundaries that achieved very close to asymptotic accuracy levels (see Table 1). When feedback was provided, young participants sacrificed accuracy to more closely approach the RROB value. Older participants remained near asymptotic accuracy.

Figure 7.

Functions relating overall accuracy to boundary separation in college-aged and older adults in Experiment 2. The first row shows results with accuracy feedback and the second shows results without feedback. The functions were constructed using parameter values averaged over participants. On each plot, the average actual boundary value is marked with a solid line and the average RROB value is marked with a dashed line.

Summary

The results show that boundary adjustment processes differ across age groups. Older participants set very similar boundaries with and without task feedback, suggesting that they do not flexibly adjust their boundaries. As in the first experiment, older participants adopted a level of conservativeness that allowed them to closely approach asymptotic accuracy levels. In contrast, younger participants adjusted their boundaries to avoid disadvantageous speed accuracy tradeoffs when they received accuracy feedback.

The results of Experiment 2 are consistent with the first experiment in that we obtained aging effects, but we did observe some inconsistency in the exact age at which differences begin to appear. In Experiment 1, college-aged and 60–74 year old adults did not differ in terms of deviation from the RROB value. However, a large age effect did appear in a sample of participants aged 75–85. In Experiment 2, a population of 60–74 year olds had substantially higher deviation scores than young participants. Taken together, these experiments may suggest that the exact timing of aging effects in boundary adjustment processes differs from task to task. However, the 60–74 year olds came close to asymptotic accuracy levels in both Experiment 2 and in the accuracy conditions from Experiment 1 (see Table 1). Therefore, it is possible that the 60–74 year olds set their boundaries to minimize avoidable errors in both experiments, and the boundary values that satisfied this criterion just happened to be closer to the RROB values in Experiment 1 than in Experiment 2.

Experiment 3

The results of the first two experiments suggest that boundary optimization processes differ across age groups. One limitation of the first two datasets is that they involve a single fit to all of the trials; thus, there is no way to see dynamic adjustment processes at work. In the third experiment, young and older participants completed a series of eight sessions of the asterisk task, and diffusion model fits were performed for each session. We evaluated changes in boundary optimality across sessions for each age group.

Method

Experimental Tasks

Experiment 3 used a numerosity task as in Experiment 2. For Experiment 3, 19 college-aged and 17 older adults (60–74) completed eight sessions with accuracy feedback provided for each session. These data were collected as part of a paper that is in preparation (Thapar, Ratcliff, & McKoon, in preparation).

Diffusion Model Fits and Analysis Methods

Data were fit with the same model that was used in Experiment 2 separately for each subject and each session. We also used the same optimality routines as in the feedback condition from Experiment 2. The average parameter values are reported in Table 3. Boundaries were wider for older than for young participants. Moreover, the boundary width for young participants decreased across sessions whereas boundary width for older participants remained relatively constant. The quality of evidence extracted from the stimuli was very similar for the two age groups and remained relatively constant across sessions. Older participants did show increases in drift rates with increasing practice, but the across-trial standard deviation in drift rates increased as well. For both groups, both the mean non-decision time and the variability in non-decision time decreased across sessions. Non-decision times were longer for the older participants. The drift criterion showed a slight bias for the “small” response (bottom boundary) for both age groups, and the bias appeared to grow slightly across sessions. Starting points were always very close to the midpoint of the corresponding boundary value.

Table 3.

Parameter values from Experiment 3

	Parameter
Age and Session	a	z	sz	ν1	ν2	ν3	ν4	η	Ter	st	dc	po
College
1	.140	.062	.085	.458	.363	.225	.076	.154	392	162	.021	.002
2	.127	.059	.077	.505	.319	.269	.091	.163	375	122	.033	.013
3	.114	.054	.057	.467	.395	.250	.076	.137	357	120	.037	.004
4	.109	.050	.059	.504	.400	.255	.083	.137	358	106	.046	.013
5	.109	.051	.060	.502	.401	.265	.104	.147	348	102	.037	.011
6	.100	.047	.064	.508	.413	.282	.090	.146	341	093	.047	.011
7	.109	.052	.068	.523	.410	.275	.099	.180	349	100	.047	.010
8	.105	.049	.060	.519	.417	.284	.101	.162	342	91	.050	.021
60–74
1	.207	.093	.061	.443	.327	.198	.068	.164	479	159	.025	.002
2	.201	.094	.042	.477	.354	.216	.069	.147	463	112	.036	.000
3	.200	.094	.041	.555	.425	.256	.090	.177	454	128	.041	.002
4	.209	.099	.050	.587	.461	.273	.098	.178	448	114	.047	.001
5	.207	.099	.050	.635	.492	.299	.100	.198	449	113	.047	.006
6	.211	.101	.060	.695	.534	.323	.105	.199	445	115	.056	.003
7	.221	.107	.055	.693	.547	.331	.113	.213	432	98	.044	.002
8	.206	.097	.056	.674	.528	.325	.108	.200	427	97	.053	.004

Note: a is boundary separation, z is starting point, s_z is the range in starting point variation, ν₁–ν₄ are the drift rates for the four difficulty conditions from easiest to hardest, η is the standard deviation in drift rates, T_er is the average non-decision component of RT, s_t is the range of variation in T_er, dc is the drift criterion, and p_o is the proportion of trials with response time contaminants.

Results and Discussion

Reward rate analyses

Figure 8 shows the deviation scores for Experiment 3. Boundary settings for both young and older participants were wider than the RROB values on average, but young participants had substantially lower deviation scores compared to older participants. The young participants’ deviation scores decreased as they gained experience with the task. The data appear to show a slight reverse trend from Session 6 to Sessions 7 and 8, but this probably reflects random variability. In contrast, older participants showed no evidence of decreasing deviation scores across sessions.

Figure 8.

Deviation scores for young and older participants across training sessions in Experiment 3. Deviations were measured as the actual boundary minus the corresponding RROB value. Each point represents an individual participant, and the lines connect the means from each session. The RROB value averaged over sessions and participants is reported on each plot.

To statistically explore how the deviation scores changed across sessions, we performed separate linear trend analyses for young and older participants. Young participants showed a significant linear decrease across sessions, F(1,16) = 9.748, p = .007, η²_p = .379. Older participants showed no evidence of change across sessions, F(1,17) = .11, ns, η²_p = .007.

Comparison to asymptotic accuracy levels

Figure 9 shows the accuracy functions obtained by averaging parameters across all sessions and all participants within each age group. The results were very similar to the feedback condition from Experiment 2. Older participants used boundaries that allowed them to get very close to asymptotic accuracy levels. Their deviation from asymptotic accuracy started very low on the first session and actually decreased across subsequent sessions down to nearly .01 by session 8. As noted, the older participants used stable boundaries across the sessions, and the change in the deviation scores reflects changes in other parameters, such as the slight increase in drift rates. Young participants showed larger deviations from asymptotic accuracy levels, which allowed them to more closely approximate the RROB value. The deviations generally increased with practice, which reflects the decrease in boundary separation across sessions.

Figure 9.

Functions relating overall accuracy to boundary separation in college-aged and older adults in Experiment 3. The functions were constructed using parameter values averaged over participants and over sessions. On each plot, the average actual boundary value is marked with a solid line and the average RROB value is marked with a dashed line.

Summary

Experiment 3 provides more evidence that young and older participants differ in how they adjust boundaries to balance speed and accuracy. Young participants persistently optimized their boundaries as they became more practiced at the decision task, whereas older participants maintained boundaries that were much higher than the RROB value throughout all of the sessions. As in the previous experiments, older participants performed near asymptotic accuracy levels.

General Discussion

Our results provide a new perspective on the common finding that young and older participants adopt different levels of conservativeness in decision tasks (Baron & Matilla, 1989; Hertzog et al., 1993; Rabbitt, 1979; Salthouse, 1979; Smith & Brewer, 1985, 1995). Across a variety of tasks, our analyses showed no substantial differences in the level of conservativeness needed to optimize reward rate across the age groups. That is, if reward rate were the only factor determining participants’ boundary settings, then all of the age groups would have used similar boundary values. The age-related differences in boundary separation that we observed reflected differences in the deviation of actual boundary values from the RROB. In the first experiment, 75–85 year old adults showed larger deviations from the RROB value than either college-aged participants or 60–74 year old adults. This pattern held across all tasks and instruction conditions, although the age differences were smaller with speed instructions than with accuracy instructions. In Experiment 2, young and older (60–74 year old) adults both showed large deviations from the RROB value with no accuracy feedback. With feedback, young participants moved their boundaries closer to the RROB value, whereas older participants did not adjust their boundaries. In the third experiment, young participants had smaller deviations from the RROB value overall, and their deviation scores decreased as they completed more sessions of the task. Older participants showed no evidence of decreasing their deviation from the RROB value with task practice.

If a participant uses a boundary near the RROB value, this signifies that the participant is sensitive to imbalances in the speed-accuracy tradeoff. Moving the boundary above the RROB value results in small gains in accuracy in relation to the cost in speed, and moving the boundary below the RROB value results in small gains in speed relative to the cost in accuracy (see Figure 3). Older participants are generally less sensitive to these tradeoffs than young participants. Older participants maintain boundaries that are much higher than the RROB value even though a lower boundary could result in substantially faster decisions with a relatively small change in accuracy.

Comparing the accuracy values achieved at the older participants’ boundary values to asymptotic accuracy values shows that older participants are unwilling to make unnecessary errors to hasten their responding. The older participants were consistently very close to the maximum accuracy attainable given infinite boundary separation. Across all of the experiments (excluding speed conditions), the older participants were within .05 of the maximum attainable accuracy in all but one task. Although the 60–74 year old group in Experiment 1 was similar to the young group in terms of deviation from the RROB, even these older adults came close to asymptotic accuracy levels, suggesting that they may have used a similar boundary adjustment strategy as the oldest age group in Experiment 1 and the 60–74 year olds in Experiments 2 and 3. In short, young participants set a pace that compromised between speed and accuracy, whereas older participants set a pace that all but eliminated avoidable errors.

Of course, optimality can be defined in many ways, and our analyses evaluate optimality in the context of a single model (the diffusion model) using a single reward index (reward rate). Certainly, participants that are far from optimal by these standards may be optimal by other standards. However, defining boundary optimality in terms of reward rate in the diffusion model is particularly elucidating. The diffusion model has been the most successful model for fitting accuracy and response time distributions in two-choice decision tasks (Ratcliff & Smith, 2004), and it has proven quite useful for exploring age-based differences in performance (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff, Thapar, & McKoon, 2001, 2003, 2004, 2006a, 2006b, 2007; Thapar et al., 2003; Spaniol et al., 2006; Spaniol et al., 2008). Using reward rate to evaluate optimal boundaries offers an objective zero point on the speed-accuracy continuum. Comparing a participant’s actual boundary value to this zero point quantifies the extent to which the participant is willing to accept relatively large increases in decision time for relatively small increases in accuracy, or vice versa.

Replicating previous work (Bogacz et al., 2006; Bogacz et al., in press; Simen et al., in press), our participants tended to set boundaries that were wider than the RROB value, with the only exception coming from young participants on speed blocks in the brightness and letter discrimination tasks. There are several reasons why participants may generally overshoot the RROB value. Evaluating Figure 2 shows that reward rate decreases sharply below the RROB value, but the decrease is more gradual above the RROB value (Bogacz et al., 2006). That is, missing the RROB value by a certain distance on the low side represents a more “unbalanced” tradeoff between speed and accuracy than missing the RROB value by the same distance on the high side. Considering that participants have imperfect estimates of their accuracy and average trial time, they will always have some degree of uncertainty as to which boundary positions lead to the highest reward rate. Faced with uncertainty, the safe bet is to set a boundary that is wider than the RROB value.

The fact that participants are consistently more conservative than the RROB value could also reflect the use of a reward index with additional penalties for error responses (Maddox & Bohil, 1998). Bogactz et al. (2006) discuss several reward indices with weighting factors to emphasize the influence of errors on boundary optimization. We did not apply these indices, because they are only useful when constraints can be placed on the weighting factors; for example, when participants get blocks of trials at different difficulty levels and a single weighting factor is used across all levels of difficulty (difficulty conditions were mixed within blocks in all of the experiments that we analyzed). When weights are unconstrained, subjective reward indices are uninformative because a weighting factor can be defined that makes any boundary value the optimal boundary (e.g., a participant with very wide boundaries would get a very high weight on accuracy).

Could a subjective reward index with weights for accuracy emphasis explain the differences between the boundaries of young and older participants? Although we cannot directly evaluate whether or not our participants were optimizing a weighted reward index, several aspects of our results are inconsistent with the idea that young and older adults use the same boundary adjustment processes with only quantitative differences in weights. In Experiments 2 and 3, older participants showed no evidence of adjusting their boundaries in response to feedback and task practice, whereas young participants responded to both of these variables. Just as these factors helped young participants approach the RROB value, feedback and practice should have helped older participants find the boundary values that optimized a weighted reward index. The fact that their boundaries did not change in response to these variables strongly suggests that older participants were not attempting to optimize a weighted combination of speed and accuracy. These results point to a qualitative difference in the boundary adjustment processes of young and older adults. As we have suggested, this qualitative difference appears to be that young participants attempt to balance speed and accuracy whereas older participants simply minimize avoidable errors.

The notion that older participants only seek to minimize avoidable errors explains why they used similar boundaries with and without task feedback in Experiment 2. Even without feedback, participants experience trials where they make a response only to realize it was an error. Older participants could adjust their boundaries to minimize this experience regardless of the feedback provided. The instruction effects in Experiment 1 also suggest that an unwillingness to make avoidable errors contributes to deviations from the RROB in older participants. That is, the speed-emphasis instructions may have altered older participants’ strategy from a monolithic concern with accuracy to a focus on balancing speed and accuracy, which could explain why age effects on boundary optimality were attenuated. Hertzog et al. (1993) also report indirect evidence that older participants close the gap with younger participants in terms of reward rate when instructions emphasize speed. In a mental rotation task, these researchers asked participants to emphasize speed, emphasize accuracy, or balance speed and accuracy. These instructions led to similar changes in RT for young and older participants. However, the decrease in RT induced by speed instructions was accompanied by a relatively large decrease in accuracy for young participants but little change in accuracy for older participants. Consistent with our results, this suggests that older participants typically make large sacrifices in speed for little gain in accuracy, and speed emphasis instructions bring them to a more balanced speed-accuracy compromise.

Previous research reinforces our finding that young participants adjust their response boundaries more readily than older participants. Trial-by-trial RT analyses reported by Smith and Brewer (1995) suggest that one difference between young and older participants is that the former are more likely to “experiment” with their boundaries. These researchers report a task in which young and older participants both performed at very high levels of accuracy and had nearly identical functions relating accuracy to speed. Despite these similarities, the age groups appeared to have very different strategies for controlling response time. Younger participants had fairly frequent runs of fast, lower-accuracy trials, which suggests that they made exploratory decreases in boundary settings. This exploration allowed them to find a point where they could both respond quickly and maintain high accuracy. In contrast, older participants had many responses on the flat region of the RT-accuracy function, where increases in response time led to little or no improvements in accuracy. Instead of exploring faster responses, they persistently responded more slowly than was required to maintain high accuracy.

In many of the tasks we report, older participants had drift rates that were comparable to the younger participants, yet the two groups showed marked differences in conservativeness. Hertzog and colleagues (Rogers, Hertzog, & Fisk, 2000; Touron & Hertzog, 2004; Touron, Swaim, & Hertzog, 2007) have thoroughly investigated another task in which older participants maintain more cautious responding compared to younger participants even when they are matched on task ability. These researchers used a task in which participants had to decide whether a candidate word pair was a member of a comparison set. The comparison set remained on the screen throughout the experiment, so participants could use the slow “look-up” strategy of searching the list to make accurate decisions. However, candidate word pairs were repeated, so participants could also respond based on their memory for the words in the set, which significantly decreased the time needed to come to a decision but ran the risk of errors. Not surprisingly, older participants were more reliant on the slow look-up strategy and younger participants were more likely to use a faster memory strategy (Rogers et al., 2000). More to the point, this was true even when analyses were limited to word pairs that were previously successfully retrieved and when both young and older participants learned the word set to a criterion before beginning the task (Touron & Hertzog, 2004). Even when older participants could use the memory strategy just as effectively as younger participants, they were more likely to engage in a look-up strategy compared to the younger group. Interestingly, older participants can be prompted to make more use of the memory strategy when they are provided with monetary incentives (Touron et al., 2007), and this flexibility is similar to our finding that older participants close the gap with younger participants when provided with speed-emphasis instructions.

Researchers must understand differences in boundary optimization processes to correctly interpret aging effects seen in a decision task. Consider a task in which young and older adults achieve similar levels of accuracy, but older adults are significantly slower than young adults. This RT difference would often be interpreted as a performance deficit for the older participants. However, the same result would be expected if young and older participants have the same ability to perform the task, but older participants use boundaries that inflate RT with little gain to accuracy. For example, Ratcliff (2008) found that only non-decision time differed between young and older adults in a response signal paradigm; that is, no aspect of the decision process showed age-related declines. Nevertheless, older adults set substantially wider boundaries on free response blocks (i.e., blocks with no response signals). Our results reveal that these boundary differences result from different boundary setting strategies: Older participants adjust boundaries to minimize avoidable errors regardless of the cost to speed, whereas young participants adjust boundaries to avoid disadvantageous speed-accuracy tradeoffs and consequently come relatively close to the RROB value.