Simulation study of chiral two dimensional ultraviolet (2DUV) spectroscopy of the protein backbone

Abstract

Amide n –π^* and π-π^* excitations around 200 nm are prominent spectroscopic signatures of the protein backbone, which are routinely used in ultraviolet (UV) circular dichroism for structure characterization. Recently developed ultrafast laser sources may be used to extend these studies to two dimensions (2D). We apply a new algorithm for modelling protein electronic transitions to simulate two-dimensional ultraviolet (2DUV) photon echo signals in this regime and to identify signatures of protein backbone secondary (and tertiary) structure. Simulated signals for a set of globular and fibrillar proteins and their specific regions reveal characteristic patterns of helical and sheet secondary structures. We investigate how these patterns vary and converge with the size of the structural motif. Specific chiral polarization configurations of the UV pulses are found to be sensitive to aspects of the protein structure. This information significantly augments that available from linear circular dichroism.

Introduction

The diverse functionality of proteins derives from the variety of stable and flexible three-dimensional geometrical structures.¹ Numerous proteins have evolved, each contributing to specific biological function. Two broad classes of structures can be distinguished: fibrous and globular. The first class of proteins form long fibers; they are usually insoluble in water and perform mostly structural functions. Globular proteins are mesoscopic balls of polypeptide chains. Their functionality ranges from hormones and enzymes to antibodies and cell structural elements. Helical and sheet structural motifs can often be recognized in globular proteins. Fibrillar proteins can be made of long fibers with helical or sheet-like secondary structure. Probing the structure of proteins and their transformations is essential for understanding fundamental cell biology as well as for protein engineering.

The atomistic structure of proteins, if they can be crystallized, can be determined using X-ray crystallography. Nuclear Magnetic Resonance (NMR) techniques can give structures in solution. However, some large proteins cannot be studied using such techniques. Examples are amyloid fibrils (due to insolubility) and intermediate steps in protein folding (due to limited time resolution). In this paper, we study the possibility of unravelling and/or refining protein structure using optical methods. Two-dimensional (2D) resonant laser spectroscopy in the infrared and the visible regions has become an important technique for studying vibrational and electronic excitations of molecules and their complexes.² These properties are unique for specific molecular structures and the underlying electronic dynamics. 2D spectroscopy^3–15 is very sensitive to electronic correlations and ultrafast electronic dynamics in proteins and other systems, such as molecular and semiconductor nanostructures. It has great potential for structure refinement, but is still not mature enough to be routinely applied.

Circular dichroism (CD) spectroscopy in the 180–220 nm UV region is a well-established technique for estimating protein secondary structure content.¹⁶ It relies on a fundamental property of the interaction between light and matter: isotropic chiral matter tends to rotate the polarization plane of linearly-polarized light and the rotation angle is intimately related to the bulk size and extent of structural chirality.¹⁷ While it is not possible to construct the structure using solely CD data, characterization of structural motifs is possible: α-helical proteins show a strong positive peak at 190 nm and usually a negative red-shifted doublet (208 and 222 nm). Sheet-containing proteins are less rigidly organized¹⁸ and their CD spectra vary from one protein to the other. However, their common feature is a negative amplitude at 180 nm, a positive band at 195 nm and usually a negative broad peak at approximately 215 nm.¹⁹ The positive features are usually weaker for sheet-like than for α-helical proteins. Elaborate numerical methods based on least-square fitting, singular value decomposition, neural network analysis, etc., have been applied to extract the content of various structural motifs from experimental CD spectra.^20–22 A considerable effort has been devoted to simulate the CD spectra of proteins. Efficient protein parametrization schemes have been developed using a Frenkel exciton (matrix) model. Woody and co-workers have optimized a set of semiempirical parameters, where some parameters were obtained by fitting to experiment.²³ Hirst and co-workers have developed an ab-initio parametrization, where all transition parameters and inter-group couplings are calculated from first-principles electronic structure calculations.^18,24 This latter parametrization has a greater predictive capacity, since the parameters are not derived empirically from experiments.

Molecular dynamics (MD) simulations are gradually acquiring the capacity to unravel the structure of peptides and small proteins.^25–28 2D spectroscopy simulations based on MD trajectories have been successfully employed in conjunction with 2DIR photon echo experiments to probe protein structure and fast folding processes and can be used to evaluate the quality of different MD methods.¹⁴ UV spectroscopy provides a different observation window, which has the advantage over IR, because it can reach shorter pulse durations (5 fs compared to 50 fs), and higher quality polarization control. The UV region is also important for specific photo-physical protein processes, photochemical reactions of peptide bonds and radiation damage. In a previous study of 2DUV,²⁹ we have used two exciton parametrization models, the first-principles one¹⁸ and the semiempirical one,²³ and we used a diagonal Gaussian disorder of transition energies to model the spectral linewidth. Both parametrization models yielded very similar absorption and CD spectra of myoglobin. The 2DUV, however, showed different signals and can, thus, be used to refine the model. In this paper, we employ a newly developed, quantum mechanics/molecular mechanics (QM/MM) approach³⁰ to improve the modelling of the amide electronic transition energies. Compared to the protein model of earlier work,¹⁸ where the transition energy is fixed and independent of the amino acid configuration, we allow the transition energy to fluctuate with the MD trajectory, using an electrostatic model. In contrast to our previous study,²⁹ the new model defines the transition frequency fluctuations from the microscopic electrostatic interaction between the amide groups, side chains and water. Our new model is transferable to different solvents and environments (e.g. membranes) and can accurately describe spectral line broadenings in various UV experiments. Simulations of absorption and CD based on this model³⁰ showed that the water fluctuations are fast and induce homogeneous spectral broadenings. Side chains fluctuations, however, are much stronger and slower and cause a large inhomogeneous broadening. This dominates the CD signal and some of the fine details of the spectra are washed out. The 2DUV photon echo technique has the capacity to eliminate certain types of inhomogeneities and improve the resolution. Recent advances in laser technology have led to the development of coherent ultrashort pulses in the UV.³¹ Ultrafast attosecond broadband UV and XUV pulses under development could make 2DUV feasible.^32–35 Here we simulate 2D UV signals of protein backbone of several proteins and their segments and demonstrate that the cross-peaks in 2DUV carry unique signatures of protein structure.

Methods

Several simulation techniques for nonlinear optical signals of molecular systems and their complexes relevant for the resonant electronic spectroscopy have been developed.^14,15,36 We use a computational protocol based on the exciton model, i.e., the matrix of single-exciton transition energies and inter-group (and intra-group) interactions calculated using electrostatic interactions between transition charge densities. The level scheme for each amide n–π^* and π–π^* transitions, their transition dipoles and interamide interactions are implemented as in the package DichroCalc.^18,37

Fluctuations in the molecular environment induce spectral broadenings. To account for these effects we use a QM/MM approach. We consider a dilute solution so that interactions between distinct protein molecules are negligible. MD simulations of a single protein molecule in water were performed with 1 fs timestep using the NAMD 2.7 program,²⁵ with the CHARMM27²⁶ force field, and the TIP3P water model,³⁸ and cubic periodic boundary conditions. Long-range electrostatic interactions were computed using particle-mesh Ewald (PME);^27,28 and a real space cutoff of 12 Å was used for nonbonded interactions. The NPT ensemble was used. All MD simulations started with a 5000 step minimization and 600 ps heating from 0 K to room temperature 310 K. After a 2 ns equilibration, we simulated a 16 ns trajectory and recorded structures every 400 fs. The protein structures were stable during the MD simulations. An ensemble of 2000 MD snapshots was recorded for every 400 fs.

The electronic transitions are described by the Hamiltonian

$${\widehat{H}}_s=\sum _{ma}{\epsilon }_{ma}^{(s)}{\widehat{B}}_{ma}^{†}{\widehat{B}}_{ma}+\sum _{\mathit{manb}}^{m\ne n}{J}_{ma,nb}^{(s)}{\widehat{B}}_m^{†}{\widehat{B}}_n,$$ (1)

where m denotes the peptide unit and a represents the transition of the unit (either n–π^* or π–π^*) and (s) denotes the snapshot. ${\epsilon }_{ma}^{(s)}$ represents the transition energy of a state of mth unit and $J_{ma,nb}^{(s)}$ denotes the resonant coupling. The exciton creation ( ${\widehat{B}}_{ma}^{†}$) and annihilation (B̂_ma) operators have commutation relations $[{\widehat{B}}_{ma},{\widehat{B}}_{nb}^{†}]={\delta }_{mn}(1-2{\widehat{B}}_{mb}^{†}{\widehat{B}}_{ma})$.

The transition energies of the mth peptide unit, ε_ma, were calculated by considering the electric field at this unit induced by water, the remaining peptide groups, and the amino acid side chains, as described in ref.30 The inter-amide interactions and transition amplitudes were calculated from the DichroCalc package.¹⁸ Single-exciton eigenstates were calculated by numerical diagonalization of Eq. (1). This model reproduces realistic spectral broadening effects based on a MD trajectory using an electrostatic model.³⁰

The 2DUV signal is obtained using four coherent short time-ordered laser pulses, labeled by their wavevectors k₁, k₂, k₃ and k₄. The laser pulses have the same carrier frequency and are resonant with peptide backbone electronic transitions. The signal is detected at direction k₄ = −k₁ + k₂ + k₃ as a function of three delay times: t₁ - between pulses k₁ and k₂, t₂ - between pulses k₂ and k₃, and t₃ - between pulses k₃ and k₄. The 2D spectrum is obtained by two-dimensional Fourier transform t₁ → Ω₁ and t₃ → Ω₃. We set the second delay t₂ to zero. The 2DUV signal was calculated in the quasiparticle representation,¹⁵ whereby each exciton is considered as a quasi-particle moving in real space. If two excitons approach the same amide group, they scatter due to Pauli exclusion. The scattering matrix was calculated by eq 325 of ref.15 We then calculate the homogeneous two-dimensional k_I photon echo signal for this snapshot (s) using eqs. 119–122, 127 in ref.15 A single-exciton dephasing rate (homogeneous broadening), γ=250 cm⁻¹ was added to represent the spectral linewidth induced by fast fluctuations of water molecules. The Hamiltonian and the homogeneous signal is calculated by this procedure at each snapshot of the full MD trajectory. The full inhomogeneous signal is obtained by averaging over 2000 MD snapshots for absorption and CD spectra, and 500 MD snapshots for 2D signals. All calculated 2DUV spectra were normalized to 1, and then were plotted from −R to R (0 < R < 1) to enhance weak features.

The UV region relevant for the spectroscopy of the peptide backbone is from 180 nm to 220 nm. A 200 nm photon has period, T = 0.67 fs. We assume a Gaussian pulse envelope as a function of frequency. The length of pulse with five optical periods is 3.33 fs (FWHM). Its spectral bandwidth is 8840 cm⁻¹ (the variance of the Gaussian shape is 3754 cm⁻¹). That approximately corresponds in wavelength to 35 nm bandwidth (FWHM). We used these pulse shape parameters with a carrier central frequency ω₀ = 52000 cm⁻¹ (192 nm) so that the full absorption band is covered (the full CD band is broader). Calculations were performed for both xxxx and xxxy polarization configurations: xxxx configuration is the simplest; xxxy is, like CD, induced by molecular chirality. We, thus, denote CD and 2D xxxy signals as Chirality Induced (CI). They are ~ 100 times weaker than regular ones, but have better structural resolution.

It can be shown using response function theory, that the CD signal corresponds to the linear response function xy tensor component, where the excitation is at x polarization and the detection is polarized perpendicularly at y.³⁹ The 2D spectrum at xxxy polarizations corresponds to the case where the first excitation has y polarization, and the second excitation has x polarization, just like in CD. The remaining two xx polarized interactions (absorption-like) perform the detection. The diagonal section of the 2DUV spectrum corresponds to the case where the excitation and the detection have the same energies, so the excited states are detected directly without interaction with other transitions (no coherent or incoherent energy transfer is involved). In this case, the diagonal of the 2DUV xxxy spectrum reflects the detection of CD-like features, which appear similar to the CD spectrum. Finite pulse bandwidths and non-linear rescaling of peak amplitudes may distort this relation. The same consideration applies to 2DUV xxxx and linear absorption, which corresponds to the xx type linear response function. Therefore, the diagonal of the 2D xxxx spectrum should reflect the absorption spectrum. Both xxxx and xxxy pulse configurations can be realized in a collinear pulse configuration. For notation and details see.¹⁵

Results

Connecting 2D signals to secondary structure elements

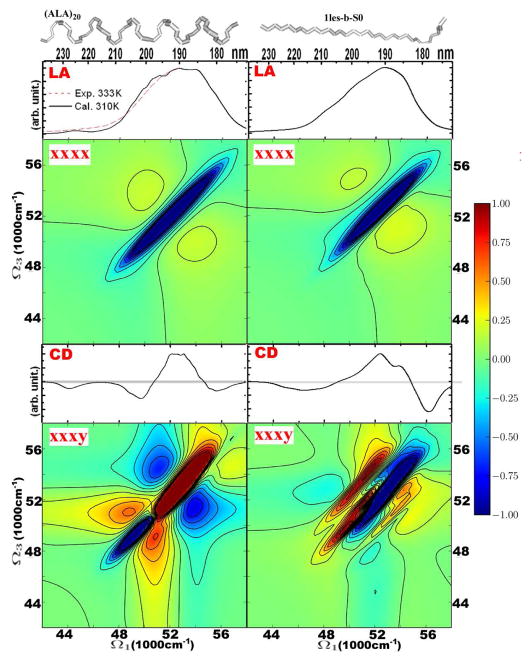
We first present the 2DUV spectra of typical protein structural motifs. In Figure 1 we compare the spectra of extended and helical conformations of the peptide backbone, shown in the upper panels: the helical fragment is a small polyalanine α-helix and the strand is excised from lentil lectin (Protein Data Bank code 1les). For completeness we also show linear absorption (LA) and CD spectra. The two LA signals are similar and show very broad asymmetric peaks at 53000 cm⁻¹. These features are mapped approximately onto the diagonal line (Ω₃ = −Ω₁) of the non chiral 2DUV xxxx spectrum. For the helix and the sheet it shows strong diagonal features and relatively weak crosspeaks. The patterns consist of negative (green-to-blue) and positive (green-to-red) features. The diagonal negative peak of the helix is slightly broader than that of the strand. The crosspeaks in the spectrum of the helix are symmetrically distributed around the negative diagonal peak, while the lower crosspeak (on the Ω₃ axis) of the extended strand is stronger.

Figure 1.

Dependence of the linear and 2D signals on the backbone configuration: helical (left column) versus extended strand (right column). From top to bottom: structures, absorption, 2DUV xxxx, CD, 2DUV xxxy. The extended strand is taken from lectil lectin (Thr1-Phe11 of chain C in 1les.pdb, from Protein Data Bank) and the α-helical conformation is a 20 residue poly-alanine chain. The 2DUV spectra normalization (R) factors: for helical xxxx – 0.35, xxxy – 0.16; strand xxxx – 0.38, xxxy – 0.31.

We now turn to CI signals. The CD spectrum of the two conformations is very different below 50000 cm⁻¹: for the strand there is a single broad negative peak centered at 45500 cm⁻¹, while the helix shows a negative doublet (44000 and 48000 cm⁻¹).^20,23 The chirality-induced 2DUV signal xxxy is much richer. The spectra along the diagonal approximately reflect the CD in the 48000 to 56000 cm⁻¹ region. The diagonal section of the strand spectrum has a negative peak at 54000 cm⁻¹ and a positive peak at 49500 cm⁻¹. Strong crosspeaks asymmetrically appear on both sides of the negative and positive peaks. The 2DUV pattern of the helical structure is markedly different. The negative 54000 cm⁻¹ diagonal peak of the strand shifts to lower values of Ω₃ and a strong positive peak develops at 52000 cm⁻¹. The positive peak of the strand at 49500 cm⁻¹ corresponds to the negative peak at 48000 cm⁻¹ in the helix. This spectral redistribution around the diagonal results in a relatively symmetric crosspeak pattern. The crosspeak symmetry in both the xxxx and xxxy spectra is, thus, attributed to the helical structure and its interactions between neighboring turns of the helix.

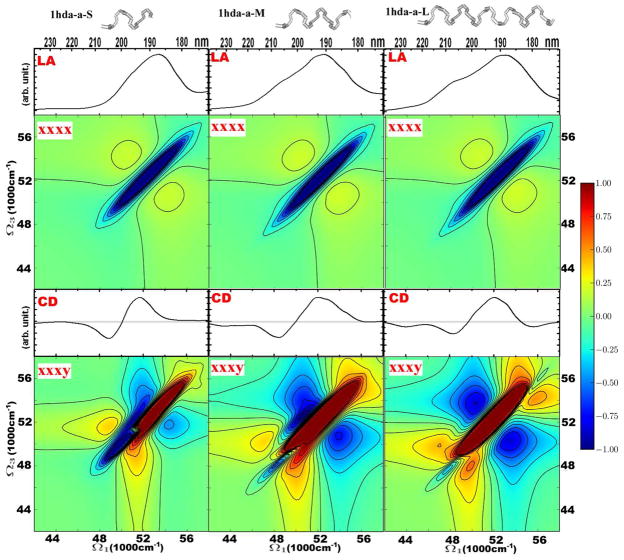
We next explore how the symmetric crosspeak pattern develops with the length of the helix. In Figure 2 we show the 2DUV signals for three helical segments with different lengths excised from hemoglobin (PDB code: 1hda). We label the three helical segments as short (S), medium (M) and long (L). Their structures are shown at the top of Figure 2: S contains two helical turns, M has three and L comprises five helical turns. The absorption of these helices demonstrates the development of the 49000 cm⁻¹ shoulder with helix length. The variation of 2DUV xxxx with the helix length is relatively weak: the length of the negative region on the diagonal increases from the short to the medium helix. There are stronger differences in the CI signals. Differences in CD are mostly apparent in the growth of the negative 44000 cm⁻¹ peak with helix length. The negative diagonal peak at 48000–50000 cm⁻¹ significantly varies in the 2DUV xxxy spectra for different helices. That peak is strong for the small helix and gradually decreases with helix length. It could, thus, be used to determine the effective length of helices in globular proteins.

Figure 2.

Linear and 2DUV signals of helical motifs of different lengths. The helices are taken from hemoglobin (PDB file 1hda.pdb): 1hda-a-S – Pro124-Asp129 of chain D; 1hda-a-M –Pro124-Val134 of chain D; 1hda-a-L – Pro124-His143 of chain D. From top to bottom: structures, and absorption, 2DUV xxxx, CD, and 2DUV xxxy spectra. The 2DUV spectra normalization (R) factors: for S xxxx – 0.37, xxxy – 0.23; M xxxx – 0.35, xxxy – 0.12; L xxxx – 0.35, xxxy – 0.11.

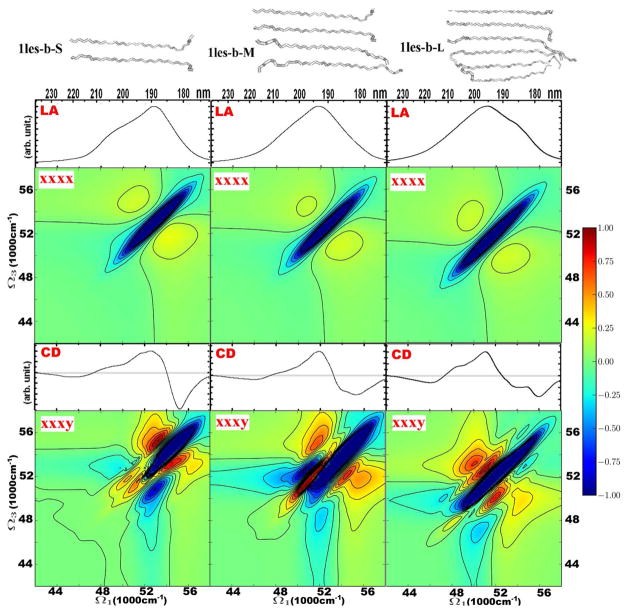
In Figure 3 we depict the variation of the 2DUV signal with the size of the sheet motif. Three motifs were taken from lectin: small (S), medium (M) and large (L). S has two strands, M has four and L six, in each case making an antiparallel beta sheet. The absorption signals of all three motifs are very similar. The 2D xxxx spectra of the sheets are also very similar and feature a single diagonal peak at 51200 cm⁻¹. The chiral CD spectra differ mostly in the shape of dispersive region between 48000 cm⁻¹ and 56000 cm⁻¹. These changes can be rationalized as follows. There is a gradual increase of a positive shoulder at 50000 cm⁻¹ with the size of the sheet. These differences are amplified in the chiral 2D xxxy spectra in the 48000–52000 cm⁻¹ region. The main negative diagonal peak becomes more elongated with the sheet size. We also notice a variation in the fine structure of the crosspeaks.

Figure 3.

Linear and 2DUV signals of the β -sheets of various sizes. The sheet elements were obtained from lectin (PDB file 1les.pdb) as follows. 1les-b-S is made of two strands: Thr1-Phe11 of chain C, and Val37-Leu46 of chain D of lectin (PDB file 1les.pdb). 1les-b-M is made of four strands: Thr1-Phe11 of chain C, Val37-Leu46 of chain D, Val60-Val70 of chain C, and Glu158-Ala169 of chain C. 1les-b-L is made of six strands: Thr1-Phe11 of chain C, Val37-Leu46 of chain D, Val60-Val70 of chain C, Glu158-Ala169 of chain C, Val1-Pro11 of chain D, and Val37-Leu46 of chain D. From top to bottom: structures, and absorption, 2DUV xxxx, CD, and 2DUV xxxy spectra. The 2DUV spectra normalization (R) factors: for S xxxx – 0.35, xxxy – 0.34; M xxxx –0.37, xxxy – 0.32; L xxxx – 0.36, xxxy – 0.12.

2D UV signals of globular and fibrillar proteins

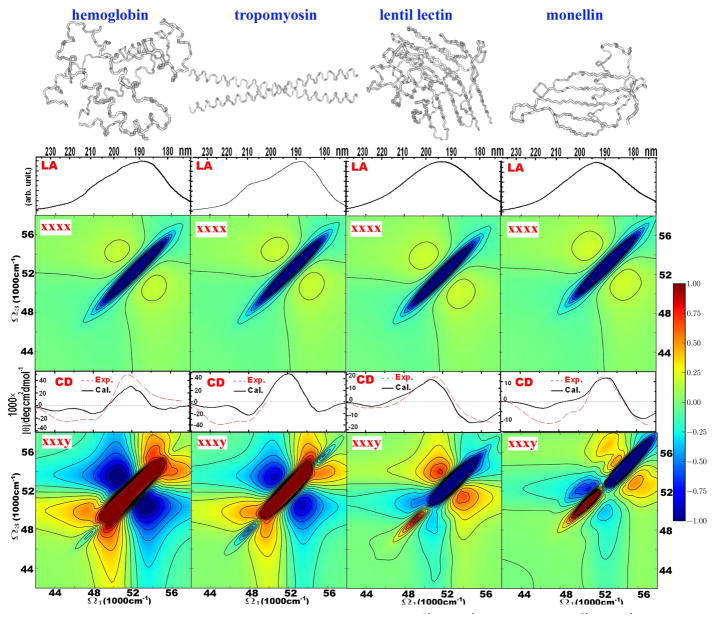
In Figure 4, we present the 2DUV spectra of four proteins with characteristic secondary and tertiary structures. Hemoglobin (PDB code 1hda) is a globular protein made of inter-connected helices. Less than 20 per cent is non-helical. Rabbit skeletal alpha-tropomyosin (2d3e) is a long helical protein, that forms fibers. Its core consist of two inter-twined α-helices. Lentil lectin (1les) is mostly a twisted β-sheet globular protein. Monellin (1mol) is a small globular protein made of a sheet and an α-helix, which allows us to study both structural motifs and their interactions.

Figure 4.

Simulated linear and 2D signals of helical proteins, hemoglobin (PDB code 1hda), leptin (1ax8), tropomyosin (2d3e), and of sheet-containing proteins, lentil lectin (1les), monellin (1mol). From top to bottom: structures, and absorption, 2DUV xxxx, CD, 2DUV xxxy spectra. Simulated CD is given in absolute units. The 2DUV spectra normalization (R) factors: for hemoglobin xxxx – 0.38, xxxy – 0.07; for tropomyosin xxxx – 0.36, xxxy – 0.11; for lentil lectin xxxx – 0.33, xxxy – 0.14; for monellin xxxx – 0.32, xxxy – 0.21.

The absorption spectra of these proteins are similar – they do not vary when many amides are involved. The same can be concluded for the 2DUV xxxx signal of these proteins, which is almost identical, showing one strong negative diagonal peak and a pair of weaker positive crosspeaks, positioned symmetrically on both sides of the diagonal. The CD features agree with experiment: the CD spectra of helical proteins have all features observed experimentally. Likewise, the CD spectra of the sheet-like proteins are similar to each other and to the experimental sheet spectra. The 2DUV CI xxxy signals of the proteins show rich spectral features, which strongly depend on structure. Helical proteins show a very strong positive diagonal peak at around 52000 cm⁻¹. The pattern is symmetric along the diagonal for the regular long helices (tropomyosin). The asymmetry in the hemoglobin spectrum can, thus, be attributed to the less regular distribution of the helices and is thus a signature of specific tertiary structure. Sheet-containing proteins show a very strong diagonal negative peak at 54000 cm⁻¹. Since lectin has a large content of sheet and monellin is a mixture of helix and sheet, this difference can be related to the strength of the positive diagonal peak at 50000 cm⁻¹ correlating with the helical content in monellin. Overall, the sheets show weaker crosspeaks than the helices.

Discussion

We have investigated the variation of 2DUV signals with respect to the size and geometry of secondary structure motifs. The absorption spectrum and the nonchiral xxxx 2DUV signal does not depend strongly on the secondary structure of a protein. The signal is dominated by a single negative diagonal peak and crosspeaks are weak, indicating that the amide π–π^* transition is dominated by inhomogeneities and inter-amide interactions are weak. This is markedly different from the amide vibrational bands, where 2DIR spectroscopy shows strong crosspeak patterns.

Our previous simulation of 2DUV spectra of helical proteins used a cruder parametrization of amide transitions.²⁹ The present simulation parameters are more accurate and show much better agreement with CD experiments especially for helical proteins. Our previous simulations showed stronger crosspeaks in the 2D signals. This arose from smaller dephasing rates, so the peaks across the diagonal (|Ω₃| = Const −|Ω₁|) were narrower, their overlap was smaller and this provided less cancellation. In the present model, the 250 cm⁻¹ homogeneous dephasing rate was estimated from absorption lineshapes by including only water-induced fluctuations. Inhomogeneity was obtained by adding averaging over fluctuations of the whole protein. In this way we simulate all broadening mechanisms microscopically, and the simulated spectra must be more accurate. The weak cross-peaks in the simulated 2D xxxx signal is the indication that the inter-amide electrostatic interaction is weak compared to the amide transition energy fluctuations.

We observed a strong dependence of the chiral xxxy 2DUV signal on the secondary structure. This signal shows characteristic patterns for sheets and helices. By comparing signals of different helical proteins, we conclude that the helical protein signal is dominated by a strong positive diagonal peak. The signal for different proteins is very similar; however, the differences indicate sensitivity to tertiary structure.

Can the observed features be related to long-range structural order of proteins, which is preserved through hydrogen bonding? To address this issue, we should determine whether 2DUV spectra depend on nearest-neighbor interactions, which are a function of rotation angles between neighbouring peptide groups or on long-range electrostatic interactions that may be inherent in specific helical or sheet structures. Since the inter-amide interactions are very weak (see 2DUV xxxx signals), we expect that long-range interactions do not a play significant role in shaping 2DUV of the proteins. Instead, the diagonal features depend on the dihedral angles between neighboring amides through the resulting shifts in the transition energies. That is why the negative diagonal feature of a single extended strand is similar to that of the whole β-sheet. We also found that some non-helical proteins show a strong positive peak in the 2DUV xxxy signal (not shown). This can be related to specific turns in the protein structure: the helical and extended strand (or sheet structure) have different angles between neighboring amides. The difference between diagonal features in the 2DUV xxxy signals, thus, originates from different local configurations. The crosspeaks between these diagonal peaks, whilst weak, are induced by the long-range interactions.

Another important question addressed here is the variation of the 2DUV spectra with the size of specific structural motifs. Our simulations showed that only the crosspeak regions of the chirality induced xxxy 2DUV signal is sensitive to the size. This supports the conclusion that the cross-peaks may be related to the long-range interactions between amide groups. However, the spectral variation with size (for helices and for sheets) is not monotonic in this set of protein structures and it is difficult to establish the relation between the size of a structural motif and the 2DUV spectrum.

Further studies are necessary to explore these issues in more detail. Our 2DUV simulations demonstrate the high sensitivity of the chirality induced 2D signals to the secondary structure of proteins. Other types of 2D signals have been used in electronic spectroscopy of photosynthetic molecules^40,41 and semiconductor quantum wells⁴² to reveal electronic correlations of excitons. These signals may be informative in UV studies of proteins as well.t

Coherent 2D experiments in the UV protein-backbone region will become available in the near future. It is important to develop efficient and accurate simulation models. Our simulations include few important assumptions. (i) We assumed that only single excitation can occupy an amide group. This corresponds to neglect of excited state absorption of amide groups into their electronic states lying around ~100000 cm⁻¹ (from their ground states). Such electronic states (Rydberg-like) are substantially destabilized in condensed phases relative to the gas phase and appear to have a limited influence. (ii) We neglected charge-tranfer (CT) states of the protein backbone.⁴³ These may be important in shaping higher-energy (180 nm) area of UV spectra.⁴⁴ (iii) Electronic interactions with near-resonant side-chain excitations were neglected. (iv) We used a simple dephasing model as induced by fast water molecule fluctuations. It is, however, known that the water molecule fluctuation correlation function may extend to picoseconds;⁴⁵ thus, the homogeneous model (Markovian approximation) may fail. Other fluctuations were assumed to be much slower than the experimental timescale. A full fluctuation analysis may be performed in the future. (v) Dissipative energy transport between amides was neglected. This may not be significant factor for our simulation scheme, but it may affect spectral lineshapes through lifetime broadening. (vi) The 2DUV signal was simulated for a laser carrier frequency of 52000 cm⁻¹ with a 8000 cm⁻¹ bandwidth enhancing the π–π^* transitions close to this region. By tuning the carrier frequency we can enhance different electronic transitions and the resulting signal may show different patterns. Using laser pulses with different central frequencies (two- or three-color setup) may enhance the crosspeak regions. The full bandwidth of the amide CD in UV region is 170–250 nm, which corresponds to ~18000 cm⁻¹. Different sections of this bandwidth may be studied using state of the art laser techniques.