Abstract
The two proton transfer reactions catalyzed by ketosteroid isomerase (KSI) involve a dienolate intermediate stabilized by hydrogen bonds with Tyr14 and Asp99. Molecular dynamics simulations based on an empirical valence bond model are used to examine the impact of mutating these residues on the hydrogen-bonding patterns, conformational changes, and van der Waals and electrostatic interactions during the proton transfer reactions. While the rate constants for the two proton transfer steps are similar for wild-type (WT) KSI, the simulations suggest that the rate constant for the first proton transfer step is smaller in the mutants due to the significantly higher free energy of the dienolate intermediate relative to the reactant. The calculated rate constants for the mutants D99L, Y14F, and Y14F/D99L relative to WT KSI are qualitatively consistent with the kinetic experiments indicating a significant reduction in the catalytic rates along the series of mutants. In the simulations, WT KSI retained two hydrogen-bonding interactions between the substrate and the active site, while the mutants typically retained only one hydrogen-bonding interaction. A new hydrogen-bonding interaction between the substrate and Tyr55 was observed in the double mutant, leading to the prediction that mutation of Tyr55 will have a greater impact on the proton transfer rates for the double mutant than for WT KSI. The electrostatic stabilization of the dienolate intermediate relative to the reactant was greater for WT KSI than for the mutants, providing a qualitative explanation for the significantly reduced rates of the mutants. The active site exhibited highly restricted motion during the proton transfer reactions, but small conformational changes occurred to facilitate the proton transfer reactions by strengthening the hydrogen-bonding interactions and by bringing the proton donor and acceptor closer to each other with the proper orientation for proton transfer. Thus, these calculations suggest that KSI forms a preorganized active site, but that the structure of this preorganized active site is altered upon mutation. Moreover, small conformational changes due to stochastic thermal motions are required within this preorganized active site to facilitate the proton transfer reactions.
I. Introduction
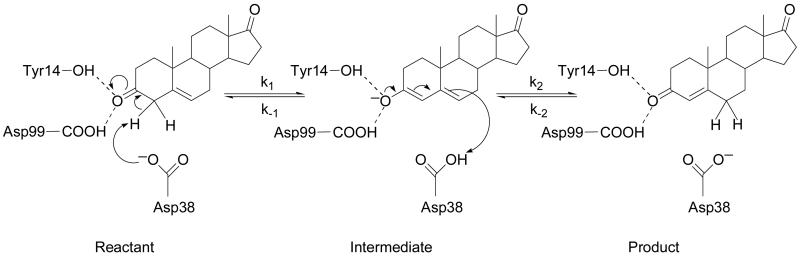
The enzyme Δ5-3-Ketosteroid isomerase (KSI) catalyzes the isomerization of 3-oxo-Δ5-steroids to their Δ4-conjugated isomers by the two-step proton transfer mechanism depicted in Figure 1. KSI enzymes from Pseudomonas putida and Commamonas testosteroni bacteria have been studied extensively. Both experimental1-9 and computational10-19 approaches indicate that the catalytic efficiency of KSI is strongly influenced by electrostatic stabilization and hydrogen bonding. As shown in Figure 1, this enzyme mechanism involves a dienolate intermediate that is stabilized by hydrogen bonds with Tyr14 and Asp99 in the active site. (In the present paper, the residues are numbered according to Commamonas testosteroni KSI.) The catalytic relevance of these residues has been investigated experimentally by kinetic studies on mutant forms of KSI.2, 3, 20-34 Mutation of these residues has been shown to significantly reduce the catalytic efficiency of KSI. Specifically, mutation of Asp99 to Leu decreases kcat by 102.1, mutation of Tyr14 to Phe decreases kcat by 103.4, and the corresponding double mutation decreases kcat by 104.6 in Pseudomonas putida KSI.3 These trends were also observed for single mutants of Commamonas testosteroni KSI,2, 20 where mutation of Asp99 to Ala decreases kcat by 103.7 and mutation of Tyr14 to Phe decreases kcat by 104.7.
Figure 1.
Schematic depiction of the proton transfer reactions catalyzed by KSI. In the first step, the proton transfers from the C4 atom of the substrate to the Asp38 residue. In the second step, the proton transfers from the Asp38 residue to the C6 atom of the substrate. The reactant, intermediate, and product states of the overall reaction are labeled.
The objective of this paper is to use molecular dynamics (MD) simulations to understand the impact of mutating Tyr14 and Asp99 on the two proton transfer reactions catalyzed by KSI. We perform calculations on both the D99L and Y14F single mutants and the Y14F/D99L double mutant of KSI from Commamonas testosteroni bacteria with the Δ5-androstene-3,17-dione (5-AND) substrate. As in our previous study of wild-type (WT) KSI,19 the simulations are based on a potential energy surface described by an empirical valence bond (EVB) model.35 We calculate the free energy profiles along the collective reaction coordinate for both proton transfer steps of all three mutants. We also analyze the hydrogen-bonding patterns, van der Waals and electrostatic interactions, and conformational changes during the proton transfer reactions. Our results are consistent with the experimental data on the mutants and provide insight into the catalytic roles of these hydrogen-bonding residues. This work differs from previous theoretical studies of KSI in that we investigate mutant forms of KSI and analyze changes in hydrogen bonding, local and global conformations, and ligand-enzyme interactions along the reaction coordinate from the substrate to the dienolate intermediate to the product. These calculations lead to a physical explanation for the significantly reduced rates of the mutants, the identification of a new hydrogen-bonding interaction between the substrate and Tyr55 for the double mutant, and an experimentally testable prediction concerning mutation of Tyr55.
This paper is organized into the following sections. The computational methods used to model the two proton transfer reactions are described in Section II. The results from the simulations are presented in Section III. The first part of this section analyzes the free energy profiles and relative rate constants, while the second part analyzes the hydrogen bonding patterns, electrostatic interactions, and conformational changes accompanying the proton transfer reactions. Our conclusions are presented in Section IV.
II. Methods
A. Theory
We used a two-state empirical valence bond (EVB) potential35 to model the electronic potential energy surface for each proton transfer reaction shown in Figure 1. The two EVB states correspond to the Reactant and the Intermediate for the first step and to the Intermediate and the Product for the second step. These two proton transfer reactions are thought to be sequential with negligible coupling between the Reactant and Product states, thereby enabling us to model them with two separate two-state EVB potentials. The ground state electronic potential energy surface for each proton transfer reaction is obtained from the lowest energy eigenvalue of the corresponding 2×2 EVB Hamiltonian. The details of this EVB potential are provided elsewhere.19
For each two-state EVB model, the diagonal matrix elements V11 and V22 of the EVB Hamiltonian were represented by a modified AMBER99 forcefield with a constant energy shift Δ included in V22.19, 36, 37 The constant energy shift Δ and the coupling V12 between the two states were determined by fitting the calculated rates for WT KSI to the experimentally determined rate constants for the forward and backward reactions.38, 39 Based on the WT KSI data from the present paper, these parameters are Δ = 1.8 kcal/mol and V12 = 99.5 kcal/mol for the first step and Δ = −14.5 kcal/mol and V12 = 93.1 kcal/mol for the second step. These parameters are similar to the values obtained from previous MD simulations of WT KSI,19 and the minor differences are due to typical statistical errors associated with MD. Moreover, these parameters are assumed to be the same for the WT and mutant KSI simulations. Thus, we did not fit any parameters to experimental data for the mutants.
The potential of mean force (PMF) for each proton transfer reaction was calculated as a function of a collective reaction coordinate defined as
| (1) |
This energy gap reaction coordinate includes motions of the entire solvated enzyme. The reaction was driven from the reactant to the product state using a series of mapping potentials defined as35
| (2) |
where the mapping parameter λ is varied between zero and unity. The PMF was obtained by propagating a series of classical MD trajectories according to these mapping potentials and combining the results to obtain the complete PMF for the unbiased EVB potential using the weighted histogram analysis method (WHAM)40-43 or umbrella integration.44-46 Note that the energy gap reaction coordinate Λ is used only for binning purposes, and its magnitude is not physically meaningful because it depends on the details of the forcefield determining the energy of the excited electronic state, which is not relevant for these MD simulations performed on the ground electronic state potential energy surface.
Within the framework of transition state theory (TST), the rate constant is given by
| (3) |
where kTST is the TST rate constant and κ is the transmission coefficient accounting for dynamical recrossings of the dividing surface. An expression for the TST rate constant in terms of the PMF along a general reaction coordinate has been derived.47-49 In this study, we used the simpler form
| (4) |
where β = 1/kBT, kB is the Boltzmann constant, and ΔG‡ is the free energy barrier determined directly from the PMF. In our previous study of WT KSI, we showed that the results are similar using the two different forms of the TST rate constant.19
Furthermore, we calculated the transmission coefficient κ using the reactive flux approach50-54 and included the nuclear quantum effects associated with the transferring hydrogen nucleus with the quantized classical path method55-58 in our previous work.19 We found that the transmission coefficient decreases the rate and the nuclear quantum effects increase the rate by approximately the same amount in WT KSI, so the inclusion of both effects together does not significantly impact the rate constant.19 Specifically, the dynamical barrier recrossings decrease the rate constants by a factor of ~3, and nuclear quantum effects of the transferring hydrogen nucleus increase the rate constants by a factor of ~8 for WT KSI. Moreover, we do not expect the trends in the rate constants for the mutant KSI enzymes to be strongly influenced by dynamical barrier recrossings or nuclear quantum effects. Thus, these effects were not included in the calculations of the rate constants for the present study.
B. Simulation Details
The starting structures for the mutant KSI simulations were obtained from our previous study on WT KSI.19 The initial structure for this previous study was based on the second dimeric unit in the 2.3 Å resolution crystal structure (PDB 1QJG)59 of Commonas testosteroni Δ5-3-ketosteroid isomerase complexed with equilenin (EQU), which is an analog for the Intermediate state. The equilenin was replaced with the naturally occurring substrate, and the protonation states were determined from the 1BUQ solution NMR structure.60 The mutated residues Asn38 and Ile83 were restored to Asp and Thr, respectively, as in WT KSI. The Asp38Asn mutant was used for the crystal structure determination because it binds steroid analogues more tightly and mimics the protonated form of Asp38 in the Intermediate state.59 The protein was immersed in a periodically replicated truncated octahedron box of 6837 explicit TIP3P rigid water molecules61, 62 with 6 Na+ ions to maintain charge neutrality. The system was equilibrated using a simulated annealing procedure involving MD for an isobaric, isothermal ensemble (NPT) at systematically increasing temperatures, followed by additional MD for a canonical ensemble (NVT) at 298 K. The details of the system preparation and equilibration are provided elsewhere.19 For the starting structures in the present study, we chose snapshots obtained after more than 2 ns of NVT MD in the Intermediate state (i.e., λ = 0.95 for the first proton transfer step and λ = 0.05 for the second proton transfer step).
The initial states of the mutant enzymes were prepared from these starting structures as follows. The D99L, Y14F, and Y14F/D99L mutant forms of KSI were created using the profix utility in the JACKAL protein modeling package.63, 64 The mutated residues were optimized (i.e., the energy was minimized with respect to their coordinates) with the remaining protein and water molecules fixed. Then the active site residues and the substrate were optimized with the remaining protein and water molecules fixed. Subsequently, the water molecules and ions were optimized while keeping the protein fixed, and finally the entire system was optimized. The final stage of equilibration for each mutant consisted of 200 ps of NVT MD at 298 K. All of these equilibration steps were performed in the Intermediate state (i.e., λ = 0.95 for the first proton transfer step and λ = 0.05 for the second proton transfer step).
A modified version of the DLPROTEIN package65 was used for these simulations. For data collection, the MD trajectories were propagated at 298 K for a canonical ensemble (NVT) with a time step of 1 fs. The hydrogen atoms bonded to heavy atoms were constrained to their equilibrium distances with the SHAKE algorithm.66 The Smooth Particle Mesh Ewald method67 was used to calculate the electrostatic interactions. The temperature was maintained with a Nosé -Hoover thermostat.68, 69 The PMF was generated for WT and the three mutant KSI enzymes using the exact same procedure. The results for WT KSI are qualitatively similar to the data obtained previously for WT KSI.19 All tables and figures in the present paper were generated from the current data.
To generate the PMF, a series of MD trajectories propagated according to different mapping potentials was started from the Intermediate state for both proton transfer reactions. For the first proton transfer step, the windows with λ = 0.95 and λ = 0.90 were started from the corresponding equilibrated structure described above. For the second proton transfer step, the windows with λ = 0.05 and λ = 0.10 were started from the corresponding equilibrated structure described above. Each subsequent window was started from the configuration of the previous window after 10 ps of equilibration. For each window, an initial optimization followed by equilibration with 100 ps of MD was performed prior to data collection. A total of 19 different mapping potentials with values of λ = 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90 and 0.950 was used for each proton transfer step. Two independent sets of trajectories were propagated for each proton transfer step, starting from the same equilibrated configuration but different initial velocities in the first window. We collected 600 ps of data for each mapping potential in both sets of trajectories, leading to a total of 23 ns of data collection for each proton transfer step of each enzyme. Although the simulation timescale is significantly shorter than the timescale associated with the catalytic rate constant, the use of mapping potentials provides information along the entire range of the reaction coordinate corresponding to the proton transfer reactions, assuming sufficient equilibration and sampling in each window.
III. Results
A. Relative rate constants
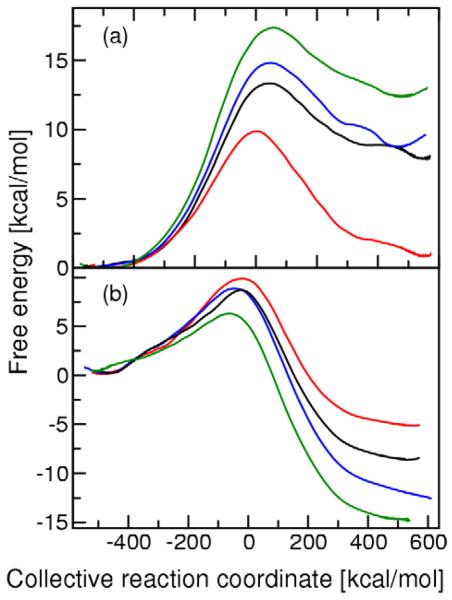
As described above, we generated 23 ns of MD data for the WT and the three mutant forms of KSI for both proton transfer steps. We used WHAM40-43 to generate the PMF curves for the two proton transfer reactions for the WT and mutant KSI enzymes. For comparison, we also used umbrella integration44-46 to generate the PMF curves and found the barrier height to be the same to within 0.5 kcal/mol for these two methods. The PMF curves for the two proton transfer steps of all three mutants are depicted in Figure 2. For each mutant we generated separate PMF curves for the two independent data sets to test convergence and reproducibility. These calculations suggest that the error in the PMF barrier due to numerical procedures is ~1.0 kcal/mol. The corresponding TST rate constants for the mutants are presented in Table 1. As mentioned above, the EVB parameters V12 and Δ were determined so that the TST rate constants for WT KSI reproduce the experimentally estimated forward and backward rate constants for each proton transfer step.38, 39
Figure 2.
Potential of mean force (PMF) curves for (a) the first proton transfer step and (b) the second proton transfer step catalyzed by KSI. These profiles are depicted for the WT (red), D99L mutant (black), Y14F mutant (blue), and Y14F/D99L double mutant (green) forms of KSI. For both steps, all curves are shifted so that the reactant is at zero energy, although mechanistically the product of the first step is the same as the reactant of the second step, following rotation of the Asp38 carboxylate group.
Table 1.
Rate constants for the two proton transfer reactions catalyzed by WT and mutant forms of KSI.
| Rate constantsa,b |
WT | D99L | Y14F | Y14F/D99L |
|---|---|---|---|---|
| k1 | 1.7 × 105 | 5.7 × 102 | 44 | 0.90 |
| k−1 | 5.6 × 105 | 6.8 × 108 | 1.5 × 108 | 8.1 × 108 |
| k2 | 2.1 × 105 | 8.6 × 105 | 1.1 × 106 | 2.8 × 107 |
| k−2 | 40 | 0.40 | 6.6 × 10−4 | 1.2 × 10−3 |
The EVB parameters used in all calculations for this table were V12 = 99.5 kcal/mol and Δ = 1.8 kcal/mol for the first step and V12 = 93.1 kcal/mol and Δ = −14.5 kcal/mol for the second step. These parameters were determining by fitting to the experimental rate constants for WT KSI given in Ref. 38, 39.
All rate constants were calculated with Eq. (4) and are given in s−1.
Figure 2 illustrates that the mutations increase the free energy of the Intermediate state relative to the Reactant and Product states. As a result, the free energy barrier increases for the first proton transfer step and decreases for the second proton transfer step upon mutation. This trend is quantified in Table 1, which indicates that the forward rate constant decreases for the first proton transfer step and increases for the second proton transfer step upon mutation. For WT KSI, the experimentally measured rate constants imply that the rate constants for the two proton transfer steps are similar.38, 39 In contrast, our calculations indicate that the rate constant of the first proton transfer step is significantly smaller than the rate constant of the second step for the mutant KSI enzymes because of the destabilized Intermediate state. The calculated forward rate constant for the first proton transfer step decreases by 102.5, 103.6, and 105.3 for the D99L, Y14F, and Y14F/D99L mutants, respectively, relative to the WT rate constant. This trend is qualitatively consistent with the experimental data showing that kcat is decreased by 102.1, 103.4, and 104.6 for the D99L, Y14F, and Y14F/D99L mutants of Pseudomonas putida KSI,3 and kcat is decreased by 103.7 and 104.7 for the D99A and Y14F mutants of Commamonas testosteroni KSI.2, 20 Note that kcat depends on other rate constants in the overall enzymatic reaction,38 so only the qualitative trends can be compared.
We also calculated kcat for the WT and mutant KSIs using the expression given in Ref. 38. Since this expression depends on the rate constant of product release, we assumed either that the rate constant for product release is the same in the mutants as in WT KSI or that the rate constant for product release is much larger than the forward rate constant of the first proton transfer step for the mutants. Using either assumption, the calculated kcat is decreased by 104.6, 105.0, and 106.0 for the D99L, Y14F, and Y14F/D99L mutants, respectively, relative to WT KSI. The qualitative trend in these calculated values of kcat is consistent with the experimental data. Note that the effects of the two mutations are only partially additive in the double mutant, suggesting the possibility of a cooperative interaction.70
B. Hydrogen bonding in the active site
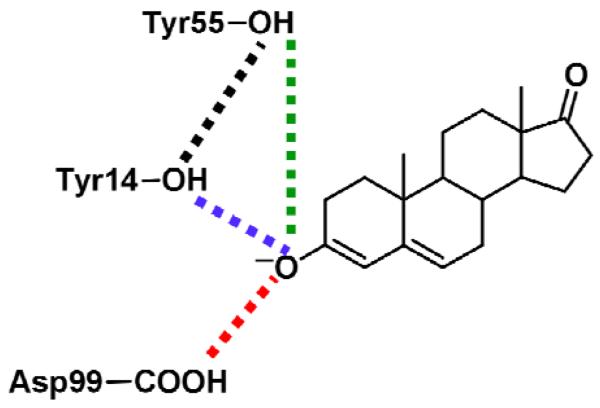
We examined the impact of the mutations on the catalytically important hydrogen bonds formed in the active site. As discussed above, hydrogen bonds formed by the substrate with Tyr14 and Asp99 play a crucial role in stabilizing the dienolate intermediate. In addition to examining these catalytically important hydrogen bonds, we also analyzed the hydrogen bonds formed by Tyr55 with Tyr14 and, in some cases, with the substrate. These hydrogen bonds are depicted schematically in Figure 3. Kinetic experiments indicate that the catalytic effects of mutating the Tyr55 residue are relatively minor,20 although the crystal structure of the Tyr55Phe mutant suggests that Tyr55 may play a role in positioning the Tyr14 residue.29 In order to investigate these hydrogen bonds during the proton transfer reactions, we calculated thermally averaged hydrogen bond donor-acceptor distances along the entire range of the collective reaction coordinate for both steps. For this purpose, the thermally averaged distances for the unbiased EVB potential were calculated from the MD trajectories propagated with mapping potentials using methodology related to the WHAM procedure, as described previously.19
Figure 3.
Schematic depiction of the hydrogen-bonding interactions analyzed in Figure 4.
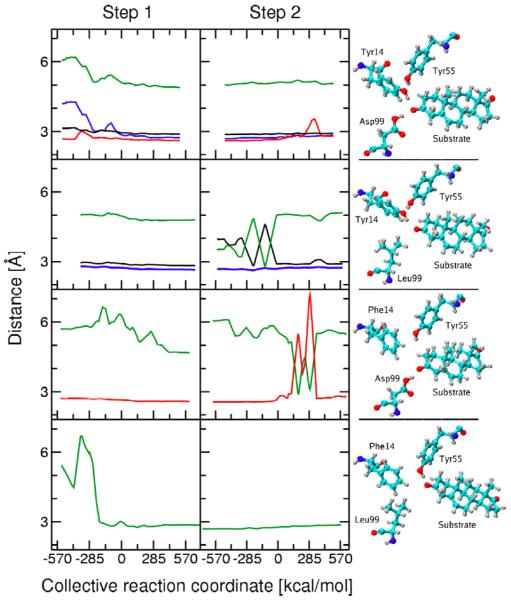
Figure 4 depicts the changes in these hydrogen bond distances during both proton transfer reactions for the WT and three mutant KSI enzymes. These figures were generated from the first data set. The analogous figures generated from the second independent data set are qualitatively similar and are provided in Supporting Information. Figure 4 also depicts snapshots from the MD trajectories corresponding to the Intermediate state, where the dienolate is stabilized by hydrogen-bonding interactions in the active site. These snapshots illustrate the hydrogen-bonding patterns for each mutant, as well as the structural rearrangements that occur within the active site upon mutation. We found that a single hydrogen-bonding pattern tends to dominate for each window (i.e., for a trajectory generated with a particular mapping potential), although in some cases we did observe changes in hydrogen bonding within a single window.
Figure 4.
Thermally averaged distances calculated along the collective reaction coordinate for the first (left) and second (right) proton transfer reactions catalyzed by KSI. Snapshots of the hydrogen-bonding pattern in the active site for the Intermediate state are also depicted. The results for the WT, D99L, Y14F, and Y14F/D99L mutants are given from top to bottom. The thermally averaged hydrogen bond donor-acceptor distances between the substrate O3 atom and Tyr14 (blue), between the substrate O3 atom and Asp99 (red), between the substrate O3 atom and Tyr55 (green), and between Tyr14 and Tyr55 (black) are shown. The distances are not shown for the mutated residue. The color coding is depicted in Figure 3.
In the D99L mutant, the mutation of aspartic acid to leucine eliminates one of the key hydrogen bonds to the substrate. Figure 4 indicates that hydrogen bonds between Tyr14 and both the substrate O3 and Tyr55 are present during the first proton transfer step, as observed in WT KSI. In contrast to WT KSI, where the hydrogen bond between the substrate and Tyr14 forms during the first part of this step, the hydrogen bond between the substrate and Tyr14 is present from the beginning of this step in the D99L mutant. For the second proton transfer step, the hydrogen bond between Tyr14 and the substrate is also maintained throughout the entire reaction. In this step, however, Tyr55 alternates between forming a hydrogen bond with either Tyr14 or the substrate O3 for the first part and forms a stable hydrogen bond with Tyr14 for the second part of the reaction.
In the Y14F mutant, the mutation of tyrosine to phenylalanine eliminates the other key hydrogen bond to the substrate. Figure 4 indicates the presence of a hydrogen bond between the substrate O3 and Asp99 throughout the first proton transfer step and most of the second proton transfer step. Near the end of the second step, this hydrogen bond disappears for short intervals during which the substrate forms a hydrogen bond with Tyr55 instead. In this regime, however, the product is partially dissociating, so the MD results become less reliable.
In the Y14F/D99L double mutant, both critical hydrogen bonds to the substrate are eliminated. In this case, Figure 4 illustrates the presence of a new hydrogen bond between Tyr55 and the substrate O3. This hydrogen bond is formed near the beginning of the first proton transfer step and is maintained throughout both proton transfer reactions, although the hydrogen bond distance gradually increases toward the end of the second step. Based on kinetic experiments indicating that this mutant is catalytically active,3 we conjecture that this hydrogen-bonding interaction partially compensates for the absence of hydrogen bonds formed by the substrate with Tyr14 and Asp99.
This analysis indicates that when the native hydrogen-bonding interactions are eliminated, structural rearrangements within the active site occur to stabilize the dienolate intermediate by forming new hydrogen-bonding interactions. An example of a new interaction is the hydrogen bond formed between the substrate and Tyr55 in the Y14F/D99L double mutant and sporadically in the D99L mutant. In the mutants, typically the substrate oxygen atom O3 is hydrogen bonded to only one residue, rather than to both Tyr14 and Asp99 as in WT KSI. As a result, the dienolate intermediate is stabilized enough for the mutants to be catalytically active but not enough to achieve rates as fast as WT KSI. These observations are consistent with the PMF curves depicted in Figure 2 and the rate constants given in Table 1.
C. Conformational changes and electrostatics
As in our previous simulations of WT KSI,19 we observed relatively small conformational changes within the active site that facilitate the proton transfer reactions. Specifically, the proton donor-acceptor distance decreases to ~2.67 Å near the transition state of each proton transfer reaction to enable the hydrogen to transfer. Here the proton donor and acceptor, respectively, are the substrate C4 carbon atom and the Asp38 oxygen atom for the first step and the Asp38 oxygen atom and the substrate C6 carbon atom for the second step. In addition, Asp38 exhibits a significant reorientation relative to the substrate between the first and second proton transfer steps to accommodate proton transfer to the C6 atom of the substrate after accepting a proton from the C4 atom of the substrate. These types of conformational changes are essential to the catalytic activity of the enzyme. They are not significantly affected by the mutation of Asp99 and Tyr14, however, and hence are similar for the WT and mutant KSI enzymes.
To investigate the overall structural changes in the protein occurring during the catalytic reaction, we generated thermally averaged structures for the reactant state, transition state, and product state of both proton transfer reactions. These structures were generated from MD trajectories obtained with mapping potentials corresponding to λ = 0.05, 0.50, and 0.95 for each proton transfer step. The thermally averaged structure for each mapping potential was generated by minimizing the RMSD over all configurations,71 followed by a weighting and averaging procedure that provides results for the unbiased EVB potential.19 Note that this process may lead to non-physical bond distances and angles in the side chains and therefore was used to analyze only the global changes in protein structure.
For each mutant, we calculated the average RMSD among the six thermally averaged structures spanning the two proton transfer reactions using the VMD program.72 The average RMSD values for the backbone atoms of the entire protein, the active site residues, and the mobile loop Tyr88-Lys92 are given in Table 2. Here the active site residues are defined to be those containing an atom within 5 Å of the substrate C4 atom or any atom in the Tyr14 or Asp99 residues. The RMSD values for the mutant and WT KSI enzymes are similar, with slightly lower values for WT KSI. The relatively low average RMSD values for the active site are consistent with experimental studies indicating that the active site exhibits highly restricted motion during the proton transfer reactions.7, 9, 73, 74 The larger average RMSD values for the loop Thr88-Lys92 indicate that this loop is more mobile than the active site. Several other mobile loops that were observed in previous simulations of WT KSI19 were also observed in the mutant forms of KSI.
Table 2.
Average RMSD values b among six thermally averaged structuresc along the reaction pathway for WT and mutant forms of KSI.
| Region | WT | D99L | Y14F | Y14F/D99L |
|---|---|---|---|---|
| Entire enzyme | 0.54 | 0.65 | 0.68 | 0.55 |
| Active sitea | 0.26 | 0.33 | 0.30 | 0.27 |
| Tyr88 to Lys92 | 1.12 | 1.74 | 1.62 | 1.08 |
The active site region consisted of all residues containing an atom within 5Å of the substrate C4 atom or any atom of Tyr14 or Asp99.
All RMSD values were calculated for backbone atoms using the VMD program and are given in Å.
The six thermally averaged structures are the reactant, transition state, and product for both proton transfer steps.
Table 3 provides the average van der Waals and electrostatic interaction energies between the substrate ligand and the enzyme for the WT and mutant KSI enzymes over the course of the two proton transfer reactions. These interaction energies were averaged over configurations sampled with 600 ps of MD for the Reactant, Intermediate, and Product, generated using mapping potentials with λ = 0.05 and 0.95 for the first proton transfer step and λ = 0.95 for the second proton transfer step. The virtually constant van der Waals interaction energies imply that no major structural rearrangements occur in the active site during proton transfer. The stronger electrostatic interaction energy for the Intermediate than for the Reactant and Product arises in part from the transfer of the positively charged proton to Asp38 and the resulting redistribution of electronic charge in the substrate. As shown by previous calculations of the hydrogen-bonding interaction energies for WT KSI,19 this enhanced electrostatic interaction energy is also due to the strengthening of the hydrogen bonds between the substrate oxygen and active site residues (i.e., Asp99, Tyr14, or Tyr55) for the dienolate intermediate. Note that the electrostatic interaction energies are slightly weaker for the mutants than for WT KSI. This difference is consistent with the observation that the mutants exhibit only one hydrogen-bonding interaction, while the WT KSI exhibits two hydrogen-bonding interactions, between the substrate and the active site. Moreover, the electrostatic stabilization of the Intermediate relative to the Reactant is 71 kcal/mol for WT KSI and 60-64 kcal/mol for the mutant forms of KSI. This difference in relative electrostatic interaction energies contributes to the higher free energy of the Intermediate relative to the Reactant in the mutant forms, as depicted in Figure 2.
Table 3.
Electrostatic and van der Waals interaction energiesa between the substrate and KSI for different states along the reaction pathway.
| KSI | Electrostatic | van der Waals | ||||
|---|---|---|---|---|---|---|
| Reactant | Intermediate | Product | Reactant | Intermediate | Product | |
| WT | −30 | −101 | −27 | −26 | −24 | −26 |
| D99L | −24 | −84 | −23 | −26 | −25 | −25 |
| Y14F | −27 | −91 | −23 | −26 | −25 | −27 |
| Y14F/D99L | −19 | −83 | −21 | −26 | −24 | −25 |
Interaction energies given in kcal/mol.
IV. Conclusions
In this study, we performed MD simulations of the two proton transfer reactions catalyzed by the D99L, Y14F, and Y14F/D99L mutant forms of KSI. The free energy profiles along a collective reaction coordinate illustrate that the mutations destabilize the dienolate intermediate relative to the reactant and product, thereby increasing the free energy barrier for the first proton transfer step and decreasing the free energy barrier for the second proton transfer step. While the rate constants for the two proton transfer steps are similar in WT KSI, our simulations suggest that the rate constant of the first proton transfer step is smaller than the rate constant of the second step in all three mutant forms of KSI. The calculated catalytic rate constant was found to decrease along the following series of KSI enzymes: WT, D99L, Y14F, and Y14F/D99L. This trend in the calculated rate constants is qualitatively consistent with kinetic experiments on these mutants. Analysis of the hydrogen-bonding patterns, conformational changes, and van der Waals and electrostatic interactions during the proton transfer reactions provides insight into the physical basis for these trends in the rate constants.
Our simulations illustrated that the mutants typically retain one hydrogen-bonding interaction between the substrate oxygen atom O3 and the active site, while the WT KSI retains two hydrogen-bonding interactions. We observed a new hydrogen bonding interaction between the substrate and Tyr55 in the double mutant and occasionally in the D99L single mutant. Moreover, the electrostatic interaction energy between the substrate and the enzyme for the Intermediate relative to the Reactant is ~8 kcal/mol greater for WT KSI than for the mutant forms of KSI. These observations provide a qualitative explanation for the experimental measurements showing that the mutant KSI enzymes are still catalytically active but exhibit lower catalytic rates. The calculations also predict that a hydrogen bond between Tyr55 and an intermediate analog such as equilenin would be observed in the crystal structure of the double mutant and that mutation of Tyr55 to Phe would have a greater impact on the proton transfer rates for the double mutant than for WT KSI.
In addition, the simulations illustrated that the van der Waals interactions between the substrate and the enzyme remain relatively constant during the two proton transfer reactions and that the RMSD of the active site among thermally averaged structures spanning both reactions is only ~0.3 Å. These observations suggest that the active site exhibits highly restricted motion during the proton transfer reactions, as also indicated by experimental studies.7, 9, 73, 74 Nevertheless, as shown previously for WT KSI,19 changes in the proton donor-acceptor distances and the angles between the substrate and Asp38, which serves as the proton acceptor and donor, must accompany the proton transfer reactions.
The high catalytic efficiency of KSI has been postulated to arise predominantly from a preorganized active site,18, 75-77 and previous simulations illustrated a significant reduction of the reorganization energy in KSI.14, 15 Our simulations indicate that the active site exhibits highly restricted motion during the two proton transfer reactions for WT and the mutant forms of KSI. The calculations also illustrate that mutation of the catalytically important Asp99 and Tyr14 residues leads to structural rearrangements within the active site to retain hydrogen-bonding interactions between the substrate and the enzyme. Thus, these calculations are consistent with the postulate that KSI forms a preorganized active site for both the WT and mutant forms of KSI, but the structure of this preorganized active site is altered upon mutation. Moreover, this preorganized active site still allows for relatively small conformational changes that facilitate the proton transfer reactions by strengthening the hydrogen bonds between the substrate and active site residues, as well as by bringing the proton donor and acceptor closer to each other with the proper orientation for proton transfer.19 Such conformational changes are due to stochastic thermal motions of the protein and substrate as they sample the multidimensional free energy landscape.78 Thus, both the concepts of a preorganized active site and conformational sampling are important for this enzyme reaction.
Supplementary Material
Acknowledgments
We thank Alexander Soudackov and Dan Herschlag for helpful discussions. This work was funded by NIH Grant No. GM56207.
Footnotes
Supporting Information Available: Table 1 and Figures 2 and 3 generated with the second independent data set; snapshot structures for the Reactant, Intermediate, and Product of the overall reaction for the three mutants. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Zhao Q, Abeygunawardana C, Talalay P, Mildvan AS. Proc. Nat. Acad. Sci. USA. 1996;93:8220–8224. doi: 10.1073/pnas.93.16.8220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu ZR, Ebrahimian S, Zawrotny ME, Thornburg LD, Perez-Alvarado GC, Brothers P, Pollack RM, Summers MF. Science. 1997;276:415–418. doi: 10.1126/science.276.5311.415. [DOI] [PubMed] [Google Scholar]
- 3.Choi G, Ha N-C, Kim SW, Kim D-H, Park S, Oh B-H, Choi KY. Biochemistry. 2000;39:903–909. doi: 10.1021/bi991579k. [DOI] [PubMed] [Google Scholar]
- 4.Kraut DA, Sigala PA, Pybus B, Liu CW, Ringe D, Petsko GA, Herschlag D. PLoS Biology. 2006;4:501–519. doi: 10.1371/journal.pbio.0040099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mildvan AS, Massiah MA, Harris TK, Marks GT, Harrison DHT, Viragh C, Reddy PM, Kovach IM. J. Mol. Struct. 2002;615:163–175. [Google Scholar]
- 6.Sigala PA, Fafarman AT, Bogard PE, Boxer SG, Herschlag D. J. Am. Chem. Soc. 2007;129:12104–12105. doi: 10.1021/ja075605a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sigala PA, Kraut DA, Caaveiro JMM, Pybus B, Ruben EA, Ringe D, Petsko GA, Herschlag D. J. Am. Chem. Soc. 2008;130:13696–13708. doi: 10.1021/ja803928m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kraut DA, Churchill MJ, Dawson PE, Herschlag D. ACS Chemical Biology. 2009;4:269–273. doi: 10.1021/cb900016q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sigala PA, Caaveiro JMM, Ringe D, Petsko GA, Herschlag D. Biochemistry. 2009;48:6932–6939. doi: 10.1021/bi900713j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Oh KS, Cha S-S, Kim D-H, Cho H-S, Ha N-C, Choi G, Lee JY, Tarakeshwar P, Son HS, Choi KY, Oh B-H, Kim KS. Biochemistry. 2000;39:13891–13896. doi: 10.1021/bi001629h. [DOI] [PubMed] [Google Scholar]
- 11.Kim KS, Oh KS, Lee JY. Proc. Nat. Acad. Sc. USA. 2000;97:6373–6378. doi: 10.1073/pnas.97.12.6373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pan Y, McAllister MA. Journal of Molecular Structure (Theochem) 2000;504:29–33. [Google Scholar]
- 13.Park H, Merz KM., Jr. J. Am. Chem. Soc. 2003;125:901–911. doi: 10.1021/ja0208097. [DOI] [PubMed] [Google Scholar]
- 14.Feierberg I, Aqvist J. Biochemistry. 2002;41:15728–15735. doi: 10.1021/bi026873i. [DOI] [PubMed] [Google Scholar]
- 15.Feierberg I, Aqvist J. Theoretical Chemical Accounts. 2002;108:71–84. [Google Scholar]
- 16.Mazumder D, Kahn K, Bruice TC. J. Am. Chem. Soc. 2003;125:7553–7561. doi: 10.1021/ja030138s. [DOI] [PubMed] [Google Scholar]
- 17.Warshel A, Sharma PK, Chu ZT, Aqvist J. Biochemistry. 2007;46:1466–1476. doi: 10.1021/bi061752u. [DOI] [PubMed] [Google Scholar]
- 18.Kamerlin SCL, Sharma PK, Chu ZT, Warshel A. Proceedings of the National Academy of Sciences (USA) 2010;107:4075–4080. doi: 10.1073/pnas.0914579107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chakravorty DK, Soudackov AV, Hammes-Schiffer S. Biochemistry. 2009;48:10608–10619. doi: 10.1021/bi901353v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuliopulos A, Mildvan AS, Shortle D, Talalay P. Biochemistry. 1989;28:149–159. doi: 10.1021/bi00427a022. [DOI] [PubMed] [Google Scholar]
- 21.Xue L, Talalay P, Mildvan AS. Biochemistry. 1991;30:10858–10865. doi: 10.1021/bi00109a008. [DOI] [PubMed] [Google Scholar]
- 22.Austin JC, Spiro TG, Kuliopulos A, Mildvan AS. Protein Science. 1992;1:259–270. doi: 10.1002/pro.5560010208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brothers PN, Blotny G, Qi L, Pollack RM. Biochemistry. 1995;34:15453–15458. doi: 10.1021/bi00047a009. [DOI] [PubMed] [Google Scholar]
- 24.Kim SW, Choi KY. J. Bacteriol. 1995;177:2602–2605. doi: 10.1128/jb.177.9.2602-2605.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhao Q, Abeygunawardana C, Gittis AG, Mildvan AS. Biochemistry. 1997;36:14616–14626. doi: 10.1021/bi971549m. [DOI] [PubMed] [Google Scholar]
- 26.Qi L, Pollack RM. Biochemistry. 1998;37:6760–6766. doi: 10.1021/bi972745w. [DOI] [PubMed] [Google Scholar]
- 27.Thornburg LD, Henot F, Bash DP, Hawkinson DC, Bartel SD, Pollack RM. Biochemistry. 1998;37:10499–10506. doi: 10.1021/bi980099a. [DOI] [PubMed] [Google Scholar]
- 28.Pollack RM, Thornburg LD, Wu ZR, Summers MF. Arch. Biochem. Biophys. 1999;370:9–15. doi: 10.1006/abbi.1999.1384. [DOI] [PubMed] [Google Scholar]
- 29.Kim D-H, Jang DS, Nam GH, Choi G, Kim J-S, Ha N-C, Kim M-S, Oh B-H, Choi KY. Biochemistry. 2000;39:4581–4589. doi: 10.1021/bi992119u. [DOI] [PubMed] [Google Scholar]
- 30.Thornburg LD, Goldfeder YR, Wilde TC, Pollack RM. J. Am. Chem. Soc. 2001;123:9912–9913. doi: 10.1021/ja016683f. [DOI] [PubMed] [Google Scholar]
- 31.Choi G, Ha N-C, Kim M-S, Hong B-H, Oh B-H, Choi KY. Biochemistry. 2001;40:6828–6835. doi: 10.1021/bi002767+. [DOI] [PubMed] [Google Scholar]
- 32.Houck WJ, Pollack RM. J. Am. Chem. Soc. 2004;126:16416–16425. doi: 10.1021/ja046819k. [DOI] [PubMed] [Google Scholar]
- 33.Jang DS, Cha HJ, Cha S-S, Hong BH, Ha N-C, Lee JY, Oh B-H, Lee H-S, Choi KY. Biochem. J. 2004;382:967–973. doi: 10.1042/BJ20031871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kraut DA, Sigala PA, Fenn TD, Herschlag D. Proceedings of the National Academy of Sciences (USA) 2010;107:1960–1965. doi: 10.1073/pnas.0911168107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. John Wiley & Sons, Inc.; New York: 1991. [Google Scholar]
- 36.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr., Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. Journal of the American Chemical Society. 1995;117:5179–5197. [Google Scholar]
- 37.Wang J, Cieplak P, Kollman PA. Journal of Computational Chemistry. 2000;21:1049–1074. [Google Scholar]
- 38.Hawkinson DC, Eames TCM, Pollack RM. Biochemistry. 1991;30:10849–10858. doi: 10.1021/bi00109a007. [DOI] [PubMed] [Google Scholar]
- 39.Hawkinson DC, Pollack RM, Ambulos NP., Jr. Biochemistry. 1994;33:12172–12183. doi: 10.1021/bi00206a021. [DOI] [PubMed] [Google Scholar]
- 40.Ferrenberg AM, Swendsen RH. Phys. Rev. Lett. 1988;61:2635–2638. doi: 10.1103/PhysRevLett.61.2635. [DOI] [PubMed] [Google Scholar]
- 41.Ferrenberg AM, Swendsen RH. Phys. Rev. Lett. 1989;63:1195–1198. doi: 10.1103/PhysRevLett.63.1195. [DOI] [PubMed] [Google Scholar]
- 42.Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 43.Roux B. Comput. Phys. Commun. 1995;91:275–282. [Google Scholar]
- 44.Kastner J, Thiel W. J. Chem. Phys. 2005;123:144104. doi: 10.1063/1.2052648. [DOI] [PubMed] [Google Scholar]
- 45.Kastner J, Thiel W. J. Chem. Phys. 2006;124:234106. doi: 10.1063/1.2206775. [DOI] [PubMed] [Google Scholar]
- 46.Chakravorty DK, Kumarasiri M, Soudackov AV, Hammes-Schiffer S. Journal of Chemical Theory and Computation. 2008;4:1974–1980. doi: 10.1021/ct8003386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Watney JB, Soudackov AV, Wong KF, Hammes-Schiffer S. Chem. Phys. Lett. 2006;418:268–271. [Google Scholar]
- 48.Carter EA, Ciccotti G, Hynes JT, Kapral R. Chem. Phys. Lett. 1989;156:472–477. [Google Scholar]
- 49.Schenter GK, Garrett BC, Truhlar DG. J. Chem. Phys. 2003;119:5828–5833. [Google Scholar]
- 50.Neria E, Karplus M. J. Chem. Phys. 1996;105:10812–10818. [Google Scholar]
- 51.Bennett CH. Algorithms for Chemical Computation. American Chemical Society; Washington, DC: 1997. [Google Scholar]
- 52.Keck JC. J. Chem. Phys. 1960;32:1035–50. [Google Scholar]
- 53.Anderson JB. J. Chem. Phys. 1973;58:4684–92. [Google Scholar]
- 54.Chandler D. A story of rare events: From barriers, to electrons, to unknown pathways. In: Berne BJ, Ciccotti G, Coker DF, editors. Classical and Quantum Dynamics in Condensed Phase Simulations. World Scientific; Singapore: 1998. pp. 3–23. [Google Scholar]
- 55.Hwang J-K, Chu ZT, Yadav A, Warshel A. J. Phys. Chem. 1991;95:8445–8448. [Google Scholar]
- 56.Hwang J-K, Warshel A. J. Phys. Chem. 1993;97:10053–10058. [Google Scholar]
- 57.Hwang J-K, Warshel A. J. Am. Chem. Soc. 1996;118:11745–11751. [Google Scholar]
- 58.Wang Q, Hammes-Schiffer S. J. Chem. Phys. 2006;125:184102. doi: 10.1063/1.2362823. [DOI] [PubMed] [Google Scholar]
- 59.Cho H-S, Ha N-C, Choi G, Kim H-J, Lee D, Oh KS, Kim KS, Lee W, Choi KY, Oh B-H. J. Biol. Chem. 1999;274:32863–32868. doi: 10.1074/jbc.274.46.32863. [DOI] [PubMed] [Google Scholar]
- 60.Massiah MA, Abeygunawardana C, Gittis AG, Mildvan AS. Biochemistry. 1998;37:14701–14712. doi: 10.1021/bi981447b. [DOI] [PubMed] [Google Scholar]
- 61.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Journal of Chemical Physics. 1983;79:926–935. [Google Scholar]
- 62.Mahoney MW, Jorgensen WL. Journal of Chemical Physics. 2000;112:8910–8922. [Google Scholar]
- 63.Xiang Z, Honig B. J. Mol. Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
- 64.Xiang JZ, Honig B. JACKAL: A Protein Structure Modeling Package. Columbia University & Howard Hughes Medical Institute; New York: 2002. [Google Scholar]
- 65.Melchionna S, Cozzini S. DLPROTEIN Version 2.1 Molecular Dynamics Software Package for Macromolecules. INFM Udr SISSA, Trieste; Italy: 2001. [Google Scholar]
- 66.Ryckaert JP, Ciccotti G, Berendsen HJC. J. Comput. Phys. 1977;23:327. [Google Scholar]
- 67.Darden T, York D, Pedersen L. Journal of Chemical Physics. 1993;98:10089–10092. [Google Scholar]
- 68.Nose S. Molecular Physics. 1984;52:255–68. [Google Scholar]
- 69.Hoover WG. Physical Review A. 1985;31:1695–7. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 70.Mildvan AS, Weber DJ, Kuliopulos A. Arch. Biochem. Biophys. 1992;294:327–40. doi: 10.1016/0003-9861(92)90692-p. [DOI] [PubMed] [Google Scholar]
- 71.van der Spoel D, Lindahl E, Hess B, van Buuren AR, Apol E, Meulenhoff PJ, Tieleman DP, Sijbers ALTM, Feenstra KA, van Drunen R, Berendsen HJC. GROMACS. 2004;3.2 [Google Scholar]
- 72.Humphrey W, Dalke A, Schulten K. Journal of Molecular Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 73.Zhao Q, Li Y-K, Mildvan AS, Talalay P. Biochemistry. 1995;34:6562–6572. doi: 10.1021/bi00019a038. [DOI] [PubMed] [Google Scholar]
- 74.Zhao Q, Abeygunawardana C, Mildvan AS. Biochemistry. 1996;35:1525–1532. doi: 10.1021/bi9525381. [DOI] [PubMed] [Google Scholar]
- 75.Rajagopalan PTR, Benkovic SJ. The Chemical Record. 2002;2:24–36. doi: 10.1002/tcr.10009. [DOI] [PubMed] [Google Scholar]
- 76.Wolfenden R. Acc. Chem. Res. 1972;5:10–18. [Google Scholar]
- 77.Jencks WP. Catalysis in Chemistry and Enzymology. 2nd ed. Dover; New York: 1987. [Google Scholar]
- 78.Benkovic SJ, Hammes GG, Hammes-Schiffer S. Biochemistry. 2008;47:3317–3321. doi: 10.1021/bi800049z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.