Genetic dissection and prognostic modeling of overt stroke in sickle cell anemia

Abstract

Sickle cell anemia (SCA) is a paradigmatic single gene disorder caused by homozygosity with respect to a unique mutation at the β-globin locus. SCA is phenotypically complex, with different clinical courses ranging from early childhood mortality to a virtually unrecognized condition. Overt stroke is a severe complication affecting 6–8% of individuals with SCA. Modifier genes might interact to determine the susceptibility to stroke, but such genes have not yet been identified. Using Bayesian networks, we analyzed 108 SNPs in 39 candidate genes in 1,398 individuals with SCA. We found that 31 SNPs in 12 genes interact with fetal hemoglobin to modulate the risk of stroke. This network of interactions includes three genes in the TGF-β pathway and SELP, which is associated with stroke in the general population. We validated this model in a different population by predicting the occurrence of stroke in 114 individuals with 98.2% accuracy.

Stroke is a severe vascular complication of SCA, more frequent in affected individuals under the age of 20. Although recovery may be complete, stroke can cause permanent brain damage and even death. Trans-cranial Doppler flow studies can predict the likelihood of stroke in children with SCA, but only 10% of individuals with abnormal trans-cranial Doppler values will have stroke in the year after the study, and stroke will occur in ~19% individuals with normal trans-cranial Doppler values¹. More accurate prognostic methods would therefore help to target prophylactic treatments, such as transfusion² or hydroxyurea, to individuals at highest risk^3,4.

In individuals with SCA, the products of modifier genes may interact to determine the likelihood of stroke and other complications. SNPs in VCAM1 (ref. ⁵), IL4R and ADRB2 (ref. ⁶) are significantly associated with stroke in SCA subjects. Furthermore, the risk of stroke is reduced in individuals with α-thalassemia⁷, and increased fetal hemoglobin (HbF) levels are associated with reduced risks for other complications⁸. To identify the genetic basis of stroke in individuals with SCA, we selected 80 candidate genes involved in vasoregulation, inflammation, cell adhesion, coagulation, hemostasis, cell proliferation, oxidative biology and other functions. We analyzed 108 SNPs in these genes in 1,398 African Americans with SCA, 92 subjects with reported overt stroke and 1,306 subjects without, enrolled in the Cooperative Study of Sickle Cell Disease (CSSCD)⁹. Extensive clinical information was available for each of these individuals (Supplementary Table 1 online).

Genetic dissection of a complex trait requires disentangling the web of interactions among genes, environment and phenotype^10–12. To model these relationships, we carried out a multivariate analysis using Bayesian networks, multivariate dependency models that account for simultaneous associations and interactions among multiple genes and their interplay with clinical and physiological factors. Bayesian networks have been already applied to the analysis of several types of genomic data (gene expression¹³, protein-protein interactions¹⁴ and pedigree analysis¹⁵), and their modular nature makes them ideal for analyzing large association studies. Furthermore, Bayesian networks can be used for prognosis: a network capturing the relationship between genotypes and phenotype can be used to compute the probability that a new individual with particular genotype will have the phenotype of interest^15,16.

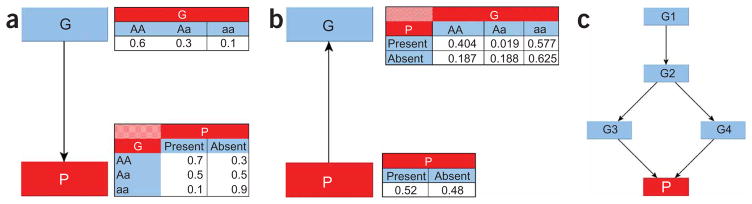
A Bayesian network is a directed acyclic graph in which nodes represent random variables and arcs define directed stochastic dependencies quantified by probability distributions. Figure 1 depicts three Bayesian networks, starting with a simple network describing the dependency of a phenotypic character P on a single SNP G (Fig. 1a). The graph decomposes the joint probability distribution of the two variables into the product of the marginal distribution of G (the parent node) and the conditional distribution of P (the child node) given G. The marginal and conditional probability distributions are sufficient to define the association between P and G because their product determines the joint probability distribution. This property persists when we invert the direction of the arc in the graph (Fig. 1b) and when we expand the graphical structure to include several variables (Fig. 1c): the overall association is measured by the joint probability distribution that is still defined by the product of each child-parent conditional distribution. This modular nature of a Bayesian network is due to the conditional independences among the variables encoded by the directed acyclic graph¹⁶: the graph specifies the set of parents of each node as those having an arc pointing directly to it, and each node becomes independent of its predecessors given the parent nodes. This modular representation captures complex dependency models (able to integrate associations between SNPs and phenotype; associations between SNPs due to linkage disequilibrium or evolutionary patterns¹⁷; and interaction processes linking SNPs, phenotype and modulating factors¹⁸) with a small number of parameters. Reducing the number of parameters allows us to ‘learn’ large dependency networks from comparatively small data sets, and well-established techniques exist to develop Bayesian networks from data in an almost automated manner¹⁶.

Figure 1.

Examples of Bayesian network structures. (a) A simple Bayesian network with two nodes representing a SNP (G) and a phenotype (P). The probability distribution of G represents the genotype distribution in the population, and the conditional probability distribution of P describes the distribution of the phenotype given each genotype. (b) The association between G and P can be reversed using Bayes theorem. (c) A Bayesian network linking four SNPs (G1–G4) to a phenotype P. The phenotype is independent of the other SNPs, once we know the SNPs G3 and G4. The joint probability distribution of the network is fully specified by the five distributions representing the distribution of G1 (two parameters), of G2 given G1 (six parameters), of G3 given G2 (six parameters), of G4 given G2 (six parameters) and of P given G3 and G4 (nine parameters). The full probability distribution requires 81 × 2 − 1 = 161 parameters; this network requires only 29.

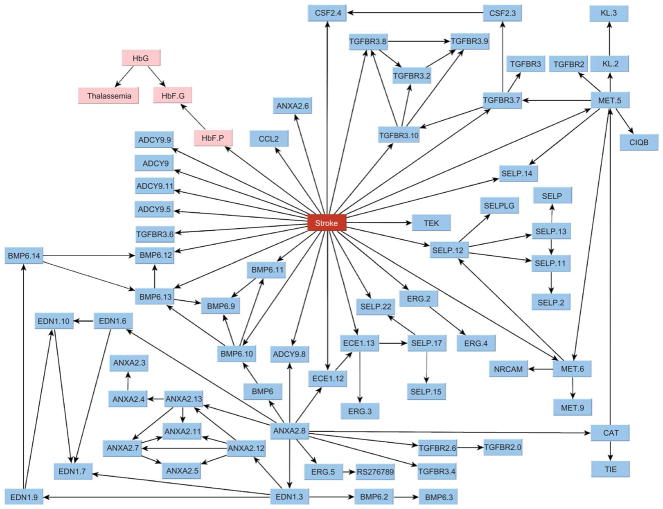
We focused on those networks that describe the dependencies of genotypes on phenotype, because analysis conditional on phenotype reduces the complexity of the search¹⁸ and can identify larger sets of associations between SNPs and phenotype. This modeling strategy describing the diagnostic rather than prognostic associations is commonly used in data mining to build predictive models in large data sets¹⁹. Figure 2 shows the overall dependency network that we identified, linking 69 SNPs in 20 genes, HbF levels, total hemoglobin concentration and coincidence of α-thalassemia to stroke. Thirty one SNPs in 12 genes interact with HbF to modulate the risk of stroke. Of these, 25 SNPs in 11 genes are directly associated with the phenotype, meaning that they have the largest independent effect on the prediction of risk of stroke. The strength of the dependency of each of these nodes is summarized by the odds of the model with the dependency versus the model without the dependency (Table 1). The conditional probability tables quantifying the network are estimated from the data (Supplementary Table 2 online).

Figure 2.

The Bayesian network describing the joint association of 69 SNPs with stroke. Nodes represent SNPs or clinical factors; the numbers after each gene distinguish different SNPs on the same gene. SNP are shown as blue nodes; their rs numbers are given in Supplementary Table 4 online. Clinical variables (HbF.G, fetal hemoglobin (g dL⁻¹); HbF.P, fetal hemoglobin (%); HbG, total hemoglobin concentration; Thalassemia, heterozygosity or homozygosity with respect to a 3.7-kb α-thalassemia deletion) are shown as pink nodes. Twenty-five SNPs in ADCY9, ANXA2, BMP6, CCL2, CSF2, ECE1, ERG, MET, SELP, TEK and TGFBR3 are directly associated with the phenotype and have the largest independent effect on the risk of stroke. Note the association of stroke with several SNPs in ADCY9, BMP6, MET, SELP and TGFBR3, which usually reduces the possibility of false positives¹⁸.

Table 1.

Summary information for the genes and the clinical variable HbF directly associated with stroke

Gene	Position	SNP	Bayes factora	Single geneb
				Accuracy (%)	Contribution (%)
ADCY9	16p13.3	rs437115	3	71.93	2
		rs2238432	98
		rs2238426	3,381
		rs2072338	638
		rs2283497	10
ANXA2	15q22.2	hCV26910500	1.68 × 108	43.86	2
BMP6	6p24.3	rs267196	2.31 × 1016	83.33	5
		rs267201	1.92 × 10103
		rs408505	4.06 × 10101
		rs449853	2.20 × 1057
CCL2	17q11.2	rs4586	844	55.14	1
CSF2	5q23.3	rs25882	1.19 × 10198	50.88	1
ECE1	1p36.12	rs212528	1.55 × 104	13.15	0.20
		rs212531	2.34 × 1080
ERG	21q22.2	rs989554	62	42.98	1
MET	7q31.2	rs38850	68	23.68	1
		rs38859	1.58 × 1039
SELP	1q24.2	rs2420378	1.90 × 1010	80.70	7
		rs3917733	2.84 × 1034
		rs3753306	2.32 × 1065
TEK	9p21.2	rs489347	2	8	1
TGFBR3	1p22.1	rs284875	443,992	50.88	2
		rs2148322	68,988
		rs2765888	41,968
		rs2007686	1,739
HbF (%)			482	72.81	1

^aBayes factor of the model associating the SNP to stroke versus the model of independence.

^bThe accuracy of a single gene is the proportion of individuals whose phenotype is correctly predicted using only the SNPs in this gene. Single gene contribution is the loss of predictive accuracy when all SNPs of this gene are removed. Both single gene accuracy and contribution were measured on the independent test set of 114 individuals.

The network dissects the genetic basis of stroke into 11 genes whose variants have a direct effect on the disease that is modulated by HbF levels and 9 genes whose variants are indirectly associated with stroke. An example is the cluster of five SNPs in EDN1 that is associated with SNPs in ANXA2 and BMP6. Both EDN1 and BMP6 are on chromosome 6 (at 6p24.1 and 6p24.3, respectively), and their association suggests that this chromosomal region may be associated with an increased risk of stroke. ANXA2 has a regulatory role in cell surface plasmin generation²⁰; EDN1 might be a potent vasoconstrictor and mitogen secreted in response to hypoxia²¹, supporting the hypothesis that EDN1 antagonists may be useful in the prevention and treatment of sickle vaso-occlusive crises. Our model suggests that variants in BMP6 are the strongest risk factors, whereas variants in EDN1 are associated with stroke through BMP6 and ANXA2 but are not as relevant for risk prediction. Stroke is also directly associated with variants in TGFBR3 and indirectly associated with variants in TGFBR2, which have essential, nonredundant roles in TGF-β signaling²². BMP6 is part of the TGF-β superfamily, and the simultaneous association of three genes with functional roles in TGF-β signaling suggests that this pathway might be involved with increased risk of stroke. This conjecture is further supported by the association of stroke with CSF2, a protein necessary for the survival, proliferation and differentiation of leukocyte progenitors. Variants in SELP are associated with stroke in the general population²³; our analysis confirms its important, though insufficient, prognostic role.

By decomposing the overall distribution into interrelated modules, the network summarizes all relevant dependencies without losing the multigenic nature of stroke. Using the network in Figure 2, we can compute the probability distribution of the phenotype (stroke) given the genotype of any SNP and, conversely, compute the conditional distribution of any genotype given values of other variables in the network. In this way, the model is able to describe the determinant effects of genetic variants on stroke, to predict the odds for stroke of new individuals given their genotypes and to find the most probable combination of genetic variants leading to stroke.

Table 2 reports the risk of stroke predicted by the network in Figure 2 for some genotypes and shows the impossibility of predicting this risk using individual SNPs. For example, homozygosity (TT) with respect to BMP6.10 is, by itself, associated with both negligible and very large risk, and only the simultaneous consideration of other SNPs can determine the actual risk of stroke. This situation is confirmed by the analysis of single-gene accuracy and contribution (Table 1), highlighting the small effect of individual genes. On the other hand, the 98.5% predictive accuracy reached by the model in fivefold cross-validation shows the determinant role of the simultaneous presence of all SNPs and their interplay with clinical variables for the correct prediction of stroke susceptibility.

Table 2.

Stroke prediction

Risk	ANXA2.6	BMP6.10	BMP6.12	SELP.14	TGFBR3.10	ERG.2	n
0.007 (0–0.03)	AG	TT	TT	CT	CT	AG	1
0.06 (0–0.38)	AG	TT	TT	CT	CC	AG	4
0.185 (0.09–0.30)	AA	TT	CT	CC	CC	AA	50
0.727 (0.61–0.83)	AA	TT	CC	CC	CC	AA	64
0.868 (0.70–0.97)	GG	TT	CC	CC	CC	AA	21
0.968 (0.79–1)	GG	TT	CC	CT	CC	AA	8

Risk of stroke in 5 years and 95% credible intervals (in parentheses), given particular genotypes of the SNPs in some genes directly associated to stroke in the network in Figure 2. We used an exact probabilistic algorithm¹⁵ to compute the odds for stroke predicted by the network in Figure 2, given the genotypes in the table. The last column (n) reports the frequency of individuals of each genotype.

We validated our results in a different population by predicting the occurrence of stroke in 114 individuals not included in the original study: 7 with reported stroke and 107 without, a proportion consistent with the phenotype distribution in the original cohort study. Our model predicted the correct outcome for all 7 individuals with stroke and for 105 of 107 individuals without stroke, with a 100% true positive rate and a 98.14% true negative rate, for an overall predictive accuracy of 98.2%. Figure 3 shows the difference between the predictive probabilities of stroke, which show that the predictions were not only correct but also inferred with high confidence. The individuals with stroke were not part of the original cohort study. The 107 individuals without stroke were part of the original study but were not used to build the Bayesian network. For these subjects, the follow-up period was 5.2 ± 2 years (mean ± s.d.), and their age at the beginning of the study was 22 ± 2.6 years (mean ± s.d.; Supplementary Table 1). Because the risk of stroke in individuals with SCA decreases rapidly after the age of 10 years (ref. ²⁴), these individuals without stroke provide a reliable test set.

Figure 3.

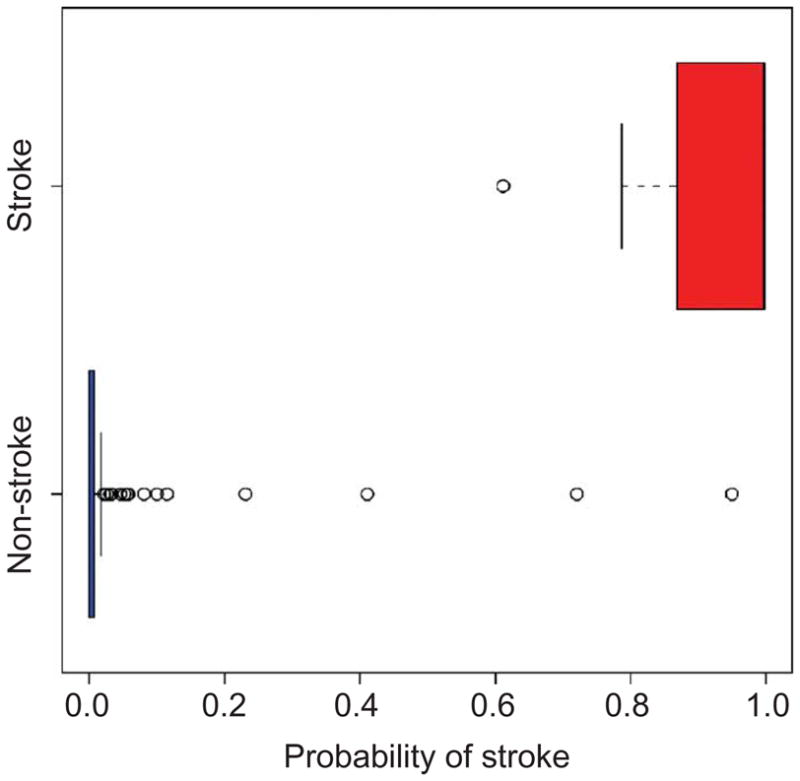
Box plot of the predictive probability of stroke (risk in 5 years) in an independent set of 7 individuals with stroke and 107 individuals without stroke. The plot shows a split of the predictive probabilities between these two outcomes: the predictive probabilities of stroke in the 7 individuals with stroke are >0.6, whereas the predictive probabilities of stroke in the 107 individuals without stroke are close to 0 (for only 2 individuals is the probability >0.5). The predictive probabilities are given in Supplementary Table 5 online.

For comparison, we also built a logistic regression model using stepwise regression. The model captured as significant only 5 SNPs (in SELP and BMP6) of the 25 identified by the Bayesian network model, and HbF (Supplementary Table 3 online), with a consequent decrease of predictive accuracy (Supplementary Fig. 1 online). Predictive validation of this regression model on the same independent set produced ten errors in the individuals without stroke (a false positive rate of 0.09) and three errors in the individuals with stroke (a false negative rate of 0.43), with an overall accuracy of 88%.

Another feature highlighted by the network is that although SNPs on the same gene tend to neatly cluster together, some dependencies extend across different genes and, sometimes, across chromosomes. These patterns support the emerging view¹⁷ that physical distance between two polymorphisms is not the only arbiter of their association: their time of origin (as reflected by their distribution) and their evolutionary history shape a web of relationships far more complex than that allowed by physical distances alone. Dependencies between SNPs across different chromosomes can also be explained by their interactions to determine other vaso-occlusive complications of SCA, such as osteonecrosis, priapism and acute chest syndrome^2,8. This explanation is consistent with the design of our study, which included individuals with at least one vaso-occlusive complication of SCA. For example, the web of interactions linking the SNPs in TGFBR2 (on chromosome 3) and BMP6 (on chromosome 6) can be explained by their simultaneous association to osteonecrosis²⁵, a known complication of SCA affecting 30% of individuals with SCA.

The inadequacy of traditional analysis methods can be a crucial impediment to the identification of the genetic basis of complex traits in large association studies^12,18,26,27. Our results show the promise of Bayesian networks for the identification, representation and prognostic use of the genetic basis of complex traits. The predictive accuracy of our model is also a step toward the development of accurate prognostic tests to identify individuals at risk of stroke and to help select better treatment options. Understanding the genetic networks modulating the likelihood of stroke may provide additional insights into the pathogenesis of the disease and suggest new therapeutic targets. Although further investigation is required to establish the causative role of these genetic markers, our results support the emerging hypothesis that stroke in individuals with SCA is a complex trait caused by the interaction of multiple genes⁶. The presence among the risk factors of genes already associated with stroke, such as SELP, suggests that some genetic factors predisposing to stroke are shared by both individuals with SCA and stroke victims in the general population, and that our model may offer some insights into the genetic basis of the third leading cause of death in the US.

METHODS

Data collection

Between October 1978 and September 1988, the first phase of the CSSCD enrolled 4,082 African Americans from 23 clinical centers across the US⁹. Newborns and any individual who had visited a participating clinic for any medical reason between 1975 and 1978 were eligible for participation. Except for newborns, who were enrolled throughout the study period, enrollment was closed in May 1981. Subjects were observed for 5.2 ± 2 years (mean ± s.d.). Five years after the start of the CSSCD, blood samples were obtained for the determination of α-thalassemia and the β-globin gene cluster haplotype. DNA from this sample was also deposited in a repository controlled by the US National Institutes of Health; this DNA was used for SNP genotyping. We limited our genotyping to samples from individuals with SCA (homozygous with respect to the hemoglobin S gene) with or without coincident α-thalassemia, who presented at least one vaso-occlusive complication of SCA. The CSSCD database provided the clinical information about the subphenotypes of SCA, including overt stroke, osteonecrosis, acute chest syndrome, painful episodes, leg ulceration, renal failure, priapism and proliferative retinopathy. Information about other clinical features, including HbF levels, systolic and diastolic blood pressure, and gender, was also collected. The DNA samples were used to genotype 235 SNPs in 80 candidate genes.

Strokes were classified by the investigator at each center on the basis of the available clinical and imaging studies. For our analysis, we considered only those individuals with a confirmed history of or incident complete nonhemorrhagic stroke, documented by imaging studies. Ninety-five percent of the individuals classified as having infarctive stroke underwent computed tomography scan, brain scan or magnetic resonance imaging at the time of the event. Magnetic resonance imaging information was not collected before December 1986. A detailed description of stroke in individuals who participated in the CSSCD was reported previously²⁸. This study was reviewed and approved by the Institutional Review Board of Boston University School of Medicine. Samples from individuals with stroke of the independent validation set were obtained from the Medical College of Georgia and the University of Mississippi Medical Center, with the approval of their respective Institutional Review Boards.

Genotyping

DNA samples were used for SNP genotyping by high-throughput mass spectrometry. We selected SNPs with population frequency information and heterozygosity values >0.2 in the candidate genes from dbSNP and the Celera database. We compared the amplification primers used in all reactions with the SNP database to ensure that there were no hidden SNPs in the amplification priming site that would result in inaccurate genotyping. We used the Sequenom Mass Spectrometry HME assay for genotyping²⁹. We amplified the region containing the SNP by PCR, treated it with shrimp alkaline phosphatase, hybridized it to with a primer upstream of the polymorphism and extended the primer with a combination of a normal and a di-deoxy dNTP that corresponds to the SNP. We then removed salt from the sample and analyzed the primer extension products on a Bruker Biflex II Mass Spectrometer. For assay design, we tagged the amplification primers. The melt temperature of the unique portion of the amplification primers was 56–58 °C and the product size was 80–150 bp. The mass of the detecting primer was 4,000–8,000 Da. We assembled multiplex groups of five to eight SNPs, with similar sequence context, into single reactions for analysis. We assembled information about phenotypes, clinical features and genotypes into a large database and assigned a unique identifier to each sample to anonymize the data.

Statistical analysis

Of the 235 SNPs genotyped in CSSCD subjects, 116 were not included in the statistical analysis either because they were monomorphic or because the primers failed. Of the remaining 118 SNPs, we included in the analysis those with <30% missing genotypes satisfying Hardy Weinberg equilibrium in the individuals with stroke, for a total of 108 SNPs in 39 candidate genes. Continuous variables were discretized into four bins with equal frequencies.

To build the Bayesian network, we used a popular Bayesian approach³⁰ implemented in the program Bayesware Discoverer. The program searches for the most probable network of dependency given the data. To find such a network, the Discoverer explores a space of different network models, scores each model by its posterior probability conditional on the available data and returns the model with maximum posterior probability. This probability is computed by Bayes theorem as p(M|D) ∝ p(D|M)p(M), where p(D|M) is the probability that the observed data are generated from the network model M and p(M) is the prior probability encoding knowledge about the model M before seeing any data. We assumed that all models were equally likely a priori, and so p(M) is uniform and p(M|D) becomes proportional to p(D|M), a quantity known as marginal likelihood. The marginal likelihood averages the likelihood functions for different parameters values and is calculated as p(D|M) = ∫ p(D|θ)p(θ)dθ, where p(D|θ) is the traditional likelihood function and p(θ) is the parameter prior density. For categorical data in which p(θ) follows a Dirichlet distribution, the integral p(D|M) = ∫ p(D|θ)p(θ)dθ has a closed-form solution¹⁶ that is computed in product form as p(D|M) = Π_i p(D_i|M_i), where M_i is the model describing the dependency of the ith variable on its parent nodes and D_i are the observed data of the ith variable¹⁶. The factorization of the marginal likelihood implies that a model can be learned locally, by selecting the most probable set of parents for each variable and then joining these local structures into a complete network, in a procedure that closely resembles standard path analysis. This modularity property allows us to assess, locally, the strength of local associations represented by rival models. This comparison is based on the Bayes factor that measures the odds of a model M_i versus a model M̃_i by the ratio of their posterior probabilities p(M_i|D_i)/p(M̃_i|D_i) or, equivalently, by the ratio of their marginal likelihoods ρ = p(D_i|M_i)/p(D_i|M̃_i). Given a fixed structure for all the other associations, the posterior probability p(D_i|M_i) equals ρ/(1 + ρ) and a large Bayes factor ρ implies that the probability p(D_i|M_i) is close to one, meaning that there is very strong evidence for the associations described by the model M_i versus the alternative model M̃_i. When we explore different dependency models for the ith variable, the posterior probability of each model depends on the same data D_i.

To reduce the search space, we used a bottom-up search strategy known as the K2 algorithm³⁰. We specified the space of candidate models to be explored by imposing a search order on the database variables in which older SNPs (more uniformly distributed in the population) were tested as children of more recent SNPs (asymmetrically distributed SNPs). Results of simulations that we have carried out suggest that this heuristic leads to better networks with largest marginal likelihood. We focused on models in which the phenotype is the root node of the network and the genotypes can be either conditionally dependent or marginally independent of it. As in traditional regression models, in which the phenotype is dependent on the genotypes, this inverted dependency structure can represent the association of independent as well as interacting SNPs with the phenotype¹⁶. But this structure is also able to capture more complex models of dependency¹⁹, because the marginal likelihood measuring the association of each SNP with the phenotype is functionally independent of the association of other SNPs with the phenotype. In contrast, in regression structures, the presence of an association between a SNP and the phenotype affects the marginal likelihood measuring the association between the phenotype and other SNPs, reducing the set of SNPs that can be detected as associated with the phenotype. In our Bayesian network, the nodes associated with the phenotype are the children nodes of stroke (26 nodes that are directly associated with stroke) and the parents of the children nodes (6 nodes that are associated to stroke, given the common children nodes).

The Bayesian network induced by this search procedure was quantified by the conditional probability distribution of each node given the parents nodes. The conditional probabilities were estimated as

$$p(x_{ik}\mid {\pi }_{ij})=\frac{{\alpha }_{\mathit{ijk}}+n_{\mathit{ijk}}}{{\alpha }_{ij}+n_{ij}},$$

where x_ik represents the state of the child node, π_ij represents a combination of states of the parent nodes, n_ijk is the sample frequency of (x_ik,π_ij) and n_ij is the sample frequency of π_ij. The parameters α_ijk and α_ij = Σ_k α_ijk encode the prior distribution with the constraint Σ_j α_ij = α for all j, as suggested¹⁶. We chose α = 8 by sensitivity analysis¹⁶.

Predictive validation

To assess the robustness of the network to sampling variability, we first used fivefold cross-validation in which we partitioned the original data set into five nonoverlapping subsets that we used for learning the network dependency. We then used each network to predict the phenotypes of the individuals not included in the learning process and measured the accuracy by the frequency of individuals for whom the correct phenotypes were predicted with probability >0.5. We calculated the predictive probability of stroke, given evidence in the network, using the clique algorithm¹⁶ implemented in Discoverer. We determined the predictive accuracy of the models using an independent set of 114 individuals with SCA, including 7 individuals with stroke who were not part of the multicenter study and 107 individuals randomly selected from the original database for whom we had a complete medical history and who were not used to build the Bayesian network model. We used the model to predict the phenotypes of these individuals and to assess the predictive accuracy by the frequency of individuals for whom the correct phenotypes were predicted with probability >0.5.

Logistic regression

We built a logistic regression model to identify the SNPs associated with the phenotype using the stepwise procedure implemented in the R program, which uses the Akaike information criterion in the forward step. We then selected the significant regressors (P < 0.05).

URLs

The network and a tutorial introduction to the use of Bayesian networks in genomics are available from our website (http://genomethods.org/sca/). dbSNP is available at http://www.ncbi.nlm.nih.gov/SNP/. The program Bayesware Discoverer is available at http://www.bayesware.com/.