Orientation Determination of Interfacial β-sheet Structures in Situ

Abstract

Structural information such as orientations of interfacial proteins and peptides is important for understanding properties and functions of such biological molecules, which play crucial roles in biological applications and processes such as antimicrobial selectivity, membrane protein activity, biocompatibility, and biosensing performance. The α-helical and β-sheet structures are the most widely encountered secondary structures in peptides and proteins. In this paper, for the first time, a method to quantify the orientation of the interfacial β-sheet structure using a combined Attenuated Total Reflectance Fourier Transformation Infrared Spectroscopic (ATR-FTIR) and Sum Frequency Generation (SFG) vibrational spectroscopic study was developed. As an illustration of the methodology, the orientation of tachyplesin I, a 17-amino acid peptide with an anti-parallel β-sheet, adsorbed to polymer surfaces as well as associated with a lipid bilayer was determined using the regular and chiral SFG spectra, together with polarized ATR-FTIR amide I signals. Both the tilt angle (θ) and the twist angle (ψ) of the β-sheet at interfaces are determined. The developed method in this paper can be used to obtain in situ structural information of β-sheet components in complex molecules. The combination of this method and the existing methodology that is currently used to investigate α-helical structures will greatly broaden the application of optical spectroscopy in physical chemistry, biochemistry, biophysics, and structural biology.

1. Introduction

Structural information such as orientations of interfacial proteins and peptides are important for understanding properties and functions of such biological molecules, which play crucial roles in a variety of biological applications and processes. For example, the adsorbed proteins on a biomedical material surface determine the biocompatibility of the material. Surface immobilized proteins serve as sensing units for biosensors; their interfacial structures play crucial roles in biosensing performance. Membrane associated proteins are important for trans-membrane transport and cellular communication. The structure and orientation of antimicrobial peptides in cell membranes control their activity and selectivity. In order to study the interfacial orientation of complex proteins, it is necessary to examine orientations of common secondary structures that are components of interfacial peptides and proteins. The most commonly seen secondary structures are α-helices and β-sheets. We have developed systematic means to determine interfacial orientation of α-helices.^1–3 In this research, we will present a systematic way to study orientation of β-sheet structure on surfaces/at interfaces.

The β-sheet structure was first proposed by Astbury in 1931; that model was not accurate until the refinements made by Pauling and Corey in 1953.⁴ It is a widely distributed secondary structure found in a diverse range of proteins. Many membrane-associated proteins and peptides have β-sheet or β-barrel components. Determining the orientation of this structure, is therefore crucial in having a detailed understanding of the protein’s functional mechanisms.⁵ Transformational changes of protein components to β-sheets have also been observed and are believed to be crucial malfunctions that lead to diseases such as mad cow disease and Creutzfeldt-Jakob disease.^6,7 The formation of β-sheets at the interface can lead to the accumulation of fibrous structures that can disrupt cellular processes.⁷ These amyloid β-peptide (Aβ-) fibrous plaques can accumulate on the brain, leading to Alzheimer’s disease.⁸ The occurrence of β-sheet structures in membrane-associated proteins as well as in Aβ-plaques raises much interest about β-sheet orientation. The ability to determine the structural information of the β-sheets, including orientation of β-sheets at interfaces and on surfaces, could aid in the understanding of such important protein behaviors.

A wide range of spectroscopic techniques have been applied to the study of interfacial proteins and peptides. For instance, Attenuated Total Reflectance Fourier Transform Infrared spectroscopy (ATR-FTIR) and Raman spectroscopic techniques have been extensively used to study surface proteins/peptides, providing orientation information of these molecules while they are adsorbed on surfaces.^9–32 Nuclear Magnetic Resonance (NMR) techniques have also been successfully applied to determine detailed structural information regarding membrane-associated proteins/peptides, including interaction mechanisms of adsorbed proteins/peptides.^33–43

Recently, a nonlinear optical spectroscopy, sum frequency generation (SFG) vibrational spectroscopy, has been developed into a powerful technique to investigate surfaces and interfaces.^44–64 SFG measures the second order nonlinear response of a system, χ⁽²⁾, which is intrinsically surface sensitive, allowing peptides and proteins to be selectively studied while they are in interfacial environments such as in lipid bilayers or on polymer surfaces. In addition, SFG has been demonstrated to be an extremely sensitive technique, allowing interfacial proteins and peptides to be studied in situ and at physiological concentration.^58,65–87 Protein (or peptide) - membrane interactions can also be studied in real time, revealing adsorption kinetics as well as orientation and structural changes as the proteins interact with surfaces or cell membranes. Therefore, in comparison with ATR-FTIR, Raman spectroscopy and NMR, SFG has many significant advantages such as superb detection limit, near background free detection and real time in situ study capability. SFG has been successfully applied to the orientation determination of interfacial α-helices.^{1–3, 85} Combination of SFG measurements with linear optical spectroscopic studies (e.g., ATR-FTIR studies) has been used to determine complicated orientation distribution of α-helices.

In this work, we successfully applied the bond additivity model to calculate the IR transition dipole moment, the Raman polarizability and eventually the SFG hyperpolarizability of the anti-parallel β-sheet. The hyperpolarizability tensor components are related to the SFG chiral and achiral signal strength, which allows for the orientation analysis of this particular structure at interfaces. Using combined ATR-FTIR and SFG studies, both the tilt angle and the twist angle of a β-sheet peptide, tachyplesin I, on polymer surfaces and in a lipid bilayer were deduced using the vibrational amide I signals. The possibility of determining the orientation of β-sheet structure is of great importance in the structural analysis of large proteins which consist of both α-helical and β-sheet structures. The orientation information of these proteins now can be investigated by two independent yet complementary SFG approaches (by studies of α-helical and β-sheet components) in situ in real time.

2. Experimental

2.1 Materials

C-terminal amidated tachyplesin I (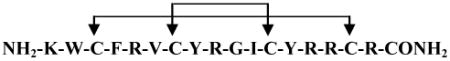) was purchased from GenScript USA Inc. (Piscataway, NJ) with >95% purity. Polystyrene (PS) used in this research was PS standard, purchased from Scientific Polymer Products Inc, with a molecular weight of 393,400. The sulfonated PS (s-PS) was prepared from such PS standard. The sulfonation reaction has been described previously.⁸⁶ PS and PS with 15% sulfonation were used for the SFG experiments. Both the lipids, hydrogenated and deuterated 1,2-dipalmitoyl (D26)-sn-glycero-3-phosphoglycerol (DPPG and dDPPG), used in this research were purchased from Avanti Polar Lipids Inc (Alabaster, AL).

2.2 Lipid bilayer deposition

Single lipid bilayers, which can have two different leaflets, were prepared on CaF₂ right angle prisms (Altos Photonics, Bozeman, MT). Langmuir-Blodgett and Langmuir-Schaefer (LB/LS) methods were used to deposit the proximal and then the distal leaflets, respectively. A KSV2000 LB system and ultrapure water from a Millipore system (Millipore, Bedford, MA) were used throughout the experiments for bilayer preparation. The bilayer was immersed in water inside a 2-mL reservoir during the experiment and a small amount of water could be added to the reservoir to compensate for evaporation when needed for long timescale experiments. For tachyplesin I-bilayer interaction experiments, 10 μL of 0.25 mg/ml tachyplesin I solution was injected into the reservoir. A magnetic micro-stirrer was used at a rate of 100 rpm to ensure a homogeneous concentration distribution of peptide molecules in the subphase below the bilayer.

2.3 SFG

The details of our SFG setup and experimental design have been previously described.^{2, 66} Polymer films were prepared by spin coating 1 wt% polymer solutions onto CaF₂ prisms at a speed of 2400 rpm. Spectra were collected in ssp (s-SFG, s-visible, p-IR), ppp and spp polarizations using our previously reported near total reflection geometry.^78,81

2.4 ATR-FTIR

The ATR-FTIR spectra were collected on a Nicolet 550 spectrometer (Thermo Fisher Scientific. Inc., MA, USA). A thin polymer film was solution cast onto a germanium substrate from a 0.1 wt % polymer solution. 50 μL of 0.05 mg/ml tachyplesin I solution in D₂O (Sigma Aldrich, St. Louis, MO) was injected into the ATR trough, and S and P polarized spectra were collected approximately one hour after the injection of peptide. The chamber was purged with nitrogen before and during the data collection, and the spectra were collected using 256 scans/spectrum.

3. Orientation determination of β-sheet

The SFG hyperpolarizability tensor, β, can be described as a tensor product of the IR transition dipole moment and the Raman polarizability tensor,^3,44,88,89

$${\beta }_{\mathit{lmn},q}\propto \frac{\partial {\alpha }_{lm}^{\ast }}{\partial Q_q}\frac{\partial {\mu }_n}{\partial Q_q}$$ (1)

where l, m, and n are the molecular coordinates, $\frac{\partial {\alpha }_{lm}}{\partial Q_q}$ and $\frac{\partial {\mu }_n}{\partial Q_q}$ are the Raman polarizability and IR dipole moment derivatives with respect to the normal mode coordinate of the q^th vibrational mode, respectively. Throughout this paper these derivatives will be referred to as the components of the Raman polarizability tensor and IR transition dipole moment. As equation 1 indicates, if both the IR transition dipole moment and the Raman polarizability tensor are known, the SFG hyperpolarizability tensor for the vibrational mode of interest can be deduced. It is widely accepted that the anti-parallel β-sheet adopts D₂ symmetry.^90–92 Applying this symmetry point group, the Raman polarizability tensor and the IR transition dipole of the four peptide units that comprise the β-sheet repeating unit can be projected onto the molecular coordinate system using the bond additivity model. This treatment is similar to that used by Higgs for helical molecules.¹³

3.1 Anti-parallel β-sheet structure and D₂ point group symmetry

The anti-parallel β-sheet belongs to D₂ symmetry. For a structure with D₂ point group symmetry, there are three IR active (B₁, B₂ and B₃) and four Raman active amide I vibrational modes (A, B₁, B₂ and B₃). The four modes are:^92–96

$$\begin{array}{l}\nu (0,0)={\nu }_0+D_{10}+D_{01}+D_{11}=1668{cm}^{-1}\\ \nu (0,\pi )={\nu }_0+D_{10}-D_{01}-D_{11}=1685{cm}^{-1}\\ \nu (\pi ,0)={\nu }_0-D_{10}+D_{01}-D_{11}=1636{cm}^{-1}\\ \nu (\pi ,\pi )={\nu }_0-D_{10}-D_{01}+D_{11}=1723{cm}^{-1}\end{array}$$ (2)

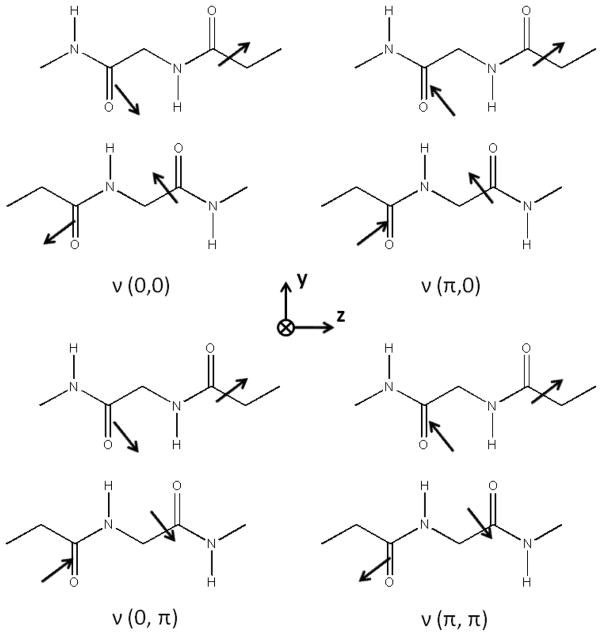
where ν₀ is the unperturbed peptide unit frequency and D₁₀ and D₀₁ account for the intrachain and interchain couplings, respectively. The term D₁₁ represents the coupling of the transition dipoles between adjacent strands. A graphical illustration of these four vibrational modes is presented in Figure 1.

Figure 1.

Four amide I vibrational modes of a repeating unit of an anti-parallel β-sheet. For each mode, the peptide units 1, 2, 3, and 4 refer to the lower right unit, the lower left unit, the upper left unit, and the upper right unit, respectively.

3.2 The Raman polarizability tensor of an anti-parallel β-sheet

The Raman tensor for the amide I mode (Figure 2) has been proposed by Tsuboi and colleagues by investigating Raman spectra of a uniaxial tetragonal aspartame.³⁰ For β-sheet structures, the principle x-axis of Tsuboi’s polarizability tensor is found to be significantly more in line with the C=O bond; this tilt angle is only 22 degrees (instead of 34.5 degrees in α-helical structures).⁹⁵ This refinement was made by adjusting this tilt angle so that the Raman intensity ratio $\frac{I_{cc}}{I_{bb}}$ matches the experimental observations on Bombyx mori silk ( $\frac{I_{cc}}{I_{bb}}=0.304$), Nephila edulis spidroin ( $\frac{I_{cc}}{I_{bb}}=0.406$), S. c. ricini fibroin silk ( $\frac{I_{cc}}{I_{bb}}=0.257$), and fowl feather barb ( $\frac{I_{cc}}{I_{bb}}=0.429$).^94,95,97 For the β-sheet, the polarizability tensor can be written in the given molecular frame as defined in Figure 2.

Figure 2.

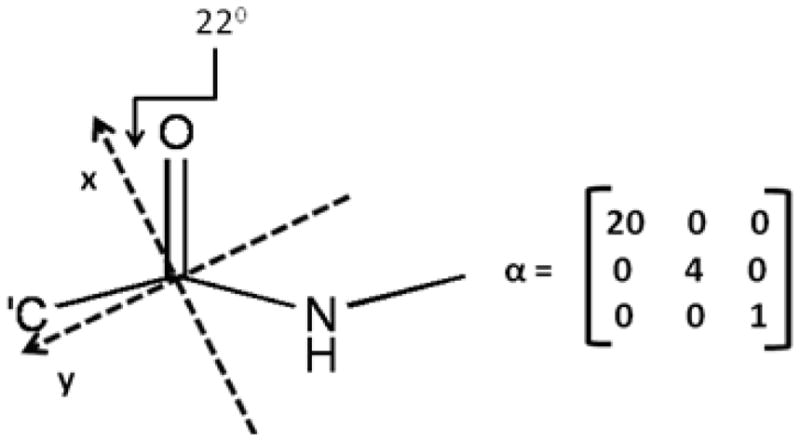
A peptide unit and its transition Raman polarizability tensor in the given molecular frame

Given this polarizability tensor and its corresponding molecular frame, an Euler transformation can be used to impose this tensor in the molecular coordinate system onto the four peptide units of the Pauling-Corey β-sheet. The Euler transformation used here follows the z-y-z convention, which has a matrix in the form of

$$\xi =\left(\begin{array}{ccc}cos(\varphi )cos(\theta )cos(\psi )-sin(\varphi )sin(\psi )& cos(\varphi )cos(\theta )sin(\psi )+sin(\varphi )cos(\psi )& -cos(\varphi )sin(\theta )\\ -sin(\varphi )cos(\theta )cos(\psi )-cos(\varphi )sin(\psi )& -sin(\varphi )cos(\theta )sin(\psi )+cos(\varphi )cos(\psi )& sin(\varphi )sin(\theta )\\ sin(\theta )cos(\psi )& sin(\theta )sin(\psi )& cos(\theta )\end{array}\right)$$ (3)

and the rotations are carried out using equation (4).

$${\alpha }_{\mathit{xyz}}=\xi {\alpha }_{\mathit{abc}}{\xi }^T$$ (4)

We define a positive rotation as a rotation in the counter-clockwise direction. The four Euler angle sets used to rotate the peptide units comprising the β-sheet repeating unit from Tsuboi’s frame into Pauling-Corey’s frame are: (ψ₁=292°, θ₁= 120°, ϕ₁= 0°), (ψ₂=112°, θ₂= 240°, ϕ₂= 0°), (ψ₃=112°, θ₃= 60°, ϕ₃= 0°) and (ψ₄=292°, θ₄= 300°, ϕ₄= 0°). The first Raman polarization tensor of the anti-parallel β-sheet structure in the Pauling-Corey coordinate system can be calculated as:

$${\alpha }_1=\left(\begin{array}{ccc}-0.19& 0.46& -0.87\\ 0.93& 0.37& 0\\ 0.32& -0.80& -0.50\end{array}\right)\left(\begin{array}{ccc}20.00& 0& 0\\ 0& 4.00& 0\\ 0& 0& 1.00\end{array}\right){\left(\begin{array}{ccc}-0.19& 0.46& -0.87\\ 0.93& 0.37& 0\\ 0.32& -0.80& -0.50\end{array}\right)}^T=\left(\begin{array}{ccc}2.31& -2.77& -2.27\\ -2.77& 17.50& 4.80\\ -2.27& 4.80& 4.93\end{array}\right)$$ (5)

The four resulting Raman polarization tensors after the rotation are

$$\begin{array}{l}{\alpha }_1=\left(\begin{array}{ccc}2.31& -2.77& -2.27\\ -2.77& 17.50& 4.80\\ -2.27& 4.80& 4.93\end{array}\right),{\alpha }_2=\left(\begin{array}{ccc}2.31& -2.77& 2.27\\ -2.77& 17.50& -4.80\\ 2.27& -4.80& 4.93\end{array}\right),\\ {\alpha }_3=\left(\begin{array}{ccc}2.31& 2.77& 2.27\\ 2.77& 17.50& 4.80\\ 2.27& 4.80& 4.93\end{array}\right),{\alpha }_4=\left(\begin{array}{ccc}2.31& 2.77& -2.27\\ 2.77& 17.50& -4.80\\ -2.27& -4.80& 4.93\end{array}\right).\end{array}$$ (6)

The transition Raman polarizability tensor of the A, B₁, B₂ and B₃ modes of the repeating unit of the β-sheet structure can be calculated from these Raman polarizability tensors, with the consideration of the phase of the amide I mode for each peptide unit (shown in Figure 1) in the A, B₁, B₂ and B₃ modes.

A mode:

$${\alpha }_{\nu (0,0)}={\sum }_{i=1}^4{\alpha }_i=\left(\begin{array}{ccc}9.24& 0& 0\\ 0& 70.00& 0\\ 0& 0& 19.72\end{array}\right)$$ (7)

B₁ mode:

$${\alpha }_{\nu (0,\pi )}=cos(\pi ){\alpha }_1+cos(\pi ){\alpha }_2+cos(0){\alpha }_3+cos(0){\alpha }_4=\left(\begin{array}{ccc}0& 11.08& 0\\ 11.08& 0& 0\\ 0& 0& 0\end{array}\right)$$ (8)

B₂ mode:

$${\alpha }_{\nu (\pi ,0)}=cos(0){\alpha }_1+cos(\pi ){\alpha }_2+cos(\pi ){\alpha }_3+cos(0){\alpha }_4=\left(\begin{array}{ccc}0& 0& -9.08\\ 0& 0& 0\\ -9.08& 0& 0\end{array}\right)$$ (9)

B₃ mode:

$${\alpha }_{\nu (\pi ,\pi )}=cos(\pi ){\alpha }_1+cos(0){\alpha }_2+cos(\pi ){\alpha }_3+cos(0){\alpha }_4=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -19.20\\ 0& -19.20& 0\end{array}\right)$$ (10)

As seen from these modes, the A mode dominates the Raman spectra of the anti-parallel β-sheet structures, which was also experimentally observed.⁹⁴

3.3 IR transition dipole moment of an anti-parallel β-sheet

The calculation of the IR transition dipole moment of the individual peptide unit comprising one repeating unit of the anti-parallel β-sheet structure (shown in Figure 3)⁹⁸ has been reported by Marsh.⁹² We slightly modified Marsh’s projection by transforming the dipole moment of the peptide unit into Tsuboi’s frame, followed by a transformation into the Pauling-Corey frame using the Euler transformation that was introduced previously in section 3.2. We have verified the outcome of this approach (projection followed by rotation) with the results obtained from the conventional projection to ensure that the proper rotational operations were performed. The final calculated dipole moments of the four peptide units are

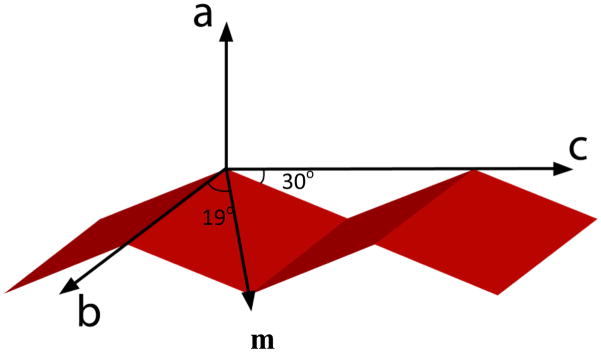
Figure 3.

Orientation of the IR transition dipole moment of the individual peptide unit comprising the anti-parallel β-sheet structure. The dipole moment lies in the plane that is inclined at an angle of 30° to the strand axis, and makes an angle of 19° to the axis that connects the two successive α-carbons of the two strands.

$${\mu }_1=\left(\begin{array}{c}-0.16\\ 0.95\\ 0.28\end{array}\right),{\mu }_2=\left(\begin{array}{c}0.16\\ -0.95\\ 0.28\end{array}\right),{\mu }_3=\left(\begin{array}{c}-0.16\\ -0.95\\ -0.28\end{array}\right),{\mu }_4=\left(\begin{array}{c}0.16\\ 0.95\\ -0.28\end{array}\right)$$ (11)

From these transition dipole moments of the four individual peptide units in a β-sheet repeating unit, one can see that the symmetric A mode is inactive in IR spectroscopy. The overall transition dipole moment of the B₁, B₂ and B₃ vibrational modes can be calculated: ⁹³

B₁ mode:

$${\mu }_{\nu (0,\pi )}=cos(\pi ){\mu }_1+cos(\pi ){\mu }_2+cos(0){\mu }_3+cos(0){\mu }_4=\left(\begin{array}{c}0\\ 0\\ -1.12\end{array}\right)$$ (12)

B₂ mode:

$${\mu }_{\nu (\pi ,0)}=cos(0){\mu }_1+cos(\pi ){\mu }_2+cos(\pi ){\mu }_3+cos(0){\mu }_4=\left(\begin{array}{c}0\\ 3.80\\ 0\end{array}\right)$$ (13)

B₃ mode:

$${\mu }_{\nu (\pi ,\pi )}=cos(\pi ){\mu }_1+cos(0){\mu }_2+cos(\pi ){\mu }_3+cos(0){\mu }_4=\left(\begin{array}{c}0.64\\ 0\\ 0\end{array}\right)$$ (14)

The calculated overall dipole moment is indeed supported by the experimental observations with a strong peak at 1635 cm⁻¹. This low frequency mode was assigned to the B₂ representation, while the high frequency absorption peak at 1685 cm⁻¹ was assigned to be the B₁ representation. If we define the molecular (a, b, c) frame to be superimposed with the lab (x, y, z) coordinate system, the B₂ mode of the β-sheet structure is y polarized, and the B₁ mode is z polarized. As one can see from the calculated dipole moments, the strong mode is along the y axis, which belongs to the B₂ representation. Additionally, the calculated intensity ratio between the B₁/B₂ modes agrees fairly well with the value reported by Choi et al. Applying normal mode analysis of the amide I vibrations, Choi reported the B₁/B₂ intensity to be around 0.11 versus our calculated value of 0.09. However, Choi’s calculation predicts quite different peak centers for the B₁ and B₂ modes as previously done by the work of Miyazawa, Tsuboi, Krimm and Marsh.⁹⁹

3.4 SFG data analysis for anti-parallel β-sheet structures based on the calculated IR transition dipole moment and Raman polarizability tensor

The SFG hyperpolarizability tensor, β, is a third-rank tensor with 27 elements. It is a tensor product of the Raman polarizability tensor and the IR transition dipole moment. Hence, a vibrational mode is only SFG active when it is both IR and Raman active. Therefore, B₁ (components μ_c and α_ab), B₂ (μ_b and α_ac) and B₃ (μ_a and α_bc) vibrational modes of the anti-parallel β-sheet are SFG active. Conventionally, chiral signal was believed to arise primarily from the double resonance SFG process, in which the Raman tensor is asymmetric.^100,101 However, Shen and colleagues used perturbation theory of vibrational SFG to predict that the generation of chiral signal is plausible in vibrational SFG without the requirement of an asymmetric Raman tensor.^100,102 Evidentially, our laboratory has also experimentally observed strong chiral vibrational SFG signal with the anti-parallel β-sheet, which was also predicted by Simpson and coworkers.^81,103

In this paper we report the SFG achiral signal observed in ssp polarization combination and the SFG chiral signal observed in spp polarization.^81,104

$${\chi }_{\mathit{ssp}}^{(2)}=L_{\mathit{yyz}}{\chi }_{\mathit{yyz}}^2$$ (15)

$${\chi }_{\mathit{spp}}^{(2)}=L_{\mathit{yxz}}{\chi }_{\mathit{yxz}}^{(2)}+L_{\mathit{yzx}}{\chi }_{\mathit{yzx}}^{(2)}$$ (16)

The normalized Fresnel factors L_yyz, L_yzx and L_yxz are calculated to be 11.0, 5.2 and 1.0, respectively for our experimental geometry which has been described in our previous publications.^2,65 These Fresnel coefficients were normalized relative to L_yxz so that the refractive index of the interfacial medium (PS/peptide solution interface and lipid bilayer with the peptides) does not need to be determined explicitly.

To relate the molecular SFG hyperpolarizability, β_abc, to the macroscopic SFG susceptibility, ${\chi }_{\mathit{xyz}}^{(2)}$, we use a set of three Euler angles ϕ, θ, and ψ representing the in-plane rotation, the tilt angle and the twist angle, respectively. The transformation matrix therefore can be written as

$$\begin{array}{l}R=(R_3(\varphi )R_2(\theta )R_1(\psi ))\\ =\left(\begin{array}{ccc}cos(\varphi )& sin(\varphi )& 0\\ -sin(\varphi )& cos(\varphi )& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}cos(\theta )& 0& -sin(\theta )\\ 0& 1& 0\\ sin(\theta )& 0& cos(\theta )\end{array}\right)\left(\begin{array}{ccc}cos(\psi )& sin(\psi )& 0\\ -sin(\psi )& cos(\psi )& 0\\ 0& 0& 1\end{array}\right)\\ =\left(\begin{array}{ccc}cos(\varphi )& sin(\varphi )& 0\\ -sin(\varphi )& cos(\varphi )& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}cos(\theta )cos(\psi )& cos(\theta )sin(\psi )& -sin(\theta )\\ -sin(\psi )& cos(\psi )& 0\\ sin(\theta )cos(\psi )& sin(\theta )sin(\psi )& cos(\theta )\end{array}\right)\\ =\left(\begin{array}{ccc}cos(\varphi )cos(\theta )cos(\psi )-sin(\varphi )sin(\psi )& cos(\varphi )cos(\theta )sin(\psi )+sin(\varphi )cos(\psi )& -cos(\varphi )sin(\theta )\\ -sin(\varphi )cos(\theta )cos(\psi )-cos(\varphi )sin(\psi )& -sin(\varphi )cos(\theta )sin(\psi )+cos(\varphi )cos(\psi )& sin(\varphi )sin(\theta )\\ sin(\theta )cos(\psi )& sin(\theta )sin(\psi )& cos(\theta )\end{array}\right)\end{array}$$ (17)

Please notice that eqn (17) is the same as eqn (3). Using this transformation, the ${\chi }_{\mathit{xyz}}^{(2)}$ components can be related to hyperpolarizability components of anti-parallel β-sheet.

The macroscopic SFG susceptibility quantity, ${\chi }_{\text{xyz}}^{(2)}$, can be described by the molecular hyperpolarizability tensor components: ^{44,89,105–108}

$${\chi }_{\mathit{IJK}}^{(2)}={\sum }_{i^{\prime }{j}^{\prime }{k}^{\prime }=x^{\prime }{y}^{\prime }{z}^{\prime }}{N}_S\langle R_{I{i}^{\prime }}{R}_{J{j}^{\prime }}{R}_{K{k}^{\prime }}\rangle {\beta }_{i^{\prime }{j}^{\prime }{k}^{\prime }}$$ (18)

The three vibrational modes of the anti-parallel β-sheet can be observed in the laboratory coordinate system by the following relations:⁸¹ B₁ mode:

$$\begin{array}{l}{\chi }_{\text{yyz}}^{(2)}={\text{N}}_{\text{s}}({cos}^3(\theta )cos(\psi )sin(\psi )-cos(\theta )cos(\psi )sin(\psi ))\ast {\beta }_{\text{abc}}\\ {\chi }_{\text{zzz}}^{(2)}=-2{\text{N}}_{\text{s}}({cos}^3(\theta )cos(\psi )sin(\psi )-cos(\theta )cos(\psi )sin(\psi ))\ast {\beta }_{\text{abc}}\\ {\chi }_{\text{yzx}}^{(2)}=\frac{1}{2}{\text{N}}_{\text{s}}({sin}^2(\theta ){sin}^2(\psi )-{sin}^2(\theta ){cos}^2(\psi )){\beta }_{\text{abc}}\\ {\chi }_{\text{yxz}}^{(2)}=0\end{array}$$ (19)

B₂ mode:

$$\begin{array}{l}{\chi }_{\text{yyz}}^{(2)}={\text{N}}_{\text{s}}({cos}^3(\theta )cos(\psi )sin(\psi )-cos(\theta )cos(\psi )sin(\psi ))\ast {\beta }_{\text{acb}}\\ {\chi }_{\text{zzz}}^{(2)}=-2{\text{N}}_{\text{s}}({cos}^3(\theta )cos(\psi )sin(\psi )-cos(\theta )cos(\psi )sin(\psi ))\ast {\beta }_{\text{acb}}\\ {\chi }_{\text{yzx}}^{(2)}=-\frac{1}{2}{\text{N}}_{\text{s}}({cos}^2(\theta )-{sin}^2(\theta ){cos}^2(\psi ))\ast {\beta }_{\text{acb}}\\ {\chi }_{\text{yxz}}^{(2)}=0\end{array}$$ (20)

B₃ mode:

$$\begin{array}{l}{\chi }_{\text{yyz}}^{(2)}={\text{N}}_{\text{s}}({cos}^3(\theta )cos(\psi )sin(\psi )-cos(\theta )cos(\psi )sin(\psi ))\ast {\beta }_{\text{bca}}\\ {\chi }_{\text{zzz}}^{(2)}=-2{\text{N}}_{\text{s}}({cos}^3(\theta )cos(\psi )sin(\psi )-cos(\theta )cos(\psi )sin(\psi ))\ast {\beta }_{\text{bca}}\\ {\chi }_{\text{yzx}}^{(2)}=\frac{1}{2}{\text{N}}_{\text{s}}({cos}^2(\theta )-{sin}^2(\theta ){sin}^2(\psi ))\ast {\beta }_{\text{bca}}\\ {\chi }_{\text{yxz}}^{(2)}=0\end{array}$$ (21)

In the above equations, ${\chi }_{\text{xyz}}^{(2)}$ can be measured using different polarization combinations of the input and output beams in SFG experiments. The hyperpolarizability quantities β_abc, β_acb and β_bca can be calculated from the Raman tensors and IR transition dipoles, details of which can be found in the supporting information:

$$\begin{array}{l}{\beta }_{\mathit{abc}}=11.08\ast (-1.12)=-12.41\\ {\beta }_{\mathit{acb}}=-9.08\ast 3.80=-34.50\\ {\beta }_{\mathit{bca}}=-19.20\ast 0.64=-12.29\end{array}$$ (22)

Equations (18) to (21) show clearly that SFG vibrational spectroscopy is a technique in which signal strength is dependent on the orientation of the oscillators and is intrinsically sensitive to asymmetric systems (or systems with no inversion symmetry). It was questioned previously whether SFG can be used to study β-sheet structure due to its semi-symmetric structure. We successfully detected both chiral and achiral SFG amide I signals from interfacial β-sheet structures, even though such signals are weak.^81,84 This demonstrates the feasibility of using SFG to study β-sheet structure. However, no quantitative orientation information on interfacial β-sheet structure has ever been obtained.

According to the above equations, measured ${\chi }_{\text{xyz}}^{(2)}$ values and calculated hyperpolarizability quantities, tile angle θ and twist angle ψ can be determined. For example, from the above equations, the relationship between the SFG susceptibility ratio $\frac{{\chi }_{\mathit{ssp}{B}_2}^{(2)}}{{\chi }_{\mathit{spp}{B}_2}^{(2)}}$ and the two orientation angles θ and ψ is shown in Figure 4a, illustrating the ability to determine the two orientation angles based on observed SFG signal. Figure 4b shows the relationship between the SFG susceptibility component ${\chi }_{\mathit{ssp}}^{(2)}$ of the B₁ mode and the tilt (θ) and twist angle (ψ) of the β-sheet. The same relationship for the B₂ mode is displayed in Figure 4c.

Figure 4.

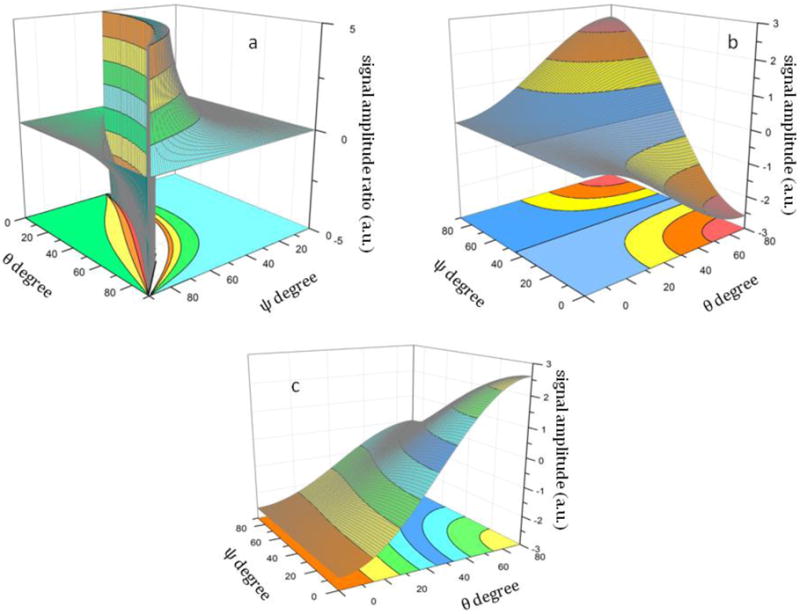
The relationship between the SFG susceptibility a). $\frac{{\chi }_{\mathit{ssp}{B}_2}^{(2)}}{{\chi }_{\mathit{ssp}{B}_2}^{(2)}}$ ratio; b.) ${\chi }_{B1\mathit{spp}}^{(2)}$ c.) ${\chi }_{B2\mathit{spp}}^{(2)}$ and the tilt (θ) and twist angle (ψ) of the β-sheet

In principle, all three SFG active modes, which are related to the molecular hyperpolarizability components β_abc, β_acb and β_bca (equations 19, 20 and 21), can be observed using SFG. However, given that β_acb is roughly 3 times higher than the next strongest vibrational mode (9 folds stronger in intensity), we will focus on the detection of achiral and chiral signals of the B₂ vibrational mode for the orientation analysis of the anti-parallel β-sheet, if the B₂ mode is observed experimentally. We will also demonstrate the feasibility of applying the interference enhancement method to enhance the chiral signal in situations in which none of the chiral signals is observed directly, as in the case of tachyplesin I adsorbed onto a lipid bilayer. The spp spectrum was deduced by using interference between ssp and spp, where the visible polarization was tuned ±20° away from the p polarization.⁸¹

$$I(\pm 20)=K{\mid {\chi }_{\mathit{ssp}}^{(2)}sin(\pm 20)+{\chi }_{\mathit{ssp}}^{(2)}cos(\pm 20)e^{-i\mathrm{\Delta }\varphi }\mid }^2$$ (23)

Where K is a constant and is the phase difference between ${\chi }_{\mathit{ssp}}^{(2)}$ and ${\chi }_{\mathit{ssp}}^{(2)}$.

4. Experimental Results and Discussion

4.1 The interaction between tachyplesin I and polystyrene (PS) polymer surface

SFG spectra were collected from the PS/tachyplesin I solution (~700 nM) using different polarization combinations such as ssp (s-SFG, s-visible, p-IR, Figure 5a) and spp (Figure 5b). As we discussed in our previous publication⁸¹, ssp polarization combination can be used to probe achiral signal, while spp polarization probes the chiral signal of the molecule. The ssp signal (Figure 5a) has several contributions which are centered at 1635 cm⁻¹, 1642 cm⁻¹, 1665 cm⁻¹, 1685 cm⁻¹ and 1730 cm⁻¹, dominated by the 1635 cm⁻¹ and 1730 cm⁻¹ peaks. These signals correspond to the B₂ mode, unordered structure, β-turns/unordered structures, B₁/inter-β-strand and B₃/side chains, respectively.^20,81,92 The spp spectrum (Figure 5b) is dominated by a peak centered at 1635 cm⁻¹, belonging to the B₂ mode. A very weak peak centered at 1685 cm⁻¹ from the B₁ mode, along with two weak bands at 1615 cm⁻¹ and 1710 cm⁻¹, are also observed. As we discussed above, we can obtain some orientation information of the anti-parallel β-sheet structure of tachyplesin I using the signal strength measured in these two polarization combinations (ssp and spp). This is different from the α-helix orientation analysis in which the ppp and ssp signal strength ratio is used. Due to the D₂ symmetry point group of the β-sheet structure, orientation information of this structure includes both the tilt angle (θ) and the twist angle (ψ). Because the SFG measurements in ppp and ssp polarization combination for the D₂ symmetry point group are not independent to each other; their intensity ratio stays constant (about 2.0), regardless of the β-sheet orientation. Therefore the signal strength ratio measured in the ssp and ppp polarization combinations cannot be used for orientation determination here.

Figure 5.

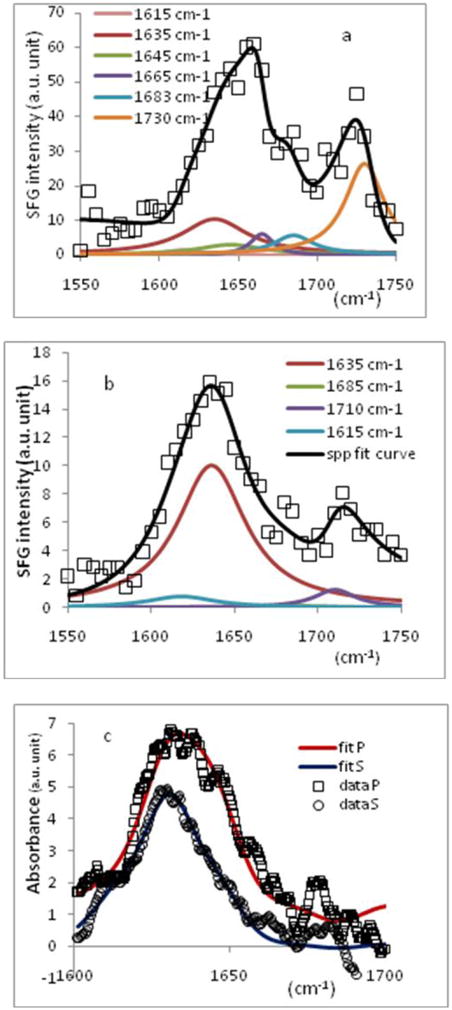
Amide I spectrum of tachyplesin I (~700 nM) adsorbed onto PS surface in a.) SFG ssp polarization combination; b.) SFG spp polarization combination and c.) ATR-FTIR amide I band obtained in s and p polarizations.

In this paper, the average orientation of tachyplesin I on a PS surface was determined by combining the results from ATR-FTIR and SFG measurements. Polarized ATR-FTIR spectra collected from the PS/tachyplesin I solution interface are presented in Figure 5c. The orientation determination methodology using ATR-FTIR of the anti-parallel β-sheet has been previously reported by Marsh.⁹² Assuming the staggering of the hydrogen bond between the adjacent strands is by one peptide unit, the strand tilt angle with the sheet was calculated to be 35° (or 60° if the staggering is caused by two peptide units).¹⁰⁹ The tilt angle, θ, of the β-sheet structure can be written as

$$R^{\mathit{ATR}}(\mathit{amide}I)=\frac{E_x^2}{E_y^2}+\frac{2({\mathit{cos}}^2\theta )}{3-({\mathit{cos}}^2\theta )}\frac{E_z^2}{E_y^2}$$ (24)

where E_x, E_y and E_z are the components of the electric field vector.

Combining ATR-FTIR with the SFG measurements, the following equations can be used to determine the complete orientation of the β-sheet.

$$\{\begin{array}{c}{R}^{\mathit{ATR}}(\mathit{amide}I)=\frac{E_x^2}{E_y^2}+\frac{2({\mathit{cos}}^2\theta )}{3-({\mathit{cos}}^2\theta )}\frac{E_z^2}{E_y^2}\\ {\chi }_{\mathit{ssp}}^{(2)}=L_{\mathit{yyz}}{\chi }_{\mathit{yyz}}^{(2)}=L_{\mathit{yyz}}{\text{N}}_3(\langle {cos}^3(\theta )\rangle \langle cos(\psi )\rangle \langle sin(\psi )\rangle -\langle cos(\theta )\rangle \langle cos(\psi )\rangle \langle sin(\psi )\rangle )\ast {\beta }_{\text{acb}}\\ {\chi }_{\mathit{ssp}}^{(2)}=L_{\mathit{yxz}}{\chi }_{\mathit{yxz}}^{(2)}=L_{\mathit{yzx}}{\chi }_{\mathit{yzx}}^{(2)}=-\frac{1}{2}{L}_{\mathit{yzx}}{\text{N}}_3(\langle {cos}^2(\theta )\rangle -\langle {sin}^2(\theta )\rangle \langle {cos}^2(\psi )\rangle )\ast {\beta }_{\text{acb}}\end{array}$$ (25)

From experimental measurements the ratio $\frac{{\chi }_{\mathit{ssp}}^{(2)}}{{\chi }_{\mathit{ssp}}^{(2)}}$ was found to be 1.04 (Figures 5a and 5b), and the R^ATR was determined to be 0.95 (Figure 5c). After inputting the appropriate radiation electric field vectors (E_x, E_y, E_z), we obtained two sets of solutions (θ= 76°, ψ= 86°) and (θ= 76°, ψ= 43°) for equations (25). However, according to the spectral fitting results of the chiral signal observed with spp polarization combination (Figure 5b), there was no discernable B₁ mode, which excludes the solution set with ψ= 86° which would give relatively strong signal in B₁ mode (Figure 4b). Therefore the tilt and twist angles for tachyplesin I at the PS/tachyplesin I solution are 76° and 43°, respectively. It is worth mentioning that around this particular orientation, the measured SFG signal ratio has a steep orientation angle dependent slope, therefore the orientation deduced should be relatively accurate.

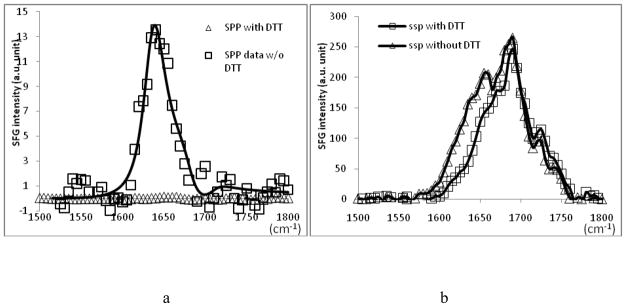
In addition to the PS, we also applied a similar method to study molecular interactions between tachyplesin I and sulfonated polystyrene (s-PS). Similarly, both SFG chiral and achiral amide I signals were observed (Figure 6). To ensure that the observed SFG signal is indeed from the β-sheet structure, dithiothreitol (DTT) was added to the interaction medium before the additions of the peptide, which can denature the native structure of tachyplesin I by breaking the disulfide bonds. With the presence of DTT in the interaction medium, after the addition of the peptide, no chiral signal was observed from the s-PS/tachyplesin I solution interface in spp polarization combination and the ssp spectrum underwent a significant blue shift (these spectra can be found in the supporting material). The blue shift seen in the ssp spectrum corresponds to the loss of β-sheet signal centered at 1635 cm⁻¹. The disappearance of the chiral signal and the spectral change in the achiral signal after the addition of DTT indicates the original chiral signal and the 1635 cm⁻¹ peak in the ssp spectrum are contributed by the β-sheet structure. The detailed data analysis suggests a slightly different orientation of tachyplesin I at the s-PS/tachyplesin I solution interface.

Figure 6.

SFG amide I spectrum of tachyplesin I adsorbed to s-PS surface with and without addition of DTT in a). spp polarization combination and b.) ssp polarization combination

4.2 The interaction between tachyplesin I and lipid bilayer

Tachyplesin I is an effective antimicrobial peptide that interacts with bacterial and mammalian cell membranes differently.^110,111 Using SFG, we successfully probed different interactions and orientations of tachyplesin I in both model mammalian and bacterial cell membranes. In brief, tachyplesin I does not bind effectively onto zwitterionic lipids such as 1-Palmitoyl-2-Oleoyl-sn-Glycero-3-Phosphocholine (POPC) or 1,2-Dimyristoyl-sn-Glycero-3-Phosphocholine (DMPC), which are similar to the major components of mammalian cell membranes. On the other hand, it binds quickly to the negatively charged lipid such as 1-Palmitoyl-2-Oleoyl-sn-Glycero-3-[Phospho-rac-(1-glycerol)] (POPG) and 1,2-Dipalmitoyl-sn-Glycero-3-Phosphoglycerol (DPPG) by the aid of the electrostatic attraction. PG lipids are the main components of bacterial cell membranes. We also obtained the SFG amide I achiral and chiral signal of membrane bound tachyplesin I (Figures 7a and 7b). The achiral signal from the peptide is relatively strong; however, the chiral signal could not be observed directly using the spp polarization combination. The interference enhancement method, which was discussed in our previous publication⁸¹, was implemented to deduce the weak chiral signal. A chiral spp spectrum was deduced, dominated by a clear peak centered at around 1685 cm⁻¹, featuring the B₁ vibrational mode (Figure 7b). By combining the signal strengths of the B₁ and B₂ modes, the orientation angles of tachyplesin I on the DPPG/deuterated DPPG (dDPPG) lipid bilayer can be estimated (Figure 4b and 4c): the tilt angle (θ) has a range of 75–90 degrees and the twist angle (ψ) has a range of 75–90 degrees. Tachyplesin I evidently adopts quite a different twist angle on DPPG/dDPPG lipid bilayer than it does on PS or sPS polymer surfaces. The different twist angles must be caused by the different molecular interactions between tachyplesin I and polymer surfaces and between tachyplesin I and negatively charged lipids. We believe that this is the first time the orientation information (θ, ψ) of antimicrobial peptides with β-sheet structure in cell membranes is determined using vibrational spectroscopies. Such information is important in understanding molecular mechanisms of interactions between β-sheet peptides and cell membranes, aiding in the design and development of improved anti-microbial peptides with β-sheet structures.

Figure 7.

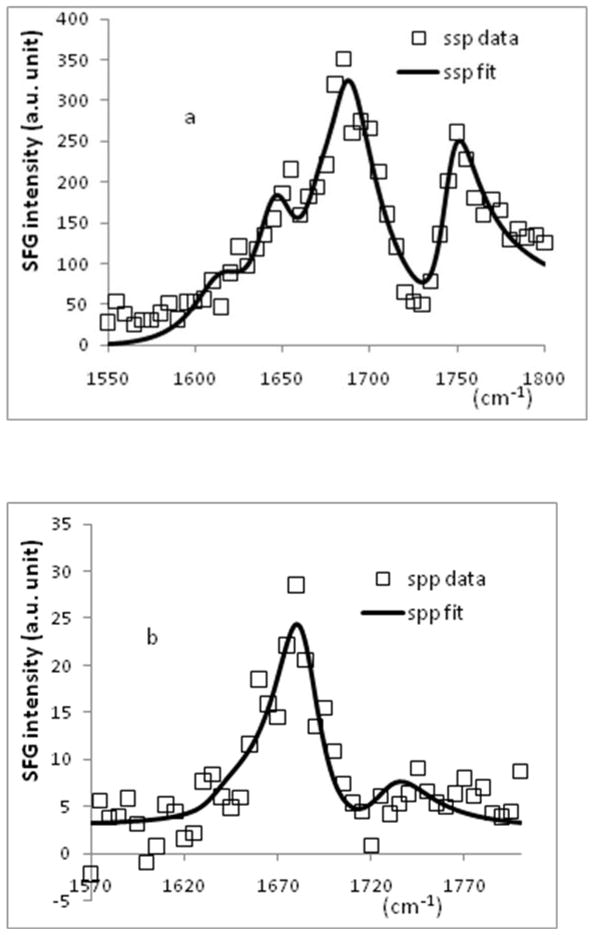
SFG spectrum of tachyplesin I (~700 nM) adsorbed onto DPPG/dDPPG lipid bilayer in a.) ssp polarization combination and b.) spp polarization combination.

Conclusion

In this paper, for the first time, a systematic method for determining β-sheet orientation on surfaces using SFG vibrational spectroscopy together with ATR-FTIR was presented. Using the bond additivity model, the IR transition dipole and the Raman polarizability tensor were calculated for the β-sheet structure. From the calculated IR dipole and Raman polarizability, the molecular hyperpolarizability was found, which was used to determine the tilt angle (θ) and the twist angle (ψ) of the β-sheet at different interfaces. Using SFG, the chiral and achiral components of the B₂ vibrational mode were selectively probed and were ultimately used to deduce the orientation of tachyplesin I adsorbed to a PS surface. The relative SFG signal intensities of B₁ and B₂ modes were then used to determine the orientation angles of tachyplesin I in DPPG/dDPPG lipid bilayers. This methodology can be applied to the study of β-sheets and β-sheet containing proteins on surfaces such as polymer surfaces or cell membranes in situ, with the capability of performing real time studies on conformational changes that occur in many interfacial proteins. In the future, various signal enhanced methods will be adopted to directly probe modes other than B₂ to provide additional measured parameters to determine more complicated orientations or orientation distributions. Coupled with previously reported orientation analysis of α-helices,¹ this method lends itself to the study of larger and more complex interfacial proteins that have α-helix and/or β-sheet components.

Biographies

Khoi Nguyen received his first bachelor’s degree in electrical engineering from the Institute of Telecommunications of Saigon in 2002. He then received two bachelor’s degrees in mathematics and chemistry from the New Mexico Institute of Mining and Technology in 2006. He graduated with a PhD degree in chemistry from the University of Michigan in 2009. Currently he is an assistant professor in the School of Biotechnology, International University, National University of Ho Chi Minh City.

John King received his B.S. degree in chemistry from The State University of New York at Fredonia in 2009. He is currently a graduate student at the University of Michigan in Ann Arbor, working towards his Ph.D. in physical chemistry.

Zhan Chen received his B.S. degree in chemistry from Peking University in 1988. He then received his M.S. degree in physics from Institute of Physics, Chinese Academy of Sciences in 1991. After he worked in Institute of Physics for two years as a research scientist, he went to the Department of Chemistry at the University of California at Berkeley in 1993. He received his Ph.D. degree in 1998, advised by Prof. Herbert Strauss. He then worked as a postdoctoral research fellow in Prof. Gabor Somorjai’s group at Berkeley. He started his own research group in 2000 at the University of Michigan. Currently he is a professor of Chemistry there. His research is to understand molecular structures of polymers and biological molecules at interfaces.