Abstract
Several studies have investigated the relationship between click-evoked auditory brainstem responses (ABRs) and loudness growth in human listeners. While some of these studies have reported promising results, showing a correlative relationship between click ABR and loudness growth as a function of level, additional studies are necessary to determine if similar results can be obtained with frequency-specific stimuli and more specific details of the loudness function can be derived from ABR recordings. The aims of this study, therefore, were to (1) develop a fully objective procedure that segments specific features of evoked, tone-burst ABR recordings, (2) investigate the feasibility of using information derived from these recordings for estimating frequency-specific loudness-growth functions, and (3) determine to what extent the loudness-growth estimation performance through ABR can be improved by controlling for residual noise levels and parametric fitting. Results from eight normal-hearing listeners using 1- and 4-kHz stimuli show that the average mean-square error of the loudness-growth estimation obtained through the procedure is comparable to that of standard psychoacoustical procedures used to estimate loudness growth. The data set has been made publicly available at www.physionet.org.
INTRODUCTION
The use of frequency-specific stimuli (tone bursts) for estimating loudness-growth functions from auditory brainstem responses (ABRs) could provide objective, frequency-specific information, potentially useful for hearing-aid fitting for patients not capable of performing psychoacoustical tasks. Several studies have attempted to find a relationship between ABR and loudness growth as a function of level (Pratt and Sohmer, 1977; Wilson and Stelmack, 1982; Babkoff and Pratt, 1984; Davidson et al., 1990; Serpanos et al., 1997; Gallego et al., 1999). (See Table 1 for a detailed summary.)
Table 1.
List of previous studies that have examined the relationship between ABR parameters and loudness growth. See text for more details on each study.
| Study | Stimulus | Number of trials (per level) | Noise control method | Level ranges (dB) | Psycho. procedure | # listeners (age) | ABR-loudness estimate method | Comparison method | Result |
|---|---|---|---|---|---|---|---|---|---|
| Pratt and Sohmer (1977) | Clicks | 200–300 | NA | 0–75 (steps of 5) | ME per single click | 22 normals (young) | Power fits to amp., latency, and area | Student's T-Test on the Coefficients | Correlation with amp., but authors claim results are inconclusive |
| Wilson and Stelmack (1982) | Clicks | 4096 | NA | 55–90 (step of 5) | ME per click train | 36 normals (mean 19.3) | Power fits to amp, latency of waves I through VI | Correlation coefficient and comparison of power coefficients | No significant effect found |
| Babkoff et al. (1984) (reanalysis ofPratt and Sohmer 1977) | Clicks | 200–300 | NA | 0–75 (steps of 5) | ME per single click | 22 normals (young) | Power fits to latency corrected for asymptote | Comparison of exponents | Latency exponent showed close agreement with loudness |
| Davidson et al. (1990) | Clicks | 8192 | NA | 20–100 (steps of 10) | ME per click train | 10 normals (22–24) 3 HI | Wave V amplitude | Rank order correlation | A significant correlation was found |
| Serpanos et al. (1997) | Clicks | 4000 | 0.025 mV reject | 20–90 nHL | ME and MP per click train | 10 normals (mean 34.7) 20 HI (mean 50.1) | Wave V latency | Direct correlation | Correlation was found for normals and HI with flat HL. No correlation was found for HI with sloping HL |
| Gallego et al. (1999) | Electric Clicks | 2000 | NA | 20–40 | Categorical scaling (seven levels) | 14 cochlear implantees | Wave latencies and amplitudes | ANOVA with loudness level | Waves II and V amplitudes and wave II latency were significant |
A few patterns can be observed from the list of studies that investigated ABR and loudness growth. First, the studies relied on an expert clinician to subjectively label the ABR waveform in order to identify particular peak amplitudes and latencies. These specific peak amplitudes and latencies were analyzed as a function of level in an attempt to establish a relationship with loudness growth. However, because the entire ABR waveform undergoes systematic changes as a function of level (amplitude, morphology, and latency), it is possible that a simple, objective measure that utilizes the entire ABR waveform could yield a more accurate and robust estimate of loudness growth than just the examination of a single feature. Second, it is well known that the amplitude of the ABR waveform can have a significant amount of variability due to the non-stationary nature of the background noise (Don and Elberling, 1996). Despite this well known characteristic of noise in ABR recordings, no attempt was made to control or quantify the ABR residual-noise1 power as a function of stimulus level in any of these studies. Although, for example, Serpanos et al. (1997) did apply an artifact rejection threshold, this does not guarantee that the residual noise levels are equal across all stimuli levels. Controlling for, or reporting, the residual noise levels can be valuable in determining a minimum quality level for an accurate estimation (possibly reducing the number of required trials), and in understanding the effects of this confounding variable in the estimation of loudness growth from ABR. Third, several of these studies have attempted to test if the relationship between particular ABR features and loudness growth exists through the use of linear, correlational analysis techniques. While in general this might seem reasonable, it is important to remember that loudness growth exhibits strong non-linear behavior due to compressive mechanisms. Thus, a linear correlation analysis may be inaccurate in that it will only assess the degree to which the linear component of the ABR feature matches the linear component of the loudness-growth function and may only, to some degree, trivially result from the fact that characteristics of the ABR waveform and loudness-growth functions are strongly correlated with level. A more robust measure of agreement between loudness-growth functions and ABR loudness-growth estimates is the mean-square-error (MSE) between the two curves. Finally, while some of these studies do suggest a relationship between ABR and loudness, no study, to the best of the authors’ knowledge, attempted to investigate any relationship between loudness growth and frequency-specific evoked ABR.
There are several challenges present in the use of the tone bursts instead of clicks to elicit evoked ABR. Tone-burst ABRs (TBABRs) can have a significantly lower signal-to-noise ratio, due in part to a narrower peak excitation on the basilar membrane, which results in a less synchronized neural response and an overall smaller number of neurons responding (for review, see Hall, 2006; Burkard et al., 2007). In addition, stimuli at different frequencies and levels can yield very different wave morphologies. The change in wave morphology of the evoked ABR waveform across stimulus level typically requires an expert-clinician observer in order to segment and classify the average response, making the overall measurements and analysis subjective. It is clear that an accurate, automatic analysis and segmentation of the evoked ABR waveform can potentially reduce the operational costs, analysis time, interpretive training, and the variability of the results.
Another important issue in establishing a relationship between TBABRs and loudness growth is the ability to control for, or at least assess, residual noise levels in the average TBABR as a form of quality measure. This is particularly important for evoked ABR because it is well known that noise sources can have significant variability in power throughout the duration of a single session of measurements (Don and Elberling, 1994; Don et al., 1994; Silva, 2009). Because loudness-growth estimation via evoked ABR (or TBABR) requires the comparison of several waveforms acquired across a wide range of levels, it is important to consider the residual noise levels of these averaged recordings as possible confounding factors or as additional sources of variability in the estimation procedure. Silva (2009) presented a new method based on the fixed-single-point (FSP) statistic (Don et al., 1984) that estimates residual noise levels on averaged waveforms under discrete, non-stationary noise sources. The ability to use this new method when comparing TBABRs measured across different levels can allow a better control for the variability due to differences in residual noise (i.e., the variability due to the quality of the average waveforms).
This study aims to extend the results of the previous studies by considering the following:
-
(a)
the use of frequency-specific stimuli (tone bursts) instead of clicks to help provide better frequency-specific estimates of loudness growth from ABR
-
(b)
the development of a signal processing scheme that estimates loudness growth from the TBABR waveform in an objective manner, eliminating the need for expert-clinician labeling (i.e., segmentation) and helping to provide a purely objective measure
-
(c)
controlling for residual noise levels through the use of a SNR-estimation procedure (Silva, 2009) to help account for non-stationary background noise activity
-
(d)
comparing results using the MSE and two psychoacoustical procedures: cross-modality matching (CMM) and magnitude estimation (ME). These two procedures will serve as ideal references and the MSE between the two of them will yield a reference MSE related to the inherent psychoacoustical variability in estimating individual loudness-growth functions using standard procedures (i.e., a rough estimate of the minimum achievable MSE)
-
(e)
comparing results with loudness growth estimated using tone-burst otoacoustic emissions (TBOAEs) as an alternative physiological measure. A previous study (Epstein and Silva, 2009) examined a procedure in which a specific approach to TBOAE measurements might be useful for estimating loudness growth at 1 kHz, but not at 4 kHz (likely due to stimulus ringing from the ear canal). Concurrent recording of ABR and TBOAEs is relatively simple and this TBOAE loudness estimation procedure will be used as an additional physiological reference at 1 kHz. In addition, the TBOAE MSE performance at 4 kHz will provide us with a convenient upper bound on the MSE. This is because the TBOAE estimation procedure at 4 kHz is linear and very strongly correlated with stimulus intensity (Epstein and Silva, 2009), thus generating a trivial loudness-growth estimation scenario in which the detailed characteristics of loudness growth are overlooked.
-
(f)
the data set has also been made publicly available at www.physionet.org (Goldberger et al., 2000) in order to allow other investigators to examine, analyze, and compare these data.
METHODS
Listeners
Eight listeners with normal hearing (four females, four males) ages 19–31 participated in the experiment. No listener had a history of hearing difficulties, and their audiometric thresholds did not exceed 15 dB HL at octave frequencies from 250 Hz to 8 kHz (ANSI, 1996). Additionally, all listeners had normal middle-ear function as determined via a clinical exam. Listeners were arbitrarily tested using their right ears.
Stimuli
The tone bursts used were 1-kHz tones with 4-ms duration and 4-kHz tones with 1-ms duration. The tone bursts were multiplied with a Gaussian window and then end-padded with silence to generate a stimulus length of 41.7 ms. This 2-cycle-up-2-cycle-down window duration with no plateau helped ensure consistent root mean square (rms) values, equal spectral dispersion on a logarithmic scale, and a good ABR response to transient stimuli (these parameters are recommended by Hall, 2006). The stimulus levels ranged from approximately 5 dB below each listener’s threshold to 100 dB peak-equivalent sound pressure level (peSPL) in steps of 5 dB. Levels matched the specifications of the voltage-to-level conversion provided by Etymotic Research (Elk Grove, Village, IL) for the ER-10C apparatus.
For the CMM and ME procedures, each stimulus presentation consisted of 12 concatenated 41.7-ms intervals in order to generate a train of tone bursts that lasted approximately 0.5 s. This train was presented in place of a single tone-burst in order to compensate for any potential temporal-integration effects resulting from the continuous, rapid presentation of stimuli in the ABR∕TBOAE procedure (Buus et al., 1997; Florentine et al., 1996; Zwicker and Fastl, 1999). Levels were determined by a pressure-proportional voltage-to-level conversion based on calibration levels measured in a 6-cc coupler (B&K 4152, Nærum, Denmark).
Apparatus
The stimuli were generated in MATLAB (2007b) running on Windows 2000 for CMM and MATLAB (2006b) for Ubuntu for TBOAEs, TBABRs, and ME, and converted from digital (48-kHz sampling frequency) to analog using a 32-bit Lynx Two soundcard. The analog signal was then passed through either a Tucker–Davis Technologies (TDT) (Alachua, FL) HB6 (CMM) or a TDT HB7 (TBOAEs, TBABRs, and ME) headphone buffer and presented monaurally via Sony MDR-V6 headphones (CMM) or the two transducers of the Etymotic ER-10C (TBOAEs, TBABRs, and ME) to a listener inside a double-walled, sound-attenuating booth. The different transducers resulted from laboratory limitations at the time of testing. During the TBOAE and TBABR measurements, the recordings from the ER-10C were converted from analog to digital (48-kHz sampling frequency) via a Lynx Two soundcard. Routine calibration for each system was performed to test for proper wiring and ER-10C output in a plastic 2-cc syringe coupler provided by Etymotic. For the TBOAEs, TBABRs, and ME, all levels were determined using the rms of the windowed signal relative to the specifications, which were provided by Etymotic and verified by doing an actual in ear measurement for a single listener using a Fonix 6500-CX real-ear system.
Loudness growth estimation through CMM
Listeners were presented with six repetitions of the stimulus for each level from 10 to 100 dB peSPL in random order and asked to cut a string to be “as long as the sound is loud.” After the listener cut each string, they taped it into a notebook and turned the page. Two blocks of trials were run separately, one for each of the two test frequencies. If a particular stimulus was not heard, no string was cut. Threshold values estimated from the CMM data were calculated in three steps. First, a psychometric function was estimated by measuring the percentage of trials that the listeners provided a string for each peSPL (i.e., they heard a sound). After the first step, a first-order polynomial was fitted between the data-point at the lowest peSPL level that had a 100% response rate and the data-point at the highest peSPL that had a 0% response rate. The threshold value was finally estimated by the peSPL value of the fitted first-order polynomial that yielded an estimated 50% response on the psychometric curve.
The loudness estimate for each level was the transformed geometric mean of the string lengths produced for that level. The transformation was performed in response to the finding that CMM, though it provides access to the details of the shape of the loudness function for individual listeners, yields functions with shallower slopes than other procedures (Epstein and Florentine, 2005). As such, a string-length multiplicative correction factor was determined by using a least-squares fit to match the average group data to a power function with an exponent equal to 0.3, widely used as a simple first approximation of the general form of the loudness function (Hellman and Zwislocki, 1963; Stevens and Guirao, 1964; Stevens, 1955, 1957, 1961). This correction factor was then applied to the individual data. The final loudness-growth curve was subtracted by an offset in order to yield a zero-mean loudness curve for comparison with loudness curves obtained through other modalities
Estimates for the slope of the loudness-growth function of the CMM data were obtained by determining a least-squares best fit line to the CMM data points. The slope of the fitted line was multiplied by a factor of 10 in order to yield slope values in terms of the exponent of a power function, which is a common way of describing loudness slope (Stevens, 1955).
Loudness growth estimation through ME
A second psychoacoustical estimate of the loudness-growth function was obtained by using a magnitude-estimation procedure. Listeners were presented with a series of tone bursts and asked to enter a numerical value that corresponded to the loudness of the stimulus. The listeners were told that they could give any positive number and were told to enter 0 only if no sound was heard. They were also encouraged to use decimals. The stimuli consisted of tone bursts from 10 to 100 peSPL in 5 dB steps (19 stimuli) presented in a random order. Blocks were separated by frequency. For each of the two frequencies tested (1 and 4 kHz) there was a practice test in which each level was presented only once in order to get the listener acquainted with the overall stimuli range.
The final estimate for a specific level was calculated from the geometric mean of the nonzero numbers. If a listener entered 0 more than four times for a given level, that level was not used (treated as sub-threshold) during data analysis. Threshold values estimated from the ME data were calculated in similar manner to that described in Sec. 2D (i.e., fitting a first-order polynomial to the psychometric function estimated from the percentage of nonzero responses at each level). Loudness-growth power-function exponent estimates were obtained in the same manner as those for the CMM data.
TBOAE and TBABR recordings
The TBABRs were recorded simultaneously with the TBOAEs in a sound-attenuating, electrically shielded booth. Listeners had three electrodes affixed to them (Grass F-E10ND, West Warwick, RI, with adhesive solid gel): the non-inverting electrode was positioned on the forehead, the inverting electrode was positioned on the ipsilateral mastoid (behind the ear), and the ground electrode positioned on the contralateral mastoid. Listeners were scrubbed with alcohol at the locations prior to the electrode placement. The electrode signal was then sent to a GRASS QP511 Quad AC Amplifier, where it was band-pass filtered from 30 to 3000 Hz, amplified by a factor of 50,000, sent to a 32-bit Lynx Two soundcard (outside the booth), and sampled at 48 kHz. Stimuli were presented in blocks of 1000 trials (about 41.7 ms per trial, at a presentation rate of about 24 Hz). Each block of trials was repeated on average eight times for each level yielding about 8000 recordings per level. For each level, two averages of TBOAE recordings were made. The first average consisted of a weighted mean (Elberling and Wahlgreen, 1985) of all the trials in the first half (about 4000 trials), the second average consisted of a weighted mean of all the trials in the second half (about 4000 trials). The weight for each block of trials was defined as the inverse of the estimated noise variance for that block of trials divided by the sum of all the weights (Elberling and Wahlgreen, 1985). These averages were the basis for the loudness estimation procedure described in Epstein and Silva (2009). For each frequency, the stimuli were presented in ascending order from approximately 5 dB below the listener’s threshold to 100 dB peSPL in steps of 5 dB. Threshold was determined from the maximum threshold of the CMM or ME procedure. For the ABR recordings, an artifact rejection threshold of 50 μV was applied. Throughout the experiment, a computer outside the booth displayed for the current level, two weighted sub-averages of the evoked response (along with their correlation), the estimated SNR as a function of trial, the estimated electric and acoustic noise variances as a function of trial, and the estimated power of weighted average as a function of blocks of trials. The variability in these statistics as a function of trial was used to detect any possible changes in the recording settings (such as transducer replacement, external noise interference, or electrode changes). The experimenter would monitor for any signs of a consistent increase in electric or acoustic noise-variability of an order of magnitude or higher and flag that for later quality checks. After the experiment was finished, all listeners were examined for any physical displacement of electrodes and transducers. No listeners reported any displacements of apparatus and no displacements were observed. Additionally, post analysis of residual noise (electric noise variance) for each SPL did not reveal any displacement trend as a function of level or total experiment duration.
Estimation of loudness from TBOAEs
The procedure used to estimate the loudness growth from TBOAEs was exactly the same as that described by Epstein and Silva (2009). Briefly, the loudness estimation procedure for a single level was done by taking the cross-spectrum of two independent weighted average responses within the time and frequency ranges determined by the parameters (window delay, window size, and F-ratio). The final loudness estimation for the particular level was given by summing all the positive real components of the estimated cross-spectrum. For the present analysis, the following parameters were held fixed: window delay=10 ms, window size=20 ms, window type=Hanning, F-ratio=2, where window delay determines the onset of the temporal analysis window, window size determines the length of the temporal analysis window, window type is the type of window that is applied to the data, and F-ratio is a parameter that determines the frequency bandwidth of the spectral analysis window.
Two additional loudness-growth estimates were obtained from the TBOAE procedure by using two different function fits. These two smoothed estimates were done in order to provide additional references for the evoked potential estimation procedures that utilize the same noise control methods.
Estimation of loudness from TBABRs
The estimation of loudness growth from TBABR consisted of three unique stages: a segmentation stage, a point-estimate stage, and a noise-control stage. The goal of segmentation stage was to select specific regions of the final averaged ABRs that were to be used in the point-estimate stage. The point-estimate stage calculates a single statistic from a given segmented waveform (i.e., the point estimate used in this experiment was either maximum amplitude or rms value). This point is assumed to be an estimate of the loudness at a particular level. Finally, the noise-control stage consists of the methods that attempt to correct for different residual noise levels in the TBABR waveforms due to the non-stationary nature of the background noise and irregularities in the shape of the estimated loudness function.
Stage 1—Segmentation
Eight different segmentation techniques were used for segmenting the weighted average evoked response: fullblock, abrblock, amlrblock, waveVamp, amlramp, fullsync, abrsync, and amlrsync (see Table 2 for details on each). All of the procedures were applied on the weighted averages of the recorded evoked responses. The first three segmentation techniques—fullblock, abrblock, and amrlblock—consisted of simply applying a rectangular window to a predefined time region of the evoked response. The fullblock selected the fixed region of the evoked response between 0.5 (after offset) and 41.5 after the stimulus onset. The abrblock technique selected a fixed region of the evoked response between 0.5 (after offset) and 21 ms after the stimulus onset (the early component of the evoked response). The amlrblock selected a fixed region of the evoked response between 20 and 41.5 ms after stimulus onset (late part of the response). The amlrblock response was selected based on some previous findings by Madell and Goldstein (1972) that suggest that this late response, also known as auditory middle latency response (AMLR), might show some correlation with loudness growth. The AMLR also has higher amplitude than the ABR, which might make the AMLR more robust to noise artifacts.
Table 2.
Summary of the different segmentation procedures used.
| Name | Summary | Range (ms after stimulus) |
|---|---|---|
| Fullblock | Full waveform in the specific range | 0.5 (after offset) −41.5 ms |
| Abrblock | Full waveform in the specific range | 0.5 (after offset) −21 ms |
| Amlrblock | Full waveform in the specific range | 20–41.5 ms |
| WaveVamp | Positive Maximum in the specific range | adaptive, starting level at 4.5–10 ms |
| Amlramp | Absolute maximum in the specific range | adaptive, starting level at 20–41.5 ms |
| Fullsync | Selected regions based on dot product | segmented, 0.5 (after offset) −41.5 ms |
| Abrsync | Selected regions based on dot product | segmented, 0.5 (after offset) −21 ms |
| Amlrsync | Selected regions based on dot product | segmented, 20–41.5 ms |
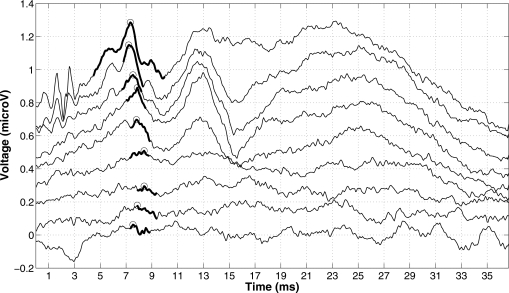
The next two segmentation techniques—waveVamp and amlramp—are based on an attempt to select well-known, specific regions of interest in the evoked response waveform that are often used by expert clinicians. The waveVamp method is an attempt to identify the amplitude of the wave V component of the ABR waveform. In order to maintain objective analysis, an algorithm attempting to simulate these expert-clinician assessments was utilized. It is initiated by selecting the largest amplitude within 4.5 and 10 ms after the stimulus onset in the evoked responses recorded at the highest SPL. The wave V component is then tracked down through lower levels by searching for the largest amplitude in the time window 0.5 ms before and 1 ms after the peak time calculated at the previous higher level. Figure 1 shows an example of how this procedure works with one data set. The amlramp segmentation procedure is exactly the same as that of waveVamp procedure except that the initial time region is between 20 and 41.5 ms after the stimulus onset and the search is performed over maximum absolute peak (as opposed to maximum positive peak in the waveVamp method).
Figure 1.
Example of how the waveVamp segmentation procedure works on one individual. The procedure is initiated by selecting the maximum between 4.5 and 10 ms after the stimulus onset at the highest recorded level (top). Subsequent wave V locations are determined by selecting the maximum peak within 0.5 ms before and 1 ms after the peak location of the previous level. The bold sections represent the regions over which the maxima were taken and the circles represent selected peaks. The waveforms in this figure were shifted vertically by an arbitrary amount for ease of comparison.
The last three procedures (fullsync, abrsync, and amlrsync) segment the evoked responses based on the degree of similarity between the current responses and the responses at the previous higher level. (It is assumed that the overall signal shape between two waveforms is similar if they were obtained at a close SPL.) The three procedures are essentially the same with the only modification being the time regions in which they are allowed to operate, with fullsync operating through 0.5 (after offset) and 41.5 after the stimulus onset, abrsync operating from 0.5 (after offset) through 21 ms after the stimulus onset, and amlrsync operating from 20 through 41.5 ms after the stimulus offset. The first step in this procedure is to obtain a time-aligned version of the evoked response obtained at a higher level with the current evoked response by selecting the time-lag that yields the maximum cross-correlation between the waveform at the previous higher level and at the current level waveforms (where n corresponds to the sample number and N is the number of samples)
| (1a) |
| (1b) |
The estimated optimal time lag of the previous level with respect to the current level, , is constrained to be within an equivalent 2-ms range (if then is set to 0). The cross-correlation between the two weighted averaged waveforms, , has length of N*2−1 and is estimated using the procedure used by Orfanidis (1996)
| (2) |
The time-aligned waveform of the previous higher level is then used to select regions on the current waveform by performing a two-step process. The first step divides each waveform into K sections of fixed length w. For each of the K sections, the dot-product (i.e., the cross-correlation at 0 lag between the signals) f(k) is calculated between the two waveforms
| (3a) |
| (3b) |
| (3c) |
Notice that a high positive value of f(k) implies a high degree of similarity between the two segments, a small value of f(k) implies a lack of similarity, and a high negative value of f(k) implies a high degree of similarity but with one of the signals inverted (multiplied by −1). The second step consists of generating a binary gating signal from f(k) by applying a threshold and multiplying the gating signal g(k) with the original waveform
| (4a) |
| (4b) |
where is the final segmented signal from and floor( ) is a function that rounds a number to the next smallest integer. The term g(floor((n∕w))) is equivalent to applying a zero-order-hold of w samples to the gating signal g(k) so that it has length equal to .
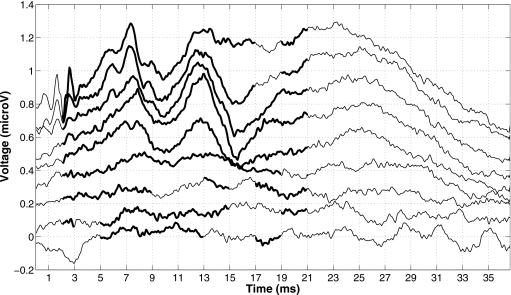
Figure 2 shows an example of the abrsync segmentation procedure on real data (using an arbitrary threshold set to th=0 and a time window length of 2 ms). The bold region is the segmented ABR—the regions for which the dot product between the current ABR and a time-aligned ABR from the next higher level exceeded a threshold value (indicating a degree of similarity between the two waveforms). The evoked responses have been shifted vertically for ease of comparison.
Figure 2.
Example of the abrsync segmentation procedure performed for one individual. The bold section represents the segmented region that was used for loudness estimation. The waveforms have been shifted vertically by an arbitrary amount for ease of comparison.
Stage 2—Point estimation
The purpose of the second stage, which is the point estimate stage, was to yield a single-point estimate of loudness for given a segmented evoked response waveform. The recorded waveforms were made zero-mean prior to any calculation of the point estimates. Two point estimates were used: the logarithm of the power of the waveform and the logarithm of the peak amplitude. The peak-amplitude point estimate was used only for the segmentation procedures waveVamp and amlramp.
Stage 3—Residual noise control
The third and final stage of the loudness-growth estimation procedure, which is the residual noise control stage, consists of attempts to minimize and control for differences in residual noise levels between the point estimates obtained at different SPLs. Two different parametric noise-control methods were implemented: wpoly, and INEX (INflected EXponential function; Epstein and Silva, 2009) fitting. These methods used residual noise estimates obtained through the weighted nonstationary fixed-multiple-point (WNS FMP) statistic, as described by Silva (2009). The WNS Fmp statistic is a modification of the FSP statistic (Don et al., 1984) that can account for measurements collected under noise sources of different powers over a variable number of trials and under normal or weighted (a.k.a., Bayesian) averaging schemes. The WNS Fmp uses an estimate of the trial-by-trial noise covariance matrix to determine the residual background noise level (for further details, see Silva 2009).
The first noise control method investigated, which is the wpoly, consists of weighted polynomial fitting to the estimated loudness growth function across L different levels (Scharf, 1991). The weighted polynomial fitting attempts to minimize the residual noise effects by applying weights to the fit that are inversely proportional to the residual noise power of each level. It is a simple polynomial regression fit, in which the P×1 polynomial coefficients θa are given by Scharf (1991)
| (5) |
where H is a L×P matrix that represents the independent variables for which the Pth order polynomial is to be evaluated (in this case, the independent variable is the stimulus SPL), are the data points to be fitted, and W is an L×L weighting matrix set to be diagonal and defined in terms of the inverse of the estimated residual noise level for each weighted average
| (6) |
The final loudness estimate for each level is then estimated by evaluating the polynomial at the respective SPL L
| (7) |
For this method the maximum polynomial order was set to 5. This is the same order as the INEX loudness-fitting model, which is a modified version of the classical Stevens power function, as described by Florentine and Epstein (2006) and Buus and Florentine (2001), and assigned specific equation parameters in Epstein and Silva (2009). The polynomial order was allowed to decrease automatically if the order was bigger than the number of data points or if the matrix H′WH was close to singular or badly scaled (i.e., if any of the singular values was close to zero).
The second noise control method, INEX fitting, was a parametric approach that involved fitting shifted versions of the INEX function (Epstein and Silva, 2009) INEX(i−x) to the point estimates obtained at each level i and selecting the best overall fit based on the combination of weighted MSE and the estimated residual noise at each level . Thus the estimated loudness growth at level L using the INEX fitting is given by
| (8a) |
| (8b) |
where the estimated optimal shift of the INEX function is given by
| (9) |
M being the total number of levels measured and is the point loudness estimate for level i. Table 3 provides a summary of the noise control procedures.
Table 3.
Summary of the different noise control methods described.
| Noise control name | Summary |
|---|---|
| Wpoly | Operates on full set of point estimates. Weighted polynomial fitting, weights proportional to inverse of residual noise levels. |
| INEX fitting | Operates on full set of point estimates. Best fit determined from weighted combination of MSE and residual noise level. |
RESULTS
Psychoacoustical results
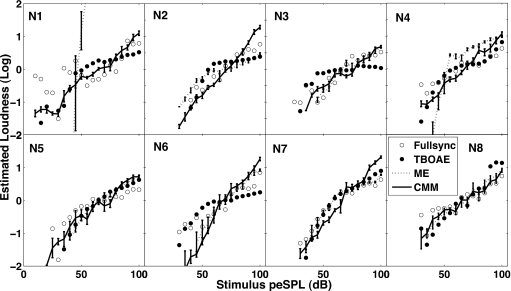
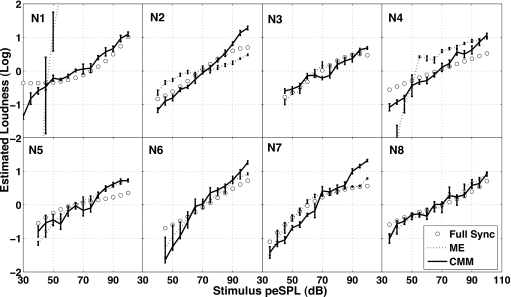
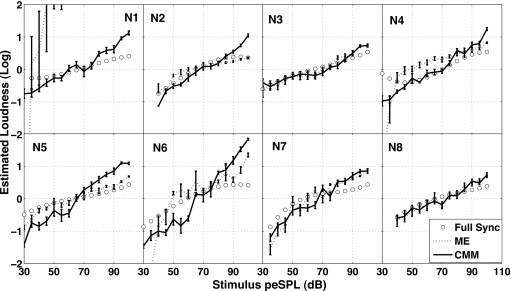
Figures 34 show the individual results for the psychoacoustical loudness-growth data (along with the physiological estimates) obtained for the eight normal-hearing listeners in response to 1- and 4-kHz tone-bursts (all functions were arbitrarily shifted to have zero mean). Most of the listeners yielded consistent loudness functions in the sense that their CMM data were in reasonable agreement with their ME data. (See Tables 4, 5 for mean square “error” differences between the two.) Some listeners, however, showed a clear discrepancy between their CMM and ME data: N1 at 1 and 4 kHz, N3 at 1 kHz, and N4 at 1 kHz. The discrepancy had a consistent pattern in that the ME was lower than CMM at near threshold levels. This could be the result of edge effects (i.e., mechanical∕motor limitations when cutting short strings for near-threshold levels), altering the shape of the CMM function at low levels. Hellman and Meiselman (1988) also found that the perception of line-length is non-linear at low levels, resulting in shallower slopes in loudness estimates involving line length. A careful observation of the MSE between the psychoacoustical MSE (Tables 4, 5) shows that N1 is clearly an outlier. This is not surprising, since N1 did not perform the magnitude-estimation task the same way as the other listeners at very low levels (even though the listener was reinstructed several times). At very low levels, rather than giving numerical estimates of the perceived loudness, the listener appeared to instead approach responding by correlating the number of zeros after the decimal point to loudness. At moderate levels, however, the listener seemed to do the task properly. The listener’s data were not discarded because it is possible that this behavior could also occur in a larger group of listeners, and such an outlier will yield more realistic comparisons of the magnitude-estimation loudness growth variability across other studies. Due to this outlying effect, results are reported both in terms of mean and median (analysis done using geometric mean yielded quantitatively similar results to that using the median).
Figure 3.
Individual loudness-growth estimates for 1 kHz tone bursts. Loudness is presented in arbitrary, zero-mean units.
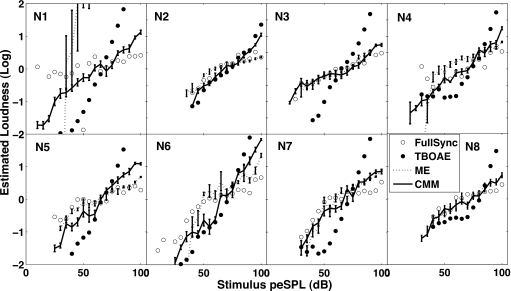
Figure 4.
Individual loudness-growth estimates for 4 kHz tone bursts. Loudness is presented in arbitrary, zero-mean units.
Table 4.
Statistics on the psychoacoustical measurement of loudness growth as a function of peSPL for 1-kHz tone bursts. The columns represent (from left to right): listener, mean-square-error between CMM and ME, CMM threshold, ME threshold, CMM slope, ME slope, average standard error on the CMM procedure, and average standard error on the ME procedure.
| Lst | MSE (CMM vs. ME) | CMM TH | ME TH | CMM slope | ME slope | CMM stderr | ME stderr |
|---|---|---|---|---|---|---|---|
| N1 | 35.84 | 10 | 30 | 0.27 | 2.33 | 0.08 | 0.91 |
| N2 | 0.24 | 30 | 30 | 0.41 | 0.19 | 0.07 | 0.04 |
| N3 | 0.03 | 35 | 45 | 0.25 | 0.26 | 0.06 | 0.06 |
| N4 | 0.54 | 30 | 35 | 0.31 | 0.50 | 0.08 | 0.12 |
| N5 | 0.03 | 20 | 40 | 0.31 | 0.29 | 0.12 | 0.05 |
| N6 | 0.04 | 35 | 45 | 0.51 | 0.38 | 0.15 | 0.12 |
| N7 | 0.11 | 30 | 35 | 0.42 | 0.29 | 0.09 | 0.06 |
| N8 | 0.01 | 30 | 35 | 0.25 | 0.27 | 0.09 | 0.09 |
| Mean | 4.60 | 27.5 | 36.87 | 0.34 | 0.57 | 0.09 | 0.18 |
| Median | 0.07 | 30 | 35 | 0.31 | 0.29 | 0.09 | 0.07 |
| St.dev. | 12.62 | 8.45 | 5.93 | 0.09 | 0.71 | 0.02 | 0.29 |
Table 5.
Statistics on the psychoacoustical measurement of loudness growth as a function of peSPL for 4-kHz tone bursts. The columns represent (from left to right): listeners, mean-square-error between CMM and ME, CMM threshold, ME threshold, CMM slope, ME slope, average standard error on the CMM procedure, and average standard error on the ME procedure.
| Lst | MSE (CMM vs. ME) | CMM TH | ME TH | CMM slope | ME slope | CMM stderr | ME stderr |
|---|---|---|---|---|---|---|---|
| N1 | 66.03 | 10 | 25 | 0.29 | 2.28 | 0.10 | 1.31 |
| N2 | 0.11 | 40 | 35 | 0.30 | 0.16 | 0.06 | 0.04 |
| N3 | 0.01 | 20 | 30 | 0.18 | 0.19 | 0.07 | 0.08 |
| N4 | 0.38 | 20 | 30 | 0.29 | 0.33 | 0.09 | 0.08 |
| N5 | 0.13 | 25 | 30 | 0.35 | 0.18 | 0.09 | 0.05 |
| N6 | 0.39 | 25 | 30 | 0.46 | 0.41 | 0.12 | 0.13 |
| N7 | 0.06 | 30 | 35 | 0.32 | 0.32 | 0.10 | 0.08 |
| N8 | 0.00 | 30 | 35 | 0.24 | 0.23 | 0.07 | 0.10 |
| Mean | 8.39 | 25 | 31.25 | 0.30 | 0.51 | 0.09 | 0.23 |
| Median | 0.12 | 25 | 30 | 0.30 | 0.27 | 0.09 | 0.08 |
| St.dev. | 23.29 | 8.86 | 3.53 | 0.08 | 0.72 | 0.01 | 0.43 |
The second columns of the Tables 4, 5 show the MSE between the CMM and the ME loudness growth estimates. It is clear that for both frequencies, listener N1 was an outlier with the MSE being an order of magnitude higher than the average. Therefore the median was also used as a measure of central tendency of the data. The thresholds were slightly higher for ME than for CMM for both frequencies, about 5 dB higher for the median (although there is significant overlap with the standard deviation). This minor difference was most likely due to different apparatus setup between CMM and ME. While on average, the 4-kHz threshold was lower than the 1-kHz threshold, individual analysis showed no consistent trend or pattern: eight thresholds were lower for 4 kHz than 1 kHz, and eight were lower for 1 kHz than 4 kHz (pooled CMM and ME threshold data). It is likely that this difference in threshold is a combination of measurement variability, greater sensitivity at 4 kHz, and greater temporal integration at 1 kHz as a result of the longer duration of the 1-kHz signal. The mean (median) estimated slope at 1 kHz was 0.34 (0.31) for CMM and 0.56 (0.29) for ME. For 4-kHz stimuli, the mean (median) estimated linear slope was 0.30 (0.30) for CMM and 0.51 (0.27) for ME. The slightly higher than expected ME mean estimates resulted from outlier N1. Figures 34 show that the ME loudness growth estimate obtained from N1 is not consistent with other listeners and not even consistent with N1’s CMM loudness growth estimates (the median values for the ME slopes are, however, more consistent with the literature). Both methods yielded consistent slope estimates across frequencies, but the CMM method was more reliable in the sense that the standard deviation for the slope estimates (last row) was an order of magnitude smaller than that of ME (0.09 vs. 0.71 for 1 kHz, and 0.08 vs. 0.72 for 4 kHz). This observation is consistent with similar studies that use CMM and ME (e.g., Serpanos et al., 1998; Collins and Gescheider, 1989). The average estimated slope was within the range of those reported in the literature: Epstein and Florentine (2005) reported a mid-to-high-level slope of about 0.18 (using uncorrected CMM), Hellman (1991) reported a slope of 0.3, Serpanos et al. (1998) reported a value of 0.32, Collins and Gescheider (1989) reported a value of 0.292, McFadden (1975) observed individual values between 0.14 and 0.24, and Stevens (1966) reported a value of 0.32. The MSE error (Tables 4, 5) from these two standard psychoacoustical procedures serves as benchmark data from which the accuracy of the evoked-potential loudness estimates are assessed.
TBABR recordings
Table 6 shows statistics describing the evoked response recordings. The wave V TBABR latency was estimated for the highest level only using the waveVamp procedure (location of maximum peak within 4.5–10 ms). The measurements are in qualitative agreement with literature (Hall, 2006) in that the average latency for the 1 kHz (7.3 ms) was longer than that for the 4 kHz tone (6.4 ms). Columns 3 and 5 describe the average (across level) residual noise levels for the responses using the WNS Fmp estimate (in μV2). There is a general consistency across listeners in that the residual noise power levels were within a 0.001 μV2 magnitude range. While the standard deviation of the mean residual noise level for 1 kHz (last row third column) was an order of magnitude lower than the total group mean (third to last row, third column), the standard deviation of the mean for the 4 kHz measure was within the same magnitude of the total group mean (the mean at 4 kHz was also twice as large as the mean at 1 kHz). The same pattern is seen on the distribution of standard deviations of the average residual noise levels (fourth and sixth columns). It is not clear why there is such a pattern.
Table 6.
Statistics for the TBABR recordings on eight normal listeners (see text for details). The names represent: V Lat—Wave V latency, Ave Noise—average residual noise power (ηV2) across peSPL, and Std Noise—standard deviation of the residual noise power (ηV2) across peSPL (see text for detail).
| Lst | V Lat (1 kHz) | V Lat (4 kHz) | Ave noise (1 kHz) | Std noise (1 kHz) | Ave noise (4 kHz) | Std noise (4 kHz) |
|---|---|---|---|---|---|---|
| N1 | 7.3 | 6.1 | 1.3 | 1.2 | 2.3 | 0.9 |
| N2 | 6.5 | 6.4 | 1.5 | 0.4 | 4.6 | 2.4 |
| N3 | 7.9 | 6.2 | 2.8 | 1.6 | 0.8 | 0.3 |
| N4 | 7.3 | 4.5 | 1.0 | 0.3 | 1.1 | 0.4 |
| N5 | 7.8 | 6.1 | 0.8 | 0.4 | 3.1 | 2.4 |
| N6 | 6.9 | 9.9 | 0.9 | 0.1 | 2.4 | 3.3 |
| N7 | 7.8 | 5.9 | 0.3 | 0.3 | 1.6 | 0.6 |
| N8 | 7.5 | 6.3 | 0.8 | 0.1 | 0.6 | 0.2 |
| Ave | 7.3 | 6.4 | 1.4 | 0.5 | 2.0 | 1.3 |
| Median | 7.4 | 6.1 | 1.3 | 0.3 | 1.9 | 0.7 |
| Std | 0.4 | 1.5 | 0.6 | 0.5 | 1.3 | 1.2 |
TBABR and TBOAE loudness growth estimation with no noise control
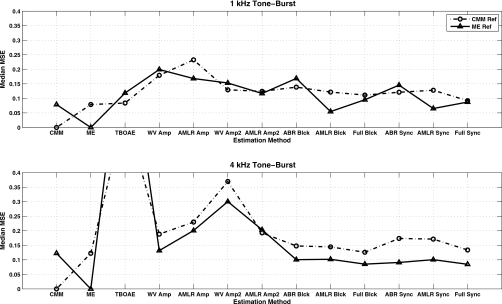
Figure 5 shows the results in terms of the median MSE calculated across the eight normal listeners for loudness growth estimation obtained through psychoacoustical procedures, TBOAE, and the ten different types of loudness estimation through evoked potentials (with no noise control). Tables 7, 8 show the individual data used to compute for the averages shown in Fig. 5. For the 1-kHz stimulus, the median MSE of the TBOAE procedures (CMM 0.083 and ME 0.118) as well as the amlrsync (CMM 0.127 and ME 0.065) and fullsync (CMM 0.092 and ME 0.087) result in nearly the same MSE as the “optimal” psychoacoustical procedures (0.078). For the 4-kHz tone-burst stimulus, however, the TBOAE yields the highest median MSE (CMM 0.692 and ME 0.949), but the amlrsync (CMM 0.171 and ME 0.1) and fullsync (CMM 0.133 and ME 0.084) still result in nearly the same MSE as the optimal psychoacoustical procedures (0.122).
Figure 5.
Median MSE between the psychoacoustical and physiological loudness growth estimates for all eight normal listeners. The legend on the bottom graph also applies to the top graph (both plots span different ordinate ranges).
Table 7.
Individual MSE between CMM and all other procedures at 1 (top) and 4 kHz (bottom).
| ME | TBOAE | WV amp | AMLR amp | WV amp2 | AMLR amp2 | ABR block | AMLR block | Full block | ABR sync | AMLR sync | Full sync | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N1 | 35.847 | 0.086 | 0.157 | 0.269 | 0.154 | 0.262 | 0.197 | 0.330 | 0.267 | 0.174 | 0.351 | 0.273 |
| N2 | 0.240 | 0.227 | 0.200 | 0.264 | 0.078 | 0.112 | 0.035 | 0.111 | 0.061 | 0.037 | 0.125 | 0.074 |
| N3 | 0.031 | 0.122 | 0.056 | 0.066 | 0.153 | 0.147 | 0.080 | 0.055 | 0.053 | 0.091 | 0.066 | 0.074 |
| N4 | 0.546 | 0.066 | 0.204 | 0.200 | 0.077 | 0.120 | 0.158 | 0.152 | 0.120 | 0.150 | 0.148 | 0.099 |
| N5 | 0.039 | 0.038 | 0.158 | 0.166 | 0.105 | 0.128 | 0.119 | 0.082 | 0.101 | 0.089 | 0.074 | 0.085 |
| N6 | 0.042 | 0.483 | 0.422 | 0.376 | 0.206 | 0.139 | 0.292 | 0.131 | 0.220 | 0.276 | 0.130 | 0.201 |
| N7 | 0.115 | 0.080 | 0.475 | 0.330 | 0.395 | 0.116 | 0.382 | 0.142 | 0.173 | 0.336 | 0.132 | 0.152 |
| N8 | 0.012 | 0.081 | 0.070 | 0.115 | 0.033 | 0.082 | 0.088 | 0.023 | 0.042 | 0.071 | 0.030 | 0.051 |
| Median | 0.078 | 0.083 | 0.179 | 0.232 | 0.129 | 0.124 | 0.138 | 0.121 | 0.111 | 0.121 | 0.127 | 0.092 |
| N1 | 66.035 | 1.479 | 0.309 | 0.370 | 0.445 | 0.472 | 0.302 | 0.199 | 0.200 | 0.314 | 0.233 | 0.197 |
| N2 | 0.110 | 0.031 | 0.168 | 0.144 | 0.504 | 0.123 | 0.082 | 0.078 | 0.071 | 0.143 | 0.076 | 0.073 |
| N3 | 0.012 | 1.106 | 0.071 | 0.084 | 0.172 | 0.094 | 0.029 | 0.059 | 0.022 | 0.041 | 0.047 | 0.019 |
| N4 | 0.389 | 0.236 | 0.207 | 0.284 | 0.149 | 0.262 | 0.215 | 0.185 | 0.147 | 0.233 | 0.233 | 0.161 |
| N5 | 0.135 | 0.893 | 0.405 | 0.589 | 0.294 | 0.661 | 0.199 | 0.253 | 0.233 | 0.204 | 0.274 | 0.253 |
| N6 | 0.391 | 0.270 | 0.585 | 0.581 | 0.556 | 0.309 | 0.541 | 0.425 | 0.419 | 0.519 | 0.532 | 0.442 |
| N7 | 0.067 | 0.901 | 0.144 | 0.175 | 0.485 | 0.080 | 0.096 | 0.103 | 0.104 | 0.085 | 0.109 | 0.106 |
| N8 | 0.008 | 0.311 | 0.037 | 0.078 | 0.267 | 0.047 | 0.041 | 0.047 | 0.041 | 0.036 | 0.052 | 0.038 |
| Median | 0.122 | 0.602 | 0.188 | 0.229 | 0.369 | 0.192 | 0.147 | 0.144 | 0.126 | 0.173 | 0.171 | 0.133 |
Table 8.
Individual MSE between ME and all other procedures at 1 (top) and 4 kHz (bottom).
| CMM | TBOAE | WV amp | AMLR amp | WV amp2 | AMLR amp2 | ABR block | AMLR block | Full block | ABR sync | AMLR sync | Full sync | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N1 | 35.847 | 35.791 | 39.311 | 41.497 | 36.534 | 40.789 | 40.645 | 42.369 | 41.657 | 40.077 | 42.674 | 41.752 |
| N2 | 0.240 | 0.061 | 0.020 | 0.027 | 0.202 | 0.119 | 0.167 | 0.048 | 0.096 | 0.155 | 0.050 | 0.081 |
| N3 | 0.031 | 0.175 | 0.051 | 0.080 | 0.082 | 0.113 | 0.034 | 0.052 | 0.026 | 0.041 | 0.063 | 0.037 |
| N4 | 0.546 | 0.592 | 1.095 | 1.016 | 0.808 | 0.702 | 1.011 | 0.959 | 0.909 | 1.002 | 0.958 | 0.817 |
| N5 | 0.039 | 0.008 | 0.228 | 0.197 | 0.178 | 0.122 | 0.174 | 0.080 | 0.124 | 0.150 | 0.082 | 0.113 |
| N6 | 0.042 | 0.254 | 0.216 | 0.182 | 0.089 | 0.046 | 0.150 | 0.038 | 0.094 | 0.140 | 0.042 | 0.088 |
| N7 | 0.115 | 0.014 | 0.182 | 0.124 | 0.127 | 0.022 | 0.169 | 0.010 | 0.023 | 0.121 | 0.005 | 0.014 |
| N8 | 0.012 | 0.053 | 0.112 | 0.153 | 0.052 | 0.093 | 0.124 | 0.056 | 0.078 | 0.097 | 0.066 | 0.085 |
| Median | 0.078 | 0.118 | 0.199 | 0.168 | 0.152 | 0.116 | 0.168 | 0.054 | 0.095 | 0.145 | 0.065 | 0.087 |
| N1 | 66.035 | 59.828 | 70.979 | 71.827 | 70.185 | 71.787 | 71.476 | 70.232 | 70.293 | 71.320 | 70.851 | 70.410 |
| N2 | 0.110 | 0.200 | 0.155 | 0.035 | 0.722 | 0.147 | 0.027 | 0.022 | 0.021 | 0.064 | 0.032 | 0.025 |
| N3 | 0.012 | 1.005 | 0.087 | 0.101 | 0.166 | 0.091 | 0.020 | 0.086 | 0.030 | 0.027 | 0.077 | 0.025 |
| N4 | 0.389 | 0.893 | 0.588 | 0.836 | 0.443 | 0.899 | 0.786 | 0.900 | 0.793 | 0.815 | 0.952 | 0.808 |
| N5 | 0.135 | 1.633 | 0.086 | 0.187 | 0.057 | 0.258 | 0.023 | 0.036 | 0.026 | 0.025 | 0.046 | 0.031 |
| N6 | 0.391 | 0.804 | 0.441 | 0.670 | 0.253 | 0.472 | 0.401 | 0.400 | 0.362 | 0.363 | 0.496 | 0.369 |
| N7 | 0.067 | 1.014 | 0.108 | 0.214 | 0.322 | 0.068 | 0.144 | 0.117 | 0.122 | 0.117 | 0.123 | 0.126 |
| N8 | 0.008 | 0.313 | 0.051 | 0.089 | 0.277 | 0.050 | 0.056 | 0.049 | 0.047 | 0.049 | 0.053 | 0.043 |
| Median | 0.122 | 0.949 | 0.131 | 0.200 | 0.300 | 0.203 | 0.100 | 0.101 | 0.085 | 0.090 | 0.100 | 0.084 |
The estimation of loudness growth through TBOAEs does show a difference with respect to frequency regardless of which psychoacoustical procedure is used to estimate loudness growth. This observation and the MSE results are in agreement with the previous study (Epstein and Silva, 2009). In fact, the TBOAE estimates at 4 kHz (CMM 0.602 and ME 0.949) might be used as a loose upper bound on the quality of the estimation. Since it has been suggested that TBOAE estimations of loudness growth at 4 kHz, using the previously described procedure, are essentially linear with respect to the stimulus, these MSE results can be thought of as related to the trivial scenario of estimating loudness growth via stimulus intensity alone and ignoring any perceptual or physiological response. The evoked-potentials estimation also seems to be consistently worse for CMM than for ME at 4 kHz. In general it seems like the “sync” segmentation procedures (fullsync, abrsync, and amlrsync) are the ones that yield the lower MSEs of the physiological responses, in addition to showing robustness across stimulus frequency. Their median performances are within the same range as the psychoacoustical references (and similar to the TBOAE at 1 kHz). Figures 34 show the individual loudness growth estimates obtained through CMM, ME, and TBOAEs, and using the fullsync procedures on the evoked response. The smallest MSE for the fullsync procedure at 1 kHz was given by listener N8 for CMM (0.0511) and N7 for ME (0.0140). The smallest MSE for the fullsync procedure at 4 kHz was given by listener N3 for CMM (0.0191) and listener N2 for ME (0.0255). The overall smallest MSE was 0.005 (N7 at 1 kHz between ME and amlrsync) and the overall largest MSE was 71.827 (listener N1 at 4 kHz between ME and amlramp). The listener that showed the most consistency within the psychoacoustical procedures (N8, MSE=0.008 at both 1 and 4 kHz), also yielded among the best MSE on the fullsync procedure across conditions (Table 7, 8, last column).
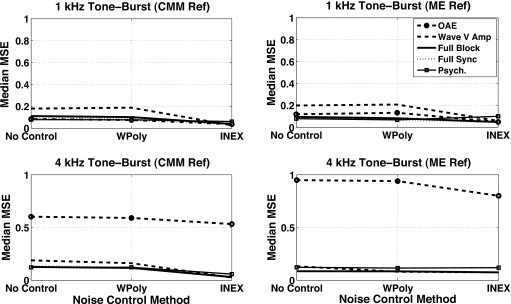
TBABR loudness growth estimation noise control and parametric fitting
Figure 6 compares the results in terms of the median MSE calculated across the eight normal listeners for loudness growth estimation obtained using the two different noise control methods. For the psychoacoustical procedures and TBOAE, the noise control methods were applied with the residual weights all set to 1 (uniform) across all SPLs. In general, the parametric noise control using the INEX function yielded the lowest median MSE. The weighted polynomial fitting, in some cases (especially at 4 kHz), yields a small improvement in the MSE. The noise-control methods also seem to have a very small advantage when used on the ME estimation data with the CMM treated as the reference loudness growth (first column). The noise-control methods yielded the greatest benefit to the wave V amp procedure at 1 kHz.
Figure 6.
Median MSE for five different loudness growth procedures according to the noise control method applied. For the psychoacoustical and TBOAE procedures, the noise control was used with all residual weights being equal (uniform) across SPL.
Figures 78 show the individual loudness growth estimation for the fullsync procedure using the INEX noise control method along with the CMM and ME raw data for comparison. The results were similar using the wpoly noise control method, not shown here. There is some individual variability, but many listeners showed good agreement between the physiological and psychoacoustical estimates for both noise control methods.
Figure 7.
Individual loudness-growth estimation for 1-kHz tone burst using CMM, ME, and full sync procedures with INEX noise control applied to fullsync. Loudness is presented in arbitrary, zero-mean units.
Figure 8.
Individual loudness growth estimation for 4-kHz tone burst using CMM, ME and fullsync procedures with weighted polynomial noise control applied to fullsync. Loudness is presented in arbitrary, zero-mean units.
Generally, the ABR-derived loudness and psychoacoustical measures matched well, always within a relative scope of similarity. If a more precise examination is performed to see whether all listeners behaved similarly, there is some notable variability. In examining individual fits in Figs. 78 (Tables 7, 8), it is important to note several limitations in the presentation of data. First, all curves are zero-mean presentations such that the absolute value at any point or range of points is not the relevant point of comparison, but rather the similarity of the slope as a function of level or within a range of levels. Second, there is great variability in psychoacoustical procedures, resulting in most researchers recommending that while these procedures are excellent for group assessments, they are limited in usefulness when examining individual loudness growth (see Epstein and Florentine, 2005, 2006; McFadden, 1975 for discussion). As such, it is not surprising that the listeners with the smallest internal variability (see error bars as well as Tables 7, 8) also showed the best correspondence with ABR results (see particularly listeners N3 and N8). As discussed earlier, listener N1 showed difficulty with ME, so the correspondence between ME and ABR estimates is poor, but the relationship with CMM is reasonable, but not exceptional particularly at low levels. This may have resulted from overestimation of low-level ABR-derived loudness due to an elevated noise floor. Other listeners also show a similar pattern of shallow ABR functions at low levels (N5 at 1 kHz, N6 at both frequencies, and N7 at 4 kHz). In many cases, ABR estimates match one of the psychoacoustical estimates well, but are less consistent with the other psychoacoustical measure (N7 at 1 kHz, N2 at 4 kHz, and N5 at 4 kHz). Still others fall between the psychoacoustical measures (N2 and N4 at 1 kHz) or match well except for within a certain range (N4 at 4 kHz at low levels). Overall, there is relative consistency between measures and a better-than-correlational relationship between loudness estimated here from ABR and the psychoacoustical standards it has been compared with.
SUMMARY AND CONCLUSIONS
This work has investigated the feasibility of using frequency specific TBABR to objectively estimate loudness growth in humans. Several signal processing schemes were developed to extract specific features of the auditory evoked responses without the need for an expert clinician. Specific statistics (i.e., power) from these segmented waveforms were measured and compared as a function of stimulus level in order to determine if they bear any resemblance to the individual loudness growth functions. The MSE between the estimated loudness growth from TBABRs and two standard psychoacoustical procedures, CMM and ME, show that the procedures developed here can operate close to the performance range of the two psychoacoustical procedures and yield smaller overall MSE than loudness growth estimates obtained through TBOAEs (see Tables 7, 8), particularly at 4 kHz (albeit at a significant increase data collection time). In contrast to any known previous work, the procedure that yielded the overall best performance (fullsync) utilized the average power of portions of the waveform response that were synchronized across level through the entire response time (0.5–41.5 ms after stimulus offset). Additional improvements on loudness growth estimation through TBABRs were obtained by controlling for residual noise levels (i.e., the quality of the recorded response) through parametric fitting either using weighted polynomials or shifted INEX functions.
ACKNOWLEDGMENTS
The authors wish to thank Dr. Jeremy Marozeau for contributing to the initial development of the software for the recording of the evoked responses, Dr. Ying-Yee Kong for assistance with calibration of apparatus, Nora Rosenfeld, Shoshannah Kantor, and Gwen Deevy for assistance with data collection, and Maria Zilberberg for assistance with editing the manuscript. This work was supported by the Capita Foundation and NIH (Grant No. NIDCD 1R03DC009071).
Footnotes
Residual noise is defined here as the amount of noise left on the final averaged waveform.
References
- MATLAB version (2006b). Natick, Massachusetts: The MathWorks, Inc.
- MATLAB version (2007b). Natick, Massachusetts: The MathWorks, Inc.
- ANSI (1996). “American national standard specification for audiometers,” ANSI S3.6-1996.
- Babkoff, H., and Pratt, H. (1984). “Auditory brainstem evoked potential latency-intensity functions: A corrective algorithm,” Hear. Res. 16, 243–249. 10.1016/0378-5955(84)90113-8 [DOI] [PubMed] [Google Scholar]
- Burkard, R. F., Don, M., and Eggermont, J. J. (2007). Auditory Evoked Potentials: Basic Principles and Clinical Application (Lippincott Williams & Wilkins, Baltimore, MD: ). [Google Scholar]
- Buus, S., and Florentine, M., 2001, “Modifications to the power function for loudness,” in Proceedings of the Fechner Day 2001, Pabst, Berlin, pp. 236–241.
- Buus, S., Florentine, M., and Poulsen, T. (1997). “Temporal integration of loudness, loudness discrimination, and the form of the loudness function,” J. Acoust. Soc. Am. 101, 669–680. 10.1121/1.417959 [DOI] [PubMed] [Google Scholar]
- Collins, A. A., and Gescheider, G. A. (1989). “The measurement of loudness in individual children and adults by absolute magnitude estimation and cross-modality matching,” J. Acoust. Soc. Am. 85, 2012–2021. 10.1121/1.397854 [DOI] [PubMed] [Google Scholar]
- Davidson, S. A., Wall, L. G., and Goodman, C. M. (1990). “Preliminary studies on the use of an ABR amplitude projection procedure for hearing aid selection,” Ear Hear. 11, 332–339. 10.1097/00003446-199010000-00003 [DOI] [PubMed] [Google Scholar]
- Don, M., and Elberling, C. (1994). “Evaluating residual background noise in human auditory brain-stem responses,” J. Acoust. Soc. Am. 96, 2746–2757. 10.1121/1.411281 [DOI] [PubMed] [Google Scholar]
- Don, M., and Elberling, C. (1996). “Use of quantitative measures of auditory brain-stem response peak amplitude and residual background noise in the decision to stop averaging,” J. Acoust. Soc. Am. 99, 491–499. 10.1121/1.414560 [DOI] [PubMed] [Google Scholar]
- Don, M., Elberling, C., and Waring, M. (1984). “Objective detection of averaged brainstem responses,” Scand. Audiol. 13, 219–228. [DOI] [PubMed] [Google Scholar]
- Don, M., Ponton, C. W., Eggermont, J. J., and Masuda, A. (1994). “Auditory brainstem response (ABR) peak amplitude variability reflects individual differences in cochlear response time,” J. Acoust. Soc. Am. 96, 3476–3491. 10.1121/1.410608 [DOI] [PubMed] [Google Scholar]
- Elberling, C., and Wahlgreen, O. (1985). “Estimation of auditory brainstem response, ABR, by means of Bayesian inference,” Scand. Audiol. 14, 89–96. [DOI] [PubMed] [Google Scholar]
- Epstein, M., and Florentine, M. (2005). “A test of the equal-loudness-ratio hypothesis using cross-modality matching functions,” J. Acoust. Soc. Am. 118, 907–913. 10.1121/1.1954547 [DOI] [PubMed] [Google Scholar]
- Epstein, M., and Florentine, M. (2006). “Loudness of brief tones measured by magnitude estimation and loudness matching,” J. Acoust. Soc. Am. 119, 1943–1945. 10.1121/1.2177592 [DOI] [PubMed] [Google Scholar]
- Epstein, M., and Silva, I. (2009). “Analysis of parameters for the estimation of loudness from tone-burst otoacoustic emissions,” J. Acoust. Soc. Am. 125, 3855–3864. 10.1121/1.3106531 [DOI] [PubMed] [Google Scholar]
- Florentine, M., Buus, S., and Poulsen, T. (1996). “Temporal integration of loudness as a function of level,” J. Acoust. Soc. Am. 99, 1633–1644. 10.1121/1.415236 [DOI] [PubMed] [Google Scholar]
- Florentine, M., and Epstein, M. (2006). “To honor Stevens and repeal his law (for the auditory system),” in Proceedings of the Fechner Day, St. Albans, England.
- Gallego, S., Garnier, S., Micheyl, C., Truy, E., Morgon, A., and Collet, L. (1999). “Loudness growth functions and EABR characteristics in digisonic cochlear implantees,” Acta Oto-Laryngol. 119, 234–238. 10.1080/00016489950181738 [DOI] [PubMed] [Google Scholar]
- Goldberger, A. L., Amaral, L. A. N., Glass, L., Hausdorff, J. M., Ivanov, P. Ch., Mark, R. G., Mietus, J. E., Moody, G. B., Peng, C. K., and Stanley, H. E. (2000). “PHYSIOBANK, PHYSIOTOOLKIT, and PHYSIONET: Components of a new research resource for complex physiologic signals,” Circulation 101, e215–e220. [DOI] [PubMed] [Google Scholar]
- Hall, J. W. (2006). New Handbook for Auditory Evoked Responses (Allyn & Bacon, Inc., Boston, MA: ). [Google Scholar]
- Hellman, R. P. (1991). “Loudness scaling by magnitude scaling: Implications for intensity coding,” in Ratio Scaling of Psychological Magnitude: In Honor of the Memory of S. S. Stevens, edited by Gescheider G. A. and Bolanowski S. J., (Erlbaum, Hillsdale, NJ: ). [Google Scholar]
- Hellman, R. P., and Meiselman, C. H. (1988). “Prediction of individual loudness exponents from cross-modality matching,” J. Speech Hear. Res. 31, 605–615. [DOI] [PubMed] [Google Scholar]
- Hellman, R. P., and Zwislocki, J. J. (1963). “Monaural loudness function at 1000 cps and interaural summation,” J. Acoust. Soc. Am. 35, 856–865. 10.1121/1.1918619 [DOI] [Google Scholar]
- Madell, J. R., and Goldstein, R. (1972). “Relation between loudness and the amplitude of the early components of the averaged electroencephalic response,” J. Speech Hear. Res. 15, 134–141. [DOI] [PubMed] [Google Scholar]
- McFadden, D. (1975). “Duration-intensity reciprocity for equal loudness,” J. Acoust. Soc. Am. 57, 702–704. 10.1121/1.380496 [DOI] [PubMed] [Google Scholar]
- Orfanidis, S. J. (1996). “Optimum Signal Processing. An Introduction,” 2nd Edition, Prentice-Hall, Englewood Cliffs, NJ. [Google Scholar]
- Pratt, H., and Sohmer, H. (1977). “Correlations between psychophysical magnitude estimates and simultaneously obtained auditory nerve, brain stem and cortical responses to click stimuli in man,” Electroencephalogr. Clin. Neurophysiol. 43, 802–812. 10.1016/0013-4694(77)90003-7 [DOI] [PubMed] [Google Scholar]
- Scharf, L. (1991). “Statistical signal processing: Detection, estimation, and time series analysis,” in Addison-Wesley Series in Electrical and Computer Engineering: Digital Signal Processing (Addison-Wesley Publishing Company Inc., Reading, MA: ). [Google Scholar]
- Serpanos, Y. C., O’Malley, H., and Gravel, J. S. (1997). “The relationship between loudness intensity functions and the click-ABR wave V latency,” Ear Hear. 18, 409–419. 10.1097/00003446-199710000-00006 [DOI] [PubMed] [Google Scholar]
- Serpanos, Y. C., O’Malley, H., and Gravel, J. S. (1998). “Cross-modality matching and the loudness growth function for click stimuli,” J. Acoust. Soc. Am. 103, 1022–1032. 10.1121/1.421218 [DOI] [PubMed] [Google Scholar]
- Silva, I. (2009). “Estimation of postaverage SNR from evoked responses under non-stationary noise,” IEEE Trans. Biomed. Eng. 56, 2123–2130. 10.1109/TBME.2009.2021400 [DOI] [PubMed] [Google Scholar]
- Stevens, J. C., and Guirao, M. (1964). “Individual loudness functions,” J. Acoust. Soc. Am. 36, 2210–2213. [Google Scholar]
- Stevens, S. S. (1955). “The measurement of loudness,” J. Acoust. Soc. Am. 27, 815–827. 10.1121/1.1908048 [DOI] [Google Scholar]
- Stevens, S. S. (1957). “Concerning the form of the loudness function,” J. Acoust. Soc. Am. 29, 603–606. 10.1121/1.1908979 [DOI] [Google Scholar]
- Stevens, S. S. (1961). “To honor Fechner and repeal his law,” Science 133, 80–86. 10.1126/science.133.3446.80 [DOI] [PubMed] [Google Scholar]
- Stevens, S. S. (1966). “Brightness and loudness as a function of stimulus duration,” Percept. Psychophys. 1, pp. 319–327. [Google Scholar]
- Wilson, K., and Stelmack, R. (1982). “Power functions of loudness magnitude estimations and auditory brainstem evoked responses,” Percept. Psychophys. 31, 561–565. [DOI] [PubMed] [Google Scholar]
- Zwicker, E., and Fastl, H. (1999). “Psychoacoustics: Facts and models,” Springer Series in Information Sciences (Springer, New York: ), Vol. 22. [Google Scholar]