Communications: Drift and diffusion in a tube of periodically varying diameter. Driving force induced intermittency

Abstract

We show that the effect of driving force F on the effective mobility and diffusion coefficient of a particle in a tube formed by identical compartments may be qualitatively different depending on the compartment shape. In tubes formed by cylindrical (spherical) compartments the mobility monotonically decreases (increases) with F and the diffusion coefficient diverges (remains finite) as F tends to infinity. In tubes formed by cylindrical compartments, at large F there is intermittency in the particle transitions between openings connecting neighboring compartments.

Mobility μ₀ and diffusion coefficient D₀ of a point Brownian particle in a cylindrical tube are independent of the driving force. This is not true for a tube of varying diameter. In this paper we discuss how a uniform driving force F affects the particle motion in cylindrically symmetric tubes formed by identical compartments of two different shapes, spherical and cylindrical, schematically shown in Figs. 1a, 2a. Neighboring compartments are connected by openings of radius a, through which the particle can go from one compartment to the other. On times when the particle displacement significantly exceeds the compartment length l, it is convenient to characterize the motion by effective mobility μ_eff(F), or effective drift velocity v_eff(F)=μ_eff(F)F, and effective diffusion coefficient D_eff(F). Both μ_eff(0) and D_eff(0) are smaller than their counterparts in a purely cylindrical tube because of periodic entropy wells and barriers for the particle motion along the tube axis. The major focus of the present paper is on the F-dependences of the effective mobility and diffusion coefficient in tubes of the two types as well as on the particle transit times between neighboring openings. Similar problems of transport in the presence of periodic entropy barriers have attracted a lot of attention in recent years.^{1, 2, 3, 4, 5} The reason is that entropy barriers are ubiquitous. They are found in porous media and nanomaterials as well as in biological cells and cellular compartments. Traditionally these problems are considered for diffusing point particles, i.e., effects of inertia and hydrodynamic interactions are neglected.^{1, 2, 3, 4, 5}

Figure 1.

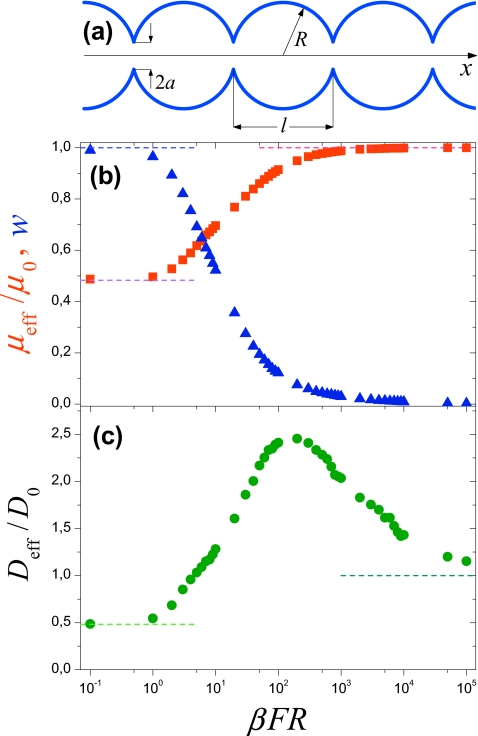
(a) Schematic representation of the tube formed by spherical compartments. (b) Effective mobility and (c) diffusion coefficient of a point particle in such a tube found in Brownian dynamics simulations at ν=a∕R=0.3 $\left(l∕R=2\sqrt{1-{\nu }^2}\approx 1.91\right)$ are shown by squares and circles, respectively, while triangles in panel (b) show function w(F), Eq. 7. Dashed lines represent asymptotic behaviors of the corresponding quantities. μ_eff and D_eff were calculated by mapping motion of the particle onto the random walk among the openings and using the formulas for μ_eff and D_eff derived in Ref. 13. The results were obtained by averaging over 2.5×10⁴ transitions among the openings. If the trajectory crossed the compartment wall, the step was rejected. The dimensionless time step $\Delta \tilde{t}=D\Delta t∕R^2$ was different at different values of the driving force: $\Delta \tilde{t}={10}^{-6}$ at βFR≤1, $\Delta \tilde{t}={10}^{-6}∕\left(\beta FR\right)$ at βFR≥1. The error in our numerical results is smaller than the size of the symbols in the figure.

Figure 2.

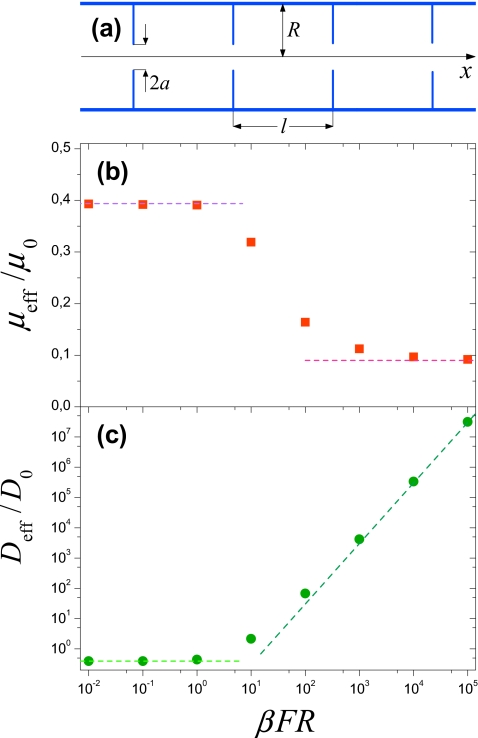
(a) Schematic representation of the tube formed by cylindrical compartments. (b) Effective mobility and (c) diffusion coefficient of a point particle in such a tube found in Brownian dynamics simulations at ν=a∕R=0.3 and l∕R=2 are shown by squares and circles, respectively. Dashed lines represent asymptotic behaviors of the corresponding quantities. μ_eff and D_eff were calculated using the first two moments of the particle displacement, which were obtained by averaging over 10⁵ trajectories. If the trajectory crossed the tube wall (the partition), only the displacement along the tube axis (normal to the axis) was accepted. The dimensionless time step $\Delta \tilde{t}=D\Delta t∕R^2$ was different at different values of the driving force:$\Delta \tilde{t}\times {10}^7=20\left(\beta FR\le 10\right)$, 5 (βFR=10²,10³), 3.2 (βFR=10⁴), 1.25 (βFR=10⁵). The number of time steps increased from 5×10⁷ at small F to 1.2×10⁸ at large F, so that the length of the trajectories varied from 15R²∕D at large F to 100R²∕D at small F. The error in our numerical results is smaller than the size of the symbols in the figure.

At F=0 the major approach to the problem is based on the Fick–Jacobs equation⁶ generalized by Zwanzig⁷ and Reguera and Rubi;⁸ a more sophisticated approach has been developed by Kalinay and Percus.⁹ The generalized Fick–Jacobs equation is a one-dimensional Smoluchowski equation that describes diffusion in the entropy potential. For one-dimensional Brownian motion in a regular periodic potential it has been shown¹⁰ that (i) the effective mobility monotonically increases with F from μ_eff(0)<μ₀ to μ_eff(∞)=μ₀, where μ₀ is the particle mobility in the absence of the periodic potential; (ii) dependence D_eff(F) is nonmonotonic: first it increases from D_eff(0)<D₀ to its maximum value, which is larger than the particle diffusion coefficient in the absence of the periodic potential D₀, and then decreases approaching D_eff(∞)=D₀ from above as F→∞. Similar behavior of μ_eff(F) and D_eff(F) in the case of entropy potentials has been reported in recent papers^{1a, 2a} devoted to the particle motion in quasi-two-dimensional periodic systems (slits of periodically varying width).

The question arises whether the effect of an external driving force on Brownian motion in periodic entropy potentials is always similar to that on motion in a periodic regular potential or not. In the present paper we show that dependences μ_eff(F) and D_eff(F) are qualitatively different when the tube is formed by cylindrical compartments (cc) separated from each other by infinitely thin periodic partitions containing circular openings in their centers [Fig. 2a]. In such a tube ${\mu }_{\text{eff}}^{\text{cc}}\left(F\right)$ monotonically decrease with F [Fig. 2b] from ${\mu }_{\text{eff}}^{\text{cc}}\left(0\right)$ to ${\mu }_{\text{eff}}^{\text{cc}}\left(\infty \right)$ given by

$${\mu }_{\text{eff}}^{\text{cc}}\left(\infty \right)={\mu }_0{\nu }^2,\nu =a∕R,$$ (1)

where R is the tube radius. Effective diffusion coefficient, $D_{\text{eff}}^{\text{cc}}\left(F\right)$, monotonically increases with F [Fig. 2c] approaching its large-F asymptotic behavior,

$$D_{\text{eff}}^{\text{cc}}\left(F\right)=\frac{{\nu }^4}{4}\left[\text{ln}\left(\frac{1}{{\nu }^2}\right)-1+{\nu }^2\right]{\left(\beta FR\right)}^2{D}_0,$$ (2)

where β=1∕(k_BT) with the standard notations k_B and T for the Boltzmann constant and absolute temperature. At the same time, when the tube is formed by spherical compartments (sc) [Fig. 1a], dependences ${\mu }_{\text{eff}}^{\text{sc}}\left(F\right)$ and $D_{\text{eff}}^{\text{sc}}\left(F\right)$ are similar to those reported in Refs. ^{1a, 2a, 10}. In this case ${\mu }_{\text{eff}}^{\text{sc}}\left(F\right)$ monotonically increases with F [Fig. 1b] from ${\mu }_{\text{eff}}^{\text{sc}}\left(0\right)$ to ${\mu }_{\text{eff}}^{\text{sc}}\left(\infty \right)={\mu }_0$, while $D_{\text{eff}}^{\text{sc}}\left(F\right)$ first increases from $D_{\text{eff}}^{\text{sc}}\left(0\right)$ to its maximum value which is larger than D₀, and then decreases approaching $D_{\text{eff}}^{\text{sc}}\left(\infty \right)=D_0$ from above asF→∞ [Fig. 1c]. In addition to unconventional behavior of ${\mu }_{\text{eff}}^{\text{cc}}\left(F\right)$ and $D_{\text{eff}}^{\text{cc}}\left(F\right)$, motion in the tube separated into cylindrical compartments has another interesting feature: when the driving force is large enough, there are two different scenarios of the particle transition between neighboring openings, fast and slow. In other words, there is intermittency¹¹ in the transitions.

We begin our discussion of the dependences μ_eff(F) and D_eff(F) with consideration of the limiting cases of very small and very large driving force. Small-F asymptotic behavior of μ_eff(F) can be found using known results for D_eff(0) and the Einstein relation. For the tube formed by spherical compartments of radius R connected by circular openings of radius $a=\sqrt{R^2-l^2∕4}$, it has been shown⁴ that $D_{\text{eff}}^{\text{sc}}\left(0\right)\approx \left(6\nu ∕\pi \right)D_0$, if ν<0.2, and $D_{\text{eff}}^{\text{sc}}\left(0\right)\approx \left[3\nu ∕\left(2+{\nu }^2\right)\right]D_0$, if 0.2<ν≤1, where $\nu =a∕R=\sqrt{1-l^2∕\left(4R^2\right)}$. This leads to

$${\mu }_{\text{eff}}^{\text{sc}}\left(0\right)=\beta D_{\text{eff}}^{\text{sc}}\left(0\right)\approx {\mu }_0\times \{\begin{array}{cc}6\nu ∕\pi ,& \nu <0.2\\ 3\nu ∕\left(2+{\nu }^2\right),& 0.2<\nu \le 1.\end{array}\phantom{\}}$$ (3)

Asymptotic behaviors of ${\mu }_{\text{eff}}^{\text{sc}}\left(F\right)$ and $D_{\text{eff}}^{\text{sc}}\left(F\right)$ in the opposite limiting case can be found using the observation that when F→∞ the particle spends practically all time in the cylinder of radius a surrounding the tube axis [Fig. 1b]. As a consequence, the particle is unaware about variation of the tube diameter, and its effective mobility and diffusion coefficient are identical to those in a cylindrical tube, ${\mu }_{\text{eff}}^{\text{sc}}\left(\infty \right)={\mu }_0$, $D_{\text{eff}}^{\text{sc}}\left(\infty \right)=D_0$.

For the tube formed by cylindrical compartments of radius R and length l, with l>R, it has been shown^5b that $D_{\text{eff}}^{\text{cc}}\left(0\right)\approx \left\{2l\nu f\left(\nu \right)∕\left[\pi R+2l\nu f\left(\nu \right)\right]\right\}{D}_0$, where f(ν)=(1+1.37ν−0.37ν⁴)∕(1−ν²)². Then the Einstein relation leads to

$${\mu }_{\text{eff}}^{\text{cc}}\left(0\right)=\beta D_{\text{eff}}^{\text{cc}}\left(0\right)\approx \frac{2l\nu f\left(\nu \right)}{\pi R+2l\nu f\left(\nu \right)}{\mu }_0.$$ (4)

To find the large-F asymptotic behaviors of ${\mu }_{\text{eff}}^{\text{cc}}\left(F\right)$ and $D_{\text{eff}}^{\text{cc}}\left(F\right)$, Eqs. 1, 2, we use the fact that infinitely thin partitions do not affect the equilibrium uniform distribution of the particle over the tube radius. The distribution at arbitrary value of the driving force is given by p_eq(ρ)=1∕(πR²), where ρ is the radial coordinate of the particle counted from the tube axis in the cylindrical coordinate system (x,ρ), in which x denotes the particle coordinate along the tube axis. The radial distribution is obtained from the three-dimensional distribution of the particle position in the tube by integrating this distribution over x from minus to plus infinity. When |ρ|>a, strong driving force presses the particle to the partition, so that the particle does not move along the tube until it reaches the opening due to its radial diffusion. As a result, at large F the uniform equilibrium radial distribution is organized as follows. Its fraction 1−ν² is mainly localized near the partitions, while the rest is spread in the cylinder of radius a connecting the openings. This distribution differs qualitatively from its counterpart in the tube formed by spherical compartments where the particle spends all the time in the cylinder connecting the openings. Mean displacement of the particle along the tube axis, ⟨Δx(t|F)⟩, observed for a sufficiently long time t is given by

$$⟨\Delta x\left(t|F\right)⟩={\mu }_{0}F⟨{\tau }_a\left(t\right)⟩,$$ (5)

where ⟨τ_a(t)⟩ is the mean residence time spent inside the circle of radius a by the particle that diffuses inside the larger circle of radius R, which is concentric with the smaller circle. Because of the ergodicity ⟨τ_a(t)⟩=ν²t, t→∞, and hence, ⟨Δx(t|F)⟩=μ₀ν²Ft that leads to the result given in Eq. 1.

To derive the expression for $D_{\text{eff}}^{\text{cc}}\left(F\right)$ given in Eq. 2, consider the variance of the particle displacement for a long time t, ${\sigma }_{\Delta x}^2\left(t|F\right)=⟨{\left[\Delta x\left(t|F\right)\right]}^2⟩-{⟨\Delta x\left(t|F\right)⟩}^2=2D_{\text{eff}}^{\text{cc}}t$. At large F, ${\sigma }_{\Delta x}^2\left(t|F\right)$ is due to the fluctuations of the particle residence time in the circle of radius a,

$${\sigma }_{\Delta x}^2\left(t|F\right)\approx {\mu }_0^2{F}^2{\sigma }_{{\tau }_a}^2\left(t\right),F\to \infty ,$$ (6)

where ${\sigma }_{{\tau }_a}^2\left(t\right)=⟨{\left[{\tau }_a\left(t\right)\right]}^2⟩-{⟨{\tau }_a\left(t\right)⟩}^2$ is the variance of this residence time. Using the exact asymptotic expression for the variance derived in Ref. 12, ${\sigma }_{{\tau }_{\alpha }}^2\left(t\right)={\nu }^4\left[\text{ln}\left(1∕{\nu }^2\right)-1+{\nu }^2\right]\left[R^2∕\left(2D_0\right)\right]t$, t→∞, we arrive at the result in Eq. 2.

We find functions μ_eff(F) and D_eff(F) over the entire range of F by Brownian dynamics simulations performed by numerical integration of the stochastic equation of motion using the forward Euler algorithm (see more details in the figure captions). This is done at ν=a∕R=0.3 for both tube geometries; the compartment lengths for the tubes of the two types, respectively, are $l_{\text{sc}}=2R\sqrt{1-{\nu }^2}\approx 1.91R$ and l_cc=2R. The results presented in Figs. 1b, 1c, 2b, 2c show that both μ_eff(F) and D_eff(F) have qualitatively different behaviors in tubes of the two types. This happens in spite of the fact that the radii of the connecting openings are identical and the compartment lengths are close.

For the tube formed by spherical compartments, we also found mean times spent by the particle outside and inside the cylinder of radius a surrounding the tube axis, ⟨τ_out(F)⟩ and ⟨τ_in(F)⟩, respectively. In Fig. 1b we show the ratio of these times, ⟨τ_out(F)⟩∕⟨τ_in(F)⟩, multiplied by the ratio of the corresponding volumes, V_in∕V_out, where V_in=πa²l andV_out=(πl∕3)(2R²+a²)−V_in. We denote the product of the two ratios by w(F),

$$w\left(F\right)=\frac{⟨{\tau }_{\text{out}}\left(F\right)⟩V_{\text{in}}}{⟨{\tau }_{\text{in}}\left(F\right)⟩V_{\text{out}}}.$$ (7)

Because of the ergodicity w(0)=1. As shown in Fig. 1b, w(F) monotonically decreases with F since the fraction of time spent by the particle inside the cylinder increases with F. As F→∞, w(F)→0 since the particle spends practically all time in the cylinder. This contrasts sharply with the particle behavior in the tube formed by cylindrical compartments. In such a tube the fraction of time spent by the particle in the narrow cylinder of radius a is independent of the strength of the driving force and equal to ν²=a²∕R², so that w(F)=1. Note that localization of the particle probability density in the central part of the elementary cell induced by the driving force has been reported in quasi-two-dimensional periodic systems.^1b

To gain additional insight into the driving force effect on the particle motion, we studied the distributions of the particle transit time τ between neighboring openings in tubes of the two types. The mean transit time, ⟨τ⟩=l∕[μ_eff(F)F], monotonically decreases as F increases. The large-F asymptotic behaviors of ⟨τ⟩ in tubes of the two types are different,

$$⟨{\tau }_{\text{sc}}⟩=\frac{l_{\text{sc}}}{{\mu }_{0}F},⟨{\tau }_{\text{cc}}⟩=\frac{l_{\text{cc}}}{{\mu }_{0}F{\nu }^2},$$ (8)

where we have used ${\mu }_{\text{eff}}^{\text{sc}}\left(\infty \right)={\mu }_0$ and ${\mu }_{\text{eff}}^{\text{cc}}\left(\infty \right)={\mu }_0{\nu }^2$, Eq. 1. At large F the probability density of the transit time in the tube formed by spherical compartments φ_sc(τ) takes its limiting form, φ_sc(τ)=δ[τ−l_sc∕(μ₀F)]. As a consequence, in such a tube the moment ratios $⟨{\tau }_{\text{sc}}^n⟩∕{⟨{\tau }_{\text{sc}}⟩}^n$ tend to unity as F→∞.

In tubes formed by cylindrical compartments the situation is different. Here at large F the transit time probability density in addition to a delta-function-like peak centered at τ=l_cc∕(μ₀F) has a long tail. Because of this tail ⟨τ_cc⟩ is ν⁻²=R²∕a² times larger than the pick center time, l_cc∕(μ₀F). During rare slow transitions, which are responsible for the tail, the particle diffuses at |ρ|>a that maintains its uniform distribution over the cross section of the tube. Consider a particle that made N⪢1 transitions between neighboring openings in a tube with cylindrical compartments at large F. Let λ be the fraction of slow transitions contributing into the tail. Then 1−λ is the fraction of fast transitions of duration l_cc∕(μ₀F). Denoting the mean duration of a slow transition by ⟨τ_out⟩, we can write the mean residence times spent by the particle inside and outside the cylinder of radius a, respectively, as (1−λ)Nl_cc∕(μ₀F) and λN⟨τ_out⟩. Since the distribution over the cross section is uniform, the ratio of these times is equal to a²∕(R²−a²)=ν²∕(1−ν²). Using this we obtain

$$\frac{\lambda }{1-\lambda }=\frac{l_{\text{cc}}\left(1-{\nu }^2\right)}{{\mu }_{0}F⟨{\tau }_{\text{out}}⟩{\nu }^2}.$$ (9)

This shows that the fraction of slow transitions tends to zero as F→∞, λ∝1∕F.

Thus, the pattern of the particle transitions between neighboring openings is as follows. Series of many fast transitions, during which the particle stays in the cylinder of radius a, are interrupted by slow transitions, during which the particle travels outside the cylinder. Such intermittency in transitions occurs when F is large enough so that the fast transit time l_cc∕(μ₀F) is much shorter than time R²∕D₀ associated with the slow transitions.

The intermittency also manifests itself in the F-dependence of the moment ratios, $⟨{\tau }_{\text{cc}}^n⟩∕{⟨{\tau }_{\text{cc}}⟩}^n$. Table 1 shows these ratios found in simulations as a function of F. As F→∞ the ratios with n≥2 diverge, while for the tube formed by spherical compartments similar moment ratios tend to unity. The divergence is a consequence of the long tail in the probability density φ_cc(τ) that is due to the slow transitions between neighboring openings. The rate of divergence increases with n. It can be shown that $⟨{\tau }_{\text{cc}}^n⟩∕{⟨{\tau }_{\text{cc}}⟩}^n\propto F^{n-1}$, F→∞. Numerical results presented in Table 1 support this estimation of the asymptotic F-dependence of the moment ratios.

Table 1.

Transit time moment ratios found in Brownian dynamics simulations for a tube formed by cylindrical compartments at ν=a∕R=0.3 and l∕R=2. Different numbers of the transit times N were used to find the moments at different values of the driving force: N×10⁶=1 (βFR=0,1), 8 (βFR=10), 20 (βFR=10²), 3×10² (βFR=10³), 10³ (βFR=10⁴), and 7×10³ (βFR=10⁵).

βFR	$⟨{\tau }_{\text{cc}}^2⟩∕{⟨{\tau }_{\text{cc}}⟩}^2$	$⟨{\tau }_{\text{cc}}^3⟩∕{⟨{\tau }_{\text{cc}}⟩}^3$	$⟨{\tau }_{\text{cc}}^4⟩∕{⟨{\tau }_{\text{cc}}⟩}^4$
0	1.79	4.76	16.9
1	1.71	4.22	13.7
10	1.69	4.28	14.4
102	5.00	44.6	540
103	31.2	1.8×103	1.3×105
104	260	1.2×105	7.5×107
105	2.5×103	1.1×107	6.4×1010

In summary, the main result of the present paper is that there are two patterns of the particle motion under the action of strong driving force in tubes of periodically varying diameter. The pattern realized in the tube formed by cylindrical compartments differs qualitatively from its counterpart in the tube formed by spherical compartments. As a consequence, dependences of the effective mobility and diffusion coefficient on the driving force are qualitatively different (Figs. 12). In addition, in the tube formed by cylindrical compartments there is intermittency in the particle transitions between neighboring openings. To emphasize the striking difference between the dependences, we compare the dependences ${\mu }_{\text{eff}}^{\text{sc},\text{cc}}\left(F\right)$ and $D_{\text{eff}}^{\text{sc},\text{cc}}\left(F\right)$ in tubes with similar parameters, namely, the same radius of the connecting openings, a=0.3R, and close values of the compartment lengths,$l_{\text{sc}}=2R\sqrt{1-{\nu }^2}\approx 1.91R$ and l_cc=2R. It would be interesting to learn how these dependences change when the compartment lengths and the opening radii vary. These studies are in progress.

After the manuscript was submitted, Marchesoni¹⁴ has published some of the results discussed above in a short note. These results are the formula for the effective mobility in the tube formed by cylindrical compartments at F→∞, Eq. 1, and its counterpart at F→0, Eq. 4, in the limiting case of small openings, ν=a∕R→0, when f(ν)=1.