An in Vivo Automated Shimming Method Taking into Account Shim Current Constraints

Abstract

Many in vivo imaging techniques require magnetic field homogeneity in the volume of interest. Shim coils of the second and third order spherical harmonics have been used successfully to compensate for complicated field variations caused by the human anatomy itself. The available currents of these coils are invariably limited. In this note we demonstrate that these limits significantly affect the optimal shim condition. We propose an automated in vivo shimming method for arbitrary volumes of interest using 3-dimensional (3D) field maps. This method is a modification of previous works using least-squares criteria. The main difference is that a constrained optimization is performed in vivo under the current limits of the shim coils, which improved the field homogeneity significantly over simple truncations of the least-squares solutions. This shimming method was used with head scans of five normal volunteers on a 4.0 tesla scanner. A fast double-echo sequence was used to obtain field maps, and a new field uniformity measure was derived for this method. The field mapping sequence was tested against a standard single-echo Dixon sequence used by previous investigators, and the stability of the shimming method was tested by repeated studies on the same subject.

INTRODUCTION

A highly uniform magnetic field in the volume of interest (VOI) is essential to many imaging techniques. Two factors contribute to the spatial variation of the magnetic field, the inherent field distribution of the magnet itself, and the susceptibility field of the subject being imaged. In living subjects the latter is significant because tissues have magnetic susceptibilities on the order of several parts per million. The tissue-air interfaces and soft tissue-bone interfaces in the body lead to the spatially dependent susceptibility fields (1–4). Shim coils of up to the 5th order spherical harmonics are available on large volume scanners to restore the field homogeneity. Because over a dozen shim coils have to be adjusted, an automated method is necessary for in vivo optimization. One successful approach is to obtain the field map of the VOI through imaging, and calculate the shim current values that minimizes the field variation, given the knowledge of the field produced by each shim coil (5–11). The field generated by each shim coil is limited by the maximum power supply to that coil. Higher order shim coils usually produce weaker fields with the same power supply, because of the self-canceling nature of the coil winding. For high field imaging experiments such as brain and cardiac studies at 4T, the susceptibility field is high enough that the required shim currents for some higher order shims are many times the current limits. A simple solution to this problem is to truncate the required values at the current limits. We attempt to demonstrate that, compared with such simple truncations, a true constrained optimization significantly improves the field homogeneity. One concern about performing constrained optimization in vivo is the computation time. We designed an efficient algorithm that is tailored to the specific problem of shimming, the total computation time on a Sun Sparc 2 workstation is no more than 3 min. This shimming method aims to optimize the field homogeneity within a VOI specified by the operator during the shimming procedure. It consists of the basic steps proposed by previous authors (6–9, 11): the field maps of the shim coils are collected in advance as basis functions; when the subject is positioned in the scanner, the field distribution of the VOI is collected with a field-mapping sequence; an algorithm is used to calculate the shim current values that minimizes the field variation, which is usually defined as a function of the field over the VOI; the shim currents are supplied into the shim coils; the center frequency is adjusted under the shimmed condition. What is new in this method is a fast constrained optimization algorithm that finds the true optimal shim current values within the available current limits, and a double-echo field mapping sequence that is optimized for its imaging time and motion compensated to the first order. The double-echo sequence was checked and adjusted in advance to ensure that gradient pulse imperfections do not cause significant errors in the field map. The problem of the chemical shift of lipid signals will be discussed in the Discussion section.

MATERIALS AND METHODS

This shimming method was performed for 4T head scans on five normal volunteers. For each volunteer three different shimming procedures were performed: manually shimming the three linear coils only; using the automated shimming routine with simple truncations at the shim current limits; using the automated shimming routine with the constrained optimization program. The resulted field maps were collected after each of the three shimming procedures, and the field homogeneity was compared. The stability of the automated shimming method was tested by shimming the same region of a head several times, and comparing the solutions. The overall shimming time is less than 11 min at present, and will be shortened with a digital interface between the computer and the shim power supplies.

This shimming method was implemented on a 4T whole-body scanner with a GE omega console and an Oxford superconducting magnet. The shim coils were connected to the Oxford Shim Power Supply. The available shim coils were “Z,” “X,” “Y,” “Z2,” “XY,” “YZ,” “XZ,” “X2-Y2,” “Z3,” “Z2X,” “Z2Y,” “ZXY,” “Z(X2-Y2),” “X3,” and “Y3.” The corresponding associated Legendre polynomials are z, x, y, z²−(x²+y²)/2, xy, yz, xz, x²−y², z³−3z(x²+y²)/2, z²x−x(x²+y²)/4, z²y−y(x²+y²)/4, zxy, z(x²−y²), x³−3x²y, and y³−3y²x. The current limits were plus-minus two amps. The linear shims were able to generate 4.7 ppm field offset on the surface of a 20-cm sphere placed at the iso-center of the magnet; the second order shims were capable of 1.1 ppm on the surface of a 20-cm diameter sphere; the third order coils were able to generate 0.3 ppm on the surface of a 20-cm sphere. The field of a shim coil per ampere of current was calibrated with the same field mapping sequence that was used in the in vivo shimming. A baseline 3-dimensional (3D) image was collected on a water phantom with a (25-cm)³ field of view (FOV) and all shim currents set to zero. The matrix size was 64 × 64 × 64. The field map of the central spherical region of 15 cm diameter was obtained. A shim coil was then supplied with a known current, and a field map of the spherical region was again taken. The two field maps were subtracted to give the field of the shim coil. The field map of a shim coil was then fitted to a polynomial of the same order as its intended Legendre polynomial, using a standard least-squares fitting routine provided in the IDL graphics language. This polynomial (its Cartesian derivatives, as described later) was used in the in vivo shimming process. Most shim coils were found to be well behaved. The less accurate shim coils were “Z3” and “Z2X.”

Five normal volunteers (four male, one female, age 24–28) underwent three different shimming procedures. A field map was collected after each shim to evaluate and compare the different methods. The VOI was defined as a 10-mm thick transaxial slice positioned above the frontal sinuses of the head. The first shimming method was to manually adjust only the three linear coils (“X,” “Y,” “Z”). A projection profile of the 10-mm slice in the slice selection direction was taken continuously while the linear shim currents were adjusted, until the area under the profile was maximized, and the echo of the slice profile was centered. The center frequency was then checked by taking a spectrum of the slice, to ensure that the frequency was centered at the peak of the spectrum. If this was not the case, the frequency was recentered and the shimming procedure was iterated.

The second shimming procedure performed on the volunteers was a simplification of the full automated shimming method. It consisted of collecting the field map of the VOI, calculating the optimal shim currents, input the current values to the shim power supplies, and recentering the radio frequency (RF). The simplification occurs at the shim current optimization algorithm. Instead of a constrained optimization, a standard least-squares optimization was used, and any current values that exceeded the current limits were truncated at the limits.

The third shimming procedure was the proposed automated shimming method. It was identical to the second shimming procedure, except that a constrained optimization was performed on the shim current values.

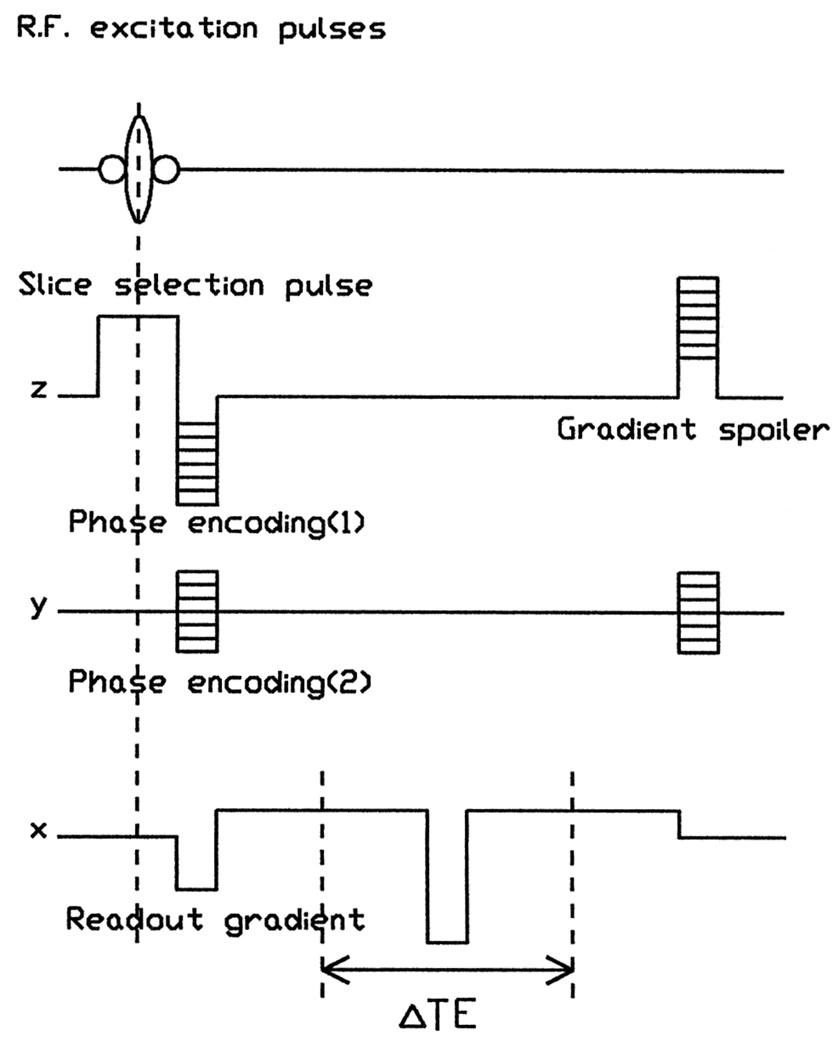
The sequence used to map the field distribution was a gradient-recalled, double-echo sequence shown in Fig. 1. For each RF excitation, two successive echoes were collected, with a readout defocusing pulse in between. The phase encoding pulses were rewound after each scan to maintain a steady state, and a gradient spoiler pulse was added in the slice selection direction. For a pixel at location (x, y, z), the phase difference between the signals from the two echoes is given by Δϕ = γB(x, y, z)(ΔTE) mod 2π, where ΔTE is the time interval between the two echoes. By unwrapping the phase difference map, the “mod 2π” dependence is removed, and the magnetic field distribution can be obtained. In general, many field mapping methods have been proposed by previous investigators of field map-based shimming methods. Roughly speaking they could be classified into two categories. One is spectroscopic imaging, where the spectrum of each pixel is obtained, either through volume selective techniques (12), or through 3DFT or 4DFT methods (3, 7, 13, 14). These methods are relatively immune to the chemical shift artifact of lipids, because lipid signals can be explicitly excluded from the spectra.

FIG. 1.

The gradient-recalled, double-echo pulse sequence used for field mapping. In the readout direction, two gradient-recalled echoes were collected with a readout defocusing pulse in between. The two echo times are 5.3 and 9.3 ms. The acquisition time for each echo is 0.8 ms. The slice selection pulse is 2 ms long. The repetition time of the sequence is 60 ms.

The drawback is the long scan time, which is a significant factor for in vivo applications. The other category is phase difference methods (6, 8–11, 15). These methods derive the local B₀ field from the phase difference of two images of different spin evolution times. The double-echo sequence used in this shimming method belongs to the second category. It is a variant of the 2-point Dixon method (15). The difference is that two echoes are collected in one scan to shorten the overall scan time. In reference to Fig. 1, the readout gradient pulses are symmetric with respect to the midpoint between the two echoes, and have a zero time integral between the two echoes, this ensures that motion-related phase shifts are the same in both echoes, and do not affect the field map.

Compared with a Dixon sequence with a single echo acquisition (8, 15), a source of inaccuracy in this sequence is the imperfections in the readout defocusing gradient pulse between the two echoes, which results in an artificial gradient in the acquired field map. This problem was corrected with a small correction term in the amplitude of the readout defocusing gradient pulse. Another source of artifact is the chemical shift of the lipid signals. This is deferred to the Discussion section.

With the double-echo sequence, a 64 × 64 × 16 image was collected on a transaxial slice above the frontal sinuses of the head. The echo times of the two echoes were 5.3 and 9.3 ms, respectively. The other parameters were slice thickness = 10 mm, FOV = 256 × 256 × 16 mm, matrix size = 64 × 64 × 16, TE of first echo = 5.3 ms, TE of second echo = 9.3 ms, TR = 60 ms, α° = 30°, NEX = 1. A VOI was defined via an interactive IDL routine. A signal level threshold was used to remove noisy pixels in the VOI. The phase maps from the two echoes were subtracted to give the phase difference map. This phase difference map was unwrapped in the VOI, using the algorithm proposed by Axel and Morton (16). This algorithm finds the location of the discontinuity lines in the phase map by comparing a pixel with its nearest neighbors.

The unwrapped phase difference map may still have a constant offset from the real field map. As described below, the B₀ variation measure is defined in terms of the Cartesian derivatives of the field, the constant offset therefore does not affect the results.

To find the optimal shim currents, a target function that measures the B₀ field variation needs to be defined. Previous investigators, including Prammer et al. (6), Tropp et al. (7), Schneider and Glover (8), Webb and Macovski (9), Gruetter and Boesch (10), Van Zijl et al. (11), used variations of the least-squares definition:

$${{\displaystyle {\int }_{\mathrm{\text{ROI}}}\left[B(x,y,z)-\langle B\rangle \right]}}^{2}dxdydz,$$ [1]

where 〈B〉 is the average field in the VOI. Prammer et al. (6) also discussed the Chebychev norm, defined as the peak-to-peak span of the B₀ field in the VOI. In the new automated shimming method, we attempted to link the target function to the overall signal intensity of the VOI. The target function is defined according to the following criterion: assuming that the spin density in the VOI is uniform, the optimal shim should maximize the total signal intensity of all the pixels in the VOI. Let the size of a pixel be L_x × L_y × L_z, the magnetic field be B, the gyromagnetic ratio be γ, the echo time difference be ΔTE. Note that the pixel dimensions L_x × L_y × L_z are of the actual imaging study, not necessarily the same as those used in the shimming procedure. If the pixel is not unusually large, the field variation within a pixel is mainly due to its first order derivatives. Assuming a perfect point response function, the signal intensity of the pixel can be written as

$$\begin{array}{l}S={\displaystyle {\int }_{-L_x/2}^{L_x/2}\mathit{\text{dx}}}{\displaystyle {\int }_{-L_y/2}^{L_y/2}\mathit{\text{dy}}}{\displaystyle {\int }_{-L_z/2}^{L_z/2}\mathit{\text{dz}}{s}_0{e}^{i\gamma \mathrm{\Delta }\mathit{\text{TE}}\left(\frac{\partial B}{\partial x}x+\frac{\partial B}{\partial y}y+\frac{\partial B}{\partial z}z\right)}}\\ ={\displaystyle {\int }_{-L_x/2}^{L_x/2}\mathit{\text{dx}}}{\displaystyle {\int }_{-L_y/2}^{L_y/2}\mathit{\text{dy}}}{\displaystyle {\int }_{-L_z/2}^{L_z/2}\mathit{\text{dz}}}·s_0[1+i\gamma \mathrm{\Delta }\mathit{\text{TE}}\left(\frac{\partial B}{\partial x}x+\frac{\partial B}{\partial y}y+\frac{\partial B}{\partial z}z\right)-\frac{{(\gamma \mathrm{\Delta }\mathit{\text{TE}})}^2}{2}{\left(\frac{\partial B}{\partial x}x+\frac{\partial B}{\partial y}y+\frac{\partial B}{\partial z}z\right)}^2+\cdots ],\end{array}$$ [2]

where s₀ is the signal per unit volume. If the phase spread within one pixel over the echo time is not too severe, we can keep only the leading correction term in the expansion and write

$$\begin{array}{l}S=s_0{\displaystyle {\int }_{-L_x/2}^{L_x/2}\mathit{\text{dx}}}{\displaystyle {\int }_{-L_y/2}^{L_y/2}\mathit{\text{dy}}}{\displaystyle {\int }_{-L_z/2}^{L_z/2}\mathit{\text{dz}}}·\left[1-\frac{{(\gamma \mathrm{\Delta }\mathit{\text{TE}})}^2}{2}{\left(\frac{\partial B}{\partial x}x+\frac{\partial B}{\partial y}y+\frac{\partial B}{\partial z}z\right)}^2\right]\\ =s_0{L}_x{L}_y{L}_z\{1-\frac{{(\gamma \mathrm{\Delta }\mathit{\text{TE}})}^2}{24}[{\left(\frac{\partial B}{\partial x}\right)}^2{L_x}^2+{\left(\frac{\partial B}{\partial y}\right)}^2{L_y}^2+{\left(\frac{\partial B}{\partial z}\right)}^2{L_z}^2]\}.\end{array}$$ [3]

Therefore, to maximize the sum of the signal intensity of all pixels in the VOI, the following quantity should be minimized:

$$D={\displaystyle \sum _{\mathit{\text{VOI}}}\left[{\left(\frac{\partial B}{\partial x}\right)}^2{L_x}^2+{\left(\frac{\partial B}{\partial y}\right)}^2{L_y}^2+{\left(\frac{\partial B}{\partial z}\right)}^2{L_z}^2\right].}$$ [4]

The quantity D is used as the target function to be minimized by the optimal shim currents. Note, however, that in real imaging studies the point response function is not perfect, and is dependent on the masking or filtering schemes used for the k-space data. Thus, the weighting of the gradients in Eq. [4] is not simply the dimensions of the pixel, but the second order moments of the point response functions. Here, for the purpose of generality and simplicity, a perfect point response function is assumed. To calculate the function D, the field derivatives at a pixel are calculated by subtracting the field values of its nearest neighbors, and divide the difference by twice the pixel dimension. For example, if the pixel dimensions of the field maps are L_x′ × L_y′ × L_z′, for a pixel at position n_x, n_y, n_z,

$$\frac{\partial B(n_x,n_y,n_z)}{\partial x}=\frac{B(n_x+1,n_y,n_z)-B(n_x-1,n_y,n_z)}{2{L^{\prime }}_x}.$$ [5]

If the original field map is B₀, the fields of the shim coils with unit current supply are f_i, i = 1 to 15 (15 available shim coils), the currents in the shim coils are c_i, the corrected field is then

$$B(\{c_i\})=B_0+{\displaystyle \sum _{i=0}^{15}{c}_i{f}_i}.$$ [6]

Substituting Eq. [6] into Eq. [4], the target function D can be written as

$$\begin{array}{l}D\left(\left\{C_i\right\}\right)={\displaystyle \sum _{\mathit{\text{VOI}}}[{\left(\frac{\partial B_0}{\partial x}+{\displaystyle \sum _{i=0}^{15}{c}_i\frac{\partial f_i}{\partial x}}\right)}^2{L_x}^2+{\left(\frac{\partial B_0}{\partial y}+{\displaystyle \sum _{i=0}^{15}{c}_i\frac{\partial f_i}{\partial y}}\right)}^2{L_y}^2}+{\left(\frac{\partial B_0}{\partial z}+{\displaystyle \sum _{i=0}^{15}{c}_i\frac{\partial f_i}{\partial z}}\right)}^2{L_z}^2]\\ ={\displaystyle \sum _{\mathit{\text{VOI}}}\left[{\left(\frac{\partial B_0}{\partial x}\right)}^2{L_x}^2+{\left(\frac{\partial B_0}{\partial y}\right)}^2{L_y}^2+{\left(\frac{\partial B_0}{\partial z}\right)}^2){L_z}^2\right]}+{\displaystyle \sum _{i=0}^{15}{\displaystyle \sum _{j=0}^{15}{c}_i{c}_j}{\displaystyle \sum _{\mathit{\text{VOI}}}\left(\frac{\partial f_i}{\partial x}\frac{\partial f_j}{\partial x}{L_x}^2+\frac{\partial f_i}{\partial y}\frac{\partial f_j}{\partial y}{L_y}^2+\frac{\partial f_i}{\partial z}\frac{\partial f_j}{\partial z}{L_z}^2\right)}}+{\displaystyle \sum _{i=0}^{15}{c}_i{\displaystyle \sum _{\mathit{\text{VOI}}}\left(\frac{\partial B_0}{\partial x}\frac{\partial f_j}{\partial x}{L_x}^2+\frac{\partial B_0}{\partial y}\frac{\partial f_i}{\partial y}{L_y}^2+\frac{\partial B_0}{\partial z}\frac{\partial f_i}{\partial z}{L_z}^2\right)}}.\end{array}$$ [7]

Define the symmetric Hessian matrix Q as

$$Q_{\mathit{\text{ij}}}={\displaystyle \sum _{\mathit{\text{VOI}}}\left(\frac{\partial f_i}{\partial x}\frac{\partial f_j}{\partial x}{L_x}^2+\frac{\partial f_i}{\partial y}\frac{\partial f_j}{\partial y}{L_y}^2+\frac{\partial f_i}{\partial z}\frac{\partial f_j}{\partial z}{L_z}^2\right)},$$ [8]

define the projection P_i as

$$P_i={\displaystyle \sum _{\mathit{\text{VOI}}}\left(\frac{\partial B_0}{\partial x}\frac{\partial f_i}{\partial x}{L_x}^2+\frac{\partial B_0}{\partial y}\frac{\partial f_i}{\partial y}{L_y}^2+\frac{\partial B_0}{\partial z}\frac{\partial f_i}{\partial z}{L_z}^2\right)},$$ [9]

define the original measure D₀ as

$$D_0={\displaystyle \sum _{\mathit{\text{VOI}}}\left[{\left(\frac{\partial B_0}{\partial x}\right)}^2{L_x}^2+{\left(\frac{\partial B_{0_2}}{\partial y}\right)}^2{L_y}^2+{\left(\frac{\partial B_0}{\partial z}\right)}^2{L}^2\right],}$$ [10]

Eq. [7] can now be written as

$$D(\{c_i\})=D_0+{\displaystyle \sum _{i=0}^{15}{\displaystyle \sum _{j=0}^{15}{c}_i{Q}_{ij}{c}_j}}+{\displaystyle \sum _{i=0}^{15}2c_i{P}_i}.$$ [11]

This is the target function to be minimized. In all the studies the pixel size was chosen to be L_x:L_y:L_z = 1:1:3 to reflect the pixel geometry of a typical transaxial image.

If the current values {c_i} are not limited, minimizing D({c_i}) in Eq. [11] simply gives the least-squares solution

$$c_i=-{\displaystyle \sum _j{Q}_{ij}^{-1}{P}_j}.$$ [12]

This was the solution used in the second shimming procedure performed on all the volunteers. The matrix Q was inverted using a Gaussian elimination routine provided in the IDL language. The condition of the inversion was reported by this routine in a status variable. In all our studies the inversion was well conditioned. The solution (Eq. [12]) invariably exceeded the current limits on most of the second and third order shim coils. In the second shimming procedure, the solution was truncated at the exceeded boundaries.

Alternatively, using an algorithm based on Powell (17), a constrained minimization of D({c_i}) can be performed fairly quickly on a Sparc 2 workstation. This was done in the third shimming procedure, the result was compared with the manual shimming procedure and the simple truncation method. The Appendix contains the description of the constrained algorithm. In the next section the results of the three different shimming methods are described. The stability of the constrained optimization method was also tested by performing the complete procedure twice on the same subject, and comparing the resulted shim current values.

RESULTS

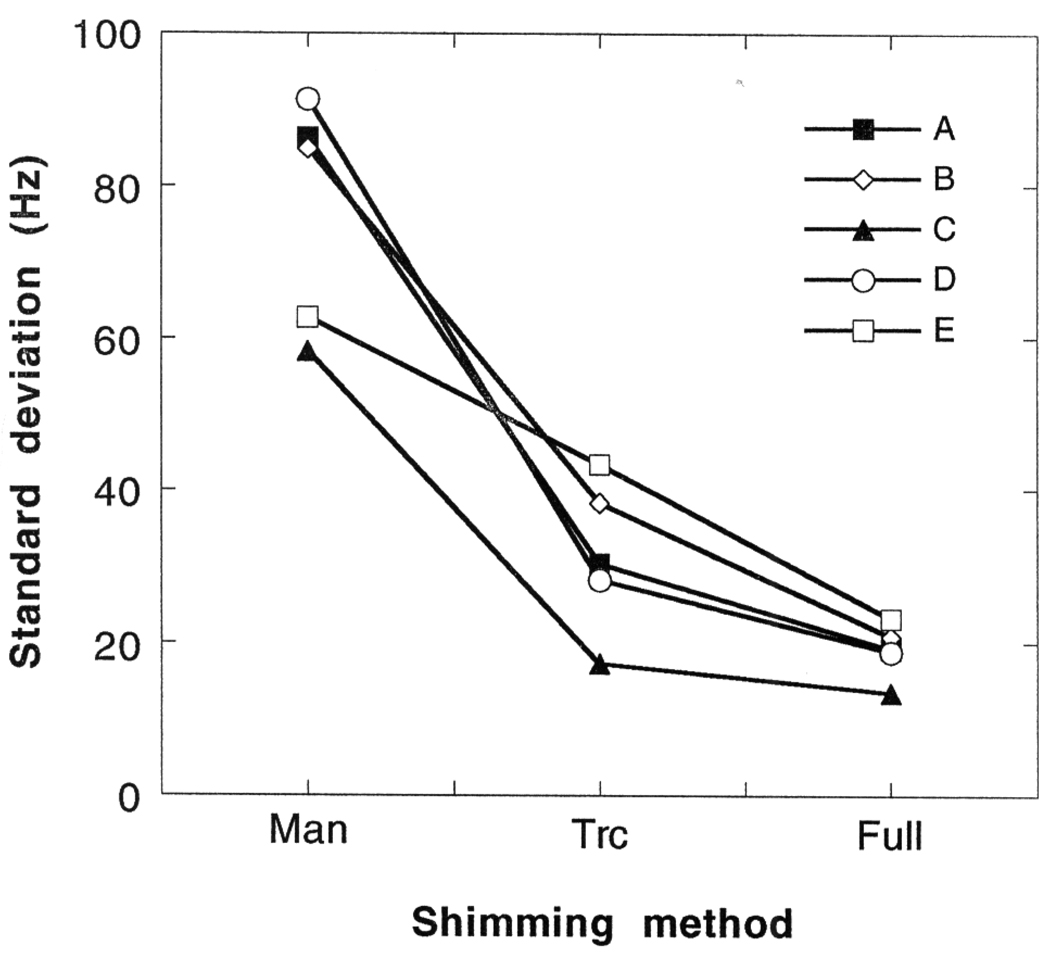
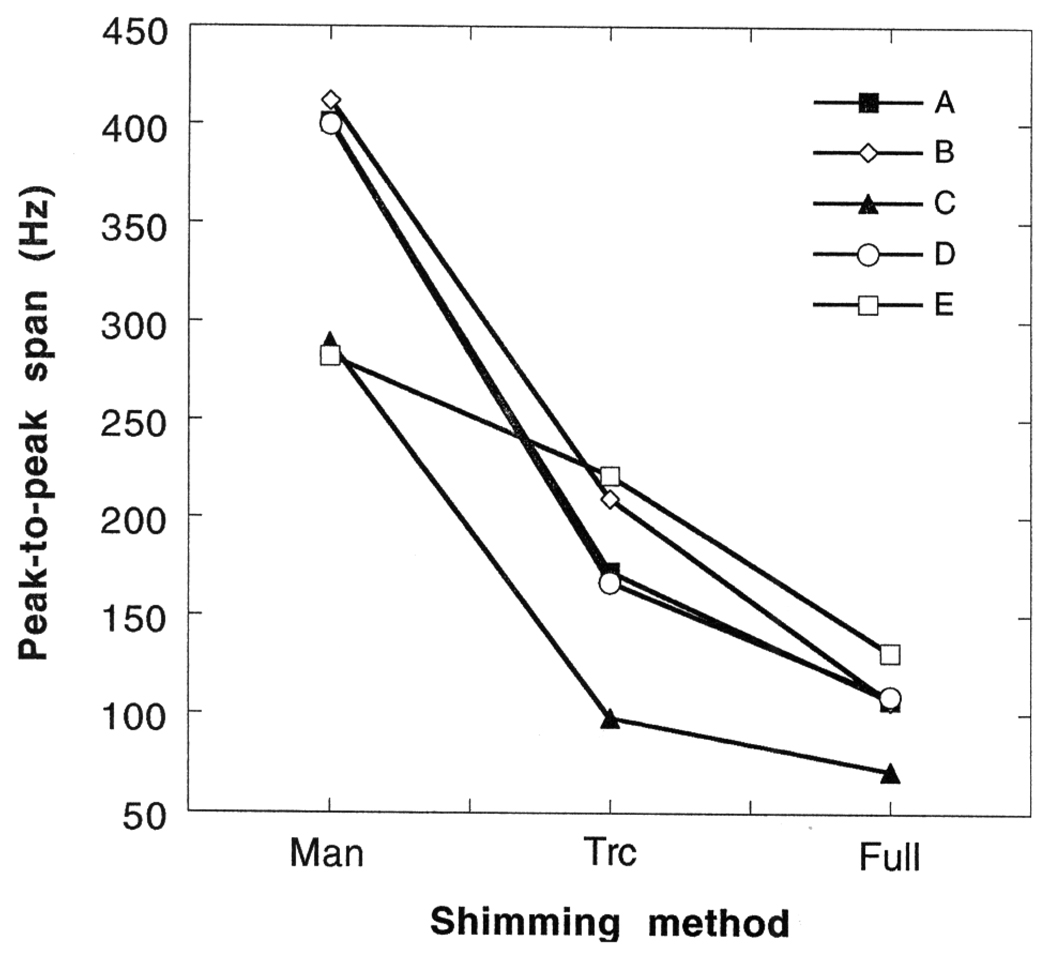
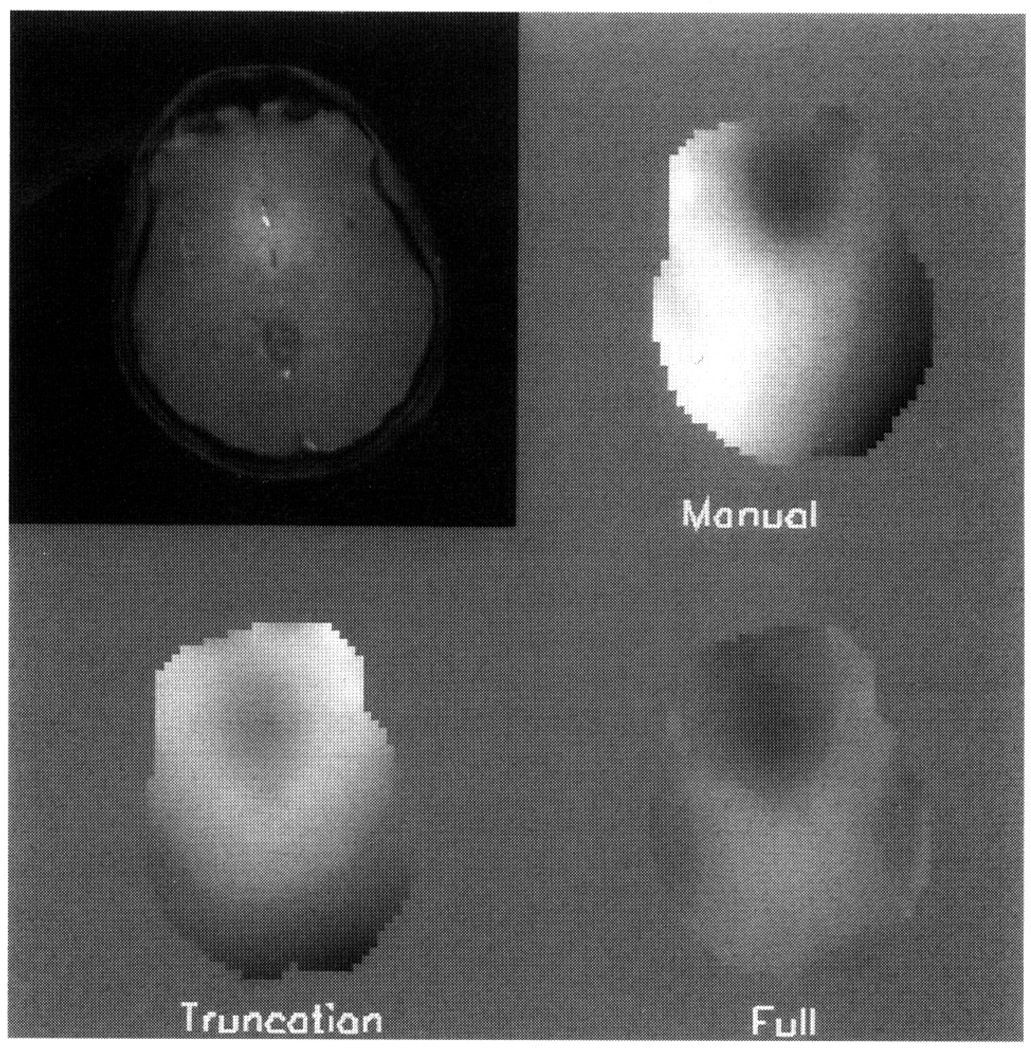
As described above, the three shimming procedures were performed on five normal volunteers (hereafter referred to as “A” to “E”) in approximately the same region of the brain. The first procedure consisted of shimming the slice profile manually with the three linear coils, this will be called “manual shim” in the following discussion; the second procedure is a simplified version of the complete automated shimming method, the difference being that a least-squares solution is used with simple truncations at the current limits, it will be called the “truncation shim”; the third procedure uses the proposed constrained optimization algorithm to find the true optimum within the current limits, and will be called the “full shim.” After each procedure the B₀ map was acquired to give the effect of the shim. The results are compared in terms of the achieved target measure D, the standard deviation of B₀ in the VOI, and the peak-to-peak difference of B₀ in the VOI (6, 9). In all three categories the truncation shim significantly improved over the manual shim, and the full shim consistently made improvement over the truncation shim. The value of the target function D after the three shimming procedures are tabulated in Table 1. The standard deviation of the B₀ field after the shimming procedures is plotted in Fig. 2. The peak-to-peak difference values are plotted in Fig. 3. All three indices of B₀ homogeneity showed large improvement from the manual shim to the truncation shim. When applying the full shim, the target function D showed 3.5–27% improvement; the B₀ standard deviation was further reduced from the truncation shim by 22–46%; the peak-to-peak difference in B₀ was further reduced by 27–49%. The field maps of volunteer “E” is illustrated in Fig. 4. The upper left image is an anatomical image of the slice that was shimmed. The sequence used was a GRASS sequence, with the parameters slice thickness = 8 mm, FOV = 256 mm, matrix size = 256 × 256, TE = 6.5 ms, TR = 100 ms, α° = 30°, NEX = 1.

Table 1.

Values of the Target Function D for the Five Volunteers (Denoted “A” to “E”) after Each of the Three Shimming Procedures

Subject	“A”	“B”	“C”	“D”	“E”
Dmanual	1079	2166	622	1256	904.7
Dtruncated	77.0	101.4	41.0	82.6	90.5
Dfull	67.9	73.9	32.8	79.4	72.0

The target function D measures the amount of variation in the B₀ field over the VOI. For all volunteers D was successively reduced from manual through truncated to full shim current optimization techniques.

FIG. 2.

The standard deviation of the B₀ field in the VOI after the three shimming methods for the five volunteers. The volunteers are referred to as “A” to “E.” The three shimming methods are labeled as “Man” for the manual shim procedure, “Trc” for the truncation shim procedure, and “Full” for the full shim procedure. The successive improvement from the manual shim to the full shim is apparent.

FIG. 3.

The peak-to-peak span of the B₀ field in the VOI after the three shimming procedures for the five volunteers. The volunteers are referred to as “A” to “E.” The three shimming procedures are labeled as “Man” for the manual shim procedure, “Trc” for the truncation shim procedure, and “Full” for the full shim procedure. The improvement from the truncation shim to the full shim is evident.

FIG. 4.

The field maps of volunteer “E” after each of the three shimming procedures. The upper left image is an anatomical image of the slice collected with a GRASS sequence. The parameters of the sequence were slice thickness = 8 mm, FOV = 256 mm, matrix size = 256 × 256, TE = 6.5 ms, TR = 100 ms, α° = 30°, NEX = 1. The field maps were collected after the three shimming procedures. The parameters of the field mapping sequence were slice thickness = 10 mm, FOV = 256 × 256 × 16 mm, matrix size = 64 × 64 × 16, TE of first echo = 5.3 ms, TE of second echo = 9.3 ms, TR = 60 ms, α° = 30°, NEX = 1. The center slice of the 3D field maps are shown here. The three maps are displayed in the same gray scale of 279 Hz for the full range.

The three B₀ maps were acquired after the three shimming procedures, and displayed in the same scale (279 Hz over the full gray scale). For this volunteer the D measure was reduced by 20% from the truncation shim to the full shim; the improvement of the standard deviation was 46%; the peak-to-peak difference was reduced by 41%. The improvement of the full shim over the truncation shim is consistent and well worth the extra 10- to 20-s computation time. In the full shim field map of Fig. 4, the dark region in the front-center of the VOI was not completely compensated. This region represents local B₀ variations of high order spatial dependence, and the amplitude of the variation is beyond the strength of the shim coils. Such local B₀ variations are caused by the various air-tissue interfaces present in the head (3, 4). The full shim solutions of different volunteers can be substantially different, as shown between volunteers “D” and “E” in Table 2. For this reason this procedure was designed to operate in vivo for each specific VOI and each volunteer. The specificity of individual volunteers is likely caused by the variations in the positions and the curvatures of the air-tissue interfaces near the VOIs.

Table 2.

Truncation Shim and Full Shim Solutions of the Five Volunteers in Amps

	A		B		C		D		E
	Ctrc	Cfull	Ctrc	Cfull	Ctrc	Cfull	Ctrc	Cfull	Ctrc	Cfull(1)	Cfull(2)
Z	−0.357	−0.376	0.0059	−0.151	−0.354	−0.379	−0.287	−0.316	−0.252	−0.250	−0.263
Z2	2.00	2.00	1.15	1.34	2.00	2.00	2.00	2.00	−0.103	1.42	1.43
Z3	0.007	−2.00	2.00	2.00	−1.92	−2.00	1.79	−0.610	−1.00	2.00	2.00
X	−0.137	−0.051	−0.599	−0.101	−0.040	0.040	−0.326	−0.008	−0.358	0.151	0.149
Y	−0.912	−0.927	−0.923	−1.03	−0.860	−0.897	−0.947	−0.952	−0.948	−0.944	−0.943
ZX	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00
ZY	2.00	2.00	2.00	2.00	1.85	2.00	2.00	2.00	2.00	2.00	2.00
XY	−0.249	0.843	−0.103	0.787	0.474	0.954	0.060	0.786	0.828	1.07	1.08
X2–Y2	0.438	−0.347	−1.71	−1.47	−0.511	−0.693	0.810	0.615	−0.451	−0.455	−0.527
Z2X	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00
Z2Y	−1.28	2.00	2.00	2.00	2.00	2.00	−0.615	2.00	−0.253	2.00	2.00
ZXY	−2.00	2.00	−2.00	−1.07	−2.00	−2.00	−2.00	0.601	−1.49	−1.07	−1.15
Z(X2–Y2)	2.00	2.00	2.00	2.00	0.674	−2.00	2.00	0.429	2.00	−2.00	−2.00
X3	−2.00	−2.00	−2.00	−2.00	−2.00	−2.00	−2.00	−2.00	−2.00	−2.00	−2.00
Y3	−2.00	−1.93	−1.79	−2.00	−2.00	−2.00	−2.00	−2.00	−1.24	−2.00	−2.00

For volunteer “E” the full shim procedure was performed twice to demonstrate the stability of the method, the solutions are labeled C_full⁽¹⁾ and C_full⁽²⁾.

To test the stability of the automated shimming method, it was performed twice in the same region of volunteer “E.” All steps of the shimming procedure were repeated, including the field mapping and the definition of the VOI. The solutions were tablulated in Table 2. The similarity of the two solutions indicates that the signal-to-noise ratio of the phase maps is adequate to give stable results.

DISCUSSION

The automated shimming procedure proposed above is capable of optimizing the B₀ uniformity in any VOI in vivo under shim power supply limits. The target function is in the form of a quadratic function of the B₀ spatial derivatives. The same constrained optimization algorithm can also be used for other quadratic target functions, such as the square of the B₀ standard deviation in the VOI. It is demonstrated here that the simple least-squares solution often requires unrealistic shim current values. The true constrained optimum is very different from a simple truncation of the least squares solution, and significantly improves the B₀ homogeneity as measured by the B₀ standard deviation and the peak-to-peak difference. On the 4T scanner used for these studies, the current limits on all the shim coils were plus-minus 2 amperes. This value could be higher on other scanners. However, the unconstrained solution usually requires unrealistically high currents, for example, the least squares solution of volunteer “E” demanded 28 amps on the “Z2X” coil, the same solution of volunteer “B” demanded 17 amps on the “Z3” coil. It is also probable that in other regions of the body the B₀ variation due to local susceptibility changes can be more severe, and even larger current values can be required. These current values are unlikely to be available on many high field scanners due to coil heating and power supply problems, thus the constrained optimization method becomes necessary.

The double-echo field mapping sequence of the shimming procedure does not have special provisions for the chemical shift artifact of lipid signals. This artifact is a common problem in field map based shimming methods. Various solutions have been proposed for this problem. Spectroscopic imaging methods can avoid this problem by picking the water peak from the spectra to form the field map. This method was adopted in another implementation of this shimming method for cardiac imaging (18). However, the scan time was usually 7 min or longer. With phase map methods, a Dixon type technique was proposed by Schneider and Glover (8) to avoid the effect of the lipid signals on the phase maps. While this method is effective at lower field strengths, our experience with Dixon type methods at 4T were not satisfactory due to the broad spectral width of the lipid signals. Other techniques such as fat suppression with spectral-spatial excitation (9) depend on a relatively well shimmed starting condition, which again was often not the case at 4T. When applying the shimming method to head scans, we adopted the approach of excluding lipid dominated pixels from the VOI (6) for its reliability and simplicity. For other regions where the distinction between lipid and water pixels are not obvious (such as the heart), methods such as the 4DFT spectroscopic sequence may be necessary.

The time to complete the shimming process was less than 11 min. The field mapping sequence takes 1 min 11 s on a GE Omega spectrometer; saving the data file over a local network to a Sun Sparc 2 station and converting the data to the format of the IDL language take 1 to 3 min, depending on the condition of the network. On the Sun station, the amount of time to specify the VOI depends on the VOI itself and the operator, and normally takes between 30 s to 2 min. The calculation on the Sun station takes 2 to 3 min, with most of the time devoted to calculating the Hessian matrix Q. The shim current solution is printed out on a hard copy and manually input into the Oxford Shim Power Supply’s control panel, this step takes about 2 min. Lastly it takes about 0.5 min to re-center the RF frequency after shimming. The overall shimming time can be reduced substantially with a direct digital interface between the computers and the shim power supplies and a better data link between the spectrometer and the Sun workstation.

APPENDIX

The target function to be minimized is D({c_i}) in Eq. [11]. The variables {c_i} are bound by the positive and negative current limits. The following program is based on an algorithm proposed by Powell (17) for quadratic programming. The algorithm is simplified for the shimming problem, where the Hessian matrix Q is invertible and positive definite, and the variables {c_i} are bound within an N-dimensional rectangle, N being the number of shim coils. The program successively adds on the relevant constraints that will bound the final optimal solution, and in this process reduces the search to subspaces of lower dimensions. This is repeated until the solution is completely determined. A relevant constraint is defined as a current limit that is present in the final constrained optimal solution. The program consists of the following steps:

1. Determine the least-squares solution {c*_i} of D({c_i}) according to Eq. [12]. If {c*_i} meets all the current constraints, it is the final solution; if not, go to step (b).

2. Truncate {c*_i} at the exceeded limits to yield the truncation solution {c_i^t}. Calculate the gradient vector of the target function D at {c_i^t}:

   $$g_i=2Q_{\mathit{\text{ij}}}{c}_j^t+2P_i.$$ [A1]

For each current value c*_k that exceeded the current limit and is truncated to c_k^t, if c_k^t is the negative limit, and the gradient vector component g_k ≥ 0, or if c^t_k is the positive limit and g_k ≤ 0, then this constraint is relevant and c_k will be fixed at c_k^t. Otherwise, the constraint is not yet relevant, and the current value is allowed to vary. When all the truncated current values are examined this way, two cases may arise. One is that all the current values are bound by constraints, and all the constraints are relevant. In this case {c_k^t} is the optimal solution. The other is that some current values are allowed to vary, either because they are not constrained, or because their constraints are not relevant. In this case, the variable currents {c_j} define a subspace “S” of the initial variable space, the relevant constraints {c_k} define a complement set of currents “R.” The form of the target function D is then defined in the subspace S by substituting the relevant constraints (the fixed c_k^ts) into Eq. [11]:

$$D(\{c_j\})={D^{\prime }}_0+{\displaystyle \sum _{j\epsilon S}{\displaystyle \sum _{l\epsilon S}{c}_j{Q}_{jl}{c}_l}}+{\displaystyle \sum _{j\epsilon S}2c_j{P^{\prime }}_j},$$ [A2]

where

$${P^{\prime }}_j=P_j+{\displaystyle \sum _{k\epsilon R}{Q}_{jk}{c_k}^t},$$ [A3]

and

$${D^{\prime }}_0=D_0+{\displaystyle \sum _{k\epsilon R}{\displaystyle \sum _{m\epsilon R}{c_k}^t{Q}_{km}{c_m}^t}}.$$ [A4]

The program returns to step (a) using the new definition of D in Eq. [A2] and repeats the process until the solution is determined.