Abstract
Objective
Calibration errors in distortion-product otoacoustic emission (DPOAE) measurements due to standing waves cause unpredictable changes in stimulus and DPOAE response level. The purpose of this study was to assess the extent to which these errors affect DPOAE test performance. Standard calibration procedures use sound pressure level (SPL) to determine specified levels. Forward pressure level (FPL) is an alternate calibration method that is less susceptible to standing waves. However, FPL derivation requires prior cavity measurements, which have associated variability. In an attempt to address this variability, four FPL methods were compared with SPL: a reference calibration derived from 25 measurements prior to all data collection and a daily calibration measurement, both of which were made at body and room temperature.
Design
Data were collected from 52 normal-hearing and 103 hearing-impaired subjects. DPOAEs were measured for f2 frequencies ranging from 2 to 8 kHz in half-octave steps, with L2 ranging from −20 to 70 dB SPL (5-dB steps),. At each f2, DPOAEs were measured in five calibration conditions: SPL, daily FPL at body temperature (daily body), daily FPL at room temperature (daily room), reference FPL at body temperature (ref body), and reference FPL at room temperature (ref room). Data were used to construct receiver operating characteristic (ROC) curves for each f2, calibration method and L2. From these curves, areas under the ROC curve (AROC) were estimated.
Results
The results of this study are summarized by the following observations: (1) DPOAE test performance was sensitive to stimulus level, regardless of calibration method, with the best test performance observed for moderate stimulus-level conditions. (2) An effect of frequency was observed for all calibration methods, with the best test performance at 6 kHz and the worst performance at 8 kHz. (3) At clinically applicable stimulus levels, little difference in test performance among calibration methods was noted across frequencies, except at 8 kHz. At 8 kHz, FPL-based calibration methods provided superior performance compared with the standard SPL calibration. (4) A difference between FPL calibration methods was observed at 8 kHz, with the best test performance occurring for daily body calibrations.
Conclusions
With the exception of 8 kHz, there was little difference in test performance across calibration methods. At 8 kHz, AROCs and specificities for fixed sensitivities indicate that FPL-based calibration methods provide superior performance compared with the standard SPL calibration for clinically relevant levels. Temperature may have an impact on FPL calculations relative to DPOAE test performance. Although the differences in AROC among calibration procedures were not statistically significant, the present results indicate that standing-wave errors may impact DPOAE test performance and can be reduced by using FPL, although the largest effects were restricted to 8 kHz.
I. Introduction
Distortion-product otoacoustic emissions (DPOAEs) are byproducts of an active mechanical process within the cochlea that are associated with normal hearing (Brownell, 1983) and can be recorded in the ear canal with a sensitive microphone (e.g., Kemp, 1978). This feature has resulted in the widespread application of OAE measurements as a screening tool that can objectively assess auditory status. Measurements of DPOAEs are made in a sealed ear canal, which helps to reduce background ambient noise. Prior to recording DPOAEs, an initial calibration measurement of the stimulus level in the ear canal is typically completed. This information is then used to adjust the voltage delivered to the transducers in order to achieve specified levels. Almost without exception, calibration is accomplished by measuring sound pressure with the same probe microphone that will be used to measure DPOAE level. Under these circumstances, it is assumed that the sound pressure level (SPL) recorded at the probe microphone accurately represents the quantity of sound entering the ear. However, the plane of the probe microphone is located approximately 15–20 mm from the adult eardrum. Previous research has shown that interactions between incident and reflected sound waves within the ear canal, called standing waves, can cause errors in estimates of both stimulus and DPOAE level of up to 20 dB (Dreisbach & Siegel, 2001; Scheperle et al., 2008; Siegel, 1994; Siegel & Hirohata, 1994; Whitehead et al, 1995a).
Theoretically, standing-wave problems are greatest when the distance between the probe microphone and the eardrum is a quarter wavelength of the stimulus frequency. In this case, partial cancellation of the sound wave occurs resulting in a pressure magnitude that is lower at the plane of the probe than it is at the eardrum. The recording software will then adjust the input voltage to achieve the desired SPL, based on the incorrect estimate of level at the plane of the probe, which results in an underestimation of the SPL at the eardrum. As a consequence, the level at the eardrum will exceed the specified level in these conditions. In an average adult ear, frequencies at or below 2 kHz have long wavelengths relative to the length of the ear canal, so that the SPL is more uniform throughout the ear canal (Siegel, 2007). As a result, errors in estimated levels are unlikely to be large. However, frequencies above 2 kHz have shorter wavelengths resulting in standing waves that may introduce large calibration errors at the plane of the probe. In addition, individual ear-canal characteristics (curvature and diameter) and eardrum impedances cause variability in the frequencies at which standing waves occur (Dirks & Kincaid, 1987; Gilman & Dirks, 1986; Siegel, 2007; Stinson, 1985), making it difficult to predict errors across individuals. In turn, calibration errors may introduce diagnostic errors at these higher frequencies due to standing waves. Although the frequencies at which standing waves occur will be shifted to higher frequencies in infants and young children, due to the smaller size of their ear canals, the effects still occur. As DPOAEs are often used to help monitor or evaluate hearing changes in high-frequency regions (e.g., Delehaye et al., 2008; Dhooge et al., 2006; Knight et al., 2007; Ress et al., 1999; Stavroulaki et al., 2001), correct estimates of stimulus levels may be important for accurate cochlear assessment.
Sound intensity level (SIL) and forward pressure level (FPL) are alternate calibration methods that are resistant to standing-wave interactions within the ear canal. These quantities can be measured by a microphone when certain characteristics of the sound source have been determined from prior measurements in cavities with known acoustic impedances. While several studies have investigated the calibration variability of these alternate methods and found less error and more consistent measurements (e.g., Neely & Gorga, 1998; Scheperle et al., 2008), no data exist to demonstrate that calibration procedure has an influence on the accuracy with which DPOAEs predict auditory status.
Although both SIL and FPL calibrations resulted in less variability compared to SPL calibrations, and were less affected by standing waves, no calibration method is without error. For example, differences in sound-source characteristics have been noted for cavity calibrations performed both at body and at room temperature (Scheperle et al., 2008). Neely and Gorga (1998) proposed that warming the calibration tubes to body temperature would approximate the same temperature as when the probe is inserted into the ear canal. This factor may be important because as temperature changes, the speed of sound changes, which was found to produce phase shifts in source impedance and source pressure (e.g., Neely & Gorga, 1998). However, just as there are no reports to suggest that calibration procedure, in general, affects DPOAE test performance, no data exist comparing DPOAE test performance when calibrations are performed at body versus room temperature. Determining test performance in relation to the temperature at which the calibration procedures are performed is clinically relevant because it is easier to perform calibrations at room temperature than body temperature.
FPL and SIL calibrations, although resulting in smaller errors than SPL calibration, did not produce the same sound-source characteristics across repeated calibrations, regardless of the temperature at which the calibrations were performed (Neely & Gorga, 1998; Scheperle et al., 2008). Scheperle et al. noted variability in daily cavity measurements for both FPL and SIL. This variability potentially reflects measurement errors during cavity calibrations. If errors exist in cavity calibration due to measurement errors, then it might be possible to reduce the magnitude of these errors by using a reference cavity-calibration measurement compared to a daily cavity-calibration measurement.
Previous research has shown that SIL and FPL calibration methods have similar influence on DPOAE level (Scheperle et al., 2008); however, FPL-based calibrations may be preferable for the following reasons. First, FPL calibration measures use the same pressure reference as SPL, which could assist in comparisons within the clinic and potentially increase the likelihood of implementation. Second, Scheperle et al. (2008) report that constant-level sound presentations during SIL calibrations were perceived as extremely loud and led to subjects discomfort for higher sound levels and higher frequencies. Apparently, constant-FPL stimuli maintain more nearly constant loudness across frequency compared to constant-SIL stimuli. Therefore, even though SIL and FPL calibration methods are similar in that they are more resistant to standing-wave errors than SPL, this study focused on DPOAE test performance following SPL and FPL calibrations, for the reasons described above.
The goal of the present study was to determine whether calibration method influences the accuracy with which auditory status is inferred from DPOAE measurements. Specifically, the objectives of this study were (1) to determine the extent to which DPOAE test performance improves with FPL calibration methods, compared to calibrations based on SPL, (2) to determine if the temperature at which the FPL calibrations are performed influences test performance, (3) to evaluate the influence of calibration for frequencies where errors are anticipated and for frequencies at which errors are not expected, (4) to determine whether repeated cavity-calibration measurements prior to data collection result in more reliable estimates, reduce the magnitude of calibration errors, and improve test performance, and (5) to determine whether an “optimal” FPL calibration file measured prior to data collection is superior to a calibration file that is measured on the same day on which the DPOAE data are collected.
II. METHODS
A. Subjects
Data were collected from 155 subjects (52 normal-hearing and 103 hearing-impaired), ranging from 11 to 75 years in age. A wide age range was selected because standing-wave errors are dependent on ear-canal characteristics such as length, diameter and eardrum impedance (Gilman & Dirks, 1986; Siegel, 2007), which varies across age. Normal hearing was defined as behavioral thresholds ≤ 20 dB HL (ANSI S3.6, 2004) for octave frequencies between 0.25 and 8 kHz, as well as the inter-octave frequencies of 3 and 6 kHz. A subject was labeled as hearing impaired if a behavioral threshold was >20 dB HL for any test frequency used during DPOAE measurements. Individuals were included only if they demonstrated normal middle-ear function as evaluated by otoscopic inspection and a 226-Hz tympanogram (peak compensated, static acoustic admittance between 0.3 and 1.8 mmhos and tympanometric pressure peak (TPP) between −100 and +50 daPa) on the day of testing, as well as air-bone gaps of ≤ 10 dB. If both ears met the inclusion criteria, then the ear with the TPP closest to 0 daPa and/or easiest probe insertion was chosen. While subjects were divided into normal-hearing and hearing-impaired categories, for the purposes of data analysis, an ear was classified as hearing impaired on a frequency-by-frequency basis, which resulted in different numbers of impaired ears depending on frequency. Among the group with hearing loss, subjects were recruited without regard to degree or configuration of hearing loss, in an effort to assure that the results will generalize to an unselected population of clinic patients.
B. Equipment Specifications
All measurements, including probe-source calibrations, Thevenin-equivalent calculations, FPL conversions, and DPOAE measurements were performed using custom-designed software (EMAV version 3.01; Neely & Liu, 1994). A probe-microphone system (Etymotic Research, ER-10C) was used for stimulus presentation and response recording with a 24-bit soundcard (CardDeluxe, Digital Audio Labs) housed in a PC. Separate channels of the soundcard were used to generate the two primary tones (f1 and f2), which were mixed acoustically in the ear canal. The probe-microphone system was modified to remove 20 dB of attenuation so that measurements were possible at 70 dB in all ears.
C. Calibration Cavities
Use of a pressure-sensitive microphone to perform FPL calibrations requires a series of prior measurements to estimate Thevenin-equivalent source characteristics of the sound sources (loudspeakers) within the ER-10C probe. Source impedance and pressure are needed to estimate load impedance, which is needed to convert SPL to FPL. A set of cylindrical cavities with known acoustic impedance was used to estimate source impedance and pressure (Allen, 1986; Keefe, Ling, & Bulen, 1992; Møeller, 1960; Rabinowitz, 1981).
The calibration procedure used in the present study was modeled after the one described in Scheperle et al. (2008). A cavity set was constructed out of five brass tubes (11/32 inches outside diameter, 8 mm inside diameter) that were 83, 54.3, 40, 25.6, and 18.5 mm in length. In addition, a coupler was created by gluing a short (20 mm) section of the same diameter tube inside a slightly longer (30 mm) section of a slightly-larger diameter tube (3/8 inches outside diameter). The foam ear-tip of the ER-10C probe was compressed and inserted into the smaller end of the coupler. The coupler effectively extended the tube length by about 3 mm. The use of this coupler was intended to remove (or at least reduce) variability associated with probe placements as the probe is moved from cavity to cavity during calibration. The lengths of the tubes were selected so that with the coupler in place, resonant peaks would occur approximately at 2, 3, 4, 6 and 8 kHz, the same frequencies that are the focus of the measurements in this study.
D. Calibration Procedures
A wideband-chirp stimulus with a sampling rate of 32 kHz was presented to each tube in the cavity set and the pressure response of each loudspeaker (source) was measured with the probe microphone. EMAV initially estimates the length of the tube based on the first spectral notch, which theoretically occurs when L = λ/4, where L is the length of the cavity and λ is the wavelength of the spectral frequency. For cylindrical tubes of known length, an ideal expression for cavity impedance (Zc) is
where k is the wave number and Z0 is the characteristic impedance of the probe microphone (Keefe et al., 1992). Z0 can be determined by
where ρ is the density of air, c is the speed of sound, and A is the area. Cavity impedance may be calculated when the length, diameter and temperature of the cavity are known (Keefe, 1984). The calculated impedance, or theoretical impedance, of a cylindrical cavity is so sensitive to length that the initial length estimate EMAV calculates based on the frequency of the first spectral notch is only assumed to be an approximation. Together, theoretical cavity impedance and measured pressure (Pc) allows for a least-squares estimate of source impedance (Zs) and source pressure (Ps). The agreement between the measured cavity pressure and the calculated source pressure are expressed as an error value derived by EMAV. Because the theoretical impedance is sensitive to length, EMAV recalculates the source pressure with slight changes to the length to find the best agreement between these measurements. An error value of less than 1 generally indicates good agreement. Although somewhat arbitrary, previous work has shown that this rule results in reliable estimates of source impedance and pressure (Scheperle et al., 2008).
In situ calibration, performed in the ear (load), was completed in each subject to measure the pressure response in the ear (Pl). Source impedance and source pressure are used in combination with load pressure to determine the impedance of the ear canal, (Zl):
Once these values are known, SPL is converted to FPL by the equation
where P+ is the forward pressure wave1. EMAV computes FPL based on the cavity measurements and saves the transform to a file that is accessed prior to the DPOAE measurement, at which time the levels of the primaries (f1 and f2) are adjusted.
Based on previous reports that temperature may affect cavity calibrations (Neely & Gorga, 1998; Scheperle et al., 2008), measurements were performed in cavities at room temperature and heated (with a heating pad) to 96–102 °F, which approximates body temperature. Neely and Gorga (1998) found that when performing repeated source-pressure and impedance measurements there was variability among the results, depending on temperature, a pattern that was also observed by Scheperle et al. (2008). During preliminary cavity-calibration measures, variability was observed that might be attributed to differences in insertion or compression of the foam tip.
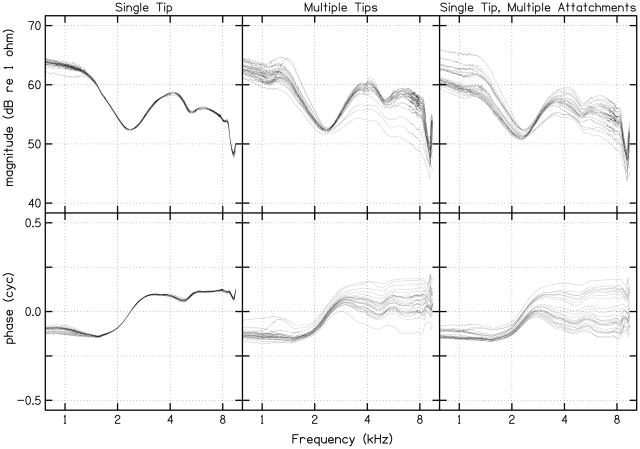
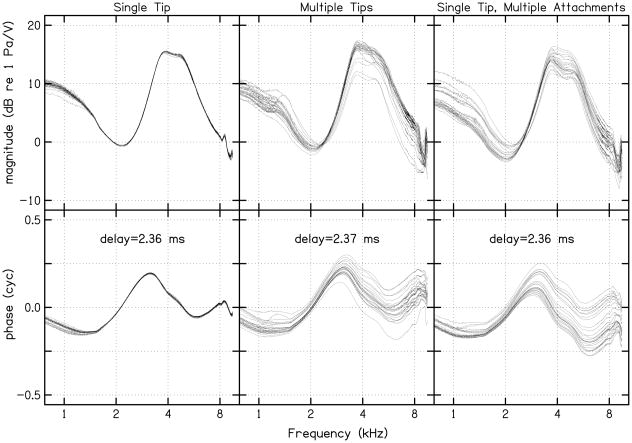
Initially, 25 cavity calibrations were completed at both body and room temperature using only one standard (adult) foam ear tip, which remained in the coupler for all measurements. In contrast to observations made by Scheperle et al., little or no deviation was seen in repeated impedance (left column, Fig. 1) and pressure (left column, Fig. 2) measurements. A second series of 25 measurements were completed at body and room temperature, but this time using a new foam ear tip for each calibration measure. Variability among the repeated measures increased, and was equivalent to those observed by Scheperle et al. (see second column of Figs. 1 and 2). In an effort to identify the source of this variability, a third set of 25 measurements were completed (only at room temperature) using the same foam ear tip, but with the ear tip removed, allowed to re-expand, and reinserted into the coupler before each new calibration (right column, Figs. 1 and 2). Once again, variability in the source pressure and impedance measurements was observed that was similar to that seen following repeated measurements with a new ear tip each time (compare middle and right columns of Figs. 1 and 2). In light of these results, it appears that the variability may be attributable to differences in compression of the foam ear tip, whether it be the same or a different foam ear tip for each trial. Given these observations, it was decided that the calibration measurement that exhibited the lowest error value (from all preliminary calibration measurements at each temperature) would be selected as the reference calibration measure. As a result, the calibration measurement selected for the reference at room temperature was one completed using the single tip (the first set of preliminary measurements) while the reference at body temperature was one completed using multiple tips.
FIGURE 1.
Twenty-five calculations of source impedance from the calibration cavities performed at room temperature using a single standard foam ear tip, which remained in the coupler for all measurements (first column), using a different standard foam ear tip (second column), and using the same standard foam ear tip but removing it from the coupler before each set of measurements (third column). The characteristics for only one sound-source channel are plotted. Each line in each panel represents one of the 25 measurements. The 25 cavity calibrations at body temperature, although not shown, exhibited the same pattern.
FIGURE 2.
Twenty-five calculations of source pressure from the same calibration cavities used in Fig. 1. The delay values in the bottom panels represent the time difference between stimulus generation and response recordings by the soundcard. The values plotted in the bottom row demonstrate the phase values after the number of cycles occurring within the time delay were subtracted out. The 25 cavity calibrations at body temperature, although not shown, exhibited the same pattern.
In addition to the reference calibration condition, a daily calibration measure at both body and room temperature was used. Source impedance and pressure responses from one day to the next are expected to vary in a manner that is similar to the variability shown in the middle and left panels of Figs. 1 and 2, respectively. By testing with both reference calibrations (determined from the best calibration measurements prior to data collection) and daily calibration (just prior to data collection on each day) at both room and body temperature, we were able to test the effects of temperature, and the influence of when the calibration measurements are made relative to data collection.
E. Procedures
In-situ calibration was performed on each subject with the same DPOAE probe and chirp stimulus used for source calibration. DPOAEs were measured for f2 frequencies ranging from 2 to 8 kHz in half-octave steps, with a fixed primary-frequency ratio (f2/f1) of approximately 1.22, and levels determined by the equation, L1 = 0.4L2+39 (Kummer et al., 1998, 2000). This level paradigm, known as the scissor paradigm due to the increasing level difference of the primaries with decreasing stimulus level, is in widespread use because it is thought to produce the largest DPOAE response, on average, in individuals with normal hearing. At each f2 frequency, DPOAEs were measured in five calibration conditions: SPL, daily FPL at body temperature (daily body), daily FPL at room temperature (daily room), reference FPL at body temperature (ref body), and reference FPL at room temperature (ref room). The order of conditions was counterbalanced across subjects. Input/output (I/O) functions were measured at each f2 frequency for every calibration condition (for a total of 25 conditions). In every case, testing began at L2 = 70 dB, depending on the condition, and decreased in 5-dB steps. To increase data-collection efficiency, I/O measurements were terminated once the DPOAE level no longer exceeded the noise floor by 3 dB (i.e., testing stopped when the signal-to-noise ratio (SNR) was < 3 dB). This approach was implemented so that no time was spent collecting data for conditions in which a reliable response would not be observed.
Measurement at each stimulus condition (every combination of f2, L2, and calibration method) continued until one of the following three stopping criteria was met: the noise floor was ≤ −25 dB SPL, 32 seconds of artifact-free averaging had expired, or the SNR was > 60 dB. These rules were chosen so that the measurement would never stop on SNR and (ideally) would end on the noise-level rule. The noise-level stopping rule was selected conservatively in relation to system distortion, such that no measurements would be made for conditions in which the observed distortion could be coming from the measurement system. Noise level was estimated as the level in the 2f1−f2 frequency bin, and in five frequency bins on either side of the distortion product frequency. It was possible to include the 2f1−f2 frequency bin in the noise estimate by alternately storing 2-second samples of the recorded response in one of two buffers. The contents of the two buffers were subtracted and then power-averaged over the eleven frequency bins (2f1−f2 plus the five bins on either side) to provide an estimate of the noise level. The buffers were summed and the level in the 2f1−f2 frequency bin was used to provide an estimate of the DPOAE level.
F. Data Analysis
Clinical decision theory was used to analyze the data, which were used to construct receiver operating characteristic (ROC) curves for each f2, calibration method and L2 (Swets, 1988; Swets, & Pickett, 1982). From these curves, areas under the ROC curve (AROC) were estimated. In order to determine if any of the AROC among the five calibration conditions differed significantly, a measure of expected variance within an ROC curve was computed. The following equation (Bamber, 1975) was used to provide an approximate upper bound on AROC variance ( ):
where A is the AROC and NL represents the number of subjects in the lesser of the two groups (normal hearing or hearing impaired). To determine if DPOAE test performance using SPL calibration differed from FPL calibration, this measure of variance was computed on the SPL calibration method at each f2 and L2. Once the variance was determined, standard deviations were estimated by taking the square root of the variance. A significant difference in test performance among calibration methods was defined as any AROC value differing by greater than 2 standard deviations from any other calibration test condition. As will be described in greater detail, no calibration method differed in test performance significantly. In addition, Cohen’s d effect size was computed to determine the strength of these findings. This measure was completed by dividing the difference between SPL and FPL AROC values by the standard deviation.
III. RESULTS
A. DPOAE I/O Functions and DPgrams from Individual Normal and Impaired Ears
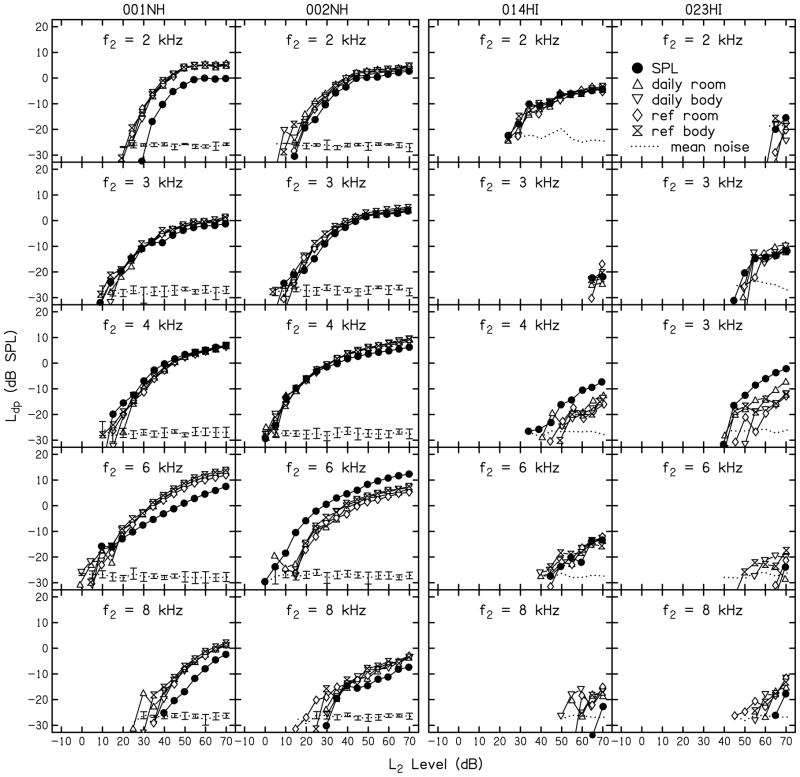
DPOAE input/output (I/O) functions from two normal-hearing and two hearing-impaired subjects at each of the five f2 frequencies for all calibration methods (SPL, ref room, ref body, daily room, daily body) are shown in Fig. 3. Data are represented at the f2 frequency (as opposed to alternatives, such as the geometric mean between f1 and f2), based on the assumption that the primary interaction between f1 and f2 occurs at or near the f2 place in the cochlea (i.e., the distortion source for the DPOAE) (e.g., Brown and Kemp, 1984; Harris et al., 1992; Kummer et al., 1995; Gaskill and Brown, 1996). Data from separate subjects are shown in each column while the data for each of the five f2 frequencies are shown in different rows. The parameter within each panel is calibration method that was used to calculate L2. For some calibration methods, data are not present at and below some L2 levels because data collection terminated once the DPOAE level (Ld) no longer exceeded the noise floor by 3 dB. The dotted lines near the bottom of each panel represent the average noise level across the calibration condition. The noise floor showed little variability across calibration methods as demonstrated by the error bars plotted for the normal-hearing subjects. Error bars were not plotted for hearing-impaired subjects because many DPOAE responses overlapped with the noise floor (SNR ≈ 0 dB), making it hard to distinguish between Ld and noise. The observation of minimal variability in noise levels is not surprising because of the measurement-based stopping rule, which resulted in data collection stopping when the noise level was ≤ −25 dB SPL.
FIGURE 3.
DPOAE I/O functions from two normal-hearing and two hearing-impaired subjects are shown in separate columns. Each row provides data for a different f2 frequency. The parameter within each panel is calibration method (SPL, ref room, ref body, daily room, daily body). The mean noise level (dotted lines) represents the average noise levels for all five calibration conditions. Error bars represent the standard deviations calculated from the noise level observed among the five calibration methods. Standard deviations around the mean noise levels are not provided in the panels depicting data from hearing-impaired subjects for the reasons described in the text.
The I/O functions for the normal-hearing subjects are consistent with previously reported measurements of DPOAE I/O functions in humans (e.g., Lonsbury-Martin et al, 1990; Nelson and Kimberley, 1992; Gorga et al. 1994; Stover et al., 1996; Dorn et al., 2001). Responses were measured over a wide dynamic range at all five f2 frequencies, although the L2 range over which responses were measured was smaller at 8 kHz. The reduced dynamic range at 8 kHz might be attributed to the stimulus conditions used in the present study, which were not optimal at this frequency (Neely et al., 2005; Johnson et al., 2006). However, a decision was made to use the scissor paradigm (Kummer et al., 1998, 2000) because of its widespread use and the need to apply a stimulus paradigm that was the same for both normal-hearing and hearing-impaired subjects. The DPOAE I/O functions in the impaired ears differed from those seen in ears with normal hearing in several ways. At some frequencies, even at high levels of stimulation, reliable responses above the noise floor were not observed. At other frequencies, responses were observed for stimuli limited to higher levels. Rarely, the I/O function was similar to what was observed in normal ears (2 kHz responses for subject # 014HI, a condition for which, in this subject, the behavioral threshold was 20 dB HL).
The DPOAE I/O functions based on the five calibration methods mainly overlapped. This outcome is expected, at least for the four FPL-based calibrations. However, when they did separate, it was usually the case that the function based on SPL calibrations (which are susceptible to standing-wave problems) differed from the others. SPL-based I/O functions were sometimes above and sometimes below the I/O functions based on FPL calibrations. One possible explanation might be that, depending on frequency and subject, the standing waves resulted in either an underestimation or overestimation of level at the eardrum for SPL calibrations. An underestimation of level at the eardrum would result in an increase in the voltage to the loudspeakers to erroneously compensate so that target levels are achieved. This hypothesis is consistent with the I/O functions at 6 kHz for subject #002NH and 4 kHz for subjects #014HI and #023HI. While cancellation due to standing-wave interactions at the plane of the probe might be a larger affect, summation at the plane of the probe also may occur (with a maximum effect that the estimated level at the probe is 6 dB higher than the incident sound wave, or FPL). For DPOAEs measured using the SPL calibration method under these circumstances, the voltage driving the loudspeaker will be reduced, potentially resulting in lower DPOAE levels, which is consistent with the observations at 2, 6 and 8 kHz for subject # 001NH and at 8 kHz for subject # 002NH. Somewhat surprisingly, differences were observed among calibration procedures at 2 kHz, a frequency for which standing-wave effects were not anticipated. Although unexpected and not easily explained, this observation highlights the individual variability that exists during ear-canal calibrations. It should be noted, however, that, whenever differences in Ld relative to calibration procedure were observed, the differences were less than 10 dB.
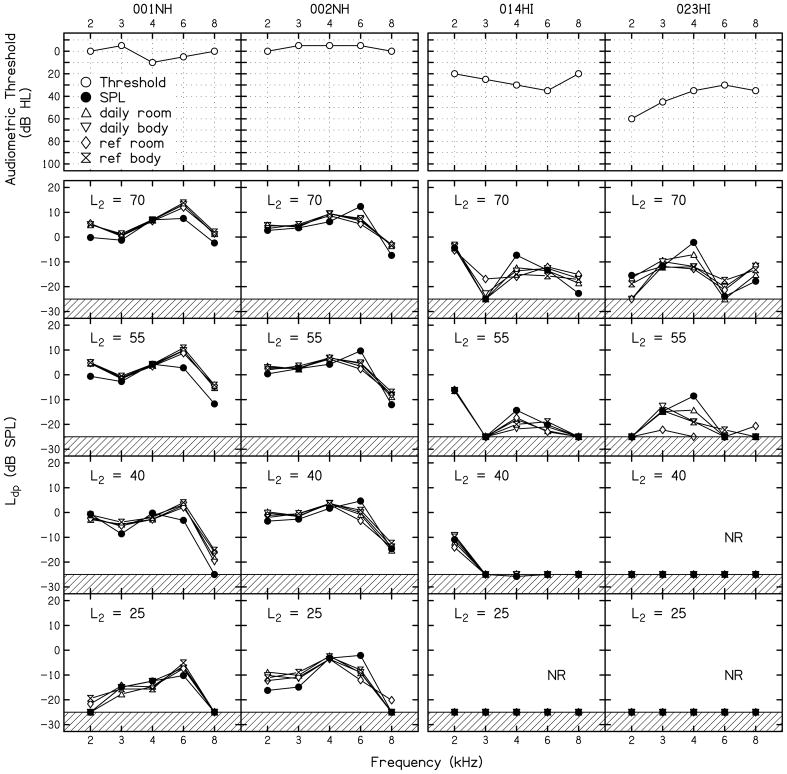
DPgrams were constructed from the previously reported I/O functions (both normal-hearing and hearing-impaired subjects), and are presented in Fig. 4 in order to give a sense of the diagnostic errors that may occur when DPOAEs are used to classify an ear as normal hearing or hearing impaired. Figure 4 shows the subjects’ pure-tone audiograms in the first row, followed by DPgrams at four different L2 levels. The data obtained from all five calibration conditions are represented within each panel. The hashed lines at the bottom of each panel represent a conservative estimate of the level at which system distortion might be observed. It is also why a noise stopping rule of −25 dB SPL was selected. The DPgrams from the two normal-hearing subjects demonstrate responses at all f2 frequencies for all but the lowest L2. This is the expected outcome for individuals with normal hearing. It may be of interest to note, however, that no response was observed in one case at L2 = 40 dB and f2 = 8 kHz following SPL calibration. For L2 = 25 dB, an absent DPOAE was observed more frequently, including conditions in which FPL calibrations were used. In the context of test performance, decisions regarding auditory status are based on the presence of DPOAEs. A condition in which no response is observed, therefore, would be considered consistent with hearing loss. However, these subjects have normal hearing. Those conditions for which no response was observed, therefore, would result in false-positive errors if used in the clinic. These data suggest that the use of low-level stimuli would have an adverse effect on test performance by driving up the false-positive rate, an observation made previously (Stover et al., 1996; Johnson et al., 2007). For the two hearing-impaired subjects, there were conditions (L2 = 70 and 55 dB) for which these ears produced responses with SNRs that would classify them as normal hearing. Furthermore, Ld using SPL calibrations were larger for the FPL methods at 4 kHz (a frequency for which behavioral thresholds were 30 and 35 dB HL for these subjects) for all levels at which a response was observed. For conditions in which a response is observed but hearing loss exists, false-negative errors would occur because ears with hearing loss might be misdiagnosed as having normal hearing. These errors occurred for high-level stimuli, and, potentially, might be more of an issue when data are collected following SPL calibrations, at least in these subjects. It is interesting to note that in one of these subjects, hearing loss was not present at all frequencies (2 and 8 kHz for #014HI). At 2 kHz, a response is present in this subject at most levels, with no response occurring only at L2 = 25 dB. This ear would be classified as hearing impaired at 2 kHz if the stimulus condition used to collect DPOAE data was L2 = 25 dB, an unlikely error because this L2 is not used in the clinic. At 8 kHz, the audiogram classified this ear as normal hearing; however, a DPOAE was observed only when L2 = 70 dB. Even for this stimulus level, the Ld collected using the SPL-based calibration was barely above the noise floor, which may be interpreted as consistent with hearing loss.
FIGURE 4.
Audiograms (top row) followed by DPgrams at four L2 levels for the same subjects whose DPOAE I/O functions were shown in Fig. 3. The data obtained from all five calibration conditions are represented within each panel. The hashed lines at the bottom of each panel represent a conservative estimate of the level at which system distortion might be observed, as described in the text. .
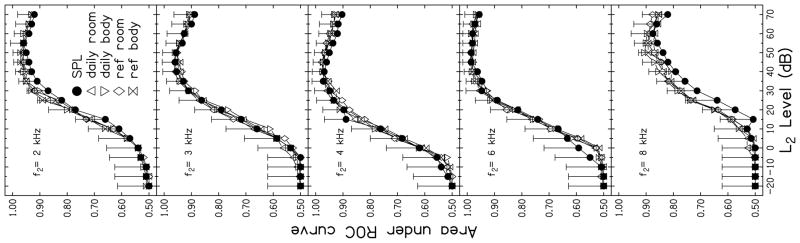
B. Influence of Level on Test Performance
The DPgrams shown in Fig. 4 demonstrate that stimulus level influences DPOAE output level, regardless of the calibration method that was used prior to data collection. The extent to which level affects test performance is demonstrated in Fig. 5, where AROC is plotted as a function of L2. Each panel represents data for a different f2 frequency while the parameter within each panel is calibration method. Error bars indicate 2 standard deviations from the SPL-based calibration function, based on the equation described earlier in which the upper bound of variance was calculated. Test performance, as described by AROC, was near chance levels for low stimulus levels (AROC = 0.5). At every frequency, AROC increased as L2 increased up to an L2 of about 50 or 55 dB. For higher stimulus levels, AROC decreased, indicating a decrease in test performance. This level effect is consistent with previous research (i.e., Whitehead et al., 1995b). At low levels, ears with hearing-loss will not produce a DPOAE response, which would have a positive impact on the hit rate. Unfortunately, many normal-hearing ears did not produce a response at these low levels as well, resulting in an increase in the false-alarm rate and an overall decrease in AROC. In fact, neither normal-hearing or hearing-impaired ears produced responses for low-level stimuli, meaning that, for these stimulus conditions, there would be an equal likelihood of committing a false-positive and a false-negative error. For high-level stimulus conditions, the likelihood of normal-hearing ears producing a response increased, decreasing the false-alarm rate, but at these high levels, some ears with hearing loss produced DPOAE responses, which, in turn, decreased the hit rate. For moderate-level stimuli, the highest AROC was observed because these stimulus conditions resulted in the lowest combined error rate, although perfect test performance was never achieved, as evident in the fact that an AROC of 1.0 was never observed.
FIGURE 5.
Areas under the ROC curves as a function of L2. Each panel represents data for a different f2 while the parameter within each panel is calibration method. Error bars indicate 2 standard deviations from the SPL-based calibration function, using the variance estimate, as described in the body of the manuscript.
The largest outcome observed in the present study related to the influence of stimulus level on test performance. This outcome was larger than both frequency and calibration effects. Still, these lesser effects also were observed. For example, AROCs at 8 kHz were lower than those observed for other f2 frequencies. This observation is consistent with other reports showing poorer test performance at 8 kHz, compared to mid to high frequencies (e.g., Gorga et al. 1993, 1997, 2007; Kim et al., 1996; Stover et al., 1996). The best test performance (i.e., the highest AROC) was observed at 6 kHz, closely followed by 2, 3 and 4 kHz.
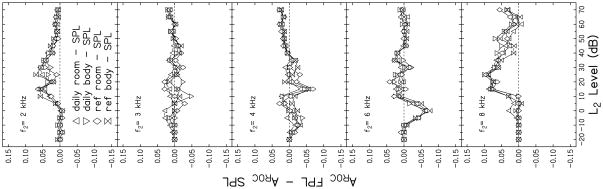
Differences in AROC related to calibration method are more difficult to see in Fig. 5. However, there are a few frequencies and levels for which a separation between the calibration methods occurred. For example, at both 2 and 8 kHz, AROC was lower for SPL calibrations compared to the FPL calibrations. In an effort to better visualize differences related to calibration method, AROC for SPL calibration (AROC SPL) at each L2 was subtracted from the AROC that was observed for data that were obtained following the four FPL calibrations (AROC FPL) at equivalent levels. These differences are plotted as a function of L2 in Fig. 6. Each panel represents results for a different frequency. The dashed line drawn at 0 within each panel serves as a reference. Values above this line indicate conditions for which test performance following FPL calibration was better than performance following SPL calibration, while values falling below this line represent conditions in which SPL achieved better test performance. There are several conditions in which SPL-based calibrations resulted in better test performance (3, 4, 6 kHz). However, SPL calibrations resulted in higher AROC only at low levels, which were conditions that resulted in overall lower AROC, compared to the AROC that was observed at moderate stimulus levels. Overall test performance was sufficiently poor for these low-level stimulus conditions that they would not be used in the clinic. Therefore, the differences seen at low L2 levels are of little clinical relevance. However, for moderate levels (levels at which overall test performance was better and which are more likely to be used in the clinic), there are some frequencies for which FPL calibrations resulted in better test performance than SPL. It is also important to note that it was never the case that FPL calibration resulted in a lower AROC compared to the AROC observed for SPL calibrations when the stimulus condition resulting in the overall highest AROC (and, therefore, best test performance) were used. The largest difference between AROCs for SPL and FPL conditions at L2 levels of clinical interest occurred at 8 kHz. In some cases at this frequency, AROCs differed by more than 0.05. At first glance, this may seem like a relatively small difference. However, AROC can range only from 0.5 to 1.0; thus, a difference of 0.05 represents a 10% change in AROC.
FIGURE 6.
Differences between SPL AROC and FPL AROC as a function of L2. Each panel represents results for a different f2. The dashed line indicates no difference in AROC between calibration methods. Values above this line indicate conditions for which test performance following FPL calibration was better than performance following SPL calibration, while values falling below this line represent conditions in which SPL achieved better test performance.
Effect-size calculations at L2 = 50 dB, a clinically relevant stimulus condition as the best test performance was observed for all calibration methods around this stimulus level, were completed to provide a general description of the magnitude of these differences between SPL- and FPL-based performances. Only the FPL condition that resulted in the largest difference when compared to SPL was used. According to Cohen (1992), an effect size of 0.2, 0.5 and above 0.8 represent small, moderate and large effects, respectively. Calculations revealed a large effect at 8 kHz (1.53), a moderate effect at 2 and 4 kHz (0.73 and 0.65, respectively), and a small effect at 3 and 6 kHz (0.15 and 0.04, respectively). However, there was no condition in which the AROC for FPL calibrations was greater than 2 standard deviations above the AROC for data collected following SPL calibrations, even with a large effect at 8 kHz. Thus, the observed differences in AROC related to calibration method failed to achieve statistical significance.
C. Specificity and Sensitivity
ROC curves and estimates of AROC provide a complete description of test performance by providing hit and false-alarm rates for all values of the experimental measure (DPOAE level in this case). Clinically, however, it may be necessary to select test criteria that minimize one error at the expense of increasing the other. For example, under some circumstances, it may be reasonable to select criteria that minimize the false-positive rate, allowing the miss rate to increase. In other circumstances, it might be more appropriate to select a criterion such that the miss rate is minimized, knowing that the use of this criterion will increase the false-positive rate. Furthermore, the ROC curve and estimates of AROC include conditions that might never be used in the clinic. For example, AROC represents the hit rate averaged across all false-alarm rates up to 100%. However, it is unlikely that criteria would be selected for clinical use that would result in such high false-alarm rates. Rather, it is more likely that criteria would be selected that result in a more limited range of false-alarm rates. In fact, estimates of AROC, which include all false-alarm rates from 0 to 100%, may obscure important differences in test performance for conditions (i.e., false-alarm rates) that might be used clinically.
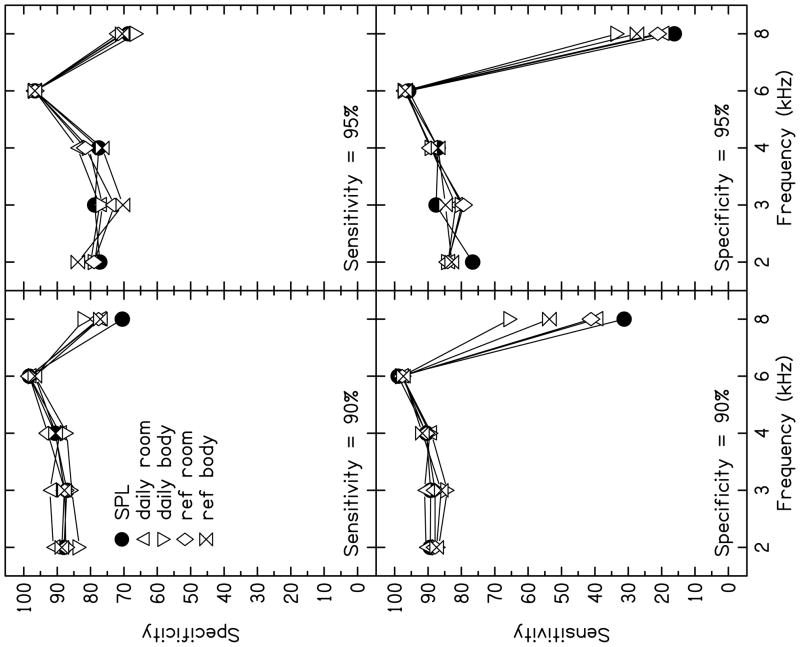
Evaluating test performance as a function of fixed sensitivity or specificity may be preferable to using AROC values because the latter estimates are based on hit rates averaged across all false-alarm rates. Figure 7 shows specificity as a function of frequency for two fixed sensitivities in the top row, while sensitivity as a function of frequency for two fixed specificities are plotted in the bottom row. These results are based on data collected when L2 = 50 dB, the condition for which overall test performance was best (Fig. 5). As seen in the top row (fixed sensitivity), specificities were similar for most f2 frequencies, with the exception of 8 kHz. Specificity was highest (i.e., false-alarm rates are lowest) at 6 kHz in all calibration conditions, while the specificity at 8 kHz for fixed sensitivities was lower than it was for other frequencies. In addition, at 8 kHz, data collected following SPL calibration demonstrated the lowest specificity values over other calibration conditions, but only for the case when sensitivity was fixed at 90%. When sensitivity was fixed at 95%, there were no significant differences among calibration procedures at 8 kHz, although performance was still poorer at this frequency. When the sensitivity was fixed at 95% (i.e., more stringent criteria were selected making it harder to pass the test), specificity decreased for 2, 3 and 4 kHz, which is expected because there was no test with perfect test performance. Stated another way, an increase in sensitivity will be accompanied by a decrease in specificity, consistent with the observations in the top row of Fig. 7.
FIGURE 7.
Specificity (top panel) and sensitivity (bottom panel) as a function of frequency for two fixed sensitivities and specificities (90 and 95%) for the condition in which L2 = 50 dB. The parameter within each panel is calibration method.
Fixing specificity and determining sensitivity resulted in trends that were similar to those observed when sensitivity was fixed. Again, 6 kHz performed the best (highest sensitivities for fixed specificities), while slightly lower sensitivities were observed for 2, 3, and 4 kHz. However, at 8 kHz, low sensitivity values were observed for all calibration conditions, especially SPL calibration. This means that, at 8 kHz, a high sensitivity cannot be achieved without a high false-alarm rate. It is also interesting to note that SPL resulted in the lowest sensitivity for fixed specificities, especially when specificity was fixed at 90%, a condition for which daily FPL calibration at body temperature resulted in a sensitivity that was nearly 40% higher than the sensitivity that was observed following SPL calibration. When specificity was increased to 95%, sensitivity decreased for all f2 frequencies (with the possible exception of 6 kHz), but this effect was especially evident at 8 kHz for all calibration conditions. The difference between calibration conditions also decreased, but it was still the case that SPL resulted in the lowest sensitivity while daily body resulted in the highest sensitivity. Thus, when the analyses were restricted to conditions that might be used clinically (i.e., the L2 resulting in the best overall test performance, and sensitivities or specificities that might be acceptable in the clinic), effects of calibration procedures were observed, although they were restricted to 8 kHz.
DISCUSSION/CONCLUSIONS/SUMMARY
The results of this study are summarized by the following observations:
DPOAE test performance was sensitive to stimulus level, regardless of calibration method, with the test performance peaking for moderate stimulus conditions. This finding is consistent with previously reported results (Whitehead et al., 1995b; Stover et al., 1996; Johnson et al., 2007).
An influence of frequency was observed for all calibration methods, with the best test performance at 6 kHz and the worst performance at 8 kHz.
At stimulus levels that would be appropriate for clinical use, little difference in test performance among calibration methods was noted across frequencies, except at 8 kHz. At 8 kHz, FPL-based calibration methods provided superior performance compared with the standard SPL calibration. However, the size of the influence was not large, making it difficult to achieve statistical significance.
In addition, a difference between FPL calibration methods was also observed at 8 kHz, with best test performance occurring for daily body calibrations. Therefore, temperature may have an impact on FPL calculations relative to DPOAE test performance, although improvements in test performance over SPL were observed for all FPL calibrations, regardless of temperature.
A. Stimulus Level and Calibration Method
Clinically, stimulus conditions that result in poorer test performance are not of interest; however, some of the differences in performance observed at lower and higher stimulus conditions provide insight into the effects of standing-wave errors. At moderate stimulus levels, a difference in FPL and SPL test performance (as estimated by AROC) was not observed for most f2 frequencies, except at 8 kHz. These results may be due, in part, to a ceiling effect, as 3, 4, and 6 kHz had high AROC values for all calibration methods. Low and high stimulus level results in lower test performance across frequencies, eliminating the ceiling effect and allowing one to analyze standing wave effects across frequencies. As shown in Fig. 6, SPL calibration produced higher AROC values compared to any FPL calibrations when L2 was below 30 dB for frequencies 3, 4 and 6 kHz. These are frequencies for which standing-wave errors are expected because of the shorter wavelengths relative to the length of the ear canal. It is possible that for these low stimulus conditions, standing-wave errors occurred, causing an under-estimation of level at the eardrum, which, in turn, led to an increase in voltage at the back of the loudspeaker. As a consequence, the level at the eardrum was higher than the specified level, increasing the likelihood that a normal-hearing ear would produce a response. Recall that many normal-hearing ears fail to produce a DPOAE response at low stimulus levels (see the level effects on AROC in Fig. 5). If the level at the eardrum was increased (knowingly or not) above some supposed low level at which many normal-hearing ears do not produce a response, then it is likely that more normal ears will produce a response, thus driving down the false-alarm rate for SPL-based functions. This hypothesis might explain findings in Fig. 6, where AROC for SPL was higher than it was for FPL calibrations.
The opposite effect is predicted at high stimulus levels. If the level at the eardrum is underestimated from SPL calibrations due to cancellation at the plane of the probe as a result of standing waves, then the voltage would be increased to even higher levels. At high levels, there is a tendency for AROC to decrease (Fig. 5), presumably because some ears with hearing loss produce responses at these levels. Thus, the observations of higher AROC for FPL calibrations at higher levels may be a result of the same standing-wave problem that explains the higher AROC at low levels for SPL calibrations (Fig. 6). Another explanation for poorer test performance with SPL compared to FPL calibrations is that an increase in level may also lead to higher system distortion, which increases at high stimulus levels. The generation of system distortion would increase the false-negative rate because one might erroneously conclude that a biological response was present when, in fact, the distortion was generated by the hardware.
B. Frequency and Calibration Method
In general, there was a similar effect of frequency regardless of calibration method. Test performance was the best at 6 kHz, closely followed by 2, 3 and 4 kHz, while 8 kHz had the lowest AROC values. Reasons for poorer test performance at 8 kHz have been attributed to higher system distortion (Gorga et al. 1997), the use of non-optimal stimulus conditions (Johnson et al., 2006; Neely et al., 2005) and/or standing-wave errors at this frequency. However, the influence of calibration method was observed, although the effects were not large. As shown in Fig. 5, the poorest performance at 8 kHz was observed following SPL calibrations. All FPL calibrations resulted in better test performance than the SPL calibration. Assuming that system distortion would not be a factor at moderate and low stimulus levels, it is possible that standing-wave errors contributed to poorer performance of 8 kHz in this and in previous studies. However, even with the improvement in performance that was observed when data were collected following FPL calibrations, test performance was still poorer at 8 kHz compared to the other four frequencies. Thus, errors associated only with calibration cannot completely account for the poorer test performance when f2 = 8 kHz. Nonetheless, 8 kHz was the only frequency in which a large effect of calibration method was observed, although not statistically significant.
The lack of significance between calibration methods may be a consequence of having too few subjects for the number of comparisons being made or due to selecting test performance criteria that may be insufficiently focused on test conditions commonly used in clinical practice. Since AROC equals the average hit rate across all false-alarm rates, including false-alarm rates that would never be utilized in the clinic, this may have inadvertently decreased our chances for observing any significant calibration-based differences in DPOAE test performance. If partial areas under the ROC curve, for which only lower false-alarm rates that would be acceptable in everyday clinical situations, were used in a statistical analysis, a larger difference may have been observed at 8 kHz and perhaps even at other frequencies. The summary provided in Fig. 7, in which only portions of the ROC curves were considered, suggests that this might be the case. It is the case that 8 kHz is a frequency not often used in clinical testing presumably because of poorer test performance, compared to other frequencies. This is unfortunate because many cochlear insults first manifest themselves at higher frequencies. Being unable to make measurements at 8 kHz that are as reliable as similar measurements at lower frequencies limits our ability to obtain information about sensory disorders during early stages.
In addition to the impact of standing wave errors on 8-kHz test performance, Neely et al. (2005) and Johnson et al. (2006) investigated optimal stimulus-level paradigms and found that the use of the Kummer et al. (1998, 2000) equation does not describe stimulus conditions resulting in the largest responses for 8 kHz, at least in normal-hearing subjects. Instead, Neely et al. (2005) and Johnson et al. (2006) observed that much higher L1 levels were required in order to produce the largest DPOAEs at 8 kHz. In fact, not only were larger DPOAEs noted when individual optimal level differences were obtained, but in addition, intersubject variability decreased and DPOAE I/O functions became more similar across frequency. The data shown in Fig. 3 indicate that 8 kHz had a different I/O function than the other test frequencies, as it had a much smaller dynamic range for the normal hearing subjects. Perhaps test performance at 8 kHz could improve if optimal level paradigms were used in conjunction with FPL calibration methods. Further study in which optimal stimulus conditions are used while comparing calibration methods would be needed to evaluate this hypothesis.
C. Differences in FPL Calibration Methods
Test performances across frequency and calibration method were similar, with the exception of 8 kHz. At 8 kHz, not only were there differences in test performance between SPL and FPL calibrations, there also were differences among the four FPL calibration methods. Given that moderate stimulus levels are of clinical interest because they result in the best test performance, our discussion on the differences among FPL calibration methods will be limited to L2 = 50 dB. Figure 8 plots specificities for fixed sensitivities and vice versa. There is little difference among calibration procedures for frequencies ≤ 6 kHz. However, differences were observed among all calibration procedures, including the four FPL conditions, at 8 kHz for the clinically relevant sensitivity and specificity values used in this figure. The FPL calibration method that resulted in the highest AROC value for L2 = 50 dB, and produced the largest sensitivity values for fixed specificities was the daily body calibration. In fact, the daily body calibration resulted in a 10–40% improvement in sensitivity for a fixed specificity of 90% over the other calibration methods. The largest difference (40%) was observed between the sensitivities following daily body calibration and SPL calibration. The calibration method that used a reference condition at body temperature (ref body) resulted in the next highest sensitivities for fixed specificities, suggesting that deriving FPL from measurements at body temperature improves test performance, at least at 8 kHz but it is still the case that daily calibrations provided the best performance. Differences between estimates of test performance at body temperature (daily body versus ref body) may be attributed to the imprecise heating process that was implemented to attain body temperature for calculating the Thevenin-equivalent source characteristics. It has yet to be determined whether the improvement in performance following daily FPL calibrations at body temperature is sufficient to justify the additional requirements associated with its use.
In contrast to calibrations performed at body temperature, no difference was observed between the daily room and the ref room FPL calibrations based on AROC values (see Fig. 5), for sensitivities at fixed specificities, or for specificities at fixed sensitivity (see Fig. 7). This observation would have simplified the use of FPL calibrations if room-temperature calibrations resulted in similar performance, compared to daily body-temperature calibrations, which, unfortunately, was not the case.
D. Clinical Implications
It may be difficult to argue to change to a calibration method that requires additional measurements prior to measuring the DPOAE, particularly since there was little if any difference noted among the test performance achieved by different calibration methods. However, at 8 kHz, a frequency for which poorer test performance has consistently been observed (e.g., Gorga et al., 1993, 1997; Stover et al, 1996), a change in calibration methodology may be beneficial. Unfortunately, the calibration method that resulted in the highest AROC value, as well as the highest sensitivity for fixed specificity, was the daily calibration method at body temperature, which is also the calibration method that would be the most difficult to implement clinically. Even so, all FPL calibrations resulted in better performance at 8 kHz, compared to SPL. For protocols that are designed to monitor changes in hearing as a result of ototoxicity or in relation to hearing conservation, measuring 8 kHz accurately may be desirable, given that higher frequencies are more susceptible to cochlear damage (e.g., Delehaye et al., 2008; Dhooge et al., 2006; Knight et al., 2007; Ress et al., 1999; Seixas et al., 2004; Stavroulaki et al., 2001). Furthermore, it can be argued that a calibration technique that results in more accurate level measurements, regardless of the impact on test performance, should be implemented.
E. Conclusions
In summary, with the exception of 8 kHz, there was little difference in test performance related to calibration methods. However, at 8 kHz AROCs and specificities for fixed sensitivities indicate that FPL-based calibration methods provide superior performance compared with the standard SPL calibration, an observation that was true for the moderate stimulus levels that typically are used in the clinic. Temperature may have an impact on FPL calculations relative to DPOAE test performance (with daily calibrations at body temperature resulting in the best performance), although improvements in test performance over SPL were observed for all FPL calibrations, regardless of temperature. Perhaps the lack of statistical significance relates to the fact that test performance is generally good at all of the frequencies used in the present study (with the exception of 8 kHz), even though these are frequencies at which standing-wave issues are thought to occur. Given this “ceiling effect”, it may be the case that a larger sample is needed to detect statistical significance. Although the results were not statistically significant, the present results suggest that standing-wave errors may impact DPOAE test performance and can be reduced by using FPL, especially at 8 kHz.
Acknowledgments
Work supported by the NIH (NIDCD T35 DC008757, R01 DC002251 R01 DC008318, P30 DC004662). We would like to thank Sandy Estee for help with subject recruitment. The data summarized in this paper were collected during the summer of 2008 when Sienna Burke and Abby Rogers were trainees in our short-term research training program.
Footnotes
A derivation of FPL is provided in the Appendix of Scheperle et al. (2008)
References
- Allen JB. Measurement of eardrum acoustic impedance. In: Allen JB, Hall JL, Hubbard A, Neely ST, Tubis A, editors. Peripheral Auditory Mechanisms. Springer-Verlag; New York: 1986. pp. 44–51. [Google Scholar]
- ANSI. ANSI Report No. S3.6. American National Standards Institute; New York: 2004. Specifications for audiometers. [Google Scholar]
- Bamber D. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. J Math Pychol. 1975;12:387–415. [Google Scholar]
- Brown AM, Kemp DT. Suppressibility of the 2f1−f2 stimulated acoustic emissions in gerbil and man. Hear Res. 1984;13:29–37. doi: 10.1016/0378-5955(84)90092-3. [DOI] [PubMed] [Google Scholar]
- Brownell W. Observations on a motile response in isolated outer hair cells. In: Webster WR, Aitken L, editors. Mechanisms of Hearing. Montash University Press; Australia: 1983. pp. 5–10. [Google Scholar]
- Delehaye E, Capobianco S, Bertetto IB, Meloni F. Distortion-product otoacoustic emission: Early detection in deferoxamine induced ototoxicity. Auris Nasus Larynx. 2008;35:198–202. doi: 10.1016/j.anl.2007.05.001. [DOI] [PubMed] [Google Scholar]
- Dhooge I, Dhooge C, Geukens S, De Clerck B, De Vel E, Vinck BM. Distortion product otoacoustic emissions: An objective technique for the screening of hearing loss in children treated with platin derivatives. Int J Audiol. 2006;45:337–343. doi: 10.1080/14992020600582117. [DOI] [PubMed] [Google Scholar]
- Dirks DD, Kincaid GE. Basic acoustic considerations of ear canal probe measurements. Ear Hear. 1987;8:60S–67S. doi: 10.1097/00003446-198710001-00002. [DOI] [PubMed] [Google Scholar]
- Dorn PA, Konrad-Martin D, Neely ST, Keefe DH, Cry E, Gorga MP. Distortion product otoacoustic emission input/output functions in normal-hearing and hearing-impaired human ears. J Acoust Soc Am. 2001;110:3119–3131. doi: 10.1121/1.1417524. [DOI] [PubMed] [Google Scholar]
- Dreisbach LE, Siegel JH. Distortion-product otoacoustic emissions measured at high frequencies in humans. J Acoust Soc Am. 2001;110:2456–2469. doi: 10.1121/1.1406497. [DOI] [PubMed] [Google Scholar]
- Gaskill SA, Brown AM. Suppression of human acoustic distortion product: Dual origin of 2f1−f2. J Acous Soc Am. 1996;100:3260–3274. doi: 10.1121/1.417210. [DOI] [PubMed] [Google Scholar]
- Gilman S, Dirks DD. Acoustics of ear canal measurement of eardrum SPL in simulators. J Acoust Soc Am. 1986;80:783–793. doi: 10.1121/1.393953. [DOI] [PubMed] [Google Scholar]
- Gorga MP, Neely ST, Bergman BM, Beauchaine KL, Kaminski JR, Liu Z. Towards understanding the limits of distortion product otoacoustic emission measurements. J Acoust Soc Am. 1994;93:1494–1500. doi: 10.1121/1.410227. [DOI] [PubMed] [Google Scholar]
- Gorga MP, Neely ST, Bergman BM, Beauchaine KL, Kaminski JR, Peters J, Jesteadt W. Otoacoustic emissions from normal-hearing and hearing-impaired subjects: Distortion product responses. J Acoust Soc Am. 1993;93:2050–2060. doi: 10.1121/1.406691. [DOI] [PubMed] [Google Scholar]
- Gorga MP, Neely ST, Johnson TA, Dierking DM, Garner CA. In: Otoacoustic Emissions: Clinical Application. 3. Robinette MS, Glattke TJ, editors. Thieme Medical Publishers, Inc; New York: 2007. pp. 197–225. [Google Scholar]
- Gorga MP, Neely ST, Ohlrich B, Hoover B, Redner J, Peters J. From laboratory to clinic: A large scale study of distortion product otoacoustic emissions in ears with normal hearing and ears with hearing loss. Ear Hear. 1997;18:440–455. doi: 10.1097/00003446-199712000-00003. [DOI] [PubMed] [Google Scholar]
- Harris FP, Probst R, Xu L. Suppression of the 2f1-f2 otoacoustic emission in humans. Hear Res. 1992;64:133–141. doi: 10.1016/0378-5955(92)90175-m. [DOI] [PubMed] [Google Scholar]
- Johnson TA, Neely ST, Garner CA, Gorga MP. Influence of primary-level and primary-frequency ratios on human distortion product otoacoustic emissions. J Acoust Soc Am. 2006;119:418–28. doi: 10.1121/1.2133714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson TA, Neely ST, Kopun JG, Dierking DM, Tan H, Converse C, Kennedy E, Gorga MP. Distortion product otoacoustic emissions: Cochlear-source contributions and clinical test performance. J Acoust Soc Am. 2007;122:3539–3553. doi: 10.1121/1.2799474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keefe DH. Acoustical wave propagation in cylindrical ducts: Transmission line parameter approximations for isothermal and nonisothermal boundary conditions. J Acoust Soc Am. 1984;75:1386–1391. [Google Scholar]
- Keefe DH, Ling R, Bulen JC. Method to measure acoustic impedance and reflection coefficient. J Acoust Soc Am. 1992;91:470–485. doi: 10.1121/1.402733. [DOI] [PubMed] [Google Scholar]
- Kemp DT. Stimulated acoustic emissions from within the human auditory system. J Acoust Soc Am. 1978;64:1386–1391. doi: 10.1121/1.382104. [DOI] [PubMed] [Google Scholar]
- Kim DO, Paparello J, Jung MD, Smurzynski J, Sun X. Distortion product otoacoustic emission test of sensorineural hearing loss: Performance regarding sensitivity, specificity and receiver operating characteristics. Acta Otolaryngol. 1996;116:3–11. doi: 10.3109/00016489609137705. [DOI] [PubMed] [Google Scholar]
- Knight KR, Kraemer DF, Winter C, Neuwelt EA. Early changes in auditory function as a result of platinum chemotherapy: Use of extended high-frequency audiometry and evoked distortion product otoacoustic emissions. J Clin Oncol. 2007;25:1190–1195. doi: 10.1200/JCO.2006.07.9723. [DOI] [PubMed] [Google Scholar]
- Kummer P, Janssen T, Arnold W. Suppression tuning characteristics of the 2f1−f2 distortion product otoacoustic emission and its relationship to auditory sensitivity in normal hearing and cochlear hearing loss. J Acoust Soc Am. 1995;103:3431–3444. doi: 10.1121/1.423054. [DOI] [PubMed] [Google Scholar]
- Kummer P, Janssen T, Arnold W. The level and growth behavior of the 2f1−f2 distortion product otoacoustic emission and its relationship to auditory sensitivity in normal hearing and cochlear hearing loss. J Acoust Soc Am. 1998;103:3431–3444. doi: 10.1121/1.423054. [DOI] [PubMed] [Google Scholar]
- Kummer P, Janssen T, Hulin P, Arnold W. Optimal L1 − L2 primary-tone level separation remains independent of test frequency in humans. Hearing Research. 2000;146:47–56. doi: 10.1016/s0378-5955(00)00097-6. [DOI] [PubMed] [Google Scholar]
- Lonsbury-Martin BL, Harris FP, Stagner BB, Hawkins MD, Martin GK. Distortion product emissions in humans I. Basic properties in normally hearing subjects. Ann Otol Rhinol Laryngol. 1990;99:3–14. [PubMed] [Google Scholar]
- Møeller AR. Improved technique for detailed measurements of the middle ear impedance. J Acoust Soc Am. 1960;32:250–257. [Google Scholar]
- Neely ST, Gorga MP. Comparison between intensity and pressure as measures of sound level in the ear canal. J Acoust Soc Am. 1998;104:2925–2934. doi: 10.1121/1.423876. [DOI] [PubMed] [Google Scholar]
- Neely ST, Johnson TA, Gorga MP. Distortion-product otoacoustic emission measured with continuously varying stimulus level. J Acoust Soc Am. 2005;117:1248–1259. doi: 10.1121/1.1853253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neely ST, Liu Z. Technical Memo No. 17. Boys Town National Research Hospital; Omaha, NE: 1994. EMAV: Otoacoustic emission averager. [Google Scholar]
- Nelson DA, Kimberley BP. Distortion-product emissions and auditory sensitivity in human ears with normal hearing and cochlear hearing loss. J Speech Hear Res. 1992;35:1142–1159. doi: 10.1044/jshr.3505.1142. [DOI] [PubMed] [Google Scholar]
- Rabinowitz WM. Measurement of the acoustic input immittance of the human ear. J Acoust Soc Am. 1981;70:1025–1035. doi: 10.1121/1.386953. [DOI] [PubMed] [Google Scholar]
- Ress BD, Sridhar KS, Balkany TJ, Waxman GM, Stagner BB, Lonsbury-Martin BL. Effects of cis-platinum chemotherapy on otoacoustic emissions: The development of an objective screening protocol. Otolaryngol Head Neck Surg. 1999;121:693–701. doi: 10.1053/hn.1999.v121.a101567. [DOI] [PubMed] [Google Scholar]
- Scheperle RA, Neely ST, Kopun JG, Gorga MP. Influence of in-situ sound level calibration on DPOAE variability. J Acoust Soc Am. 2008;4:288–300. doi: 10.1121/1.2931953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seixas NS, Kujawa SG, Norton S, Sheppard L, Neitzel R, Slee A. Predictors of hearing threshold levels and distortion product otoacoustic emissions among noise exposed young adults. Occup Environ Med. 2004;61:899–907. doi: 10.1136/oem.2003.009209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JH. Ear-canal standing waves and high-frequency sound calibration using otoacoustic emission probes. J Acoust Soc Am. 1994;95:2589–2597. [Google Scholar]
- Siegel JH. Calibrating otoacoustic emission probes. In: Robinette MS, Glattke TJ, editors. Otoacoustic Emissions: Clinical Application. 3. Thieme Medical Publishers, Inc; New York: 2007. pp. 403–427. [Google Scholar]
- Siegel JH, Hirohata ET. Sound calibration and distortion product otoacoustic emissions at high frequencies. Hearing Research. 1994;80:146–152. doi: 10.1016/0378-5955(94)90106-6. [DOI] [PubMed] [Google Scholar]
- Stavroulaki P, Apostolopoulos N, Segas J, Tsakanikos M, Adamopoulos G. Evoked otoacoustic emissions – an approach for monitoring cisplatin induced ototoxicity in children. Int J Pediatr Otorhinolaryngol. 2001;59:47–57. doi: 10.1016/s0165-5876(01)00455-4. [DOI] [PubMed] [Google Scholar]
- Stinson MR. The spatial distribution of sound pressure within scaled replicas of the human ear canal. J Acoust Soc Am. 1985;78:1596–1602. doi: 10.1121/1.392797. [DOI] [PubMed] [Google Scholar]
- Stover L, Gorga MP, Neely ST. Toward optimizing the clinical utility of distortion product otoacoustic emission measurements. J Acoust Soc Am. 1996;100:956–967. doi: 10.1121/1.416207. [DOI] [PubMed] [Google Scholar]
- Swets JA. Measuring the accuracy of diagnostic systems. Science. 1988;240:1285–1293. doi: 10.1126/science.3287615. [DOI] [PubMed] [Google Scholar]
- Swets JA, Pickett RM. Evaluation of Diagnostic Systems: Methods from Signal Detection. New York: Academic Press; 1982. [Google Scholar]
- Whitehead ML, McCoy MJ, Lonsbury-Martin BL, Martin GK. Dependence of distortion-product otoacoustic emissions on primary levels in normal and impaired ears. I Effects of decreasing L2 below L1. J Acoust Soc Am. 1995a;97:2346–2358. doi: 10.1121/1.411959. [DOI] [PubMed] [Google Scholar]
- Whitehead ML, Stanger BB, Lonsbury-Martin BL, Martin GK. Effects of ear-canal standing waves on measurements of distortion-product otoacoustic emissions. J Acoust Soc Am. 1995b;98:3200–3214. doi: 10.1121/1.413810. [DOI] [PubMed] [Google Scholar]