Abstract
We present a simple and highly accurate computational method for operon prediction, based on intergenic distances and functional relationships between the protein products of contiguous genes, as defined by STRING database (Jensen,L.J., Kuhn,M., Stark,M., Chaffron,S., Creevey,C., Muller,J., Doerks,T., Julien,P., Roth,A., Simonovic,M. et al. (2009) STRING 8–a global view on proteins and their functional interactions in 630 organisms. Nucleic Acids Res., 37, D412–D416). These two parameters were used to train a neural network on a subset of experimentally characterized Escherichia coli and Bacillus subtilis operons. Our predictive model was successfully tested on the set of experimentally defined operons in E. coli and B. subtilis, with accuracies of 94.6 and 93.3%, respectively. As far as we know, these are the highest accuracies ever obtained for predicting bacterial operons. Furthermore, in order to evaluate the predictable accuracy of our model when using an organism's data set for the training procedure, and a different organism's data set for testing, we repeated the E. coli operon prediction analysis using a neural network trained with B. subtilis data, and a B. subtilis analysis using a neural network trained with E. coli data. Even for these cases, the accuracies reached with our method were outstandingly high, 91.5 and 93%, respectively. These results show the potential use of our method for accurately predicting the operons of any other organism. Our operon predictions for fully-sequenced genomes are available at http://operons.ibt.unam.mx/OperonPredictor/.
INTRODUCTION
Operons can be defined as a gene or set of genes arranged contiguously on the same transcriptional strand of a genome sequence, which are co-transcribed in the same transcription unit (TU). Due to the biological relevance of operons for coordinating the expression of metabolically or functionally related genes in bacterial organisms, different computational protocols have been devised for identifying them, in the fast growing set of fully-sequenced genomes. These protocols may include neural networks (NN) (1,2), hidden Markov modes (3–5), support vector machines (6), Bayesian probabilities (7–9), genetic algorithms (10), decision tree-based classification (5) and graph-theoretic techniques (8,11), among others. In principle, the genes that constitute any operon can be defined by the regulatory elements that delimit their transcription start (promoter) and their transcription end (terminator). At the present time, accuracy for computationally identifying promoters and transcription terminators is restricted only to canonical or almost canonical cases, therefore other genome characteristics have been considered for the in silico identification of operons and some of the most important ones are as follows: (i) Transcription direction of the genes: this is a straight forward way of identifying the boundaries of certain operons, as genes in opposite strands always form part of different operons. (ii) Intergenic distances between contiguous genes: this is the second most widely used parameter for operon prediction (1,2,5–10,12–15), as the intergenic distances between contiguous genes of the same operon are generally shorter than the distance between contiguous genes of different operons. (iii) Expression gene pattern: this can be evaluated from microarray analyses and has been used to identify genes from the same operon, as these tend to have highly correlated values (7,13). Unfortunately, microarray gene expression data is only available for few organisms. (iv) Functional relationships between proteins encoded in an operon, as these genes commonly share similar or closely related functions (1,2,8–10,13,15). (v) Conserved metabolic pathway of the enzymes encoded by the genes of the operon (2,6,11,13,14). (vi) Conserved gene neighborhood; which implies a tendency of the genes in an operon to be preserved across phylogenetically related organisms (2,5,6,8–10,13–15). (vii) Phylogenetic profiles; indicating a general trend for a set of genes to be simultaneously present or absent in closely related organisms (2,5,6,8–10,13–15).
Despite extensive work employing all the different computational approaches and genomic characteristics of the operons, the best predictive accuracies obtained for the model organisms Escherichia coli and Bacillus subtilis trained with their corresponding known operon data set were 93 and 90%, respectively (5). As expected, these accuracy values decreased significantly when training and testing data sets did not correspond to the same organism. For example, the most accurate prediction for B. subtilis using a decision tree-based algorithm trained with an E. coli data set was only 83% (5). In our opinion, all predictive methods should rely on general data obtained from common features observed in the set of fully-sequenced genomes, in order to guarantee extensive predictive effectiveness. Nevertheless, a clear tendency observed in the above-mentioned operon predictive methods is that most of them only exploit either a single or a limited set of the information which is available from metabolic pathways, expression gene patterns, functional relationships or other sources, but as far as we know, none has considered simultaneously all of the above mentioned sources of data wisely integrated. In the light of this concern, we investigated the possibility of using the precompiled scores from the STRING database that reflect the functional associations of different proteins (16). STRING is a carefully curated database that integrates four main different types of data: (i) Genomic context based on gene fusion, gene neighborhood and phylogenetic profiles. (ii) Primary evidence extracted from experimentally derived protein–protein interactions and gene co-expression experiments, by means of literature curation. (iii) Manually curated pathway databases. (iv) Automatic literature mining in order to discover co-mentioned genes. All predicted or imported interactions are benchmarked on metabolic maps in the KEGG database (Kyoto Encyclopedia of Genes and Genomes) (8). Finally, STRING carefully assesses and integrates all these data in order to obtain a single confidence score for all protein interactions. In this work, we integrated the intergenic distance values and the STRING scores, using a neural network, to accurately predict the operon structures in a set of fully-sequenced genomes.
MATERIALS AND METHODS
Generation of operonic and non-operonic gene pair data sets
As in many other operon prediction studies, we used E. coli and B. subtilis as our reference organisms for evaluating the accuracy of our predictions, as these organisms represent the best characterized bacteria in terms of experimentation. The collection of the E. coli operons used in our study was taken from the RegulonDB database version 6.4 (17). This database contains information about 2663 E. coli operons, which existence was corroborated by different types of evidence, some classified as strong, for example, RNA polymerase footprinting, primer extension or S1 mapping; and other as weak, such as that inferred from mutant phenotype or by computational promoter identification, among other examples. In our study, we considered only the 344 E. coli operons that were included in the group of operons corroborated by strong evidence. From this set of operons, we identified 493 operonic gene pairs (contiguous genes of the same operon). The collection of B. subtilis operons was taken from DBTBS database (18). In this case, the number of predicted operons was 1153, but only 509 of these were corroborated by strong evidence, such as northern blotting. This former group of operons contains 698 operonic gene pairs. On the other hand, the set of non-operonic gene pairs was identified with reference to their 5′ and 3′ operon gene borders and their corresponding upstream and downstream adjacent genes, when transcribed in the same direction. A similar approach for defining non-operonic data sets has previously been taken by other research groups (5,8,10,19,20). In this way, we obtained 386 and 433 non-operonic gene pairs from E. coli and B. subtilis, respectively. The lists of operons from E. coli and B. subtilis that were corroborated by strong experimental evidence and considered in our analysis are available in the Supplementary Tables S1 and S2).
Intergenic distances and STRING scores for genes within operon, directons and TU borders
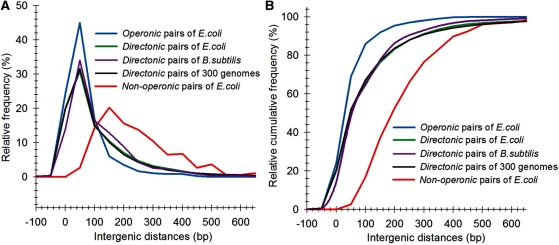
The intergenic distance between contiguous genes is one of the most commonly used parameter to predict the operon structures of genomes (1,2,5–10,12–15). Furthermore, it has been found that the intergenic distance is the best single predictor of operons in E. coli (7). In accordance with (12), we found that in E. coli, the intergenic distances of operonic gene pairs tend to be shorter than intergenic distances of directonic gene pairs (adjacent genes on the same strand with no intervening gene transcribed in the opposite one) and even more significantly shorter than the intergenic distances between non-operonic gene pairs (Figure 1A and B). For example, in the case of operonic gene pairs of E. coli, we found that 69% of them have intergenic distances of <50 bp. A similar value of 65% was obtained when the set of directonic gene pairs was considered. Contrarily, only 4% of non-operonic gene pairs have an intergenic distance of <50 bp.
Figure 1.
Frequency distributions of intergenic distances of operonic, non-operonic and directonic gene pairs of E. coli, B. subtilis and directonic gene pairs of 300 non-redundant genomes, at 50 bp intervals. (A) Relative frequency percentage. (B) Relative cumulative frequency. The intergenic distance profiles of directonic gene pairs of E. coli, B. subtilis and the mean values obtained from our 300 non-redundant genomes (S3) are almost the same (are overlapped). Note: negative intergenic distances are from adjacent genes where DNA sequence overlapped with each other.
In order to analyze if aforementioned intergenic distance tendency was not restricted to E. coli, we repeated our analysis in a set of public available fully-sequenced genomes. To avoid over-representation of certain organisms [e.g. at the present time, there are 12 different fully-sequenced E. coli strains at the NCBI database (http://www.ncbi.nlm.nih.gov/), the analysis was done considering only a set of 300 non-redundant genomes. These non-redundant genomes were selected based on the similarity of their genetic distances, evaluated from a multiple sequence alignment of their corresponding 16S rRNA sequences and the PROTDIST program of the J. Felsenstein’s PHYLIP phylogeny inference package program. The name list of these 300 organisms is available in the Supplementary Table S3. As it can be seen in Figure 1A and B, the distribution of the mean values of intergenic distances of the genes within directions in our set of 300 non-redundant genomes is similar to the one observed in E. coli and B. subtilis. This result upholds the idea of using intergenic distance as a valuable parameter for operon prediction, although we do not discard the idea that for some specific organisms, intergenic distances may differ importantly, as it has been previously documented (22). We believe that this variability can be taken into account in new prediction algorithms as new experimental data on operon architectures are available.
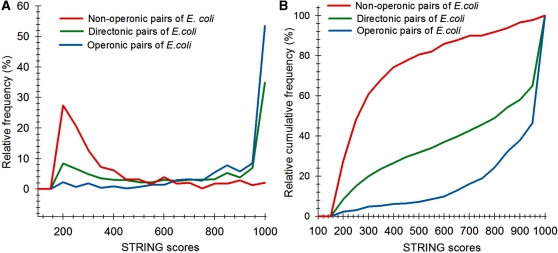
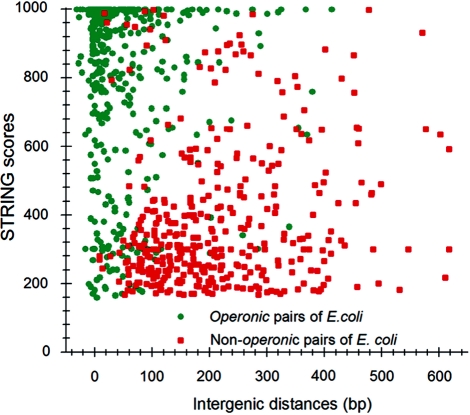
Following the method used to calculate inergenic distances, we obtained distinctive frequency distributions for the STRING scores of the E. coli operonic, directonic and non-operonic genes pairs (Figure 2A and B). STRING considers two different kind of interacting entities to evaluate their confidence scores: (i) proteins from a particular organism or (ii) groups of orthologous proteins spanning multiple organisms, as defined by the COG database (Clusters of Orthologous Groups of proteins) (23). In order to make our operon prediction method as general as possible, we opted for the latter option to retrieve the COG functional association scores from the STRING web page (http://string.embl.de). From the profiles shown in Figure 2A and B, it is clear that a great fraction of the genes within operons (62%) or directons (42%) have significantly high STRING scores (above 900), whereas, most of the genes at the border of the operons (68%) have notably low STRING scores (below 400). In order to examine the relationship between intergenic distance and STRING scores, we generated a scatter plot for operonic and non-operonic gene pairs (Figure 3). From these results, it is clear that operonic gene pairs are generally characterized by short intergenic distance and high STRING scores, whereas contrastingly, non-operonic gene pairs manifest greater distances and lower STRING score values.
Figure 2.
Comparison of the frequency distribution of STRING scores of E. coli operonic, non-operonic and directonic gene pairs. (A) Relative frequency percentage. (B) Relative cumulative frequency.
Figure 3.
Relationship between intergenic distances (horizontal axis) and STRING scores (vertical axis) of E. coli operonic and non-operonic gene pairs.
Clustering of orthologous genes that lack COG assignation
As previously mentioned, our operon prediction method is based on the functional relationship of proteins as defined by the STRING database. This relationship has been established for the different groups of orthologous genes of the COG database (23). Nevertheless, it is important to consider that for a significant number of genes, there are not corresponding COG groups; consequently, there are not STRING score assignations for them and thus, is not possible to make any operon prediction with our methodology. For example, only 3612 out of the 4493 annotated genes in the model organism E. coli have a COG assignation, whereas only 3290 out of the 4225 genes of B. subtilis have been annotated in the COG database. This lack of COG assignation may be even more significant among a considerable number of less well characterized organisms. As a first instance to consider all these genes that lack a COG assignation in our operon predictions, we performed a clustering procedure to identify groups of orthologous genes. To this end, we performed BLAST comparisons (18) to identify bi-directional best hits among our set of fully-sequenced genomes. We then used these bi-directional best hit relationships to identity different groups of orthologous proteins using an agglomerative clustering algorithm (24). This procedure was also performed to identify orthologous clusters of non-coding genes, such as rRNAs, tRNAs and small RNAs. The new orthologous groups generated by the above clustering procedure were designated as Remained Orthologous Groups (ROGs), where each ROG has at least three orthologous genes to ensure that they are indeed conserved during evolution and not just shared by chance. In this manner, we expanded the original set of 4873 COGs (23) by the addition of our 8901 new ROGs, 8539 corresponding to protein-coding genes and 362 to non-coding genes. To avoid over-representation of particular organisms in the clustering procedure the analysis described previously was performed considering only our set of 300 non-redundant genomes.
Extrapolating the STRING scores of the COG groups to our new set of ROG gene clusters
As a second instance to consider those genes without COG assignation in our operon prediction method, we deduced functional relationship sores for our ROG groups. Based on the STRING scores and the neighborhood conservation of adjacent genes, we obtained by extrapolation STRING-like scores for our new set of ROG groups in such a way that the set of STRING scores, originally defined for COGs versus COGs groups, was expanded to also include the relationships of COGs versus ROGs, and ROGs versus ROGs groups. For this purpose, we developed a metric of neighborhood conservation between any two groups of orthologous genes. We considered two genes to be neighbors if they were transcribed in the same direction, if there were no more than three genes between them and if the mean of their intergenic distances did not exceed 375 bp. This cutoff distance was established taking twice the SD (165 bp) from the mean (45 bp) of intergenic distances of adjacent genes for the set of operons found in E. coli and B. subtilis. In this way, we were not restricted to only consider adjacent gene neighbors separated by nothing higher than a specific cutoff value, as was the case in (2,10,13,14,19–21); or to windows of a certain size, without taking into account the number of genes inside them, as was the case in (22,25); or to windows that included a certain number of genes, regardless of the intergenic distances between them, as was the case in (6,8,9). Our flexible definition of gene neighbors is consistent with the characteristics observed in real operons (26) and allowed us to analyze the relationships of most of the genes from the same TUs in our set of 300 non-redundant genomes, with a minimal risk of including false positive elements.
In order to determine the STRING-like assignments between all the COGs and ROGs groups, we implemented the following procedure:
Identification of all gene neighbors of our set of 300 genomes
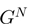 with COG assignation. Let
with COG assignation. Let 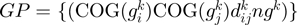 be the set of gene neighbors, where
be the set of gene neighbors, where 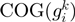 and
and 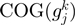 are the corresponding COGs of the genes at the position
are the corresponding COGs of the genes at the position 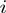 and
and 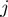 of the
of the 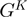 genome, respectively. For every
genome, respectively. For every 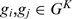 and
and 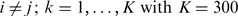 ;
; 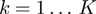 with
with 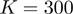 ;
; 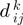 as the observed distance between
as the observed distance between 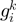 and
and 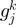 (in terms of the number of genes in between) along
(in terms of the number of genes in between) along 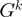 ;
; 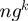 is the number of genes in the genome
is the number of genes in the genome 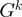 .
.Definition of a function
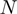 of the form
of the form 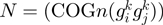 where
where 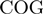 is a COG pair and
is a COG pair and 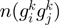 is a neighborhood conservation score for each gene pair in our set of genomes, which is defined as:
is a neighborhood conservation score for each gene pair in our set of genomes, which is defined as:
| (1) |
where 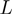 is the log-likelihood for each COG pair that belongs to the set
is the log-likelihood for each COG pair that belongs to the set 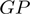 to be related. The log-likelihood score is computed as the probability of
to be related. The log-likelihood score is computed as the probability of 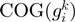 and
and 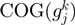 to be neighbors taking into account certain gene and COG family characteristics and this is computed as:
to be neighbors taking into account certain gene and COG family characteristics and this is computed as:
| (2) |
where 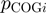 and
and 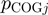 are the relative frequencies of
are the relative frequencies of 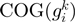 and
and 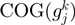 present in
present in 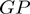 , considering the number of elements in the COG groups to which the genes
, considering the number of elements in the COG groups to which the genes  and
and 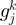 belong;
belong; 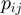 is the frequency of
is the frequency of 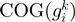 and
and 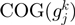 in
in 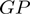 divided by the number of different genomes having the COGs neighbors
divided by the number of different genomes having the COGs neighbors 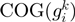 and
and 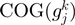 and
and 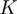 (300, number of non-redundant sequenced genomes).
(300, number of non-redundant sequenced genomes).
By using these variables, we assessed the probability of two COGs being functionally related in terms of their: (a) neighborhood conservation involving mainly their neighbor frequency; the greater the frequency, the greater the conservation and thus the more significant their relationship. (b) Number of genes between them; the fewer the genes between them the more significant is their contribution. (c) Number of elements in the COG families; bigger families have more probability of appearing by chance in any genome and consequently, their contribution is less significant, and (d) Genome size in terms of number of genes; as in COG families, the bigger the genome, the less significant is their contribution. Regarding this aspect, we noted that 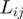 is very small, when
is very small, when 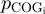 ,
, 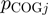 ,
, 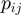 and/or
and/or 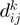 are small. In agreement with (5), we observed that small
are small. In agreement with (5), we observed that small 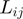 values are generally associated with gene pairs that are functionally related (5). In this way, a larger
values are generally associated with gene pairs that are functionally related (5). In this way, a larger 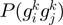 implies stronger significance in terms of the functional relationship between
implies stronger significance in terms of the functional relationship between 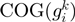 and
and 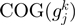 . The neighborhood conservation function
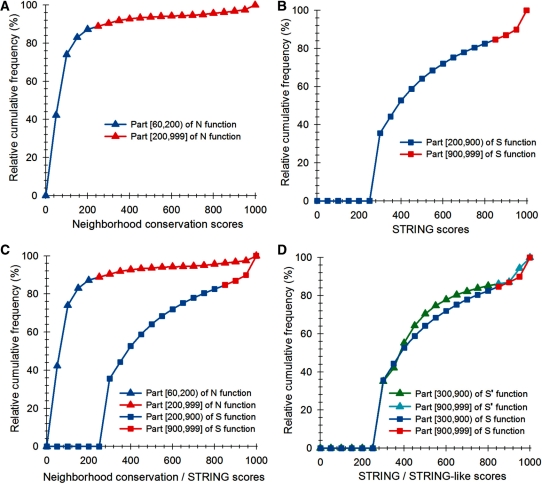
. The neighborhood conservation function  is shown in Figure 4A. As evident in this figure,
is shown in Figure 4A. As evident in this figure,  can be defined by two intervals; the first interval ranges from 60 to 199.99 and the second ranges from 200 to 999.
can be defined by two intervals; the first interval ranges from 60 to 199.99 and the second ranges from 200 to 999.
Definition of
 function of the form
function of the form 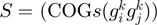 , where
, where 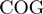 is a COG pair and
is a COG pair and 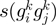 is the STRING functional association score (16). Considering that the COG database has 4873 COGs, in theory 11 870 628 different COG versus COG associations should exist, nevertheless referring to the STRING database, only 2 085 550 of these associations have significant values. The frequency distribution of these values is presented in Figure 4B. As in the case of the
is the STRING functional association score (16). Considering that the COG database has 4873 COGs, in theory 11 870 628 different COG versus COG associations should exist, nevertheless referring to the STRING database, only 2 085 550 of these associations have significant values. The frequency distribution of these values is presented in Figure 4B. As in the case of the  function, we noted that the
function, we noted that the 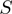 function can be defined by two different intervals, the first one ranges from 200 to 899.99, and the second interval from 900 to 999. Moreover, we also observed that the first interval of this function includes most of the total data, 86.7%, which resembles the great data accumulation of 88.5% in the first interval of the
function can be defined by two different intervals, the first one ranges from 200 to 899.99, and the second interval from 900 to 999. Moreover, we also observed that the first interval of this function includes most of the total data, 86.7%, which resembles the great data accumulation of 88.5% in the first interval of the 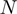 function.
function.Definition of a
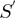 function by matching
function by matching 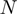 to
to 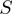 using a piecewise continuous approximation, applying two different equations corresponding to each one of the
using a piecewise continuous approximation, applying two different equations corresponding to each one of the 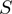 intervals (Figure 4C and D). The correlation of
intervals (Figure 4C and D). The correlation of 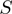 and
and 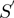 was found to be 82%.
was found to be 82%.The neighborhood conservation scores of each pair of COGs versus ROGs, and ROGs versus ROGs groups were evaluated as previously carried out in the first and second steps of the neighborhood conservation analysis for the COGs versus COGs groups.
A STRING-like value for each pair of COGs versus ROGs, and ROGs versus ROGs groups was evaluated using the equations that define the
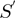 function described in the previous step. Following this method, 95.5% of the genes in our set of 300 non-redundant genomes could be functionally related to any other gene by either a STRING or a STRING-like score.
function described in the previous step. Following this method, 95.5% of the genes in our set of 300 non-redundant genomes could be functionally related to any other gene by either a STRING or a STRING-like score.Finally, the smallest STRING or STRING-like score value considered in our procedure was defined as 300. This score corresponds to the functional relationship value between genes by which the operon predictions of our NN are exclusively based on the intergenic distance of the gene pairs, as it is explained in the next section of our article.
Figure 4.
(A) Neighborhood conservation function of the form 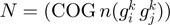 where
where 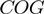 is an orthologous group pair from COG database and
is an orthologous group pair from COG database and 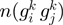 is its neighborhood conservation score in our set of 300 non-redundant genomes. (B) STRING
is its neighborhood conservation score in our set of 300 non-redundant genomes. (B) STRING 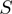 function of the form
function of the form 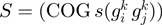 where
where 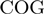 is an orthologous group pair and
is an orthologous group pair and 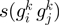 is its STRING functional association score. (C)
is its STRING functional association score. (C) 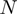 function intervals that will be approximated to
function intervals that will be approximated to 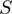 function intervals (blue with blue interval and red with red one) using a lineal piecewise continuous approximation. (D)
function intervals (blue with blue interval and red with red one) using a lineal piecewise continuous approximation. (D) 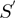 function resulted by matching
function resulted by matching 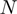 to
to 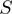 functions.
functions. 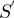 represents our STRING-like score.
represents our STRING-like score.
Constructing a neural network for operon prediction
As the relationship of the intergenic distances and STRING scores do not define the nature of the operonic and non-operonic gene pairs in a linear dependent manner (Figure 3), we implemented a multilayer perceptron artificial NN. The idea behind of a NN is to provide a desired output target for given input data once it is trained. The design of our NN involved three main steps: (i) Input data pre-processing carried out by normalizing the intergenic distances and STRING scores in the same range of the NN activation function [−1,1] in order to avoid an exponential calculation overflow and to ensure that the range for each feature does not influence the performance of the NN. (ii) Selection of appropriate network architecture by testing different configurations of NN multilayer topologies, varying the number of layers and neurons for each layer; in our case, two-layers/two-one-neurons network architecture was selected. The neuron activation function applied was the hyperbolic tangent, producing both positive and negative values, tending to yield faster training. (iii) Selection of the training algorithm, in our case we used the quick propagation algorithm which optimizes the weights of the network during the training (supervised learning) phase in order to minimize the error between the network output and the desired output in terms of the training data (27). Other network functions and training algorithms were tested but none of them gave results which were as good as the ones obtained with our selected network, or the differences were insignificant (data not shown). The desired outputs have values of either 0 or 1; 1 for gene pairs that belong to the same operon and 0 for gene pairs that do not belong to the same operon. Besides this, our NN estimates an associated confidence value for each prediction, which is normalized between 0 and 1. A value greater than 0.5 indicates that the corresponding gene pair belongs to the same operon, predicting that the greatest accuracy for confidence values will be near to 0 or near to 1, and the lowest accuracy will be near to 0.5. (iv) In this study, the conventional one-training-and-one-testing validation was performed in order to obtain the accuracy of the NN. In this senses, the input data was randomly divided into 80% used as the training set and 20% as the testing set. Besides this, we made a k-fold cross-validation to estimate how good generalization can be made by the NN. For this, the data was randomly divided to k mutually exclusive and approximately equal size subsets. The classification algorithm was trained and tested k times, in our case 9. In each case, one of the folds was taken as test data and the remaining folds were added to form training data. Thus, k different test results exist for each training-test configuration. The average of these test errors was only 5.2% with a 2.6% standard deviation.
Performance measurement
As previously undertaken in the case of other operon prediction studies (1,2,5–7,14,25), we calculated the sensitivity, specificity and accuracy values of our predictions, as follows:
| (3) |
| (4) |
| (5) |
Where TP (true positives) represent the number of operonic gene pairs correctly predicted among all known operonic gene pairs; FN (false negatives) represent the number of operonic gene pairs incorrectly predicted as non-operonic gene pairs; TN (true negatives) represent the number of correctly predicted non-operonic gene pairs in known non-operonic gene pairs and FP (false positives) represent the number of non-operonic gene pairs incorrectly predicted as operonic gene pairs.
RESULTS
Accuracy of operonic and non-operonic gene pair predictions
We evaluated the efficacy of our method for three different cases. (i) First, we estimated the accuracy of our NN to predict E. coli operonic and non-operonic gene pairs that have COG assignation, using intergenic distance values and STRING scores. (ii) Secondly, to evaluate the efficiency of our deduced STRING-like scores to predict operonic and non-operonic gene pairs, we repeated the analysis on the same data as that used in the first case, replacing the original input STRING scores of our NN with those from the STRING-like scores. (iii) Finally, to test the integrated accuracy of our NN using intergenic distance values and STRING or STRING-like scores, we predicted the complete set of operonic and non-operonic gene pairs in E. coli and B. subtilis.
Escherichia coli operonic and non-operonic gene pair predictions, using intergenic distances and STRING scores
Due to its simplicity and its predictive relevance, the intergenic distance between adjacent genes has become one of the parameters most frequently used in operon prediction methodologies and likewise it is one of the parameters employed in this work. The best predictive accuracy achieved in an E. coli operon prediction analysis, considering intergenic distances as the only data source has been reported to be 74% (12). We obtained a similar accuracy (79%) using an NN that we specifically implemented to use intergenic distances as the only input data. As predicted, the performance of this NN increased significantly, when besides intergenic distances, the NN was also trained with the functional relationships of gene products, as defined in the STRING database (16). Since STRING scores have only been established for groups of orthologous proteins COGs (23), our predictions for the original E. coli set of 493 operonic and 386 non-operonic gene pairs were restricted to 435 operonic and 309 non-operonic gene pairs that had a COG assignation. The predictive performance of our NN in this data set was 94.8%, with a sensitivity of 95.8% and a specificity of 93.4%.
Escherichia coli operonic and non-operonic gene pair predictions, using intergenic distances and STRING-like scores
As previously commented, not all the genes in a genome belong to a specific COG group and thus, the functional relationships with other genes have not been defined in the STRING database. For example, almost 20% of the E. coli genes lack a COG assignation because; either they are not translated into proteins, or their polypeptide product does not have a corresponding orthologous family, and thus our NN cannot make any prediction for them.
In order to overcome this problem, we have derived a set of STRING-like scores based on the neighborhood conservation of adjacent genes, as previously described in the above sections. The results obtained from our NN applying the STRING-like scores were compared with the previous results of the NN using the original STRING scores. Interestingly, we found that the performance of our NN using the derived STRING-like scores was only slightly inferior to the NN using the STRING scores, as it achieved an accuracy of 92.8%, a sensitivity of 91.4% and a specificity of 93.9%. This result validates our extrapolation procedure for obtaining the STRING-like scores and gives us an indirect idea of the NN performance for predicting operonic and non-operonic gene pairs that are part of our ROG groups.
Escherichia coli operonic and non-operonic gene pair predictions, using intergenic distances and the combined values of STRING and STING-like scores
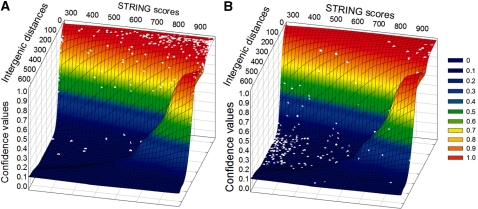
The accuracy of our NN in the complete set of an organism’s gene pairs is obtained considering both, the STRING and the STRING-like scores, in addition to the data for intergenic distance. First, we evaluated the performance of our NN for predicting E. coli operonic and non-operonic gene pairs. Figure 5A shows the distribution of the gene pairs that according to RegulonDB (17) are part of the same operon, whereas Figure 5B corresponds to gene pairs that are part of different operons. A great number of predictions are correctly located in characteristic operonic and non-operonic areas, whereas only a very small number of predictions were found not to be consistent with the reported data compiled in the RegulonDB database (17). From these figures, it can be seen that two kinds of inconsistency exist in terms of predictions. The first kind lies close to the borderline of our NN for distinguishing operonic from non-operonic gene pairs. These inconsistencies emerge as a natural consequence of being near the cutoff values when applying any binary classification method. It is worth noting that in our method, the set of gene-pairs close to the ‘twilight zone’ is very small. The second kind of inconsistency corresponds to exceptional cases that may arise from incorrect genome annotations, incorrect interpretation of the experimental data, or a possible mistake in the RegulonDB curation. Examples of inconsistencies due to an incorrect genome annotation are found with hypothetical small genes which have no experimental data to corroborate their existence. When these kind of hypothetical genes are close to real genes, the NN predicts that the gene pairs are part of the same operon, even though this may not be the case. An example of this kind of error corresponds to the inconsistency found for ribF and the hypothetical yaaY gene, which are separated only by 7 bp and thus our NN predicts them as operonic gene pairs. Neverthess, in RegulonDB these genes are considered to be part of different operons since a transcription start site for ribF has been defined within yaaY, supporting the possibility that this is not a real gene (28,29). On the other hand, a clear example of an inconsistency due to imprecise data curation is found in the htrE-yadM gene-pair involved in the pilus assembly process. In E. coli, these genes are separated by only 16 bp and are commonly contiguous to each other in different Proteobacteria genomes. Nevertheless, based on only one article with a partial characterization of the ecpD-htrE-yadM-yadL-yadK-yadC (30), these genes were annotated in RegulonDB as part of different operons. A second example of this kind of likely and inexact curated data is found in the accD-folC gene-pair coding for the acetyl-CoA carboxylase β subunit and the folylpolyglutamate synthase proteins, respectively. In certain Proteobacteria, the intergenic region of these genes is very small or even non-existent, thus they are very likely to be part of the same operon. Besides this, the functional relationship between their corresponding products is remarkably high, nevertheless RegulonDB considered these genes to be part of different operons based on only one article where the authors suggested the monosistronic nature of these genes (31).
Figure 5.
Three-dimensional (3D) operon confidence predictions in terms of intergenic distances and STRING or STRING-like scores. Different colors represent the confidence of a gene pair to be part of the same operon or not, with dark red for operon and blue for non-operon. (A) Distribution of gene pairs that in conformity with RegulonDB (17), are part of the same operon. (B) Distribution of gene pairs that in conformity with RegulonDB (17), are part of different operons.
Considering the results mentioned earlier, the accuracy obtained using our NN based method for the complete E. coli set of operonic and non-operonic gene pairs was 94.6%, with a sensitivity of 95.2% and a specificity of 93.9%. As far as we know, this is the highest accuracy which has been obtained using computational methods to predict bacterial operons.
Unbiased performance of our operon predictive protocol
In order to test the predictive performance of our NN in other organisms apart from E. coli, we analyzed the B. subtilis genome. It is important to note that B. subtilis is an organism which is phylogenetically distant from E. coli and that the training procedure for our NN was done exclusively with data coming from the E. coli, thus there was no bias to B. subtilis introduced here, or during any other step in our methodology. In this case, we obtained slightly smaller accuracy; 93.6%, with a sensitivity of 92.9% and a specificity of 94.9%. It is worth noting that a common problem with most of the operon prediction algorithms is that they do not tend to generalize well from one genome to another. In fact, examples exist of algorithms that have attained important accuracy values when the training data set and the operon predictions corresponded to the same organism, but which presented a significant accuracy reduction when tested on other organisms. For example, one of the best algorithms developed in our days obtained an accuracy of 93.7% for predicting E. coli operons trained with E. coli data, but observed a significant accuracy reduction of 11% when the same algorithm was used to predict B. subtilis operons (5). More significant accuracy reductions, from 11 to 30%, have been observed with most of the published algorithms when the training data, and the operon predictions, corresponded to different organisms [reviewed in (32)]. This was not the case for our E. coli trained NN when predicting B. subtilis operons, where the accuracy reduction was only 1.3%. In order to further validate the unbiased performance of our operon predictive protocol, we trained our NN using a B. subtilis data set and then, we successfully predicted the operons of B. subtilis and E. coli with high prediction accuracies of 94.5 and 91.5%, respectively.
Individual contribution of the STRING variables on the operon predictions
As it was previously mentioned, the STRING confident scores are evaluated from the weighted values coming from different kind of sources. In order to evaluate the relative contribution of these sources in the overall accuracy prediction of our method, we repeated our operon prediction analysis in E. coli; in this case, using a NN with two-layers/seven-one-neurons network architecture with intergenic distances and the individual STRING sources, as input data. The data considered for this comparative analysis only included the set of operonic genes for which there is a STRING score associated to a COG group. Interestingly, the accuracy obtained by this new NN was only slightly better (95.0 versus 95.6%), than the one obtained with our original two-layers/two-one-neurons NN. The relative contribution of the variables in this new two-layers/seven-one-neurons NN is as follows: intergenic distance: 22.8%, gene neighborhood: 29.5%, gene fusion: 0.3%, gene co-occurrence: 1.1%, gene co-expression: 6.4%, experimental derived protein–protein interactions: 4.3%, information coming from other databases: 9.3% and automatic literature mining: 26.3%.
NN training and overtraining
A neural network is trained in order to establish a pattern for a given set of input data. Nevertheless, when a NN is over-trained, it will produce random outputs for unseen input data. In order to confirm that our final NN was not over-trained, we randomly split the E. coli known data set 10 times and used these subsets independently to train, validate, test and calculate their corresponding prediction accuracies. The average difference between the prediction error rates was <0.4%, and the standard deviation for the differences was only 0.03%. These low values clearly indicate that our NN is not over-trained.
Web interface
We devolved Operons database (http://operons.ibt.unam.mx/OperonPredictor/) in order to make our set of high-quality operon predictions available to the scientific community. Operons database includes predictions for 300 sequenced prokaryotic genomes, organized into a relational database. We provide two different types of information for each genome: (i) all its operons and (ii) all its directonic gene pairs. For each operon, our database provides its gene names, gene GIs and gene locus tags. Correspondingly, for each directonic gene pair, Operons database reports whether these are predicted to be in the same operon and the estimated confidence for the prediction. Values near to 1 (operonic gene pairs) or 0 (non-operonic gene pairs), are high-confidence predictions, whereas values near to 0.5 are low-confidence. Operons database is implemented using MySQL as the database management system, Tomcat as its web server, and Servlets Java, CSS and Javascript to implement the dynamic web pages.
DISCUSSION
We have developed a simple and highly accurate method which successfully predicted the operon structure of nearly all the experimentally determined operons in the model organisms E. coli and B. subtilis. One of the fundamental advantages of our method over other previously reported algorithms is the use of the STRING scores that wisely integrates the information coming from different kind of sources, such as gene neighborhood, gene fusion, gene co-occurrence, gene co-expression, protein–protein interactions, compiled information of other databases and text mining, to determine the functional relationship between proteins. In order to make our predictive method as general as possible, we used the STRING scores associated to the set of orthologous proteins as defined in the COG database. For genes without a COG assignation, we developed a STRING-like metric by an extrapolation procedure based on the gene neighborhood conservation. Interestingly, we found that the accuracy of a NN using this extrapolated STRING-like score as input is greater than a similar NN using the direct values coming from the gene neighborhood conservation. In this manner, using the intergenic distance, STRING and SRTING-like scores as input to our NN, we managed to predict the opreonic/non-operonic nature of every single gene of any genome.
As far as we know, the accuracies reach for our model organisms E. coli and B. subtilis (94.6 and 93.3%, respectively) are one of the highest ever obtain by a predictive method. Furthermore, we have found that some of the exceptional inconsistencies between our operon predictions and the compiled data could arise as a consequence of an incorrect genome annotation of inexistent genes, mistakes in the database curation, or even by an incorrect interpretation of the experimental data, and not necessarily by an erroneous prediction of our method. Taking this fact into consideration, it is likely to think that the accuracy of our method could be even higher than the reported in the ‘Results’ section of our article and in fact, could be placed it close to the maximum of 100%.
Our method is based on the intergenic distances between contiguous genes and the functional relationship scores of the STRING database between the different groups of orthologous proteins, as defined in the COG database. Nevertheless, the operon predictions done by our method are not restricted to those genes with a COG assignation. An important number of genes exist which have not been annotated in the COG database, and for these we successfully defined new groups of orthologous genes and obtained a set of equivalent STRING-like scores. (16). As the STRING functional relationship scores are determined in an unbiased way and efficiently integrates a large amount of information from different sources and types of evidences, the predictions of our NN are considerably less influenced by the bias imposed by a training procedure which uses one specific organism, and thus this constitutes a suitable protocol for operon predictions both, for existing or for future sets of fully-sequenced genomes.
FUNDING
CONACyT (grants 60127-Q and SALUD-2007-C01-68992) to E.M.; DGAPA (IN212708) to E.M. Funding for open access charge: National Council on Science and Technology, México.
Conflict of interest statement. None declared.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
ACKNOWLEDGEMENTS
We thank Shirley Ainsworth for bibliographical assistance, Ricado Ciria, Juan Manuel Hurtado, Arturo Ocadiz, Alma Martinez and Abel Linares for computer support and Maria Luisa Tabche for critical review of the manuscript.
REFERENCES
- 1.Chen X, Su Z, Xu Y, Jiang T. Computational prediction of operons in Synechococcus sp. WH8102. Genome Inform. 2004;15:211–222. [PubMed] [Google Scholar]
- 2.Tran TT, Dam P, Su Z, Poole FL, Adams MW, Zhou GT, Xu Y. Operon prediction in Pyrococcus furiosus. Nucleic Acids Res. 2007;35:11–20. doi: 10.1093/nar/gkl974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yada T, Nakao M, Totoki Y, Nakai K. Modeling and predicting transcriptional units of Escherichia coli genes using hidden Markov models. Bioinformatics. 1999;15:987–993. doi: 10.1093/bioinformatics/15.12.987. [DOI] [PubMed] [Google Scholar]
- 4.Tjaden B, Haynor DR, Stolyar S, Rosenow C, Kolker E. Identifying operons and untranslated regions of transcripts using Escherichia coli RNA expression analysis. Bioinformatics. 2002;18(Suppl. 1):S337–S344. doi: 10.1093/bioinformatics/18.suppl_1.s337. [DOI] [PubMed] [Google Scholar]
- 5.Dam P, Olman V, Harris K, Su Z, Xu Y. Operon prediction using both genome-specific and general genomic information. Nucleic Acids Res. 2007;35:288–298. doi: 10.1093/nar/gkl1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang GQ, Cao ZW, Luo QM, Cai YD, Li YX. Operon prediction based on SVM. Comput. Biol. Chem. 2006;30:233–240. doi: 10.1016/j.compbiolchem.2006.03.002. [DOI] [PubMed] [Google Scholar]
- 7.Bockhorst J, Craven M, Page D, Shavlik J, Glasner J. A Bayesian network approach to operon prediction. Bioinformatics. 2003;19:1227–1235. doi: 10.1093/bioinformatics/btg147. [DOI] [PubMed] [Google Scholar]
- 8.Edwards MT, Rison SC, Stoker NG, Wernisch L. A universally applicable method of operon map prediction on minimally annotated genomes using conserved genomic context. Nucleic Acids Res. 2005;33:3253–3262. doi: 10.1093/nar/gki634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Westover BP, Buhler JD, Sonnenburg JL, Gordon JI. Operon prediction without a training set. Bioinformatics. 2005;21:880–888. doi: 10.1093/bioinformatics/bti123. [DOI] [PubMed] [Google Scholar]
- 10.Jacob E, Sasikumar R, Nair KN. A fuzzy guided genetic algorithm for operon prediction. Bioinformatics. 2005;21:1403–1407. doi: 10.1093/bioinformatics/bti156. [DOI] [PubMed] [Google Scholar]
- 11.Zheng Y, Szustakowski JD, Fortnow L, Roberts RJ, Kasif S. Computational identification of operons in microbial genomes. Genome Res. 2002;12:1221–1230. doi: 10.1101/gr.200602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Salgado H, Moreno-Hagelsieb G, Smith TF, Collado-Vides J. Operons in Escherichia coli: genomic analyses and predictions. Proc. Natl Acad. Sci. USA. 2000;97:6652–6657. doi: 10.1073/pnas.110147297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Okuda S, Kawashima S, Kobayashi K, Ogasawara N, Kanehisa M, Goto S. Characterization of relationships between transcriptional units and operon structures in Bacillus subtilis and Escherichia coli. BMC Genomics. 2007;8:48. doi: 10.1186/1471-2164-8-48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yan Y, Moult J. Detection of operons. Proteins. 2006;64:615–628. doi: 10.1002/prot.21021. [DOI] [PubMed] [Google Scholar]
- 15.Romero PR, Karp PD. Using functional and organizational information to improve genome-wide computational prediction of transcription units on pathway-genome databases. Bioinformatics. 2004;20:709–717. doi: 10.1093/bioinformatics/btg471. [DOI] [PubMed] [Google Scholar]
- 16.Jensen LJ, Kuhn M, Stark M, Chaffron S, Creevey C, Muller J, Doerks T, Julien P, Roth A, Simonovic M, et al. STRING 8–a global view on proteins and their functional interactions in 630 organisms. Nucleic Acids Res. 2009;37:D412–D416. doi: 10.1093/nar/gkn760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gama-Castro S, Jimenez-Jacinto V, Peralta-Gil M, Santos-Zavaleta A, Penaloza-Spinola MI, Contreras-Moreira B, Segura-Salazar J, Muniz-Rascado L, Martinez-Flores I, Salgado H, et al. RegulonDB (version 6.0): gene regulation model of Escherichia coli K-12 beyond transcription, active (experimental) annotated promoters and Textpresso navigation. Nucleic Acids Res. 2008;36:D120–D124. doi: 10.1093/nar/gkm994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic local alignment search tool. J. Mol. Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- 19.Ermolaeva MD, White O, Salzberg SL. Prediction of operons in microbial genomes. Nucleic Acids Res. 2001;29:1216–1221. doi: 10.1093/nar/29.5.1216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Janga SC, Moreno-Hagelsieb G. Conservation of adjacency as evidence of paralogous operons. Nucleic Acids Res. 2004;32:5392–5397. doi: 10.1093/nar/gkh882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen X, Su Z, Dam P, Palenik B, Xu Y, Jiang T. Operon prediction by comparative genomics: an application to the Synechococcus sp. WH8102 genome. Nucleic Acids Res. 2004;32:2147–2157. doi: 10.1093/nar/gkh510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Price MN, Huang KH, Alm EJ, Arkin AP. A novel method for accurate operon predictions in all sequenced prokaryotes. Nucleic Acids Res. 2005;33:880–892. doi: 10.1093/nar/gki232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tatusov RL, Fedorova ND, Jackson JD, Jacobs AR, Kiryutin B, Koonin EV, Krylov DM, Mazumder R, Mekhedov SL, Nikolskaya AN, et al. The COG database: an updated version includes eukaryotes. BMC Bioinformatics. 2003;4:41. doi: 10.1186/1471-2105-4-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Remm M, Storm CE, Sonnhammer EL. Automatic clustering of orthologs and in-paralogs from pairwise species comparisons. J. Mol. Biol. 2001;314:1041–1052. doi: 10.1006/jmbi.2000.5197. [DOI] [PubMed] [Google Scholar]
- 25.Li G, Che D, Xu Y. A universal operon predictor for prokaryotic genomes. J. Bioinform. Comput. Biol. 2009;7:19–38. doi: 10.1142/s0219720009003984. [DOI] [PubMed] [Google Scholar]
- 26.Wolf YI, Rogozin IB, Kondrashov AS, Koonin EV. Genome alignment, evolution of prokaryotic genome organization, and prediction of gene function using genomic context. Genome Res. 2001;11:356–372. doi: 10.1101/gr.gr-1619r. [DOI] [PubMed] [Google Scholar]
- 27.Kim HB, Jung SH, Kim TG, Park KH. Fast learning method for back-propagation neural network by evolutionary adaptation of learning rates. Neurocomputing. 1996;11:101–106. [Google Scholar]
- 28.Kamio Y, Lin CK, Regue M, Wu HC. Characterization of the ileS-lsp operon in Escherichia coli. Identification of an open reading frame upstream of the ileS gene and potential promoter(s) for the ileS-lsp operon. J. Biol. Chem. 1985;260:5616–5620. [PubMed] [Google Scholar]
- 29.Miller KW, Bouvier J, Stragier P, Wu HC. Identification of the genes in the Escherichia coli ileS-lsp operon. Analysis of multiple polycistronic mRNAs made in vivo. J. Biol. Chem. 1987;262:7391–7397. [PubMed] [Google Scholar]
- 30.Raina S, Missiakas D, Baird L, Kumar S, Georgopoulos C. Identification and transcriptional analysis of the Escherichia coli htrE operon which is homologous to pap and related pilin operons. J. Bacteriol. 1993;175:5009–5021. doi: 10.1128/jb.175.16.5009-5021.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li SJ, Cronan JE., Jr Growth rate regulation of Escherichia coli acetyl coenzyme A carboxylase, which catalyzes the first committed step of lipid biosynthesis. J. Bacteriol. 1993;175:332–340. doi: 10.1128/jb.175.2.332-340.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brouwer RW, Kuipers OP, van Hijum SA. The relative value of operon predictions. Brief. Bioinform. 2008;9:367–375. doi: 10.1093/bib/bbn019. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.