A Versatile Gene-Based Test for Genome-wide Association Studies

Abstract

We have derived a versatile gene-based test for genome-wide association studies (GWAS). Our approach, called VEGAS (versatile gene-based association study), is applicable to all GWAS designs, including family-based GWAS, meta-analyses of GWAS on the basis of summary data, and DNA-pooling-based GWAS, where existing approaches based on permutation are not possible, as well as singleton data, where they are. The test incorporates information from a full set of markers (or a defined subset) within a gene and accounts for linkage disequilibrium between markers by using simulations from the multivariate normal distribution. We show that for an association study using singletons, our approach produces results equivalent to those obtained via permutation in a fraction of the computation time. We demonstrate proof-of-principle by using the gene-based test to replicate several genes known to be associated on the basis of results from a family-based GWAS for height in 11,536 individuals and a DNA-pooling-based GWAS for melanoma in ∼1300 cases and controls. Our method has the potential to identify novel associated genes; provide a basis for selecting SNPs for replication; and be directly used in network (pathway) approaches that require per-gene association test statistics. We have implemented the approach in both an easy-to-use web interface, which only requires the uploading of markers with their association p-values, and a separate downloadable application.

Main Text

Gene-based tests for association are increasingly being seen as a useful complement to genome-wide association studies (GWAS).¹ A gene-based approach considers association between a trait and all markers (usually SNPs) within a gene rather than each marker individually. Depending on the underlying genetic architecture, gene-based approaches can be more powerful than traditional individual-SNP-based GWAS. For example, if a gene contains more than one causative variant, then several SNPs within that gene might show marginal levels of significance that are often indistinguishable from random noise in the initial GWAS results. By combining the effects of all SNPs in a gene into a test-statistic and correcting for linkage disequilibrium (LD), the gene-based test might be able to detect these effects. Gene-based tests are also ideally suited for network (or pathway) approaches to interpreting the findings from GWAS.^2–7 These approaches are necessarily gene centric and require a measure of the relative importance of each gene to the phenotype of interest. The gene-based approach also reduces the multiple-testing problem of GWAS by only considering statistical tests for ∼20,000 genes per genome as opposed to testing more than half a million SNPs in a typical GWAS.

Ideally, a gene-based test statistic can be obtained with permutations, where LD structure and other possible confounding factors, such as gene size, will be accounted for. Computing a gene-based test for basic GWAS designs via permutations is conceptually simple and is currently implemented as the “set-based test” in the PLINK software package⁸; however, heavy computational requirements have restricted this method from being adopted on a genome-wide scale. Other gene-based tests, such as those based on genetic distances⁹ or entropy,¹⁰ are often also restricted to situations where individual genotype information is available or to specific GWAS designs (usually case-control designs). There are several important situations in which permutations or existing methods cannot be used; these include family-based GWAS, GWAS meta-analyses based on summary data, and DNA-pooling-based GWAS. In contrast, our approach, called VEGAS (versatile gene-based association study), only requires individual marker p values in order to allow computation of a gene-based p value, and it can be applied to virtually any association study design. The method tests the evidence for association on a per-gene basis by summarizing either the full set of markers (typically SNPs) in the gene or a subset of the most significant markers (for example, the 10% most significant SNPs). For some genes, an approach considering all the markers might be the most powerful; for others, focusing on just the most associated markers might be apt. The true underlying genetic architecture is seldom known in advance. The default gene-based test in our implementation and in the following examples uses the full set of markers in the gene. Our approach takes account of LD between markers in a gene by using simulation based on the LD structure of a set of reference individuals from a HapMap phase 2 population (CEU [Utah residents with ancestry from northern and western Europe]; CHB and JPT [Han Chinese in Beijing, China and Japanese in Tokyo, Japan]; or YRI [Yoruba in Ibadan, Nigeria]), which provides approximately ∼2.1 million autosomal SNPs,¹¹ or a custom set of individuals if genotype information is available.

Our method assigns SNPs to each of 17,787 autosomal genes according to positions on the UCSC Genome Browser hg18 assembly. In order to capture regulatory regions and SNPs in LD, we define gene boundaries in this case as ± 50 kb of 5′ and 3′ UTRs. Then, for a given gene with n SNPs, association p values are first converted to upper-tail chi-squared statistics with one degree of freedom (df). The gene-based test statistic is then the sum of all (or a pre-defined subset) of the chi-squared 1 df statistics within that gene. If the SNPs are in perfect linkage equilibrium, the test statistic will have a chi-squared distribution with n degrees of freedom under the null hypothesis. Because this is unlikely to be the case, however, the true null distribution given the LD structure (and hence p values that correlate accordingly) will need to be taken into account. Ideally, one would achieve this by performing a large number of permutations; however, this is very computationally intensive, requires individual genotype information, and assumes that individuals are unrelated. Instead, our Monte Carlo approach makes use of simulations from the multivariate normal distribution and is both much faster and agnostic regarding the GWAS design.

For a gene with n SNPs, we simulate an n-element multivariate normally distributed vector with mean 0 and variance Σ, the n × n matrix of pairwise LD (r) values. A vector of n independent, standard, normally distributed random variables is first generated and then multiplied by the Cholesky decomposition matrix of Σ – that is, the n × n lower triangular matrix C, such that CC^T = Σ. The new random vector, $Z=\left(z_1,z_2\dots z_n\right)$, will have a multivariate normal distribution, $Z\sim N_n\left(0,\sum \right)$. Z is then transformed into a vector of correlated chi-squared 1 df variables, $Q=\left(q_1,q_2\dots q_n\right)$, $q_i=z_i^2$. The simulated gene-based test statistic is then the sum of all (or a predefined subset) of the elements of Q and will have the same approximate distribution as our observed gene-based test statistic under the null hypothesis. A large number of multivariate normal vectors are simulated, and the empirical gene-based p value is the proportion of simulated test statistics that exceed the observed gene-based test statistic.

We have implemented VEGAS in both an easy-to-use web-interface or as a downloadable application for Linux and Unix. The only user inputs required are a text file consisting of two columns: SNP rs-name and association p value, along with specification of the reference population (CEU, CHB and JPT, or YRI). The downloadable version also allows the use of custom individual genotypes if available, as well as specification of gene boundaries. Pairwise LD correlation matrices are calculated in PLINK. The R corpcor package is used to correct for non-positive definite correlation matrices,¹² and multivariate normal random vectors are simulated with the mvtnorm package.¹³ The number of simulations per gene is determined adaptively. In the first stage, 10³ simulations will be performed. If the resulting empirical p value is less than 0.1, 10⁴ simulations will be performed. If the empirical p value from 10⁴ simulations is less than 0.001, the program will perform 10⁶ simulations. At each stage, the simulations are mutually exclusive. For computational reasons, if the empirical p value is 0, then no more simulations will be performed. An empirical p value of 0 from 10⁶ simulations can be interpreted as p < 10⁻⁶, which exceeds a Bonferroni-corrected threshold of p < 2.8 × 10⁻⁶ (≈0.05/17,787; this threshold is likely to be conservative given the overlap between genes). The user may select whether to perform the gene-based test on the full set of SNPs within a gene, a specified percentage of the most significant SNPs, or just the single most significant SNP. Because the program depends upon the output from other programs, it is important to take correct GWAS quality-control measures to account for issues such as population stratification or pooling errors before using VEGAS.

Using a test with permutations as the “gold standard,” we compared the results from VEGAS to those from the PLINK set-based test⁸ with permutations (with parameters --set-p1 --set-r21 --maf 0.01) on a GWAS for height in 3,611 unrelated Australian individuals drawn from community-based twin studies conducted from 1980 to 2004. Several recent genetic studies of other traits,^14–16 have used these samples and have described genotype and phenotype data cleaning. In brief, height was corrected for age and sex before being converted to standard z scores. PLINK was used for performing genome-wide association, from which the results were used in our method. For a given set of SNPs, the PLINK set-based test initially performs a standard association test and then uses the average association test statistic across these SNPs as the “set-based” test statistic (VEGAS uses the sum rather than average; the two methods are equivalent in calculations of empirical p values). Then, for the permutation procedure, the phenotypes are randomly shuffled among individuals, and the process is repeated several thousand times, from which an empirical p value is obtained. Because of computational limitations, we only performed the PLINK set-based test on 413 genes on chromosome 22 with 10⁴ permutations each. To see how both tests deal with more significant genes, we performed 10⁶–10⁷ permutations on seven additional genes. These genes were chosen on the basis of having p values < 10⁻³ when VEGAS was applied across all chromosomes. across all chromosomes. The results from both tests are shown in Figure 1, which compares the corresponding −log₁₀(p value)s from the PLINK set-based test and VEGAS for 420 genes. For the majority of genes, both methods produced very similar results. Correlation between the p values was very high (Pearson r = 0.999), as was that between the rankings (Spearman ρ = 0.998). Thus, in addition to being agnostic toward GWAS design, a major advantage of our method over permutations is speed. The PLINK set-based test on our computer took ∼12 hr to compute the 413 chromosome 22 genes plus 2 days for the seven additional genes. In contrast, our approach with 10³ to 10⁶ simulations per gene computed the same set of genes in less than thirty minutes.

Figure 1.

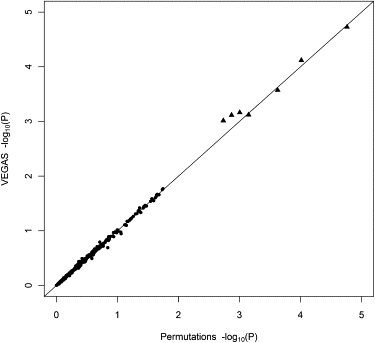
Comparison of the −log₁₀(p value)s from the PLINK Set-Based Test and VEGAS on a GWAS of Height in 3,611 Individuals

The PLINK set-based test was performed on 413 genes on chromosome 22 with 10⁴ permutations (circles) and on seven genes on other chromosomes; these were selected on the basis of having the smallest p values from the VEGAS analysis, at 10⁶ to 10⁷ permutations (triangles). The p values from VEGAS were obtained by running 10³ to 10⁷ multivariate normal simulations per gene. The straight diagonal line indicates a 1:1 relationship.

We selected nine nonoverlapping genes of various sizes on chromosome 22 to further investigate the type I error rate of our method compared to those from permutations. The previous height data were permuted 1000 times. VEGAS and the PLINK set-based test were applied to the association results of each permutation for each of the genes. The comparison of the p values for each of the nine genes is shown in Figure S1. Overall, there does not appear to be any major bias involved with VEGAS. Nevertheless, it should be noted that our method will produce spurious results if the incorrect reference population, and hence LD structure, is used. Biases toward smaller p values will occur if the reference population is older than the study population, and larger p values will occur in the opposite situation. When the same 420 genes and 3611 Australian individuals were used, running VEGAS with the HapMap CEU population as the reference produced results comparable to those from permutation (Figure S2A), whereas using the HapMap YRI population produced significant biases toward smaller p values (Figure S2B). Slight biases might also potentially occur for genes with a non-positive definite LD correlation matrix. In our dataset, this was a property of ∼80% of genes, inhibiting the direct use of Cholesky decomposition. For these genes, the nearest positive semidefinite matrix is estimated with the R corpcor package.^12,17 Matrices that require a large adjustment might explain some of the discrepancy between VEGAS and permutations, although as seen in Figure 1, this does not appear to have a major effect.

Under some genetic architectures, a more powerful gene-based method may be to consider only the most significant SNP in a gene rather than the full set of SNPs and then correct this SNP's association p value for gene size and other possible confounders. Our approach can readily be applied to this situation. For a gene with n SNPs, recall the simulated vector of n correlated chi-squared 1 df variables, $Q=\left(q_1,q_2\dots q_n\right)$. For the “Top-SNP” method, we define Q_max as the simulated test statistic of the maximum element of Q. Then, by simulating a large number of Q_max test statistics, the empirical gene-based p value is the proportion of simulated Q_max test statistics that exceed the observed test statistic of the most significant SNP in the gene.

Using the same 420 genes as in our previous analysis with the full set of SNPs, we compared the VEGAS Top-SNP method and permutations (Figure 2). Note that in this case, we ran our own permutations by using R rather than the PLINK set-based test because the two methods are not equivalent. As with the test considering the full set of SNPs, VEGAS produces results very similar to those from permutations. Correlation between the p values was very high (Pearson r = 0.996), as was that between the rankings (Spearman ρ = 0.996).

Figure 2.

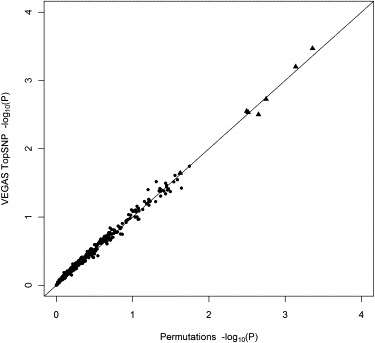
Comparison of the −log₁₀(p value)s from Permutations and VEGAS When Only the Single Best SNP from Each Gene Is Considered

Results are based on a GWAS of height in 3611 individuals. Permutations were performed on 413 genes on chromosome 22 with 10³ permutations and on seven additional genes with 10⁵–10⁶ permutations. The p values from VEGAS were obtained from 10³–10⁶ multivariate normal simulations per gene. The straight diagonal line indicates a 1:1 relationship.

Our method of using the full set of SNPs per gene was applied to two situations where permutation tests are not applicable: a family-based GWAS for height, where permutation cannot account for phenotypic correlation between family members, and a DNA-pooling GWAS for melanoma (MIM 155600), where individual genotype information is not available. For height, we included an extra 7,935 relatives of those in our original GWAS of 3,611 unrelated individuals. These consisted of parents, offspring, siblings, twins, and other family members, all typed with the same SNP chip as the unrelated individuals used in the first calculation. The results of the family-based association analysis were previously published in Liu, et al.¹⁸ Table 1 lists the 15 most significant height-associated genes obtained from VEGAS. One gene, the previously implicated HHIP (MIM 606178; p = 1 × 10⁻⁶),^19–21 exceeded a Bonferroni corrected threshold of p < 2.8 × 10⁻⁶. Overall, nine of the top 15 genes have been previously implicated in published GWAS of height at genome-wide significance.²² It remains to be seen whether any of the remaining genes play a role in height. The gene NMUR1 (MIM 604153; p = 6.05 × 10⁻⁴) is a G-protein-coupled receptor and is also involved in neuropeptide signaling, similar to the previously implicated GPR126 (MIM 612243; p = 5 × 10⁻⁶). Height might also be mediated by MFAP2 (MIM 156790; p = 3.71 × 10⁻⁴) through its role as a glycoprotein component of connective-tissue microfibrils,²³ for which normal connective-tissue development is essential for height growth. Mutations in other microfibril components have been linked to Marfan syndrome (MIM 154700), a genetic disorder characterized by skeletal overgrowth.²⁴ These results suggest that despite having a relatively small sample size for a GWAS for height, the gene-based test has the potential to identify novel genes. In a two-stage GWAS, the most significant genes may also be used as a basis for selecting SNPs for replication samples.

Table 1.

VEGAS Results for the 15 Most Significant Genes from a Family-Based GWAS for Height in 11,536 Individuals

Chromosome	Gene	Number of SNPs	Start Position	Stop Position	Test Statistic	p Value	Best SNP	SNP p Value
4	HHIPa	26	145786622	145879331	263.505	10−6	rs1812175	1.06 × 10−9
6	GPR126a	23	142664748	142809096	169.912	5 × 10−6	rs6570507	2.16 × 10−7
8	CHCHD7a	4	57286868	57293730	31.82	3.2 × 10−5	rs7833986	2.20 × 10−4
6	HMGA1a	6	34312627	34321986	38.934	8.4 × 10−5	rs1776897	6.71 × 10−6
15	ADAMTSL3a	85	82113841	82499597	344.52	1.34 × 10−4	rs7183263	3.89 × 10−7
4	LCORLa	30	17453940	17632474	222.748	1.38 × 10−4	rs6817306	7.63 × 10−6
20	GDF5a	10	33484562	33489441	81.199	1.78 × 10−4	rs4911494	1.39 × 10−4
12	HMGA2a	34	64504506	64646338	147.824	3.00 × 10−4	rs8756	4.26×10−7
1	MFAP2	15	17173585	17180668	76.961	3.71 × 10−4	rs11203280	6.03 × 10−4
17	C17orf78	5	32807097	32823775	27.012	5.31 × 10−4	rs8067120	1.80 × 10−3
6	HIST1H3Ga	16	26379124	26379591	86.062	5.77 × 10−4	rs10946808	2.48 × 10−5
2	NMUR1	18	232096114	232103426	102.955	6.05 × 10−4	rs1434519	3.29 × 10−5
4	ADH5	26	100211152	100228954	142.218	8.01 × 10−4	rs1042364	2.45 × 10−4
8	SPATC1	8	145158594	145174003	58.172	8.30 × 10−4	rs3936211	7.35 × 10−4
2	EMX1	13	72998111	73015528	60.278	9.62 × 10−4	rs10183113	3.71 × 10−6

^aThese genes have been implicated in previous GWAS of height.²² The signal in HIST1H3G is driven by a variant previously implicated in the neighboring HIST1H1G.

For melanoma, the gene-based test was performed on the results from a GWAS that used pooled DNA in 1354 melanoma cases and 1291 controls. The sample was originally part of a larger previously published GWAS for melanoma,²⁵ and pooling and association methods are described in that study. This study was performed with the approval of the appropriate ethics committee and with informed consent from all participants.

As for height, the results from the gene-based test are consistent with our current understanding of the genetics of melanoma (Table 2). Overall, all of the top 15 genes are in regions known to harbor melanoma-susceptibility genes. Seven genes identified are located on 20q11.22, the region originally implicated by Brown et al.²⁵ and containing the skin pigmentation gene ASIP (MIM 600201); these include MAP1LC3A (MIM 601242; p < 10⁻⁶), PIGU (MIM 608528; p = 2 × 10⁻⁶), DYNLRB1 (MIM 607167; p = 7 × 10⁻⁶), TP53INP2 (p = 4.7 × 10⁻⁵), and NCOA6 (MIM 605299; p = 1.38 × 10⁻⁴). ASIP itself, however, was nonsignificant (p = 0.116). Given the size of this associated region, it could be the case that a distant enhancer rather than nonsynonymous or proximal regulatory elements is driving the association with ASIP. Similarly, a large number of associated genes are also located on 16q24.3; the most significant of these genes was DEF8 (p = 4 × 10⁻⁵). Given that DEF8 lies ∼30 kb downstream of the known melanoma-susceptibility gene, MC1R (MIM 155555), it is likely that this signal is driven by variants in and around MC1R, which was only nominally significant (p = 1.30 × 10⁻³), rather than DEF8 itself. Likewise, the gene RXFP3 (p = 1.95 × 10⁻⁴) is adjacent to SLC45A2 (MIM 606202; p = 8.91 × 10⁻³), a known melanoma-susceptibility gene, and MYEF2 (p = 4 × 10⁻⁶) is adjacent to SLC24A5 (MIM 609802; p = 2.34 × 10⁻³), a gene associated with skin pigmentation.

Table 2.

VEGAS Results for the 15 Most Significant Genes from a DNA-Pooling GWAS for Melanoma in 1354 Cases and 1291 Controls

Chromosome	Gene	Number of SNPs	Start Position	Stop Position	Test Statistic	p Value	Best SNP	SNP p Value
20	MAP1LC3A	59	32598352	32611810	762.618	<10−6	rs910873	1.00 × 10−16
20	PIGU	93	32612006	32728750	964.294	2 × 10−6	rs910873	1.00 × 10−16
15	MYEF2	25	46218920	46257850	50.865	4 × 10−6	rs2470102	4.18 × 10−4
20	DYNLRB1	58	32567864	32592423	548.265	7 × 10−6	rs910873	1.00 × 10−16
20	SNTA1	39	31459423	31495359	242.906	9 × 10−6	rs291695	6.60 × 10−11
16	DEF8	73	88542651	88561968	318.251	4.0 × 10−5	rs1805007	3.33 × 10−16
20	TP53INP2	44	32755808	32764898	312.611	4.7 × 10−5	rs4417778	5.35 × 10−9
20	NCOA6	81	32766238	32877094	563.953	1.38 × 10−4	rs4911442	2.71 × 10−10
20	CDK5RAP1	55	31410305	31452998	260.851	1.53 × 10−4	rs291695	6.60 × 10−11
5	RXFP3	48	33972247	33974099	138.421	1.95 × 10−4	rs35389	1.31 × 10−8
16	C16orf55	49	88251710	88265176	244.276	3.12 × 10−4	rs258322	1.34 × 10−7
16	MGC16385	59	88563701	88566443	218.033	3.99 × 10−4	rs8049897	9.74 × 10−7
16	DPEP1	58	88207216	88232340	248.214	4.54 × 10−4	rs12918773	4.47 × 10−7
16	CHMP1A	52	88238344	88251630	248.105	4.60 × 10−4	rs258322	1.34 × 10−7
16	SPG7	73	88102305	88151675	370.214	4.66 × 10−4	rs4785686	2.76 × 10−7

Although VEGAS was able to produce results equivalent to those obtained through permutations at a fraction of the time taken, as well as replicate several known height- and melanoma-associated genes, there are several situations in which use of the gene-based test is limited. The effectiveness of VEGAS, along with other gene-based methods, is determined by the underlying genetic architecture of the gene and phenotype of interest. Although gene-based methods are more powerful than single-marker analysis for identifying significant genes with multiple causal variants, the converse is also true. If a gene contains only one causal variant, then the inclusion of a large number of nonsignificant markers into the gene-based test will dilute this gene's significance. The correct genetic model to use is seldom known in advance, although our method can be performed on a specified subset of markers or just the single most significant marker rather than all markers in a gene. Similarly, the use of ± 50 kb to define gene boundaries is an arbitrary choice. Large boundaries mean that some markers are included in multiple genes, resulting in a situation similar to our results for melanoma, where it may be difficult to pinpoint the causal gene when multiple adjacent genes are statistically significant. Specifying stringent boundaries, however, may not fully capture regulatory regions or those SNPs in high LD with variants in the gene. Moreover, given that the majority of SNPs so far identified in GWAS are found in nongenic regions,²⁶ these SNPs would not be included in any gene-centric analysis at all. For these reasons, gene-based methods should not be seen as a replacement for traditional single-marker association studies but rather should be seen as a complement to GWAS and an essential step for network- and pathway-based approaches. We offer our gene-based test not as a definitive solution to the problem but also as one tool in the complex-trait geneticist's toolbox for post-GWAS analysis.

Web Resources

The URLs for data presented herein are as follows:

• corpcor, http://strimmerlab.org/software/corpcor

• mvtnorm, http://cran.r-project.org/package=mvtnorm

• Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim

• PLINK, http://pngu.mgh.harvard.edu/∼purcell/plink

• R, http://www.r-project.org

• UCSC Genome Browser, http://genome.ucsc.edu

• VEGAS, http://genepi.qimr.edu.au/general/softwaretools.cgi