Sample size considerations for GEE analyses of three-level cluster randomized trials

SUMMARY

Cluster randomized trials in health care may involve three instead of two levels, for instance, in trials where different interventions to improve quality of care are compared. In such trials, the intervention is implemented in health care units (“clusters”) and aims at changing the behavior of health care professionals working in this unit (“subjects”), while the effects are measured at the patient level (“evaluations”). Within the generalized estimating equations (GEE) approach, we derive a sample size formula that accounts for two levels of clustering: that of subjects within clusters and that of evaluations within subjects. The formula reveals that sample size is inflated, relative to a design with completely independent evaluations, by a multiplicative term that can be expressed as a product of two variance inflation factors, one that quantifies the impact of within-subject correlation of evaluations on the variance of subject-level means and the other that quantifies the impact of the correlation between subject level means on the variance of the cluster means. Power levels as predicted by the sample size formula agreed well with the simulated power for more than 10 clusters in total, when data was analyzed using bias-corrected estimating equations for the correlation parameters in combination with the model-based covariance estimator or the sandwich estimator with a finite sample correction.

1. Introduction

Cluster randomized trials, i.e. trials which randomize intact groups of individuals (“clusters”) instead of the individuals themselves, have become common in health and health care research (Donner and Klar, 2000; Murray, 1998; Murray, Varnell, and Blitstein, 2004; Campbell, Donner, and Klar, 2007; Ukoumunne et al., 1999). They are a natural design choice when an intervention aims to improve patients health by innovating the provision of health care around the patient (Donner and Klar, 2000). The intervention is then implemented at the level of health care professionals (e.g. clinicians, physicians, nurses, caregivers) or health service units (e.g. practices, hospitals), while the hypothesized favorable effects are measured at the level of the patients. Trials such as these have two levels: subjects (e.g. patients) are nested within clusters (e.g. physicians). As a more recent development, cluster randomized trials with three levels have begun to find application in health care research. An example is the Dutch Helping Hands trial which compares two strategies to improve adherence to hand hygiene guidelines in hospitals. Each strategy is implemented in a subset of the wards (“clusters”), and subsequently nurses (“subjects”) are observed with respect to their level of guideline adherence in opportunities for hand hygiene (“evaluations”). Data from trials such as these are correlated in ‘twofold’ nested fashion: evaluations (hand hygiene opportunities) are correlated within subjects (nurses) that are, in turn, correlated within clusters (wards). The statistical analysis method used and therefore the corresponding sample size calculation needs to take account of this twofold nested correlation structure. Statistical models that account for such clustering fall into two categories, depending on the interpretation of their regression parameters: population-averaged (marginal) or cluster-specific (conditional) models. Each approach has its own merits (Preisser, Lu, and Qaqish, 2008; Preisser, 2004) but for covariates that do not vary within clusters, population-averaged model parameters have an easy interpretation, while the interpretation of cluster-specific model parameters may be difficult or misleading. To illustrate, consider the model parameter for treatment in a cluster trial. In a population-averaged model, it describes how the response average changes across the subsets of the population defined by treatment. In a cluster-specific model, the treatment parameter is specific for a given cluster and describes the difference in response when that particular cluster would have been observed in the control condition and in the treatment condition, which is an unobserved effect, because each cluster is observed in one condition only. For this reason, population-averaged models have been recommended for analyzing cluster-specifc covariates (Zeger, Liang, and Albert, 1988; Neuhaus, Kalbfleisch, and Hauck, 1991; Heagerty, 1999).

Sample size and statistical power for a cluster-specific model of a three level cluster randomized trial have recently been considered, viz. a linear mixed model for continuous responses (Heo and Leon, 2008). In this paper, we focus on a population-averaged model for three-level cluster randomized trials fitted with generalized estimating equations (GEE) and we derive a GEE-sample size formula for a post-test design. Furthermore, we conduct a simulation study to evaluate the accuracy (practical applicability) of this formula. The evaluation is complicated, however, because the standard covariance estimator of GEE (the empirical sandwich estimator) has inflated type I errors when the number of clusters is small, typically below 40 (Kauermann and Carroll, 2001; O'Brien and Fitzmaurice, 2004). Approaches to deal with small samples have been proposed (Mancl and DeRouen, 2001; Fay and Graubard, 2001; Pan and Wall, 2002; Morel, Bokossa, and Neerchal, 2003; Kauermann and Carroll, 2001). We validate the sample size formula with simulated test size (empirical type I error rate) and power of Wald tests that are based on a small sample correction to the empirical standard error due to Kauermann and Carroll (2001). For comparison, also the performance of the Wald test with the model-based standard error and the Wald test with small sample correction due to Mancl and DeRouen (2001) was investigated. Finally, the Dutch Helping Hands trial is used to illustrate the proposed sample size formula.

2. Statistical Model

Typically, a response is observed under certain characteristics or conditions that may affect it and these may be at the level of evaluation, subject and/or cluster level. Consider a population-averaged (marginal) model where evaluation $k=1,\dots ,n_e^{ij}$ of subject $j=1,\dots ,n_s^i$ in cluster i = 1, . . . , N yields a response y_ijk which is observed given a covariate vector X_ijk = (x_ijk1, . . . ,x_ijkp)^t. Let μ_ijk = E(y_ijk|X_ijk) be the marginal mean response given X_ijk i.e. μ_ijk is the mean response of a population of cluster-subject-evaluations that is characterized by X_ijk. The relation of the covariates and the marginal mean is described in a generalized linear model (GLM) as $g\left({\mu }_{ijk}\right)=X_{ijk}^t\beta$ where β is a p × 1 vector of regression parameters to be estimated from the data and g(μ_ijk) the link function. The covariance structure is defined by within-cluster correlations and marginal variances $var(y_{ijk}\mid X_{ijk})=\tilde{\varphi }\nu \left({\mu }_{ijk}\right)$ where ν(μ_ijk) is the variance function and $\tilde{\varphi }$ is the scale parameter. We employ a ‘nested exchangeable’ (‘nested compound symmetry’) correlation structure, i.e. 1) the correlation between evaluations within the same subject is constant (corr(x_ijk,x_ijk′) = r for k ≠ k) and 2) the correlation between evaluations in the same cluster, but of different subjects is constant (corr(x_ijk, x_ij′k′) = ρ for j ≠ j).

3. GEE and the three level exchangeable correlation structure

Let $Y_{ij}={(y_{ij1},\dots ,y_{ij{n}_e^{ij}})}^t$, ${\mu }_{ij}={({\mu }_{ij1},\dots ,y_{ij{n}_e^{ij}})}^t$, and $X_{ij}={(X_{ij1},\dots ,X_{ij{n}_e^{ij}})}^t$ be the $n_e^{ij}\times 1$ response vector, $n_e^{ij}\times 1$ marginal mean response vector, and $n_e^{ij}\times p$ covariate matrix of subject j in cluster i, respectively. Furthermore, let $Y_i={(Y_{i1},\dots ,Y_{i{n}_e^{ij}})}^t$ and ${\mu }_i={({\mu }_{i1},\dots ,{\mu }_{i{n}_e^{ij}})}^t$ be the vector of responses and marginal mean responses of the subjects in cluster i, respectively. GEE is an approach for fitting the GLMs for correlated data using a multivariate analogue of the quasi-score function (Wedderburn, 1974). Define D_i = ∂μ_i/∂β and let $V_i=\tilde{\varphi }{A}_i^{1∕2}{R}_i{A}_i^{1∕2}$ be a ‘working covariance matrix’ for Y_i, where A_i is a diagonal matrix with elements ν(μ_ijk) and R_i = R_i(α) is a ’working correlation matrix that may vary across clusters but is specified by a common parameter vector α, e.g. α = (r, ρ)^t. Then, the three level exchangeable correlation structure defined in section 2 is

$$R_i=\rho J_{n_s{n}_e}+(r-\rho )BDia{g}_{n_s}\left(J_{n_e}\right)+(1-r)I_{n_s{n}_e}$$

where $J_s=1_s{1}_s^t$ where 1_s is an s-column vector of ones, BDiag_t(A) is a block diagonal matrix with matrix element A replicated t times, and I_u is the identity matrix of dimension u. The combinations (p, r) for which R_i is positive definite, can be determined using the SAS/IML macro provided in web appendix 1.

The GEE estimate $\widehat{\beta }$ is obtained by solving ${\Sigma }_i^N{D}_i^t{V}_i^{-1}(Y_i-{\mu }_i)=0$. Any consistent estimate of α may be used (Liang and Zeger, 1986). Fast computation, even in cases of large clusters common to cluster trials, and in the extension to unbalanced data, is provided by calculation of an expression (see web appendix 2 for the derivation) that avoids matrix inversion

$$R_i^{-1}=\frac{\rho }{\varphi \gamma }\rho J_{n_s{n}_e}+\frac{r-\rho }{(1-r)\gamma }BDia{g}_{n_s}\left(J_{n_e}\right)+\frac{1}{1-r}{I}_{n_s{n}_e}$$ (1)

To provide a degree of correction to the small sample bias of α estimates, we use the set of “matrix adjusted” estimating equations (MAEE) described in (Preisser, Lu, and Qaqish, 2008). Asymptotically (i.e. when N is sufficiently large), $\widehat{\beta }$ has a multivariate normal distribution with mean β and covariance estimated by the model-based variance estimator

$$V_R^{model}={\widehat{\Sigma }}_1^{-1}={\left(\sum _{i=1}^N{D}_i^t\left(\widehat{\beta }\right)V_i^{-1}\left(\alpha \right)D_i\left(\widehat{\beta }\right)\right)}^{-1}$$

or by the sandwich estimator

$$V_R^{sandwich}={\widehat{\Sigma }}_1^{-1}{\widehat{\Sigma }}_0^{-1}{\widehat{\Sigma }}_1^{-1}\text{where}{\widehat{\Sigma }}_0=\sum _{i=1}^N{D}_i^t\left(\widehat{\beta }\right)V_i^{-1}\left(\alpha \right)B_i(Y_i-{\widehat{\mu }}_i){(Y_i-\widehat{\mu })}^t{B}_i{V}_i^{-1}\left(\alpha \right)D_i\left(\widehat{\beta }\right)$$

Sandwich estimators provide valid inference regardless of the correct specification of R_i, provided the number of clusters is sufficiently large, whereas the consistency of the model-based variance estimator requires correct specification of the correlation structure. In the sandwich estimator, B_i are matrices that may be defined to provide a partial correction to the small sample bias of the uncorrected sandwich estimator of Liang and Zeger (1986) that is given by B_i = I_ni, where $n_i=n_s^i{n}_e^{ij}$ is the total number of evaluations in the ith cluster). Defining the cluster leverage (Lu et al., 2007) as $H_i=D_i{\Sigma }_1^{-1}{D}_i^t{V}_i^{-1}$, the small sample (i.e. when the number of clusters is small) correction of Mancl and DeRouen is given by B_i = (I_ni – H_i)^–1 and that of Kauermann and Carroll by B_i = (I_ni – H_i)^–1/2 (Lu et al., 2007).

In finite samples, Lu et al. (2007) reported that bias correction for α-estimation via MAEE mildly improved the confidence interval coverage of the marginal mean regression parameters β based upon the model-based covariance estimator but such correction had essentially no effect on procedures that used sandwich estimators. On the other hand, MAEE may substantially reduce the bias of the estimator of, and improve inference on, α (Preisser et al., 2008). The three-level cluster randomized design with nested exchangeable correlation structure can be analyzed with the general purpose software made available at http://www.bios.unc.edu/jpreisse.

4. Sample size and statistical power

4.1 General formula for the two-sample case

Suppose the treatment assignment is coded in the last column of the clusters covariate matrices $X_i={(X_{i1},\dots ,X_{i{n}_e^{ij}})}^t$ and the corresponding last parameter of β is β_p. The asymptotic variance of $\sqrt{N}({\widehat{\beta }}_p-{\beta }_p)$ is determined by the (p, p)th (right-lower) corner element of $\widehat{cov}\left\{\sqrt{N}(\widehat{\beta }-\beta )\right\}$. To account for the uncertainty in estimating the variance, we will use t-percentiles in the Wald tests i.e. $({\widehat{\beta }}_p-{\beta }_p)∕SE\left({\widehat{\beta }}_p\right)$, where $SE\left({\widehat{\beta }}_p\right)=\sqrt{{\sigma }_{\beta }^2}$ and ${\sigma }_{\beta }^2=Var({\widehat{\beta }}_p-{\beta }_p)$ will be referred to a t-distribution with N – p degrees of freedom. The statistic of interest is the difference (on the link function scale) in the mean response of all evaluations in the control clusters and that in the intervention clusters. Asymptotically, the power to detect a difference β_p of size b, with a two-sided type I error rate α given by sample size N is approximately

$$power={\Phi }_{t,N-p}\left(t_{\alpha ∕2,N-p}+\frac{\sqrt{N}\sqrt{b^2}}{\sqrt{{\sigma }_{\beta }^2}}\right)$$ (2)

where Φ_t,n is the cumulative distribution function of the t-distribution with n degrees of freedom. Conversely, the approximate number of clusters required to provide power 1 – γ satisfies the relation

$$N={\left(t_{\alpha ∕2,N-p}+t_{\gamma ,N-p}\right)}^2\frac{{\sigma }_{\beta }^2}{b^2}$$

where t_α,Np is the 100α% percentile from the t-distribution with N – p degrees of freedom. For power and sample size calculations, we assume the (co)variances to be known i.e. ${\sigma }_{\beta }^2={\left({\Sigma }_1^{-1}\right)}_{p,p}$. In the calculation of the sample size below, we assume that the total of N clusters is divided in πN clusters in the control arm and (1 – π)N clusters in the intervention arm. Furthermore, we assume the GLM model has no further covariates (p = 2). We restrict to post-test only designs i.e. g(μ_ijk) = β₁x_1ijk + β₂x_2ijk (x₁ is only 1s, x₂ is the cluster level treatment indicator). In other words: X_ijk = [x_1ijk, x_2ijk] = [1, x_2ijk] is a two-column matrix with the first column consisting of ones and the second column consisting of the treatment indicator.

4.2 Variance inflation factor

A simplification we make in the sample size calculations is that all clusters are of the same size (same number of subjects in each cluster and same number of evaluations in each subject) and have the same type of correlation structure, i.e. the correlation matrix R is the same for all clusters. Generalizing the calculations of Shih for continuous and binary outcomes (Shih, 1997) shows ${\sigma }_{\beta }^2=va{r}_0∕\left(1^t{R}^{-1}1\right)$, where 1^tR^–11 is the sum of all matrix elements of the inverse of the correlation matrix R, and var₀ is proportional to the variance without account of clusterings (see 4.3 and 4.4 below). For the three level exchangeable correlation matrix, it is shown in web appendix 2 that 1^tR^–11 = (n_sn_e)/ϕ where

$$\varphi ={\varphi }_s{\varphi }_e\text{with}{\varphi }_e=1+(n_e-1)r,{\varphi }_s=1+(n_s-1){\rho }_{s,n_e}\text{and}{\rho }_{s,n_e}=\frac{n_e\rho }{1+(n_e-1)r}.$$ (3)

Here ρ_s,ne is the correlation between mean evaluation scores of two different subjects within the same cluster. The variance inflation factor ϕ for the three level design is the product of variance inflation factors from 2-level designs operating within subjects at the evaluation level and within clusters at the subject level. Equivalently, ϕ = 1 + (n_e – 1)r + n_e(n_s – 1)ρ, the variance inflation factor that applies to a maximum likelihood analysis of a three level hierarchical cluster randomized trial (Heo and Leon, 2008). Note the GEE variance inflation factor is the same for continuous as well as binary outcome, as in the two-level cluster randomized designs (Shih, 1997). It reduces to the familiar variance inflation factor of the two-level design (subjects nested within clusters), when one evaluation per subject is taken (n_e = 1).

4.3 Sample size for continuous outcomes

Under the identity link function, the marginal mean model is μ_ijk = β₁+β₂x_2ijk with variance var(y_ijk|X_ijk) = ν(μ_ijk) = σ². Then ${\sigma }_{\beta }^2={\sigma }^2∕\left\{\pi (1-\pi )1^t{R}^{-1}1\right\}$ (Shih, 1997), so that the sample size is a solution to

$$N=\frac{{\left(t_{\alpha ∕2,N-2}+t_{\gamma ,N-2}\right)}^2}{b^2}\frac{{\sigma }^2\varphi ∕\left\{\pi (1-\pi )\right\}}{n_s{n}_e}$$ (4)

4.4 Sample size for binary outcomes

The marginal mean model is now logit(μ_ijk) = β₁ + β₂x_ijk with variance var(y_ijk|X_ijk) = ν(μ_ijk) = μ_ijk(1–μ_ijk). The difference to be detected is b = log(P₀/(1–P₀))–log(P₁/(1–P₁)). Analogous to Shih (1997):

$${\sigma }_{\beta }^2=\left\{\frac{1}{\pi P_0(1-P_0)}+\frac{1}{(1-\pi )P_1(1-P_1)}\right\}∕\left(1^t{R}^{-1}1\right)$$ (5)

so that the required number of clusters is a solution to

$$N=\frac{{\left(t_{\alpha ∕2,N-2}+t_{\gamma ,N-2}\right)}^2}{b^2}\frac{\varphi [{\left\{\pi P_0(1-P_0)\right\}}^{-1}+{\left\{(1-\pi )P_1(1-P_1)\right\}}^{-1}]}{n_s{n}_e}$$ (6)

For two-level binary data (n_e = 1), ϕ = 1 + (n_s – 1)ρ and our sample size formula reduces to that of Shih (1997), formula (10). For one level binary data (n_e = n_s = 1), ϕ = 1 and the sample size formula reduces to that of the two-sample Wald test for logistic regression, formula (5) in Vaeth and Skovlund (2004), noting that the variance of this Wald test statistic is 1.

In principle, equation (4) and (6) have to be solved iteratively, but a practical approach is to substitute z-percentiles for the t-percentiles and multiply the result by the factor (N+1)/(N−1) (p. 118 of Steel and Torrie (1980)).

5. Simulation study

5.1 Simulation design

As we expected that the accuracy of the sample size formula would be less for binary than for continuous outcomes, we restricted the validation of our sample size formula to binary outcomes. Correlated binary data for the model given in section 4.4 were generated using SAS/IML according to the method of Qaqish (2008), see web appendix 3. Since our interest was in cluster randomized studies with a small to moderate total number of clusters, we varied the total number of clusters (N) from 6 to 56 and we took ρ much smaller than r: (r, ρ) = (0.60, 0.05), (0.10, 0.005). We varied across the simulation scenarios the number of subjects per cluster (n_s) from 5 to 50 and the number of evaluations (n_e) from 2 to 6 (see Table 1). Regression parameters β₁ and β₂ were determined according to specifications of the probabilities of an event in the two treatment groups: p₀ and p₁ for control and intervention clusters, respectively. For evaluation of test size β₂ was set 0. The correct models for marginal mean and correlations were fit using GEE in combination with matrix adjusted estimating equations (MAEE) for a and four estimators for the variance of ${\widehat{\beta }}_2$: the model-based estimator (MB), the uncorrected sandwich estimator (rob), the sandwich estimator with the small sample correction due to the Kauermann and Carroll correction (KC) and that of Mancl and DeRouen (MD). From 1000 simulations, test size and power were estimated as the proportion of times $\mid {\widehat{\beta }}_2∕SE\left({\widehat{\beta }}_2\right)\mid >t_{0.975,N-2}$, when β₂ = 0 and β₂ ≠ 0, respectively, where t_0.975,N–2 is 97.5th percentage point of the t-distribution with N – 2 degrees of freedom, and SE denotes the standard error. The questions addressed by the simulation study are: 1) what is the minimal number of clusters needed so that the different Wald tests (based on different variance estimators) for H₀ : β₂ = 0 provide type I error rates near the nominal 0.05 level and 2) for those Wald tests that best maintain the type I error rate near the nominal level in small samples: how well do the power levels predicted by the sample size formula agree with empirical power generated by the simulation experiment?

Table 1.

Simulated scenarios, predicted power (Pred) by (2) and (5), and simulated power using the model-based variance estimator (MB) and the Kauermann and Caroll correction of the sandwich estimator (KC)

p0	p1	ρ	r	ns	ne	VIF	N	Preda	KCb	MBc
0.5	0.2	0.03	0.6	5	2	1.84	18	0.817	0.841	0.842
0.5	0.2	0.03	0.6	5	4	3.28	16	0.810	0.817	0.824
0.5	0.2	0.03	0.6	10	2	2.14	12	0.846	0.850	0.853
0.5	0.2	0.03	0.6	10	4	3.88	10	0.800	0.774	0.770
0.5	0.2	0.03	0.6	20	2	2.74	8	0.827	0.804	0.810
0.5	0.2	0.005	0.1	5	2	1.14	12	0.823	0.836	0.837
0.5	0.2	0.005	0.1	5	4	1.38	8	0.825	0.774	0.780
0.5	0.2	0.005	0.1	10	2	1.19	8	0.876	0.842	0.844
0.5	0.2	0.005	0.1	10	4	1.48	6	0.902	0.807	0.812
0.5	0.2	0.005	0.1	20	2	1.29	6	0.933	0.865	0.870
0.3	0.1	0.03	0.6	5	2	1.84	28	0.814	0.847	0.853
0.3	0.1	0.03	0.6	5	6	4.72	24	0.810	0.834	0.844
0.3	0.1	0.03	0.6	10	2	2.14	18	0.836	0.861	0.874
0.3	0.1	0.03	0.6	10	4	3.88	16	0.824	0.839	0.847
0.3	0.1	0.03	0.6	20	2	2.74	12	0.830	0.838	0.84
0.25	0.1	0.03	0.6	10	5	4.75	22	0.795	0.821	0.835
0.25	0.1	0.03	0.6	12	5	5.05	20	0.802	0.809	0.811
0.25	0.1	0.03	0.6	14	5	5.35	18	0.794	0.804	0.810
0.25	0.1	0.03	0.6	20	4	5.08	16	0.815	0.836	0.833
0.25	0.1	0.03	0.6	30	3	4.81	14	0.822	0.832	0.827
0.25	0.1	0.03	0.6	50	2	4.54	12	0.816	0.803	0.801
0.2	0.1	0.03	0.6	10	2	2.14	46	0.798	0.810	0.814
0.2	0.1	0.03	0.6	20	2	2.74	30	0.796	0.789	0.793
0.2	0.1	0.005	0.1	5	6	1.62	24	0.795	0.814	0.810

^apredicted power

^bsimulated power using sandwich estimator with Kauermann and Carroll correction

^csimulated power using model-based variance estimator

5.2 Simulation results

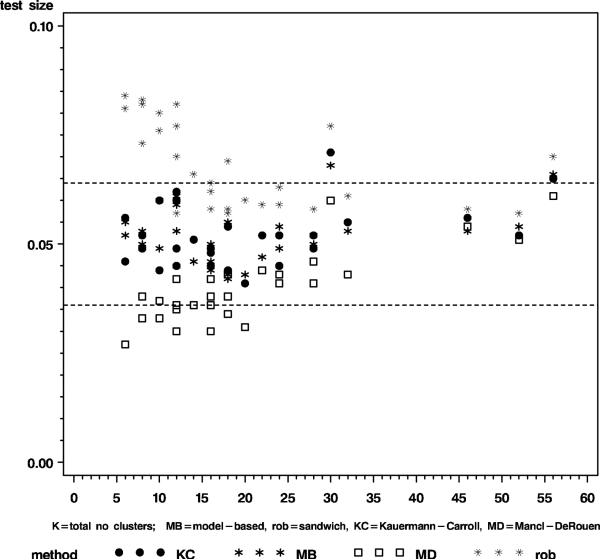
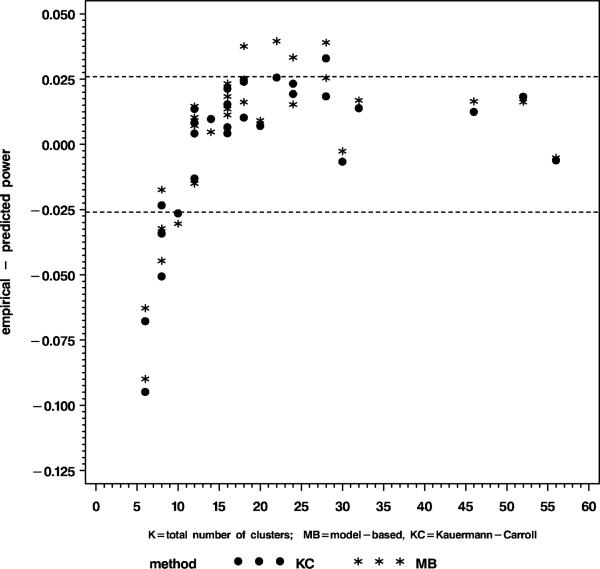
The convergence rate exceeded 99% for all simulated cases. To assess whether the test size was nominal and the power level as predicted by the sample size formula (6) was accurate, we considered a simulated test size between 3.6% and 6.4% to be compatible with a true test size of 5% and we considered a power level that differs at most 2.6% from the predicted level to be in agreement with the sample size formula. The rationale for this is that a true test size of 0.05 and power 0.80-0.90 have (approximate) standard errors of 0.7% and 1.3%, respectively, based on the binomial standard error . Figure 1 summarizes the results for test size. The test size of the model-based variance estimator (MB) and the sandwich estimator with Kauermann-Carroll correction (KC) was near nominal, even for as few as six clusters. The Mancl-DeRouen (MD) variance estimator gave test sizes below 6.4%, but was too conservative ( < 3.6%) for fewer than 20 clusters. Not surprisingly, test sizes for the robust variance estimator were inflated. Figure 2 and Table 1 provide the power results for the best two performing methods from Figure 1. The power of tests based on MB and KC corresponded well with that of formula (6) when the number of clusters was greater than 10, but was up to 5% smaller than predicted for N = 8, and up to 10% smaller for N = 6.

Figure 1.

Test size of the model-based covariance estimator (MB) and the sandwich estimators with no correction (rob), the Kauermann and Carroll correction (KC), or Mancl and DeRouen correction (MD)

Figure 2.

Power of the model-based covariance estimator (MB) and the sandwich estimator with the Kauermann and Carroll correction (KC)

6. Application

The variance inflation factor (3) implies that many different combinations (N, n_s, n_e) of total number of clusters, number of subjects per cluster, and number of evaluations per subject provide the same level of power to detect a given effect. Therefore, it is worthwhile to assess the feasibility of several scenarios in a particular application, the Helping Hands Trial. Hospital acquired infections are a burden to patients and the health care system, while the (most effective) obvious preventive measure, hand hygiene, is simple as well as underutilized. The Helping Hands trial (Netherlands Organization for Health Research and Development ZonMw, grant nr 80-007028-98-07101) compares two strategies to enhance adherence to hygiene guidelines. The first focuses on the nurses (training, feedback) and the wards (facilities), while the second strategy adds elements based on social influence in groups (norms and target setting within the nurse team). Randomization and implementation is done at the ward level and targets at changing nurse behavior. However, a binary outcome reflects whether guidelines are followed for each hand hygiene opportunity.

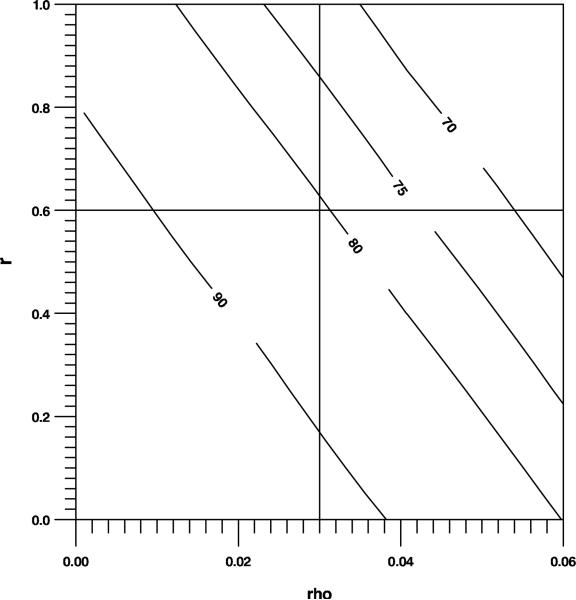
The researchers expect that the standard and extended strategy will result in an adherence of 60% and 70%, respectively. Uncorrected for correlation, the total sample size for a 1: 1 allocation is N₀ = 718 (formula (4) with ϕ = 1). It is reasonable to suppose that the behavior of an individual nurse with respect to hand hygiene is rather consistent (r = 0.6) and that the sharing of a common (working) environment results in some correlation of nurses's evaluations within a ward (ρ = 0.3). The researchers can make ca. 3 evaluations on ca. 15 nurses in each ward. Calculating for the number of wards (clusters) from n_s = 15 and n_e = 3, gives N = 58. Figure 3 illustrates how sensitive power is for uncertainty in ρ and r: power remains above 75% when ρ ≤ 0.04 (given r = 0.6) and when r ≤ 0.84 (given ρ = 0.03). The region depicted falls entirely in the range (ρ, r) for which R is positive definite.

Figure 3.

Power as a function of r and ρ (Section Application)

7. Discussion

The nested exchangeable correlation structure in a three level model for a posttest only trial is a direct generalization of the exchangeable correlation structure that is commonly used in two-level cluster randomized trials. It is suitable when the lowest level units are exchangeable within the middle level units and the middle level units are exchangeable within the highest level units. In the Helping Hands trial, evaluation of adherence to hygiene guidelines is nested within nurses which are nested within wards. As all the nurses in a ward share the same program, the nurses within wards are considered exchangeable. Since the evaluations ‘measure’ an underlying property or trait of a nurse (hygiene behavior), it is reasonable to suppose these evaluations are exchangeable within nurse. Another example where a nested exchangeable correlation is reasonable is when students are nested within classes within schools. The nested exchangeable correlation structure proposed in this paper is also applicable to nested cross-sectional cluster randomized trials (Murray, 1998; Preisser, Lohman, and Rathouz, 2002; Feldman and McKinlay, 1994), where clusters are measured repeatedly, but the subjects in those clusters are different for different times. For example, in the pretest-posttest the cross-sectional design discussed in Preisser et al. (Preisser et al., 2003), pairs of within-cluster observations from the same time are assumed to have one correlation e.g. r), while those from different times are assumed to have another (e.g., ρ). Notwithstanding the use of the same correlation structure, the respective variance inflation factors and test statistics differ: a pretest-posttest is employed in Preisser et al. (2003) versus a posttest in the Helping Hands trial.

The fact that the variance inflation factor derived for GEE equals the variance inflation factor of a mixed effects model for continuous outcomes leads to some interesting observations. First, this illustrates that power calculations for GEE Wald tests can be derived from appropriate summary statistics (Preisser et al., 2003; Preisser et al., 2007), in this case the treatment mean. Second, this equality of variance inflation factors conveys a bonus: the optimal allocation of units to the three levels that was derived for continuous 3-level random effects models (Moerbeek, Van Breukelen, and Berger, 2000; Teerenstra et al., 2008) can be identified as the optimal allocation for both continuous and binary 3-level GEE analyses. Despite the similarity in the variance inflation factor in the mixed effects and GEE analysis, there is also a difference: the correlations in the GEE framework are allowed to be negative unlike in mixed effects models. However, negative correlations are uncommon in cluster randomized trials (Donner and Klar, 2000). A conspicuous detail is that the variance inflation factor of GEE is the same for both continuous as binary outcomes. Shih observed this earlier for two-level cluster randomized trials (Shih, 1997): following his calculations, it can be seen that the variance inflation factor for posttest designs only depends on the correlation matrices of the clusters (Pan and Wall, 2002; Shih, 1997) and this generalizes easily to more than 2 levels.

A simplification we made in the sample size calculations is that all clusters are of the same size (same number of subjects in each cluster and same number of evaluations in each subject). Research into the impact of varying cluster size for ordinary (two-level) cluster randomization showed that the coefficient of variation of the cluster sizes enters the (simplified) sample size formulas (Manatunga, Hudgens, and Chen, 2001; van Breukelen, Candel, and Berger, 2007; Eldridge, Ashby, and Kerry, 2006). We expect similar results for the three level case, but this is subject of future research.

In practice, not only treatment but also other (influential) covariates are often included in the analysis model. Generally, this will decrease the (residual) variance (Murray and Blitstein, 2003) and increase the power, so that the sample size formula presented will be conservative. However, also the number of degrees of freedom for the test statistic will be reduced (Section 4.1). In cluster trials with (very) few clusters, this may offset any gain due to variance reduction and may actually result in a loss of power.

Our simulation study showed that the MAEE in combination with the model-based covariance estimator and the Kauermann-Carroll (KC) corrected covariance estimator had near nominal test size and power levels in agreement with the sample size formula down to a total number of clusters of 10. In contrast, the Mancl-DeRouen (MD) corrected covariance estimator resulted in too conservative test size. An explanation for this is that MD consistently overestimates the variance when the number of clusters is small (Lu et al., 2007). Our findings at first glance appear to contradict those of Lu et. al (2007) who recommend the MD variance estimator over KC for the analysis of cluster trials. However, their recommendation were based on the construction of confidence intervals using standard normal quantiles, whereas t-quantiles were employed in this paper. In more apparent harmony with the results reported here, Lu et al. (2007) found that for a cluster level covariate (such as the treatment indicator in a cluster randomized trial), KC tends to have better coverage (again, using standard normal quantiles) than MD, but this observation was restricted to small cluster sizes (e.g., size four or six).

Intuitively, one would expect that a sample size calculation based on a model-based covariance estimator followed by an analysis using a robust covariance estimator would result in some loss in precision and hence power in small samples. For large samples (many clusters), the proposed sample size formula will accurately characterize the behavior (i.e., power and Type I error) of the GEE test statistics, since the robust GEE covariance estimator is a consistent estimator for the (assumed) true model-based covariance matrix. In small samples, the robust GEE covariance estimator tends to underestimate the true covariance matrix and the increased variability of the sandwich estimator is known to adversely affect the small sample performance of test statistics. This led to the proposal of finite sample corrections to the sandwich estimator (Kauermann and Carroll, 2001) evaluated in this paper. Our simulation study shows that for moderately sized cluster randomized trials, an analysis using the robust covariance estimator with KC correction has power as predicted by the sample size calculation based on the model-based covariance matrix.

An entirely different situation occurs if sample size calculations are based on an incorrectly specified model-based covariance matrix, so that the planned power is not likely to be realized. Nonetheless, the GEE analysis based on a robust covariance estimator is a consistent estimator of the (unknown) true variance under a correctly specified model for the marginal mean, whereas use of an incorrectly specified model-based covariance matrix in the analysis will give invalid results. Although the ‘robust-GEE’ analysis would be valid, it would likely be under- or overpowered. Following Rochon (1998), one could specify a sample size formula for GEE based on a “robust covariance matrix” with the understanding that two covariance models are being specified, a (assumed) true covariance matrix (e.g., whose structure may vary across specified subpopulations) and a working covariance matrix to be specified in the GEE at the analysis stage (e.g., Rochon, 1998).

As a practical conclusion, MAEE in combination with the model-based or KC-corrected covariance estimator protects the type I error in a GEE analysis of 3-level cluster randomized trials that have as few as three clusters per condition (at least in the specific model treated here). Moreover, when using either of these two analysis methods, the sample size calculation (variance inflation factor) presented is accurate for planning a three level cluster randomized trial with at least 5 clusters per condition.