The Influence of the Oxygen Atom Acceptor on the Reaction Coordinate and Mechanism of Oxygen Atom Transfer From the Dioxo-Mo(VI) Complex, Tp^iPrMoO₂(OPh), to Tertiary Phosphines

Abstract

The oxygen atom transfer reactivity of the dioxo-Mo(VI) complex, Tp^iPrMoO₂(OPh) (Tp^iPr = hydrotris(3-isopropylpyrazol-1-yl)borate), with a range of tertiary phosphines (PMe₃, PMe₂Ph, PEt₃, PBuⁿ₃, PEt₂Ph, PEtPh₂ and PMePh₂) has been investigated. The first step in all the reactions follows a second-order rate law indicative of an associative transition state, consistent with nucleophilic attack by the phosphine on an oxo ligand, viz. Tp^iPrMoO₂(OPh) + PR₃ → Tp^iPrMoO(OPh)(OPR₃). The calculated free energy of activation for the formation of the OPMe₃ intermediate (Chem. Eur. J. 2006, 12, 7501) is in excellent agreement with the experimental ΔG^‡ value reported here. The second step of the reaction, i.e., the exchange of the coordinated phosphine oxide by acetonitrile, Tp^iPrMoO(OPh)(OPR₃) + MeCN → Tp^iPrMoO(OPh)(MeCN) + OPR₃, is first-order in starting complex in acetonitrile. The reaction occurs via a dissociative interchange (I_d) or associative interchange (I_a) mechanism, depending on the nature of the phosphine oxide. The activation parameters for the solvolysis of Tp^iPrMoO(OPh)(OPMe₃) (ΔH^‡ = 56.3 kJ mol⁻¹; ΔS^‡ = −125.9 J mol⁻¹ K⁻¹; ΔG^‡ = 93.8 kJ mol⁻¹) and Tp^iPrMoO(OPh)(OPEtPh₂) (ΔH^‡ = 66.5 kJ mol⁻¹; ΔS^‡ = −67.6 J mol⁻¹ K⁻¹; ΔG^‡ = 86.7 kJ mol⁻¹) by acetonitrile are indicative of I_a mechanisms. In contrast, the corresponding parameters for the solvolysis reaction of Tp^iPrMoO(OPh)(OPEt₃) (ΔH^‡ = 95.8 kJ mol⁻¹; ΔS^‡ = 26.0 J mol⁻¹ K⁻¹; ΔG^‡ = 88.1 kJ mol⁻¹) and the remaining complexes by the same solvent are indicative of an I_d mechanism. The equilibrium constant for the solvolysis of the oxo-Mo(V) phosphoryl complex, [Tp^iPrMoO(OPh)(OPMe₃)]⁺, by acetonitrile was calculated to be 1.9 × 10⁻⁶. The oxo-Mo(V) phosphoryl complex is more stable than the acetonitrile analogue, whereas the oxo-Mo(IV) acetonitrile complex is more stable than the phosphoryl analogue. The higher stability of the Mo(V) phosphoryl complex may explain the phosphate inhibition of sulfite oxidase.

Introduction

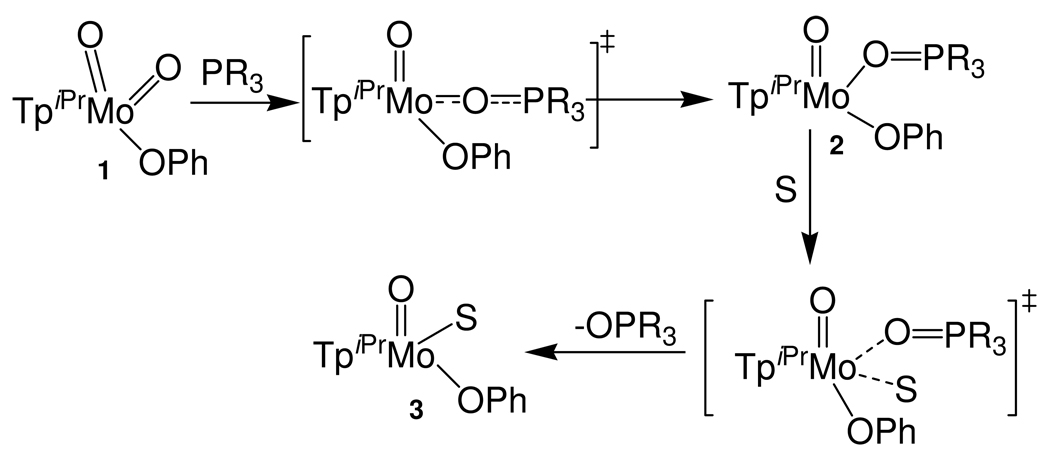
The transfer of an oxygen atom between competent centers is a fundamental reaction in chemistry and biology, and in past decades reactions of this type have been extensively investigated.^1–9 Many pterin-containing molybdenum enzymes catalyze oxygen atom transfer (OAT) chemistry, as the metal center shuttles between +6 and +4 oxidation states. Prominent examples include the oxidation of sulfite to sulfate by sulfite oxidase and the reduction of dimethyl sulfoxide (DMSO) to dimethyl sulfide (DMS) by DMSO reductase. For sulfite oxidase, the resting state of the enzyme has a dioxo-Mo(VI) center that is transformed into an oxo-Mo(IV) center upon substrate oxidation and there are a number of chemical models for reactions of this type. Studies from several laboratories have demonstrated that a variety of discrete dioxo-Mo(VI) complexes can undergo OAT reactions with oxygen atom acceptors producing oxidized species such as tertiary phosphine and arsine oxides, sulfoxides, N-oxides, or sulfate.^{6, 10–24} While tertiary phosphines are not physiological substrates, they are often the preferred substrates in models studies. The relevance of such reactions to enzymes is highlighted by the observation that OAT between DMSO and a water-soluble tertiary phosphine (PC₆H₁₂N) is catalyzed by DMSO reductase.²⁵ Trimethylphosphine has also been used as an acceptor of the oxygen atom of DMSO in a voltammetric study of DMSO reductase.²⁶ Our studies have provided important insights into the reactions of dioxo-Mo(VI) trispyrazolylborate complexes, e.g., reactions of tertiary phosphines with Tp^iPrMoO₂(OPh) (1 ; Tp^iPr = hydrotris(3-isopropylpyrazol-1-yl)borate),^27–30 and Tp^*MoO₂X (Tp^*=hydrotris(3,5-dimethylpyrazol-1-yl)borate; X= Cl, SPh); these insights appear to have broad relevance to metal-mediated OAT reactions.^31–36 We have shown that the reactions occur in two steps, the first involving the generation of isolable oxo-Mo(IV) phosphoryl complexes (2), the second their solvation to yield solvent coordinated oxo-Mo(IV) complexes (Scheme I). Kinetics and computational studies have probed the interplay of steric and electronic factors in the formation of the phosphoryl intermediates, which have been isolated and thoroughly characterized.

Scheme I.

It is generally believed that the first step in OAT from dioxo-Mo(VI) centers to tertiary phosphines involves nucleophilic attack of the phosphine on an empty Mo=O π* orbital, while the other oxo-group acts in a ‘spectator’ capacity.^{37, 38} Thus, the initial reaction is dependent on the nucleophilicity of the phosphine – the higher the nucleophilicity, the faster the rate of reaction. Of course, any increase in the electrophilicity of the oxo-donor center would also enhance the reaction rate.³⁹ In addition to the electronic effects, the steric properties of the phosphine, as defined by the Tolman’s cone angle,^{40, 41} also impact on the reaction rate and the stability of the phopshoryl product. This first step of the OAT reaction (Scheme I) is associative in nature and has a negative entropy of activation.

The second step of the reaction, i.e., ligand exchange or solvolysis of the oxo-Mo(IV) phosphoryl complex, is poorly understood. The solvolysis of Tp^iPrMoO(OPh)(OPEt₃) and Tp^iPrMoO(OPh)(OPMePh₂) to give Tp^iPrMoO(OPh)(MeCN) (3) occurs via a dissociative interchange (I_d) mechanism, associated with a positive entropy of activation.^{42, 43} However, in principle, this reaction can proceed by dissociative or associative pathways (or an intermediate interchange pathway) depending on the nature of the phosphine oxide and solvent. To date, there have been no extensive studies of the dependence of the rates and mechanisms of these reactions (Scheme 1) on the nature of the tertiary phosphine.

Here, we report detailed kinetics studies of the reactions of 1 with the tertiary phosphines, PMe₃, PMe₂Ph, PEt₃, PBuⁿ₃, PEt₂Ph, PEtPh₂ and PMePh₂. These reactions produce 3 and the corresponding phosphine oxide via one of the following oxo-Mo(IV) phosphoryl complexes:

• Tp^iPrMoO(OPh)(OPMe₃) (2a)

• Tp^iPrMoO(OPh)(OPMe₂Ph) (2b)

• Tp^iPrMoO(OPh)(OPEt₃) (2c)

• Tp^iPrMoO(OPh)(OPEt₂Ph) (2d)

• Tp^iPrMoO(OPh)(OPBuⁿ₃) (2e)

• Tp^iPrMoO(OPh)(OPMePh₂) (2f)

• and Tp^iPrMoO(OPh)(OPEtPh₂) (2g).

We show that the first step in all the reactions proceeds via an associative transition state, consistent with a mechanism involving nucleophilic attack by the phosphine on an oxo ligand of the complex. Further, we demonstrate that the rates of formation of the phosphoryl complexes (2) vary linearly with the phosphine cone angle. Most significantly, we have established that step 2 of the OAT reaction can proceed by dissociative or associative mechanisms and that the rate-limiting step in the overall reaction can be switched depending on the phosphine employed. Finally, we have used electrochemical data and a thermodynamic square scheme to calculate the stability constants for the exchange of OPMe₃ and NCMe at oxo-Mo(IV) and -Mo(V) centers. Our results show that the phosphoryl ligand forms a more stable complex with Mo(V) than Mo(IV), which may provide a rationale for phosphate inhibition of sulfite oxidase detected by EPR spectroscopy.^{44, 45}

Experimental

Materials and Methods

All solvents, except the NMR solvents and acetonitrile, were distilled from sodium, deoxygenated using the freeze-pump-thaw technique, and stored inside a glove-box until needed. The acetonitrile used in this study was triple-distilled from KMnO₄, CaH₂ and then P₄O₁₀, and was stored anaerobically. The NMR solvents that were used in the characterization of the Tp^iPrMoO(OPh)(OPR₃) complexes were dried by flushing them through an activated alumina micro-column inside a glove-box, while those employed to record the spectra of 1 were used as received. In addition, all solutions were prepared under an argon atmosphere using standard Schlenk techniques and gas-tight syringes.

Complexes 1, 2b and 2f were prepared as previously reported,^28–30 while complexes 2a, 2c–2e and 2g were prepared and studied in situ, from the reactions of 1 with ~ 2- to 5-fold excess of the desired phosphine in dry benzene or acetonitrile. The acetonitrile complex, 3, was characterized in situ, and was produced by solvolysis of 2a–2g, through standing in acetonitrile solution.

NMR spectra of 1 were recorded on a Bruker 300 MHz NMR spectrometer either in CD₃CN or in C₆D₆. NMR spectra for the characterization of the intermediates were recorded on a Varian 500 MHz spectrometer, with ³¹P spectra referenced to PPh₃ in C₆D₆ solution (NMR data can be found in the Supporting Information).

Electrochemistry

Electrochemical measurements were carried out using a Bioanalytical Systems (BAS) model CV-50W voltammetric analyzer. Voltammograms were recorded with a standard three-electrode system consisting of a Pt-disk working electrode, an Ag/Ag⁺ reference electrode, a Pt-wire auxiliary electrode, and tetra-n-butylammonium perchlorate (TBAP) as the charge carrier. All voltammograms were internally referenced with ferrocene (Fc), and the potentials are reported with respect to the Fc⁺/Fc couple without correcting for junction potential. All electrochemical work was performed at room temperature inside a nitrogen-filled glove-box.

Kinetics

The majority of the kinetics investigations were conducted by recording electronic spectral changes on a Cary 14 spectrophotometer with an OLIS 14 version 2.6.99 operating system connected to a constant-temperature water-circulation bath. However, some of the single-wavelength and repeat-scan measurements were conducted on a Cary 3E diode array spectrophotometer with a Varian operating system or a Hewlett-Packard 8452A diode array spectrophotometer at room temperature. All UV-visible kinetics measurements were conducted using an anaerobic cuvette that was oven-dried and cooled under an argon flow.

Reaction of Tp^iPrMoO₂(OPh) with PR₃

The basic procedure of the kinetics studies has been detailed elsewhere.^{27, 28} Kinetic runs were conducted under pseudo first order conditions with excess tertiary phosphine. The reactions were conducted in acetonitrile by monitoring the change in the absorption spectra either near 300 nm, 680 nm or 910 nm over a temperature range of ~30 °C (depending on the compound from 0–38 °C, supporting information). The second order rate constants were calculated from the pseudo first order rates as a function of phosphine concentration. These rate constants normalized for the concentration of the Mo-complex and the normalized rate constants were used to calculate the activation parameters from the Arrhenius and Eyring relations (eqns 1 and 2, respectively).

$$\text{ln}k=\text{ln}(A)\cdot e^{\left(\frac{-E_a}{R\cdot T}\right)}$$ eqn 1

$$\text{ln}\left(\frac{k\cdot h}{k_b\cdot T}\right)=-\frac{\mathrm{\Delta }{H}^{*}}{\mathit{\text{RT}}}+\frac{\mathrm{\Delta }{S}^{*}}{R}$$ eqn 2

For the second order reactions with the phosphines, the activation parameters were calculated from the rate constants normalized for concentration of the molybdenum complex.

Solvolysis of Tp^iPrMoO(OPh)(OPR₃)

The kinetics of the solvolysis of the phosphoryl complexes were conducted in acetonitrile using either isolated or in situ generated Tp^iPrMoO(OPh)(OPR₃) complexes. The presence of excess solvent ensured pseudo-first order conditions. The rate of the solvolysis reaction of a related compound, Tp^*MoO(Cl)(OPMe₃), in mixed benzene-acetonitrile solvent follows linear relation with the acetonitrile concentration, the rate of the reaction is slower at a lower acetonitrile concetration.⁴⁶ In the current system, formation of dimeric compounds complicates the mixed solvent reaction and was not followed further in mixed solvent system. The pseudo first order rates were corrected for acetonitrile concentration (19.2 M) with the assumption that the rate follows first order with respect to acetonitrile concentration. The activation parameters were derived from the variable temperature corrected rates. This correction has small effect on the activation parameters.²⁸

Results

Electrochemistry

Room temperature cyclic voltammograms (CVs) of complexes 1, 2a–2g and 3 were recorded in acetonitrile. Complex 1, exhibited a one-electron Mo(VI/V) redox couple, while the Mo(IV) complexes exhibited an Mo(V/IV) redox couple. The redox potentials measured are listed in Table 1. It is interesting to note that the solvent coordinated species 3 exhibited a redox potential of −316 mV, which is 348 to 388 mV more positive than the redox potentials of its phosphoryl precursors. Thus, the Mo(V) state is easier to achieve when an acetonitrile ligand, rather than a phosphoryl ligand, is coordinated in the oxo-Mo(IV) center.

Table 1.

Electrochemical data in acetonitrile at 22 °C.

Complex	E1/2, mV (ΔEp, mV)
TpiPrMoO2(OPh), 1	−1183 (73)
TpiPrMoO(OPh)(OPMe3), 2a	−664 (126)
TpiPrMoO(OPh)(OPMe2Ph), 2b	−688 (61)
TpiPrMoO(OPh)(OPEt3), 2c	−685 (109)
TpiPrMoO(OPh)(OPEt2Ph), 2d	−685 (78)
TpiPrMoO(OPh)(OPBun3), 2e	−700 (85)
TpiPrMoO(OPh)(OPMePh2), 2f	−704 (79)
TpiPrMoO(OPh)(OPEtPh2), 2g	−681 (118)
TpiPrMoO(OPh)(NCMe), 3	−316 (112)

Kinetics of the Reactions of Tp^iPrMoO₂(OPh) with PR₃

Solutions of yellow 1 react with tertiary phosphines producing green to gold-colored solutions containing oxo-Mo(IV) phosphoryl complexes, Tp^iPrMoO(OPh)(OPR₃) (2a–2g). All reactions follow a second order rate law, being dependent on the concentrations of both the complex and phosphine (Scheme 1). The oxo-Mo(IV) complexes exhibit two low energy d-d transitions, assigned to d_xy → d_xz/d_yz transitions, that are absent in the dioxo-Mo(VI) precursor; for example, the lowest energy transition is observed around 910 nm (ε ~ 110 M⁻¹ cm⁻¹) for 2c and at 900 nm (ε ~ 92 M⁻¹ cm⁻¹) for 2f. These low-energy transitions were monitored for the kinetics measurements.²⁸

Reactions were conducted under pseudo-first order conditions while optimizing the highest concentration of the phosphines to allow reactions to be followed with conventional spectrophotometry. Depending on the phosphine and its concentration, higher temperature reactions lead to side reactions and limited the accessible (higher) temperature range. The variable temperature rate constants (see Supporting Information) provided the activation parameters listed in Table 2.

Table 2.

Activation parameters for formation of the phosphoryl complexes, 2a–2g.

Complex formed	Ea kJ mol−1	lnA	R2	ΔH‡ kJ mol−1	ΔS‡ J mol−1 K−1	R2	ΔGf‡298 kJ mol−1
TpiPrMoO(OPh)(OPMe3), 2a	77.1 (±12.2)	24.1 (±5.1)	96.4	74.6 (±12.3)	−53.1 (±42.1)	96.2	90.4
TpiPrMoO(OPh)(OPMe2Ph), 2b	45.1 (±3.9)	11.4 (±1.7)	99.2	43.0 (±4.0)	−157.2 (±14.0)	99.1	89.8
TpiPrMoO(OPh)(OPEt3), 2c	50.9 (±1.9)	12.5 (±0.8)	99.6	48.4 (±1.9)	−149.2 (±6.4)	99.5	92.9
TpiPrMoO(OPh)(OPEt2Ph), 2d	69.2 (±6.1)	19.7 (±2.5)	99.2	66.8 (±5.9)	−88.8 (±20.2)	99.2	93.2
TpiPrMoO(OPh)(OPBun3), 2e	85.6 (±10.1)	26.1 (±4.1)	97.9	83.2 (±10.5)	−36.2 (±35.6)	97.7	94.0
TpiPrMoO(OPh)(OPMePh2), 2f	75.9 (±3.8)	21.8 (±1.5)	99.6	73.4 (±3.7)	−71.9 (±2.3)	99.5	94.8
TpiPrMoO(OPh)(OPEtPh2), 2g	85.0 (±3.3)	24.4 (±1.3)	99.9	82.5 (±3.3)	−50.3 (±0.1)	99.8	97.5

Kinetics of the solvolysis of Tp^iPrMoO(OPh)(OPR₃)

Kinetics investigations of the solvolysis reactions of isolated 2c and 2f have been reported elsewhere;²⁸ in the present work, they were conducted by in situ generation of the phosphoryl complexes from 1 and the appropriate phosphine. Likewise, complexes 2a, 2b and 2d–2f were investigated following their in situ generation from 1, and monitored at the d-d band at ~900 nm. The rate constants at different temperatures are listed in the Supporting Information. From these rate constants the activation parameters were calculated; the results are listed in Table 3. From the entropy of activation it is evident that that at least in two cases (compounds 2a and 2g) the nature of the transition state is different from the others. The data summarized, included the differences noted above, have been reproduced on a number of occasions.

Table 3.

Activation parameters for solvolysis reaction in MeCN of 2a–2g.

Complex	Ea kJ mol−1	lnA	R2	ΔH‡ kJ mol−1	ΔS‡ Jmol−1 K−1	R2	ΔGs‡298 kJ mol−1
TpiPrMoO(OPh)(OPMe3), 2a	56.3 (±10.9)	11.4 (±4.3)	96.4	56.3 (±10.9)	−125.9 (±35.5)	96.4	93.8
TpiPrMoO(OPh)(OPMe2Ph), 2b	109.3 (±4.6)	34.8 (±1.9)	99.8	109.3 (±4.6)	69.3 (±16.1)	99.8	88.6
TpiPrMoO(OPh)(OPEt3), 2c	95.8 (±1.1)	29.6 (±0.5)	99.9	95.8 (±1.1)	26.0 (±3.9)	99.9	88.1
TpiPrMoO(OPh)(OPEt2Ph), 2d	94.6 (±10.1)	29.7 (±4.2)	97.3	94.6 (±10.1)	26.7 (±35.0)	97.3	86.7
TpiPrMoO(OPh)(OPMePh2), 2f	96.1 (±5.9)	31.4 (±2.5)	99.6	96.1 (±5.9)	40.4 (±20.6)	99.6	84.1
TpiPrMoO(OPh)(OPEtPh2), 2g	66.5 (±15.1)	18.3 (±6.2)	95.2	66.5 (±15.1)	−67.6 (±51.7)	95.2	86.7

Discussion

The results presented in the preceding section confirm that of the reduction of 1 by tertiary phosphines proceeds through two steps in acetonitrile. The first step involves the formation of an oxo-Mo(IV) phosphoryl intermediate while the second step involves its solvolysis to produce the acetonitrile complex, 3, with release of oxidized substrate. Below, we discuss the mechanism of both steps and the relative importance of the steps with respect to the properties of the phosphines.

For step 1, a negative entropy of activation is observed in each reaction. The negative entropy of activation is indicative of an associative transition state as expected for a bimolecular reaction.^{28, 31} Here, the enthalpy of activation is the dominant contributor to the free energy of activation and this implicates a significant degree of bond breaking and making in the transition state. However, the difference in the enthalpy of activation is relatively large (ΔΔH^‡ ≈ 40 kJ mol⁻¹), which may reflect the difference in basicity of the phosphines and/or the steric interactions in the transition state.

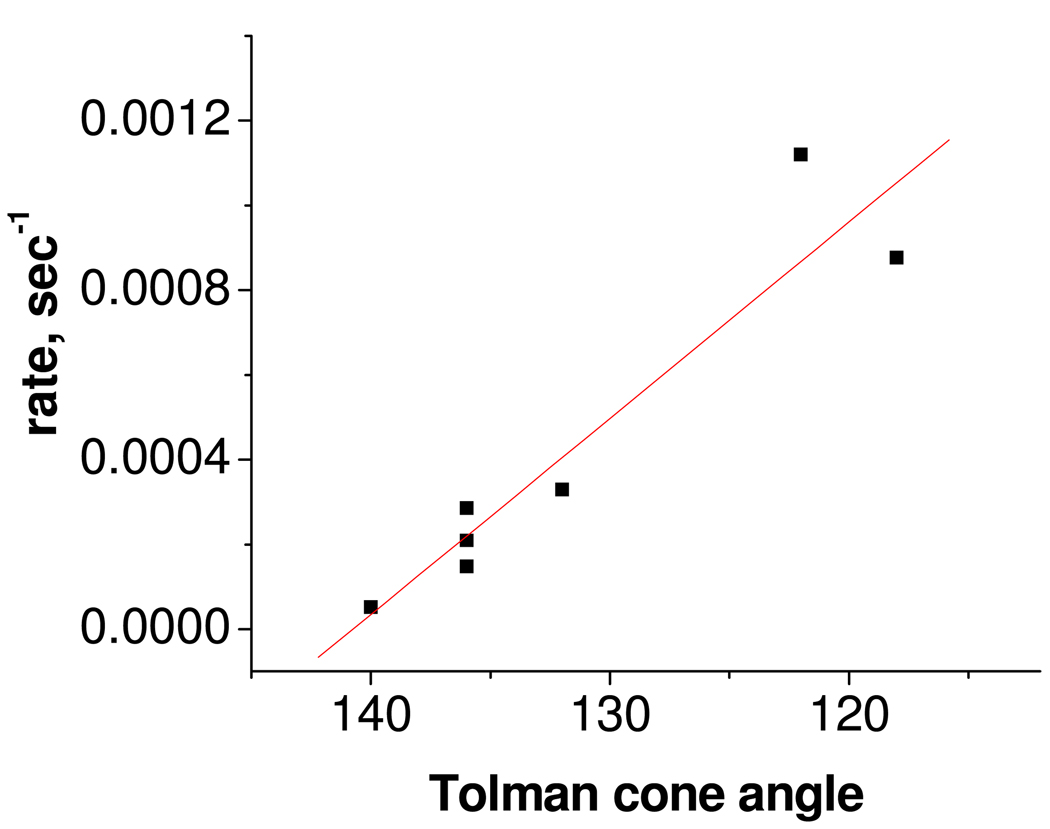
Conventionally, it is thought that the transition state is formed by direct nucleophilic attack of the phosphine on an empty Mo=O π* orbital of the metal complex. Thus, one would expect the reaction rate to be dependent on the nucleophilicity of phosphines, viz., the greater the nucleophilicity of the phosphine, the faster the reaction rate and vice versa. A good marker of the nucleophilicity of the phosphines is their pK_a’s. However, no linear correlation between the reaction rate and the pK_a of the phosphine was observed, implying that the nucleophilicity of the phosphine is not the dominant factor controlling reaction rate. In contrast, the reaction rate does depend on the steric bulk of the phosphine, increasing with decreasing phosphine cone angle as shown in Figure 1. The linear relation indicates that in sterically crowded Tp^iPr complexes, the steric bulk of the phosphines has an important influence on reaction rate, which is consistent with our ‘energy controlled pocket’ hypothesis.^{29, 34–36} Recently, we have suggested²⁸ a reciprocity in the nucleophilic attack of the phosphine to the terminal oxo-functionality, where the lone pair of the terminal oxo ligand attacks the antibonding orbitals of the phosphorus; this is also consistent with the current results.

Figure 1.

Correlation (R² =94%) between the rates of formation of the phosphoryl complexes with the phosphine cone angles.

We have previously investigated the mechanistic details of the solvolysis reaction (step 2),²⁸ however, the effect of the phosphine oxide on this reaction has not been assessed. In acetonitrile solution, the reaction is pseudo-first order, the rate being dependent only on the concentration of the complex. The solvolysis reaction follows a second order reaction. The enthalpic and entropic contributions to the solvolysis reaction (Table 4) also reflect leaving group dependence, a similar trend to that observed for the formation reaction. The enthalpic contribution remains the dominant factor in the overall free energy of activation. The entropy of activation shows a large variation from +69 to −126 J mol⁻¹ K⁻¹. A positive entropy of activation is indicative of a dissociative mechanism with a less crowded transition state, whereas a negative entropy of activation is indicative of an associative mechanism involving a more crowded transition state. It is important to consider that pure dissociative or associative reactions are two extreme cases, and many reactions can follow an intermediate type reaction mechanism, such as I_a (associative interchange) and I_d (dissociative interchange) type mechanisms. In the I_a and I_d-type mechanisms, true identification of the nature of the transition state becomes more complex as both mechanisms involve varying degrees of simultaneous bond making and breaking.^{42, 43} In this system, the solvolysis reactions appear to follow an I_d-type mechanism for the majority of the complexes, but follow an I_a-type mechanism in reactions involving 2a and 2g. Interestingly, despite the entropic variability, the free energy of activation varies by only ~ 9 kJ mol⁻¹.

Table 4.

Formation (k_f) and solvolysis (k_s) rate constants of complexes (2a–2g).

Complex	kf × 105 (sec−1) (Step 1)	ks × 105 (sec−1) (Step 2)	ks/kf
TpiPrMoO(OPh)(OPMe3), 2a	87.7	22.3	0.3
TpiPrMoO(OPh)(OPMe2Ph), 2b	112.1	179.6	1.6
TpiPrMoO(OPh)(OPEt3), 2c	32.8	228.5	6.9
TpiPrMoO(OPh)(OPEt2Ph), 2d	28.5	403.5	14.1
TpiPrMoO(OPh)(OPMePh2), 2f	14.8	1144.2	77.1
TpiPrMoO(OPh)(OPEtPh2), 2g	5.1	403.2	78.6

^ak_f and k_s relate to the formation and solvolysis reactions, respectively. All reaction rates were calculated for 298K from the activation parameters.

The reaction rates of steps 1 and 2 of these reactions are listed in Table 4. The rate of the reaction is dependent on the nature of the leaving group, i.e., the phosphoryl group. Thus, Table 4 shows that the rates of solvolysis of 2a and 2f differ by a factor of ~50. This leaving group dependence is most clearly reflected in the enthalpies of activation of the two steps, which favor formal loss of OPMe₃ by ~40 kJ mol⁻¹ (Table 3). More explicitly, the enthalpy of activation for leaving group, OPMe₃, is nearly half of that of the leaving group, OPMePh₂, which may reflect the bond strength of the two phosphoryl complexes. The activation barrier to the solvolysis of (2a–2g), expressed as ΔG_s^‡, shows a narrow range with an average ΔΔG_s^‡ of ~9 kJ mol⁻¹ at 298 K. At 298 K, the entropic term (TΔS^‡) contributes towards the free energy of activation accounting for approximately 11% of the total free energy in 2d and 40% of the total free energy in 2a. A pure dissociative mechanism would require a higher ΔH^‡, which is indicative of bond breaking, and in more associative mechanism the transition state is more stabilized and hence a lower HΔ^‡ is expected.

The identification of the rate-limiting step in these OAT reactions is a significant outcome of the present study. Although the seven substrates employed are similar in their geometry about the central phosphorus atom, PBuⁿ₃ and PEt₃ are expected to have a higher degree of conformational flexibility. On the other hand, PMePh₂ and PEtPh₂ have a lower basicity due to the electron withdrawing effects of the phenyl rings. However, the latter phosphines are more sterically encumbered, which should result in a higher enthalpic contribution and a diminished rate of reaction. These two competing factors determine the overall reaction profiles. The ratio of the reaction rates for different substrates, as shown in Table 4, serves as a good indicator of the rate-limiting step. In most cases, the release of the phosphine oxide is the faster process, thus nucleophilic attack by the phosphine (step 1) becomes rate limiting. However, in the case of PMe₃, the rate of formation of the phosphoryl complex is the faster process thus, solvolysis becomes rate limiting. Therefore, by changing the substrate slightly one can indeed alter the nature of the rate-limiting step in the overall process.

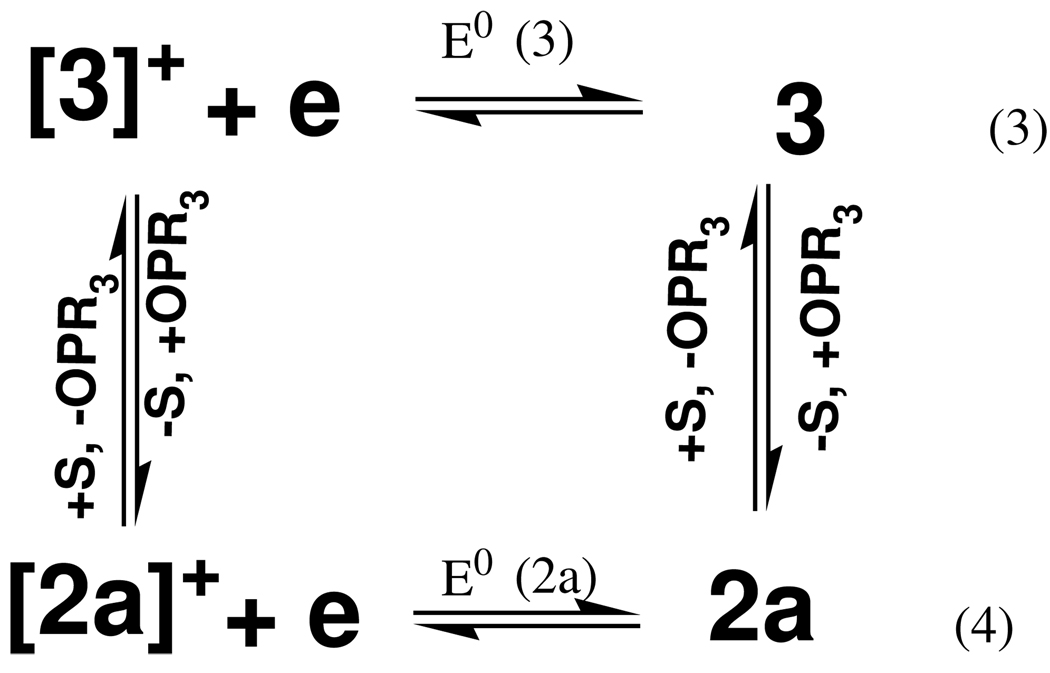
With the electrochemical data for the phosphoryl and acetonitrile complexes in hand, thermodynamic square schemes describing the reaction can be constructed.⁴⁷ One such scheme is shown in Scheme II, where the redox processes are defined by eqns 3 and 4 (the horizonal components of the Scheme). The two vertical equilibrium processes describe the exchange of phosphine oxide (OPMe₃) and acetonitrile (S) ligands. The equilibrium on the left is for (oxidized) Mo(V) complexes, while that on the right is for (reduced) Mo(IV) complexes. In the Mo(IV) system, the equilibrium lies towards the solvent-coordinated species. The free energy

$${[3]}^{+}+2\mathrm{a}\rightleftharpoons 3+{[2\mathrm{a}]}^{+}$$ (5)

difference for the OPMe₃ system has been calculated to be 0.40 kJ mol⁻¹ in favor of the solvated complex 3 (with release of OPMe₃).²⁸ This free energy leads to an equilibrium constant for the solvolysis of the oxo-Mo(IV) phosphoryl complex (K^IV) of 1.2. The corresponding equilibrium constant for the Mo(V) state can be calculated considering the redox cross reaction as shown in eqn 5. The equilibrium constant for this reaction K^cr = K^IV/K^V = exp [(F/RT)(E⁰(3)-E⁰(2a))] = 6.4 × 10⁵. From this one calculates the equilibrium constant for the solvolysis of the oxo-Mo(V) phosphoryl complex (K^V) as 1.9 × 10⁻⁶. This implies that in the Mo(V) system, the phosphoryl complex is considerably more stable thermodynamically than the acetonitrile complex. The higher stability of the phosphoryl-Mo(V) complex could arise from a number of factors. Firstly, occupation of the potentially π* O–P orbitals in the two-electron reduced Mo(IV) form would lead to a weakening of the Mo–O bond. Secondly, oxidation to Mo(V) would increase the effective nuclear charge of the metal center, leading to stabilization by the phosphoryl oxygen. This stabilization would derive from the ability of the phosphoryl ligand to adopt canonical forms that lead to a partial negative charge on oxygen. Ongoing investigations in our laboratory will further investigate these aspects.

Scheme II.

Themodynamic differentiation of ligand binding as a function of metal oxidation state is fundamental to metalloenzyme behavior and function. In the case of sulfite oxidase, the enzyme is inhibited by phosphate.⁴⁸ In principle, phosphate can bind to either the Mo(IV) or Mo(V) states of sulfite oxidase. However, only an EPR-active Mo(V) form has been detected.^49–51 The results reported here support the view that phosphate binding to Mo(V) is thermodynamically favored over binding to the Mo(IV) state and that the EPR-active species is responsible for the inhibition of the enzyme. Whether the phosphate-bound Mo(V) form of the enzyme can be converted to a catalytically competent enzyme by reduction to Mo(IV) and subsequent displacement of “inhibitor” phosphate is yet to be experimentally established but would be predicted on the basis of the results reported herein.

Summary

The kinetic and mechanistic details of the OAT reactions between Tp^iPrMoO₂(OPh) and a variety of tertiary phosphines have been investigated. The reactions occur in two steps, the first being the formation of an oxo-Mo(IV) phosphoryl intermediate, the second being solvolysis of the phosphoryl intermediate. As shown previously,^{28, 31} the first step is bimolecular and involves an associative transition state. However, the mechanism of second step is dependent on the phosphine. In the majority of cases, a dissociative mechanism is favored; however, in two cases, an associative transition state is indicated by the negative entropy of activation. Under the two step model, the rate-limiting step is generally the first nucleophilic attack of the phosphine on the dioxo-Mo(VI) complex. However, this is not the situation in reactions involving PMe₃. Thus, the choice of substrate can make a difference to the rate-limiting step as well as dictating the mechanism of the reaction. The reaction rate follows a linear correlation with the phosphine cone angle suggesting steric influences play a significant role in this system. Calculation of the equilibrium constant for the solvolysis of the Mo(V) cation, [Tp^iPrMoO(OPh)(OPMe₃)]⁺, using the square diagram in Scheme II, indicates that the phosphoryl-Mo(V) complex is more stable than the related acetonitrile complex, a result in stark contrast to the situation in the analogous Mo(IV) complexes.