Geodesic Shooting for Computational Anatomy

Abstract

Studying large deformations with a Riemannian approach has been an efficient point of view to generate metrics between deformable objects, and to provide accurate, non ambiguous and smooth matchings between images. In this paper, we study the geodesics of such large deformation diffeomorphisms, and more precisely, introduce a fundamental property that they satisfy, namely the conservation of momentum. This property allows us to generate and store complex deformations with the help of one initial “momentum” which serves as the initial state of a differential equation in the group of diffeomorphisms. Moreover, it is shown that this momentum can be also used for describing a deformation of given visual structures, like points, contours or images, and that, it has the same dimension as the described object, as a consequence of the normal momentum constraint we introduce.

1. Introduction

Over the past several years we have been studying natural shapes using homogeneous orbits of imagery constructed via the action of transformation groups on exemplars or templates. The mathematical structure of group action as a model in image analysis has been pioneered by Grenander [13], the idea being to introduce the group actions in the very nature of the objects themselves, through the notion of deformable templates. Roughly speaking, a deformable template simply is an “object or exemplar” I_temp on which a group G acts and generates, through the orbit 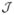= G · I_temp, a whole family of new objects. The interest of this approach is to concentrate the modeling effort on the group G, and not on the family of objects .

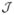Since the earliest introduction by Silicon Graphics Incorporated of special purpose graphics hardware for object rendering, group action as a model in image analysis has been the subject of a wide range of research in computer vision. Naturally, the analytical and computational properties of the low-dimensional matrix Lie groups form the core dogma of modern Computer graphics. In sharp contrast, however, for the study of imagery generated from natural or biological shapes, the finite dimensional matrix groups are replaced by their infinite dimensional analogue, the more general diffeomorphisms [7, 11, 16, 22, 23, 36].

The anatomical orbit or deformable template is made into a metric space with a metric distance between elements by constructing curves through the space of diffeomorphisms connecting them; the length of the curve becomes the basis for the construction, the metric distance corresponding to the geodesic shortest length curves. This gives rise to a natural variational problem describing the geodesic flows between elements in the orbit, with the solution of the associated Euler-Lagrange equations giving the optimal flow of diffeomorphisms and thus the metric between the shapes. The obtained setting shares several similarities with the mechanics of perfect fluids, for which the Euler-Lagrange equation has been derived by Arnold (Eq. (1) of [2]) for the group of divergence-free volume-preserving diffeomorphisms. As well these results become another example of the general Euler-Poincaré principle of [19] applied to an infinite dimensional setting.

Interestingly, as emphasized by Arnold [1] in his study, one of the most beautiful aspects of studying diffeomorphisms with a Lie group point of view is that many fundamental aspects which can be proved in the finite dimensional case can be formally extended to retrieve well-known equations of mechanics. One of the purposes of this paper is to develop infinite dimensional analogues, for the study of high dimensional shapes via diffeomorphisms, of several of the well known properties of Lie groups in rigid body mechanics. In particular we shall focus on the interpretation of the Euler equation as an expression of the evolution of the generalized momentum of diffeomorphoc flow of least energy in both Eulerian and Lagrangian coordinates.

Such a point of view will link our geodesic formulation to a conservation of momentum law in Lagrangian coordinates providing a powerful method for studying and modeling diffeomorphic evolution of shape. It will imply that the momentum of the diffeomorphic flow at any place along the geodesic can be generated from the momentum at the origin, thus providing the vehicle for geodesic generation via shooting.

This same conservation of momentum of the diffeomorphic flow, allows us to derive equations for the geodesic evolution of the elements in the orbit $I_t=I\circ {\phi }_t^{-1}$, t ∈ [0, 1], I ∈ 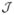. This unifies various geodesic evolutions associated with orbits of sparse finite dimensional landmarked shapes as well as the evolutions of dense images. Of special interest is the fact that for the special case of image matching, geodesic evolution of elements in the orbit links us to the notion of normal motion familiar to the rapidly growing community working in level set methods. Interestingly, as we show, the momentum of the diffeomorphic flow is normal to the level sets associated with geodesic motion. By solving the partial differential equations which are associated with the conservation of momentum, we will be able to control by specifying the initial conditions (within a specific class of momentum which depends on the considered imaging problem) a wide range of arbitrarily large deformations; this provides new possibilities for learning shape models of deformable templates, or for designing new numerical matching procedures.

This second point of view in terms of the conservation of momentum law also sheds new light on a large number of high dimensional evolution based Active Model Methods in Computer Vision, including active snakes and contours [6, 12, 18, 20, 29, 31, 37, 40, 41, 43], active surfaces and deformable models [8, 9, 21, 24, 25, 28, 30, 33, 39, 40, 42]. In such approaches vector fields are defined which give the boundary manifold of the shape some velocity of motion, usually following the gradient of an energy to form an attractive force to pull the boundary. The power of such methods is that they parameterize motion only associated with a submanifold of the imagery, not the entire extrinsic background space. For example, to deform a planar simply connected shape via an active contour method, the dimension of the motion is determined by the dimension of the boundary of the region, which is substantially less than the dimension of the plane. Historically such approaches have not been studied globally as diffeomorphic action. In fact it is well known that such methods cannot prevent self intersection nor ensure topological consistency, for which the addition of other constraints become necessary [14, 15]. From the conservation law in Lagrangian coordinates describing geodesic motion in the metric space of diffeomorphic action, we introduce the normal momentum motion which constrains the momentum to the bounding manifold, and extends the velocity of motion of the shape to the entire background space, thereby giving the global property that the resulting integrated vector field generates a diffeomorphism on the entire extrinsic space. This in turn carries the smooth submanifold diffeomorphically. As the analysis shows, this global property seems to be required to generate geodesic motions.

2. The Basic Set Up

2.1. Right Invariant Metric on Group of Diffeomorphisms

The basic component of our models is the group of one-to-one, smooth, transformations (diffeomorphisms) of a bounded subset Ω ⊂ ℝ^d. In this paper, we consider diffeomorphisms emerging as flows of non-autonomous differential equations. A time dependent vector field on Ω is a function:

$$\begin{array}{r}v:[0,1]\times \mathrm{\Omega }\to {\mathbb{R}}^d\\ (t,x)\mapsto v(t,x)\end{array}$$

(v(t, x) will also be denoted v_t(x)). The associated ordinary differential equation is

$$\frac{dy}{dt}=v_t(y).$$

The flow of this ODE is a function φ^v which depends on time and space, such that

$$\frac{\partial {\phi }^v}{\partial t}(t,x)=v_t\left({\phi }_t^v(x)\right)$$

and φ(0, x) = x for all x ∈ Ω. We will also use the notation ${\phi }_t^v(x)$ for φ(t, x) and

$${\phi }_s^{v-1}={\phi }_t^v\circ {\phi }_s^{v-1}.$$ (1)

It is well-known that, under some smoothness conditions on v, such ${\phi }_t^v$ is at all times a diffeomorphism of Ω.

The groups that we consider are precisely composed with such flows ${\phi }_1^v$ for v belonging to a specified functional class. More precisely, we assume that a Hilbert space ℊ is given, the element of which being smooth enough vector fields on Ω, and denote the norm and inner product on this space by || ||_ℊ, 〈,〉_ℊ. We now define (following [35]) the group G as the set of functions ${\phi }_1^v$ for time-dependent vector fields v satisfying

$${\int }_0^1{\left|\right|v_t\left|\right|}_{\text{g}}dt<\infty ,$$

i.e. for v belonging to L¹([0, 1], ℊ). We will always assume that ℊ can be embedded in the space of ( $C_0^1(\mathrm{\Omega },{\mathbb{R}}^d)$, || ||_{1, ∞}), containing vector fields on Ω, which vanish on ∂Ω, where

$${\left|\right|w\left|\right|}_{1,\infty }={\left|\right|w\left|\right|}_{\infty }+{\left|\right|dw\left|\right|}_{\infty }.$$

From this definition, it appears that the main ingredient in the construction of G is the Hilbert space ℊ.

Fixing v ∈ ℊ, one can define the linear form w ↦ 〈v, w〉_g, which will be denoted Lv. We therefore have the identity

$$(Lv,w)\doteq {\langle v,w\rangle }_{\text{g}}$$

(we use the standard notation (M, w) for the linear form M applied to w). By definition, Lv belongs to the dual, ℊ^* of ℊ, and L can be seen as an operator L: ℊ → ℊ^* (this is the canonical duality operator of ℊ on its dual). As we shall see, this operator turns out to be a key feature in our analysis. For the moment, we point out the fact that Lv is a linear form on ℊ which is a space of smooth vector fields. Therefore, Lv itself can be a singular object (a generalized function, or a distribution). Here are a few examples of distributions M which qualify as elements of ℊ^*, under our running assumption that ℊ is embedded in the space of C¹ functions:

1. L¹ vector fields of Ω: if ψ: Ω ↦ ℝ^d is integrable, define

   $$(M,v)={\int }_{\mathrm{\Omega }}{\langle \psi (x),v(x)\rangle }_{{\mathbb{R}}^d}dx$$

2. Let now μ be any measure on Ω, and ψ be μ integrable. Define

   $$(M,v)={\int }_{\mathrm{\Omega }}{\langle \psi (x),v(x)\rangle }_{{\mathbb{R}}^d}d\mu (x)$$

3. Dirac measures: as a particular case of the previous, define, for x ∈ Ω and a ∈ ℝ^d,

   $$(M,v)={\langle a,v(x)\rangle }_{{\mathbb{R}}^d}$$

   This will be denoted $M={\delta }_x^{\ast }(a)\in {\text{g}}^{\ast }$.

4. Differential operators: if (f_{i, j}, 1 ≤ i, j ≤ d) are integrable functions, define

   $$(M,v)=\sum _{i,j=1}^d{\int }_{\mathrm{\Omega }}{f}_{ij}\frac{\partial v_i}{\partial x_j}dx$$

It is important to notice that, although L is defined in a rather abstract way in the previous lines, numerical procedures to compute geodesics can be derived most of the time from the knowledge of its inverse (of Green kernel) K = L⁻¹. This K is a smoothing kernel, the choice of which, within a specific range of available kernels, being the starting point of any practical procedure. We do not detail numerical algorithms in this paper, but the reader can refer to [4, 5, 17, 23] for examples of choices of K.

2.2. Energy and Momenta

Consider a time-dependent diffeomorphism v ∈ L¹([0, 1], ℊ), and let ( ${\phi }_{0t}^v$, t ∈ [0, 1]) be the associated flow, defined in the previous section. Along time, each point x ∈ Ω, considered as a particle, evolves on the trajectory $t\mapsto {\phi }_{0t}^v(x)$, its velocity at time t being by definition $v_t({\phi }_{0t}^v(x))$. In other terms, for y ∈ Ω, v_t(y) is the instantaneous velocity of the particle which is at y at time t. It is called the Eulerian velocity at y at time t.

So, at each time, we have an Eulerian velocity field, y ↦ v_t(y), and we define the kinetic energy of the system to be $E(v_t)=\frac{1}{2}{\left|\right|v_t\left|\right|}_{\text{g}}^2$. The total energy spent during the deformation path now is

$$E_{\text{total}}(v)=\frac{1}{2}{\int }_0^1{\left|\right|v_t\left|\right|}_{\text{g}}^{2}dt.$$

Note that, in classical fluid mechanics, the kinetic energy is the sum of particle kinetic energies, which, for a homogeneous fluid with mass density given by ρ yields

$${\left|\right|v_t\left|\right|}^2=\frac{\rho }{2}{\int }_{\mathrm{\Omega }}\mid v_t(y){\mid }^{2}dy.$$

This is the L² norm of v, which cannot be used in our context, since we require that ℊ is embedded in $C_0^1$ (we need some kind of Sobolev norms). However, in analogy with standard mechanical systems, we may define the global momentum of the system at time t to be the linear form M_t ∈ ℊ^* such that E(v_t) = (M_t, v_t)/2, which, with the notation of the previous section, yields.

$$M_t=L{v}_t.$$

So, if v_t is the Eulerian velocity field at time t, the momentum at time t is given by Lv_t. It will be called the momentum in Eulerian coordinates.

2.3. Lagrangian and Eulerian Frames

The Eulerian frame, as introduced above, describes mechanical quantities as they are observed in the current configuration at each time. The Lagrangian frame, on the contrary, describes quantities as seen from the initial configuration. For example, the diffeomorphism ${\phi }_{0t}^v(x)$ provides the position at time t of the particle which was at x at time 0, which is a Lagrangian notion. For the velocity, we create a Lagrangian velocity field by pulling back the previously defined velocity v_t, setting

$$\begin{array}{l}{v}_t^l(x)=\frac{d}{ds}{\left({\phi }_t^{-1}({\phi }_{t+s}(x))\right)}_{\mid s=0},\\ \text{i}.\text{e}.v_t^l={(d{\phi }_t)}^{-1}(v_t\circ {\phi }_t).\end{array}$$

The operation

$$v\mapsto (d\phi )v\circ {\phi }^{-1}$$

defines a fundamental Lie group operation, and is called the adjoint action of G on its Lie algebra (which here is ℊ), denoted Ad_φv. We have obtained the relation

$$v_t=A{d}_{{\phi }_t}{v}_t^l.$$

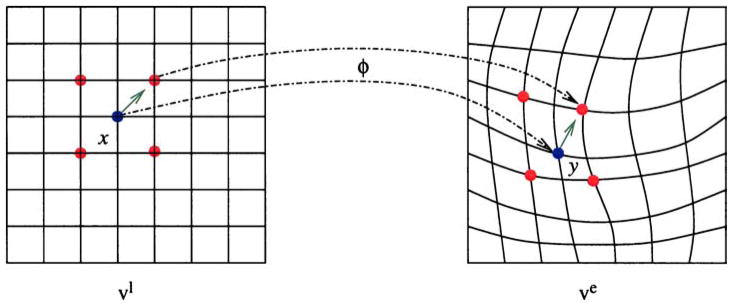
To interpret the adjoint action pictorially, the new vector field under the adjoint action v → (dφ)v ◦ φ⁻¹ has to be interpreted as the transformation of v under the deformation generated by φ. Figure 1 shows how the field v^l at location x is transported by the flow to the value v(y) at location y = φ(x) by pushing forward (using φ) the Lagrangian frame on which v^l is drawn. Note that the orientation of the vector v(x) drawn on the deformed sheet is also changed (through the action of (dφ)).

Figure 1.

Here is represented the deformation obtained by pulling back the Eulerian frame associated with v^e and represents pictorially the adjoint action.

2.4. Momentum in Eulerian and Lagrangian Coordinates

The momentum M_t = Lv_t, which has been defined in Eulerian coordinates, also admits a Lagrangian version. It can be computed by expressing the kinetic energy at time t, which is (Lv_t, v_t)/2, under the form $(M_t^l,v_t^l)/2,M_t^l$, being then the Lagrangian momentum. This is straightforward, since, by definition of an adjoint operator:

$$(L{v}_t,v_t)=(L{v}_t,A{d}_{{\phi }_t}{v}_t^l)=(A{d}_{{\phi }_t}^{\ast }L{v}_t,v_t^l).$$

This leads to the definition $M_t^l=A{d}_{{\phi }_t}^{\ast }L{v}_t$ for the momentum in Lagrangian coordinates. The Lagrangian frame takes here the role of a Galilean, or reference frame, and we will retrieve below the fundamental principle of mechanics, which states that the Lagrangian momentum is constant over time along any energy minimizing path. Before this, we make a brief interuption in our discussion to describe the relation between the classical mechanics of a rigid body, and geodesic equation in matrix Lie groups. This simple description will help to understand the formalism in our infinite dimensional group of diffeomorphisms.

3. Euler Equation and Conservation of the Momentum for Lie Groups of Matrices

In this part, we derive the Euler equation for extremal paths of the kinetic energy in the case of Lie groups of matrices. This derivation is well-known in the context of classical solid mechanics [1], but this simpler case, which can be derived completly without too much technicalities, may be helpful to understand the case of diffeomorphisms.

Let G ⊂ ℳ_d(ℝ) be a Lie group of d × d matrices with Lie algebra ℊ. The case of interest is when G is a group of 3D rotations, which models the position of a rigid body with fixed center of mass. In this case, ℊ is the vector space of antisymmetric 3 × 3 matrices. Let t ↦ g_t be a trajectory in this group. Then, the angular velocity a_t ∈ ℊ is given by the equation $\frac{d{g}_t}{dt}=g_t{a}_t$. This is to be related to our previous definition of Eulerian velocity, which was

$$\frac{d{\phi }_t}{dt}=v_t\circ {\phi }_t$$

in which the (left) product of matrices is replaced by the (right) composition of functions.

Returning to the matrix case, we define the kinetic energy at time t to be (Ja_t, a_t)/2, for some symmetric positive definite operator J: ℊ → ℊ^*. In the case of the rigid body, the angular velocity can be identified to a 3-vector ω_t, and J can be seen as a 3 × 3 matrix which only depends on the geometry of the object, called the inertia operator and, with some abuse of notation,

$$(J{a}_t,a_t)=(J{\omega }_t,{\omega }_t).$$

(note that here the notation (,) refers to the sum of products of coordinates, i.e. the usual inner product on Euclidean spaces, after identification between ℊ and ℊ^*). The total energy is

$$E(g)=\frac{1}{2}{\int }_0^1(J{a}_t,a_t)dt.$$

We retrieve again the analogy with the diffeomorphisms by letting

$${\langle a,b\rangle }_{\text{g}}=(Ja,b)$$

so that J takes the role of L in the previous section.

We now compute the Euler equation for least energy paths between two fixed endpoints g₀ and g₁. We recall that the Lie bracket on ℊ is [a, b] = ab − ba.

Theorem 1

The Euler-Lagrange equation for the kinetic energy is given by

$$\frac{\partial Ja}{\partial t}-a{d}_a^{\ast }(Ja)=0.$$ (2)

where $a{d}_a^{\ast }:{\text{g}}^{\ast }\to {\text{g}}^{\ast }$ is defined by duality through the equalities $(a{d}_a^{\ast }f,b)=(f,a{d}_{a}b)=(f,[a,b])$.

Proof

Let (t ↦ g₀(t)) be an extremal curve for the kinetic energy and ((t, h) ↦ g(t, h)) be a smooth deformation around h = 0 (g(t, 0) = g₀(t)): Let a(t, h) and A(t, h) be such that

$$\frac{\partial g}{\partial t}=ga\text{and}\frac{\partial g}{\partial h}=gA.$$ (3)

Writing $\frac{{\partial }^{2}g}{\partial t\partial h}=\frac{{\partial }^{2}g}{\partial h\partial t}$, we get $\mathit{gAa}+g\frac{\partial a}{\partial h}=\mathit{gaA}+g\frac{\partial A}{\partial t}$ i.e.

$$\frac{\partial a}{\partial h}=\frac{\partial A}{\partial t}+[a,A]=\frac{\partial A}{\partial t}+{\text{ad}}_{a}A.$$ (4)

The curve A(t, h) can vary freely in ℊ, with boundary conditions A(0, h) = A(1, h) = 0. From

$$\frac{d}{dh}{\left(\int {\langle a,a\rangle }_{\text{g}}dt\right)}_{\mid h=0},$$

we get

$$\int {\langle a,\frac{\partial A}{\partial t}+a{d}_{a}A\rangle }_{\text{g}}dt=\int \left(Ja,\frac{\partial A}{\partial t}+{\text{ad}}_{a}A\right)dt=0$$ (5)

Using the duality relation, we get $(Ja,{\text{ad}}_{a}A)=({\text{ad}}_a^{\ast }(Ja),A)$ so that by integration by part, we finally obtain the Euler equation

$$\frac{\partial Ja}{\partial t}-{\text{ad}}_a^{\ast }(Ja)=0.$$ (6)

We know from Lagrangian mechanics that the motion of a body with inertial operator J without external forces are extremal paths of the kinetic energy. Hence, Eq. (6) is the evolution equation of a body. We recognize in this equation the momentum to the body $M_t^b\doteq J{a}_t$ and the Euler equation is then:

$$\frac{\partial M^b}{\partial t}-{\text{ad}}_a^{\ast }(M^b)=0.$$ (7)

The momentum in the body here is to relate to the momentum in Eulerian coordinates for diffeomorphisms. However, if we study the motion of the body in a fixed static reference frame, the momentum to the space denoted here M^s should remain constant in the absence of external forces. The momentum to the space is defined from M^b_t by a change of reference frame:

$$M_t^b\doteq A{d}_{g_t^{-1}}^{\ast }(M_t^b)$$ (8)

where ${\text{Ad}}_g^{\ast }$ is the co-adjoint representation which is defined by duality through the equalities: ${\text{(Ad}}_g^{\ast }f,b)=(f,{\text{Ad}}_{g}b)=(f,gb{g}^{-1})$. We derive from the evolution equation for M^b, given by the Euler equation (7), the conservation of the momentum to the space M^s:

Theorem 2

Along extremal curves for the kinetic energy, M^s is constant:

$$\frac{d{M}^s}{dt}=0.$$ (9)

Proof

Indeed, we have

$$\left(\frac{d{M}_t^s}{dt},b\right)=\frac{d}{dt}(M_t^s,b)=\frac{d}{dt}(J{a}_t,{\text{Ad}}_{g_t^{-1}}b)$$

Since, $\frac{d}{dt}({\text{Ad}}_{g_t^{-1}})=-{\text{ad}}_{a_t}{\text{Ad}}_{g_t^{-1}}$, we get finally using Euler Eq. (6),

$$\begin{array}{l}\left(\frac{d{M}_t^s}{dt},b\right)=\left(\frac{\partial Ja}{\partial t}-{\text{ad}}_a^{\ast }(Ja),{\text{Ad}}_{g_t^{-1}}b\right)\\ =0.\end{array}$$ (10)

Thus, from the conservation of the momentum to the space, $M_t^s\equiv M_0^s$, we deduce that

$$J{a}_t={\text{Ad}}_{g_t}^{\ast }(L{a}_0),$$ (11)

or equivalenty, for any b ∈ ℊ:

$$(J{a}_t,b)=(J{a}_0,{\text{Ad}}_{g_t}b)$$ (12)

These results are in fact true for any Lie-group with a left-invariant metric. As we now investigate, they can be formally extrapolated also for infinite dimensional groups of diffeomorphisms.

4. Geodesic Evolution of the Diffeomorphism and Conservation of Momentum

4.1. Euler Equation as Evolution Equation for the Momentum in Eulerian Coordinates

The derivation of the Euler equation for extremal paths of the kinetic energy in the case of finite-dimensional Lie groups can be carried out in full generality within the Lie theory framework, to lead to the law of conservation of momentum. A general computation can be found in [1]. In our infinite dimensional case, a rigorous derivation of this law is much harder, and must most of the time be obtained directly from variational and functional analysis arguments rather than with purely algebraic Lie group derivations. However, it is interesting, and quite informative, to use these derivations to obtain a formal proof of the conservation of momentum, without wondering too much about the well-posedness of the expressions. This will be done in the next paragraphs.

The first Euler equation provides the variations of the momentum in Eulerian coordinates. Before stating it, we need some definitions:

Definition 1

The adjoint action Ad of G on ℊ and the associated adjoint action ad of ℊ on itself are given with their dual operators Ad^*, ad^* by

$$\begin{array}{l}{\text{Ad}}_{\phi }w=(d\phi )w\circ {\phi }^{-1},\\ ({\text{Ad}}_{\phi }^{\ast }f,w)=(f,{\text{Ad}}_{\phi }w)\end{array}$$ (13)

$$\begin{array}{l}{\text{ad}}_{v}w=[v,w]=(dv)w-(dw)v,\\ ({\text{ad}}_v^{\ast }f,w)=(f,{\text{ad}}_{v}w).\end{array}$$ (14)

with φ ∈ G, w ∈ ℊ, f ∈ ℊ^*.

Already at this point, one can point out the difficulty of the infinite dimensional problem: at the difference with the matrix case, if v, w belong to ℊ, it cannot be guaranteed that it is still so for [w, v] = (dw)v − (dv)w: in situations of interest, ℊ is, in fact, not a Lie algebra: Ad_φw and ad_vw do not necessarily belong to ℊ. As a consequence, the definition of ${\text{ad}}_v^{\ast }f$ which has been given cannot hold without some restriction on f, in order to be able to extend it to vector fields which are brackets of elements of ℊ. We however proceed with such formal computation without addressing these issues.

The geodesics are extremal curves for the kinetic energy. They satisfy an Euler equation giving the variation of the momentum in terms of the co-adjoint action operator on the momentum.

Statement 1

The Euler equation for the kinetic energy is given by

$$\frac{\mathit{dLv}}{dt}+a{d}_v^{\ast }(Lv)=0.$$ (15)

When Lv ∈ H (i.e. it is a function), one has

$${\text{ad}}_v^{\ast }Lv=\text{div}(Lv\otimes v)+d{v}^{\ast }Lv.$$ (16)

where div(u ⊗ v) = duv + div(v)u.

These equations, which are derived below, are special cases of the Euler-Poincaré principle, described, for example in [19]. Equation (15) is formally identical to Eq. (2) in the matrix case, excepted for a sign difference arising from the switch from a left-invariance in the matrix case to a right-invariance in the diffeomorphism case.

Formal Justification

This is exactly as in the matrix case. Here again, let (t ↦ φ_t) be extremal and ((t, ε) ↦ φ_t,ε) be a smooth deformation around ε = 0, with the abuse of notation φ_t,0 = φ_t. Denote $\frac{\partial {\phi }_{t,\epsilon }}{\partial t}=v_{t,\epsilon }\circ {\phi }_{t,\epsilon },\frac{\partial {\phi }_{t,\epsilon }}{\partial \epsilon }={\eta }_{t,\epsilon }\circ {\phi }_{t,\epsilon },\frac{\partial v_{t,\epsilon }}{\partial \epsilon }=h_{t,\epsilon }$, still denoting v_t,0 = v_t, η_t,0 = η_t and h_t,0 = h_t. Our first step is to express h_t in function of the other variables. For this, write

$$\frac{{\partial }^2\phi }{\partial \epsilon \partial t}=\frac{{\partial }^2\phi }{\partial t\partial \epsilon }$$

which yields

$$h_t\circ {\phi }_t+d_{{\phi }_t}{v}_t{\eta }_t\circ {\phi }_t=\frac{\partial {\eta }_t}{\partial t}\circ {\phi }_t+d_{\phi t}{\eta }_t{v}_t\circ {\phi }_t$$

or (applying ${\phi }_t^{-1}$ on the right to both terms) gives

$$h_t=\frac{\partial {\eta }_t}{\partial t}+d{\eta }_t{v}_t-d{v}_t{\eta }_t=\frac{\partial {\eta }_t}{\partial t}+[{\eta }_t,v_t].$$

The¹ first variation of the energy is given by

$$\begin{array}{l}\frac{d}{d\epsilon }{\int }_0^1{\left|\right|v_{t,\epsilon }\left|\right|}_{\text{g}}^{2}dt\\ =2{\int }_0^1{\langle v_t,h_t\rangle }_{\text{g}}dt\\ ={\int }_0^1{\langle v_t,\frac{d{\eta }_t}{dt}+[{\eta }_t,v_t]\rangle }_{\text{g}}dt\\ ={\int }_0^1\left(L{v}_t,\frac{d{\eta }_t}{dt}\right)dt-{\int }_0^1(L{v}_t,a{d}_{v_t}{\eta }_t)dt.\end{array}$$

Since φ_t is extremal, this expression vanishes for all η (with η₀ = η₁ = 0), and a last integration by parts yields

$$\frac{dL{v}_t}{dt}+a{d}_{v_t}^{\ast }L{v}_t=0,$$

which is Eq. (15).

We now prove Eq. (16) under the assumption that Lv is a function. By definition

$$\begin{array}{l}(a{d}_v^{\ast }Lv,w)=(Lv,\mathit{dvw}-\mathit{dwv})\\ =(d{v}^{\ast }Lv,w)-(Lv,\mathit{dwv})\end{array}$$

and the conclusion comes from Stokes’ theorem which states that (since v and w vanish on ∂Ω)

$$(\text{div}(Lv\otimes v),w)=-(Lv,dw.v).$$

It appears that the Euler equation (15) with ${\text{ad}}_v^{\ast }Lv=\text{div}\mathit{vLv}+d{v}^{\ast }Lv$ has been derived in [26] and subsequently [22] directly as the Euler-Lagrange equation for the kinetic energy by analytical means. This has been originally proved by Arnold in [3] for the motion of impressible fluid which corresponds to the case L = Id with the constraint div v = 0.

4.2. Conservation of Momentum in Lagrangian Coordinates

The Euler equation (15) is the evolution of the momentum in Eulerian coordinates. We recognize in this equation the momentum M_t ≐ Lv_t; the momentum in Eulerian coordinates evolves in time so as to balance the co-adjoint of the momentum thereby satisfying the associated Euler equation $\frac{d{M}_t}{dt}+a{d}_{v_t}^{\ast }(M_t)=0$ for extremal paths. However, the momentum in Lagrangian coordinates, identified in the introduction as $M_t^l={\text{Ad}}_{{\phi }_t}^{\ast }(M_t)$, remains constant in the absence of external forces, $\frac{d}{dt}{M}_t^l=0$.

Statement 2

Along extremal curves for the kinetic energy, $M_t^l$ is constant:

$$\frac{d{M}_t^l}{dt}=0.$$ (17)

In particular, we have for all w ∈ ℊ,

$$(L{v}_t,w)=(L{v}_0,{(d{\phi }_t)}^{-1}w\circ {\phi }_t).$$ (18)

Formal Derivation

Indeed, fix w ∈ ℊ and let $f(\epsilon )=(M_{t+\epsilon }^l,w)$. We have, on the first hand $f^{\prime }(0)=(\frac{d{M}_t^l}{dt},w)$, and on the second hand (derivatives being evaluated at time ε = 0)

$$\begin{array}{l}{f}^{\prime }(0)=\frac{d}{d\epsilon }(L{v}_{t+\epsilon },{\text{Ad}}_{{\phi }_{t+\epsilon }}w)\\ =\left(\frac{dL{v}_t}{dt},{\text{Ad}}_{{\phi }_t}w\right)+\left(L{v}_t,\frac{d}{d\epsilon }A{d}_{{\phi }_{t+\epsilon }}w\right)\end{array}$$

Note here that Ad_φ◦φ′= Ad_φ Ad_φ′. Now, if φ₀ = id and $\frac{d{\phi }_{\epsilon }}{d_{\epsilon }}=v$ at ε = 0, we have for any w′,

$$\begin{array}{l}\frac{d}{d\epsilon }({\text{Ad}}_{{\phi }_{\epsilon }}{w}^{\prime }){\mid }_{\epsilon =0}=\frac{d}{d\epsilon }\left((d{\phi }_{\epsilon })w^{\prime }\circ {\phi }_{\epsilon }^{-1}\right){\mid }_{\epsilon =0}\\ =dv(w^{\prime })-d{w}^{\prime }(v)=a{d}_v{w}^{\prime }.\end{array}$$ (19)

Applying this to w′ = Ad_φt−1 and v = v_t, we get

$$\begin{array}{l}{f}^{\prime }(0)=\left(\frac{dL{v}_t}{dt},{\text{Ad}}_{{\phi }_t}w\right)+(L{v}_t,a{d}_{v_t}A{d}_{{\phi }_t}w)\\ =\left(\frac{dL{v}_t}{dt}+a{d}_{v_t}^{\ast },A{d}_{{\phi }_t}w\right)=0\end{array}$$

by Eq. (15). This completes the proof,

$$\left(\frac{d{M}_t^l}{dt},w\right)=0.$$

Although the conservation of momentum has only been derived from formal arguments, we can check that, when it is satisfied, the generated deformation paths do provide extremal curves of the kinetic energy. The perturbation of the end point of the path ( ${\phi }_{0t}^v$, t ∈ [0, 1]) at time 1 under a perturbation $v_t^{\epsilon }$ of v_t is given by [22]:

$$\frac{d}{d\epsilon }{\phi }_{01}^{v^{\epsilon }}(x)={\int }_0^1{d}_{{\phi }_{0s}^v}{\phi }_{s1}^v(h_s\circ {\phi }_{0s}^v)ds.$$ (20)

with $h_s(x)=\frac{d{v}_s^{\epsilon }(x)}{d\epsilon }$, the derivative being taken at ε = 0 (we have used the notation of Eq. (1)). Assume that this expression vanishes (so that the end point ${\phi }_{01}^{v^{\epsilon }}$ remains unchanged). The first variation of the kinetic energy is given by ${\int }_0^1{\langle v_t,h_t\rangle }_{L}dt={\int }_0^1(L{v}_t,h_t)dt={\int }_0^1(L{v}_0,d_{{\phi }_{0t}}{\phi }_{t0}{v}_t\circ {\phi }_{0t})dt$. Now, using (20) and the fact that d_φ0t φ_t1 = d_φ00 φ₀₁d_φ0t φ_t0, we get easily that ${\int }_0^1{d}_{{\phi }_{0t}}{\phi }_{t0}{v}_t\circ {\phi }_{0t}dt=0$ so that, by linearity,

$${\int }_0^1{\langle v_t,h_t\rangle }_{L}dt=\left(L{v}_0,{\int }_0^1{d}_{{\phi }_{0t}}{\phi }_{t0}{h}_t\circ {\phi }_{0t}dt\right)=0.$$ (21)

4.3. Coadjoint Transport of Structures Along a Geodesic

For M ∈ ℊ^*, the evolution $t\mapsto {\text{Ad}}_{{\phi }_t^{-1}}^{\ast }M$ is called coadjoint transport. The fact that the momentum evolves by coadjoint transport along a geodesic implies the conservation of several properties whenever they are initially true, for Lv₀. These properties will turn out to be of main importance for image processing applications.

In this section, we assume that M₀ = Lv₀ is given, and that the coadjoint transport $M_t=L{v}_t=A{d}_{{\phi }_{t0}}^{\ast }(M_0)$ is well defined at all considered times.

4.3.1. Coadjoint Evolution of the Support

Let Supp(M) denote the support of a momentum M ∈ ℊ^*. It is defined by the complementary of the union of all open sets Ω′ ⊂ Ω which are such that (M, w) = 0 whenever w ∈ ℊ vanishes outside Ω′. We have the property:

Statement 3

If $M_t={\text{Ad}}_{{\phi }_{t0}}^{\ast }(M_0)$, then

$$\text{Supp}(M_t)={\phi }_{0t}^v(\text{Supp}(M_0))$$

Indeed, assume that M₀ vanishes Ω′ ⊂ Ω. Let w have its support included in φ_0t (Ω′). Then (M_t, w) = (M₀, dφ_0t)⁻¹ w ◦ φ_0t and w ◦ φ_0t vanishes outside Ω′, which implies that (M_t, w) = 0. Thus Supp(M_t) ⊂ φ_0t (Supp(M₀)), and the reverse inclusion is true by inverting the roles of M₀ and M_t.

As a first example, consider the case when M₀ is finitely supported, and more precisely a sum of Dirac measures. This is legitimate since our hypotheses on L imply that Dirac measures belong to ℊ^*, therefore have the form Lv₀ for some v₀ ∈ ℊ. So, we assume that

$$(M_0,w)=\sum _i{\langle a_i,w(x_i)\rangle }_{{\mathbb{R}}^d},$$ (22)

where (x_i)_1≤i≤n is a finite family of points in Ω (landmarks) and (a_i)_1≤i≤n is a finite family of vectors in ℝ^d. We write $M_0={\sum }_{i=1}^n{\delta }_{x_i}^{\ast }{a}_i$, where, by definition

$$\begin{array}{l}{\delta }_x^{\ast }a:\text{g}\to \mathbb{R}\\ w\mapsto \langle a,w(x)\rangle \end{array}$$ (23)

Denoting x_i (t) ≐ φ_t (x_i), we obtain the fact that M_t is supported on {x₁(t), …, x_N (t)}. More precisely, a rapid computation shows that

$$M_t=\sum _{i=1}^n{\delta }_{x_i(t)}^{\ast }{a}_i(t)$$ (24)

with

$$a_i(t)={(d_{x_i(t)}{\phi }_{t0})}^{\ast }{a}_i$$ (25)

so that the momentum remains a sum of Dirac measures. This is a special case of the property considered in the next section.

4.3.2. Coadjoint Transport of Measure

Measure-based momenta are given by

$$(M,w)={\int }_{\mathrm{\Omega }}\langle {\nu }_0,w\rangle d{\mu }_0$$ (26)

where μ₀ is a measure on Ω and ν₀ is measurable and μ₀-integrable. They generate a large class of geodesic evolutions, and have the attractive property that the momentum Lv_t can be explicitly computed from the momentum at the origin.

Statement 4

Assume that (M₀, w) = ∫_Ω〈ν₀, w〉dμ₀ then the linear momentum functional evolves according to

$$\begin{array}{l}(M_t,w)={\int }_{\mathrm{\Omega }}{\langle {\nu }_t,w\rangle }_{{\mathbb{R}}^d}d{\mu }_t\text{where}\\ {\nu }_t(x)={(d_x{\phi }_{t0})}^{\ast }{\nu }_0\circ {\phi }_{t0}(x),{\mu }_t\doteq \mu \circ {\phi }_{t0},\end{array}$$ (27)

i.e. μ_t (A) = μ(φ_t0(A)) for any measurable set A.

The statement follows straightforwardly from the substitutions

$$\begin{array}{l}(M_t,w)={\int }_{\mathrm{\Omega }}{\langle {\nu }_0(x),({(d{\phi }_{0t})}^{-1}w\circ {\phi }_{0t})(x)\rangle }_{{\mathcal{R}}^d}d\mu (x)\\ ={\int }_{\mathrm{\Omega }}{\langle d_{{\phi }_{0t}}(x){\phi }_{t0}^{\ast }{\nu }_0(x),w\circ {\phi }_{0t}(x)\rangle }_{{\mathcal{R}}^d}d{\mu }_0(x)\\ ={\int }_{\mathrm{\Omega }}{\langle {\nu }_t(x),w(x)\rangle }_{{\mathcal{R}}^d}d{\mu }_t(x)\end{array}$$ (28)

Point-supported momentum evolution considered in the previous section, clearly is a particular case of this statement. As another illustration, consider the case of measures which are supported by submanifolds of Ω. In this case, the initial momentum is concentrated along the boundary Σ₀ of a k-dimensional C ¹ sub-manifold in Ω ⊂ ℝ^d.

Let σ₀ by the surface measure (given as the induced volume form on the sub-manifold) and let μ₀ be supported by Σ₀, such that for any smooth function on Ω, ∫_Ωf dμ₀ = ∫_Σ0f α₀dσ₀ for some density α₀ (not necessary positive) on the surface. Let ν₀: Ω → ℝ^d (the values of ν₀ outside Σ₀ will not be important) and define

$$(L{v}_0,w)={\int }_{{\mathrm{\sum }}_0}{\langle {\nu }_0,w\rangle }_{{\mathbb{R}}^d}{\alpha }_{0}d{\sigma }_0.$$ (29)

Using Statements 3 and 4, we get that the tranported measure μ_t is located on the transported sub-manifold Σ_t ≐ φ_t (Σ₀) (whose smoothness is preserved by the regularity of the diffeomorphisms in G) and can be written as μ_t = α_t σ_t where σ_t is the k-dimensional volume measure on Σ_t. Moreover, if ν_t = d(φ_t0)^*γ₀ ◦ φ_t0, Statement 4 gives us the evolution of the momentum

$$(L{v}_t,w)={\int }_{{\mathrm{\sum }}_t}\langle {\nu }_t,w\rangle {\alpha }_{t}d{\sigma }_t(y).$$ (30)

In the case where the sub-manifold is Ω itself, then σ_t = σ₀ is the Lebesgue’s measure λ on Ω, and α_t = α₀ ◦ φ_t,0|dφ_t,0|.

4.3.3. Coadjoint Transport of Orthogonality

The last property transported by geodesic evolution which is considered here is the normality with respect to a smooth submanifold of Ω. Since normality will be extensively studied in the next section, we here provide an illustration in a particular case.

Assume that ν₀, in Eq. (26) can be expressed as

$${\nu }_0=\sum _{i=1}^r{b}_0^i\nabla f_0^i$$ (31)

where ${(b_0^i)}_{1\le i\le r}$ and ( $f_0^i$) are two families of functions on Ω and 1 ≤ r ≤ d. Then, we get from Statement 4 that

$${\nu }_t=\sum _{i=1}^r{b}_t^i\nabla f_t^i$$ (32)

where $b_t^i=b_0^i\circ {\phi }_{t,0}$ and $f_t^i=f_0^i\circ {\phi }_{t,0}$. Equation (32) can be interpreted as a normality property of the geodesic motion under initial condition (31). Indeed, let

$${\mathrm{\sum }}_0=\underset{i=1}{\overset{r}{\cap }}{(f_0^i)}^{-1}(\{0\}).$$

Assume that Σ₀ is not empty and denotes $N_0(x)=\text{Span}\{\nabla f_0^i(x)\mid 1\le i\le r\}$ for any x ∈ Σ₀. Under appropriate transversality conditions, mainly

$$r\equiv dim{N}_0,$$

Σ₀ can be equipped with a structure of (d − r)-dimensional C¹ manifold and N₀(x) is exactly the space of vectors normal to Σ at location x.

We then deduce easily that

$${\mathrm{\sum }}_t=\underset{i=1}{\overset{r}{\cap }}{(f_t^i)}^{-1}(\{0\})$$

and equality (32) implies for any x ∈ Σ_t

$${\nu }_t(x)\in N_t(x)$$ (33)

where $N_t(x)=\text{Span}\{\nabla f_t^i(x)\mid 1\le i\le r\}$ is the set of normal vectors to Σ_t at location x.

We deduce that if the momentum is normal to some k-dimensional sub-manifold Σ₀, this normality property is preserved by coadjoint transport along a geodesic.

In the case of r = 1 and $f_0^1=f_0$, Σ₀ is exactly the level set for threshold value 0 of f₀ and the normality of the initial momentum to the level sets is preserved under geodesic motion. Since the threshold value is arbitrary, we deduce that the property is true for all level sets.

5. The Normal Momentum Motion Constraint

5.1. Heuristic Analysis

The conservation of momentum is a general property of geodesics in a group of diffeomorphisms with a right invariant metric. More can be said in the situation when diffeomorphisms are associated to deformations of geometric structures or images, which is the situation of interest for our applications. In this setting we are still looking for curves with shortest length in G, but we partially relax the fixed end-point condition by the constraint that the initial template is correctly mapped to the target: because there is a whole range of diffeomorphisms which deform one given structure into another, this condition is weaker than the fixed end-point condition, which means that there are more degrees of freedom for the optimization, and therefore more constraints on the minimum. For image matching, these additional constraints may essentially be summarized by the statement the momentum along the geodesic path is at all times normal to the level sets of the image. This is what we call the normal momentum constraint, which is described in this section.

We start with a heuristic analysis, for which I₀, the image, is a smooth function defined on Ω. Let I₁ be in the orbit of I₀ for the group G of diffeomorphisms: there exists ψ ∈ G such that I₀ ◦ ψ⁻¹ = I_t. By compactness and semi-continuity arguments, one can prove the existence of a geodesic path φ = (φ_t) such that

$$d_G(\text{Id},{\phi }_1)=\underset{\varphi \in G}{inf}{d}_G(\text{Id},\varphi )\text{and}{I}_0=I_1\circ \varphi .$$ (34)

Let $\phi =({\phi }_t^v)$ be such a solution and consider a first order expansion around t = 0, φ_t(x) ≃ x + tv₀(x) so that $I_t=I_0\circ {\phi }_t^{-1}(x)\simeq I_0-t{\langle \nabla I_0,v_0\rangle }_{{\mathbb{R}}^d}$. By definition, the cost to go from I₀ to I_t is (still at first order) t|v₀|_L. However, any u ∈ ℊ such that 〈∇I₀, u〉_ℝ^d = 〈∇I₀, v₀〉_ℝ^d, will lead to the same I_t so that the least deformation cost from I₀ to I_t should be t|p_I0 (v₀)| where p_I0 (v₀) the unique solution of the minimization problem:

$$\begin{array}{l}({\mathcal{P}}_0):\underset{u\in \text{g}}{inf}\mid u{\mid }_L\text{subject}\text{to}:\\ {\langle (v_0-u)(x),\nabla I_0(x)\rangle }_{{\mathbb{R}}^d}=0,\forall x\in \mathrm{\Omega }\end{array}$$ (35)

Since ( ${\phi }_t^v$) is a geodesic path minimizing the deformation cost from I₀ to I₁, it minimizes also the deformation cost from I₀ to I_t yielding

$$v_0=p_{I_0}(v_0).$$ (36)

Introduce the set ℊ_I0 = {h ∈ ℊ | 〈∇ I₀(x), h(x)〉_ℝ^d = 0, ∀x ∈ Ω}: the constraints in 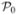can be restated as u − v₀ ∈ ℊ_I0 so that p_I0 (v) is the orthogonal projection of v on ${\text{g}}_{I_0}^{\perp }$, the space orthogonal to ℊI₀. Hence, equality (36), translates to

$$\begin{array}{l}\forall h\in \text{g}\text{such}\text{that}\text{for}\text{all}x\in \mathrm{\Omega },\langle \nabla I_0(x),h(x)\rangle =0,\\ \text{we}\text{have}{\langle v_0,h\rangle }_L=0.\end{array}$$ (37)

Now, the fact that 〈∇I₀(x), h(x)〉 ≡ 0 means that h is a vector field which is tangent to the level sets of I₀, and since 〈v₀, h〉_L = (Lv₀, h), we see that Lv₀ vanishes when applied to any such vector field, or, that Lv₀ is a linear form which is normal to the level sets of I₀.

5.2. Rigorous Result

We now pass to a rigorous derivation of this property. Since it will be interesting to also consider images which are not smooth, we provide a new definition of the set ℊ_I0. Obviously, when I₀ is smooth, h ∈ ℊ_I0 is equivalent to the fact that, for any function f which is C¹ on Ω, one has

$${\int }_{\mathrm{\Omega }}{\langle {\nabla }_x{I}_0,h(x)\rangle }_{{\mathbb{R}}^k}f(x)dx=0.$$

Applying the divergence theorem (we assume that ∂Ω is smooth enough and take advantage on the fact that elements of ℊ vanish on ∂Ω), we get

$$-{\int }_{\mathrm{\Omega }}{I}_0(x)\text{div}(hf)(x)dx=0.$$

Since this has a meaning when I₀ ∈ L²(Ω), we now define

Definition 2

When I ∈ L²(Ω), we denote

$${\text{g}}_I=\{h\in \text{g}:{\langle I,\text{div}(hf)\rangle }_{L^2}=0\text{for}\text{all}f\in C^1(\mathrm{\Omega })\}.$$

We still denote by p_I the orthogonal projection on ${\text{g}}_I^{\perp }$. The group G is assumed to be built as described in Section 2.1 (in particular ℊ is continuously embedded in C¹(Ω, ℝ^d)).

Theorem 3. (Normal Momentum Constraint)

Assume that I₀ ∈ L²(Ω) and let $\phi =({\phi }_t^v)$ be a geodesic path solution of (34). Then, for almost all t ∈ [0, 1]

$$v_t\in {\text{g}}_{I_t}^{\perp }.$$

The proof is given in Appendix A.

5.3. Examples

Consider again the case of smooth I, so that the condition h ∈ ℊ_I is equivalent to h ∈ ℊ and for all x ∈ Ω, 〈∇_x I, h(x)〉_ℝ^d = 0. Using notation (23), we get that ${\langle \nabla I_0(x),h(x)\rangle }_{{\mathbb{R}}^d}={\langle {\delta }_x^{\ast }(\nabla I_0(x)),h\rangle }_L$ so that ${\text{g}}_{I_0}={(\text{Span}\{{\delta }_x^{\ast }(\nabla I_0(x))\mid x\in \mathrm{\Omega }\})}^{\perp }$ and finally,

$${\text{g}}_I^{\perp }=\overline{\text{Span}\{{\delta }_x^{\ast }(\nabla I(x))\mid x\in \mathrm{\Omega }\}}.$$ (38)

Vector fields v such that

$$(Lv,u)={\int }_{\mathrm{\Omega }}{\langle v(x),u(x)\rangle }_{{\mathbb{R}}^d}d\mu (x),$$ (39)

where ν is normal² to the level sets of I belong to ${\text{g}}_I^{\perp }$ and it can be shown that they form a dense subset.

For non-smooth I, we can similarly introduce ω_f (I), as the unique element of ℊ such that, for h ∈ V, 〈ω_f (I), h〉 = 〈 I, div(h f)〉_L²(Ω), and conclude that

$${\text{g}}_I^{\perp }=\overline{\text{Span}\{{\omega }_f(I)\mid f\in C^1(\mathrm{\Omega },\mathbb{R})\}}.$$ (40)

This implies that any element v ∈ ℊ_I is such that Lv can be expressed as a limit

$$(Lv,u)=\underset{N\to \infty }{lim}{\int }_{\mathrm{\Omega }}I(x)\text{div}(u{f}_N)(x)dx$$

where f _N ∈ C¹(Ω, ℝ). The particular case when I is the indicator function of a smooth domain B ⊂ Ω (which can be interpreted as a smooth shape) is quite interesting. For x ∈ ∂B, let ν(x) be the outward normal to ∂Ω and denote σ_B be the uniform measure on ∂B. Then

$$\begin{array}{l}{\int }_{\mathrm{\Omega }}I(x)\text{div}(uf)(x)dx={\int }_B\text{div}(uf)(x)dx\\ ={\int }_{\partial B}f(x){\langle u(x),\nu (x)\rangle }_{{\mathbb{R}}^d}d{\sigma }_B(x).\end{array}$$

In this case, we obtain a dense subspace of ℊ_I by considering elements v ∈ ℊ such that

$$(Lv,u)={\int }_{\partial B}{\langle v(x),u(x)\rangle }_{{\mathbb{R}}^d}d\mu (x).$$ (41)

for some measure μ on ∂B (the boundary of the shape).

Remark

We close this section with a technical, but important, remark. We have called normal momentum constraint the property that v_t ⊥ ℊ_It at almost all times. We have shown that this property is always true for geodesics minimizing (34). But there is another important issue, which is how much it constrains v_t, or, in other terms, how big ℊ_I is for a given image I. That this is relevant, and sometimes non-trivial, may be seen from the following example: assume that we are in 2 dimensions (d = 2) and that I is a C¹ image, with a non-vanishing gradient, at least on a dense subset of Ω. Then, on any point x such that ∇ _x I ≠ = 0, we can de-fine in a unique way a positively oriented orthonormal frame (τ (x) ν (x)) such that ν (x) = ∇_x I/|∇_x I|. Then, if h ∈ ℊ_I and h(x) ≠ = 0, we must have h/|h| = ± τ in a small ball around x. Now h, as an element of ℊ must be smooth (depending on the choice made for L, and h/|h| has the same smoothness as h: this is impossible to achieve when τ itself is not smooth enough, which in such a case forces h(x) = 0. We thus get the property that h vanishes whenever τ (x) does not meet the smoothness requirements of ℊ, which may very well be everywhere on Ω (or on a dense subset, which is the same since h is continous), in which case ℊ_I = {0} and the constraint is void, contrary to our intuition that the momentum should be aligned with ν. We see that, for the constraint to really be effective, we need some smoothness requirement on I. Fortunately, as illustrated by the example above, this smoothness is only required for the level sets of I, which must have a smooth boundary. With such an assumption, for example, one can show that if v ⊥ ℊ_I and

$$(Lv,u)={\int }_{\mathrm{\Omega }}\langle \xi (x),u(x)\rangle d\mu (x)$$

for some measure μ on Ω and some vector field on ξ Ω, then ξ must be (μ-almost everywhere) orthogonal to the level sets of I. From a practical point of view smoothness of level sets may easily be obtained using algorithms such as mean curvature motion ([27]).

5.4. Conservation and Normality Property Check for Inexact Matching

Here, we give a brief account of situations in which proofs of conservation of momentum and the normality property can be carried on in a well-defined context, and retrieve the evolutions described in the previous section.

It is hard to make rigorous, in full generality, the variational argument we have used in the proof of Eq. (15). Notice that the well-definiteness of the conservation of momentum Eq. (17) is an issue by itself, since, when w ∈ ℊ, and φ_t is the diffeomorphism generated by a geodesic, there is a priori no reason for (dφ_t)⁻¹w ◦ φ_t) to belong to ℊ: one must be able to define Lv₀ on spaces which are bigger than ℊ, which means that Lv₀ needs to be somewhat smoother (as a distribution) than a generic element of ℊ^*.

However, there is a setting in which such a fact is true and easy to obtain: it is when the search for the geodesic is done with an approximation of the target, with some L² penalty term added to control the error. We summarize this setting in the case of landmark matching, shape matching and image matching. In these three situations, we will retrieve the coadjoint transport of measure-based momenta. In all cases, results in [11, 35] ensure the existence of minimizers of the variational problem.

5.4.1. Inexact Landmark Matching

In this section, we assume that a measured space (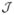, ρ), together with two measurable functions x, y: 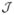→ Ω are given. The diffeomorphism φ is searched to minimize

$$U(\phi )=E(\phi )+\frac{1}{{\sigma }^2}{\int }_{\mathcal{J}}\mid y_i-\phi (x_i){\mid }^{2}d\rho (i)$$

When ρ is discrete, this relates to point-based matching, x representing the landmark original positions and y giving the landmark target positions. If we express U in function of v, this requires the minimization of

$$\stackrel{\sim }{U}(v)={\int }_0^1{\left|\right|v_t\left|\right|}_L^{2}dt+\frac{1}{{\sigma }^2}{\int }_{\mathcal{J}}\mid y_i-{\phi }_{01}^v(x_i){\mid }^{2}d\rho (i)$$

The main point here is to notice that the optimal solution v generates a geodesic in G between id and ${\phi }_1^v$.

Proposition 1

Denote ${\delta }_x^{\ast }a$ the linear form on ℊ such that $({\delta }_x^{\ast }a,v)=\langle a,v(x)\rangle$. Let v be a minimizer of Ũ. Then, letting $x_i(t)={\phi }_{0t}^v(x_i)$

$$L{v}_t=-\frac{1}{{\sigma }^2}{\int }_{\mathcal{J}}{\delta }_{x_i(t)}^{\ast }[{(d_{x_i(t)}{\phi }_{t1}^v)}^{\ast }(y_i-x_i(1))]d\rho (i)$$ (42)

Proof

The proof of this result is a direct consequence of the identity, valid for s, t ∈ [0, 1], v, h ∈ L²([0, 1], ℊ),

$${\frac{d}{d\epsilon }{\phi }_{st}^{v+\epsilon h}(x)|}_{\epsilon =0}={\int }_s^t{d}_{{\phi }_{su}^v}{\phi }_{ut}^v(h_u\circ {\phi }_{su}^v)du.$$ (43)

the proof of which being carried on with usual ODE arguments and being omitted here. It is then straightforward to obtain (42), using the definition of the linear forms ${\delta }_x^{\ast }a$, for x ∈ Ω and a ∈ ℝ^d.

Equation (42) is a conservation of momentum equation for

$$L{v}_0=-\frac{1}{{\sigma }^2}{\int }_{\mathcal{J}}{\delta }_{x_i}^{\ast }[{(d_{x_i}{\phi }_{01}^v)}^{\ast }(y_i-x_i(1))]d\rho (i).$$

When 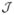is finite, this is equation (31) with $a_i=-\frac{1}{{\sigma }^2}{(d_{x_i}{\phi }_{01}^v)}^{\ast }(y_i-x_i(1))$. Equation (42) now is exactly (24), since

$$\begin{array}{l}{a}_i(t)={(d_{x_i(t)}{\phi }_{t0}^v)}^{\ast }{a}_i\\ =-\frac{1}{{\sigma }^2}{[d_{x_i(0)}{\phi }_{01}^v{d}_{x_i(t)}{\phi }_{t,0}^v]}^{\ast }(y_i-x_i(1))\\ =-\frac{1}{{\sigma }^2}{(d_{x_i(t)}{\phi }_{t1}^v)}^{\ast }(y_i-x_i(1))\end{array}$$

5.4.2. Inexact Shape Matching

We now consider the comparison of a binary set-indicator function, I₀ = 1_Ω0 (Ω̄₀ ⊂ Ω having smooth boundaries) and a smooth function I₁, through the minimization of

$$U(\phi )=E(\phi )+\frac{1}{{\sigma }^2}{\int }_{\mathrm{\Omega }}\mid {\mathbf{1}}_{{\mathrm{\Omega }}_0}\circ {\phi }^{-1}(x)-I_1(x){\mid }^{2}dx$$

over G_L. We have

Proposition 2

Let v be a minimizer of $U({\phi }_{01}^v)$ over L²([0, 1], ℊ). Then

$$L{v}_t=\frac{1}{{\sigma }^2}{\int }_{\partial {\mathrm{\Omega }}_1}\left(\frac{1}{2}-I_1\right){\delta }_{{\phi }_{1t}^v(x)}^{\ast }[{(d_{{\phi }_{1t}^v}{\phi }_{t1}^v)}^{\ast }{\nu }_1]d{\sigma }_1(x)$$ (44)

where ${\mathrm{\Omega }}_1={\phi }_{01}^v({\mathrm{\Omega }}_0)$, ν₁ is the outward normal to ∂ Ω₁ and σ₁ is the volume measure on ∂ Ω₁.

Proof

Taking a variation v + εh, the main issue is to compute the derivative of

$$\frac{1}{2}{\int }_{\mathrm{\Omega }}\mid {\mathbf{1}}_{{\mathrm{\Omega }}_0}\circ {\phi }_{10}^{v+\epsilon h}(x)-I_1(x){\mid }^{2}dx$$

This integral can be rewritten

$${\int }_{{\mathrm{\Omega }}_{01}^{v+\epsilon h}({\mathrm{\Omega }}_0)}\left(\frac{1}{2}-I_1(x)\right)dx+\frac{1}{2}{\int }_{\mathrm{\Omega }}\mid I_1(x){\mid }^{2}dx$$

Since the last term is constant, we see that the problem boils down to the computation of the derivative of the first term, which can be written, after a change of variable and letting f₁ = 1/2 − I₁,

$${\int }_{{\mathrm{\Omega }}_0}{f}_1\circ {\phi }_{01}^{v+\epsilon h}(x)\mid d_x{\phi }_{01}^{v+\epsilon h}\mid dx$$

Define u by $u\circ {\phi }_{01}^v(x)=\frac{d}{d\epsilon }{\phi }_{01}^{v+\epsilon h}(x)$. Simple computations, which can be, for example, found in [10], yields the fact that

$$\frac{d}{d\epsilon }{\int }_{{\mathrm{\Omega }}_0}{f}_1\circ {\phi }_{01}^{v+\epsilon h}(x)\mid d_x{\phi }_{01}^{v+\epsilon h}\mid dx={\int }_{{\mathrm{\Omega }}_1}\text{div}(f_{1}u)dx$$

Now the conclusion is a direct consequence of Eq. (43) and of the divergence theorem.

Here again, one straighforwardly checks that the conservation of momentum is satisfied. We have in particular

$$(L{v}_0,w)=\frac{1}{{\sigma }^2}{\int }_{\partial {\mathrm{\Omega }}_1}\left(\frac{1}{2}-I_1\right)\langle {(d_{{\phi }_{10}^v}{\phi }_{01}^v)}^{\ast }{\nu }_1,w\circ {\phi }_{10}^v(x)\rangle d{\sigma }_1(x)$$

Letting ${\mu }_0={\phi }_{01}^v({\sigma }_1)$, and ${\nu }_0(x)={(d_x{\phi }_{01}^v)}^{\ast }{\nu }_1\circ {\phi }_{10}^v(x)$ this can be rewritten

$$(L{v}_0,w)=\frac{1}{{\sigma }^2}{\int }_{\partial {\mathrm{\Omega }}_0}\left(\frac{1}{2}-I_1\circ {\phi }_{01}^v(x)\right)\langle v_0,w\rangle d{\mu }_0(x)$$

which is under the general form of a measure-based momentum.

5.4.3. Inexact Image Matching

In this section, we let I₀ and I₁ be two smooth enough (say C¹) functions defined on Ω (images). We consider the image matching problem which corresponds to minimizing, over G,

$$U(\phi )=E(\phi )+\frac{1}{{\sigma }^2}{\int }_{\mathrm{\Omega }}\mid I_0\circ {\phi }^{-1}(x)-I_1(x){\mid }^{2}dx$$

This problem is equivalent to minimizing

$${\int }_0^1{\left|\right|v_t\left|\right|}_L^{2}dt+\frac{1}{{\sigma }^2}{\int }_{\mathrm{\Omega }}\mid I_0\circ {({\phi }_{01}^v)}^{-1}(x)-I_1(x){\mid }^{2}dx$$

This matching problem has been studied, in particular in [4], to show that the optimal solution should satisfy, at each time t,

$$L{v}_t=-\frac{1}{{\sigma }^2}\mid d{\phi }_{t,1}^v\mid (I_{0t}^v-I_{1t}^v)\nabla I_{0t}^v$$ (45)

in which we have introduced the notation: $I_{0t}^v=I_0\circ {\phi }_{t0}^v,I_{1t}^v=I_1\circ {\mathrm{\Phi }}_{t1}^v$, and |dφ| for the Jacobian of φ. This equation is in fact an equation of conservation of momentum, with

$$L{v}_0=-\frac{1}{{\sigma }^2}\mid d{\phi }_{01}^v\mid (I_0-I_{10}^v)\nabla I_0$$

as can be deduced from Eq. (30), with $\alpha =-\frac{1}{{\sigma }^2}\mid d{\phi }_{01}^v\mid (I_0-I_{10}^v)$. Moreover, we can check also the normality property (31) which holds here with with r = 1 and f₀ = I₀. This allows us to conclude that for the geodesic path in the image space generated by inexact matching, the lifting of the path in G defines a geodesic for which the momentum stays normal to the level sets of the current image I₀ ◦ φ_t,0 at time t.

6. Geodesic Evolution in the Orbit

Thus far we have concentrated on the evolution of the flow of diffeomorphisms and its conservation of momentum. For all of our image understanding work we use the flow (φ_t, t ∈ [0, 1]) to act on the elements in the orbits 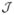of a given template I = I_temp. Now we examine the geodesic flows in the orbit {I_t = I ◦ φ_t, t ∈ [0, 1]}, I ∈ 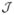, and provide the associated evolution equations.

6.1. Geodesic Evolution Equation of Landmark Points

Here we examine the finite dimensional landmark orbit denoted 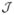_n, consisting of n-shapes I_N = (x₁, …, x_n), each landmark (x_i)_1≤i≤n is in Ω ⊂ ℝ^d; correspondingly (a_i)_1≤i≤n are a finite family of vectors in ℝ^d. Denoting by x_i (t) =̇ φ_t (x_i), the trajectory in Ω of the point x_i under the flow φ_t gives

$$L{v}_t=\sum _{i=1}^n{\delta }_{x_i(t)}^{\ast }{a}_i(t),$$ (46)

where a_i (t) = (d_xt (t) φ_t,0)^*a_i. From the identity

$$\frac{d}{dt}({(d_{x_i(t)}{\phi }_{t,0})}^{\ast })=-d_{x_i(t)}{v}_t^{\ast }{(d_{x_i(t)}{\phi }_{t,0})}^{\ast },$$ (47)

we deduce that $\frac{d{a}_i}{dt}(t)+{(d_{x_i(t)}{v}_t)}^{\ast }{a}_i(t)=0$. To prove (47), one needs to remark that

$$d_{x_i(t)}{\phi }_{t,0}=d_{{\phi }_{0,t}(x_i)}{\phi }_{t,0}={(d_{x_i}{\phi }_{0,t})}^{-1}$$

Now,

$$\begin{array}{l}\frac{d}{dt}{(d_{x_i}{\phi }_{0,t})}^{-1}=-{(d_{x_i}{\phi }_{0,t})}^{-1}\frac{d}{dt}(d_{x_i}{\phi }_{0,t}){(d_{x_i}{\phi }_{0,t})}^{-1}\\ =-{(d_{x_i}{\phi }_{0,t})}^{-1}(d_{{\phi }_{0,t}(x_i)}{v}_t{d}_{x_i},{\phi }_{0,t})\times {(d_{x_i}{\phi }_{0,t})}^{-1}\\ =d_{x_i(t)}{\phi }_{t,0}{d}_{x_i(t)}{v}_t\end{array}$$

Hence we get the following geodesic evolution in the orbit of landmarks.

Proposition 3 (Landmark Transport)

The landmarks are transported along the geodesic according to the following equations with velocity vector field satisfying

$$v_t=L^{-1}\left(\sum _{i=1}^n{\delta }_{x_i(t)}^{\ast }{a}_i(t)\right)=\sum _{i=1}^{n}K(x_i(t),·)a_i(t)$$

where K(x, y) is the Green kernel associated with L:³

$$\{\begin{array}{l}\frac{d{a}_i}{dt}(t)+{(d_{x_i(t)}{v}_t)}^{\ast }{a}_i(t)=0,\hfill \\ \frac{d{x}_i}{dt}(t)-v_t(x_i(t))=0.\hfill \end{array}$$ (49)

Note that the expression of v_t from Eq. (48) can be introduced into the system (49), yielding an evolution equation which only depends on the landmarks in the orbit.

We notice the reduction of the vector field to the range space of the Green’s kernels travelling over the landmark trajectories is as in [17].

There is a straightforward extension of this result to geodesic curve evolution, in which x(0) is a parametrized curve σ ↦ x(σ) for σ ∈ [0, L] and

$$L{v}_0={\int }_0^L{\delta }_{x(0,\sigma )}^{\ast }{\nu }_0(\sigma )d\sigma$$

where ν₀(σ) is normal to x(0). In this case, we have

$$L{v}_t={\int }_0^L{\delta }_{x(t,\sigma )}^{\ast }{\nu }_t(\sigma )d\sigma$$

with

• $\frac{\partial {\nu }_t}{\partial t}(t,\sigma )+{(d_{x(t,\sigma )}{v}_t)}^{\ast }\nu (t,\sigma )=0$,

• $\frac{\partial x}{\partial t}(t,\sigma )-v_t(x(t,\sigma )=0$.

6.2. Geodesic Image Evolution

Assume here that dμ = α (x)dx has a density with respect to Lebesgue’s measure on Ω. In this case, dμ_t = |dφ_t0|α ◦ φ_t0dx and

$$L{v}_t=\mid d{\phi }_{t0}\mid \alpha \circ {\phi }_{t0}\nabla I_t$$ (50)

From the conservation of momentum in Lagrangian coordinates for image based motion, we get for Lv₀ = α₀ ∇ I₀ that Lv_t = α_t |dφ_t,0|∇I_t where α_t = α₀ ◦ φ_t,0, I_t = I₀ ◦ φ_t,0. Let z_t = α_t |dφ_t,0| so that Lv_t = z_t ∇ I_t.

Since $\frac{d}{dt}(z_t\circ {\phi }_{0,t})=\frac{d}{dt}(\mid d_{\phi 0,t}{\phi }_{t,0}\mid {\alpha }_0)=-\text{div}(v_t)\circ {\phi }_{0,t}\mid d_{\phi 0,t}{\phi }_{t,0}\mid {\alpha }_0$ we get $\frac{d{z}_t}{dt}+d{z}_t(v_t)+\text{div}(v_t)z_t$. Moreover, we get easily $\frac{\partial I_t}{\partial t}+\langle \nabla I_t,{\nu }_t\rangle =0$. Hence we get the following geodesic evolution equation in image space.

Proposition 4 (Image Transport)

The image is transported along the geodesic according to the following equations: with vector field v_t = L⁻¹(z_t ∇I_t):

• $\frac{d{z}_t}{dt}+d{z}_t(v_t)+\text{div}(v_t)z_t=0$,

• $\frac{\partial I_t}{\partial t}+\langle \nabla I_t,v_t\rangle =0$.

Notice that these equations appear as a limit case of the evolution equations which have been studied in [34] for image comparison.

As illustrated above, the pair (I₀, μ) provides a device for modeling deformations. In the cases we have studied, I₀ was representing some geometrical structure (a curve, an image), which evolved with time accordi to the generated deformation, and μ, essentially quantifies the speed and direction of the deformation.

We get from this a natural way to represent the deformation of a template. Using Grenander’s original terminology, I₀ would precisely be the template and μ is the generator of the deformation. Thus, fixing I₀, and letting μ vary, we get a model which represents perturbations of the template.

An example of deformations of an image is provided in Fig. 2. The images have been obtained by solving Eq. (50) from an initial image g of a slice of macaque brain, and taking

Figure 2.

Three random deformations of an image.

$$\alpha (x)=\frac{X(x)}{1+\mid {\nabla }_x{I}_0\mid }$$

where X is a Gaussian process.

7. Computational Results

The following results illustrate the computation of the momentum Lv₀ = α₀∇I₀ (as described in Section 6.2) from geodesic paths between two images. These geodesics are computed using F. Beg’s implementation of image matching, as described in [4]. In these experiments, the operator L is (∇ + c Identity),² implemented via fast Fourier transform. The shooting algorithm solves the equation provided in Proposition 4 with initial condition (I₀, z₀ = α₀).

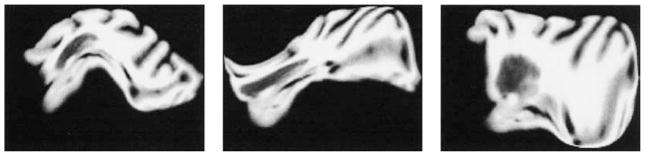
Figure 3 shows the three objects studied, a smooth Gaussian bump for shift, circles for scale, and two mitochondria examin g both forward and inverse shooting.

Figure 3.

Figure shows objects under translation (column 1), scale (column 2), and mitochondria 1 and 2.

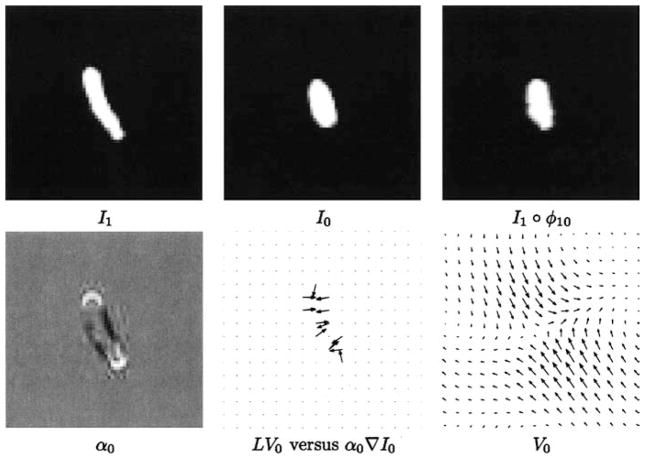
Shown in Fig. 4–6 are examples illustrating the image based momentum and the diffeomorphisms generated via geodesic shooting. Figure 4 shows the results of the translation experiment. Panels 1 and 2 show I₀ and I₁; panel 3 shows the diffeomorphism generated via geodesic shooting applied to I₀, and illustrates how solving the conservation of momentum equation allows to recover I₁ from I₀ and Lv₀.

Figure 4.

Rows 1, 2: Results from translation experiment. Panels 1, 2, and 3 show I₀, I₁, I₀ ◦ φ₁₀. Panels 4, 5 and 6 show α₀, Lv₀ versus α₀∇I₀, and V₀ and L⁻¹α∇ I₀.

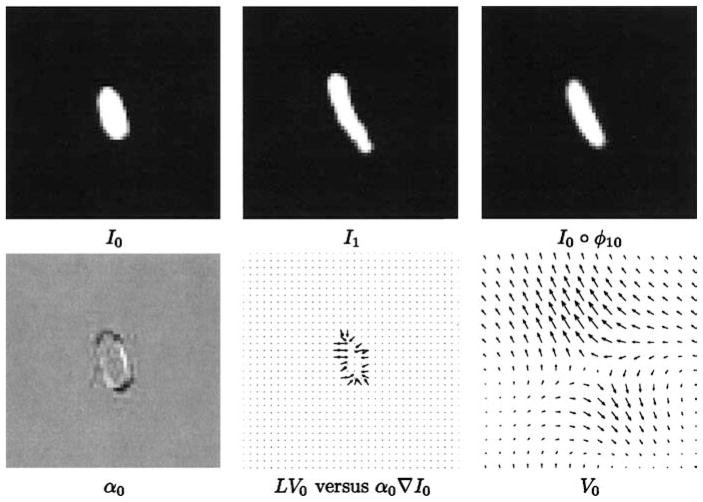
Figure 6.

Results from mitochondria 2. Panels 1, 2, and 3 show I₁, I₀, I₁ ◦ φ₁₀. Panels 4, 5 and 6 show α₀, LV₀ versus α₀∇ I₀, and V₀.

Shown in panel 4 is the density α showing the concentration near the boundary of I₀. Superposed in panel 5 are the predicted directions of the momentum, given by α₀∇I₀, and the value Lv₀ obtained from Beg’s algorithm. In almost all case they appear as one line indicating a good accuracy of the algorithm. Panel 6 indicates that the vector field V₀ demonstrating that while α and the momentum Lv₀ are highly localized, the velocity of motion extends over the entire object.

Shown in Fig. 5 are similar results for the scale experiment.

Figure 5.

Rows 1, 2: Results from scale experiment. Panels 1, 2, and 3 show I₀, I₁, I₀ ◦; φ₁₀. Panels 4, 5 and 6 show α₀, Lv₀ versus α₀∇I₀, and V₀ and L⁻¹α∇ I₀.

Shown in Fig. 6 are two sets of results for the geodesic shooting of the mitochondria. The organization of the results are the same as for the translation and scale experiments. Shown in Fig. 6 are two sets of results for the geodesic shooting of the mitochondria. The organization of the results are the same as for the translation and scale experiments.

Figure 7.

Results from mitochondria 1. Panels 1, 2, and 3 show I₀, I₁, I₀ ◦ φ₁₀. Panels 4, 5 and 6 show α₀, LV₀ versus α₀∇ I₀, and V₀.

Appendix A: Proof of Theorem 3

Proof

Since ${\text{g}}_{I_t}^{\perp }$ is closed, we have to show that for almost all t, v_t = p_It (v_t). Denote h_t =̇ v_t − p_It(v_t). For ε ∈ [0, 1], let $v_t^{\epsilon }\doteq v_t+\epsilon h_t$, and ${\phi }_t^{\epsilon }\doteq {\phi }_t^{v^{\epsilon }}$ (one can check, but we skip the argument, that t → h_t is measurable and belongs to L²([0, 1], ℊ), so that this variation is valid).

The proof essentially consists in showing that, for all 0 ≤ t ≤ 1

$$I_0\circ {\phi }_{t0}=I_0\circ {\phi }_{t0}^{\epsilon }.$$ (51)

Indeed, assume that this result is proved. Considering ε = 1 and t = 1, we deduce that $I_1=I_0\circ {\phi }_{1,0}^1$. However, since 〈h_t, v_t〉_L = 〈v_t − p_It(v_t), v_t〉_L = 0, we get $\mid v_t+h_t{\mid }_L^2=\mid v_t{\mid }_L^2-\mid h_t{\mid }_L^2$. Since t → v_t corresponds to paths with lowest kinetic energy from I₀

to I₁, we deduce that ${\int }_0^1\mid h_t{\mid }_L^{2}dt=0$ and the proof is ended.

We now return to Eq. (51). Using the formula

$$\frac{d{\phi }_{t0}(x)}{dt}=-d_x{\phi }_{t0}{v}_t(x)$$

and letting $q_t^{\epsilon }(x)={\phi }_{t0}\circ {\phi }_{0t}^{\epsilon }(x)$, we obtain

$$\begin{array}{l}\frac{\partial q_t^{\epsilon }(x)}{\partial t}=-d_{{\phi }_{0t}^{\epsilon }(x)}{\phi }_{t0}{v}_t\circ {\phi }_{0t}^{\epsilon }(x)+d_{{\phi }_{0t}^{\epsilon }(x)}{\phi }_{t0}(v_t\circ {\phi }_{0t}^{\epsilon }(x)+\epsilon h_t\circ {\phi }_{0t}^{\epsilon }(x))\\ =\epsilon d_{{\phi }_{0t}^{\epsilon }(x)}{\phi }_{t0}ht\circ {\phi }_{0t}^{\epsilon }(x)\end{array}$$

We first prove Eq. (51) under the assumption that I₀ is C¹. From the computation above, we have

$$\begin{array}{l}\frac{\partial }{\partial t}(I_0\circ q_t^{\epsilon })(x)=\epsilon \langle {\nabla }_{{\phi }_{t0({\phi }_{0t}^{\epsilon }(x))}}{I}_0,d_{{\phi }_{0t}^{\epsilon }(x)}{\phi }_{t0}{h}_t\circ {\phi }_{0t}^{\epsilon }{(x)\rangle }_{{\mathbb{R}}^d}\\ =\epsilon \langle {\nabla }_{{\phi }_{0t}^{\epsilon }(x)}{I}_t,h_t({\phi }_{t0}^{\epsilon }(x))){\rangle }_{{\mathbb{R}}^d}=0\end{array}$$

since by definition of the projection p_It (v_t), we have for any x ∈ Ω

$${\langle h_t(x),\nabla I_t(x)\rangle }_{{\mathbb{R}}^d}={\langle v_t(x),\nabla I_t(x)\rangle }_{{\mathbb{R}}^d}-{\langle p_{I_t}(v_t),\nabla I_t(x)\rangle }_{{\mathbb{R}}^d}=0.$$

This implies $I_0\circ {\phi }_{t,0}\circ {\phi }_{0,t}^{\epsilon }=I_0$ which yields Eq. (51) in this case. When I₀ is not smooth, the proof goes by showing that

$$\frac{\partial }{\partial t}{\int }_{\mathrm{\Omega }}{I}_0\circ q_t^{\epsilon }(x)f(x)dx={\int }_{\mathrm{\Omega }}{I}_t(x)\text{div}(h_t{g}_t^{\epsilon })(x)dx$$

for smooth f on Ω and $g_t^{\epsilon }\circ {\phi }_t^{\epsilon }\mid d{\phi }_t^{\epsilon }\mid =f$ which can be done either by a direct (heavy) computation, or by using a density argument, based on the fact that, by the divergence theorem, this is true for smooth I₀ (we skip the details).