Comparative Analysis of Sequence Periodicity among Prokaryotic Genomes Points to Differences in Nucleoid Structure and a Relationship to Gene Expression

Abstract

Regular spacing of short runs of A or T nucleotides in DNA sequences with a period close to the helical period of the DNA double helix has been associated with intrinsic DNA bending and nucleosome positioning in eukaryotes. Analogous periodic signals were also observed in prokaryotic genomes. While the exact role of this periodicity in prokaryotes is not known, it has been proposed to facilitate the DNA packaging in the prokaryotic nucleoid and/or to promote negative or positive supercoiling. We developed a methodology for assessments of intragenomic heterogeneity of these periodic patterns and applied it in analysis of 1,025 prokaryotic chromosomes. This technique allows more detailed analysis of sequence periodicity than previous methods where sequence periodicity was assessed in an integral form across the whole chromosome. We found that most genomes have the periodic signal confined to several chromosomal segments while most of the chromosome lacks a strong sequence periodicity. Moreover, there are significant differences among different prokaryotes in both the intensity and persistency of sequence periodicity related to DNA curvature. We proffer that the prokaryotic nucleoid consists of relatively rigid sections stabilized by short intrinsically bent DNA segments and characterized by locally strong periodic patterns alternating with regions featuring a weak periodic signal, which presumably permits higher structural flexibility. This model applies to most bacteria and archaea. In genomes with an exceptionally persistent periodic signal, highly expressed genes tend to concentrate in aperiodic sections, suggesting that structural heterogeneity of the nucleoid is related to local differences in transcriptional activity.

DNA sequences generally contain two strong periodic signals. The dominant signal has a period of 3 bp and relates to biased codon and amino acid usages in protein-coding genes. The second significant periodic signal has a period close to 10.5 bp (the average length of a helical turn of DNA in the canonical B conformation) and relates to DNA curvature and/or bendability. This periodic signal is most pronounced in the distribution of short runs of A or T (37, 39, 40). In eukaryotes, the DNA periodicity is a primary nucleosome positioning signal—the intrinsically bent DNA both facilitates wrapping of the DNA around the histone core and restricts the placement of nucleosomes (22, 35, 36, 40). The periodic pattern in the DNA sequence can influence characteristics of the chromatin and consequently the molecular interactions associated with transcription. In particular, patterns of sequence periodicity in the Caenorhabditis elegans genome are related to histone modifications, and regions with strong periodic signals are associated with germ line-specific genes, suggesting that periodicity within chromosomal segments can affect levels of gene expression (9, 12, 17).

Previous analyses of periodic signals in prokaryotic DNA sequences raised interesting questions about possible roles the sequence periodicity and concomitant DNA curvature could play in the organization of the prokaryotic nucleoid. Herzel and coworkers (13, 14, 34) noted distinct periodic patterns in archaea and bacteria, with periods close to 10 bp being most common in archaea and periods close to 11 bp prevalent in bacteria. They attributed the difference to possible distinct supercoiling propensities of bacterial and archaeal DNA: the periods shorter than the average DNA helical period of ∼10.5 bp lead to formation of left-handed superhelices corresponding to positive supercoiling, whereas periods larger than 10.5 bp promote right-handed superhelices and negative supercoiling. Based on a detailed analysis of periodic patterns in the Escherichia coli genome, Tolstorukov and coworkers (38) proposed a model in which short bent DNA segments stabilize the DNA loops that form in the bacterial nucleoid. They proffered that the DNA bending can be induced by DNA-binding proteins or by sequence periodicity that gives rise to the intrinsic bends in the absence of DNA-protein interactions. However, these studies relied on assessments of sequence periodicity in an integral form across the whole chromosome, which does not take into account variance of the periodic signal among different chromosomal regions. Our recent analysis of periodicity signatures in a diverse collection of prokaryotic genomes showed that sequence periodicity can vary significantly among different chromosomal regions, suggesting that considerations of intrachromosomal heterogeneity could be important to understand the role of sequence periodicity in prokaryotic genomes (27).

In the present work, we developed a set of computational tools for analysis of intergenomic as well as intragenomic variance of periodic sequence patterns related to DNA curvature (that is, with periods close to the DNA helical period of about 10 to 11 bp). These tools were subsequently employed to compare properties of periodic signals among 1,025 available complete prokaryotic chromosomes. Our analysis differs from the earlier work (13, 14, 34, 38) not only by using a larger data set of available complete genomes but also by including assessments of intrachromosomal heterogeneity of the periodic signal. This leads to new results that require modifications of previously proposed models for the role of sequence periodicity and intrinsic DNA curvature in prokaryotes.

MATERIALS AND METHODS

DNA sequences.

Complete DNA sequences of 1,025 prokaryotic chromosomes were downloaded from the NCBI FTP server (ftp://ftp.ncbi.nih.gov/genomes/Bacteria/). The complete list is provided in Table S1 in the supplemental material.

Periodicity plot: analysis of sequence periodicity in the whole chromosome context.

We start with a histogram of spacings between pairs of selected sequence patterns similar to that used by Herzel and coworkers (13, 14). The sequence patterns of interest center on short runs of A or T, whose periodic spacing contributes most significantly to DNA curvature (37, 39). We used three different patterns, referred to as “AT,” “AT4,” and “A2T2.” The AT method evaluates spacings between A or T nucleotides (13, 14). The AT4 method involves spacings between any of the tetranucleotides AAAA/AAAT/AATT/ATTT/TTTT (i.e., those containing dinucleotides AA, TT, and AT but not TA). This selection was motivated by a previous analysis of sequence periodicity in the E. coli genome, which used a similar definition of “A-tracts” (38). A2T2 includes dinucleotides AA/TT, whose periodic distribution dominates the nucleosome positioning signals in eukaryotes (22, 35).

The initial spacing histogram simply plots the counts N(s) of all pairs of the selected sequence motifs (AT, AT4, and A2T2) that occur at the distance s from each other (measured between the first nucleotides of each motif location). Note that the three methods AT, AT4, and A2T2 generally yield similar results (see below). The histogram N(s) is subsequently processed in a series of steps, which were designed through an analysis of extensive sequence data to reduce noise and various artifacts. First, the values N(s) are converted to odds ratios R(s) = N(s)/E(s). Values for E(s) are the expected counts estimated as E(s) = n_s p², where n_s signifies the number of times a pair of any nucleotides A, C, G, or T is found at the distance s from each other. Note that under normal circumstances n_s = L − s + 1 (L being the length of the analyzed sequence), but the more general definition allows masking out some sections of the sequence, such as genes or intergenic regions (see below). p is the probability of finding the selected pattern at any given position in the sequence estimated as p = f_A+T for the AT method, 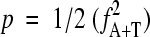for the A2T2 method, and 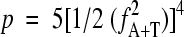for the AT4 method. f_A+T is the A+T content of the sequence at hand. The 3-bp periodic signal arising from biased codon usage in genes is subsequently removed with a 3-bp sliding-window average, yielding R′(s) = 1/3[R(s − 1) + R(s) + R(s+ 1)]. In some genomes, the R′(s) plot has a strong decreasing slope resulting from local variance in the A+T content. This slope is eliminated by subtracting a parabolic regression from the histogram, yielding 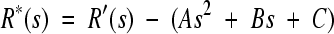, where the parameters A, B, and C define the parabola fitted to R′(s) by the least-squares method (Fig. 1a).

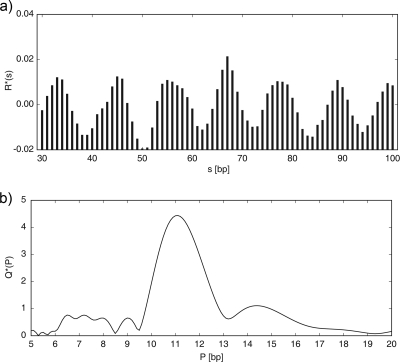
FIG. 1.

(a) Normalized histogram of spacings between AA/TT dinucleotides (the A2T2 method) in the E. coli K-12-MG1655 chromosome. The abscissa shows a distance s between a pair of AA or TT nucleotides in the DNA sequence, and the ordinate shows the normalized odds ratio R*(s) of how many times the dinucleotides AA/TT are found at this particular distance from each other. (b) Normalized power spectrum Q*(P) generated by Fourier transform from the histogram. The ordinate displays a measure of strength of a periodic signal corresponding to the period P shown by the abscissa. See Materials and Methods for details.

A section of the R*(s) plot between values s_min and s_max is converted to a power spectrum by Fourier transform. The power spectrum measures the strength of a periodic signal, Q(P), corresponding to the period P. It is defined as

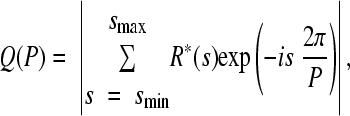where i is the imaginary unit. To allow comparisons among sequences of different properties, the power spectrum is subsequently normalized to an average value of 1 over a desired range of periods (we used the range 5 to 20 bp in this work), yielding

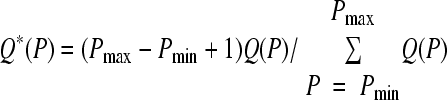(Fig. 1b). We refer to the function Q*(P) as the “periodicity plot.”

The choice of parameters s_min and s_max is important for detection of the periodic signal related to DNA curvature. Following the information in literature and our own extensive testing, we chose the range 30 to 100 bp. The upper limit is dictated by the observation that in most genomes the periodic signal extends only over distances up to 100 to 150 bp (13, 38). A lower limit of 30 bp excludes most of the signal that can arise from α-helices in proteins (α-helices involve ∼3.6 amino acids per helical turn, translating into an ∼10.8-bp period in the nucleotide sequence), which affects only a short range of distances (13, 14, 43).

Periodicity scan: sliding-window analysis of sequence periodicity.

Major peaks in the periodicity plot (Fig. 1b) indicate a strong periodic signal in the spacing of selected sequence motifs, but the plot itself does not tell whether the signal comes from a few short DNA segments or if it is widely distributed throughout the genome. In the periodicity scan, we apply the technique described above in a sliding-window mode (Fig. 2a). The shade of gray signifies the intensity of the periodic signal corresponding to the period showed by the vertical axis and the window position indicated on the horizontal axis. That is, each vertical line in Fig. 2a represents the same Q*(P) plot as in Fig. 1b corresponding to the specific window in the analyzed sequence. We used window sizes of 50, 10, and 2 kb to analyze intrachromosomal heterogeneity of the periodic signal at different scales. The window is shifted by one-half of its length at each step; that is, the adjacent windows overlap by 50% of their size.

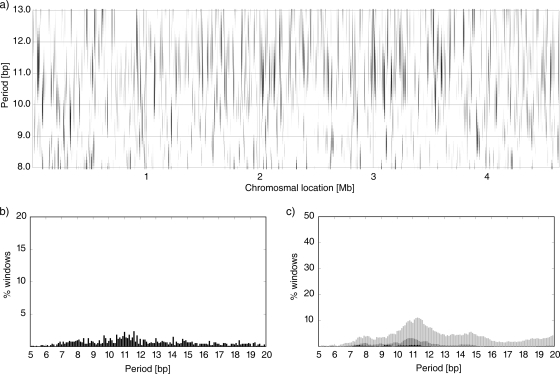
FIG. 2.

(a) Periodicity scan of the E. coli K-12-MG1655 chromosome. The signal intensity Q*(P) is signified by the level of gray for a given chromosomal location shown on the horizontal axis and the period shown on the vertical axis. The white areas correspond to Q*(P) of ≤1.5, whereas black indicates Q*(P) of ≥3.0. A 10-kb window was shifted by 5 kb at a time. (b) Percentage of windows with the strongest signal at the period indicated by the abscissa. (c) Percentage of windows with Q*(P) of ≥2.0 (light gray), ≥2.5 (dark gray), and ≥3.0 (black). See Materials and Methods for details.

Two types of summary statistics are used to further analyze the periodicity scans. The plot in Fig. 2b shows the percentage of all (partially overlapping) windows that have the strongest signal (max[Q*(P)]) at the period shown by the abscissa. In the plot shown in Fig. 2c, the ordinate signifies the percentage of all windows that have the periodic signal Q*(P) greater than some specified cutoff value for the period P.

Comparisons among genomes.

We generated the periodicity plot and periodicity scan data for all 1,025 genomes using several different sets of parameters. To simplify the comparisons among many different genomes, we use several indices that measure the strength and persistency of the periodic signal in each chromosome (Table 1). The MaxQ and PMaxQ indices describe the strongest periodic signal in the whole genome context. The other three pairs of indices reflect both the strength of the signal and its persistency at a given scale, which is determined by the sliding-window size. PMaxMax corresponds to the prevalent period throughout the chromosome, and MaxMax measures the fraction of the chromosome dominated by this period. As such, the MaxMax/PMaxMax indices measure the persistency of the dominant periodic signal but do not depend on its absolute strength. The Max2/PMax2 and Max3/PMax3 pairs of indices reflect both the strength of the signal and its persistency throughout the chromosome. Discrepancies among the PMaxMax, PMax2, and PMax3 values are indicative of weak or inconsistent signals that can arise from noise or various artifacts, such as the presence of repetitive sequences.

TABLE 1.

Summary indices used for comparisons of periodicity patterns among different DNA sequences

Index	Definition
MaxQ	Maximum value Q*(P) in the periodicity plot (the highest peak in Fig. 1b)
PMaxQ	The period P corresponding to MaxQ
Max2	The largest fraction of windows with Q*(P) ≥ 2.0 (the highest light gray peak in Fig. 2c)
PMax2	The period corresponding to Max2
Max3	The largest fraction of windows with Q*(P) ≥ 3.0 (the highest black peak in Fig. 2c)
PMax3	The period corresponding to Max3
MaxMax	The largest fraction of windows with the maximum signal at the given period ± 0.2 bp (i.e., the maximum sum of any five consecutive values in Fig. 2b)
PMaxMax	The period corresponding to MaxMax

Random simulations.

Simulations with random sequences were used to assess significance of specific MaxQ values. Ten random sequences were generated for each of the 1,025 analyzed chromosomes matching its length and overall nucleotide composition. The median MaxQ value among the resulting 10,250 random sequences was 2.0; about 9% random sequences produced MaxQ values of ≥2.5, and about 1.5% had MaxQ values of ≥3.0. Hence, while MaxQ values of ∼2 are typical of random sequences, values of ∼3 or greater are likely to reflect periodic patterns beyond random.

Data and software availability.

The raw periodicity plot and periodicity scan data (both tabular and graphical form) for the 1,025 prokaryotic chromosomes analyzed in this work can be downloaded from our laboratory web server at http://www.cmbl.uga.edu/downloads/data_sets/2010/. The programs used to generate the data written in C are available upon request from the author.

RESULTS

Periodicity plot comparisons among prokaryotes.

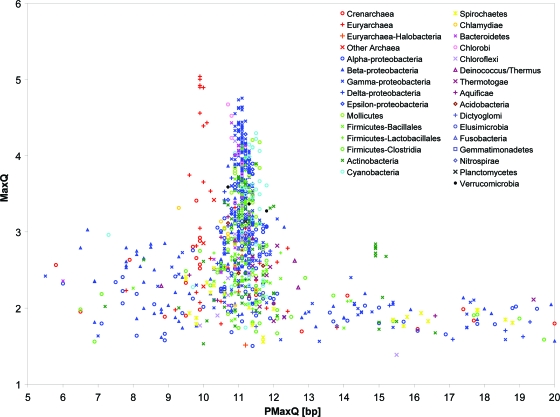
Figure 3 and Table S1 in the supplemental material show the MaxQ and PMaxQ indices for all 1,025 chromosomes analyzed with the A2T2 method (dinucleotides AA/TT) and spacing range 30 to 100 bp. Consistent with earlier work (14, 27, 34), most bacteria have PMaxQ around 11 bp or slightly higher whereas many archaea have PMaxQ near 10 bp. For genomes analyzed previously by Schieg and Herzel (34), the PMaxQ rarely differs by more than 0.1 bp from their “fitting period” (see Table S1 in the supplemental material). However, the data in Fig. 3 and Table S1 in the supplemental material show additional general tendencies characteristic of different taxonomic groups, which extend beyond the distinction between bacteria and archaea. For example, the proteobacteria (and especially gammaproteobacteria) often have a very strong periodic signal, while many clostridia have no significant signal near the 10- to 11-bp period. The predominant period PMaxQ in cyanobacteria tends to be slightly larger than that in most other bacteria. Notably, less than 50% archaeal chromosomes in our data set have PMaxQ of ∼10 bp (specifically, 31 of 66 archaea have PMaxQ in the range 9.5 to 10.5 bp) and many archaea have only a weak periodic signal (28 of the 66 have MaxQ of <2.5).

FIG. 3.

MaxQ and PMaxQ indices for 1,025 prokaryotic chromosomes using the A2T2 method and spacing ranging from 30 to 100 bp. See Table S1 in the supplemental material for tabulated data.

Some chromosomes have PMaxQ far from the DNA helical period (∼10.5 bp), but these are generally weak periodic signals with MaxQ of ∼2.0, which are typical of random sequences. Repeats can under some circumstances also generate periodic signals. For example, all strains of Mycobacterium tuberculosis and Mycobacterium bovis included in this study stand out in Fig. 3 with PMaxQ of 15 bp and MaxQ of about 2.5. This weak periodic signal is generated by pentapeptide repeats in some of the PPE family proteins and disappears when the PPE genes are masked out (data not shown). Results obtained with the AT and AT4 methods are similar to those obtained with the A2T2 method (see Fig. S1 and S2 in the supplemental material).

Assessments of intragenomic heterogeneity of the periodic signal.

A periodicity scan facilitates assessments of intrachromosomal heterogeneity of the periodic signal and its comparisons among different genomes. The E. coli chromosome was previously shown to contain a number of short (up to ∼130-bp) intrinsically bent segments, which are distributed throughout the chromosome (38). However, a periodicity scan with a 10-kb sliding window (Fig. 2) shows significant heterogeneity of the periodic signal along the chromosome. There are long sections lacking the periodic signal, and the predominant period in segments with a strong signal varies, while periods of ∼11 bp are most common.

Most prokaryotic genomes exhibit patterns similar to that for E. coli: a strong signal with an ∼11-bp period (or ∼10 bp in some archaea) when assessed from the whole chromosome but with a significant heterogeneity among different chromosomal regions in terms of both the intensity of the signal and the predominant period, as revealed by a sliding-window scan. Figure 4 shows the MaxMax and PMaxMax indices for the 1,025 analyzed chromosomes. MaxMax measures the fraction of the chromosome which shows a consistent periodic signal (within a narrow period range) regardless of the signal intensity. The data in Fig. 4 indicate that only few of the analyzed chromosomes exhibit a consistent sequence periodicity over a large part of the chromosome length. Specifically, 33 of the 1,025 chromosomes have MaxMax of ≥20. These include mostly mycoplasmas, epsilonproteobacteria, and cyanobacteria among bacterial taxa and Methanococcus as the only genus representing archaea (Fig. 4; see Table S2 in the supplemental material). The Max2 and Max3 indices, which reflect both the intensity and homogeneity of the periodic signal, show a qualitatively similar picture (see Fig. S3 in the supplemental material). The organisms with very strong and exceptionally persistent sequence periodicity throughout the chromosome (Table 2) are investigated in detail.

FIG. 4.

MaxMax and PMaxMax indices for 1,025 prokaryotic chromosomes using the A2T2 method, spacing ranging from 30 to 100 bp, and a 10-kb sliding window. See Table S2 in the supplemental material for tabulated data.

TABLE 2.

Periodicity indices for selected prokaryotes^a

Chromosome	Indexb
	PMaxMax (bp)	MaxMax (%)	PMax2 (bp)	Max2 (%)	PMax3 (bp)	Max3 (%)
Mycoplasma hyopneumoniae 232	10.9	64.8	10.8	82.12	10.9	45.25
Mycoplasma hyopneumoniae 7448	10.9	62.7	10.9	83.24	10.8	40.54
Mycoplasma hyopneumoniae J	10.9	58.33	10.6	82.78	10.8	41.67
Methanococcus maripaludis C6c	9.9	54.15	10.0	62.75	10.0	20.92
Methanococcus maripaludis C7c	10.0	51.83	9.9	61.69	9.9	19.72
Methanococcus maripaludis S2c	10.0	49.85	10.1	57.66	9.9	21.02
Methanococcus vannielii SBc	9.9	49.57	9.8	59.71	10.0	17.10
Methanococcus maripaludis C5c	10.0	48.46	10.1	61.06	10.0	17.65
Campylobacter fetus 82-40	11.3	45.07	11.4	68.17	11.3	16.62
Campylobacter concisus 13826	11.3	44.28	11.2	66.18	11.3	21.17
Mycoplasma pulmonis UAB CTIP	11.4	39.38	11.3	49.74	11.4	16.06
Mycoplasma genitalium G37	11.5	39.32	11.3	50.43	11.6	14.53
Cyanothece strain PCC 8801	11.5	37.29	11.5	58.87	11.5	14.64
Campylobacter curvus 525.92	11.4	35.19	11.5	49.11	11.4	9.87
Cyanothece strain ATCC 51142d	11.5	34.35	11.5	52.68	11.5	10.13
Trichodesmium erythraeum IMS101	11.4	33.66	11.5	50.48	11.5	11.41
Escherichia coli K-12 MG1655	11.1	8.41	11.3	11.10	10.9	0.54
Bacillus subtilis 168	8.3	5.69	10.0	7.23	7.8	0.24
Burkholderia pseudomallei K96243d	9.1	6.63	11.2	7.61	8.1	1.23
Streptomyces coelicolor A3(2)	10.6	6.17	10.5	7.55	10.1	0.35
Anabaena variabilis ATCC 29413	9.8	6.75	11.3	9.34	11.5	0.55
Deinococcus radiodurans R1d	11.4	6.60	11.0	8.11	8.9	0.38
Aquifex aeolicus VF5	10.5	11.25	10.8	15.43	7.0	0.96
Halobacterium strain NRC-1c	9.1	7.20	9.4	8.19	11.0	0.50
Pyrococcus furiosus DSM 3638c	11.2	7.33	11.2	10.99	9.1	0.79

^aAll chromosomes with the MaxMax, PMax2 or PMax3 value among the top 10 are included (top part). Some model organisms were included for comparison (bottom part).

^bSee Table 1 and Materials and Methods for definitions. The periodicity was assessed by the A2T2 method and with a 10-kb sliding window. The data for all 1,025 chromosomes, for AT and AT4 methods, and for 50-kb and 2-kb sliding windows are shown in Table S2 in the supplemental material.

^cArchaea.

^dChromosome 1.

Methanococcus maripaludis is a mesophilic, strictly anaerobic methanogen. We chose the strain S2 for detailed investigation because it is a model strain most often used in laboratory studies. Figure 5 displays the periodicity scan results with a 10-kb sliding window. The periodic signal is exceptionally persistent throughout the chromosome, with more than 50% of the 10-kb windows exhibiting a maximum between periods 9.8 and 10.2 bp. A comparison with Fig. 2 shows a striking contrast between a chromosome with a “typical” sequence periodicity (E. coli) and a chromosome with an exceptionally strong and persistent periodic signal. Few extended segments of the Methanococcus maripaludis chromosome are devoid of the periodic signal. We identified all 10-kb windows that have Q*(P) of <1.5 for 9.5 ≤ P ≤ 10.5, and we refer to those regions as “aperiodic segments.” Of 1,772 annotated genes (including both protein-coding and RNA-coding genes), 467 overlap with the aperiodic segments (see Table S3 in the supplemental material; the annotation was downloaded from the IMG database [http://img.jgi.doe.gov/]). Many of these genes are known or presumed to be highly expressed (21). For example, the list includes 37 ribosomal protein genes, 6 rRNA genes and other enzymes involved in protein biosynthesis, several multisubunit protein complexes involved in energy metabolism, particularly methanogenesis, and the S-layer protein gene, which is highly abundant in methanococci (18).

FIG. 5.

Periodicity scan of the Methanococcus maripaludis S2 chromosome. See legend to Fig. 2.

We used our previously developed method (19, 20, 29) and software (http://www.cmbl.uga.edu/software/phxpa.html) to predict highly expressed (PHX) and alien (PA) genes of the Methanococcus maripaludis genome. A total of 153 genes were identified as PHX, and 81 of those were located in the aperiodic segments (see Table S3 in the supplemental material). This is significantly more than expected if PHX genes were distributed randomly, indicating a significant bias in the distribution of PHX genes toward aperiodic segments (Table 3). In contrast, distribution of PA genes with respect to the aperiodic regions appears unbiased. Somewhat weaker but still highly significant bias with respect to PHX genes was detected in Methanococcus maripaludis C6 (see Table S4 in the supplemental material). On the other hand, Methanococcus vannielii exhibits only marginal bias of PHX genes toward aperiodic regions (see Table S5 in the supplemental material and Table 3).

TABLE 3.

Distribution of predicted highly expressed (PHX) and putative alien (PA) genes in aperiodic segments in selected genomes

Chromosome	No. of genesa
	Annotated	In aperiodic segments	All PHX	PHX in aperiodic segmentsb	All PA	PA in aperiodic segmentsb
Methanococcus maripaludis S2c	1,772	467	153	81 (40; <10−11)	22	7 (6; 0.35)
Methanococcus maripaludis C6c	1,871	412	140	56 (31; <10−5)	40	11 (9; 0.25)
Methanococcus vannielii SBc	1,729	392	113	37 (26; 0.01)	25	9 (6; 0.09)
Mycoplasma hyopneumoniae 232	728	52	28	3 (2; 0.32)	5	0 (0.4; 1.0)
Campylobacter fetus 82-40	1,775	350	94	35 (19; <10−4)	29	10 (6; 0.05)
Campylobacter concisus 13826	1,988	391	140	38 (28; 0.02)	94	65 (18; <10−24)
Campylobacter curvus 525.92	1,931	597	133	51 (41, 0.04)	89	35 (28, 0.06)
Cyanothece strain PCC 8801	4,309	1,287	489	188 (146; <10−4)	122	47 (36; 0.03)
Trichodesmium erythraeum IMS101	4,531	1,711	288	144 (109; <10−4)	245	105 (93; 0.06)

^aPHX and PA genes were identified using the software available at http://www.cmbl.uga.edu/software/phxpa.html. All are annotated protein coding and RNA genes. Pseudogenes are excluded. PHX and PA predictions are limited to protein coding genes.

^bThe expected number and P values are shown in parentheses. Probabilities were calculated from binomial distribution.

^cArchaea.

We further compared the periodicity scan data with results from RNA tiling arrays for Methanococcus maripaludis S2 (unpublished data kindly provided by Min Pan, Chris Bare, Sung Ho Yoon, Sujung Lim, John Leigh, and Nitin Baliga). These data consist of normalized RNA concentrations for tiling 60-bp probes at eight time points along the growth curve and estimated probabilities that a given probe is complementary to a transcribed region (p_exp; see reference 23 for a detailed description of the method). We divided the chromosome into partially overlapping 10-kb segments (5-kb overlap) and used the mean p_exp value for all probes from each segment on both DNA strands as a measure of transcriptional activity in that segment. These mean expression probabilities were subsequently compared with the MaxQ value for that 10-kb segment (see Fig. S4 in the supplemental material). These comparisons indicated significant negative correlations with Pearson correlation coefficients r = −0.30 (P < 0.0001) and r = −0.20 (P = 0.0003) for the AT and A2T2 methods, respectively. The AT4 method yielded an insignificant r = 0.03 (P = 0.3). The probabilities in parentheses were determined using the online calculator at http://faculty.vassar.edu/lowry/rsig.html. Notably, the segments with a very high mean probability of expression lacked a strong periodic signal (see Fig. S4 in the supplemental material).

Mycoplasma hyopneumoniae 232 possesses an even more consistent periodic signal than Methanococcus maripaludis but with a maximum at a period of 10.9 bp (see Fig. S5 in the supplemental material). The shift in the predominant period is consistent with the previously reported distinction between bacteria and archaea (14, 34). We define aperiodic segments as those with Q*(P) of <1.5 in the range 10.4 ≤ P ≤ 11.4. Only 52 of the 728 annotated genes are located in the aperiodic segments, and they include mostly hypothetical genes of unknown function (see Table S6 in the supplemental material). Only 28 genes qualify as PHX in Mycoplasma hyopneumoniae, while 5 Mycoplasma hyopneumoniae genes are PA. Neither the PHX nor the PA genes exhibit a significant bias toward aperiodic segments (Table 3). However, it is worthwhile to note that mycoplasmas lack many regulatory pathways common in other bacteria and most genes are believed to be expressed constitutively (7). Moreover, most mycoplasmas grow very slowly and likely contain few, if any, genes synthesized at rates comparable with those of the most highly expressed genes in fast-growing bacteria. Other Mycoplasma species in Table 2 (Mycoplasma pulmonis and Mycoplasma genitalium) are similar to Mycoplasma hyopneumoniae in having very few PHX and PA genes, which are distributed randomly with respect to aperiodic segments (data not shown).

The epsilonproteobacterium Campylobacter fetus 82-40 is a mammalian pathogen with motile curved rod-shaped cells, growing in microaerophilic or anaerobic environments. Its chromosome has the strongest periodic signal at a period of 11.3 bp, and we define aperiodic segments as those with Q*(P) of <1.5 in the range 10.8 ≤ P ≤ 11.8 (see Fig. S6 in the supplemental material). Of 1,775 annotated genes, 350 overlap with the aperiodic segments (see Table S7 in the supplemental material). They include 34 ribosomal proteins and several other enzymes involved in translation, proteins participating in major energy and carbon metabolism pathways, three outer membrane proteins, 4 rRNA and 24 tRNA genes, and 69 hypothetical proteins. The distribution of PHX genes is significantly biased toward the aperiodic segments (Table 3). In contrast, Campylobacter concisus 13826 and Campylobacter curvus 525.92 show only marginal bias of PHX genes toward aperiodic segments (Table 3). PA genes are very strongly concentrated in aperiodic segments in the C. concisus chromosome. In particular, the largest contiguous aperiodic region contains several phage-related genes and likely represents a genomic island acquired by lateral transfer (see Table S8 in the supplemental material).

The unicellular, nitrogen-fixing cyanobacterium Cyanothece strain PCC 8801 features a consistent periodic signal spanning most of its chromosome with a predominant period about 11.5 bp, larger than that of most bacteria (see Fig. S7 and Tables S1 and S2 in the supplemental material). We define aperiodic segments as those with Q*(P) of <1.5 in the range 11.0 ≤ P ≤ 12.0. Of 4,309 annotated genes, 1,287 overlap with the aperiodic segments, including 22 ribosomal protein genes and a number of photosynthetic enzymes but also many other genes of diverse functions (see Table S9 in the supplemental material). The bias of PHX genes toward aperiodic regions is statistically significant (Table 3). Interestingly, the periodicity scan shows a weak secondary maximum at period ∼10.0 bp (see Fig. S7b and c in the supplemental material). The strongest signal with an ∼10-bp period [Q*(P) ≥ 4.0 using the A2T2 method and a 2-kb sliding window] pertains to the region at 1,306 to 1,316 kb. We investigated whether this region could be acquired by lateral transfer from archaea. Most genes encoded in this region have top BLAST (1, 16) hits to diverse bacteria, and one, the GCN5-related N-acetyltransferase, has top hits among plants (see Table S10 in the supplemental material). Note that hits to cyanobacteria are excluded and all genes in this region are in fact more similar to genes from distant cyanobacteria than to those from noncyanobacteria. These results suggest that the 10-bp period in this region is unlikely due to lateral transfer from archaea.

Similar to most other cyanobacteria, Trichodesmium erythraeum IMS101 has the strongest periodic signal around period 11.5 bp (see Fig. S8 in the supplemental material). Of 4,531 annotated genes, 1,711 overlap with the aperiodic segments, more than a third of the genome (see Table S11 in the supplemental material). The distribution of PHX genes shows a moderate but significant bias toward aperiodic regions (Table 3).

Periodic signal in protein-coding and noncoding regions.

We tested whether the periodic signal originates in protein-coding regions, noncoding regions, or both. For the purpose of this investigation, all genome segments annotated as coding sequences (those labeled “CDS” in the features table of the GenBank files) are considered protein coding and all other segments are noncoding. After the appropriate regions were masked out, the resulting sequence was processed using the same methods that were applied to complete chromosomes. The MaxQ and PMaxQ indices for the 1,025 chromosomes restricted to protein-coding and noncoding regions are shown in Fig. S9 and S10, respectively, in the supplemental material. The results for protein-coding regions are similar to those obtained with complete chromosomes (Table 4). This is not necessarily surprising considering that in most prokaryotes about 80 to 90% of their DNA is protein coding. On the other hand, noncoding sequences comprise a small fraction of the chromosome and consist mostly of short contiguous segments (most intergenic sequences are <100 bp in length), which makes weak periodic signals more difficult to detect. Nevertheless, the periodic signals in intergenic regions are still dominated by periods about 10 to 11 bp (see Fig. S10 in the supplemental material), indicating that the sequence periodicity related to DNA bending transcends both protein-coding and noncoding segments.

TABLE 4.

Comparison of periodic signals in protein-coding and noncoding sequences among selected prokaryotes^a

Chromosome	Complete sequence		Protein coding		Noncoding
	PMaxQ (bp)	MaxQ	PMaxQ (bp)	MaxQ	PMaxQ (bp)	MaxQ
Mycoplasma hyopneumoniae 232	10.9	3.84	10.9	3.96	10.8	2.29
Methanococcus maripaludis S2b	9.9	4.90	9.9	4.91	10.0	3.11
Campylobacter fetus 82-40	11.4	3.82	11.3	3.99	11.2	2.16
Cyanothece sp. PCC 8801	11.6	4.06	11.6	4.10	11.8	2.25
Trichodesmium erythraeum IMS101	11.5	4.29	11.6	4.32	11.4	4.19
Escherichia coli K-12 MG1655	11.1	4.44	10.9	4.63	11.1	2.37
Bacillus subtilis 168	10.9	2.35	11.3	2.01	12.6	1.85
Burkholderia pseudomallei K96243c	11.0	2.51	11.1	2.49	7.8	2.12
Streptomyces coelicolor A3(2)	11.4	2.77	11.3	2.63	11.4	1.97
Anabaena variabilis ATCC 29413	11.5	2.83	11.4	2.94	9.5	2.04
Deinococcus radiodurans R1c	11.4	2.92	11.4	2.76	9.1	1.81
Aquifex aeolicus VF5	10.7	3.20	10.7	3.19	16.8	1.74
Halobacterium strain NRC-1b	11.0	2.49	10.8	2.86	19.6	2.36
Pyrococcus furiosus DSM 3638b	12.4	1.96	10.3	2.32	9.4	2.42

^aMaxQ and PMaxQ indices are shown for the complete chromosome, protein-coding regions, and noncoding regions assessed by the periodicity scan with the A2T2 method. See Table 1 and Materials and Methods for definitions.

^bArchaea.

^cChromosome 1.

Some chromosomes exhibit strong periodic signals with unexpected periods (i.e., substantially different from the ∼10.5-bp period related to DNA structure) in their noncoding sequences, most notably several Burkholderia strains, which have a strong signal at a period of 7 bp. These arise from extended tandem heptanucleotide repeats, which are common in some large prokaryotic genomes (28).

DISCUSSION

Sequence periodicity and DNA supercoiling.

Our results confirm a bimodal distribution of predominant periodicities among prokaryotes previously observed by Herzel and coworkers and ascribed to different supercoiling propensities (13, 14, 34). However, the larger collection of analyzed genomes and analysis of intrachromosomal heterogeneity of the periodic signal performed in this study provide a more nuanced picture. Less then 50% of archaeal chromosomes analyzed here exhibit a period of ∼10 bp (Fig. 3 and 4; see Tables S1 and S2 in the supplemental material). Several, mostly halobacterial chromosomes, have predominant periods close to 11 bp, similar to those of most bacterial genomes, and some archaea show only weak periodic signals that could arise from random noise. Moreover, only members of the genus Methanococcus have a strong periodic signal spanning most of the chromosome length, whereas other archaea (as well as bacteria) have majority of the chromosome devoid of a strong periodic signal (Table 2; see Table S2 in the supplemental material). Our data do not necessarily dispute the relationship between sequence periodicity and DNA supercoiling, which remains a plausible explanation for the bimodal character of predominant sequence periodicities in prokaryotes. However, archaea are not a coherent group in terms of sequence periodicity. Bacteriumlike 11-bp periodicities in some halophilic archaea and Methanopyrus kandleri were reported earlier (27, 34), and results presented here show additional differences in the distribution of the periodic signal along the chromosome. Moreover, intrachromosomal heterogeneity of the periodic signal pertinent to most bacteria and archaea suggests that even if the sequence periodicity promotes the appropriate mode of supercoiling (positive or negative) it applies only to some chromosomal regions whereas supercoiling in the rest of the chromosome is likely determined by other factors, which could include intracellular concentrations of various DNA binding proteins, gene expression patterns, or intracellular salt concentrations, among others (27).

The intrachromosomal heterogeneity of the periodic signal could also arise from a rampant lateral gene transfer between bacteria and archaea, as was proposed for Thermotoga maritima (42). However, it is unlikely that all or even most of the observed heterogeneity can be attributed to lateral transfer. Notably, when we investigated in detail an atypical region with a strong 10-bp periodicity in the otherwise >11-bp-periodic Cyanothece strain PCC 8801 chromosome, we found no indication that it may have been acquired from archaea (see Table S10 in the supplemental material).

Role of periodicity-induced DNA curvature in nucleoid packaging.

Tolstorukov et al. (38) investigated the distribution of intrinsically bent DNA segments characterized by periodically spaced A-tracts in E. coli and several other bacteria. They found that continuous bent segments generally do not exceed 100 to 150 bp in length, which is consistent with earlier results (13, 14) as well as data presented here. They also found that 70% of the bent segments are located in protein-coding regions, which appeared to contradict earlier observations that DNA curvature in prokaryotes is concentrated in intergenic regions, primarily near transcription promoters and terminators (4, 24). Our results confirm that most of the periodic signal indicative of DNA curvature originates in protein-coding regions (see Fig. S9 and S10 in the supplemental material). Tolstorukov et al. (38) proposed that the bent DNA segments play a role in the packaging of DNA in the nucleoid structure: the irregular supercoiled loops that form in the nucleoid contain sharp DNA bends, which can be stabilized by intrinsically curved DNA segments or by DNA-interacting proteins. The intrinsic bends can also drive branching of the plectonemic superhelix during nucleoid formation and thus influence topology of the DNA loops (38). Our results are generally consistent with this nucleoid packaging model. However, the observation that the periodic signal in most prokaryotic genomes is significantly heterogeneous at the scale of kilobases to tens of kilobases (Fig. 2; see Table S2 in the supplemental material) requires a modification of the model: we proffer that some sections of the chromosome can form rigid DNA loops stabilized by intrinsically bent segments, whereas other DNA loops can be dynamic or stabilized by DNA-protein interactions. The relative proportions of rigid and flexible chromosomal segments can vary dramatically among different prokaryotes. This structural heterogeneity of the nucleoid can be important in basic cellular processes such as transcription, replication, recombination, or integration of foreign DNA.

DNA periodicity and gene expression.

The observation that highly expressed genes preferentially localize at aperiodic segments in some of the analyzed genomes is consistent with the modified nucleoid packaging model and the notion that different DNA loops can have different structural characteristics. It concurs with a previous work, where DNA accessibility derived from nucleosome positioning preferences in eukaryotic chromatin was proposed as a predictor of gene transcription levels in both eukaryotic and prokaryotic microbes (41). Although bacteria do not possess the nucleosomes found in eukaryotic chromatin, the sequence periodicity is the main component of nucleosome positioning signals, and the nucleosome positioning preference can reflect DNA bending in general rather than specifically wrapping of DNA around nucleosomes. In this regard, it is interesting to note that none of the prokaryotes with a persistent periodic signal (Table 2) has very fast doubling times (i.e., less than ∼1 h). Fast growth requires high expression of a number of genes, and absence of a persistent periodic signal in fast-growing bacteria is therefore expected if sequence periodicity interferes with high rates of transcription. The relationship between sequence periodicity and gene expression in bacteria parallels earlier investigations of DNA periodicity in Caenorhabditis elegans, where a locally strong periodic signal in the DNA sequence was shown to affect both the chromatin structure and gene expression (9, 12, 17). Fig. S11 in the supplemental material shows the periodicity scan of the Caenorhabditis elegans chromosome 4, which clearly differentiates the chromosomal arms with a strong periodic signal from a mostly aperiodic region near the centromere. In E. coli, gene expression was shown to be affected by changes in DNA supercoiling (3, 30). However, these experiments used modifications to the DNA topoisomerase activity or mutations in nucleoid proteins to induce changes in DNA supercoiling, which can have different effects than intrinsic DNA bending caused by sequence periodicity.

Genomes with exceptionally persistent periodic signals.

Most prokaryotic genomes have the periodic signal concentrated in several relatively small sections of the chromosome rather than consistently distributed throughout its length (Fig. 2 and 4; see Table S2 in the supplemental material). However, some genomes stand out with a periodic signal persistently spread through a majority of the chromosome. Those with the most persistent periodic signal include multiple representatives of the genus Methanococcus, some but not all species of Mycoplasma, most epsilonproteobacteria (Campylobacter near the top of the list and Helicobacter slightly behind), some cyanobacteria (mostly of the order Chroococcales), several gammaproteobacteria (particularly Shewanella species and Pasteurellaceae but also the sulfur-oxidizing symbionts “Candidatus Ruthia magnifica” and “Candidatus Vesicomyosocius okutanii” and representatives of other clades) and some Bacteroidetes (see Table 2 and Table S2 in the supplemental material for complete list). What do these organisms have in common, and what role, if any, do the persistent periodic signal and concomitant intrinsic DNA bending have in their physiology? This collection of organisms is rather diverse in terms of taxonomy, environment, lifestyle (from free-living environmental organisms to highly specialized symbionts or pathogens), morphology, and physiology (2, 5, 10, 11), suggesting that the persistent periodic signal is not a result of adaptation to a particular environment or a characteristic of a specific clade. There are no extremophiles in the list, ruling out a role in adaptation to extreme environments. The absence of a persistent periodic signal in thermophiles is consistent with earlier observations that strong DNA curvature near promoter and terminator regions is restricted to mesophiles (4, 24). One common characteristic among the genomes with persistent periodicity is their low G+C content, but that is not necessarily surprising, considering that it is the short runs of A or T that generate the signal in the first place. Along these lines, we reported earlier that among Mycoplasma species, an excess of short (4- to 7-bp) runs of A or T is correlated with a strong periodic signal (26).

In accordance with the nucleoid packaging model (38), we proffer that the chromosomes of these organisms contain more abundant and more uniformly distributed intrinsically bent segments than typical prokaryotes. That could facilitate tighter packaging of the DNA in the nucleoid or more rigid conformation of DNA loops. In an analogy to eukaryotic chromatin (17, 33), rigid nucleoid structure could constrain transcriptional activity, which is consistent with the observation that highly expressed genes tend to concentrate in aperiodic segments. It is intriguing to speculate that the intrachromosomal heterogeneity of the periodic signal and associated DNA curvature could play a role in regulation of gene expression. It has been known that chromosomal location of genes in prokaryotes is not random, but the nonrandomness has been generally ascribed to locations relative to the origin and terminus of replication, colocalization of coexpressed genes, or evolutionary constraints related to lateral gene transfer or gene amplification (6, 8, 15, 25, 31, 32). We propose that heterogeneity of physical structure of the nucleoid reflected in the intrachromosomal variance of sequence periodicity can serve as an additional constraint on gene location, possibly by modulating the gene expression in different chromosomal regions. Differences in the character of the periodic patterns between genomes can reflect overall regulatory modes of each individual organism and/or organism-specific aspects of nucleoid structure, in particular the composition and cellular concentrations of the ensemble of DNA-interacting proteins.