On the convexity of ROC curves estimated from radiological test results

Abstract

Rationale and Objectives

Although an ideal observer’s receiver operating characteristic (ROC) curve must be convex — i.e., its slope must decrease monotonically — published fits to empirical data often display “hooks.” Such fits sometimes are accepted on the basis of an argument that experiments are done with real, rather than ideal, observers. However, the fact that ideal observers must produce convex curves does not imply that convex curves describe only ideal observers. This paper aims to identify the practical implications of non-convex ROC curves and the conditions that can lead to empirical and/or fitted ROC curves that are not convex.

Materials and Methods

This paper views non-convex ROC curves from historical, theoretical and statistical perspectives, which we describe briefly. We then consider population ROC curves with various shapes and analyze the types of medical decisions that they imply. Finally, we describe how sampling variability and curve-fitting algorithms can produce ROC curve estimates that include hooks.

Results

We show that hooks in population ROC curves imply the use of an irrational decision strategy, even when the curve doesn’t cross the chance line, and therefore usually are untenable in medical settings. Moreover, we sketch a simple approach to improve any non-convex ROC curve by adding statistical variation to the decision process. Finally, we sketch how to test whether hooks present in ROC data are likely to have been caused by chance alone and how some hooked ROCs found in the literature can be easily explained as fitting artifacts or modeling issues.

Conclusion

In general, ROC curve fits that show hooks should be looked upon with suspicion unless other arguments justify their presence.

Introduction

The history of science is the story of cyclical interaction between theoretical models and experiments. The present paper is concerned with the science of binary decision making under uncertainty and, in particular, the perspectives of receiver operating characteristic (ROC) analysis that provide a conceptual basis for nearly all applications of that science. Contemporary introductions to ROC methodology have been provided by Pepe (1), Zhou et al. (2) and Wagner et al. (3), for example.

A principal purpose of this paper is to call attention to recent refinements in the understanding of ROC models in diagnostic imaging and clinical laboratory testing. These refinements have come about through more careful scrutiny of observed data, new developments in mathematical modeling and data analysis, and a recognition of potential logical inconsistencies in the common applications and interpretations of what has become the most popular ROC paradigm. Some new developments will be recapitulated here; logical difficulties are then identified and our proposed resolution of them presented. Although our view is by no means revolutionary, we believe that it goes beyond incremental refinement. In particular, we begin by shifting attention from the diagnostic performance observed in a particular experiment to the information that such experiments provide concerning potentially improved future implementations of the technologies tested, in part because it would be unethical to discard a new diagnostic test merely on the grounds that it was employed inappropriately in a particular experiment — e.g., interpreted by observers who did not have adequate experience with the test or judged to perform poorly due to an evaluation-methodology artifact that should have been anticipated or corrected.

This paper is organized as follows. After discussing the historical emergence of ROC methodology in diagnostic assessment research, we look at some basic ROC curve shapes and define fundamental ROC concepts that are relevant to this work. We then analyze population ROC curves (those obtained when a diagnostic modality is applied to “all patients in a population”) and explore the implications and desirability of convexity. A simple algorithm will be shown to render any modality’s ROC curve convex. Subsequently, we discuss the statistics of ROC curve sampling and describe some of the conditions that can generate non-convex experimental datasets from convex population ROC curves. We will propose approaches that provide insight regarding whether a particular dataset is unlikely to have been generated by a convex population curve. We also will describe how some kinds of empirical datasets can produce fitted ROC curves with non-convex shapes that may be fitting artifacts.

Materials and methods

Some historical perspective: the NCI initiative of the late 1970s

With the arrival of the high-technology — and expensive — medical imaging revolution of the 1970s, the National Cancer Institute (NCI) initiated a contract with Bolt, Beranak, and Newman (later BBN Inc.) of Cambridge, Massachusetts, to develop a standard protocol for the collection and analysis of data to assess and compare diagnostic medical imaging technologies and other diagnostic tests. The methodology developed in that project and its results were described in a landmark paper (4) and a now-classic book (5). In brief, these publications recommended that human readers in medical imaging use an ordinal categorical scale to rate and report their levels of suspicion regarding the presence versus absence of a specified disease state, and they prescribed the use of existing binormal maximum-likelihood estimation (MLE) algorithms and software for analysis of such data within the ROC paradigm. Use of this and related reporting scales has continued to evolve (3), and the binormal-based MLE approach has continued to increase in flexibility and in the level of complexity of problems that it can address, ranging from the original work on fitting ROC curves to data from a single reader and single modality by Dorfmann and Alf (6) to testing differences between ROC curves estimated from multiple readers and/or modalities: first independent data from two or more modalities (7) and subsequently fully paired data (8), partially paired data (9) or data without truth from two modalities (10). Other methodologies not considered in this paper also have been introduced to estimate performance and/or to test differences between modalities, ranging from non-parametric methods, jackknifing, and bootstrapping to the Bayesian hierarchical models described by Pepe (1) and Wagner et al. (3) and references cited therein. ROC analysis and its generalizations are now considered widely to be the definitive methodology for assessment of “Level 2” efficacy in the conceptual hierarchy developed for assessment of medical imaging (11, 12).

The broad usefulness of the conventional binormal model has been discussed and debated extensively during the decades since its introduction. Several related cornerstones have supported use of the binormal model, despite occasional objections. First, this model does not require that data in fact arise from a pair of normal distributions, but only that they be approximately transformable to binormal by means of a monotonic transformation, which does not need to be specified. Second, a vast collection of rating data has been accumulated over the years (13–16) from psychophysical and medical diagnostic studies that seems to be very well fit by the binormal model (6). And finally, recognition of the robustness of the binormal model has led to the development of a large body of practical, broadly validated and continually up-dated software for ROC curve fitting by maximum-likelihood estimation (MLE) and statistical testing (3).

A quirk of the original binormal model, hereafter called the conventional binormal model (CvBM) in this paper, is that it can produce ROC curves with “hooks”: the slope of the curve does not decrease monotonically as one moves from left to right on the curve (17), so the curve can have a non-convex¹ shape (see Fig. 1). Such ROC curves are said to be “improper” because they cannot arise from the optimal — and arguably, more natural — use of likelihood ratio or Bayesian posterior probability as the decision variable in statistical decision-making (17). Use of likelihood ratio or posterior probability as the decision variable in a two-group classification task necessarily produces an ROC curve with monotonic slope, i.e., without hooks, which is therefore known as a “proper” ROC curve. For that reason, much work over the years has been devoted to the development of models that are constrained mathematically to avoid hooked fits and to their implementation: the so-called “proper models” (18–22). One should note in passing that “proper” ROC curves can be defined equivalently either as those that result from use of likelihood ratio (or any monotonic transformation thereof) as the decision variable or as those with monotonically decreasing slope, because the slope of any ROC curve at any operating point must equal the likelihood ratio of that curve’s decision variable at the corresponding threshold (23).

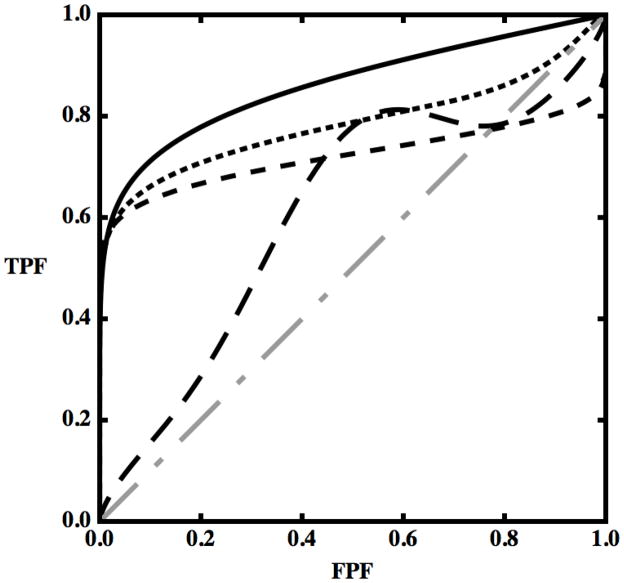
Figure 1.

Examples of ROC curves plotted together with the chance-line (dot-dashed gray line). Displayed here are a generic convex ROC curve (black), a non-convex curve with a hook but not crossing the chance-line (dotted line), a non-convex curve that crosses the chance-line (medium dashed line) and a curve that decreases, thus not being a properly defined ROC curve (long-dashed line) — see text.

Definitions of basic concepts

In this paper, mathematical terminology such as “continuous” is employed in a pragmatic rather than purist sense, because more rigorous usage would render the discussion substantially more complex without affecting its conclusions appreciably.

A patient who in fact has the disease one is trying to diagnose will be called an actually-positive case, while one who does not will be called actually-negative. This is done to preclude confusion between the positive or negative nature of a diagnostic decision, on one hand, and the actual presence or absence of the disease in question for the patient at hand, on the other.

ROC analysis can be applied to any diagnostic test that produces ordinal (i.e., inherently rank-ordered) test results. For this reason, without loss of generality we can assume that these test results are numbers (24) and that larger values imply a higher probability for the disease to be present. Cutoff values (“thresholds of abnormality” or “critical test-result values”) often are used to make binary decisions — that is, to classify each case into one of two groups: a specific decision or course of action is adopted if the test result lies above a specific numerical value (for example do further tests if a PSA level is higher than 4.0 ng/ml), whereas the complementary decision is adopted below that value. Thus, the decision strategy can be made more aggressive or more conservative simply by shifting the threshold setting.

Some medical action categories, such as those in the American College of Radiology’s BI-RADS scale (25), are (with some exceptions) inherently ordinal and as such can be used to produce ROC curves, though care may be needed to produce results that can be interpreted clearly. The concept of threshold becomes more complex in this situation, however, because the probabilities that are used to define the ordinal BI-RADS category boundaries are subjective judgments, yielding data that may differ substantially across observers. In terms of decision analysis, a reasonable model could be to assume that the various information is utilized by a statistical learning algorithm (the human observer) to produce a likelihood for the presence of the disease, whose values are then rounded into categories (4). However, it must be emphasized that there is no definitive evidence that human observers make diagnostic decisions by “computing” a likelihood and then discretizing it.

An ROC is usually plotted as a smooth, continuous curve where sensitivity, in this paper called true positive fraction (TPF), is plotted as a function of 1 – specificity, here called false positive fraction (FPF). Beginning in the lower-left corner of a unit square, related values of FPF and TPF are swept out by rendering the test progressively less strict: “operating points” on the curve with larger values of both FPF and TPF imply that less thoroughly convincing evidence is required in order to classify cases as positive (e.g., a lower “threshold” PSA value is used to classify cases as either worthy or unworthy of biopsy in testing for prostate cancer), so progressively larger fractions of both actually-positive and actually-negative cases will be classified as positive. (In accord with traditional terminology, individual points on an ROC curve sometimes will be called operating points here, because they represent particular combinations of FPF and TPF at which the diagnostic test can be “operated” by use of a particular cutoff setting.) More details can be found in the introductory documents mentioned previously (1–3). Continuous population ROC curves can be described mathematically by a latent (i.e., hypothetical and non-measurable) decision variable v, which in principle could be used to make medical decisions regarding the presence or absence of a condition with “infinitesimal” numerical precision. Setting one or more cutoffs on the value of v can be used to predict the fractions of actually-positive and actually-negative cases in a population that fall into each category on a discrete ordinal response scale, regardless of how many categories were in fact present in the actual data scale. One can easily show that (1)

$$\mathit{FPF}=1-F(v\mid -)\text{and}\mathit{TPF}=1-F(v\mid +)$$ (1)

for any v, where F is the cumulative distribution function of the random variable v over the population of interest (26), conditional upon the actual presence or absence of the medical condition in question, indicated with “+” and “−”, respectively. Throughout the following, we use v to denote both latent and actual decision-variables unless explicit distinction between the two seems necessary to avoid confusion.

Many of the following arguments distinguish explicitly between population ROC curves (what researchers usually want to estimate: the performance of a diagnostic test when it is applied to an arbitrarily large number of eligible patients, so that statistical variation is negligibly small), on one hand, and the ROC curves that are obtained from limited samples of patients (which are the only curves that can be observed in practice and must be used to infer the nature of the population curve). One should note in passing that population ROC curves are difficult to specify in the sense that disease populations are rarely invariant with time (27), which is a potentially important but rarely acknowledged limitation of many real-world assessments of medical diagnostic tests.

Although we will discuss decisions that are based only on the value of a single decision variable in the interest of simplicity, our results and conclusions can be generalized to multivariate problems. Also, with regard to samples, we will assume for simplicity that the condition in question is univocally defined and that the actual presence or absence of the condition is known with complete certainty for every case. However, our general results will apply also to ROC curves that are estimated by use of schemes that do not require knowledge of such truth (28). Many of our results will apply also to generalizations of ROC analysis that involve disease location or multiple states of truth (3), which we will not mention again here.

An ROC curve is said to be convex in this paper if, given two points A and B on the curve and a straight line s that passes between those points, there is no curve point between A and B that lies below s, for every pair of points on the curve. This is equivalent to requiring that the second derivative of TPF with respect to FPF must be negative or zero, d²TPF/dFPF² ≤ 0, or that the first derivative dTPF/dFPF is monotonically non-increasing — i.e., curve slope either is constant or decreases as one moves along the ROC curve from left to right (29). From this definition, ROC curves that contain straight line segments are considered to be convex. One should note that mathematical definitions of convexity usually do not include straight line segments and sometimes refer to situations where d²TPF/dFPF ² ≥ 0 rather than ≤ 0; however, our definition will simplify the discussion that follows here.

Figure 1 displays several curves: three with various kinds of hooks (dashed) and a convex curve (solid). One kind of hook is represented by the long-dashed curve: for part of the curve, increasing values of FPF are associated with decreasing values of TPF, so when the test is modified to yield more false positives in that range of FPF, the number of true positives decreases. Because of the inherent ordering described previously, moving a decision-variable threshold toward less strict decisions cannot decrease the value of either FPF or TPF. On the other hand, if a TPF-vs.-FPF curve were swept out by changing the way in which an image is evaluated (e.g., by modifying an automatic classifier to address data from an additional group of patients in the hope to increase sensitivity) rather than by merely changing the threshold on a decision-variable for a fixed classifier and population of patients, then in principle such a decrease in TPF could be found — e.g., because the new algorithm might classify as positive a larger proportion of actually-negative cases while at the same time reducing the fraction of actually-positive cases classified as positive, within some range of FPF. However, the resulting plot would not constitute a true ROC curve, but instead would show how sensitivity and specificity change when the decision process is changed, which is equivalent to moving among a family of ROC curves at a more or less constant decision criterion.

Two other hooked (dashed) curves are included in Fig. 1. Both increase monotonically, but one crosses the “chance-line” diagonal whereas the other doesn’t, and for this reason they are usually considered different in nature. (We note in passing that all hooked curves produced by the CvBM cross the diagonal chance line. The chance line can be thought of as the ROC curve produced by a decision variable that provides no diagnostic information about the disease in question, because it selects identical fractions of actually-positive and actually-negative cases for any cutoff setting.) These two curves are examples of the kind of ROC curves that we will discuss in the rest of this manuscript. More extremely hooked curves with sigmoidal shapes consisting of vertical and horizontal straight line segments, usually known as a “degenerate” ROCs, display essentially the same behavior as the hooked curves discussed here, so we won’t address them directly. The interested reader is referred elsewhere (30) in that regard.

Results

Population ROC curves

As mentioned above, the desire to avoid curves with hooks such as those produced by the CvBM led several research groups to introduce proper ROC curve-fitting models. At least one such model is based on the properties of an ideal observer: the proper binormal model proposed initially by Birdsall (31) and developed in detail by Metz et al. (18, 21). Ideal observers can produce only convex ROC curves (17), because they use likelihood ratio (or some monotonic transformation thereof) as the decision variable in binary decision tasks, and ROC curve slope at any operating point must equal the likelihood ratio of the decision variable at the corresponding threshold (23). However, one should note that this does not imply that convex curves can occur only when available information is used optimally, or that the proper binormal model is appropriate only for ideal observers (21). Another possible approach is to construct a model that does not allow hooks because of the latent decision-variable distributions it assumes — e.g., the bigamma model proposed by Dorfman et al. (19). Alternatively, the actually-positive population can be assumed to arise from a mixture distribution, one component of which is identical to the actually-negative distribution — often called “contamination.” Adding some distributional constraints causes such models to produce ROC curves that are always convex. One recent example of this kind of model is the “contaminated” binormal model (CBM) described by Dorfman et al. (20), which can be used to fit convex curves to datasets for which the CvBM would have produced hooked fits. Others introduced quasi-proper behavior through search models like that of Swensson (32). However, one should note that the latter model is not truly proper, because it allows hooks even though its ROC curves cannot cross the chance line.

All of these models were based on arguments at the population level and aimed at restricting population ROC curves in a way that does not allow hooks. Similarly, in the following we begin at the population level and then let the arguments suggest, explicitly or implicitly, what we consider “natural” approaches in handling hooks. We are not recommending that formal proper models should be neglected, but instead that the underlying decision variables of each process should be understood and the use of information should be optimized before one attempts to assess the clinical value of a decision process via an ROC fit.

Although some of the observations that follow are known to some investigators, they have never been analyzed systematically, to the best of our knowledge, and are not recognized widely.

Random decisions are associated with straight lines

Since an ROC curve must drop below the straight line connecting at least two of its points in order to include a hook, a natural part of our analysis of hooked curves is to review the properties of straight ROC curve segments.

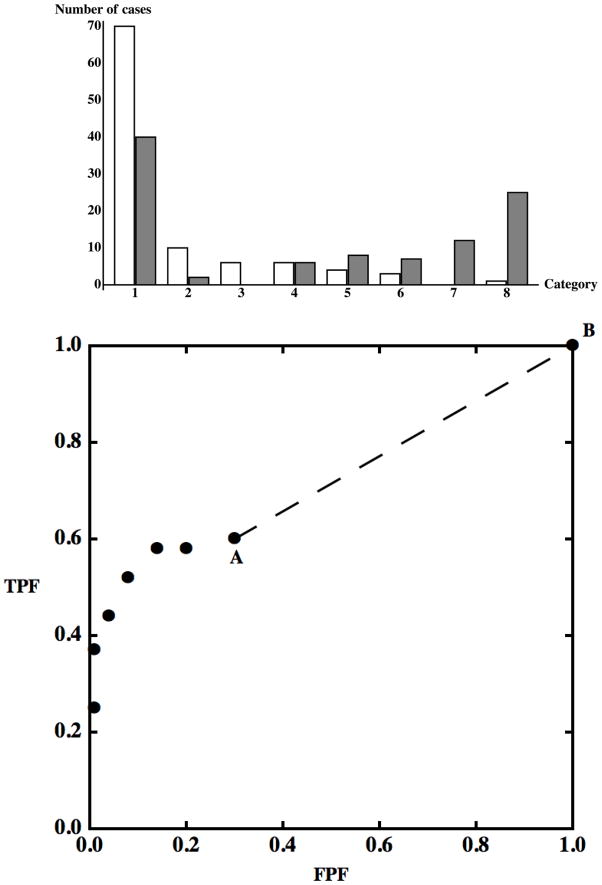
Straight-line segments are a symptom of contamination, as just defined, and they are most often associated with samples of categorical data in which the smallest or largest category is used most frequently; an example is shown in Fig. 2. If we assume that there is no sampling variability or other experimental sources of uncertainty, these plots represent the population, so the probabilities associated with each category are the population probabilities. The ROC plot in Fig. 2 has two key characteristics: it is discrete (i.e., there is “nothing” between points) and there is a large distance between points A and B. We propose to consider these characteristics while keeping in mind that an ROC curve represents the set of decisions that can be made using the available information and not just the decisions actually made in the experiment. Looking at the envelope of the first few points starting from (0,0), it seems intuitive to think of them as resulting from the discretization of some continuous decision process. Hence, if one could “undo” the discretization, the categories from 2 to 8 could be broken down into much smaller ones, perhaps even quasi-continuous values, thereby producing a continuous smooth curve. However, the last segment stands out more as a probability mass, a well-defined subset of actually-positive and actually-negative cases that cannot be split. Can we make decisions that would split category “1” just with the information we have? Let us consider the last two operating points in Fig. 2. The value FPF_A is the fraction of all actually-negative cases that would be called positive if a positive decision were made for all values v >1; likewise, TPF_A is the fraction of all actually-positive cases that would be called positive in that situation. Similarly, FPF and TPF values can be defined for point B (both of which happen to equal 1.0 for the example shown in Fig. 2). Between A and B there are specific fractions of actually-negative and actually-positive cases that we denote by p = FPF_B − FPF_A and q = TPF_B − TPF_A, respectively. Suppose that we want to split category “1” into two subcategories and assign positive cases to the first with probability λ and to the second with probability 1 − λ. For every case in category “1” we can draw a uniformly-distributed random number r ∈ [0,1]; if r > λ the case will be called positive, otherwise it will be called negative. This creates a new operating point², which with the use of some simple algebra can be shown to satisfy the relationship

Figure 2.

Upper panel. Bar chart of a simulated 8-category contaminated dataset. Actually-negative cases are displayed as white bars, actually-positive cases are displayed as gray bars. Cases in categories with a larger index have a higher probability of being actually-positive according to the hypothetical decision process we are simulating. Contamination can be observed in the category labeled “1”. Lower panel. The same dataset displayed as an ROC plot.

$$\mathit{TPF}={\mathit{TPF}}_A+(\mathit{FPF}-{\mathit{FPF}}_A)(q/p).$$

Different values of λ will produce different points on what is obviously a straight line, indicated in the plot by a dashed line segment, and we can operate at any point on this straight line between A and B by choosing an appropriate value of λ with which to compare outcomes of the random variable r. The procedure that we have described here makes no use of particular characteristics of the points A and B, so we can generalize our results in two ways. First, any discrete set of meaningful ROC points — points that represent cumulative probabilities of a decision-variable (26) — can be transformed into a well-defined and unique continuous ROC curve without using additional data: even if the decision variable is in fact discrete, we can work as if a continuous decision variable v were used to construct a continuous ROC curve through any set of ROC points. Second, if decisions are made randomly within any interval, e.g., v₁ < v ≤ v₂, the resulting ROC curve will be a straight line for the curve points corresponding to that interval. If all decisions are made randomly for all cases in the selected population, then FPF_A = TPF_A = 0 and p = q = 1, so the line is the positive diagonal of ROC space, the already introduced and well-known chance line.

It is of interest also to know what can be said about a continuous (or quasi-continuous (3)) decision-variable whose ROC curve displays one or more straight-line segments. Any point C on a straight-line segment between points A and B can be described with

$$({\mathit{FPF}}_C,{\mathit{TPF}}_C)=({\mathit{FPF}}_A+{\lambda }_{C}p,{\mathit{TPF}}_A+{\lambda }_{C}q),$$

where p and q are defined as before and λ_C is the value of λ that defines the coordinates of point C. From equation (1), it follows that the conditional cumulative distribution functions for the decision variable v, evaluated at the value v_C that yields the operating point C, must satisfy the simple relationships

$$F(v_C\mid +)=1-{\mathit{TPF}}_A-{\lambda }_{C}q\text{and}F(v_C\mid -)=1-{\mathit{FPF}}_A-{\lambda }_{C}p,$$

so

$$F(v_C\mid +)=\text{constant}+F(v_C\mid -)q/p$$

and the conditional density functions must satisfy

$$f(v_C\mid +)/f(v_C\mid -)=q/p.$$

The ratio on the left side of the latter equation is the already encountered likelihood ratio. Accordingly, all cases with test result values that correspond to thresholds on the straight-line segment have the same odds, and thus the same probability, of being actually-positive (26), independent of the value of λ_c or v_C. Using v to separate actually-positive from actually-negative cases is equivalent to making random decisions for that interval: changing the value of v is equivalent to changing the value of λ in the random decision process described in the previous paragraph. The chance-line is simply equivalent to an exclusively random decision-process in v: different values of the variable v always contain the same information about the condition of interest — the prevalence.

It is interesting to draw parallels here with contaminated ROC models such as the CBM (20). All straight line segments can be considered the product of some form of contamination for the decision-variable being analyzed because we just proved that straight-lines imply identical densities for the decision variable (apart from a scale factor, the local prevalence).

From the ROC point of view it does not matter whether the actually-positive or actually-negative cases have identical distributions over an interval, or random decisions are made within that interval, or a subset is simply a probability mass, because all three situations will produce identical sets of classification decisions.

“Hooks,” convex ROC curves and straight lines

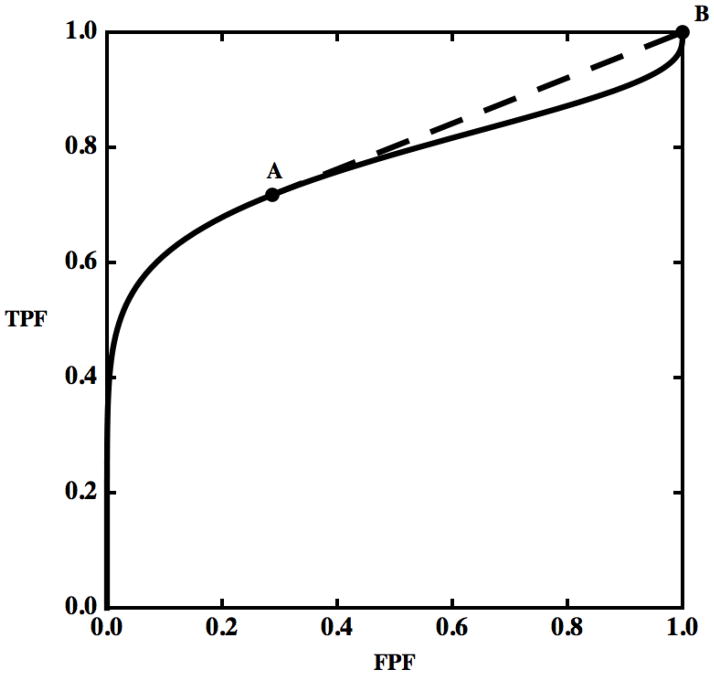
We have seen that, to include a hook, an ROC curve must drop below the straight line connecting at least two of its points, in the way that the solid curve in Fig. 3 drops below the line segment between points A and B. Moreover, all of the decisions made at operating points on the hooked curve between A and B are inferior to the decisions made at points on the straight line segment, because each such curve point has a smaller TPF value at any FPF in the range between those of A and B, or equivalently, a larger FPF at any TPF in the corresponding range (1). Finally, we have seen that, given two decision-variable cutoff settings which produce two ROC points such as A and B in Fig. 3, a decision-maker can always operate at any combination of FPF and TPF that lies on the straight line segment between those points by using a random number generator. Thus, it follows that hooks represent a decision-making strategy that always can be improved simply by introducing an element of chance. (Greater improvements are sometimes possible for each specific decision process, but they often require more complex, usually likelihood-ratio based, strategies that are beyond the scope of this discussion.)

Figure 3.

Two operating points, A and B, are shown on a hooked ROC curve. The dashed straight line segment between A and B reveals a hook that drops below it.

The following simple strategy can be used to remove all hooks from any ROC curve that is convex in the neighborhood of (FPF = 0, TPF = 0) and whose tangent there does not cross the curve, whereas trivial modifications of it apply to any ROC. Starting from (0,0), move upward and to the right on the population ROC curve to the first point, P₀, where the tangent to the curve is tangent also at another point, P₁, farther along the curve. Then by introducing the gamble described above to interpolate between points P₀ and P₁, the original ROC curve segment between P₀ and P₁ can be replaced by the straight-line segment P₀P₁ from the joint tangent. If this procedure is repeated until (1,1) is reached, the resulting ROC will be convex.³ Because this simple decision strategy improves performance, one can argue that direct use of the decision variable that produced the hook must be considered irrational (and unethical when applied to medical decisions). If we wish to compare two diagnostic modalities and one or both ROC curves currently display hooks, the argument above implies that we are obliged to consider explicitly the question of whether a meaningful comparison can be obtained without ameliorating the potential effects of the hooks in some way. On the other hand, simply reporting the empirically-hooked curve would be appropriate if the purpose of a study is to show that illogical decisions were made and there is no plan to make suggestions for future improvement of decision performance with the diagnostic modality in question. In the latter situation, one might argue that it is not important whether a hook crosses the chance line or not, because both of those situations represent irrational decision strategies that can be improved by introducing an element of chance.

A perhaps common example of a similar situation is exemplified when a binary decision process is modified because it is necessary to produce a larger sensitivity. If the modification fails to consider both sensitivity and specificity, the new algorithm might select just a few more positive cases but many more negative cases and the strategy would have moved the point on a hook. Classifying more cases as positive by use of the random strategy described above would have produced a better decision process.

Finally, one should note that the preceding arguments apply directly only to population ROC curves rather than those that are estimated from finite samples of case readings, and that removing hooks from the latter in the way described here might introduce bias in estimates of area under the ROC curve, for example.

ROC curves estimated from samples

By “sample” we mean here a sequence of decision-variable outcomes that have been obtained by applying a diagnostic procedure to a group of cases selected from the population of interest⁴. The test-result values in this sample can be ranked and an empirical ROC curve can then be constructed, starting from the largest test-result value and then progressively moving the decision-variable threshold to lower settings. Thus, empirical operating points are obtained like those in Fig. 2, where the coordinates of the point that is lowest and farthest to the left represent the combination of FPF and TPF obtained by calling “positive” those and only those cases in the sample whose decision-variable outcomes fell into the highest category (category 8 in Fig. 2); the next point to the right and up is obtained by calling positive all cases in the two highest categories (7 and 8 in Fig. 2); and so on — again, the interested reader is referred to Pepe’s book for details (1).

Finite datasets are subject to statistical sampling variations, so they produce estimates that are uncertain. The purpose of such estimates is not to determine the “true” value of some parameter in a population, which usually cannot be known exactly, but instead to determine a restricted range of population-parameters values with which available data are consistent. Often such ranges are not very narrow — i.e., estimates are not very precise. Accordingly, we must understand what a hook in an ROC curve estimate obtained from a finite sample of cases tells us — and does not tell us — about the possible shapes of the ROC curve that corresponds to an entire population of cases.

As stated above, a hook can be present either in a set of empirical operating points or in a continuous ROC curve that has been fit to such points. In the following subsections we will discuss hooks in operating points generally and then a particular but typical example of a hook in a fitted curve.

Populations with convex ROC curves can produce empirical ROCs with hooks

Population operating points represent exactly the tradeoffs that the associated decision process provides when it is used under the conditions studied (e.g., with a given number of categories in the reporting scale), and the straight lines that connect these population operating points represent the corresponding population ROC curve (again, for the given number of categories in the reporting scale, etc.). However, empirical operating points calculated from sampled data depend not only upon the population itself, but also upon the sampling process and chance. For example, when the number of cases is substantially smaller than the number of distinct rating values that those cases can have, as with continuous or quasi-continuous data, the ranked test-result samples usually consist of alternating sequences of actually-positive and actually-negative cases, and the corresponding ROC contains many hooks that plot as a staircase (e.g., figures 5.1 through 5.5 in (1)), regardless of the population from which they were sampled. This kind of hook in an empirical ROC is usually meaningless because it is an unavoidable consequence of the sampling process. Moreover, these hooks tend to be small, producing effects on estimates that are negligible when compared to the uncertainty of those estimates. On the other hand, a small number of response categories (relative to the number of cases) is more likely to cause ties between test results from actually-positive and actually-negatives cases, and therefore is more likely to produce slanted line segments between empirical operating points. However, the resulting empirical ROC may still include points that lie below the line connecting an operating point to its left and another to its right, thereby producing a configuration similar to point A in the bottom panel of Fig. 2. Moreover, such irregularities also can be due to the variability imposed naturally by chance, even when several adjacent points seem to form a hook. (When one views an empirical ROC curve, it is important to keep in mind that we are not looking at the population ROC curve, but only at a particular — and perhaps atypical — sample from it.) Simulation studies readily demonstrate how difficult it can be to guess the shape of a population ROC curve from even a moderately large sample of cases. In fact, it is not at all unusual for a convex population ROC to produce samples that includes a hook of some sort. While it is confusing and perhaps impossible to enumerate all of the scenarios that can produce a hooked empirical sample from a given convex population ROC, some general insights can be drawn from simple models. In general, our experience indicates that the probability of observing a large hook usually increases when:

• the total number of cases sampled is small;

• the ratio of actually-negative cases to actually-positive cases is far from 1;

• the population ROC curve is strongly skewed (i.e., it tends to cling to either the FPF=0 or the TPF=1 axis, but not to both); and/or

• the distribution of operating points along the population ROC curve is very uneven.

Thus, a practically relevant question arises: How unlikely it is that a particular set of empirical operating points containing hooks could have been produced from a convex population curve? The lower the probability of this occurrence, the stronger is the evidence that the process under study is producing illogical decisions and perhaps should be amended before assessing its performance or implementing it. In our experience it makes sense to consider convexity as the reference, because it is a very common characteristic of empirical ROC curves that have been determined by applying diagnostic processes to large samples drawn from the population for which the decision process was designed. On the other hand, one should keep in mind that there is no reason to expect that a decision process will produce reasonable decisions if is applied to an inappropriate population. An example of a potentially misleading evaluation of a decision process can be obtained when a radiologist is asked to classify a collection of cases that has been constructed (either by chance or by design) in a way such that some actually-malignant lesions appear more benign than any of the actually-benign lesions, or vice-versa.

Most statistical tests quantify the likelihood of an event that is at least as deviant as the one observed, rather than merely the likelihood of the observed event itself, because this provides an indication of how unusual the observed data would be if a pre-selected hypothesis were true (33). This in turn forces us to choose a relevant metric for the hook we are evaluating — e.g., a drop in TPF for a specific point, a reduction in the area under the ROC curve produced by the hook, or the number of points that deviate from convexity, as suggested by Lloyd (22). Because of the lack of a clear metric and the likely failure of a real-world sample to satisfy the simplifying assumptions that may be necessary to formulate a statistical test in closed form, we tentatively propose here a simulation-based approach, essentially following Lloyd (22). First, some strategy similar to that described in Appendix 1 is applied to render the empirical curve convex, i.e., to find the convex curve that is closest in some sense to the observed data. Then the population associated with the “corrected” curve is used as reference population and an appropriate number of randomly sampled datasets are drawn from it — i.e., from the multinomial distribution with categorical probabilities corresponding to the corrected curve. The samples are then used to estimate the probability of producing a curve with a hook metric at least as extreme as the one observed. The resulting number provides a quantitative basis for judging how likely it is that the lack of convexity was caused by chance alone. A more detailed exposition of this approach is presented in Appendix 1. The same basic idea can be used also to produce more complex tests that suit specific experimental designs. We propose the approach here for categorical data, but similar methods have been described for continuous data (22).

How non-convex ROC curve fits usually happen

In radiology, most clinical image-reading data are categorical because they represent subjective degrees of suspicion rather than empirical measurements, and usually very few reporting categories are used in the clinical practice; for example, the BI-RADS scale includes only 5 or 7 confidence-rating categories (25). However, data collected on BI-RADS and similar scales often produce hooked ROC curves (3) and this tendency is accentuated when the curves are fit by the CvBM — e.g., excellent examples of such fits can be found in reference (34). For the interested reader, Appendix 2 shows in detail how this can happen when the conventional binormal model is used to fit 5-category data and why it should be considered a fitting artifact caused by the characteristics of the model used.

Conclusions

We have shown how ROC curve hooks represent trivially irrational decision processes and as such rarely can be accepted as real in medical research.

Empirical data that display hooks should be subjected to either statistical tests or comparisons with previous experience in order to determine their likelihood of having arisen from a population ROC curve that did not contain a hook before any meaningful statement about the curve’s convexity can be made. If this likelihood is sufficiently small— i.e., if the hook appears to be real — then investigators must consider attempting to amend the decision process that they are analyzing or at least address the issue when reporting their results, because the diagnostic procedure may then be likely to produce irrationally poor diagnostic decisions under some conditions. The resulting amended decision process can then be fit, if a semi-parametric fit is desired. Unless the ROC curve is expected to be non-convex, we recommend the use of a proper model to prevent the fitting aberrations produced by the conventional binormal model. On the other hand, all of the non-parametric methods we know that can be used to remove a hook from data before computing an estimate of a decision-performance index such as AUC introduce a positive bias. Users of ROC curve fitting models must consider carefully the fits that they publish, because most commonly used goodness-of-fit measures such as deviance (33) are not affected by this type of fitting aberration, as is suggested by our example in Fig. 4 of Appendix 2, where a highly “irrational” curve can nevertheless pass very close to the experimental points and then veer off in other parts of the graph.

Although a diagnostic test might in practice be operated at sensitivity and specificity values far away from the hook in its ROC curve, thereby rendering that hook clinically irrelevant, many figures of merit — and AUC (3) in particular — can be seriously affected by these irrational decisions, thus biasing both the estimated performance and the inferences drawn from statistical testing. Use of local figures of merit, such as partial areas and FPF at a pre-selected value of TPF, can partially ameliorate these and other issues, but they can also produce negative consequences, such as a considerable loss in statistical power and the necessity of basing an assessment upon potentially arbitrarily chosen threshold values. Although discussion of these issues is beyond the scope of this paper, other publications deal with them in detail (1, 3).

Appendix 1: An algorithm to judge whether a hook is real

This appendix describes an algorithm that can be used, at least in principle, to estimate the likelihood that a particular hooked sequence of empirical operating-point estimates from a finite set of categorical test-result values could have been produced by chance from a convex population ROC curve. Similar methods have been proposed elsewhere for continuous rating data (22). The same basic idea can be used also to produce more complex tests that suit specific experimental designs.

Here we define a discrete dataset as having a hook if it provides three sequential operating points — A, B and C — in the set of the empirical operating points (including (0,0) and (1,1)) for which the middle point lies below the straight line that connects the other two points — i.e.,

$${\mathit{TPF}}_B<{\mathit{TPF}}_A+({\mathit{FPF}}_B-{\mathit{FPF}}_A)\frac{({\mathit{TPF}}_C-{\mathit{TPF}}_A)}{({\mathit{FPF}}_C-{\mathit{FPF}}_A)},$$ (A1.1)

given that FPF_A < FPF_B < FPF_C. Thus, point B must lie below the straight-line connecting A with C. It is straightforward to generalize this to a sequence of points, all of which lie below the segment connecting two points A and B, or to a dataset with multiple hooks.

If we have collected a discrete dataset on a scale that provides N_cat rating categories, and if each category j contains k_j ≥ 0 actually-negative and l_j ≥ 0 actually-positive cases, then condition (A1.1) for a hooked ROC implies that

$$(l_j/M_s)/(k_j/M_n)<(l_{j-1}/M_s)/(k_{j-1}/M_n)$$ (A1.2)

for at least some category j, where $M_n={\sum }_{j=1}^{N_{\mathit{cat}}}{k}_j$ and $M_s={\sum }_{j=1}^{N_{\mathit{cat}}}{l}_j$. A population ROC indistinguishable from that of the sampled data can be defined by assigning the population probabilities p_j = k_j/M_n and q_j = l_j/M_s to every category j, thereby causing the hypothetical population of test results to be categorical as well; thus, condition (A1.2) implies that

$$q_j/p_j<q_{j-1}/p_{j-1}.$$ (A1.3)

Notice that we have defined empirical ROC curves in terms of numbers of cases, whereas we have defined population ROC curves in terms of probability distributions.

Although the hypothetical population ROC described above will have a hook, that hook does not imply that the actual population from which the sample was drawn — and hence, from which the hypothetical population ROC was constructed — is non-convex, because every dataset is a finite sample and carries an uncertainty. As previously mentioned, in our experience large data samples from realistic experiments aimed at studying medical decisions are usually associated with convex ROC curves. This suggests that these population ROCs are usually convex. Moreover, we argued that hooked population curves imply by necessity illogical decisions. Therefore, it seems reasonable to first assume that hooks in empirical sets of ROC operating points are caused by random sampling variations and, consequently, to compute a measure of the probability of such a sampling event. For this purpose we start by defining a reference population that is both convex and “as close as possible” to the observed dataset. We define this reference population as the one that produces an ROC curve indistinguishable from the observed data, as described above, but having its subsets that deviate from convexity modified as little as possible to render the curve convex — e.g., we replace what appear to be illogical decisions with random decisions as described in Appendix 2. For categorical data this is equivalent to merging all categories that satisfy inequality (A1.3). (This process might need to be applied iteratively until all line segments that connect adjacent operating points, starting from the lower-left, have progressively decreasing slope. It does not matter from which category the merging starts, because the resulting curve will be the same; see Lloyd (22) for a more detailed description.) The merging will yield a new set of Ñ_cat ≤ N_cat categories. Each of the new categories will have actually-negative and actually-positive outcome probabilities ${\stackrel{\sim }{p}}_i={\displaystyle \sum _{j_m\le j\le j_n}}{p}_j$ and ${\stackrel{\sim }{q}}_i={\displaystyle \sum _{j_m\le j\le j_n}}{q}_j$, respectively, and expected total numbers of cases ${\stackrel{\sim }{k}}_i={\displaystyle \sum _{j_m\le j\le j_n}}{k}_j$ and ${\stackrel{\sim }{l}}_i={\displaystyle \sum _{j_m\le j\le j_n}}{l}_j$, where j_m and j_n are the first and last of the categories that were collapsed to create the new category i. In order to obtain the reference population defined above we need to split the merged categories to re-obtain a population defined over N_cat categories as the original data; in order to keep the associated curve convex we suggest to give to each of the j categories collapsed into each i category a probability equal to p_{c, j} = p̃_i (k_j + l_j)/(k̃_i + l̃_i)and q_{c, j} = q̃_i (k_j + l_j)/(k̃_i + l̃_i), respectively. In this way, for every category created from category i, the slope is identical, equal to p̃_i/q̃_i, and the weight is equal to the total number of cases that originally occupied that category.

Categorical ROC datasets can be shown to be equivalent to samples from multinomial distributions (6, 35). Now we have two multinomial distributions with category probabilities {p_{c, j}, j = 1,…, N_cat} and {q_{c, j}, j = 1,…, N_cat} and with totals of M_n and M_s actually-negative and actually-positive cases, respectively. Moreover, we know they produce a convex ROC curve. We can then generate random samples of rating data by using one of the multinomial random number generators that are provided by most statistical analysis and mathematical software packages. An index of interest (e.g., drop in AUC caused by one or more hooks or the total number of points in the hooked parts of the curve) can be computed from each sampled dataset. When a large number of samples is taken, this approach asymptotically provides the distribution of the index for the experiment of sampling M_n actually-negative and M_s actually-positive cases from the “convex” reference convex population described above. The quantiles of this distribution estimate can be used to get an idea of the probability that a test statistic at least as deviant as the one computed for the original dataset could have been produced by a convex population close to the data. For example, suppose that large values of the index of interest, y, correspond to hooks that are large in some meaningful sense and the value of this index in the original dataset is Y. Then if the simulations described above were to show that values of y as great or greater than Y occur by chance in 80% of repeated experiments, one would conclude that the observed hook can be ascribed to statistical variation, whereas if the simulations show that such values of y occur by chance in only 1% of repeated experiments, one would conclude that a hook is likely to be present in the population. Given the uncertainty usually associated with estimating ROC curve shapes, it is unlikely that this test would be very powerful in detecting that the population curve has in fact a hook. Further research will be needed to validate this approach and to determine the relationship between its type I and type II error rates — itself essentially an ROC curve! — that arises in distinguishing between hooks in empirical ROC curves that are due either to real hooks in the population ROC or to sampling variation alone. The interested reader is encouraged to perform computer simulations to determine whether these error rates are acceptable for his or her specific estimation problem.

Other methods could be employed to define a reference convex population — e.g., fit a proper ROC curve to the data (21) and then use the estimated cutoffs and distribution parameters to sample random datasets. Perhaps multiple approaches should be used to provide a more reliable understanding of the probability that, when a specific decision process is applied to the population from which a dataset was sampled, the resulting distribution of decision variables will produce a non-convex ROC curve.

Appendix 2: How hooks can happen and a way to reconsider them, with an example from published data

In this appendix we show mathematically how non-convex ROC curve fits usually happen in radiological observer studies. We consider 5-category data because 5-category rating scales have been used widely in radiological research, and we will consider only two-parameter fitting-models, as is nearly always done in practice (1, 3). Following Dorfman and Alf (6) and Ogilvie and Creelman (35), the probability of observing a specific dataset given a population model (better know as the likelihood) is given by

$$P(\overrightarrow{k},\overrightarrow{l}\mid \alpha ,\beta ,\overrightarrow{x})=M_n!M_s!\prod _{i=1}^5\frac{p_i^{k_i}{q}_i^{l_i}}{k_i!l_i!},$$ (A2.1)

where α and β are the parameters that specify the population ROC curve according to a particular model; k_i and l_i are the numbers of actually-negative and actually-positive cases in category i, respectively; $M_n={\displaystyle \sum _{i=1}^5}{k}_i;M_s={\displaystyle \sum _{i=1}^5}{l}_i$; and the vector ν⃗ represents an ordered set of category boundaries that defines the conditional response probabilities associated with each category via the equations

$$p_i=p(\alpha ,\beta ,{\nu }_{i-1},{\nu }_i)=P(x_{i-1}\le \nu \le {\nu }_i\mid \alpha ,\beta ,-)$$

and

$$q_i=q(\alpha ,\beta ,{\nu }_{i-1},{\nu }_i)=P(x_{i-1}\le \nu \le {\nu }_i\mid \alpha ,\beta ,+),$$

in which ν is the latent decision variable — e.g., see Metz for details (36). The “best fit” ROC curve usually is determined by maximum-likelihood estimation (MLE) because of its good statistical properties (33). Each such ROC curve estimate consists of the values of α,β and ν⃗ that maximize the value of an appropriate likelihood function. Usually a modified log-likelihood function is employed for numerical and other practical reasons (33):

$$LL(\overrightarrow{k},\overrightarrow{l}\mid \alpha ,\beta ,\overrightarrow{\nu })=\sum _{i=1}^5{k}_{i}log{p}_i+l_{i}log{q}_i.$$ (A2.2)

We created artificial data based on Panel D of Fig. 1 in reference (34), which represents the ROC curve of film mammography screening for premenopausal or perimenopausal women. We chose to synthesize data on the basis of information in this publication because it reports a large clinical trial in which data were collected by experienced investigators under carefully controlled conditions. We chose the particular dataset shown in Panel D of Fig. 1 in reference (34) because it displays the most obvious hook. The original data were collected on a 7-category scale, but we simplified them to 5-category data because the first three ROC operating points are essentially aligned vertically, thereby allowing the corresponding categories to be merged without affecting the maximum-likelihood estimates of the ROC curve (37). We measured the FPF and TPF values as accurately as possible from the published plot and synthesized data from similar numbers of actually-positive and -negative cases, as in reference (34). The resulting synthesized dataset consisted of test-result values for 100 actually-positive cases and 16,000 actually-negative cases. This is a highly unbalanced dataset, as is often the case in prospective clinical trials that assess the detection of diseases with low prevalence. The empirical operating points and the corresponding ROC curve estimated by our LABROC4 algorithm (37) for fitting the conventional binormal model (available upon request from http://www-radiology.uchicago.edu/krl/) are shown in Fig. 4. Our fitted curve is somewhat lower and displays a slightly more obvious hook than the original because the samples are slightly different. The standard errors of our resulting parameter estimates were similar to those reported in reference (34).

Figure 4.

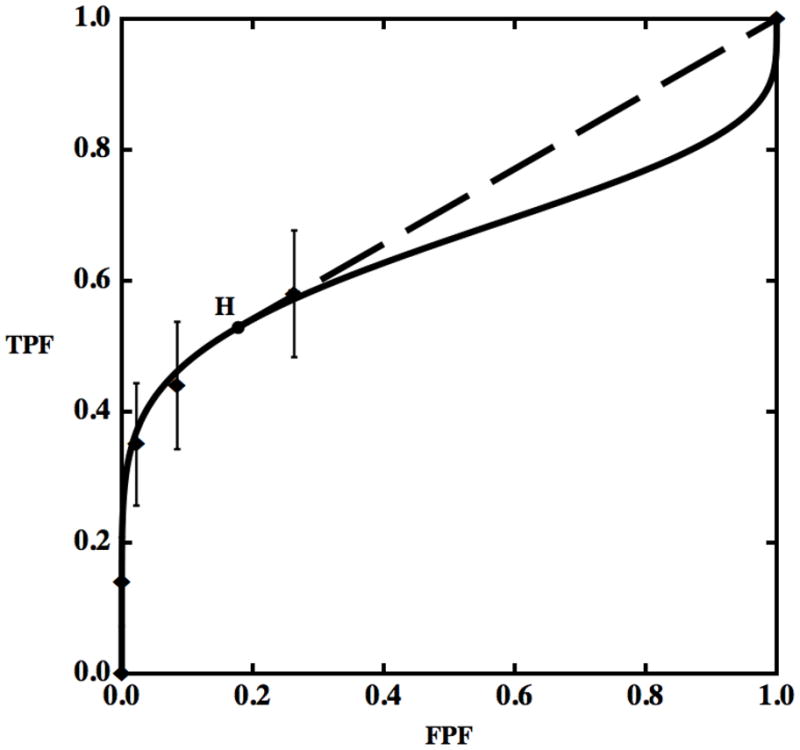
Empirical operating points (diamonds) and the fitted ROC curve (solid) for synthetic data generated from Panel D of Fig. 1 in reference (34), which describes the estimated performance of film mammography in screening for breast cancer in premenopausal or perimenopausal women. Both vertical and horizontal 95% confidence intervals for the operating points are shown by bars, but the horizontal bars are invisible here due to their very small size. Point H is the operating point on the ROC curve at which the tangent to the fitted ROC curve passes through (1,1) — i.e., the beginning of the hook, according to the definition employed in this paper. The tangent at H is shown as a dashed straight line segment.

Figure 4 displays also the estimated 95% confidence intervals on the empirical operating points, computed considering the various FPFs and TPFs as independent proportions (1). The vertical uncertainties are very large, making it impossible to determine the population curve shape with reasonable accuracy, so the estimated ROC curve must be considered only a very rough picture of what the actual population curve might be, both from our synthesized data and from the original clinical trial data (34). Therefore, these data do not provide conclusive evidence that the fit with a large hook that was obtained with the conventional binormal model should be preferred to other “more reasonable” choices. Moreover, such a fit implies that physicians would make decisions worse than random chance at FPFs larger than about 0.3, though no data were collected in that range. Although this inference may not be relevant to clinical practice, it has a substantial impact on widely-employed figures-of-merit such as area under the curve (AUC), also used in (34), and thus may adversely affect performance estimates and the statistical testing of differences thereof (1).

Point H in Fig. 4 is the position on the fitted ROC where the curve’s “hook” begins — i.e., the point where the tangent to the curve passes through (1,1). We suggest assuming that for test-result values below the threshold associated with point H (i.e., for ν < ν_H or, equivalently, for FPF > FPF_H), the test result provides no diagnostic information at all. This is equivalent to replacing the last part of the curve with the dashed straight line shown in Fig. 4. The resulting model not only seems to make more reasonable assumptions — i.e., it does not assume illogical decisions for most of the patient population — but in terms of goodness of fit the hooked and straightened curves treat the points identically and, as will be shown below, produce nearly identical likelihoods, which is an additional argument against accepting the hook. In effect, the straightened ROC curve is obtained from a contaminated model.

Notice also that the hook corresponds almost entirely to data that fell within category 1. All of those cases received the same rating, implying that the readers essentially made or could make no discrimination within those cases, practically providing an additional argument against a hook and in favor of a contaminated model because, as we have shown previously, no discrimination produces straight lines rather than hooks.

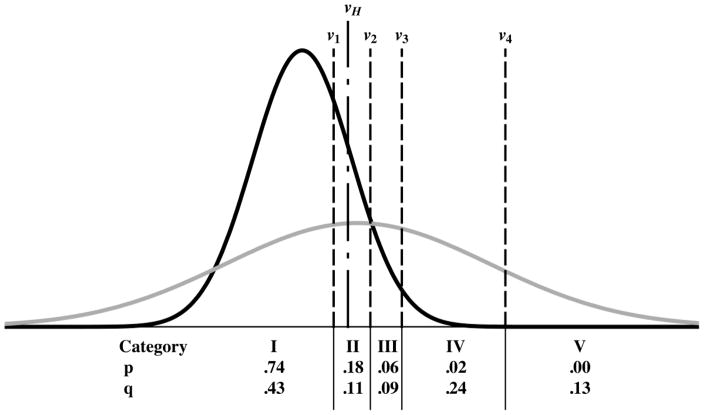
A related and important question is why maximum-likelihood estimation is producing a curve with a hook in the first place. Equation (A2.2) shows that only the total probability between cutoffs affects the likelihood and, thereby, estimation of the parameters. However, Fig. 5 shows that shapes of the parts of the actually-negative and actually-positive probability distributions that generate the hook — the parts to the left of the vertical dot-dashed line in Fig. 5, i.e., where ν < ν_H — have little effect on any of the category probabilities. The area under either density for ν < ν₁ defines the probability of obtaining a rating in category 1. Therefore, the densities when ν < ν₁ can have any shape and would still produce exactly the same category probabilities: the shapes of the densities in that region will have no effect whatsoever on the likelihood function, regardless of whether they produce a “hook,” a straight line, or a convex line as long as the category probabilities (the areas under the densities for ν < ν₁, indicated by the numbers at the bottom of Fig. 5) are kept constant. Moreover, changing the shape of the density functions below the point where the hook begins, ν_H, also would have a minimal affect on the probabilities of the numbers of ratings accrued in category 2, because it is only the portions of the density functions that lie between ν₁ and ν_H that would produce a likelihood change and it is minimal when compared to the size of the errors bars of the empirical operating points — unless very unreasonable choices are made. On the other hand, the highest category, number 5, contains no actually-negative cases. Because k₅ = 0, the actually-negative probability density above the last cutoff (ν ≥ ν₄) does not contribute to any of the terms that appear in equation (A2.2), so it does not affect the likelihood directly. However, this part of the density must be rendered as close to zero as possible in order to maximize the likelihood because, given the necessary constraint ${\sum }_{i=1}^5{p}_i=1$, the larger is p₅ the smaller are p₁ to p₄. This causes ν₄ to be selected such that the actually-negative density lies almost entirely to the left of it (as indicated in the Fig. 5, where 0.00). For the CvBM to have a sizeable actually-positive density above ν₄ either a has to be large (causing the two densities to lie far apart), but then AUC will be large and the fit to the other points will be poor, or b will have to be small (so that the variance of the actually-positive density will be large), which will allow a very good fit to the observed points, as shown in Fig. 4. However, because the normal distributions that the binormal model employs are symmetrical, this will seriously affect the shape of the upper right corner. Thus, the hook shown in the upper-right corner of Fig. 4 is produced mainly by the MLE curve-fitting algorithm’s attempting to fit the data in the lower-left corner. Hence, the hook in the fitted ROC curve not only implies illogical decisions for operating points that were not observed, but it is produced by an unrelated part of the curve due to constraints imposed by the fitting the model. We believe that fits of this kind cannot be relied upon above the last empirical operating point unless additional evidence is provided.

Figure 5.

A pair of truth-conditional probability density functions corresponding to the ROC curve shown in Fig. 4, centered around zero for the actually-negative cases and centered at a value larger than zero and much broader for the actually-positive cases. The axis scales are not indicated to simplify the plot. The four vertical dashed lines represent the cutoff settings (ν₁, ν₂, ν₃, ν₄) that produce the categorical probabilities p_i and q_i that appear in equation (2), whereas the vertical dot-dashed line indicates the particular value of ν (ν_H) that corresponds to the beginning of the hook — see text. The p_i and q_i values associated with each ordinal category, the number of which is indicated by a Roman numeral for clarity, are indicated (rounded to two decimal places) at the bottom of the figure.