Glass microneedles for force measurements: a finite-element analysis model

Abstract

Changes in developed force (0.1–3.0 μN) observed during contraction of single myofibrils in response to rapidly changing calcium concentrations can be measured using glass microneedles. These microneedles are calibrated for stiffness and deflect on response to developed myofibril force. The precision and accuracy of kinetic measurements are highly dependent on the structural and mechanical characteristics of the microneedles, which are generally assumed to have a linear force–deflection relationship. We present a finite-element analysis (FEA) model used to simulate the effects of measurable geometry on stiffness as a function of applied force and validate our model with actual measured needle properties. In addition, we developed a simple heuristic constitutive equation that best describes the stiffness of our range of microneedles used and define limits of geometry parameters within which our predictions hold true. Our model also maps a relation between the geometry parameters and natural frequencies in air, enabling optimum parametric combinations for microneedle fabrication that would reflect more reliable force measurement in fluids and physiological environments. We propose a use for this model to aid in the design of microneedles to improve calibration time, reproducibility, and precision for measuring myofibrillar, cellular, and supramolecular kinetic forces.

Introduction

Glass microneedles have been used as force probes to investigate muscle physiology for several decades. Techniques for quantifying cell kinetics were developed in the early 1980s [7], while, more recently, the technique has been adapted to quantify myofibril kinetics [3, 8]. Several types of microneedles that have been used have been based on the requirements of the specific experiment at hand. For example, to measure forces on single actin filaments, Kishino and Yanagida [7] fabricated microneedles from a 1-mm glass rod using an electrode micropipette puller to produce a tip approximately 0.3 μm in diameter and 70–100 μm in length. This microneedle was then attached to a rigid 100-μm-diameter glass rod so as to yield a force probe with stiffness between 0.5 and 5.4 pN/nm. To measure contractile forces in single myofibrils in our laboratory, we follow Poggesi's group [3, 8] and pull glass rods to produce microneedles with an approximate 6–15 μm tip diameter and a 0.02–0.66° taper. These needles are then bent at right angles (about 1 mm from the tip) using a microforge to form an L-shaped cantilever.

While specific fabrication methods vary, three problems are common to all types of microneedle cantilevers: inconsistency in manufacturing, time- and labor-intensive calibration methods, and difficulty in a priori predicting probe stiffness and frequency response. Stiffness calibration methods that commonly have been employed are (1) cross-calibration with a reference cantilever of known stiffness [4, 9], (2) inference from impulse deflection or resonance response [2, 9], and (3) inference from thermal vibrations [7, 9]. These methods produce accuracies between 5% and 40% [1, 5].

Although glass microneedles are versatile force probes with diverse applications, the time- and labor-intensive methods of calibration and the difficulty in a priori predicting needle properties (in terms of stiffness and frequency response) remain as limitations. To address these limitations, we performed a combination of experimental and modeling work to produce a more thorough engineering analysis than currently available. We investigated the effects of geometry on microneedle mechanical properties by careful direct measurement; the resulting data were then used to develop and validate a detailed model based on finite-element analysis (FEA) methods. Additionally, the results of the FEA model were used to produce a set of simple empirical equations to aid in the design and fabrication of microneedles with a specified desired stiffness. We also examined the effects of immersion in water on the frequency response of the microneedles and predict optimized needle geometries suitable for kinetic measurements in fluids. We present this report together with an online repository of our model simulation software (http://www.uic. edu/depts/mcpb/Resources/downloadable_resources/Down loadable_Resources.htm) to help others in field to reliably produce and accurately calibrate microneedles.

Methods and materials

Preparation of microneedles

1-mm×100-cm borosilicate glass rods (World Precision Instruments Inc., Item Number: GR100-4) were pulled with a Flaming/Brown style micropipette puller (Sutter Instrument Co. Model P-87) to obtain fine gradually tapered needles (taper angles between 0.02° and 0.66°). The degree of taper and tip length were controlled to obtain geometries falling between a highly tapered short length (bee-stinger 5.5-μm tip diameter:550-μm tip length) and a gradually tapered long length (microinjection 14-μm tip diameter:1,800-μm tip length). Individual microneedles were transferred to a microforging microscope (Narishige MF-9) where they were cut to different final lengths by using a hot 10-μm-diameter platinum wire. Their tips were fire-polished until smooth with resulting tip diameters ranging from 5.5 to 14 μm. By using the microforge, the microneedles were bent into a 90° cantilever at distances ranging from 512 to 1,800 μm away from the tip (cf. Fig. 1). The geometry of the needles were then characterized by carefully measuring their tip diameter (T₁), diameter immediately after the bend (T₂), diameter just before the bend (R₁), tip length (L₁), radius of the bending arc (A_RC), and the diameter of the needle shaft (R₂) at a distance (L₂) away from the bend. These parameters were sufficient to fully describe the needle geometry for our stiffness characterizing FEA model. For stiffness properties, the needles were secured in a needle holder attached to a micromanipulator. For harmonic frequency purposes, the parameter R₂ was determined after clamping the cantilevers at a distance L₂, then gluing the clamp holders to a piezoelectric displacement generator. For Young's modulus determination, the needles were pulled to get an approximate cylindrical shaft but not bent. They were then transferred to an inverted microscope (Olympus IX70) to be calibrated.

Fig. 1.

Microneedle geometry. a 1. Composite image of a sample needle after it has been heated, pulled, bent, and fire-polished resulting in a smoothened tip (scale: ten divisions=1 mm); 2. Zoomed in geometry of a real microneedle tip; 3. Tip of model geometry mesh used for simulation. b Shows a 3-D mesh that reveals measurable microneedle geometry parameters. T₁ = tip diameter, T₂ = diameter after bend, R₁ = diameter before bend, A_RC = radius of curvature of 90° bending arc, L₁ = length of tip, L₂ = length of needle shaft, R₂ = shaft diameter at fixed end. c Shows microneedle characterization by the cross-calibration method. A stage of two nanofabricated silicon–nitride cantilevers of known stiffness [4] was pushed (bottom panel) against the microneedle tip to displace it. The left cantilever acts as a reference for stage displacement while the right one (in contact with the needle) is the active cantilever. The stiffness ratio is then inversely proportional to the displacement ratio between the microneedle and the active nanofabricated cantilever (bright-field image observed at ×40 magnification)

Calibration of microneedles

Calibration of the needles for stiffness was done by the cross-calibration method using nanofabricated cantilevers (a generous gift from Dr. Gerald Pollack's group [4]). These cantilevers were created by optical lithography methods and their stiffness determined with high accuracy within 7–16% error [4]. Deflection was measured by using a Nikon filar eyepiece coupled with a ×40 objective (Fig. 1 c). These reference cantilevers were made of silicon–nitride with stiffness 12, 58, 114, 192, 359, and 621 pN/nm. The microneedle tip was placed 5–10 μm away from the silicon–nitride tip each time to ensure stability of contact (this was accounted for in the FEA model by adjusting the force application point). Each microneedle was calibrated by pushing against all six of the silicon–nitride reference cantilevers and that which gave an approximate one-to-one relative movement between the microneedle and the reference calibrating cantilever was used for stiffness calculation by comparing the deflection distances. In addition, microneedle stiffness was also determined in a subset of experiments by direct force measurement using a capacity force transducer (Aurora Scientific Inc. Model: 406A). The stiffness of the microneedles ranged from 17 to 1,402 pN/nm. To investigate the linearity of the force–deflection characteristic, a needle was calibrated several times by applying a different displacement so as to obtain a force–deflection relationship (Fig. 2).

Fig. 2.

Force–deflection relationships of real microneedles. Force–deflection relationships were measured by cross-calibration. a Static forces were applied to a pulled tapered straight cantilever beam of dimensions (in micrometer) R₁=15.7, R₂=58.1, L₁=2,574. Estimated mean stiffness: k=0.502 μN/μm. b Static forces were applied to a pulled tapered bent needle of dimensions (in micrometer) T₁=10.3, T₂=13.2, R₁=20.1, R₂=36.2, L₁=1,072, L₂=1,500, A_RC=290. Estimated mean stiffness: k=0.044 μN/μm

Measurement of resonant frequencies

A small unit containing a biphotodiode detector (SD-066, Advanced Photonix Inc, Camarillo, CA, USA) and a current-to-voltage circuit (cutoff frequency 27 kHz) was mounted on an available microscope port (Fig. 6). The entire setup was placed on a vibration-proof floating table. We plucked on the tip of individual needles with a thin glass rod mounted on the inverted microscope in bright-field mode. The data were collected by measuring differential current from the photodiode as the incident cantilever image moved across the photocells. For measurement of the harmonic frequencies in both air and water, the needles were attached to a 17-kHz piezoelectric multilayered actuator (AE0505D16, Thor Labs Inc, Newton, NJ, USA) and swept through frequencies from 5 Hz to 5 kHz. Sine waves were used to drive the piezo with small amplitudes (<±3 μm) and the data captured on a computer via a 12-bit A/D converter at 10-kHz sampling rate using Lab View 7.0. A fast Fourier transform analysis was performed using SCILAB (version 4.0) with careful attention to isolate the signals from background noise and artifacts. The microneedles were attached to the piezo in an equiplanar manner to minimize multiplane vibration. This procedure was repeated for the needles fully immersed in skinned muscle solutions [3, 8] in a temperature-controlled bath (~14°C). The solutions and temperature were used to represent the conditions under which most of our experimental measurements are made.

Fig. 6.

Schematic of calibration apparatus used to measure frequency response. A signal generator drives the piezo which is attached to the microneedle. Light is collected by the condenser and focused onto the microneedle so that it throws a shadow of the needle tip onto a biphotodiode and amplifier detector system. Vibrations from the needle cause the shadow to move across the biphotodiode, whose current differential is then processed by the amplifier and collected by a computer via a 12-bit A/D converter. The signals are then analyzed and an FFT is performed using MATLAB R2007a and SCILAB 4.0 to extract the dominant frequencies

Simulated microneedles

FEA meshing and solver programs were designed and programmed using CALCULIX 1.7. An initial Young's modulus (E) of 66.3 GPa and mass density (ρ) of 2.23 g/cm³ [6, 10, 12] for borosilicate glass were adjusted systematically and validated by solving for the model's eigenvalues at their corresponding eigenmodes, and comparing with results from the experimental resonant frequencies measured in air. A Poisson's ratio (ν) of 0.22 was chosen for the model based on published properties of borosilicate glass [6, 11], and an initial operating temperature of 25°C was used for simulating stiffness while 14°C was used for determining the harmonics in water. The finite-element building blocks for the model were chosen to have isotropic elastic properties and a nonlinear geometric consideration in their integration characteristics. The simulated needle was loaded quasistatically using an iterative Cholesky preconditioning solver, and solid boundary conditions with single-point constraints (SPC) were used on a total of 5,756, 20-node, three-dimensional quadratic, isoparametric brick elements (with reduced integration) which constituted the model. Stiffness and frequency response data for the microneedles were internally validated by simulation using the geometry dimensions and glass material properties (E, ν, and ρ).

Results

Linearity of glass microneedles

Since straight thin glass microneedles resemble a simple linear beam, it is expected that such structures should obey a close to linear force–deflection relationship. The data in Fig. 2 show that such was indeed the case not only for straight but also bent microneedle geometries. Here, experimentally determined microneedle stiffness was determined by the comparison method, either by using nanofabricated reference silicon–nitride cantilevers [4] or by direct force measurement using a sensitive force transducer (Aurora Scientific Inc. Model: 406A). By calculating point estimates of stiffness at different static forces over a wide range, both bent and straight glass microneedles were found to exhibit a close to linear force–deflection relationship.

Young's modulus

Calibration of the microneedles by numerical methods critically depends on the determination of the Young's modulus of elasticity (E) of the borosilicate glass from which we fabricate them. We determined E for the blank glass rods and found it to be 66.3±2.5 GPa (mean±SEM), a value that falls within the range of elastic modulus reported for borosilicate glass [6, 11]. In contrast, however, when we determined E for pulled glass using a variety of calibration techniques [1, 2, 4, 5, 7, 9], we found it to be on average 39.5±1.6 GPa. The annealing temperature of borosilicate glass is in the 585–600°C range. Therefore, a possible explanation could be that during microneedle manufacture (pulling and forging ~700–900°C), the glass material undergoes an annealing process which shifts E towards a relatively lower value. This can be further explained by the fact that, after pulling, the glass stays within the heating element, which cools down more slowly making it more ductile. However, once pulled, the elastic modulus E stayed within range of our reported value regardless of further cutting or bending manipulations. Furthermore, this result was independent of the time taken to pull the microneedles and the temperature used for pulling and forging; provided fabrication occurred between the temperatures for annealing (~585°C) and melting (~850°C). Thus, we used a Young's modulus of elasticity E=39.5 GPa in all subsequent FEA modeling. After determining our field variables (systems of equations to be used, boundary and initial conditions, element nodal properties, and material parameters), we modeled silicon cantilever wafer beams previously described by Stephan Weigert et al. [13] and simulated their stiffness and harmonic frequencies. Our values matched very well with the experimental values of Weigert et al. for the cantilevers in air, up to the fourth harmonic (data not shown), suggesting that our field variables and systems of equations could indeed satisfactorily describe real-life harmonics in microstructures.

Comparing FEA model with experimental data

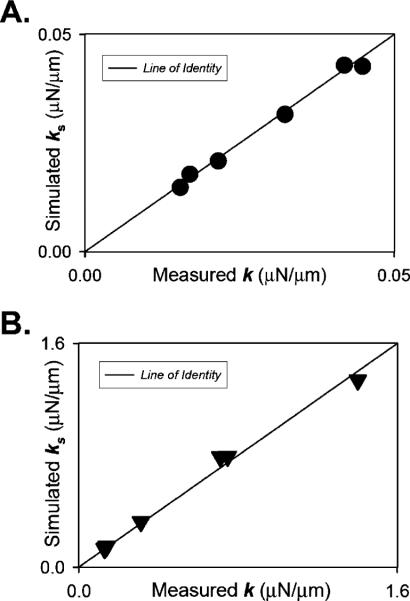
To check how closely our three-dimensional geometry mesh resembled a real needle, we overlaid it with a photographed copy of a measured real microneedle and it fitted quite well (cf. Fig. 1a). Measuring of the needle geometry parameters was done repeatedly in bright field as well as contrast imaging mode. Next, we fabricated 12 microneedles, measured their geometry parameters, and calibrated them using the techniques as employed for the data shown in Fig. 2. The needles had properties that fit the parametric geometry and stiffness boundary limits relevant for myofibril kinetic force measurements generally employed in our laboratory. Figure 3 shows FEA-modeled stiffness of these needles as function of the measured stiffness for bent microneedles with low (Fig. 3a) and high (Fig. 3b) stiffness. The data clustered closely to the line of identity; on average, the mean error between FEA model and measured stiffness was less than 8%.

Fig. 3.

Comparison of simulated to experimentally determined stiffness. Shows FEA-modeled stiffness of a sample set of 12 bent microneedles as function of the measured stiffness with low (a; 0.00–0.05-μN/μm range) and high (b; 0.10–1.50-μN/μm range) stiffness. The data clustered closely to the line of identity; on average, the mean error between FEA model and measured stiffness was less than 8%

Impact of geometry on predicted microneedle stiffness

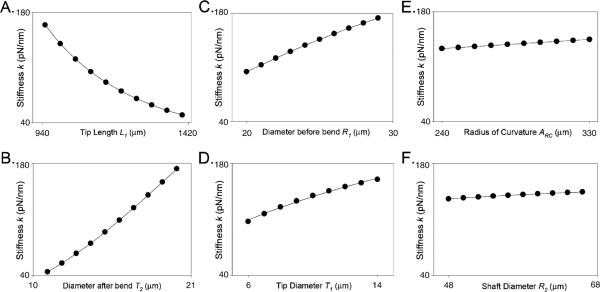
To determine the relative impact of geometry on stiffness, we simulated stiffness for 117,649 microneedles, with unique geometry parameters permuted within our defined parametric space. Figure 4 shows FEA-model-derived stiffness as function of each of the geometry parameters (note that, to facilitate comparison, the ordinate stiffness scale is identical in all panels). These data reveal that the geometry parameters L₁ (tip length) and T₂ (diameter immediately after the bend) have the largest impact on microneedle stiffness, followed by R₁ (diameter just before the bend) and T₁ (tip diameter). The parameters A_RC (radius of the bending arc), R₂ (diameter of the needle shaft), and L₂ (not shown) have only minimal impact on microneedle stiffness.

Fig. 4.

Relationships between microneedle geometry parameters and FEA stiffness. FEA model microneedle stiffness (k) obtained with gradually changing geometry parametric values. Starting at the following centroidal parametric values (μm): T₁=10, T₂=18, R₁=28, R₂=50, L₁=1,000, L₂=1,500, and A_RC=280, each parameter was varied separately while keeping all other parameters unaltered. The data were fitted to the following functions (solid line): a k = 37:80 + 9468 exp^−0:005L₁, b k=−34.45+3.15[T₂]+0.36[T₂]², c k=−135.10+15.30[R₁]−0.16[R₁]², d k=49.5[T₁]^0.45, e k=105.4+[0.125A_RC], f k=92.18+1.27[R₂]−0.007[R₂]²

Mutual information analysis

One objective of the current study was to develop a simple heuristic method to estimate the stiffness of microneedle with a known geometry. This approach complements the more rigorous and exact FEA modeling method based on continuum mechanics. In the heuristic approach, we sought to develop a predictor of microneedle stiffness that is based on a small number of parameters. To determine the best parameter set to use, we performed an analysis based on mutual entropy between the stiffness and one or more geometric parameters that can be measured. The exact set of parameters was T₁, T₂, R₁, R₂, L₁, and A_RC. We varied these independent parameters to seven discrete levels over the typical range of pulled microneedles for a total 7⁶ combinations. Based on these combinations, the stiffness was predicted using the continuum model. The predicted stiffness K_P was treated as a dependent variable discretized to 50 levels and containing roughly the same number of samples per elements. The general formula for entropy is

$$H\left(X\right)=-\sum _{i=1}^{n}p\left(x_i\right){\log }_2\left(p\left(x_i\right)\right)$$ (1)

The entropy of the independent variable k_e=5.644, a value that is roughly log₂(50) as the 50 levels with equal probability. The mutual information of two discrete random variables X and Y can be defined as:

$$I(X;Y)=-\sum _{j=1}^m\sum _{i=1}^{n}p(x_i,y_j){\log }_2\left(\frac{p(x_i,y_j)}{p\left(x_i\right)p\left(y_j\right)}\right)$$ (2)

Where p(x, y) is the joint probability distribution function of X and Y, and p(x) and p(y) are the marginal probability distribution functions of X and Y, respectively.

Our results show the highest mutual information with single independent variables as follows: I(k_e;L₁)=1.5, I(k_e; T₂)=0.2, and I(k_e;R₁)=0.05. We also computed the mutual information with the joint distribution of all pairs and triplets of the dependent variables. In summary, the largest mutual information for a pair is I(k_e;L₁, T₂)=2.5. The largest mutual information for a triplet is I(k_e;L₁, T₂, R₁)=3.2. Hence, we chose to use geometric parameters L₁, T₂, R₁, and T₁ as a small set of parameters that can account for most of the entropy in the stiffness values (4.2 out of maximum of 5.6). Results are dependent on the exact number of discretization levels chosen; however, we used different levels with essentially similar results.

Constitutive equation

As described above, mutual information analysis revealed geometric parameters L₁, T₂, R₁, and T₁ as the most impacting parameters predicting microneedle stiffness. Accordingly, an approximation of the effect of each geometry parameter on stiffness was determined by maintaining the other parameters at chosen values (centroidal values), while varying the particular parameter of interest within a useful range (cf. Fig. 4). Parametric equations from these results were used as starting points, together with quotient and product entropy analysis, to determine the following constitutive equation:

$$\log K=C_1+C_2{T}_1-C_3{T}_2+C_4{R}_1-C_5\left[\frac{L_1}{T_2}\right]$$ (3)

Where C₁, C₂, C₃, C₄, and C₅ depend on the range of microneedle stiffness applied. When applied to the entire range (5–2,800 pN/nm) of simulated microneedles (7⁶ permutations), the result was a curvilinear fit (Fig. 5) where

$$C_1=3.316\mathrm{pN}∕\mathrm{nm};C_2=0.025\mathrm{pN}∕\mathrm{nm}.\mathrm{um};C_3=0.034\mathrm{pN}∕\mathrm{nm}.\mathrm{um};C_4=0.019\mathrm{pN}∕\mathrm{nm}.\mathrm{um};C_5=0.022\mathrm{pN}∕\mathrm{nm};$$

(R²=0.95, p<0.05) and standard error of 0.138.

Fig. 5.

Constitutive equation. Parametric equations from Fig. 4 and mutual entropy analysis were used as starting points to develop a simple heuristic constitutive equation for stiffness from the four parameters with the most impact on stiffness.

When applied to the range commonly used by our group (40–160 pN/nm),

$$C_1=3.023\mathrm{pN}∕\mathrm{nm};C_2=0.027\mathrm{pN}∕\mathrm{nm}.\mu \mathrm{m};C_3=0.024\mathrm{pN}∕\mathrm{nm}.\mu \mathrm{m};C_4=0.0165\mathrm{pN}∕\mathrm{nm}.\mu \mathrm{m};C_5=0.0204\mathrm{pN}∕\mathrm{nm};$$

Where K is in piconewton per nanometer and all geometry measurements are in micrometers (R²=0.96, p<0.05) and standard error of 0.038 which translates to a standard error of 9.26 pN/nm; the pooled average data for this reduced geometry set are displayed as inset (Fig. 5) that also shows how the constitutive equation applies well within our range but then begins to deviate after 160 pN/nm.

Harmonic frequencies

The first mode of harmonic frequencies in air for our range of microneedles was between 1.02 and 2.26 kHz depending largely on the geometry of the needles and effective mass. When measured in rigor solution and also in water, the harmonic frequencies were overdamped with a damping ratio ξ of 0.26±0.05 at frequencies ranging from 410 to 820 Hz. This indicates that in fluids the harmonic frequencies are reduced drastically and consequently, for reliable interpretation of kinetic measurements, the microneedle probes should be designed to have a relatively high resonance frequency in air for better resonance response in fluids and physiological media. Our finite-element model simulation software helps achieve this (refer to online downloadable FEA model).

We simulated for harmonic frequencies of the microneedle by calculating for the eigenvalues of our FEA for a range of microneedle geometries (cf. Table 1). No preload was used so that at the start of the calculation all SPC boundary conditions, which may be nonzero due to previous steps, were set to zero. We compared our model simulation results with harmonic frequencies of real microneedles and found that, besides the first harmonic as reported in Table 1,our model could also predict microneedle frequencies up to the second harmonic in plucked mode and up to the third harmonic in swept frequency mode (data not shown). Higher harmonic modes of the real needles in swept frequency mode were obscured by noise, which may be due to possible vibration of the needle in several planes. It should be noted that, although the full FEA model could accurately predict the frequency response of a microneedle, attempts to derive a simple heuristic constitutive equation were unsuccessful.

Table 1.

Comparing measured to simulated harmonic frequencies

Tip diameter (T1/μm)	Diameter after bend (T2/μm)	Diameter before bend (R1/μm)	Bending arc (ARC/μm)	Tip length (L1/μm)	Shaft length (L2/μm)	Shaft diameter at fixed end (R2/μm)	Natural frequency in air (kHz)	Model predicted harmonic (/kHz)
12.2	19.8	32.4	288.0	1,202.0	2,508.0	40.0	1.68	1.69
11.8	21.6	28.0	248.0	1,398.0	2,512.0	49.8	2.23	2.04
10.2	14.4	14.9	292.0	1,286.0	4,326.0	72.3	1.40	1.41
9.4	12.2	14.1	242.0	988.0	3,380.0	68.0	2.26	2.25
13.8	14.8	15.2	244.0	1,680.0	3,870.0	67.8	1.02	0.952

Measured dimensions and natural frequencies of six real needles in air, compared to simulated first harmonic frequencies from our model. Our range of microneedles used falls approximately within the dimensions (μm) T₁ 6–14, T₂ 10–20, R₁ 12–33, R₂ 28–90, L₁ 500–1,800, L₂ 600–4,000, A_RC 190–390

Discussion

In measuring myofibrillar force, the aim is to design a probe that will reflect that force accurately and reliably and also function without distortion from the resonance response of the probe in the measuring medium. The difficulty in fabricating glass microneedles stems from their miniaturized sizes so that assessment by traditional macroscale methods becomes difficult. Traditional methods of stiffness calibration produce results that are accurate between 5% and 40% [1, 5] and are time-consuming. Moreover, these methods preclude a priori prediction of microneedle stiffness and frequency response characteristics. The FEA approach developed in the current study overcomes these limitations.

Capturing needle images in bright field and using pixel-measuring software (for example NiiRuler or ImageJ), the errors involved in measuring the geometry parameters are approximately 1.0 μm for L₁, L₂, and A_RC captured using a lower objective (×10) and 0.5 μm for T₁, T₂, R₁, and R₂ captured with a higher objective (×40). We estimate that such errors translate into maximum deviations of approximately 10% stiffness within the range of microneedles commonly used in our laboratory. We estimate that the FEA model itself has a systemic error of less than 2%, while the constitutive equation deviates from the model by up to 12% within the range (40–160 pN/nm). Thus, the overall error in stiffness estimation compares favorably to the traditional methods of microneedle stiffness determination with the advantage of greatly improved speed of determination and the ability to a priori predict both stiffness and frequency response.

In conclusion, we find this finite-element method to be very time saving in calibrating microneedles and find the model to be very accurate in determining stiffness. While the simple heuristic equation could be used to quickly judge the approximate ranges of microneedle stiffness, it cannot be used as an alternative for calibration. For such purpose, our FEA model is much better suited. We have made available Windows-PC and Intel Mac-OS platform executables of our FEA model simulation program to help others in field reliably produce and accurately calibrate microneedles (http://www.uic.edu/depts/mcpb/Resources/down loadable_resources/Downloadable_Resources.htm). We propose that this model would enhance future research work by saving time and ensuring precision and accuracy in microforce measurements and would add flexibility and ease to the process of calibrating microneedle force probes.