Nanofluids Research: Key Issues

Abstract

Nanofluids are a new class of fluids engineered by dispersing nanometer-size structures (particles, fibers, tubes, droplets) in base fluids. The very essence of nanofluids research and development is to enhance fluid macroscopic and megascale properties such as thermal conductivity through manipulating microscopic physics (structures, properties and activities). Therefore, the success of nanofluid technology depends very much on how well we can address issues like effective means of microscale manipulation, interplays among physics at different scales and optimization of microscale physics for the optimal megascale properties. In this work, we take heat-conduction nanofluids as examples to review methodologies available to effectively tackle these key but difficult problems and identify the future research needs as well. The reviewed techniques include nanofluids synthesis through liquid-phase chemical reactions in continuous-flow microfluidic microreactors, scaling-up by the volume averaging and constructal design with the constructal theory. The identified areas of future research contain microfluidic nanofluids, thermal waves and constructal nanofluids.

Introduction

Nanofluids, fluid suspensions of nanometer-sized particles, have recently been demonstrated to have thermal conductivities far superior to that of the liquid alone [1-4]. This and their other distinctive features offer unprecedented potential for many applications in various fields including energy, bio and pharmaceutical industry, and chemical, electronic, environmental, material, medical and thermal engineering [1-17]. State-of-the-art expositions of major advances on the synthesis, characterization and application of nanofluids are available, for example, in [1-3,16-19].

Nanofluids are research challenges of rare potential but daunting difficulty. The potential comes from both scientific and practical opportunities in many fields. The difficulty reflects the issues related to multiscales. Nanofluids involve at least four relevant scales: the molecular scale, the microscale, the macroscale and the megascale. The molecular scale is characterized by the mean free path between molecular collisions, the microscale by the smallest scale at which the law of continuum mechanics apply, the macroscale by the smallest scale at which a set of averaged properties of concern can be defined and the megascale by the length scale corresponding to the domain of interest [20,21]. By their very nature, research and engineering practice in nanofluids are to enhance fluid macroscale and megascale properties through manipulating microscale physics (structures, properties and activities). Therefore, interest should focus on addressing questions like: (1) how to effectively manipulate at microscale, (2) what are the interplays among physics at different scales and (3) how to optimize microscale physics for the optimal megascale properties. In this work, we summarize methodologies available to effectively address these central problems and identify the future research needs by taking heat-conduction nanofluids as examples.

Microscale Manipulation

The ability to manipulate at microscale depends very much on nanofluids synthesis techniques. Nanofluids have been synthesized by either a two-step approach that first generates nanoparticles and subsequently disperses them into base fluids [1-3,15-18] or a one-step physical method that simultaneously makes and disperses the nanoparticles into base fluids [22-26]. An advantage of the two-step method is that the inert gas condensation technique has already been scaled up to commercial nano-powder production [27]. Because of this and the ease with which the particle concentration and size distribution can be manipulated, most of the experimental investigations have used the two-step method [1-3,15-18]. A deficiency of the two-step technique is particles’ agglomeration during storage and dispersion in the base fluids, as a result of their high surface-to-volume ratio. Such agglomerates, in most cases, negate the unique properties associated with nanoparticles and nanofluids [1-3,15-18]. Changing the nanofluids’ PH value, adding surfactants or a suitable surface activator, or using ultrasonic or microwave vibration have been used with the two-step method to prevent nanoparticles from agglomerating [1-3,15-18]. However, typically it is rare to maintain so-synthesized nanofluids in a homogeneous stable state for more that 24 h [2].

To prevent oxidation of metallic particles, a one-step technique is preferable for synthesizing nanofluids containing metal particles. The one-step physical method developed in [22,23] involves nanoparticle source evaporation and direct condensation and dispersion into a flowing base fluid in a vacuum chamber. The method has been successfully used to synthesize nanofluids of Cu particles in ethylene glycol with small copper nanoparticles (about 10 nm) and high thermal conductivity enhancement (about 40% at the particle volume concentration of 0.3%) [23]. Another one-step physical method (the submerged arc nanoparticle synthesis system; SANSS) has also been used to synthesize nanofluids of particles in deionized water [24], CuO particles in deionized water [25] and Cu particles in the mixture of deionized water and ethylene glycol [26]. With the SANSS, the nanofluids are generated by vaporizing the solid material by the submerged arc and condensing into the base liquid in a vacuum chamber. Although these one-step physical methods are capable of synthesizing nanofluids with different nanostructures, they would be difficult to scale-up mainly because of their high cost and their demand for a vacuum.

In addition to the challenge of how to effectively prevent nanoparticles from agglomerating or aggregating, the key issue in either of these two approaches is the lack of effective means for synthesizing nanofluids with controllable microstructures due to either the limitation of available nanoparticle powers in the two-step method or the limitation of the system used in the single-step physical method. In an attempt to develop more effective techniques, a one-step chemical solution method has been recently developed [16,28-32]. The strength of the solution chemistry for synthesizing nanofluids lies in its ability to manipulate atoms and molecules in the liquid phase, thereby providing a powerful arsenal for synthesis of tailor-designed nanofluids using a bottom-up approach [16,28].

Figure 1 shows the flow chart of the chemical solution method (CSM) [16,28]. The reaction between Reactants A (e.g., Cu²⁺) and B (e.g., OH⁻) in the liquid phase yields the solution or colloid containing the precursor C (e.g., Cu(OH)₂). The additives (e.g., ammonium citrate or cetyltrimethyl ammonium bromide) are then added into the solution/colloid. Finally, the solution/colloid of the precursor C transforms into nanofluid D (e.g., CuO-particles-in-water) under ultrasonic or/and microwave irradiation.

Figure 1.

Chemical solution method (CSM) for synthesis of nanofluids: flow chart

Precursor C normally exists in the form of solution or colloid and is not, in general, the nanoparticle in the nanofluid D. Its solution or colloid can directly transform into the required nanofluids with the help of additives and external fields such as ultrasonic and microwave irradiation. Both the additives and the external fields are used to prevent nanoparticles from agglomeration and growth and thus control nanofluid microstructures.

The method has been successfully applied to produce nine kinds of nanofluids in Fig. 2[16,28-32]. The nanofluids synthesized by this method have both higher conductivity enhancement and better stability than those produced by the other methods. This method is distinguished from the others also by its controllability. The nanofluid microstructure can be varied and manipulated by adjusting synthesis parameters such as temperature, acidity, ultrasonic and microwave irradiation, types and concentrations of reactants and additives, and the order in which the additives are added to the solution [16,28].

Figure 2.

TEM/SEM images of some nanoparticles from “drying” samples of nanofluids synthesized by the chemical solution method [16,28-32] (a CePO₄ nanofibers; b octahedral Cu₂O nanoparticles; c N-vinylcaprolactam polymer-nanoparticles; d spherical Fe₃O₄ nanoparticles; e elliptic Cu nanorods; f needle-like CuO nanoparticles; g hollow CuS nanoparticles; h hollow and wrinkled Cu₂O nanoparticles; i Cu₂O(core)/CuS(shell) nanoparticles)

Problems with the CSM come mainly from the macroscale batch reactors where reactions take place:

· The CSM uses a bottom-up approach to generate nanoparticles through chemical reactions in the liquid phase, and thereby it has the potential to manipulate atoms and molecules. However, the difficulty of controlling the microscale while operating at the macroscale is insuperable.

· Mixing in a macro-scale batch reactor is usually achieved by stirring. In this case, the fluid entity is broken into fragments by circular motion. The last part of mixing takes place based on molecular diffusion. In the diffusion process, the mixing time t depends on the diffusion path d in the form of t ∝ d²/D, where D is the diffusion coefficient. Therefore, if the diffusion path becomes smaller, the mixing time becomes shorter. However, it is very difficult to make small-sized fragments by conventional stirring in solution phase. At the macroscale, therefore, mixing time is usually much larger than reaction time. The reaction rate is normally determined by the mixing time and is usually very low (reaction time: minutes–hours). Moreover, the longer mixing time and lack of effective ways to accurately control mixing also lead to poor product selectivity of competitive reactions either in parallel or in consecutive, thereby leading to poor quality of synthesized nanofluids that could contain some undesired side products.

· Generally, the heat generation rate in reaction increases in proportion to the reactor volume. Because the heat of reaction is removed through the wall of the reactor, the wall-surface-area/reactor-volume ratio, which decreases with the increasing reactor size, plays a crucial role. Therefore, heat removal capacity is also a key issue for highly exothermic and extremely fast reactions in macroreactors.

· Because of high labor and work-up demand, a batch-model operation is not commercially economical. The repeatability of nanofluids’ structures is also poor with the batch-model operation.

To resolve these critical issues, the batch-based macroreactors in the CSM can be replaced by continuous-flow microfluidic microreactors, for example, those in Fig. 3[16,33-35]. This allows a continuous and scalable (simply by numbering-up) synthesis of high-quality nanofluids with a more accurate and effective control over particle microstructures such as the size, distribution and shape. Microreactors exhibit numerous practical advantages, including safety, easy modulation and numbering-up for industrial production, when compared with traditional macroreactors. It is also advantageous that the reactions can be controlled more accurately through efficient mixing, enhanced reaction/product selectivity and effective mass and heat transfer, due to short diffusion paths and high surface-to-volume ratios at the microscale. Running the one-step chemical process in a continuous mode would not only increase its commercial viability, but also improve its repeatability significantly. Growth of nanoparticles directly in the base fluids through chemical reactions enables us to manipulate atoms and molecules in the liquid phase, thereby providing a powerful arsenal for synthesis of tailor-designed nanofluids using a bottom-up approach [16].

Figure 3.

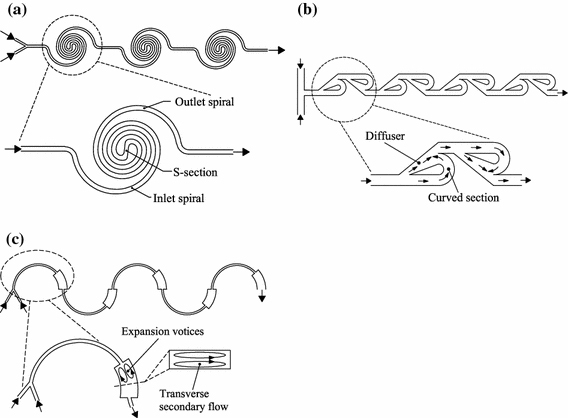
Three kinds of microfluidic reactors (a three spiral-microchannel units; b four modified-Tesla-structure units; c five semicircular-arc units)

Mixing has a decisive influence on the heat transfer, mass transfer, yield and selectivity of a reaction. Shrinking the reactor size to the microscale reduces the diffusion length between the reactant fluids, thus enhancing the mixing by molecular diffusion. The mixing by convection at the microscale is, however, weak because typically flow in microchannels is laminar with Reynolds numbers well below the threshold for turbulence. Transverse secondary flows—which arise as a result of centrifugal effects experienced by fluids traveling along a curved trajectory and continuously expand interfacial area between reagent streams through stretching, folding and breakup processes—offer an attractive possibility of providing enhanced mixing in an easily fabricated planar format by simply introducing curvature to the flow path. Expansion vortices or direct collision of slit fluid streams can also be generated by manipulating the geometrical structure of curved channels, and hence further enhance the mixing. Figure 3 shows three types of microreactors that are made of planar and smooth-walled curved microchannels on the one hand and have a rapid laminar-flow mixing on the other hand.

All three kinds of microreactors consist of several units of curved microchannels connected in series (three, four and five, respectively, in Fig. 3a–3c for illustration and example). The unit in Fig. 3a–3c is the spiral microchannel having an inlet and outlet spiral connected by a central S-shaped channel, the modified Tesla structure containing two modified Tesla microchannels in opposite directions and the semicircular arc involving an abrupt width increase over the last quarter, respectively. These microreactors can have a very rapid mixing between reactant fluids due to both the short diffusion length and the centrifugal-force-driven transverse secondary flow in curved microchannels [36-41]. The mixing is also further enhanced by the direct collision of slit fluid streams in the Tesla structure (Fig. 3b) and by the expansion vortices that arise in the horizontal plane due to an abrupt increase in the channel width (Fig. 3c) [42,43].

The centrifugal-force-driven transverse secondary flow becomes stronger following increases in the channel curvature ratio σ defined by σ = w/R (w and R are the channel width and the curvature radius, respectively) and the Dean number defined by 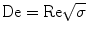(Re is the Reynolds number) [36-38]. The mixing performance thus becomes better as the Re increases for all three microreactors in Fig. 3, with consequently all working well as high-Re (Re >100) reactors. The first two types of microreactors (Fig. 3a, 3b) also work well as the low-Re (Re <10) and the intermediate-Re (10< Re <100) reactors [39,40,43], respectively, due to a very high curvature ratio σ used in the inner region of spiral microchannels in Fig. 3a and the fluid-stream direct collision in Fig. 3b.

In this microfluidic approach for nanofluids synthesis, solutions of the two reagents are injected as steady streams into a microfluidic channel at initial point (s = 0) where the reaction between them starts (t = 0). Here, s and t are the distance and time, respectively. As their mixture flows at a constant velocity v, the reaction time is linearly related to the spatial distance by t = s/v. Interactions of multiple chemical reactions in time could thus be controlled simply by varying flow velocities and by creating a network of converging and diverging channels for carrying reaction mixtures. Therefore, this approach offers simple means for controlling many chemical reactions, including when each reaction starts, for how long each reaction evolves before it is separated or combined with other reactions, and when each reaction is quenched.

Droplets and slugs formed within microfluidic channels can also serve as microreactors in the CSM for nanofluids synthesis. Figures 4 and 5 illustrate two such microfluidic systems [16]. In the first type (Fig. 4), discrete droplets are formed at the T-junction and are encapsulated by a dispersing liquid that wets the microchannel. These droplets form the dispersed phase in which the reaction between Reactants A (e.g., phosphoric acid H₃PO₄) and B (e.g., cerium nitrate Ce(NO₃)₃) occurs in the liquid phase. After separating the dispersing liquid in the separator, we can obtain nanofluids (e.g., suspensions of cerium phosphate (CePO₄) nanofibers in water, Fig. 2a). In the second type (Fig. 5), liquid slugs are separated by discrete gas bubbles generated at the T-junction of microfluidic channels. Reactions occur within the slugs that form the continuous phase. The nanofluids are collected after separating the gas bubbles in the separator. The first type differs from the second type in that reagents in droplets do not come into contact with the microchannel wall.

Figure 4.

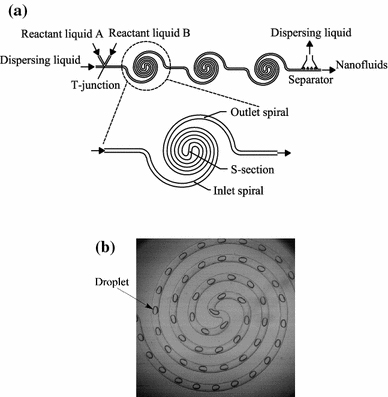
Nanofluids’ synthesis by compartmentalizing chemical reactions in microfluidic droplets: a microfluidic system; b microfluidic droplets

Figure 5.

Nanofluids’ synthesis by compartmentalizing chemical reactions in microfluidic slugs mediated by gas bubbles: a microfluidic system; b microfluidic slugs mediated by gas bubbles

The additional advantage of compartmentalizing reactions in droplets or slugs of femoliter to microliter includes the enhanced mixing from the internal recirculation within the droplets or slugs [43-46] and enhanced controllability of reactions due to the simplicity and accuracy in manipulating microfluidic droplets, bubbles and slugs in various ways [43-47]. For example, the ability to split and fuse individual droplets improves simplicity with which the reagent volume and concentrations can be controlled precisely.

Figure 6a shows the photos of some microfluidic Cu₂O nanofluids 24 h after their preparation [34], with the enhanced stability, highly monodispersed particles and reduced particle size compared with those synthesized by the CSM [31]. The particle shape can also be designed with this type of synthesis method. Figure 6b illustrates some flower-shaped Cu₂O particles that are difficult to form by the other methods [34].

Figure 6.

Microfluidic Cu₂O particles-in-water nanofluids 24 h after their preparation [34]: a stable nanofluid samples; b SEM images of flower-shaped Cu₂O particles

Therefore, microstructures of microfluidic nanofluids (the nanofluids synthesized through liquid-phase chemical reactions in microfluidic systems) can be precisely controlled by reagent fluid properties, system geometrical properties and fluid dynamical parameters such as flow rates. Intensified future effort is required to define the potential of this promising synthesis technique against an important target of controlling reactions accurately with a rapid and precise mixing. Specifically, the research focus should be on the correlations between nanofluids microstructures and controlling parameters of fluid physical/chemical/dynamical properties and microfluidic geometrical features.

Macroscale Heat Conduction

A relatively intensified effort has been made on determining nanofluid thermal conductivity from experiments, particularly for the nanofluids with spherical nanoparticles or nanotubes. While the data from these experiments have enabled some trends to be identified, there is still no consensus on the effects of some parameters such as particle size, shape, distribution and additives in the nanofluids [1-3,15-19,28,29]. There also exist wide discrepancies and inconsistencies in the reported conductivity data due to a limited understanding of the precise nature of heat conduction in nanofluids, the poor microstructure characterization and the unavailability of nanofluids with various microstructures [1-3,15-19,28,29]. In many cases, the microstructural parameters were not measured by the experimenters themselves but rather taken from the powder manufacturers’ nominal information. To reconcile these discrepancies and inconsistencies and to lay the foundations for better and more efficient designs of nanofluids, it is essential to generate nanofluids of various microstructures, characterize their microstructures by state-of-the-art instrumentation and develop precise heat-conduction model for nanofluids [16,28].

Suggested microscopic reasons for experimental finding of significant conductivity enhancement include the nanoparticle Brownian motion effect [48-53], the liquid layering effect at the liquid–particle interface [54-59], and the nanoparticle cluster/aggregate effect [60,61]. As generally accepted [1-3,15-19,62-67], however, no conclusive explanation is available. Often, the explanation by one research group is confronted by others. There is also a lack of agreement between experimental results and between theoretical models. The fact that the conductivity enhancement comes from the presence of nanoparticles has directed research efforts nearly exclusively toward thermal transport at nanoscale. The classical heat conduction equation has been postulated as the macroscale model but without adequate justification. Thermal conductivity is a macroscale phenomenological characterization of heat conduction and the conductivity measurements are not performed at the nanoscale, but rather at the macroscale. Therefore, interest should focus not only on what happens at the nanoscale but also on how the presence of nanoparticles affects the heat transport at macroscale.

In an attempt to isolate the mechanism responsible for the significant enhancement of thermal conductivity, a macroscale heat conduction model in nanofluids has been recently developed from first principles [16,20,28,68]. The model was obtained by scaling-up a microscale model for heat conduction in nanoparticles and in base fluids. The approach for scaling-up is the volume averaging with help of multiscale theorems [20,69]. The microscale model for the heat conduction in the nanoparticles and in the base fluids comes from the first law of thermodynamics and the Fourier law of heat conduction. The result shows that the presence of nanoparticles leads to a dual-phase-lagging heat conduction in nanofluids at macroscale with a potential of higher thermal conductivity. Here, we first summarize the development of this theory, then examine the macroscale manifestation of microscale physics, and finally identify the future research needs.

Microscale Heat-Conduction Models

The microscale model for heat conduction in nanofluids is well known. It consists of the field equation and the constitutive equation. The field equation comes from the first law of thermodynamics. The commonly used constitutive equation is the Fourier law of heat conduction for the relation between the temperature gradient ∇T and the heat flux density vector q[70].

Consider heat conduction in nanofluids with the base fluid and the nanoparticle denoted by β- and σ-phases, respectively. By the first law of thermodynamics and the Fourier law of heat conduction, we have the microscale model for heat conduction in nanofluids (Fig. 7)

Figure 7.

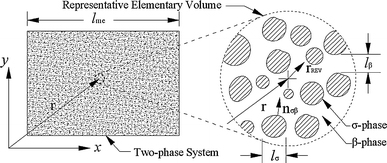
Nanofluids and representative elementary volume (REV)

Here, T is the temperature. ρ, c and k are the density, specific heat and thermal conductivity, respectively. Subscripts β and σ refer to the β- and σ-phases, respectively. A_βσ represents the area of the β–σ interface; n_βσ is the outward-directed surface normal from the β-phase toward the σ-phase, and n_βσ = −n_σβ (Fig. 7).

Macroscale Heat-Conduction Models

A macroscale model equivalent to the microscale behavior can be readily obtained by the method of volume averaging [20,69]. Consider a representative elementary volume (REV) in Fig. 7, the smallest differential volume resulting in statistically meaningful local average properties. Averaging Eqs. 1-4 over REV and applying the multiscale theorems [20] yield the macroscale model of heat conduction [16,20,28,68]:

and

where

and

V_β and V_σ are the volumes of β- and σ-phases in REV, respectively. γ_β = (1 − φ)(ρc)_β and γ_σ = φ(ρc)_σ are the β-phase and σ-phase effective thermal capacities, respectively. φ is the volume fraction of the σ—phase defined by φ = V_σ/V_REV (V_REV is the volume of REV). h and a_υ come from modeling of the interfacial flux and are the film heat transfer coefficient and the interfacial area per unit volume, respectively [16,20,68]. K_ββK_σσK_βσ and K_σβ are the effective thermal conductivity tensors, and the coupled thermal conductivity tensors are equal

When the system is isotropic and the physical properties of the two phases are constant, Eqs. 5 and 6 reduce to

and

where k_ββ and k_σσ are the effective thermal conductivities of the β- and σ-phases, respectively, and k_βσ = k_σβ is the cross effective thermal conductivity of the two phases.

Thermal Waves

Rewrite Eqs. 10 and 11 in their operator form

We then obtain an uncoupled form by evaluating the operator determinant such that

where the index i can take β or σ. Its explicit form reads, after dividing by ha_υ(γ_β + γ_σ)

where

This can be regarded as a dual-phase-lagging (DPL) heat-conduction equation with as the DPL source-related term 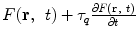and with τ_q and τ_T as the phase lags of the heat flux and the temperature gradient, respectively [68,71]. Here, is the volumetric heat source. k, ρc and α are the effective thermal conductivity, capacity and diffusivity of nanofluids, respectively. The dual-phase-lagging heat-conduction equation originates from the first law of thermodynamics and the dual-phase-lagging constitutive relation of heat flux density [68,71]. It is developed in examining energy transport involving high-rate heating in which the non-equilibrium thermodynamic transition and the microstructural effect become important associated with a shortening of the response time [68,71]. Therefore, the presence of nanoparticles shifts the Fourier heat conduction in the base fluid into the dual-phase-lagging heat conduction in nanofluids at the macroscale. This finding is significant because all results regarding dual-phase-lagging heat conduction can thus be applied to study heat conduction in nanofluids.

The presence of nanoparticles gives rise to variations of thermal capacity, conductivity and diffusivity, which are given by, in terms of ratios over those of the base fluid,

Therefore, ρc/(ρc)_β depends only on the volume fraction of nanoparticles and the nanoparticle–fluid capacity ratio. However, both k/k_β and α/α_β are affected by the geometry, property and dynamic process of nanoparticle–fluid interfaces. This dependency causes the most difficulty because it is the least precisely known feature of a nanofluid. The future research effort should thus focus on 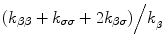to develop predicting models of thermal conductivity for nanofluids. Consider

It can be large, equal or smaller than 1 depending on the sign of 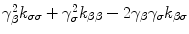. Therefore, by the condition for the existence of thermal waves that requires τ_T/τ_q < 1 [68,72], we may have thermal waves in nanofluid heat conduction when

A necessary (but not sufficient) condition for Eq. 20 is 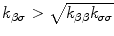. Note also that for heat conduction in nanofluids, there is a time-dependent source term 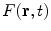in the dual-phase-lagging heat conduction (Eqs. 14 and 15). Therefore, the resonance can also occur. These thermal waves and possibly resonance are believed to be the driving force for the conductivity enhancement. When k_βσ = 0 so that τ_T/τ_q is always larger than 1, thermal waves and resonance would not appear. The coupled conductive terms in Eqs. 10 and 11 are thus responsible for thermal waves and resonance in nanofluid heat conduction. It is also interesting to note that although each τ_q and τ_T is ha_υ dependent, the ratio τ_T/τ_q is not. Therefore, the evaluation of τ_T/τ_q will be much simpler than τ_q or τ_T.

Addition of 4% of 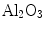particles was reported to increase thermal conductivity by a factor of 8% [73], while CuO particles at the same volume fraction enhance the conductivity by about 12% [15]. This is interesting because conductivity of CuO is less than that of . The thermal wave theory can explain this since the conductivity enhancement k/k_β equals to (k_ββ + 2k_βσ + k_σσ)/k_β (Eq. 17), which are strongly affected by nanofluids microstructures and interfacial properties/processes of nanoparticle–fluid interfaces.

Therefore, the molecular physics and the microscale physics (interactions between nanoparticles and base fluids at the microscale in particular) manifest themselves as heat diffusion and thermal waves at the macroscale, respectively. Their overall macroscopic manifestation shifts the Fourier heat conduction in the base fluid into the dual-phase-lagging heat conduction in nanofluids. When τ_T/τ_q < 1, thermal waves dominant and Eq. 14 is of a hyperbolic type [68]. When τ_T/τ_q ≥ 1, however, heat diffusion dominants and Eq. 14 is parabolic [68]. Depending on factors like material properties of nanoparticles and base fluids, nanoparticles’ geometrical structure and their distribution in the base fluids, and interfacial properties and dynamic processes on particle–fluid interfaces, the heat diffusion and thermal waves may either enhance or counteract each other. Consequently, the heat conduction may be enhanced or weakened by the presence of nanoparticles. Table 1 lists the conductivity ratio k/k_b from experiments. Here, k and k_b are the thermal conductivity of the nanofluid and the base fluid, respectively. It shows that: (1) the interaction between the heat diffusion and the thermal waves can either upgrade or downgrade fluid conductivity by the presence of higher-conductivity nanoparticles, and (2) extraordinary water conductivity enhancement (up to 153%) can be achievable by the presence of lower-conductivity oil droplets due to strong thermal waves. The reported strong thermal conductivity enhancement beyond that from the higher value of suspended nanoparticles in [23,75-79] is also the evidence of such thermal waves.

Table 1.

Measured conductivity ratio k/k_b of some nanofluids (k: nanofluid thermal conductivity; k_b: base-fluid thermal conductivity)

Nanofluids	k/kb
CePO4 nanofibers in water [28,32]	0.67–1.54
Cu2O spherical particles in water [31]	0.83–1.24
Cu2O octahedral particles in water [31]	0.89–1.24
CuS/Cu2S hollow spherical particles in water [30]	0.85–1.18
CuS/Cu2S core–shell spherical particles in water [30]	0.82–1.21
1 vol% Alumina nanorods (80 × 10 nm) in water [67]	0.92–1.18
1 vol% Alumina nanorods (80 × 10 nm) in Polyalphaolefins lubricant (PAO) + surfactant [67]	0.91–1.10
0.001 vol% Gold nanoparticles (20–30 nm) in water [67]	0.91–1.11
0.86 vol% Mn–Zn ferrite (12.9 nm) in water [67]	0.92–1.09
Corn oil droplets in water [74]	0.755–2.39
Olive oil droplets in water [28]	0.636–2.533

The immediate and intensive efforts should thus focus on: (1) solving the three closure problems in [16] analytically and numerically for unit cells with various microscale physics to find the correlation between the microscale physics and the nanofluid macroscale properties (effective thermal conductivity, effective thermal diffusivity, phase lag of the heat flux τ_q and phase lag of the temperature gradient τ_T); (2) studying the dual-phase-lagging heat conduction equation Eq. 14 analytically and numerically for various nanofluids systems to find properties of thermal waves and how they interact with the heat diffusion. Focused experiments in these areas are also in great demand for experimentally confirming the analytical/numerical findings. Such studies, together with the development of microfluidic nanofluids should lead to methodologies of controlling nanofluids macroscale properties through manipulating their microscale physics, a significant step forward toward creating nanofluids by design.

The first of Type-(1) work has recently been made in [80,81], showing that the macroscale model works very well and uncovering some important features regarding the model itself and the microstructure–conductivity correlation. For nanofluids consisting of in-line arrays of perfectly dispersed two-dimensional circular, square or hollow particles, for example, the heat conduction is diffusion-dominant so that the effective thermal conductivity can be predicted adequately by the mixture rule with the effect of particle shape and particle–fluid conductivity ratio incorporated into its empirical parameter [80]. Thermal waves appear more likely at smaller particle–fluid conductivity ratio and lower particle volume fraction, a result that agrees with the experimentally observed significant conductivity enhancement in the oil-in-water emulsion [28,74]. The computed thermal conductivity predicts some experimental data in the literature very well and shows the sensitivity to the surface-to-volume ratio [80]. The simulation results in [81] show that the radius of gyration and the non-dimensional particle–fluid interfacial area are two important parameters in characterizing the geometrical structure of nanoparticles. A non-uniform particle size is found to be unfavorable for the conductivity enhancement, while particle aggregation benefits the enhancement especially when the radius of gyration of aggregates is large [81]. Without considering the interfacial thermal resistance, larger non-dimensional particle–fluid interfacial area between the base fluid and the nanoparticles is also desirable for enhancing thermal conductivity [81]. The nanofluids with nanoparticles of connected cross-shape show a much higher (lower) effective thermal conductivity when particle–fluid conductivity ratio is larger (smaller) than 1 [81].

Megascale Optimization

In the field of nanofluid heat conduction, efforts have been nearly exclusively on correlating thermal conductivity of nanofluids with their microscale physics, as a fundamental step of searching for optimal thermal conductivity [1-3,16-19]. The attention to system megascale properties has been very limited. However, practical applications of nanofluids as the heat-conduction fluids often have a different ultimate aim such as minimization of system highest temperature and minimization of system overall thermal resistance. Therefore, interest should focus not only on optimizing nanofluid macroscale properties but also on designing nanofluids for the best system performance at megascale.

By its very nature, the microstructural optimization for the best system performance at the megascale fits well into the inverse problem in mathematics and the downscaling problem in multiscale science [20]. Both are of fundamental importance but daunting difficulty with no effective method available to resolve them at present. By following the constructal theory [82-84], a constructal approach has been recently developed in [16,85-88], which converts the inverse problem into a forward one by first specifying a type of microstructures and then optimizing system performance with respect to the available freedom within the specified type of microstructures and enables us to find the constructal microstructure (the best for the optimal system performance within the specified type of microstructures). The approach has also been applied to make a constructal design for some fundamental heat conduction systems of nanofluids with two pre-specified types of microstructures: (1) dispersed configuration in which nanoparticles are well dispersed in the base fluid [85,86], and (2) tree configuration in which nanoparticles form tree structures in the base fluid as high-conductivity channels for the heat flow [87,88]. The former is commonly used in the nanofluid field; the latter is mostly found in nature for its small flow resistance. The constructal nanofluids that maximize the system performance are not necessarily the ones with uniformly dispersed particles in base fluids [85,86]. The constructal nanofluids with the tree configuration can normally offer significantly smaller constructal overall resistance than the dispersed configuration [87]. The constructal nanofluids with the tree configuration have also some universal features of independent of: (1) some details of specified tree configuration, (2) fluid and particle properties and (3) particle overall volume fraction [88].

Therefore, the future effort is in great demand to construct nanofluids with respect to available freedoms for various systems of practical applications. Such studies will inspire the development of microfluidic nanofluids through constantly providing information regarding new nanofluids required.

Concluding Remarks

Nanofluids are a very important area of emerging technology and are playing an increasingly important role in the continuing advances of nanotechnology and biotechnology worldwide. They have enormously exciting potential applications and may revolutionize the field of heat transfer. With powerful microfluidic technology, scaling-up techniques, thermal-wave theory and constructal theory, research and engineering practice in nanofluids is entering a new era. On one side is great opportunity because these technologies empower us to address the central questions of nanofluid research and development such as effective means of microscale manipulation, interplays among physics at different scales and optimization of microscale physics for the optimal megascale properties. On the other side is greater challenge than ever before due to the difficulty related to scales and scaling.

Conventional synthesis approaches have not been satisfactory because of their inadequacies in engineering microstructures of nanofluids. Recently-developed one-step chemical solution method (CSM) takes advantage of the ability of manipulating atoms and molecules through chemical reactions in the liquid phase. However, the difficulty of controlling the microscale while operating at the macroscale is insuperable. By replacing batch-based macroreactors in the CSM by continuous-flow microfluidic microreactors of microchannels, droplets and slugs, a novel microfluidic one-step CSM is proposed for effective synthesis of high-quality nanofluids with controllable microstructures. Future research is in great demand to define the potential of this promising synthesis technique against an important target of controlling reactions accurately with a rapid and precise mixing. The success of this technology may change the way nanofluids are synthesized and applied and should also lead to progress both in creating nanofluids by design and in producing nanofluids economically at a commercial scale.

In an attempt to determine how the presence of nanoparticles affects the heat conduction at the macroscale and isolate the mechanism responsible for the reported significant enhancement of thermal conductivity, a macroscale heat-conduction model in nanofluids is rigorously developed. The model is obtained by scaling-up the microscale model for the heat conduction in the nanoparticles and in the base fluids. The approach for scaling-up is the volume averaging with help of multiscale theorems. The result shows that the presence of nanoparticles leads to a dual-phase-lagging heat conduction in nanofluids at the macroscale. Therefore, the molecular physics and the microscale physics manifest themselves as heat diffusion and thermal waves at the macroscale, respectively. Depending on factors like material properties of nanoparticles and base fluids, nanoparticles’ geometrical structure and their distribution in the base fluids, and interfacial properties and dynamic processes on particle-fluid interfaces, the heat diffusion and thermal waves may either enhance or counteract each other. Consequently, the heat conduction may be enhanced or weakened by the presence of nanoparticles. Focused efforts are required to find the correlation between the microscale physics and macroscale properties based on the three closures and to detail properties of thermal waves and how they interact with the heat diffusion.

Practical applications of nanofluids are always with an ultimate megascale goal to which nanofluid research must pay attention. The microstructural optimization for the best system performance is however a very difficult, unresolved problem of inverse type. A constructal approach is thus proposed, which is based on the constructal theory, converts the inverse problem into a forward one by first specifying a type of microstructures and then optimizing system performance with respect to the available freedom within the specified type of microstructures, and enables us to find the constructal microstructure (the best for the optimal system performance within the specified type of microstructures). Such a constructal design shows, for example, that the march toward uniformly dispersed particles in base fluids not necessarily leads to an optimal megascale performance depending on systems that use nanofluids. Our focus of future research and development should thus be not only on nanofluids themselves but also on their systems and ultimate goals. The march toward micro and nano scales must also be with the sobering reminder that useful devices are always be macroscopic and that larger and larger numbers of small-scale components must be assembled and connected by flows that keep them alive. Clearly, an intensive effort is in great demand to construct nanofluids with respect to available freedoms for various systems of practical applications.

Acknowledgments

The financial support from the Research Grants Council of Hong Kong (GRF718009 and GRF717508) is gratefully acknowledged.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.