Collaborative Double Robust Targeted Maximum Likelihood Estimation

Abstract

Collaborative double robust targeted maximum likelihood estimators represent a fundamental further advance over standard targeted maximum likelihood estimators of a pathwise differentiable parameter of a data generating distribution in a semiparametric model, introduced in van der Laan, Rubin (2006). The targeted maximum likelihood approach involves fluctuating an initial estimate of a relevant factor (Q) of the density of the observed data, in order to make a bias/variance tradeoff targeted towards the parameter of interest. The fluctuation involves estimation of a nuisance parameter portion of the likelihood, g. TMLE has been shown to be consistent and asymptotically normally distributed (CAN) under regularity conditions, when either one of these two factors of the likelihood of the data is correctly specified, and it is semiparametric efficient if both are correctly specified.

In this article we provide a template for applying collaborative targeted maximum likelihood estimation (C-TMLE) to the estimation of pathwise differentiable parameters in semi-parametric models. The procedure creates a sequence of candidate targeted maximum likelihood estimators based on an initial estimate for Q coupled with a succession of increasingly non-parametric estimates for g. In a departure from current state of the art nuisance parameter estimation, C-TMLE estimates of g are constructed based on a loss function for the targeted maximum likelihood estimator of the relevant factor Q that uses the nuisance parameter to carry out the fluctuation, instead of a loss function for the nuisance parameter itself. Likelihood-based cross-validation is used to select the best estimator among all candidate TMLE estimators of Q₀ in this sequence. A penalized-likelihood loss function for Q is suggested when the parameter of interest is borderline-identifiable.

We present theoretical results for “collaborative double robustness,” demonstrating that the collaborative targeted maximum likelihood estimator is CAN even when Q and g are both mis-specified, providing that g solves a specified score equation implied by the difference between the Q and the true Q₀. This marks an improvement over the current definition of double robustness in the estimating equation literature.

We also establish an asymptotic linearity theorem for the C-DR-TMLE of the target parameter, showing that the C-DR-TMLE is more adaptive to the truth, and, as a consequence, can even be super efficient if the first stage density estimator does an excellent job itself with respect to the target parameter.

This research provides a template for targeted efficient and robust loss-based learning of a particular target feature of the probability distribution of the data within large (infinite dimensional) semi-parametric models, while still providing statistical inference in terms of confidence intervals and p-values. This research also breaks with a taboo (e.g., in the propensity score literature in the field of causal inference) on using the relevant part of likelihood to fine-tune the fitting of the nuisance parameter/censoring mechanism/treatment mechanism.

1. Introduction

Researchers acknowledge that questions about our infinite-dimensional, semi-parametric world are not well-addressed by parametric models. More sophisticated tools are needed to wrest meaning from data. We can and should develop and utilize methods specifically designed to estimate a relatively small-dimensional precisely specified parameter within such a semiparametric model that is identifiable from the data. The ideal method would be entirely a priori specified, have desirable statistical properties, avoid reliance on ad hoc or arbitrary specifications, and be computationally feasible.

Suppose one observes a sample of independent and identically distributed observations from a particular data generating distribution P₀ in a semiparametric model, and that one is concerned with estimation of a particular pathwise differentiable parameter of the data generating distribution. A parameter should be viewed as a mapping from the semiparametric model to the parameter space (e.g., real line). A parameter mapping is pathwise differentiable at P₀ if it is differentiable along all smooth parametric sub-models through P₀, and its derivative is uniformly bounded as a linear mapping on the Hilbert space of all scores of these parametric submodels. Intuitively, a pathwise differentiable parameter is a parameter which has a finite generalized Cramer-Rao information lower bound, so that in principle, under enough regularity conditions, it is possible to construct an estimator which behaves like a sample mean of i.i.d. random variables. Due to the curse of dimensionality implied by the infinite dimension of semi-parametric models, standard (nonparametric) maximum likelihood estimation is often ill defined or breaks down due to overfitting, while, on the other hand, regularized sieve-based maximum likelihood estimation results in overly biased plug-in estimators of the target parameter of interest.

The latter is due to the fact that such likelihood based estimators seek and achieve a bias-variance trade-off that is optimal for the density of the distribution of the data itself. Since the variance of an optimally smoothed density estimator is typically much larger than the variance of a smooth (pathwise-differentiable) parameter of the density estimator, the substitution estimators are often too biased relative to their variance. That is, substitution estimators based on density estimators involving optimal (e.g., likelihood-based) bias-variance trade-off (for the whole density) are not targeted towards the parameter of interest.

Motivated by this problem with the bias-variance trade-off of maximum likelihood estimation in semiparametric models, while still wanting to preserve the log-likelihood as the principle criterion in estimation, in van der Laan and Rubin (2006) we introduced and developed a targeted maximum likelihood estimator of the parameter of interest.

The targeted maximum likelihood estimator of the distribution of the data is obtained by fluctuating an initial estimator of the relevant part of the data generating distribution with a parametric fluctuation model whose score at the initial estimator (i.e., at zero fluctuation) equals or includes the efficient influence curve of the parameter of interest, and estimating the fluctuation parameter (i.e., amount of fluctuation) with standard parametric maximum likelihood, treating the initial estimator as offset. Iteration of this targeted maximum likelihood modification step results in a so called k-th step targeted maximum likelihood estimator, and its limit in k solves the actual efficient influence curve equation defined by setting the empirical mean of the efficient influence curve equal to zero. The latter estimator we called the targeted maximum likelihood estimator, which also results in a corresponding plug-in targeted maximum likelihood estimator of the parameter of interest by applying the parameter mapping to the targeted maximum likelihood estimator.

This targeted maximum likelihood step using the fluctuation model removes bias of the initial estimator with respect to (w.r.t.) the target parameter, while increasing the variance of the estimator till the level of the semi-parametric information bound, thereby resulting in a consistent, asymptotically linear, and semi-parametric (locally) efficient estimator.

Although in a variety of applications the fluctuation model is known, e.g., randomized controlled trials with known treatment assignment and missingness mechanism, the fluctuation model typically depends on an unknown nuisance parameter, which then needs to be estimated as well. In censored data models satisfying the so called coarsening at random (CAR) assumption this nuisance parameter typically represents the censoring mechanism, and the density of the data factors in the relevant part of the density and the censoring mechanism density (e.g., Heitjan and Rubin (1991), Jacobsen and Keiding (1995), Gill et al. (1997)).

In this case, the bias reduction obtained at the targeted maximum likelihood step depends on how and how well we estimate the nuisance parameter. Specifically, the targeted maximum likelihood estimator is a so called double robust locally efficient estimator in censored data models (including causal inference models with the full data representing a collection of treatment regimen specific counterfactuals) in which the censoring mechanism satisfies the coarsening at random assumption. This means that, under regularity conditions, it is consistent and asymptotically linear if either the initial estimator is consistent or the nuisance parameter is consistent, and it is efficient in the semiparametric model if the initial estimator is consistent. Another approach for double robust locally efficient estimation is the estimating equation methodology (see, van der Laan and Robins (2003), and review below).

An outstanding open problem that obstructs the robust practical application of double robust estimators (in particular, in nonparametric censored data or causal inference models) is the selection of a sensible model or estimator of the nuisance parameter: this is particularly true when the efficient influence curve estimating equation involves inverse probability of censoring or treatment weighting, due to the enormous sensitivity of the estimator of the parameter of interest to the estimator of the nuisance parameter. A relevant recent discussion of these issues is found in Kang and Schafer (2007a), Ridgeway and McCaffrey (2007), Robins et al. (2007), Tan (2007), Tsiatis and Davidian (2007), Kang and Schafer (2007b).

Given an initial estimator, we are concerned with constructing an estimator of the nuisance parameter, that results in a better bias-variance trade-off (i.e. better MSE) for the resulting targeted maximum likelihood estimator of the target parameter than current practice. In this article we introduce a new strategy for nuisance parameter estimator selection for targeted maximum likelihood estimators that addresses this challenge by using the log-likelihood of the targeted maximum likelihood estimator (of the relevant density) indexed by the nuisance parameter estimator as the principal selection criterion. The nuisance parameter estimators needed for the targeting step are selected based on the relevant log-likelihood loss function of the resulting targeted maximum likelihood estimator, not on a loss function for the nuisance parameter itself. This approach takes into account the established fit of the initial estimator, and that the resulting estimator of the target parameter is indeed based on the relevant part of the likelihood.

Recognizing that the selected estimator of the nuisance parameter is very much a function of the goodness of fit of the initial estimator led to the development of a new theory of collaborative double robust estimation. The asymptotic linearity theory presented below involves characterizing a true minimal nuisance parameter indexed by the initial estimator limit, g₀(Q), that results in an efficient influence curve that is unbiased for the target parameter. This defines the collaborative double robustness of the efficient influence curve. Given a nested sequence of increasingly non-parametric estimators, g_δ, there is a g_δmin corresponding to g₀(Q) which makes the efficient influence curve unbiased for the target parameter. In addition, all estimates of g in the sequence that are more nonparametric than the estimator indexed by δ_min, i.e. δ > δ_min, also make the efficient influence curve unbiased for the target parameter. These results allow us to establish asymptotic linearity of the collaborative double robust targeted maximum likelihood estimator, under appropriate regularity conditions.

The theory is fascinating, and results in potentially super efficient estimators, the main intuition, in the context of CAR-censored data models, is that the covariates that enter the treatment mechanism and censoring mechanism estimator (i.e., nuisance parameter estimator) used to define the fluctuation model in the targeted maximum likelihood step should explain the difference between the initial estimator, Q_n, and the true relevant density, Q₀.

Such collaborative double robust estimators involve a variety of choices, including the choice of initial estimator and the choice of collaborative nuisance parameter estimator, but all solve the efficient influence curve equation and all rely on the collaborative nuisance parameter estimator being correctly specified so that the wished unbiasedness of the efficient influence curve is achieved in the limit. We propose using cross-validation w.r.t. a targeted loss function to select among these different collaborative targeted maximum likelihood estimators of the relevant density. In addition, we suggest the square of their influence curve or square of the efficient influence curve as a particularly suitable loss function, corresponding with selection of the estimator with minimal asymptotic variance.

An overview of relevant literature

The construction of efficient estimators of pathwise differentiable parameters in semi-parametric models requires utilizing the so called efficient influence curve, defined as the canonical gradient of the pathwise derivative of the parameter. A fundamental result of the efficiency theory is that a regular estimator is efficient if and only if it is asymptotically linear with influence curve equal to the efficient influence curve. We refer to Bickel et al. (1997), and Andersen et al. (1993). There are two distinct approaches for construction of efficient (or locally efficient) estimators: the estimating equation approach that uses the efficient influence curve as an estimating equation (e.g., one-step estimators based on the Newton-Raphson algorithm in Bickel et al. (1997)), and the targeted MLE that uses the efficient influence curve to define a targeted fluctuation function, and maximizes the likelihood in that targeted direction.

The construction of locally efficient estimators in censored data models in which the censoring mechanism satisfies the so called coarsening at random assumption (Heitjan and Rubin (1991), Jacobsen and Keiding (1995), Gill et al. (1997)) has been a particular focus area. This also includes the theory for locally efficient estimation of causal effects under the sequential randomization assumption (SRA), since the causal inference data structure can be viewed as a missing data structure on the intervention-specific counterfactuals, and SRA implies the coarsening at random assumption on the missingness mechanism, while not implying any restriction on the data generating distribution.

Gill and Robins (2001) present an implicit construction of counterfactuals as a mapping from the observed data distribution, such that the observed data structure augmented with the counterfactuals satisfies the consistency assumption and the SRA. Yu and van der Laan (2002) provide a particular explicit construction of counterfactuals from the observed data structure in terms of quantile-quantile functions, satisfying the consistency assumption and SRA. These results show that, without loss of generality, one can view causal inference as a missing data structure estimation problem. Causal graphs make explicit the real assumptions needed to claim that these counterfactuals are actually the counterfactuals of interest.

Inverse probability of censoring weighted (IPCW) estimators were originally developed to correct for confounding-induced bias in causal effect estimation. Theory for IPCW estimation and augmented locally efficient IPCW-estimator based on estimating functions defined in terms of the orthogonal complement of the nuisance tangent space in CAR-censored data models (including the optimal estimating function implied by efficient influence curve) was originally developed in Robins (1993), Robins and Rotnitzky (1992). Many papers build on this framework (see van der Laan and Robins (2003) for a unified treatment of this estimating equation methodology, and references). In particular, double robust locally efficient augmented IPCW-estimators have been developed (Robins and Rotnitzky (2001b), Robins and Rotnitzky (2001a), Robins et al. (2000b), Robins (2000a), van der Laan and Robins (2003), Neugebauer and van der Laan (2005), Yu and van der Laan (2003)).

Causal inference for multiple time-point interventions under sequential randomization was first addressed by Robins in the eighties: e.g. Robins (1986), Robins (1989).

The popular propensity score methods to assess causal effects of single time point interventions (e.g., Rosenbaum and Rubin (1983), Sekhon (2008), Rubin (2006)) have no natural generalization to multiple time-point interventions and may be inefficient (and less robust) estimators for single time point interventions, relative to the locally efficient double robust estimators such as the augmented IPCW and the targeted MLE. One crucial ingredient of these proposed methods is propensity score estimation in the absence of any knowledge of the outcomes.

Structural nested models and marginal structural models for single and multiple time point static treatment regimens were proposed by Robins as well: Robins (1997b), Robins (1997a), Robins (2000b). Many application papers on marginal structural models exist, involving the application of estimating equation methodology (IPCW and DR-IPCW): e.g., Hernan et al. (2000), Robins et al. (2000a), Bryan et al. (2003), Yu and van der Laan (2003). In van der Laan et al. (2005) history adjusted marginal structural models were proposed as a natural extension of marginal structural models, and it was shown that the latter also imply an individualized treatment rule of interest (a so called history adjusted statically optimal treatment regimen): see Petersen et al. (2005) for an application to the “when to switch” question in HIV research.

Murphy et al. (2001) present a nonparametric estimator for a mean under a dynamic treatment in an observational study. Structural nested models for modeling and estimating an optimal dynamic treatment were proposed by Murphy (2003), Robins (2003), Robins (2005a), Robins (2005b). Marginal structural models for user supplied set of dynamic treatment regimens were developed and proposed in van der Laan (2006), van der Laan and Petersen (2007) and, simultaneously and independently, in a technical report authored by Rotnizky and co-workers (2006), and Robins et al. (2008). van der Laan and Petersen (2007) also includes a data analysis application of these models to assess the mean outcome under a rule that switches treatment when CD4-count drops below a cut-off, and the optimal cut-off is estimated as well. Another practical illustration in sequentially randomized trials of these marginal structural models for realistic individualized treatment rules is presented in Bembom and van der Laan (2007).

Unified loss based learning based on cross-validation was developed in- van der Laan and Dudoit (2003), including construction of adaptive minimax estimators for infinite dimensional parameters of the full data distribution in CAR-censored data and causal inference models: see also van der Laan et al. (2006), van der Vaart et al. (2006), van der Laan et al. (2004), Dudoit and van der Laan (2005), Keleş et al. (2002), Sinisi and van der Laan (2004).

The oracle results for the cross-validation selector inspired a unified super learning methodology mapping a library of candidate estimators into a weighted combination with optimal cross-validated risk, thereby resulting in an estimator which either achieves the best possible parametric model rate of convergence up till a log-n-factor, or it is asymptotically equivalent with the oracle selected estimator that selects the best set of weights for the given data set. These results rely on the assumption that the loss function is uniformly bounded and that the number of candidates in the library is polynomial in sample size (van der Laan et al. (2007), Polley and van der Laan (2009)).

The super learning methodology applied to a loss function for the G-computation formula factor, Q₀, in causal inference, or the full-data distribution factor, Q₀, of the observed data distribution in CAR-censored data models, provides substitution estimators of the target parameter ψ₀. However, although these super learners of Q₀ are optimal w.r.t. the dissimilarity with Q₀ implied by the loss function, the corresponding substitution estimators will be overly biased for a smooth parameter mapping Ψ. This is due to the fact that cross-validation makes optimal choices w.r.t. the (global) loss-function specific dissimilarity, but the variance of Ψ(Q̂) is of smaller order than the variance of Q̂ itself.

van der Laan and Rubin (2006) integrates the loss-based learning of Q₀ into the locally efficient estimation of pathwise differentiable parameters, by enforcing the restriction in the loss-based learning that each candidate estimator of Q₀ needs to be a targeted maximum likelihood estimator (thereby, in particular, enforcing each candidate estimator of Q₀ to solve the efficient influence curve estimating equation). Another way to think about this is that each loss function L(Q) for Q₀ has a corresponding targeted loss function L(Q*), with Q* the targeted MLE algorithm applied to initial Q, and we apply the loss-based learning to the latter targeted version of the loss function L(Q). Rubin and van der Laan (2008) propose the square of efficient influence curve as a valid and sensible loss function L(Q) for selection and estimation of Q₀ in models in which g₀ can be estimated consistently, such as in randomized controlled trials.

The implications of this targeted loss based learning are that Q₀ is estimated optimally (maximally adaptive to the true Q₀) w.r.t. the targeted loss function L(Q*) using the super learning methodology, and due to the targeted MLE step the resulting substitution estimator of ψ₀ is now asymptotically linear as well if the targeted fluctuation function is estimated at a good enough rate (and only requiring adjustment by confounders not yet accounted for by initial estimator: see collaborative targeted MLE): either way, bias reduction will occur as long as the censoring/treatment mechanism is estimated consistently. Targeted MLE have been applied in a variety of estimation problems: Bembom et al. (2008), Bembom et al. (2009) (physical activity), Tuglus and van der Laan (2008) (biomarker analysis), Rosenblum et al. (2009) (AIDS), van der Laan (2008a) (case control studies), Rose and van der Laan (2008) (case control studies), Rose and van der Laan (2009) (matched case control studies), Moore and van der Laan (2009) (causal effect on time till event, allowing for right-censoring), van der Laan (2008b) (adaptive designs, and multiple time point interventions), Moore and van der Laan (2007) (randomized trials with binary outcome). We refer to van der Laan et al. (September, 2009) for collective readings on targeted maximum likelihood estimation.

1.1. Advantages of TMLE relative to augmented IPCW estimating function methodology

Even though the augmented IPCW-estimator is also double robust, targeted maximum likelihood estimation has the following important advantages relative to estimating equation methods such as the augmented-IPCW estimator: 1) the TMLE is a substitution estimator and thereby respects global constraints of model such as that one might be estimating a probability in [0, 1] or a (monotone) survival function at a finite set of points, 2) since, given an initial estimator, the targeted MLE step involves maximizing the likelihood along a smooth parametric targeted fluctuation model, it does not suffer from multiple solutions of a (possibly non-smooth in the parameter) estimating equation, 3) the TMLE does not require that the efficient influence curve can be represented as an estimating function in the target parameter, and thereby applies to all pathwise differentiable parameters 4) it can use the cross-validated log-likelihood (of the targeted maximum likelihood estimator), or any other cross-validated risk of an appropriate loss function for the relevant factor Q₀ of the density of the data, as principle criterion to select among different targeted maximum likelihood estimators indexed by different initial estimators or targeted maximum likelihood steps.

The latter allows fine tuning of initial estimator of Q₀ as well as the fine tuning of the estimation of the unknowns (e.g., censoring/treatment mechanism g₀) of the fluctuation function applied in the targeted maximum likelihood step, thereby utilizing the excellent theoretical and practical properties of the loss-function specific cross-validation selector. In particular, this property results in a collaborative double robust, and possibly super efficient, TMLE, as introduced and studied in this article, thereby adding theoretical and practical properties that go beyond the double robustness and efficiency. In contrast, the augmented-IPCW estimator cannot be evaluated based on a loss function for Q₀ alone: the augmented-IPCW estimator is not a substitution estimator $\Psi (Q_n^{*})$ for some $Q_n^{*}$ of Q₀, as is the TMLE. Instead the augmented-IPCW estimator ψ_n is a certain function of an initial Q_n and g_n, where the performance of g_n is scored based on the orthogonal loglikelihood of g₀, for which a good fit can result in bad fit of ψ₀. In trying to address these shortcomings of the augmented IPCW-estimators we converged to the targeted MLE and, subsequent refinement, the collaborative targeted MLE.

1.2. Organization of article

In Section 2 we present a description of the two stage collaborative targeted maximum likelihood methodology, the first stage representing the initial estimator, and the second stage representing the construction of a sequence of targeted maximum likelihood estimators indexed by increasingly nonparametric nuisance parameter estimators, and log-likelihood based cross-validation to select among the TMLEs and thereby select the nuisance parameter estimator. The second stage of the C-DR-TMLE can be viewed as a mapping from an initial estimator of the relevant density into a particular estimator of the nuisance parameter needed in the fluctuation function, and corresponding targeted maximum likelihood estimator using this nuisance parameter estimator in the targeted maximum likelihood step. We also provide the rational for the consistency of this C-DR-TML estimator under the collaborative double robustness assumption, relying on the earlier established oracle property of the log-likelihood-based cross-validation selector, which itself relies on the assumption that the log-likelihood loss function is uniformly bounded.

In Section 3 we define and study collaborative double robustness of the efficient influence curve. In particular, we define true nuisance parameters depending on a choice of relevant density (i.e., limit of initial estimator), which make the efficient influence curve an unbiased function for the target parameter. A collaborative targeted maximum likelihood estimator solves the efficient influence curve equation and relies on the nuisance parameter estimator to consistently estimate this true initial estimator-specific nuisance parameter or more nonparametric nuisance parameter. We also discuss alternative collaborative nuisance parameter estimators that can be used in the targeted MLE or in estimating equation methodology.

In Section 4 we prove an asymptotic linearity theorem for such collaborative double robust estimators, such as the collaborative double robust targeted maximum likelihood estimator, and discuss the conditions and implications of this theorem. In particular, this theorem provides us with influence curve based confidence intervals and tests of null hypotheses. A study of the influence curve teaches us that the C-DR-TMLE can be super efficient.

In Section 5 we consider targeted loss functions that can be used to select among different C-DR-TMLEs indexed by different initial estimators and choices of nuisance parameter estimator. These targeted loss functions can also be used to build the candidate nuisance parameter estimators within a C-DR-TMLE estimator, and thereby to construct the sequence of corresponding candidate targeted maximum likelihood estimators in the collaborative targeted maximum likelihood algorithm. Even though we enforce the use of a log-likelihood-based cross-validation selector to select among these candidate targeted maximum likelihood estimators in the C-DR-TMLE algorithm, we propose a penalized log-likelihood loss function that is more targeted towards the target parameter in the case the target parameter is borderline identifiable. This penalty is particularly important to robustify the estimation procedure in situations in which the variance of the efficient influence curve easily blows up to infinity for certain realization of the nuisance parameter estimator (e.g., close to zero inverse weights).

In section 6 we consider estimation of a causal effect in a marginal structural model, and define the collaborative double robust targeted penalized maximum likelihood estimator of the unknown parameters of the marginal structural model. In the companion paper we present a simulation study and data analysis for the C-DR-TMLE of the causal effect EY (1) − Y (0) of a binary treatment A, adjusting for baseline confounders W, based on observing n i.i.d. copies of a time-ordered data structure (W, A, Y = Y (A)).

We end this article with a discussion in Section 7, which provides a global overview.

1.3. An example to keep in mind

Although the methodology is completely general, throughout the paper we ground the discussion by referring to the following example, estimation of the additive causal effect of a binary treatment on an outcome. This example is rich enough to illustrate the ideas and methods, and has been used intensively in the causal inference literature. In this subsection we provide the notation, and objects required to define the C-DR-TMLE.

Let O = (W, A, Y = Y (A)) ∼ P₀ be an observed missing data structure on full data structure X = (W, Y (0), Y (1)) with missingness binary variable A ∈ {0, 1}. For concreteness, we consider the case that Y is binary. Suppose the model for P₀ is nonparametric, that the missingness mechanism g₀(1 | X) = P₀(A = 1 | X) = P₀(A = 1 | W) satisfies the coarsening at random assumption, and that our target parameter is the causal additive risk

$$\begin{array}{l}\Psi (P_0)={\Psi }^F(Q_0)=E_{0}Y(1)-Y(0)\\ =E_0\{E_0(Y|A=1,W)-E_0(Y|A=0,W)\},\end{array}$$

where Q₀ = (Q₀₁, Q₀₂) denotes the marginal distribution of W and conditional distribution of Y, given A, W, respectively. For notational convenience, we will suppress the F from “Full Data Parameter” in Ψ^F. We note that dP₀(O) = Q₀(O)g₀(A | X) = Q₀₁(W)Q₀₂(Y | A, W)g₀(A | X).

The efficient influence curve of Ψ at dP₀ = Q₀g₀ is given by

$$D*(Q_0,g_0)=h_{g_0}(A,W)(Y-Q_0(A,W))+Q_0(1,W)-Q_0(0,W)-\Psi (Q_0),$$

where Q₀(A, W) = E_Q0 (Y | A, W), h_g0(A, W) = A/g₀(1 | W) – (1 – A)/g₀(0 | X). We note that h_g0 also plays the role of the clever covariate in the targeted maximum likelihood fluctuation of the conditional distribution of Y, given A, W: log Q(ε)/(1 – Q(ε)) = log Q/(1 – Q) + εh_g0.

We also note that an alternative representation of the efficient influence curve is given by the augmented IPCW-representation:

$$\begin{array}{l}D*(Q_0,g_0)=\left(\frac{A}{g_0(1|X)}-\frac{1-A}{g_0(0|X)}\right)Y-\Psi (Q_0)\\ -\left(\frac{A}{g_0(1|X)}-1\right)Q_0(1,W)+\left(\frac{1-A}{g_0(0|X)}-1\right)Q_0(0,W)\\ =D_{IPCW}(g_0,{\psi }_0)-D_{CAR}(Q_0,g_0),\end{array}$$

where D_IPCW(g₀, ψ₀) = (A/g₀(1) – (1 – A)/g₀(0))Y – Ψ(Q₀) is the IPCW-estimating function, and D_CAR(Q₀, g₀) is its projection onto T_CAR defined as the sub-Hilbert space of $L_0^2(P_0)$ consisting of all functions of (A, W) with conditional mean zero, given W. Here $L_0^2(P_0)$ is the Hilbert space of functions of O endowed with inner product 〈h₁, h₂〉_P0 = E_P0h₁(O)h₂(O).

2. Collaborative double robust targeted maximum likelihood estimators

We will describe the proposed collaborative double robust targeted maximum likelihood estimators in the context of censored data models, but the generalization to general semi-parametric models is immediate. We first review targeted maximum likelihood estimation and loss-based cross-validation in order to provide a foundation for the explanation of C-DR-TMLE.

2.1. Targeted MLE in CAR-censored data model

Let O = Φ(C, X) be a censored data structure on a full data random variable X, where C denotes the censoring variable. We assume coarsening at random so that the observed data structure O ∼ P₀ has a probability distribution whose density w.r.t an appropriate dominating measure factors as dP₀(O) = Q₀(O)g₀(O | X), where Q₀ is the part of the distribution of X that is identifiable, and g₀ denotes the conditional probability distribution of O, given X, which we often refer to as the censoring mechanism. By CAR, we have g₀(O | X) = h(O) for some measurable function h. If C is observed itself, then g₀ denotes the conditional distribution of C, given X.

A semiparametric model $\mathcal{M}$ for the probability distribution P₀ of the observed data structure O is implied by a model $\mathcal{Q}$ for the full-data distribution factor Q₀, and a model $\mathcal{G}$ for the censoring mechanism g₀. The conditional distribution of O, given X, is identified by the conditional distribution of C, given X. For notational convenience, we will denote both with g₀. Let O₁, . . . , O_n be n independent and identically distributed (i.i.d.) observations of the experimental unit O with probability distribution P₀ ∈ $\mathcal{M}$. Let P_n be the empirical probability distribution of O₁, . . . , O_n which puts mass 1/n on each of the n observations.

Let Ψ : $\mathcal{M}$ → IR^d be a d-dimensional parameter that is path-wise differentiable at each P ∈ $\mathcal{M}$ (w.r.t. a class of finite dimensional paths through P) with canonical gradient D*(P): i.e., for a rich class of parametric submodels {P(δ) : δ} ⊂ $\mathcal{M}$ through P at δ = 0 with score $S\in L_0^2(P)$, $L_0^2(P)$ being the Hilbert space of mean zero functions of O endowed with inner product 〈h₁, h₂〉_P = Eh₁h₂(O) (i.e., the covariance operator), we have

$$\frac{d}{d\delta }\Psi (P(\delta )){|}_{\delta =0}=E_{P}D*(P)S.$$

Because D^*(P) is an element of the Hilbert space in $L_0^2(P)$ generated by all scores S of these parametric submodels (the so called tangent space), it is the canonical gradient D^*(P), also called the efficient influence curve at P. Any D(P) such that E_PD^*(P)S = E_PD(P)S for all scores S in the tangent space is called a gradient of the path-wise derivative. Thus the canonical gradient is the unique gradient that is an element of the tangent space. For the sake of illustration, it is assumed that Ψ(P_Q,g) = Ψ^F (Q) for some Ψ^F : i..e, the parameter of interest is a parameter of the full data distribution of X. The efficient influence curve D^*(P) at P with dP = Qg will also be denoted with D^*(Q, g).

The Targeted Maximum Likelihood estimator indexed by initial (Q, g): Given any P ∈ $\mathcal{M}$ with dP = Qg, let {P(ε) : ε} ⊂ $\mathcal{M}$ be a submodel with finite dimensional parameter ε, dominated by P, through P at ε = 0, and whose scores at ε = 0 span a finite dimensional space within $L_0^2(P)$ that includes the (components of the) efficient influence curve D^*(P) = D^*(Q, g). Because our parameter of interest is a parameter of Q₀ and the factorization dP₀ = Q₀g₀, it follows that such a fluctuation model can be chosen to only fluctuate Q with a submodel Q_g(ε) ⊂ $\mathcal{Q}$, where this fluctuation model will be indexed by g. Let dP(ε) = Q_g(ε)g be such a fluctuation model with fluctuation parameter ε. In van der Laan and Rubin (2006) we also consider fluctuation models that vary both Q and g.

At a given (Q, g), one can now define a k-th step targeted maximum likelihood version $Q_g^k(P_n)$ of Q₀ as follows. Let L(Q) = − log Q be the log-likelihood loss. Firstly, let $Q_g^1(P_n)=Q_g({\epsilon }_n^1)$, where

$${\epsilon }_n^1=\text{arg}\underset{\epsilon }{\text{min}}{P}_{n}L(Q_g(\epsilon )).$$

Here we use the notation Pf = ∫ f(o)dP(o). In general, $Q_{gn}^k=Q_g^k(P_n)=Q_g^{k-1}(P_n)({\epsilon }_n^k)$, where

$${\epsilon }_n^k=\text{arg}\underset{\epsilon }{\text{min}}{P}_{n}L(Q_g^{k-1}(P_n)(\epsilon )),k=1,.\dots$$

One iterates this updating till ${\epsilon }_n^k$ equals zero within a user supplied precision. The final update is refered to as the (iterative) targeted maximum likelihood estimator $Q_{gn}^{*}=Q_g^{*}(P_n)$, indexed by the initial starting point (Q, g).

The Targeted Maximum Likelihood estimator indexed by initial estimator and estimator of nuisance parameter: The above procedure, applied to an initial estimator $Q_n^0$, and an estimator g_n of g₀, defines the k-th step targeted maximum likelihood estimator and its limit in k, $Q_n^{*}$, as introduced and analyzed in van der Laan and Rubin (2006). By definition, the targeted maximum likelihood estimator ( $Q_n^{*}$, g_n) solves the efficient influence curve equation:

$$0=P_{n}D*(Q_n^{*},g_n).$$

Remark: Cross-validated initial estimator in the targeted MLE. If the initial estimator is an over-fit, then the bias reduction of the targeted MLE algorithm is not as effective. To protect against such cases one can use a cross-validated initial estimator. Specifically, let B_n ∈ {0, 1}ⁿ be a random variable that splits the sample in a training sample {i : B_n(i) = 0} and validation sample {i : B_n(i) = 1}, and, let $P_{n,B_n}^0$, $P_{n,B_n}^1$, denote the empirical distribution of the training and validation sample, respectively. The above targeted MLE iterative algorithm is now given by: $Q_{gn}^k=Q_g^k(P_n)=Q_g^{k-1}(P_n)({\epsilon }_n^k)$, where

$${\epsilon }_n^k=\text{arg}\underset{\epsilon }{\text{min}}{E}_{B_n}{P}_{n,B_n}^{1}L(Q_g^{k-1}(P_{n{B}_n}^0)(\epsilon )),k=1,.\dots$$

2.2. Loss-based cross-validation to select among (collaborative) targeted maximum likelihood estimators

Consider a loss function L*(Q) for Q₀ that satisfies

$$Q_0=\text{arg}\underset{Q}{\text{min}}{P}_{0}L*(Q).$$

Or, more precisely, we only require that Ψ (arg min_Q P₀L*(Q)) = Ψ(Q₀). An example of such a loss function is the the log-likelihood L*(Q)(O) = L(Q) = − log Q(O). Each loss function has a corresponding dissimilarity d(Q, Q₀) = P₀{L*(Q) – L*(Q₀)}.

Given different targeted maximum likelihood estimators, $P_n\to {\widehat{Q}}_k^{*}(P_n)$, of Q₀, for example, indexed by different initial estimators, we can use a preferred loss-function based cross-validation to select among them. Specifically, let B_n ∈ {0, 1}ⁿ be a random variable that splits the sample in a training sample {i : B_n(i) = 0} and validation sample {i : B_n(i) = 1}, and, let $P_{n,B_n}^0$, $P_{n,B_n}^1$, denote the empirical distribution of the training and validation sample, respectively. The loss-function based cross-validation selector is now defined by

$$\widehat{k}(P_n)=\text{arg}\underset{k}{\text{min}}{E}_{B_n}{P}_{n,B_n}^{1}L*({\widehat{Q}}_k^{*}(P_{n,B_n}^0)).$$

The resulting targeted maximum likelihood estimator is then given by

$${\widehat{Q}}_n^{*}={\widehat{Q}}_{\widehat{k}(P_n)}^{*}(P_n).$$

Cross-validation selector: Consider a preferred loss function that satisfies

$$\underset{Q}{\text{sup}}\frac{{\text{VAR}}_{P_0}\{L*(Q)-L*(Q_0)\}}{P_0\{L*(Q)-L*(Q_0)\}}\le M_2,$$ (1)

and that is uniformly bounded

$$\underset{O,Q}{\text{sup}}|L*(Q)-L*(Q_0)|(O)<M_1<\infty ,$$

where the supremum is over the support of P₀, and over all possible candidate estimators of Q₀ that will ever be considered. The first property (1) applies to the log-likelihood loss function and any weighted squared residual loss function, among others. The property (1) is essentially equivalent with the assumption that the loss-function based dissimilarity d(Q, Q₀) = P₀L^*(Q) – L^*(Q₀) is quadratic in a distance between Q and Q₀. The property (1) has been proven for log-likelihood loss functions and weighted L²-loss functions, and is in essence equivalent with stating that the loss function implies a quadratic dissimilarity d(Q, Q₀) (see van der Laan and Dudoit (2003)). If this property does not hold for the loss function, the rates 1/n for second order terms in the below stated oracle inequality reduce to the rate $1/\sqrt{n}$.

For such loss functions, the cross-validation selector satisfies the following (so called) oracle inequality: for any δ > 0,

$$\begin{array}{l}{E}_{B_n}\{P_{0}L({\widehat{Q}}_{\widehat{k}}(P_{n,B_n}^0)-L(Q_0)\}\le (1+2\delta )E_{B_n}\underset{k}{\text{min}}{P}_0\{L({\widehat{Q}}_k(P_{n,B_n}^0))-L(Q_0)\}\\ +2C(M_1,M_2,\delta )\frac{1+\text{log}K(n)}{np},\end{array}$$

where the constant C(M₁, M₂, δ) = 2(1 + δ)²(M₁/3 + M₂/δ) (see page 25 of van der Laan and Dudoit (2003)). This result proves (see van der Laan and Dudoit (2003) for the precise statement of these implications) that, if the number of candidates K(n) is polynomial in sample size, then the cross-validation selector is either asymptotically equivalent with the oracle selector (based on sample of size of training samples, as defined on right-hand side of above inequality), or it achieves the parametric rate log n/n for convergence w.r.t. d(Q, Q₀) ≡ P₀{L(Q) – L(Q₀)}. So in most realistic scenarios, in which none of the candidate estimators achieve the rate of convergence one would have with an a priori correctly specified parametric model, the cross-validated selected estimator selector performs asymptotically exactly as well (up till constant!) as the oracle selected estimator. These oracle results are generalized for estimated loss functions $L_n^{*}(Q)$ that approximate a fixed loss function L^*(Q). If arg min_Q $P_0{L}_n^{*}(Q)\ne Q_0$, then the oracle inequality also presents second order terms due to the estimation of the loss function.

This preferred loss function based cross-validation can now be used to select among different candidate targeted maximum likelihood estimators indexed by different initial estimators, and possibly different censoring mechanism estimators. Specifically, we will use a preferred targeted loss function to select among different collaborative targeted maximum likelihood estimators, which are just special targeted maximum likelihood estimators in the sense that g_n is estimated in collaboration with the initial Q_n.

For a given loss function L(Q), and an estimator Q̂(P_n), we will refer to P_nL(Q̂(P_n)) as the entropy of the fit Q̂(P_n). Similarly, for a loss function L₁(g) of g₀, and an estimator ĝ(P_n), we will refer to P_nL₁(ĝ(P_n)) as the entropy of ĝ(P_n). Both the preferred loss function for Q₀, as well as this loss function L₁ for g₀ represent important choices. For example, one likes to select the loss function L₁ so that the dissimilarity P₀{L₁(g) – L₁(g₀)} measures strongly how well g approaches the optimal fluctuation function implied by g₀. In other words, we need to keep in mind how g is used, namely that it is used to fit the wished fluctuation function implied by g₀. For example, if the clever covariate defining the fluctuation function is given by A – E(A/σ²(A, W) | W)/E(1/σ²(A, W) | W), as in the semiparametric regression model E(Y | A, W) – E(Y | A = 0, W) = βA, one might want to define as loss function L(θ₁(g), θ₂(g)) = w₁(A/σ²(A, W) – θ₁(W))² + w₂(1/σ²(A, W) – θ₂(W))², for weight-functions w₁, w₂ (functions of W), and θ₁, θ₂ representing the numerator and denominator of the conditional expectations in the clever covariate. Similarly, the preferred loss function for Q₀ can be tuned to represent a dissimilarity d(Q, Q₀) that measures strongly how well Ψ(Q) approximates Ψ(Q₀). We discuss such choices in more detail in a later section.

2.3. Building a collaborative estimator of censoring mechanism/nuisance parameter

A C-TMLE estimator is constructed by building a family of candidate estimators, then choosing the best among them, using cross-validation to drive the choice to Q₀. However, we also rely upon a loss function when building each candidate nuisance parameter (e.g. censoring mechanism) estimator, and it is not necessary that these two loss functions be the same. In fact, as part of building a collaborative nuisance parameter estimator in the collaborative T-MLE procedure, we couple an increase in the log-likelihood entropy of the targeted maximum likelihood estimator with an increase in the g₀-loss function specific entropy of the corresponding nuisance parameter estimator. In this manner, we arrange that, for increasing sample size, the cross-validation selector will be driven towards the selection of targeted maximum likelihood estimator with an initial estimator closer to Q₀ and simultaneously a more and more nonparametric estimator of g₀ (thereby achieving the full wished bias reduction in the limit).

That is, given a collection of candidate estimators of g₀, ordered by empirical fit w.r.t. a loss function for g₀ such as the log-likelihood, we will build a sequence of targeted maximum likelihood estimators of Q₀ ordered by log-likelihood entropy and indexed by increasingly nonparametric estimators of g₀, where the extend of being nonparamatric is measured by the L₁-entropy. Subsequently, we use the cross-validated log-likelihood for Q₀ to choose among these candidate targeted maximum likelihood estimators.

There are many possible approaches that construct such an ordered sequence of targeted maximum likelihood estimators in which a next element in the sequence has both a higher entropy for the Q₀-loss as well as a higher g₀-loss entropy for its corresponding censoring estimator. Of course, the strict ordering is not what drives the properties of the resulting estimator, but the sequence should represent an approximately monotone function in the log-likelihood entropy of Q₀ and L₁-entropy of g₀.

This procedure represents one particular approach for constructing a targeted maximum likelihood estimator that uses a collaboratively estimated nuisance parameter. We refer to any algorithm that maps into a targeted maximum likelihood estimator that uses a collaborative nuisance parameter estimator (relative to the Q-estimator), as a collaborative targeted maximum likelihood estimator.

2.4. A template for collaborative targeted MLEs

We present the following template providing a class of collaborative targeted maximum likelihood estimators.

Initial estimator of Q₀: Build an estimator Q_n of Q₀, such as a super learner based on the log-likelihood loss function L(Q), or any other loss function.

Preferred loss function for Q₀: Let L^*(Q) be a (targeted) loss function for Q₀. We note that the loss function can also be data dependent, and, in particular, the choice of loss function can depend on an initial estimator Q_n of Q₀, and corresponding collaborative estimator g_n (see DR-IPCW loss functions in van der Laan and Dudoit (2003), and our section on targeted loss functions).

Loss function for g₀: Let L₁(g) be a loss function for g₀.

Candidate estimators of censoring mechanism/nuisance parameter: For each δ in an index set, let g_nδ be a candidate estimator of g₀. Let d(δ) = P_nL₁(g_nδ) denote the entropy of g_nδ, thereby measuring how data adaptive g_nδ is, and for a maximal value d(δ) or for d(δ) approximating a maximum value we have that g_nδ is actually a consistent estimator of g₀.

Select ordered sequence of entropies for censoring mechanism (nuisance parameter) estimator

Select a sequence d⁰ > d¹ > . . . > d^K.

Select initial targeted maximum likelihood estimator: We start out with a $g_n^0$ with entropy larger than d⁰ and a corresponding targeted maximum likelihood estimator $Q_n^{*0}=Q_{n{g}_n^0}^{*}$ applied to initial estimator Q_n. We refer to the pair ( $g_n^0$, $Q_n^{*0}$) as the initial targeted maximum likelihood estimator in the sequence of targeted maximum likelihood estimators that will be constructed below.

Construct next targeted maximum likelihood estimator in sequence

We are given an current initial estimator $Q_n^k$, a current targeted maximum likelihood estimator ( $g_n^k$, $Q_n^{k*}$) in our sequence of targeted maximum likelihood estimators, with $Q_n^{k*}$ being the targeted maximum likelihood estimator applied to current initial estimator $Q_n^k$ and nuisance parameter estimator $g_n^k$. The current nuisance parameter estimator $g_n^k$ has entropy larger than d^k. We are also given k, and thereby two corresponding entropy values d^k > d^k+1. (we note that the initial estimator does not get updated at each step k, but it corresponds with one of the elements in current sequence of targeted maximum likelihood estimators)

Consider an algorithm that searches among a specified set of candidate estimators g_nδ with {δ : d^k > d(δ) > d^k+1)} with the goal of minimizing the preferred loss L^*-fit of the targeted maximum likelihood estimator, applied to initial $Q_n^k$:

$$\delta \to P_{n}L*(Q_{n\delta }^{k*}).$$ (2)

Recall that $Q_{n\delta }^{k*}$ denotes the targeted maximum likelihood estimator that uses the optimal fluctuation model identified by censoring mechanism g_nδ applied to initial estimator $Q_n^k$. Let g_nδn be the selected estimator. If either the fit is improved relative to current T-MLE $Q_n^{k*}$,

$$P_{n}L*(Q_{n{\delta }_n}^{k*})<P_{n}L*(Q_n^{k*}),$$

or the above holds for the log-likelihood loss function L(Q) = − log Q on which the targeted maximum likelihood algorithm operates, then we accept δ_n, and thereby the next targeted maximum likelihood estimator, $g_n^{k+1}=g_{n{\delta }_n}$, $Q_n^{k+1*}=Q_{n{\delta }_n}^{k*}$, in the sequence we are constructing. The algorithm now delivered its next k + 1-th targeted maximum likelihood estimator. We set k = k + 1, keep the initial estimator $Q_n^k$ unchanged, and the current targeted maximum likelihood estimator ( $g_n^k$, $Q_n^{k*}$) is now updated.

If this monotonicity condition fails to hold for both the log-likelihood fit as well as the preferred loss function fit, then we reject this δ_n, and update the initial estimator $Q_n^k$ by setting it equal to the current targeted maximum likelihood estimator $Q_n^{k*}$. We now, rerun the above procedure with initial $Q_n^k=Q_n^{k*}$, and same d^k > d^k+1. This time the resulting δ_n will always be accepted since the log-likelihood fit of a targeted maximum likelihood estimator (a maximum likelihood fluctuation of an initial estimator) is larger than the log-likelihood of initial estimator. So the algorithm now delivers the next k + 1-th targeted maximum likelihood estimator $g_n^{k+1}=g_{n{\delta }_n}$, $Q_n^{k+1*}=Q_{n{\delta }_n}^{k*}$ in its sequence. We set k = k + 1, the initial estimator is still set at $Q_n^k$, and the current targeted maximum likelihood estimator ( $g_n^k$, $Q_n^{*k}$) is now updated (the last one in sequence so far).

k-th step collaborative targeted maximum likelihood estimator:

The above algorithm maps a running current initial estimator, a current targeted MLE ( $g_n^k$, $Q_n^{*k}$) (the lastly constructed in current sequence), into a new targeted MLE ( $g_n^{k+1}$, $Q_n^{*k+1}$), and possible updated current initial estimator. We start this algorithm with k = 0, and iterate it. This now defines the k-th step collaborative targeted maximum likelihood estimator ( $g_n^k$, $Q_n^{*k}$), k = 0, 1, 2, . . . , K.

We are guaranteed that the fit of $Q_n^{*k}$ is either increasing w.r.t. the preferred loss function (most likely, since that is the loss we minimize at each step), or it is increasing w.r.t the log-likelihood loss used to define the targeted maximum likelihood step, relative to previous targeted maximum likelihood estimator $Q_n^{*k-1}$. In addition, the corresponding $g_n^k$ has a L₁-fit that is larger than the L₁-fit of $g_n^{k-1}$. At every step in which the initial estimator is updated, we also know that the log-likelihood fit is increasing.

Cross-validation to select number of iterations k in k-th step C-TMLE:

Given this sequence of k-th step collaborative targeted maximum likelihood estimators $P_n\to (Q_n^{k*}=){\widehat{Q}}^{k*}(P_n)$, using estimator $g_n^k$, it remains to select k, k = 0, 1, . . . , K.

We select k based on the cross-validated log-likelihood:

$$k_n=\underset{k}{\text{argmax}}{E}_{B_n}{P}_{n,B_n}^{1}L({\widehat{Q}}^{k*}(P_{n,B_n}^0)),$$

where the random vector B_n ∈ {0, 1}ⁿ denotes a cross-validation scheme such as V-fold cross-validation, and $P_{n,B_n}^0$, $P_{n,B_n}^1$ are the empirical probability distributions of the training sample {i : B_n(i) = 0} and validation sample {i : B_n(i) = 1}, respectively, as identified by the split vector B_n.

This finalizes the mapping from the initial estimator Q_n, and the data, into a collaborative estimator of the censoring mechanism, $g_n=g_n^{k_n}$. We refer to $Q_n^{*}=Q_n^{k_n*}$, paired with collaborative estimator g_n, as the collaborative targeted maximum likelihood estimator of Q₀.

The Collaborative (Double Robust) Targeted Maximum Likelihood Estimator: The corresponding targeted maximum likelihood estimator of ψ₀ = Ψ^F (Q₀) is given by the substitution estimator

$$\Psi (Q_n^{*})=\Psi (Q_n^{k_n*})=\Psi ({\widehat{Q}}^{k_n*}(P_n)).$$

We refer to this estimator as the collaborative (double robust) targeted maximum likelihood estimator (C-DR-TMLE or C-TMLE) of ψ₀, and we recall that it is paired with a collaborative estimator g_n.

C-TMLE solves an efficient influence curve equation: Since the C-TMLE is a targeted maximum likelihood estimator $Q_n^{k_n*}$, applying the fluctuation function with censoring mechanism estimator $g_n=g_n^{k_n}$ to the estimator $Q_n^{k_n}$, it solves the efficient influence curve equation:

$$0=P_{n}D*(Q_n^{*},g_n).$$

This is a fundamental property of the collaborative targeted MLEs driving the targeted bias reduction w.r.t. the target parameter of interest,ψ₀.

Selection among candidate C-TMLEs: The collaborative targeted maximum likelihood estimator depends on a choice of initial estimator $Q_n^0$, and choices that concern the second stage. As a consequence, one might have a set of collaborative targeted maximum likelihood estimators ( $Q_{nj}^{*}$, g_nj) indexed by such choices, j = 1, . . . , J. We can now select among these estimators $Q_{nj}^{*}$ based on loss-based cross-validation using the preferred loss function L^* for Q₀.

Selection based on empirical efficiency maximization: Since, under regularity conditions of our asymptotic linearity theorem, each j-specific C-TMLE is asymptotically linear with influence curve IC_j( $Q_j^{*}$, g_0j) (equal to D^*( $Q_j^{*}$, g_0j) plus a contribution from g_nj), we can select j as the minimizer of a (cross-validated) estimate of the variance of IC_j( $Q_j^{*}$, g_0j), or, if ψ₀ has dimension larger than 1, then we can minimize an estimate of the variance of a function of ψ₀. One could here ignore the contribution from g_nj and thus use the cross-validated or empirical variance of the efficient influence curve at the collaborative targeted maximum likelihood estimator:

$$j_n=\text{arg}\underset{j}{\text{min}}{E}_{B_n}{P}_{n,B_n}^1{\{D*({\widehat{Q}}_j^{*}(P_{n,B_n}^0),{\widehat{g}}_j(P_{n,B_n}^0))\}}^2.$$

Generalization. The above C-TMLE can also be called the collaborative minimum loss estimator. The loss function L(Q) needs to satisfy that the derivative of ε → L(Q_g(ε)) at ε = 0 for a suitably constructed path {Q_g(ε) : ε} equals the efficient influence curve D^*(Q, g), where the efficient influence curve at P only depends on Q(P) and g(P), while the target parameter Ψ(P) = Ψ^F (Q(P)) depends on P only through Q(P). No further structure is needed for the above template (such as dP = Q*g, or CAR-censored data structure).

2.5. The rationale of the consistency of the collaborative-TMLE

The C-TMLE procedure starts with an initial estimator Q_n of Q₀. Suppose that the sequence constructed in the C-TMLE template consists of a finite number K of targeted maximum likelihood estimators $Q_n^{k*}$. By construction, the last targeted maximum likelihood estimator in this sequence uses a censoring mechanism estimator that is nonparametric (maximal g₀-entropy): i.e, the nuisance parameter estimator $g_n^K$ as selected by the K-th step C-TMLE converges to the true g₀. We also know that $g_n^k$ is increasingly nonparametric in k, k = 1, . . . , K.

For simplicity, we also assume that the k-th targeted maximum likelihood estimator in the sequence is obtained by applying the targeted maximum likelihood algorithm to the previous targeted maximum likelihood estimator in sequence. This is not necessary, since we can apply the argument to the subsequence for which that is true (the elements in the sequence at which the targeted maximum likelihood update is actually carried out), but it simplifies the presentation.

Consider the limits $Q_{{kg}_k}^{*}$ of the targeted maximum likelihood estimators $Q_n^{*k}$ in our sequence, where g_k is the limit of $g_n^k$, k = 1, . . . , K, and thus g_K = g₀. We also know that $P_n\text{log}{Q}_{{nkg}_{nk}}^{*}$ is increasing in k, by the fact that each element in the sequence is a targeted maximum likelihood estimator applied to previous element in sequence (as initial estimator in the T-MLE algorithm). Therefore, $P_0\text{log}{Q}_{{kg}_k}^{*}$ is non-decreasing in k. As discussed in introduction, if the log Q is uniformly bounded in all its candidates Q, then the cross-validation selector of k is asymptotically equivalent with the oracle selector ${\tilde{k}}_n=\text{arg}\hspace{0.17em}\text{max}\hspace{0.17em}{P}_0\text{log}\hspace{0.17em}{Q}_{k{g}_{nk}}^{*}$. For n large enough, this oracle selector behaves as $\tilde{k}=\text{arg}\hspace{0.17em}{\text{max}}_k\hspace{0.17em}{P}_0\hspace{0.17em}\text{log}\hspace{0.17em}{Q}_{{kg}_k}^{*}$, where this maximum might be non-unique. One maximum is obtained at k = K, giving $P_0\hspace{0.17em}\text{log}\hspace{0.17em}{Q}_{K{g}_0}^{*}$ and, we know that $\Psi (Q_{K{g}_0}^{*})={\psi }_0$. So if k̃ = K, then the c-tmle will be consistent for ψ₀. Suppose that k̃ is actually smaller than K. Then we have, suppressing the g’s in the notation,

$$P_0\text{log}{Q}_{\tilde{k}}^{*}=P_0\text{log}{Q}_{\tilde{k}+1}^{*}=\dots =P_0\text{log}{Q}_K^{*}.$$

We know that Q^*k+1 is a T-MLE with Q^*k as initial. So the above equalities are only possible if Q^*k+1 = Q^*k for k = k̃, . . . , K – 1. Thus $Q_K^{*}=Q_{\tilde{k}}^{*}$. Since $Q_K^{*}$ is a targeted MLE at nuisance parameter g₀, it follows that $\epsilon \to P_0\text{log}{Q}_{K,g_0}^{*}(\epsilon )$ is maximized at ε = 0: compare with $P_n\hspace{0.17em}\text{log}\hspace{0.17em}{Q}_{nK}^{*}(\epsilon )$ is maximized at ε = 0 by definition of the T-MLE algorithm. Since we just showed that $Q_K^{*}=Q_{\tilde{k}}^{*}$, it also follows now

$$\epsilon \to P_0\text{log}{Q}_{\tilde{k},g_0}^{*}(\epsilon )$$

is maximized at ε = 0. In particular, this means that the derivative at ε = 0 equals zero, giving us:

$$0=P_{0}D*(Q_{\tilde{k}}^{*},g_0).$$

However, the efficient influence curve typically satisfies that P₀D^*(Q, g₀) = 0 implies Ψ(Q) = ψ₀, which then implies $\Psi (Q_{\tilde{k}}^{*})={\psi }_0$. Thus $\Psi (Q_{n\tilde{k}}^{*})$ is consistent, and thereby $\Psi (Q_{n{k}_n}^{*})$ is consistent.

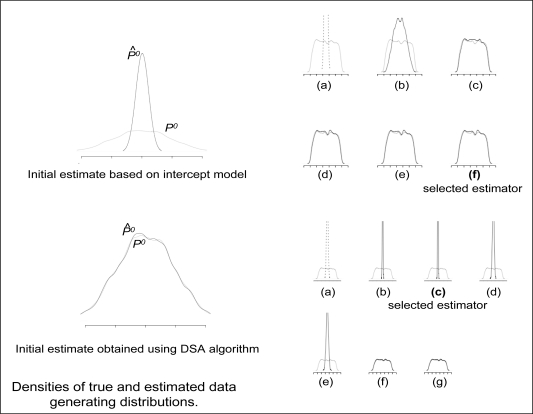
Figure 1 illustrates the collaborative nature of the construction of a sequence of increasingly data-adaptive nuisance parameter estimators, $\{g_n^1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{g}_n^K\}$, and its relation to the performance of the initial estimator. We generated 5000 observations of O = (W, A, Y) from data generating distribution dP₀ = Q₀g₀ defined as:

$$\begin{array}{l}\mathit{\text{logit}}\hspace{0.17em}(g_0(A|W))=.15W_1+.1W_2+W_3-W_4\\ Q_0(A,W)=A+3W_1-6W_2+4W_3-5W_5+3W_4\end{array}$$

where W₁ through W₅ are independent random variables ∼ N(0, 1), Y = Q₀(A, W) + ε, ε ∼ N(0, 1), and g₀ is the conditional density of A given confounding variables W = {W₁, W₂, W₃, W₄, W₅}. We applied the C-TMLE to estimate the effect of binary treatment A on outcome Y, adjusting for W, defined as ψ₀ = E_W (E(Y | A = 1, W) – E(Y | A = 0, W)).

Figure 1:

Construction of a sequence of nuisance parameter estimators based on a poor initial fit of the density (top) and a good initial fit for the density (bottom). Kernel estimates of true densities Q₀ and g₀ are shown in gray.

A kernel density estimator was applied to Y and to the predicted values of two initial estimators of Q₀ = E₀(Y | A, W), which we denote with ${\widehat{Q}}_{n,\mathit{\text{poor}}}^0$, and ${\widehat{Q}}_{n,\mathit{\text{good}}}^0$, respectively. These estimators were obtained with the D/S/A algorithm (Sinisi and van der Laan, 2004), a data-adaptive machine learning approach to model selection that was set to search over all second degree polynomials of size six. The kernel density estimates are displayed in plots on the left hand side of the figure.

In addition, we plotted the kernel density estimates of the predicted values of each set of the collaboratively-constructed candidate ĝ estimators, and we can compare them with the density of the true predictions g₀(1 | W) = P₀(A = 1|W). These are plotted on the right hand side of the figure, overlaid with the density estimator applied to the true values g₀(1 | W). When the initial fit of Q₀ is poor, the nuisance parameter estimator $g_n^k$ converges quickly to g₀ in k, and the selected candidate estimator closely approximates g₀. Plots in the bottom half of the figure shows the behavior of the C-TMLE procedure when $Q_n^0$ is a good estimate of Q₀. When the initial fit of Q₀ is good, the nuisance parameter estimator grows slowly towards g₀, and a candidate estimator that estimates a true treatment mechanism that adjusts for fewer covariates than the true treatment mechanism g₀ that was used to generate the data.

2.6. Revisiting the additive causal effect example

Recall that the targeted maximum likelihood estimator applied to an estimator, Q_n, of P(Y = 1 | A, W) is obtained by running a univariate logistic regression of Y , with offset the initial estimator, on an estimate of the univariate clever covariate h_g0(A, W) = A/g₀(1 | W) – (1 – A)/g₀(0 | W), implied by the treatment mechanism estimator, using an estimator g_n of treatment mechanism P(A = 1 | W).

The collaborative targeted maximum likelihood estimation procedure starts with computing $Q_n^0$, an initial estimator of P(Y = 1 | A, W) using super learning, and then collaboratively generating a sequence of targeted maximum likelihood estimators. These use increasingly nonparametric estimators of g₀, applied to subsequent targeted maximum likelihood updates of the initial estimator (as needed to guarantee the monotonicity in fit). In this way the sequence of constructed targeted maximum likelihood estimators has increasing log-likelihood fit. The selection of the sequence of increasingly nonparametric treatment mechanism estimators was based on maximizing the fit of the corresponding targeted maximum likelihood estimators of P(Y = 1 | A, W), as outlined in our template, thus very much driven by the outcome data. Likelihood based cross-validation selects the wished targeted maximum likelihood estimator, with its paired treatment mechanism estimator, from this sequence. It is assumed that the resulting selection of the estimator of g₀ is nonparametric enough so that the collaborative double robustness of the efficient influence curve as presented in next section is utilized, and, thereby, that our asymptotic linearity theorem in later section can indeed be applied.

A collaborative targeted maximum likelihood estimator constructed in this manner has made every effort to make the estimator of the additive causal effect as unbiased as possible. If we now construct a set of such collaborative targeted maximum likelihood estimators, possibly indexed by different initial estimators, and different ways of constructing the sequence of targeted maximum likelihood estimators, we can then select among these estimators the estimator with minimal estimated variance (based on the influence curve). To obtain an honest estimate of the variance of the resulting estimator, just as one obtained honest cross-validated risk of an estimator that internally uses cross-validation, one uses the honest cross-validated variance of the influence curve of the complete estimator, including cross-validating this final selection step that involves minimizing the variance.

3. Collaborative double robustness of estimating functions in CAR censored data models

In this section we establish a new kind of collaborative robustness of the class of estimating functions in CAR-censored data models, where, as in van der Laan and Robins (2003), the class of estimating functions is implied by the orthogonal complement of the nuisance tangent space of the target parameter Ψ : $\mathcal{M}$ → IR^d. This orthogonal complement of the nuisance tangent space equals the space spanned by the gradients of the pathwise derivative of Ψ, and thus includes the canonical gradient/efficient influence curve. The collaborative robustness result teaches us that the censoring mechanism required to obtain an unbiased estimating function at a mis-specified Q for the parameter of interest need not always condition on the whole full data structure. In fact, it teaches us that the better Q approximates Q₀ the less of an adjustment by full data random variables is necessary for the censoring mechanism to still obtain an unbiased estimating function for the parameter of interest. The precise collaborative property of (Q, g₀(Q)) such that P₀D(ψ₀, g₀(Q), Q) = 0 will be explicitly specified, where D represents the estimating function, such as the one implied by the canonical gradient.

3.1. The formal collaborative robustness result

The new form of double robustness we wish to establish is understood as follows. Consider an estimating function D(Ψ(Q), G, Q) for the parameter of interest ψ₀ that is indexed by nuisance parameters (G₀, Q₀), and which is already known to satisfy the classical double robustness property: for any G under which ψ₀ is identifiable from P_Q0,G, we have E₀D(ψ₀, G, Q) = 0 if either Q = Q₀ or G = G₀ (van der Laan and Robins (2003)). Given a Q, we are interested in the question under what conditional distribution G_0δ of censoring variable C, given a reduction X(δ) of X, will we still have P₀D(ψ₀, G_0δ, Q) = 0 and thereby that D is an unbiased estimating function for ψ at this mis-specified Q.

Firstly, we note that P₀D(ψ₀, G, Q) = P₀{D(ψ₀, G, Q) – D(ψ₀, G, Q₀)} + P₀D(ψ₀, G, Q₀), and the latter term is zero under any G that allows identifiability of ψ₀. Thus, it remains to determine for what G_0δ we will have P₀{D(ψ₀, G_0δ, Q) – D(ψ₀, G_0δ, Q₀)} = 0. This choice of G_0δ (e.g., it includes G₀ itself) is not unique but will be dependent on a difference Q – Q₀ in the sense that X(δ) has to be rich enough so that it contains a difference Q–Q₀.

By the general representation theorem for estimating functions that are orthogonal to the nuisance tangent space of the target parameter (Theorem 1.6, van der Laan and Robins (2003)), one can typically represent an estimating function D(ψ₀, G, Q) as an Inverse Probability of Censoring Weighted Estimating function D_IPCW(G, ψ₀) plus a function D_CAR(Q, G) in the tangent space T_CAR(G) of the censoring mechanism at G. The function D_CAR(Q, G) is defined as the projection of – D_IPCW(G, ψ₀) on the tangent space T_CAR(G) = {h(O) : E_G(h(O) | X) = 0} of the censoring mechanism when only assuming coarsening at random, where this projection is carried out in the Hilbert space of all functions of O with mean zero and finite variance endowed with inner product the covariance operator 〈f₁, f₂〉 = E_Q,gf₁(O)f₂(O). In other instances, the D_IPCW might depend on Q₀ through another parameter beyond ψ₀, in which case it will need to be assumed that this parameter is correctly specified.

This teaches us that P₀{D(ψ₀, G, Q) – D(ψ₀, G, Q₀)} = P₀{D_CAR(Q, G) – D_CAR(Q₀, G)}, since the IPCW-difference equals zero. This representation theorem also teaches us that for all Q we have that D_CAR(Q, G) has conditional mean zero under G, given X. In addition, this same theorem also shows that Q → D_CAR(Q, G) is linear in Q. Therefore, it remains to show that P₀D_CAR(Q – Q₀, G) = 0. Now, inspection of the proof that the conditional mean of D_CAR(Q′, G) under G equals zero for a Q′ involves typically conditioning on a rich enough reduction of X so that a particular function indexed by Q′ is fixed under the conditioning. Thus, the censoring mechanism only needs to condition on a particular function of Q – Q₀.

This is best illustrated with a concrete censored data structure. For example, consider the right censored data structures O = (C, X̄(C)), where X(t) is a time dependent process, X = (X(t) : t) represents the full data structure, and X̄(t) = {X(s) : s ≤ t} represents the sample path up till time t. For this censored data structure, one can represent the projection of D_IPCW onto T_CAR as D_CAR(Q, G) = ∫ H_Q,G(u, X̄ (u–))dM_G(u), where

$$\begin{array}{l}{H}_{Q,G}(u,\overline{X}(u-))=E_{Q,G}(D_{IPCW,G}|C=u,\overline{X}(u))-E(D_{IPCW,G}|C\ge u,\overline{X}(u))\\ d{M}_G(u)=I(C=u)-I(C\ge u)d{\Lambda }_{C|X}(u|X),\end{array}$$

and Λ_C|X is the cumulative hazard of C, given X. For details, we refer to chapter 3 in van der Laan and Robins (2003). Here dM_G(u) is a Martingale satisfying E(dM_G(u) | X̄(u), C ≥ u) = 0. Due to the linearity of the conditional expectation operator, we have D_CAR(Q – Q₀, G) = ∫ H_Q–Q0,G(u, X̄(u))dM_G(u). By conditioning on H_Q–Q0,G(u, X̄(u)) within the integral, and using E(dM_G(u) | X̄(u), C ≥ u) = 0, it follows that D_CAR(Q – Q₀, G) also has mean zero under a censoring mechanism s.t. λ_C(u | X) only depends on X̄(u) (it only depends on X̄ (u) by CAR) through H_Q–Q0,G(u, X̄(u)). One can factorize H_Q–Q0,G = H₁(G)H₂(Q – Q₀), so that adjustment in λ_C(u | X) by the time-dependent covariate H₂(Q – Q₀) (u, X̄ (u)) suffices. Alternatively, it also suffices if the censoring mechanism uses a self-iterated adjustment by H_Q–Q0,G as described later in this section. If Q approximates Q₀, this function H_Q–Q0,G(u, X̄ (u)) will be shrunk to zero, so that less conditioning becomes necessary.

The following much simpler (but in essence making the same point) example helps to further illustrate the general collaborative double robustness property of the efficient influence curve. Suppose the observed censored data structure is O = (W, Δ, ΔY) and X = (W, Y) is the full data random variable, where Δ is the censoring variable. Suppose one wishes to estimate ψ₀ = E₀Y. The efficient influence curve is given by

$$D({\psi }_0,{\Pi }_0,Q_0)=D_{IPCW}({\psi }_0,{\Pi }_0)+D_{CAR}(Q_0,{\Pi }_0),$$

where

$$\begin{array}{l}{D}_{IPCW}({\psi }_0,{\Pi }_0)=Y\frac{\Delta }{{\Pi }_0(W)}-{\psi }_0\\ D_{CAR}(Q_0,{\Pi }_0)=-E(Y|\Delta =1,W)\left(\frac{\Delta }{{\Pi }_0(W)}-1\right),\end{array}$$

∏₀(W) = P₀(Δ = 1 | W) and Q₀(W) = E₀(Y | W, Δ = 1). Consider a Q. We are interested in the question under what conditional distribution ∏_0δ of Δ, given a reduction W(δ) of W, will we still have P₀D(ψ₀, ∏_0δ, Q) = 0 and thereby that D is an unbiased estimating function for ψ at this mis-specified Q. Firstly, we note that P₀D(ψ₀, ∏, Q) = P₀{D(ψ₀, ∏, Q) – D(ψ₀, ∏, Q₀)} + P₀D(ψ₀, ∏, Q₀), and the latter term is zero under any ∏ for which P₀(∏(W) > 0) = 1. Thus, it remains to determine for what ∏_0δ P₀{D(ψ₀, ∏_0δ, Q) – D(ψ₀, ∏_0δ, Q₀)} = 0.

This teaches us that P₀{D(ψ₀, ∏, Q) – D(ψ₀, ∏, Q₀)} = P₀{D_CAR(Q, ∏) – D_CAR(Q₀, ∏)}, since the IPCW-difference equals zero:

$$P_0\{D({\psi }_0,\prod ,Q)-D({\psi }_0,\prod ,Q_0)\}=\frac{(Q-Q_0)(W)}{{\prod }_0(W)}(\Delta -{\prod }_0(W)).$$

Note that we used here that Q → D_CAR(Q, ∏) is linear in Q. Therefore, it remains to show that P₀D_CAR(Q – Q₀, ∏) = 0. This can be represented as H(Q – Q₀, ∏₀)(W)(Δ – ∏₀(W)) as above, with H(Q – Q₀, ∏₀)(W) = (Q – Q₀)(W)/∏₀(W).

The proof that the conditional mean of D_CAR(Q – Q₀, ∏) under ∏ equals zero involves conditioning on a rich enough reduction of W so that Q – Q₀ is captured by the conditioning: if (Q – Q₀)(W) only depends on W through W(δ), then

$$E\frac{(Q-Q_0)\hspace{0.17em}(W)}{{\prod }_0(W(\delta ))}(\Delta -{\prod }_0(W(\delta )))=0.$$

In particular, we have that the conditional mean of D_CAR(Q – Q₀, ∏₀), given (Q – Q₀)(W), equals zero if ∏₀(W) = P(Δ = 1 | Q – Q₀(W)). This shows that if, for example, (Q – Q₀)(W) only depends on one component W₁, then P₀D(ψ₀, ∏₀, Q) = 0 for ∏₀(W₁) = P₀(Δ = 1 | W₁), and, more general, for ∏₀(W′) with W₁ ⊂ W′ . That is, the better job Q does in approximating Q₀ the less inverse probability of missingness weighting is required to still obtain an unbiased estimating function for ψ₀.

Summary: Consider the efficient influence curve D(Q, G). Suppose we already know that for Q with Ψ(Q) = ψ₀ P₀D(Q₀, G) = 0 for all G. Given a Q with Ψ(Q) = ψ₀, characterize the set of G₀(Q)s for which P₀D(Q₀, G₀(Q)) – D(Q, G₀(Q)) = 0. For such Q and corresponding G₀(Q)’s we have P₀D(Q, G₀(Q)) = 0. Given the representation theorem for estimating functions derived from the orthogonal complement of the nuisance tangent space, it appears that we need to determine the conditional distributions G_0δ of C, given a reduction X(δ) of X, for which E₀D_CAR(Q – Q₀, G_0δ(Q)) = 0. Thus we need to determine the conditional distributions G₀(Q) of C that solves the score equation E₀D_CAR(Q–Q₀, G₀) = 0 of score D_CAR(Q–Q₀, G₀). In particular, if G₀(Q) is a MLE of a finite dimensional parameter (e.g., same dimension as ψ₀), whose score spans D_CAR(Q – Q₀, G₀), then E₀D_CAR(Q – Q₀, G₀) = 0. More generally, if G₀ is a limit of an efficient (e.g. NPMLE) estimator in a model for G₀ that has a tangent space at G₀ that contains D_CAR(Q–Q₀, G₀), then this G₀ also satisfies E₀D_CAR(Q – Q₀, G₀) = 0. In addition, a self-iterated iterative MLE, starting with arbitrary offset G, for a parameter with score D_CAR(Q – Q₀, G), at G, can be employed as well, as presented below, resulting in an updated G₀(Q) of G so that E₀D_CAR(Q – Q₀, G₀(Q)) = 0.

We will now present the general result which can be applied to any CAR-censored data model as defined and studied in van der Laan and Robins (2003).

Theorem 1 (Collaborative Double Robustness of Efficient Influence Curve/Estimating Functions)

CAR-censored data model: Let O = Φ(C, X) ∼ P₀ be a censored data structure with full data random variable X ∼ P_X0, and censoring variable C with conditional probability distribution G₀ of C, given X. Assume G₀ satisfies the coarsening at random assumption. Let g₀(C | X) = dG₀(C | X) a probability density of G₀ w.r.t. an appropriate dominating measure that satisfies coarsening at random itself. Let $\mathcal{M}$ denote the observed data model for P₀. Due to CAR, we have w.r.t. an appropriate dominating measure dP₀(O) = Q₀(O)g₀(O | X), where g₀(O | X) is only a function of O (by CAR), and Q₀ denotes the identifiable part of the full data distribution P_X0 (Gill et al. (1997)). (Here we abused notation to indicate that the conditional density of O, given X, is a deterministic function of the conditional density of C, given X, and, in fact, represents the identifiable part of the censoring mechanism G₀.) Let $\mathcal{Q}$ and $\mathcal{G}$ be models for Q₀ and G₀ which imply a model $\mathcal{M}$= {dP = Qg : Q ∈ $\mathcal{Q}$, G ∈ $\mathcal{G}$} for P₀.

Parameter of interest: Let Ψ: $\mathcal{M}$ → IR^d be pathwise differentiable parameter of interest and it is assumed that Ψ(P₀) = Ψ^F (Q₀) is only a function of Q₀. Let D^*(Q, G) be the efficient influence curve/canonical gradient of Ψ at dP = Qg.

We make the following assumptions:

Augmented “PCW”-representation of efficient influence curve:

(PCW stands for Probability of Censoring Weighted) For each Q ∈ $\mathcal{Q}$, G ∈ $\mathcal{G}$,

$$D*(G,Q)=D_{h(G,Q)}(G,Q)=D_{h(G,Q),PCW}(G,\Gamma (Q))+D_{h(G,Q),CAR}(G,Q^{\prime }),$$

for mappings (G, Q) → h(G, Q), (h, G, Q) → D_h,PCW(G, Γ(Q)), (h, G, Q′) → D_h,CAR(G, Q′(Q, G)), both defined on $\mathcal{H}$ × $\mathcal{G}$ × $\mathcal{Q}$, a parameter mapping Γ on $\mathcal{Q}$, and (G, Q) → Q′(G, Q).

(We refer to Theorem 1.3 in van der Laan and Robins (2003) for such a general representation of the efficient influence curve and, more generally, the orthogonal complement of the nuisance tangent space, where the CAR-components are elements of the tangent space T_CAR of G consisting of all functions of O with conditional mean zero, given X, under G. Under that representation, we have that E₀D_h,PCW(G₀, γ₀) = 0 and D_h,CAR(G₀, Q′) has conditional mean zero, given X, for all Q′.)

Linearity of CAR-component: Q′ → D_h,CAR(G, Q′) is linear on a set ${\overline{\mathcal{Q}}}^{\prime }$ containing {Q′(G, Q) : G, Q} in the sense that for all h ∈ $\mathcal{H}$, and all Q₁, $Q_2\in {\overline{\mathcal{Q}}}^{\prime }$

$$D_{h,CAR}(G,{Q^{\prime }}_1)-D_{h,CAR}(G,{Q^{\prime }}_2)=D_{h,CAR}(G,{Q^{\prime }}_1-{Q^{\prime }}_2).$$

Robustness for mis-specified censoring mechanism: For all Q₀ ∈ $\mathcal{Q}$ and G ∈ $\mathcal{G}$(Q₀) ⊂ $\mathcal{G}$, where (e.g.,) $\mathcal{G}$(Q₀) is defined as all censoring mechanisms G for which ψ₀ can be identified from dP = dQ₀g, we have

$$E_0{D}_h(G,Q_0)=0\mathit{\text{for}}\hspace{0.17em}\mathit{\text{all}}\hspace{0.17em}h\in \mathcal{H}.$$

Robustness of CAR-component: For a reduction X(δ) of X (i.e., X(δ) = f(X, δ) for some function f), let G_0δ be the conditional distribution of C, given X(δ).

Let ${\overline{{\mathcal{Q}}_{\delta }}}^{\prime }$ be a set within ${\overline{\mathcal{Q}}}^{\prime }$ for which for each ${\overline{Q}}^{\prime }\in {\overline{{\mathcal{Q}}_{\delta }}}^{\prime }$

$$E_0{D}_{h,CAR}(G_{0\delta },{\overline{Q}}^{\prime })=0.$$

(Typically, one can select ${\overline{{\mathcal{Q}}_{\delta }}}^{\prime }$ as all functions in ${\overline{\mathcal{Q}}}^{\prime }$ that are only functions of X through X(δ).)

Let Γ(Q) = Γ(Q₀) (typically implying Ψ(Q) = ψ₀), G_0δ ∈ $\mathcal{G}$(Q₀), and assume $Q^{\prime }-{Q^{\prime }}_0\in {\overline{{\mathcal{Q}}_{\delta }}}^{\prime }$, where Q′ = Q′(G_0δ, Q) and Q′₀ = Q′(G_0δ, Q₀). Then

$$E_{0}D*(G_{0\delta },Q)=0.$$

We also have for all G ∈ $\mathcal{G}$(Q₀)

$$E_{0}D*(G,Q_0)=0.$$

Proof. Suppose Γ(Q) = Γ(Q₀) and $Q^{\prime }-{Q^{\prime }}_0\in {\overline{{\mathcal{Q}}_{\delta }}}^{\prime }$. Let $G_0^{*}=G_{0\delta }$ be the conditional distribution of C, given X(δ), and assume it is an element of $\mathcal{G}$(Q₀).

By the “Augmented ‘PCW’-representation of efficient influence curve” assumption, we have

$$E_{0}D*(G_0^{*},Q)=E_0{D}_h(G_0^{*},Q)$$

for some h ∈ $\mathcal{H}$. Thus,

$$\begin{array}{l}{E}_{0}D*(G_0^{*},Q)=E_0{D}_h(G_0^{*},Q)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E_0\{D_h(G_0^{*},Q)-D_h(G_0^{*},Q_0)\}+E_0{D}_h(G_0^{*},Q_0).\end{array}$$

By the assumption that $G_0^{*}\in \mathcal{G}(Q_0)$, it follows that the last term $E_0{D}_h(G_0^{*},\hspace{0.17em}{Q}_0)=0$.

By the “PCW-representation” assumption we have

$$\begin{array}{l}{E}_0\{D_h(G_0^{*},Q)-D_h(G_0^{*},Q_0)\}=E_0\{D_{h,PCW}(G_0^{*},\Gamma (Q))-D_{h,PCW}(G_0^{*},\Gamma (Q_0))\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+E_0\{D_{h,CAR}(G_0^{*},Q^{\prime }(Q,G_0^{*}))-D_{h,CAR}(G_0^{*},Q^{\prime }(Q_0,G_0^{*}))\}.\end{array}$$

By the assumption that Γ(Q) = Γ(Q₀), the first term equals zero. By the “linearity of CAR-component”-assumption we have that the last term equals:

$$E_0\{D_{h,CAR}(G_0^{*},Q^{\prime })-D_{h,CAR}(G_0^{*},{Q^{\prime }}_0)\}=E_0{D}_{h,CAR}(G_0^{*},Q^{\prime }-{Q^{\prime }}_0),$$

where $Q^{\prime }=Q^{\prime }(G_0^{*},\hspace{0.17em}Q)$ and ${Q^{\prime }}_0=Q^{\prime }(G_0^{*},\hspace{0.17em}{Q}_0)$.

We assumed that $Q^{\prime }-{Q^{\prime }}_0\in {\overline{{\mathcal{Q}}_{\delta }}}^{\prime }$. Thus, by the “Robustness of CAR-component”-assumption we have that

$$E_0{D}_{h,CAR}(G_0^{*},Q^{\prime }-{Q^{\prime }}_0)=0.$$

This proves $E_0{D}^{*}(G_0^{*},\hspace{0.17em}Q)=0$. □

3.2. Examples illustrating the collaborative double robustness in censored data models

For the sake of illustration, we will now explicitly establish the collaborative double robustness of the efficient influence curve estimating function in two additional examples. These results are also corollaries of the above general Theorem 1.

3.2.1. Example I: Marginal additive causal effect in nonparametric model

We have the following double robustness result for our additive causal effect example.

Theorem 2 Let dP₀ = Q₀dG₀ be the distribution of O = (W, A, Y) and let the model for P₀ be nonparametric.

Let Ψ(Q₀) = E_Q01{E_Q02(Y | A = 1, W) – E_Q02(Y | A = 0, W)} be the parameter on this model, where it is assumed that it is identifiable from P₀. Here Q₀₁ denotes marginal distribution of W and Q₀₂ the conditional distribution of Y, given A, W. The efficient influence curve of Ψ at P = (Q, G) is given by

$$D*(Q,G)(O)=h(G)(A,W)(Y-Q_2(A,W))+Q_2(1,W)-Q_2(0,W)-\Psi (Q),$$

where Q₂(A, W) = E_Q(Y | A, W) denotes the conditional mean of Y, given A, W, under Q = (Q₁, Q₂).

Assume

$$(Q_{02}-Q_2)(A,W)=E_{Q_0}(Y-Q_2(A,W)|A,W)=f_0(A,W(Q))$$

is only a function of A, W(Q) for a W(Q) = Φ(Q₂, W) for some mapping Φ: i.e., W(Q) denotes a reduction or subset of the full vector random variable W indexed by Q.

Let dG₀(Q) be the conditional distribution of A, given W(Q). If Ψ(Q) = Ψ(Q₀), then

$$E_{P_0}D*(Q,G_0(Q))=0.$$

Or, equivalently, if we represent D^*(Q, G) as D^*(Ψ(Q), Q, G), then

$$E_{P_0}D*({\psi }_0,Q,G_0(Q))=0.$$

We also have: If Pr(P_G(A = 0 | W) * P_G(A = 1 | W) > 0) = 1, then

$$E_{P_0}D*(Q_0,\hspace{0.17em}G)=0,$$

or equivalently,

$$E_{P_0}D*({\psi }_0,Q_0,G)=0.$$

Proof. The last statement is easy and well known (e.g., van der Laan and Robins (2003)). The first statement needs to be proved, or can be derived as a corollary of Theorem 1. Note, if Ψ(Q) = ψ₀, then

$$E_{0}D*(Q,G_0(Q))=E_{0}h(G_0)(A,W(Q))(Y-Q(A,W))+Q(1,W)-Q(0,W)-{\psi }_0.$$

If E₀(Y –Q(A, W) | A, W) = f₀(A, W(Q)) is only a function of A, W(Q), then it follows by first taking the conditional mean, given A, W, and then taking the mean of A, given W(Q),

$$\begin{array}{l}{E}_{0}D*(Q,G_0(Q))=E_{0}h(G_0)(A,W(Q))f_0(A,W(Q))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+Q(1,W)-Q(0,W)-{\psi }_0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E_0{f}_0(1,W(Q))-f_0(0,W(Q))+Q(1,W)-Q(0,W)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\psi }_0.\end{array}$$

Now, note that f₀(A, W(Q)) = Q₀(A, W) – Q(A, W), which proves that the latter quantity equals zero.

□

The implication of this result is that, given an estimate Q of Q₀, we only need to estimate G₀(Q), conditioning on W(Q), or any conditional distribution that conditions on more than W(Q). Thus, if Q already succeeds in explaining most of the true regression E₀(Y | A, W), then only little inverse weighting with G₀(Q) = P(A = · | W(Q)) remains to be done. That is, the amount and manner of inverse weighting required to obtain a consistent estimator of the causal effect ψ₀ can be adapted to the approximation error of Q relative to the true regression.

3.2.2. Example II: Semiparametric regression

Let O = (W, A, Y) ∼ P₀. Assume the model E₀(Y | A, W) – E₀(Y | A = 0, W) = Aβ₀V for some V ⊂ W. If the variance of Y, given A, W, only depends on W, then the efficient score of β₀ at P₀ can be represented as

$$D*({\prod }_0,{\theta }_0,{\beta }_0)(O)=(A-{\prod }_0(W))\hspace{0.17em}(Y-A{\beta }_{0}V-{\theta }_0(W)),$$

where ∏₀(W) = E₀(A | W), and θ₀(W) = E₀(Y | A = 0, W). For the sake of illustration we will use this simpler representation, but the same double robustness applies to the general efficient influence curve representation as (e.g.) presented in van der Laan and Robins (2003).

Theorem 3 Suppose E₀(Y – Aβ₀V – θ(W) | A, W) = f₀(W(θ)) for some function f₀ of W(θ) where W(θ) = Φ(W, θ) is function of W and θ. Note that this states that θ₀(W) – θ(W) = f₀(W(θ)) is only a function of a reduction W(θ) of W. Let ∏₀(θ)(W) = E₀(A | W(θ)). Then

$$E_{0}D*({\prod }_0(\theta ),\theta ,{\beta }_0)=0$$

We also have

$$E_{0}D*(\prod ,{\theta }_0,{\beta }_0)=0$$

Proof. Only the first robustness result needs to be proved. First take the conditional mean, given A, W, which results in the term E₀(A–∏₀(θ)(W(θ))) f₀(W(θ)). Subsequently, we take the conditional mean, given W(θ), which proves it equals zero. □

3.3. Construction of collaborative double robust estimators

By using a collaborative estimator g_n(Q) of a g₀(Q) in the set of conditional distributions that conditions on the required function of Q–Q₀ (and g₀ itself), one can construct collaborative double robust estimators. For example, one could use the targeted maximum likelihood estimator applied to initial estimator Q_n and using the resulting collaborative estimator g_n(Q_n). One can also use estimating equation methodology, solving for ψ_n in 0 = P_nD^*(ψ, Q_n, g_n(Q_n)). The formal asymptotic linearity (and thereby asymptotic normality) of such estimators is studied in the next section. Our proposed collaborative targeted maximum likelihood procedure is one particular collaborative double robust targeted maximum likelihood estimator, which also involves updating the initial estimator Q_n beyond the construction of an appropriate g_n(Q_n). However, we could also simply have taken g_n(Q_n) from our proposed collaborative targeted maximum likelihood procedure, and still use the targeted maximum likelihood estimator with initial estimator Q_n. In addition, we could also have used our proposed collaborative estimator g_n(Q_n) to solve an estimating equation 0 = P_nD^*(Q_n, g_n(Q_n), ψ) = 0 in ψ.

Other methods for construction of collaborative estimators g_n(Q_n) are of interest as well. For example, one could consider a collection of one-dimensional fluctuations of Q_n and use maximum likelihood to test these fluctuations. In this manner one can select a dimension reduction involving the X-components that still significantly increase the log-likelihood (or other loss function) beyond the initial fit Q_n. One could then fit g_n by running a machine learning algorithm that only conditions on the selected components. This procedure only uses the initial estimator to obtain a dimension reduction, but from then on it uses an external procedure based on the loss function for g₀.

Given an initial estimator Q_n, another idea of interest for construction of a collaborative estimator g_n(Q_n) is the following. One first constructs a sequence of increasingly nonparametric estimators ĝ_j of g₀, j = 1, . . . , J. These estimators could already be based on a dimension reduction based on offset by initial estimator. Given an initial estimator Q̂, we select the following estimator of g₀:

$$j_n=\text{arg}\hspace{0.17em}\underset{j}{\text{min}}{\Vert E_{B_n}{P}_{n,B_n}^{1}D*(\widehat{Q}(P_{n,B_n}^0),{\widehat{g}}_j(P_n))\Vert }^2,$$

where B_n denotes a random variable in {0, 1}ⁿ defining a random split in training sample {i : B_n(i) = 0} and validation sample {i : B_n(i) = 1}, and $P_{n,B_n}^0$, $P_{n,B_n}^1$ denote the empirical probability distributions of the training and validation sample, respectively. Thus, one selects the estimator that minimizes the Euclidean norm of the cross-validated mean of efficient influence curve at the estimator Q̂. If j is too small, then P₀D^*(Q̂, g_j) will be non zero, so that j_n will always select a large enough j for n tending to infinity. If, on the other hand, j is large enough so that P₀D^*(Q̂, g_j) = 0, then the expectation of {P_nD^*(Q̂, g_j)}² will be equal to its variance which will be increasing in j, so that smaller j’s, but larger than the critical one, will be preferred. One now defines as collaborative estimator the estimator g_n(Q_n) ≡ ĝ_jn(P_n) indexed by this choice j_n.

3.4. Estimating the sufficient minimal adjustment covariate from the data

Let H(g₀, Q – Q₀) be the component that needs to be adjusted for in g₀ = g₀(Q). One could estimate this component from the data using appropriate methodology. If, given an arbitrary initial fit g, one would add H(g, Q – Q₀) as main term in a fluctuation model of g, and the fluctuation function is chosen so that the score of the coefficient of this main term at zero equals D_CAR(Q–Q₀, g₀), then the MLE-update of g will solve the wished score equation P₀D_CAR(Q – Q₀, g₀) = 0. We can refer to H(g₀, Q – Q₀) as the minimal adjustment covariate, needed to obtain the wished collaborative robustness.

The sufficient covariate H(g, Q–Q₀), that is needed to update g, depends on g itself as well, so that, even given an estimate of Q – Q₀, the above maximum likelihood update of an initial g does not work. There are two approaches that can be used to deal with this self-dependence of the minimal adjustment covariate for g.

Firstly, one can extract the few components of only Q – Q₀, and enforce nonparametric adjustment by these covariates in a fit of g₀(Q) of the censoring mechanism. In this manner, the resulting censoring mechanism estimator will estimate a true conditional distribution that conditions on covariates that imply the value of H(g₀(Q), Q – Q₀). Secondly, one can also only adjust for H(g⁰, Q–Q₀) as a main term, given an estimate g⁰, and iterate this updating process of g till convergence. In the latter case, as mentioned above, it is assumed that the score of the fluctuation of g implied by this main term extension H(g, Q–Q₀) at zero equals D_CAR(g, Q–Q₀). Let’s illustrate these two approaches with an example.

For example, in the additive causal effect example with O = (W, A, Y), ψ₀ = EY (1)–Y (0) and Y continuous, we have $H(g_0,\hspace{0.17em}Q-Q_0)=\frac{1}{g_0(1|W)}E(Y-Q|A=1,\hspace{0.17em}W)+\frac{1}{g_0(0|W)}E(Y-Q|A=0,\hspace{0.17em}W)$, and the score of ε, at ε = 0, of logistic regression model g_ε(1 | W) = 1/(1 + exp(–C⁰(W) – εH(g, Q – Q₀)), using an offset C⁰(W), is given by D_CAR(g, Q–Q₀) = H(g, Q–Q₀)(A–g(1 | W)).

One can estimate E(Y – Q|A = 1, W) and E(Y – Q|A = 0, W) with a machine learning algorithm, treating an initial estimate Q as offset (possibly cross-validated to make the offset independent of Y_i). If Y is binary, we would use Q as offset and one could estimate these Q – Q₀-components by running a logistic regression with Q as offset. Given this estimate of the two Q – Q₀-components that span H(g₀, Q – Q₀), one could now force nonparametric adjustment by these two estimated covariates in the estimate of g₀.

Alternatively, given an initial estimator $g_n^0$, one could obtain an estimate $H_n^0$ by plugging in an estimate of Q₀ – Q, and this initial $g_n^0$. One could now force in this $H_n^0$ as a main term in $g_n^0$, resulting in an updated $g_n^1$. This process is iterated till convergence. In the limit we have that g_n solves $0=P_{n}H(g_n,\hspace{0.17em}\widehat{Q-Q_0})(A-g_n(1|W))$. Here $g_n^0$ would already be a collaborative estimator of g₀(Q), such as the one proposed in our collaborative targeted maximum likelihood estimator, so that the collaborative double robustness is preserved (we do not want to only rely on correct specification of $\widehat{Q-Q_0}$, and thereby of this sufficient minimal covariate)

We do not advise starting the above iterative algorithm at a purposely misspecified estimator $g_n^0$. Instead we want to apply the above iterative algorithm at a collaborative estimator $g_n^0$, such as the one presented in our template of the C-TMLE in Section 2. For example, after having run the C-TMLE in Section 2, we would carry out a subsequent update of the resulting collaborative estimator g_n by applying the above iterative updating algorithm, starting at $g_n^0=g_n$, and using an estimator of Q₀ – Q. If we would only include this estimate of the sufficient covariate H(g₀, Q – Q₀) in g_n, then the consistency of the estimator ψ_n fully relies on correct estimation of Q – Q₀, and thereby on correct estimation of Q₀, and therefore would not utilize the collaborative double robustness of the efficient influence curve. Instead of carrying out a subsequent update of a collaborative estimator g_n using the iterative algorithm, we could incorporate an estimate H_n (or its (Q – Q₀)-components) in our proposed template for the collaborative targeted MLE by forcing it in our candidate censoring mechanism estimators.

In the above additive causal risk example, we estimate H(g, Q – Q₀) by plugging in an initial estimate g⁰ and Q – Q₀, and the iterative adjustment succeeds in its goal as long as the estimate of Q – Q₀ is correct, even if (the initial) g is misspecified. One could also use a representation such as H(g₀, Q–Q₀) = E_g0,_Q0(D_IPCW(g₀, Q) | A = 1, W) – E₀(D_IPCW(g₀, Q) | A = 0, W), and estimate the two regressions by regressing an IPCW-function indexed by g₀, Q on A, W, and evaluate it at A = 1 and A = 0, respectively. Here D_IPCW = (Y – Q){A/g₀(A | W) – (1 – A)/g₀(A | W)}. One could now apply the above iterative updating algorithm to this (non-substitution based) manner of estimating H(g₀, Q–Q₀). As shown in (e.g.) van der Laan and Robins (2003) for monotone censored data structures and causal inference data structures, involving censoring and treatment actions over time, D_CAR(Q – Q₀, g₀) does allow such a representation Σ_j H_j(g₀, Q–Q₀)(A(j)–g_0j(1 | $\mathcal{F}$(j)), where $\mathcal{F}$(j) represents the history before censoring or treatment A(j), and H_j(g₀, Q–Q₀) = E₀(D_IPCW | A(j) = 1, $\mathcal{F}$(j)) – E₀(D_IPCW | A(j) = 0, $\mathcal{F}$(j)) for some IPCW-function. The disadvantage of this approach is that it relies on g₀ representing a true conditional distribution, while in the iterative substitution based approach the main term adjustment at a possibly misspecified g still yields the wished collaborative double robustness.

4. Asymptotic linearity of collaborative double robust TMLE

The collaborative targeted maximum likelihood estimator $Q_n^{*}$ equals a k_n-th step collaborative targeted maximum likelihood estimator, and thereby equals a targeted maximum likelihood estimator with a starting estimator $Q_n^k$ (e.g., the k_n – 1-th collaborative targeted maximum likelihood estimator), and the censoring mechanism estimator g_n = g_nδn as selected in the k_n-step, given the collection of candidate estimators g_nδ indexed by δ ranging over an index set.

Thus, just like the targeted maximum likelihood estimator, the collaborative targeted maximum likelihood estimator ${\psi }_n=\Psi (Q_n^{*})$ of ψ₀ solves the efficient influence curve estimating equation

$$0=P_{n}D*(Q_n^{*},g_n,{\psi }_n).$$

For simplicity, we will make the assumption that the efficient influence curve at a P_Q,g can be represented as an estimating function in ψ: i.e., the efficient influence curve at P can be represented as D^*(Q(P), g(P), ψ(Q(P))) for some mapping (Q, g, ψ) → D^*(Q, g, ψ). However, the theorem in this section can be generalized to any efficient influence curve D^*(Q, g) at a data generating distribution P_Q,g.

It is a reasonable assumption that $Q_n^{*}$ converges to some element Q^* in the model for Q₀, where Q^* is not necessarily equal to the true Q₀. In addition, let’s assume that, for each δ, the δ-specific censoring mechanism estimator g_nδ converges to some g_0δ. For example, if δ indicates an adjustment set, then it might be assumed that g_nδ converges to the true conditional distribution, given this δ-specific adjustment set.

For a given Q, we define δ(Q) as the index δ with entropy d(δ) minimal and so that

$$P_{0}D*(Q,g_{0\delta (Q)},{\psi }_0)=0.$$

In other words, given the family of adjustments indexed by δ, δ (Q) represents the minimal adjustment necessary in the censoring mechanism to obtain the collaborative double robustness/unbiased estimating function for ψ₀. It is then a natural assumption that

$$P_{0}D*(Q,g_{0\delta },{\psi }_0)=0\text{for}\hspace{0.17em}\text{each}\hspace{0.17em}\delta \hspace{0.17em}\text{with}\hspace{0.17em}d(\delta )\ge d(\delta (Q)).$$

In other words, if one uses a more nonparametric estimator of the censoring mechanism than needed (i.e.., than δ(Q)), then one certainly obtains the wished unbiasedness.

We will assume that, as n converges to infinity, then the selected censoring mechanism estimator g_n = g_nδn converges to a fixed g_0δ0 representing the limit of a g_nδ0 , not necessarily equal to the conditional distribution, given the full X. For notational convenience, we will also denote this limit with g₀.

It is assumed that d(δ₀) ≥ d(Q^*) so that

$$0=P_{0}D*(Q*,g_0,{\psi }_0),$$

which will be the fundamental assumption for asymptotic normality of the CTMLE. In other words, it is assumed that our collaborative C-TMLE procedure selects a nonparametric enough estimator g_n for the censoring mechanism (in collaboration with $Q_n^{*}$) so that the required unbiasedness of the efficient influence curve estimating function is achieved.

To derive the influence curve of $\Psi (Q_n^{*})$, the asymptotic linearity theorem below assumes also that the limit of the selected censoring mechanism estimator satisfies

$$P_{0}D*(Q_n^{*},g_0,{\psi }_0)=o_P(1/\sqrt{n}).$$ (3)

As a consequence of this assumption (3), the influence curve does not involve a contribution requiring the analysis of a function of $Q_n^{*}$. This important simplification of the influence curve allows straightforward calculation of standard errors for the C-TMLE. The assumption (3) requires the limit g₀ to be nonparametric enough w.r.t. the actual estimator $Q_n^{*}$ so that enough orthogonality is achieved to make the contribution $P_0{D}^{*}(Q_n^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}{\psi }_0)$ second order.

Why assumption (3) holds for C-TMLE: We now explain why this assumption is reasonable for the C-TMLE.

Define $g_0(Q_n^{*})$ as $g_{0{\delta }_n^{*}}$ with ${\delta }_n^{*}=\text{min}\{\delta \hspace{0.17em}:\hspace{0.17em}d(\delta )\hspace{0.17em}\ge \hspace{0.17em}d({\delta }_0),\hspace{0.17em}{P}_0{D}^{*}(Q_n^{*},\hspace{0.17em}{g}_{0\delta },\hspace{0.17em}{\psi }_0)=0\}$. In other words, $g_0(Q_n^{*})$ corresponds with the limit of the least nonparametric estimator (among all estimators more nonparametric than the one identified by δ₀) that still yields the wished unbiasedness of the estimating function at $Q_n^{*}$, and it as close as possible to g₀ = g_0δ0.

We note that

$$\begin{array}{l}{P}_{0}D*(Q_n^{*},g_0,{\psi }_0)-D*(Q*,g_0,{\psi }_0)=P_{0}D*(Q_n^{*},g_0(Q_n^{*}),{\psi }_0)\hspace{0.17em}-D*(Q*,g_0(Q_n^{*}),{\psi }_0)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+R_n,\end{array}$$

where R_n is a second order term (like R_n1 below) involving the difference $Q_n^{*}-Q^{*}$ and $g_0(Q_n^{*})-g_0$. By definition of $g_0(Q_n^{*})$ and the fact that $Q_n^{*}$ converges to Q^*, it is reasonable to assume $g_0(Q_n^{*})\to g_0$ as n → ∞. So R_n is a second order term, so that it is reasonable to assume $R_n=o_P(1/\sqrt{n})$.

By definition of $g_0(Q_n^{*})$, we do not only have

$$P_{0}D*(Q_n^{*},g_0(Q_n^{*}),{\psi }_0)=0,$$

but also that $g_0(Q_n^{*})$ is equally or more nonparametric than g₀(Q^*) so that

$$P_{0}D*(Q*,g_0(Q_n^{*}),{\psi }_0)=0.$$

This implies now that indeed

$$P_{0}D*(Q_n^{*},g_0,{\psi }_0)=o_P(1/\sqrt{n}).$$

Finally, we note that the next theorem can be applied to any collaborative double robust estimator, as discussed in previous section, not only the collaborative double robust targeted maximum likelihood estimator.

Theorem 4 Let (Q, g, ψ) → D^*(Q, g, ψ) be a well defined function that maps any possible (Q, g, Ψ(Q)) into a function of O. Let O₁, . . . , O_n ∼ P₀ be i.i.d, and let P_n be the empirical probability distribution. Let Q → Ψ(Q) be a d-dimensional parameter, where ψ₀ = Ψ(Q₀) is the parameter value of interest. In the following template for proving asymptotic linearity of $\Psi (Q_n^{*})$ as an estimator of Ψ(Q₀), $Q_n^{*}$ represents the collaborative targeted maximum likelihood estimator, but it can be any estimator.

Let Q^* denote the limit of $Q_n^{*}$. Let g_n be an estimator and g₀ denote its limit.

Assume

Efficient Influence Curve Estimating Equation: $0=P_n{D}^{*}(Q_n^{*},\hspace{0.17em}{g}_n,\hspace{0.17em}{\psi }_n)$, where ${\psi }_n=\Psi (Q_n^{*})$.

Censoring Mechanism Estimator is Nonparametric Enough:

$$P_{0}D*(Q*,g_0,\hspace{0.17em}{\psi }_0)=0.$$

$$P_{0}D*(Q_n^{*},g_0,{\psi }_0)=o_P(1/\sqrt{n}).$$

(Above we show why the latter is indeed a second order term for the C-TMLE.)

Consistency:

$$P_0{(D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_0))}^2\to 0\hspace{0.17em}\mathit{\text{in}}\hspace{0.17em}\mathit{\text{probability}},$$

as n → ∞. And the same is assumed if one or two of the triplets $(Q_n^{*},\hspace{0.17em}{g}_n,\hspace{0.17em}{\psi }_n)$ is replaced by its limit (Q^*, g₀, ψ₀).

Identifiability/Invertibility: c₀ = –d/dψ₀P₀D^*(Q^*, g₀, ψ₀) exists and is invertible.

Donsker Class: {D^*(Q, g, Ψ(Q)) : Q, g} is P₀-Donsker, where (Q, g) vary over sets that contain ( $Q_n^{*}$, g_n), (Q^*, g_n), ( $Q_n^{*}$, g) with probability tending to 1.

Contribution due to Censoring Mechanism Estimation: Define the mapping g → Φ(g) ≡ P₀D^*(Q^*, g, ψ₀). Assume $\Phi (g_n)-\Phi (g_0)=(P_n-P_0)I{C}_{g_0}+o_P(1/\sqrt{n})$ for some mean zero function ${IC}_{g_0}\in L_0^2(P_0)$.

Second order terms: Define second order term

$$\begin{array}{l}{R}_{n1}=P_0\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-P_0\{D*(Q_n^{*},g_0,{\psi }_0)-D*(Q*,g_0,{\psi }_0)\},\end{array}$$

and assume $R_{n1}=o_P(1/\sqrt{n})$. Note R_n1 is a second order term involving difference between $Q_n^{*}-Q$ and g_n – g₀.

Define second order term

$$\begin{array}{l}{R}_{n2}=P_0\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-P_0\{D*(Q*,g_n,{\psi }_0)-D*(Q*,g_0,{\psi }_0)\},\end{array}$$

and assume $R_{n2}=o_P(1/\sqrt{n})$. Note R_n2 is a second order term involving differences g_n – g₀ and ψ_n – ψ₀.

Then, ψ_n is asymptotically linear estimator of ψ₀ at P₀ with influence curve

$$IC(P_0)=c_0^{-1}\{D*(Q*,g_0,{\psi }_0)+I{C}_{g_0}\}.$$

That is,

$${\psi }_n-{\psi }_0=(P_n-P_0)IC(P_0)+o_P(1/\sqrt{n}).$$

In particular, $\sqrt{n}({\psi }_n-{\psi }_0)$ converges in distribution to a multivariate normal distribution with mean zero and covariance matrix Σ₀ = E₀IC(P₀)IC(P₀)^⊤.

Proof: The principal equations are $0=P_n{D}^{*}(Q_n^{*},\hspace{0.17em}{g}_n,\hspace{0.17em}{\psi }_n)$ and P₀D^*(Q^*, g₀, ψ₀) = 0. So, we have

$$P_{0}D*(Q*,g_0,{\psi }_n)-D*(Q*,g_0,{\psi }_0)=-\{P_{n}D*(Q_n^{*},g_n,{\psi }_n)-P_{0}D*(Q*,g_0,{\psi }_n)\}.$$

Let $c_0=-\frac{d}{d{\psi }_0}{P}_0{D}^{*}(Q^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}{\psi }_0)$. Then,

$$\begin{array}{l}{c}_0({\psi }_n-{\psi }_0)+o(|{\psi }_n-{\psi }_0|)=(P_n-P_0)D*(Q*,g_0,{\psi }_n)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+P_n\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+P_n\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)\}.\end{array}$$

We denote the three terms on the right with I,II and III, and deal with them separately below.

I: By the Donsker condition, and consistency condition, we have

$$(P_n-P_0)\{D*(Q*,g_0,{\psi }_n)-D*(Q*,g_0,{\psi }_0)\}=o_P(1/\sqrt{n}).$$

Thus, we obtain $(P_n-P_0)D^{*}(Q^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}{\psi }_0)+o_P(1/\sqrt{n})$ as first term approximation. We refer to van der Vaart and Wellner (1996) for this empirical process theorem.

II: We have

$$\begin{array}{l}{P}_n\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)\}=\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{P}_n-P_0)\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+P_0\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)\}.\end{array}$$

The first term is $o_p(1/\sqrt{n})$ by our Donsker class condition, and consistency condition at $Q_n^{*},\hspace{0.17em}{g}_n,\hspace{0.17em}{\psi }_n$. We also have

$$P_0\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)\}=P_0\{D*(Q_n^{*},g_n,{\psi }_0)-D*(Q*,g_0,{\psi }_0)+R_{n1},$$

where

$$\begin{array}{l}{R}_{n1}=P_0\{D*(Q_n^{*},g_n,{\psi }_n)-D*(Q*,g_n,{\psi }_n)-D*(Q_n^{*},g_0,{\psi }_0)-D*(Q*,g_0,{\psi }_0)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=o_P(1/\sqrt{n}),\end{array}$$

by assumption.

R_n1 is a second order term involving $Q_n^{*}-Q^{*}$ and (g_n, ψ_n) – (g₀, ψ₀). It remains to consider the term $P_0\{D^{*}(Q_n^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}{\psi }_0)-D^{*}(Q^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}{\psi }_0)\}$, which is $o_P(1/\sqrt{n})$ by “Censoring Mechanism is Nonparametric Enough”-assumption.

III: We have

$$\begin{array}{l}{P}_n\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)=\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(P_n-P_0)\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+P_0\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)\}.\end{array}$$

The first term is $o_P(1/\sqrt{n})$ by Donsker class condition, and consistency condition at $Q_n^{*}$, g_n, ψ_n. We also have

$$P_0\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)\}=P_0\{D*(Q*,g_n,{\psi }_0)-D*(Q*,g_0,{\psi }_0)\}+R_{n2},$$

where

$$\begin{array}{l}{R}_{n2}=P_0\{D*(Q*,g_n,{\psi }_n)-D*(Q*,g_0,{\psi }_n)-D*(Q*,g_n,{\psi }_0)-D*(Q*,g_0,{\psi }_0)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=o_P(1/\sqrt{n}),\end{array}$$

by assumption. Thus the third term equals P₀D^*(Q^*, g_n, ψ₀)–D^*(Q^*, g₀, ψ₀), which, by definition, equals Φ(g_n)–Φ(g₀). We assumed that $\Phi (g_n)-\Phi (g_0)=(P_n-P_0)I{C}_{g_0}+o_P(1/\sqrt{n})$. Thus, the third term equals $(P_n-P_0){IC}_{g_0}+o_P(1/\sqrt{n})$.

We can thus conclude that

$${\psi }_n-{\psi }_0=(P_n-P_0)c_0^{-1}\{D*(Q*,g_0,{\psi }_0)+I{C}_{g_0}\}+o_P(|{\psi }_n-{\psi }_0|)+o_P(1/\sqrt{n}).$$

This implies $|{\psi }_n-{\psi }_0|=O_P(1/\sqrt{n})$, and thereby the stated asymptotic linearity. □

4.1. Statistical Inference

If Q^* = Q₀, then IC_g0 = 0, so that the influence curve reduces to the efficient influence curve D^*(Q₀, g₀, ψ₀) at a possibly weakly adjusted g₀. If g_n converges to the fully adjusted conditional distribution, given X, then we know that IC_g0 equals minus the projection of D^*(Q^*, g₀, ψ₀) onto the tangent space of the model used by g_n (van der Laan and Robins (2003), Section 2.3.7). We suggest that, even if g₀ is not the fully adjusted censoring mechanism, we will typically still have that D^*(Q^*, g₀, ψ₀) is a conservative influence curve. In other words, if Q_n starts approximating the true Q₀, then the IC_g0 contribution gets smaller and smaller, while if Q_n stays away from Q₀, then g_n starts approximating the fully adjusted g₀, in which case, inference based on D^* is conservative. This might explain why we see good coverage in our simulations based on “influence curve” $D^{*}(Q_n^{*},\hspace{0.17em}{g}_{n,\hspace{0.17em}}{\psi }_n^{*})$. If g_n corresponds with a parametric MLE estimator (for a data adaptively selected parametric model), then we propose to use the parametric delta-method to compute the analytic formula for the influence curve IC_g0 in order to obtain an accurate influence curve.

One can estimate the covariance matrix Σ = E₀ICIC^⊤ of the influence curve with the empirical covariance matrix ${\sum }_n=1/n{{\sum }_{i=1}^n\widehat{IC}(O_i)\widehat{IC}(O_i)}^{\top }$, and statistical inference can be based on the corresponding mean zero multivariate normal distribution, as usual.

4.2. Selection among difference collaborative targeted maximum likelihood estimators

Suppose that we have a set of candidate collaborative targeted maximum likelihood estimators $({\widehat{Q}}_k^{*}(P_n),\hspace{0.17em}{\widehat{g}}_k(P_n))$, k = 1, . . . , K. Suppose that each of these estimators satisfy the conditions of the theorem. For example, these might be collaborative targeted maximum likelihood estimators as defined in our template, using different initial estimators indexed by k, but the same collaborative estimator for the censoring mechanism as a function of the data and the initial estimator (thus still resulting in different realizations if the initial estimators are different). Then $\Psi ({\widehat{Q}}_k^{*}(P_n))$ is asymptotically linear with influence curve $D^{*}(Q_k^{*},\hspace{0.17em}{g}_{0k},\hspace{0.17em}{\psi }_0)$, k = 1, . . . , K. We can now select among these candidate C-DR-TMLEs by maximizing the estimated efficiency, as in Rubin and van der Laan (2008).

Specifically, let Ψ be a one-dimensional parameter. We now select the k that minimizes the cross-validated variance of the influence curve:

$$k_n=\text{arg}\hspace{0.17em}\underset{k}{\text{min}}{E}_{B_n}{P}_{n,B_n}^{1}D{*}^2({\widehat{Q}}_k^{*}(P_{n,B_n}^0),{\widehat{g}}_k(P_{n,B_n}),{\psi }_n).$$

Thus, we would use the estimator ${\psi }_n=\Psi ({\widehat{Q}}_{k_n}^{*}(P_n))$. If Ψ is multidimensional, then one needs to agree on a real valued criterion applied to the covariance matrix of the influence curve, such as the sum of the variances along the diagonal, and minimize over k the criterion of the cross-validated covariance matrix of the k-specific influence curve.

4.3. Irregular C-TMLE and super efficiency

If g_n converges to the fully adjusted g₀(· | X) (fully adjusting for X, under CAR) and $Q_n^{*}$ converges to Q₀, then it follows that ψ_n is asymptotically linear with influence curve equal to the efficient influence curve D^*(Q₀, g₀, ψ₀). So in that case, ψ_n is an asymptotically efficient estimator and thereby also a regular estimator.

Due to the particular way g_n is constructed in response to Q_n, it is easily argued that the collaborative targeted MLE can be an irregular estimator and can be super efficient by achieving an asymptotic variance that is smaller than the variance of the efficient influence curve. In particular, our previous arguments showed that if the initial estimator is a maximum likelihood estimator according to a correctly specified parametric model, then g_n will avoid nonparametric fits, thereby staying away from estimating the fully adjusted g₀ that would result in an efficient estimator in first order. In this case, by the above theorem, the influence curve of ψ_n will be equal to D^*(Q₀, g₀, ψ₀), using a non-fully adjusted g₀, so that the variance of the influence curve will be smaller than the variance of the efficient influence curve that involves a fully adjusted g₀.

The super efficiency may have very attractive features in practice. For example, there might be a covariate that is very predictive of censoring/treatment, but have no relation to the outcome. The C-TMLE will now decide to not adjust for this covariate at all in the selected censoring mechanism, and as a consequence, it might achieve the efficiency bound for the data structure excluding this covariate, but still assuming CAR, so that the C-TMLE will have smaller asymptotic variance than the efficiency bound. The resulting super efficient estimator not only shows improved precision, but also yields more reliable confidence intervals, by avoiding heavily non-robust (and harmful) operations. In most practical scenarios, such a covariate will still have a weak link with the outcome. In this case, for very large sample sizes, the C-TMLE will adjust for this covariate and thereby only be asymptotically efficient, but it will still behave as a super efficient estimator for practical sample sizes, by not adjusting for this covariate. That is, it invests in effective bias reduction focussing on covariates that are still predictive of the outcome, taking into account the already included initial estimator. This behavior is completely compatible with an estimator that aims to minimize mean squared error of the estimator of the target parameter, and certainly avoids steps that both increase bias as well as variance.

Finally, we remark that in simulations in which Q_n converges fast to the true Q₀, g_n seems to have a temptation to converge to a random choice g₀ that is beyond the required minimal censoring mechanism with probability 1. That is, likelihood based cross-validation might over-select the adjustment in the censoring mechanism relative to the minimal adjustment, and the amount of over-selection remains random (but small) for large sample sizes (this is a known property of cross-validation). This naturally results in an irregularity of the estimator. Simulations have not shown practical problems for statistical inference, but this remains an area of study.

5. Targeted loss functions implied by efficient influence curve

The template of the collaborative targeted maximum likelihood estimators is based on 1) a log-likelihood loss function (i.e., same loss function that is maximized at targeted maximum likelihood step) to select among candidate targeted maximum likelihood estimators indexed by increasingly nonparametric estimators of censoring mechanism, and 2) a preferred loss function to compare targeted maximum likelihood estimators using different censoring mechanism estimators, in order to build these candidate censoring mechanism estimators. One can also use a preferred loss function to select among different candidate collaborative targeted maximum likelihood estimators (e.g., indexed by different initial estimators).

In this section we propose targeted loss functions implied by the efficient influence curve of Ψ. Firstly, the log-likelihood can be replaced by a penalized log-likelihood that is sensitive to sparse data bias w.r.t. target parameter, as defined in next subsection This penalized log-likelihood can also play the role of the preferred loss function. In the second subsection we propose as preferred loss function the cross-validated variance of the efficient influence curve, relying on an overall collaborative estimator of censoring mechanism w.r.t. an initial estimator, or a candidate specific collaborative estimator. In the last subsection, we utilize the mean of the efficient influence curve as a criterion to generate a targeted loss function for Q that incorporates a sequence of increasingly nonparametric estimators of the censoring mechanism.

5.1. The MSE-penalized cross-validated log-likelihood

In the C-DR-TMLE we applied loglikelihood based cross-validation to select among different targeted maximum likelihood estimators, indexed by different censoring mechanism estimators. We propose here a penalized log-likelihood criterion that results in robust estimators in the context of sparse data w.r.t. the parameter of interest.

Consider candidate (e.g., collaborative) targeted maximum likelihood estimators $P_n\to {\widehat{Q}}_{\delta }^{*}(P_n)$ of the true Q₀ ∈ $\mathcal{M}$, targeting a parameter ψ₀ = Ψ(Q₀), indexed by δ. Our proposed criterion for selecting δ is

$${\delta }_n=\underset{\delta }{\text{argmax}}{E}_{B_n}{P}_{n,B_n}^1\text{log}{\widehat{Q}}_{\delta }^{*}(P_{n,B_n}^0)-MSE(P_n)(\delta ),$$

where the first term is the cross-validated log-likelihood for the candidate estimator ${\widehat{Q}}_{\delta }^{*}(P_n)$, and MSE(P_n)(δ) is an estimator of the mean squared error (variance plus bias-squared) of the substitution estimator $\widehat{\Psi }({\widehat{Q}}_{\delta }^{*}(P_n))$ as an estimator of its δ-specific limit (thus ignoring asymptotic bias). The MSE(P_n)(δ) is possibly appropriately scaled relative to the log-likelihood term. The sole motivation for the proposed additional penalty term is to make the criterion more targeted towards ψ₀, while still preserving the log-likelihood as the dominant term in regular situations: i..e, asymptotically, the penalty is negligible (in regular situations the MSE behaves as 1/n).

5.1.1. Variance of targeted maximum likelihood estimator relative to its δ-limit

If the target parameter cannot be reasonably identified from the data the log-likelihood of the targeted maximum likelihood estimator is not sensitive enough to such a singularity: in fact, on many occasions this just means that the targeted maximum likelihood algorithm will be ineffective (i.e., the maximum likelihood fluctuations get too noisy) so that in essence the log-likelihood of the initial estimator drives the selection.

Therefore it is crucial that the log-likelihood terms are penalized by a term that blows up (in the negative direction) for δ-values for which the variance (or bias, addressed in next subsection) of the targeted maximum likelihood estimator $\Psi ({\widehat{Q}}_{\delta }^{*}(P_n))$ relative to its limit ${\psi }_0(\delta )=\Psi ({\widehat{Q}}_{\delta }^{*}(P_0))$ gets large. Since we can derive the influence curve of the targeted maximum likelihood estimator $\Psi ({\widehat{Q}}_{\delta }^{*}(P_n))$ as an estimator of ψ₀(δ), this variance can be estimated with the variance of this influence curve at this targeted maximum likelihood estimator ${\widehat{Q}}_{\delta }^{*}(P_n)$. As follows from the study of TMLE in van der Laan and Rubin (2006) one can often use as approximate influence curve the efficient influence curve D^*( $Q_{\delta }^{*}$, g_δ) at the limit of the targeted maximum likelihood estimator ( ${\widehat{Q}}_{\delta }^{*}$, ĝ_δ), which simplifies the penalty while it remains equally effective.

We first define the cross-validated covariance matrix

$$\frac{\Sigma (P_n)(\delta )}{n}=\frac{1}{n}{E}_{B_n}{P}_{n,B_n}^1\{D*({\widehat{P}}_{\delta }^{*}(P_{n,B_n}^0))D*{({\widehat{P}}_{\delta }^{*}(P_{n,B_n}^0))}^{\top }\}.$$

For example, if the target parameter is 1-dimensional (i.e., d = 1), then we have

$$\frac{{\sigma }^2(P_n)(\delta )}{n}=\frac{1}{n}{E}_{B_n}{P}_{n,B_n}^1{\{D*({\widehat{P}}_{\delta }^{*}(P_{n,B_n}^0))\}}^2.$$

For example, one can define the variance term of the MSE as

$${\sigma }^2(P_n)(\delta )=a\Sigma (P_n)(\delta )a^{\top },$$

for a user supplied vector a, so that σ²(P_n)/n represents the variance estimate of the estimator of a^⊤ψ₀(δ).

Our proposal presented in the MSE-subsection below will actually have the form

$${\sigma }^2(P_n)(\delta )=\sum _{j=1}^d{a}_j^{\top }\Sigma (P_n)(\delta )a_j,$$ (4)

where a_j are the row vectors of the square root of a user supplied matrix such as the inverse of the the correlation matrix of Σ(P_n)(δ).

5.1.2. Bias of targeted maximum likelihood estimator relative to its δ-limit

We might also wish to estimate the bias of the targeted maximum likelihood estimator $\Psi ({\widehat{Q}}_{\delta }^{*}(P_n))$ relative to its limit ψ₀(δ) (even though in most applications the variance appears to drive the MSE term). For example, this could be done with the bootstrap:

$$E_{P_n}\{\Psi ({\widehat{Q}}_{\delta }^{*}(P_n^{\#}))-\Psi ({\widehat{Q}}_{\delta }^{*}(P_n))\},$$

where $P_n^{\#}$ represents the empirical distribution of a bootstrap sample $O_1^{\#},\dots ,O_n^{\#}$ from the empirical distribution P_n. However, this would be much too computer intensive in many applications in which the targeted maximum likelihood estimator involves data adaptive model or algorithm selection. By noting that a bootstrap sample corresponds on average with 2/3 of the n observations, the following analogue bias estimate can be viewed as an approximation of this bootstrap bias that only requires 3 times applying the targeted maximum likelihood estimator to a sample of size n * 2/3:

$$B(P_n)(\delta )=E_{B_{n3}}\{\Psi ({\widehat{Q}}_{\delta }^{*}(P_{n,B_n}^0))-\Psi ({\widehat{Q}}_{\delta }^{*}(P_n)\},$$

where B_n3 denotes the 3-fold cross-validation scheme.

If d = 1, then we will add to the variance term in the previous section the squared bias B(P_n)² to create a MSE-term. If d > 1, then in our proposal below we will construct an appropriate function of B(P_n) representing the analogue of the variance term (4):

$$b{(P_n)}^2(\delta )\equiv \sum _j{(a_j^{\top }B(P_n)(\delta ))}^2.$$

Additional rationale behind bias term: To provide further understanding of this kind of bias estimate B(P_n), we note the following. Let Ψ̂(P_n) be an estimator of its target Ψ̂(P₀), where it plays the role of the δ-specific targeted maximum likelihood estimator $\Psi ({\widehat{Q}}_{\delta }^{*}(P_n))$. The fundamental assumption allowing statistical inference for Ψ̂(P₀) is the assumption of asymptotic linearity:

$$\widehat{\Psi }(P_n)-\widehat{\Psi }(P_0)=(P_n-P_0)D(P_0)+R(P_n),$$ (5)

where D(P₀) is the influence curve of the estimator, and R(P_n) is the remainder. The asymptotic linearity assumption now assumes that $R(P_n)=o_P(1/\sqrt{n})$.

The representation (5) of the mapping P_n → Ψ̂(P_n) implies for any cross-validation scheme B_n

$$\begin{array}{l}B(P_n)=E_{B_n}\widehat{\Psi }(P_{n{B}_n}^0)-\widehat{\Psi }(P_n)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E_{B_n}\{\widehat{\Psi }(P_{n{B}_n}^0)-\widehat{\Psi }(P_0)\}-\{\widehat{\Psi }(P_n)-\widehat{\Psi }(P_0)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E_{B_n}\{(P_{n{B}_n}^0-P_0)D(P_0)+R(P_{n,B_n}^0)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\{(P_n-P_0)D(P_0)+R(P_n)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E_{B_n}R(P_{n,B_n}^0)-R(P_n),\end{array}$$

where we use that $E_{B_n}{P}_{n,B_n}^{0}D(P_0)=P_{n}D(P_0)$. Thus, our proposed bias estimate B(P_n) equals, for any cross-validation scheme, an average difference of the remainder applied to a subsample of size n(1–p) and the full sample of size n. Therefore, one can conclude that this term will be very sensitive to a large remainder (e.g., second order terms) in the asymptotic linearity expansion (5).

5.1.3. MSE of targeted maximum likelihood estimator relative to its δ-limit

If d = 1, then we define the MSE term as

$$MSE(P_n)(\delta )=\frac{{\sigma }^2(P_n)(\delta )}{n}+B{(P_n)}^2.$$

If d > 1, then we assume that we are provided with a user-specified d × d symmetric positive definite matrix ρ, so that the square root of this matrix ρ^1/2 exists. Our MSE term will represent the expectation of the Euclidean norm of ρ^1/2(Ψ̂ – ψ), or equivalently, the expectation of (Ψ̂ – ψ)^⊤ρ(Ψ̂ – ψ). One concrete proposal is to set ρ^1/2 equal to the square root of the inverse of an estimate of the correlation matrix of the asymptotic covariance matrix of $\sqrt{n}(\widehat{\Psi }-\psi )$, so that the linearly transformed vector has uncorrelated components.

Let a_j be the j-th row of the matrix ρ^1/2, j = 1, . . . , d. The wished MSE term is now the sum of the MSEs of the linear combination $a_j^{\top }\widehat{\Psi }$. Therefore, the MSE term is represented as

$$MSE(P_n)(\delta )=\frac{1}{n}\sum _j{a}_j^{\top }\Sigma (P_n)(\delta )a_j+n\{a_j^{\top }B(P_n)(\delta )\}.$$

This is equivalent to defining a variance term

$$\frac{{\sigma }^2(P_n)(\delta )}{n}=\frac{1}{n}\sum _j{a}_j^{\top }\Sigma (P_n)(\delta )a_j,$$

a bias term

$$b(P_n)(\delta )=\sum _j\{a_j^{\top }B(P_n)(\delta )\},$$

and defining

$$MSE(P_n)(\delta )=\frac{{\sigma }^2(P_n)(\delta )}{n}+{\{b(P_n)(\delta )\}}^2.$$

5.2. Targeted loss functions relying on a collaborative estimate of censoring mechanism

Let D^*(Q₀, g₀, ψ₀) be the efficient influence curve at dP₀ = Q₀g₀ for the parameter Ψ : $\mathcal{M}$ → IR. Consider a set of estimators Q̂^k(P_n) that are all more nonparametric than an initial estimator Q̂⁰(P_n). Let ĝ⁰ be a collaborative estimator, relative to the initial estimator Q̂⁰, so that P₀D^*(Q^0*, g⁰, ψ₀) = 0. Since, Q̂^k is more nonparametric than Q̂⁰, it is reasonable to assume that ĝ⁰ is also a collaborative estimator for Q̂^k, so that $P_0{D}^{*}(Q_{g^0}^{k*},\hspace{0.17em}{g}^0,\hspace{0.17em}{\psi }_0)=0$, where now $Q_{g^0}^{k*}$ denotes the limit of the targeted maximum likelihood estimator of Q̂^k using ĝ⁰.

We can use as criterion for selection among Q̂^k, the cross-validated estimated variance of $D^{*}(Q_{g^0}^{k*},\hspace{0.17em}{g}^0,\hspace{0.17em}\Psi (Q_{g^0}^{k*}))$, where $Q_{g^0}^{k*}$ denotes the limit of the targeted maximum likelihood estimator of Q̂^k using ĝ⁰. Of course, this is also a selection among the collaborative targeted maximum likelihood estimators ${\widehat{Q}}_{{\widehat{g}}^0}^{k*}$.

By our asymptotic linearity theorem, this selection among Q̂^k corresponds with minimizing the variance of the influence curve of the (collaborative) targeted maximum likelihood estimators $\Psi ({\widehat{Q}}_{{\widehat{g}}^0}^{k*})$ based on initial estimator Q̂^k using the collaborative estimator ĝ⁰. The crucial assumption is that ĝ⁰ is indeed a collaborative estimator estimating a true g₀ that involves enough adjustment, so that $P_0{D}^{*}(Q_{g^0}^{k*},\hspace{0.17em}{g}^0,\hspace{0.17em}{\psi }_0)=0$. However, this assumption is needed for construction of estimators of ψ₀, and is already relying on weaker assumption than double robustness.

This criterion can now be used as the preferred loss function in our template for the collaborative targeted maximum likelihood estimator to build the candidate censoring mechanism estimators. It will require obtaining a single collaborative estimator ĝ⁰ after having obtained the initial estimator: for example, one could carry out a dimension reduction based on improved fits relative to initial estimator, and estimate it with a super learner only adjusting for the selected variables.

We already discussed that the same criterion can be used to select among any set of candidate collaborative targeted maximum likelihood estimators ( ${\widehat{Q}}_{{\widehat{g}}^k}^{k*}$, ĝ^k), relying on collaborative estimators ĝ^k, so that P₀D^*(Q̂^k*, g^k, ψ₀) = 0:

$$k_n=\text{arg}\underset{k}{\text{min}}{E}_{B_n}{P}_{n,B_n}^1{D}^{*2}({\widehat{Q}}^{k*}(P_{n,B_n}^0),{\widehat{g}}^k(P_{n,B_n}^0),\Psi ({\widehat{Q}}^{k*}(P_n)).$$

However, the above only relies on a single collaborative estimator ĝ⁰, and is therefore particularly suitable for building the second stage within the collaborative targeted MLE template.

5.3. Targeted loss functions incorporating a sequence of increasingly nonparametric estimators of censoring mechanism

Consider an initial estimator Q̂. We wish to develop a criterion to select among candidate estimators of Q₀ that are more nonparametric than Q̂, such as estimators using Q̂ as offset. A special application of the loss function presented in this subsection is that Q̂ is empty. Consider a sequence of increasingly nonparametric estimators ĝ_j, j = 1, . . . , J, of g₀, which could be based on Q̂: For example, they might be based on a dimension reduction which has as goal to estimate Q₀ – Q̂. Consider the following hypothetical criterion for a candidate Q:

$$Q\to \sum _{j=1}^{J}w(j){\Vert P_{0}D*(Q,{\widehat{g}}_j(P_0))\Vert }^2,$$

for a list of weights/scalars (w(j) : j = 1, . . . , J), where ‖ · ‖ denotes a possibly weighted Euclidean norm applied to the vector of the form P₀D^*(Q, g).

Firstly, if Q = Q₀, then the criterion is minimized. In addition, let j₀(Q) be such that P₀D^*(Q, ĝ_j(P₀)) = 0 for all j ≥ j₀. Since this mean zero property holds if ĝ_j solves a score implied by Q – Q₀, it follows that the closer Q is to Q₀ the more j-specific terms within this sum are close to zero. Finally, by the fact that D^* is a gradient of the path-wise derivative of the target parameter Ψ, for j ≥ j₀, we have that P₀D^*(Q, ĝ_j(P₀)) ≈ Ψ(Q) – ψ₀ (either exact, or in first order), which shows that this criterion also targets ψ₀ (see van der Laan and Robins (2003), Section 1.4).

The cross-validated analogue of this criterion is given by

$$D_n({\widehat{Q}}^k)\equiv E_{B_n}\sum _{j=1}^{J}w(j){\Vert P_{n,B_n}^{1}D*({\widehat{Q}}^k(P_{n,B_n}^0),{\widehat{g}}_j(P_n))\Vert }^2.$$

If ψ₀ is one dimensional, a sensible choice of weights are given by the inverse of the variance of the empirical means, so that it downweights the noisy j-specific signals:

$$w{(j)}^{-1}=P_{n,B_n}^1{\{D*({\widehat{Q}}^k(P_{n,B_n}^0),{\widehat{g}}_j(P_n))\}}^2,$$

and makes the criterion D_n() unit free. Analogues of such weighting can be obtained for multi-dimensional ψ₀ as well, and are recommended.

One can add this criterion to a valid loss function such as the log-likelihood criterion L(Q̂^k), giving a more targeted loss function

$$L*({\widehat{Q}}^k)\equiv L({\widehat{Q}}^k)+D_n({\widehat{Q}}^k).$$

The additional term D_n preserves the validity of the loss function L (i.e., its minimum still identifies Q₀), while it makes the selection targeted towards ψ₀. One can add both D_n as well as the above presented MSE-penalty, where the latter is asymptotically negligible but important in sparse data (w.r.t. ψ₀) situations.

6. Example: Targeted maximum likelihood estimation of the marginal structural model

Suppose we observe O = (W, A, Y = Y (A)), where W are baseline covariates, A is a discrete treatment, and Y is a subsequently measured outcome. It is assumed that A is realized in response to the realization of W, and Y is realized in response to both W and A. The full data structure on the experimental unit is X = (W, (Y (a) : a)), so that A represents the missingness variable for the missing data structure O on X. We assume the randomization assumption: g₀(a | X) = P₀(A = a | X) = P₀(A = a | W).

Consider a marginal structural model for the full data distribution

$$E_0(Y(a)|V)=m(a,V|{\beta }_0)$$

that models the causal effect of a treatment intervention A = a on the outcome Y. For example, one might assume a simple linear model m(a, V | β₀) = β₀(a, V, aV).

Since it is often unreasonable to assume such a parametric form, but such parametric forms can still provide very meaningful projections of the true causal curve, we consider the nonparametric extensions of the parameter β₀:

$${\Psi }_h(P_0)=\underset{\beta }{\text{argmin}}{E}_{P_0}\sum _{a}h(a,V){(Q_0(a,W)-m(a,V|\beta ))}^2,$$

where Q₀(a, w) = E₀(Y | A = a, W). We have that Ψ_h(P₀) represents a projection of E₀(Y (a) | V) onto the working model m(| β₀). Specifically,

$${\Psi }_h(P_0)=\underset{\beta }{\text{argmin}}{E}_{P_0}\sum _{a}h(a,V){(E(Y(a)|V)-m(a,V|\beta ))}^2.$$

In particular, if E₀(Y (a) | V) = m(a, V | β₀), then for each h we have Ψ_h(P₀) = β₀. Without the randomization assumption and consistency assumption, we can interpret Ψ_h(P₀) as the same projection, but E(Y (a) | V) = E(E(Y | A = a, W) | V) now represents a (non-causal) dose response curve of the effect of A on Y that controls for the measured confounders W.

We note that this nonparametric extension only depends on P₀ through the conditional mean of Y, given A, W, and the marginal distribution of W. For simplicity, we will also use the notation Ψ_h(Q₀), where Q₀ now denotes both the marginal distribution of W and the conditional distribution of Y , given A, W.

The efficient estimating function for this nonparametric extension Ψ_h of β₀ is given by:

$$\begin{array}{l}{D}_h(P_0)(O)=\frac{h_1(A,V)}{g_0(A|W)}(Y-Q_0(A,W))\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _a{h}_1(a,V)(Q_0(a,W)-m(a,V|{\Psi }_h(P_0)),\end{array}$$

where $h_1(a,\hspace{0.17em}V)=h(a,\hspace{0.17em}V)\frac{d}{d\psi }m(a,\hspace{0.17em}V|\psi )$. We will assume that h₁(A, V) = d/dψ₀m(A, V | ψ₀)h(A, V) is chosen so that h₁ does not depend on ψ₀, which is easily arranged for the case that m is linear in ψ and that m is logistic linear. For example, if we use the linear form (1, a, V, aV), then, if m is linear, then we can choose h₁ = d/dψ₀m(A, V | ψ₀)g(A | V) = ((1, A, V, AV)g(A | V), and, if m is logistic linear, then we can choose h₁ = d/dψ₀m(A, V | ψ₀)/(m(1 – m)(A, V | ψ₀))g(A | V), which equals (1, A, V, AV)g(A | V), again.

Let $D_h^{*}(P_0)=-c_0^{-1}{D}_h(P_0)$ be the corresponding efficient influence curve obtained by standardizing the efficient estimating function by the negative of the inverse of the derivative matrix c₀ = d/dψ₀E₀D_h(P₀) (noting that D_h(P₀) can indeed be viewed as a function in ψ₀).

If Y is continuous and we use a normal error regression model as a working model, then a targeted maximum likelihood estimator of ψ_h0 can be obtained by adding to an initial estimator Q⁰(A, W) of E₀(Y | A, W) the d-dimensional ε-extension εC_h(g)(A, W), where

$$C_h(g)(A,W)=\frac{h_1(A,V)}{g(A|W)},$$

for some fit g of g₀, and fitting ε with maximum likelihood (i.e., least squares estimation) using Q⁰ as offset. The resulting update Q¹(A, W) is now a first step targeted maximum likelihood estimator. It is also the actual targeted maximum likelihood estimator, since iteration is not resulting in further updates (the clever covariate does not change at a targeted MLE update). One estimates the distribution of W with the empirical distribution. The estimate Q¹ and the empirical distribution of W now yields a substitution estimate of the target parameter ψ_h0. If Y is binary, the same εC_h(g)(A, W) is added on the logit scale, and ε is fitted with maximum likelihood estimation. Again, the targeted maximum likelihood estimator converges in one step.

6.1. Penalized log-likelihood for candidate treatment mechanism fits

Let Q̂(P_n) be an initial regression estimator of Q₀ = E₀(Y | A, W). For a given P_n → ĝ(P_n), let ${\widehat{Q}}_{\widehat{g}}^{*}(P_n)$ be the targeted maximum likelihood estimator corresponding with the covariate C_h(ĝ(P_n)). Let B_n be a cross-validation scheme, and let $P_{n,B_n}^1$ and $P_{n,B_n}^0$ be the empirical distributions of the validation and training sample, respectively, as identified by B_n ∈ {0, 1}ⁿ. Let

$${\widehat{\Sigma }}_{CV}(P_n)(\widehat{g})=E_{B_n}{P}_{n,B_n}^1{D}_h^{*}{({\widehat{Q}}_{\widehat{g}}^{*}(P_{n,B_n}^0),\widehat{g}(P_{n,B_n}^0))}^2$$

be the cross-validated estimate of the covariance matrix of the efficient influence curve at the estimator Q̂ and ĝ. We also consider the empirical estimate of this covariance matrix

$$\widehat{\Sigma }(P_n)(\widehat{g})=P_n{D}_h^{*}{({\widehat{Q}}_{\widehat{g}}^{*}(P_n),\widehat{g}(P_n))}^2.$$

Let

$$\widehat{B}(P_n)(\widehat{g})=E_{B_n}{\widehat{\Psi }}_{\widehat{g}}(P_{n,B_n}^0)-{\widehat{\Psi }}_{\widehat{g}}(P_n)$$

be the bias estimator for the targeted maximum likelihood estimator ${\widehat{\Psi }}_{\widehat{g}}(P_n)={\Psi }_h({\widehat{Q}}_{\widehat{g}}^{*}(P_n))$ obtained by plugging in ${\widehat{Q}}_{\widehat{g}}^{*}(P_n)$ in the parameter mapping Ψ. Here we can use three-fold cross-validation as choice for B_n.

We will penalize the log-likelihood with the an estimate of the following average mean squared error

$$\frac{1}{n}{\sum _{i=1}^{n}E\left(m(a_i,v_i|{\widehat{\Psi }}_{\widehat{g}}(P_n)))-m(a_i,v_i|{\widehat{\Psi }}_{\widehat{g}}(P_0))\right)}^2.$$

This mean squared error can be decomposed as $1/n{\sum }_{i=1}^n\text{Var}(m(a_i,\hspace{0.17em}{v}_i|{\widehat{\Psi }}_{\widehat{g}}(P_n)))$ and $1/n{\sum }_{i=1}^n{\text{Bias}}^2(m(a_i,\hspace{0.17em}{v}_i|{\widehat{\Psi }}_{\widehat{g}}(P_n)))$. The variance terms of this mean squared error can be estimated by

$$\frac{{\sigma }_i^2(\widehat{g})}{n}\equiv \frac{z{(a_i,v_i)}^{\top }\widehat{\Sigma }(P_n)(\widehat{g})z(a_i,v_i)}{n},$$

where

$${z(a_i,v_i)=\frac{d}{d\beta }m(a_i,v_i|\beta )|}_{\beta ={\widehat{\Psi }}_{\widehat{g}}(P_n)}.$$

We keep open the option that one uses either the cross-validated covariance matrix Σ̂_CV (P_n) or the empirical covariance matrix Σ̂(P_n).

The bias terms of this mean squared error can be estimated as

$$B_i(\widehat{g})\equiv E_{B_n}m(a_i,v_i|{\widehat{\Psi }}_{\widehat{g}}(P_{n,B_n}^0))-m(a_i,v_i|{\widehat{\Psi }}_{\widehat{g}}(P_n)).$$

If m is linear in β, then this reduces to

$$B_i(\widehat{g})=m(a_i,v_i|B(P_n)).$$

Thus, we obtain the following mean squared error estimate for the targeted maximum likelihood estimator Ψ̂_ĝ(P_n) for a given g-estimator:

$$\widehat{MSE}(P_n)(\widehat{g})\equiv \frac{1}{n}\sum _{i=1}^n\left\{\frac{{\sigma }_i^2(\widehat{g})}{n}+B_i{(\widehat{g})}^2\right\}.$$

We suggest that the penalized log-likelihood could also only be penalized by the empirical variance component of the MSE. Therefore, we also define

$${\sigma }^2(P_n)(\widehat{g})\equiv \frac{1}{n}\sum _{i=1}^n\frac{{\sigma }_i^2(\widehat{g})}{n}.$$

Consider now the following two penalized log-likelihood criterions for ĝ, given the initial estimator Q̂⁰:

$$L(\widehat{g}|{\widehat{Q}}^0)=\frac{1}{n}\sum _{i=1}^n{(Y_i-{\widehat{Q}}_{\widehat{g}}^{*}(P_n)(W_i,A_i))}^2+\widehat{MSE}(P_n)(\widehat{g}),$$

or

$$L(\widehat{g}|{\widehat{Q}}^0)=\frac{1}{n}\sum _{i=1}^n{(Y_i-{\widehat{Q}}_{\widehat{g}}^{*}(P_n)(W_i,A_i)))}^2+{\sigma }^2(P_n)(\widehat{g}).$$

For Y binary, the RSS is replaced by the log-likelihood of Y , given A, W.

We will use the penalized log-likelihood as loss function to build the candidate treatment mechanism estimators, according to the template for the collaborative targeted MLE in Section 2.

6.2. Algorithm for estimating the treatment mechanism based on penalized log-likelihood

Given any candidate adjustment set W^* ⊂ W, let an estimator ĝ(P_n)(W^*) of g₀(A | W^*) be specified. This allows us to define a criterion in candidate adjustment sets W^*, given the current estimator Q̂:

$$L(W*|\widehat{Q})\to L(\widehat{g}(P_n)(W*)|\widehat{Q}).$$

Thus, one can evaluate/score any given adjustment set W^* with L(W^* | Q̂).

Given Q̂, one can now use this empirical criterion in adjustment sets to construct an estimator of g₀(Q̂) with a greedy type algorithm maximizing over a set of candidate adjustment sets. One starts with the empty adjustment set and selects the best addition move among a set of candidate addition moves based on the criterion. One iterates this process until there does not exist an addition move that improves the criterion. More aggressive greedy algorithms can be implemented as well, as with any machine learning algorithm that is based on iterative local maximization of an empirical criterion. One could apply this algorithm to candidate adjustments sets that have a certain size or entropy for the corresponding ĝ(P_n)(W^*).

Alternatively, one creates a sequence of nested (increasing in size) adjustment sets $W_j^{*}$, j = 1, . . . , J, for each $W_j^{*}$ one obtains a particular estimator ĝ_j(P_n) of $g_0(A|W_j^{*})$ (e.g., using super learning), and maximizes the penalized log-likelihood criterion over all these J adjustment sets.

In our algorithm in the next subsection defining the sequence of C-TMLEs we apply this greedy algorithm to candidate estimators that are more nonparametric than the selected estimator of g₀ in the previous step.

6.3. Iteration to obtain sequence of targeted maximum likelihood estimators indexed by increasingly non-parametric estimators of treatment mechanism

Given an initial estimator Q̂ of E(Y | A, W) and a corresponding estimator ĝ(Q̂) defined above, sometimes denoted with ĝ, we define a resulting targeted maximum likelihood estimator

$${\widehat{Q}}_g^{*}(P_n)=\widehat{Q}(P_n)+{\epsilon }_{n}h(\widehat{g}(\widehat{Q})(P_n)),$$

where ε_n is the least squares estimator of the regression coefficient ε treating Q̂(P_n) as offset and h(ĝ(Q̂)(P_n)) as covariate. We can define this as a first step targeted maximum likelihood estimator based on an initial Q̂(P_n), and corresponding censoring mechanism estimator ĝ(Q̂)). Let’s denote this operation as:

$${\widehat{Q}}^1(P_n)=\widehat{Q}(P_n)+{\epsilon }_h^{1}h(\widehat{g}(\widehat{Q})(P_n)).$$

This process can now be iterated by replacing Q̂(P_n) by this update Q̂¹(P_n):

$${\widehat{Q}}^2(P_n)={\widehat{Q}}^1(P_n)+{\epsilon }_h^{2}h(\widehat{g}({\widehat{Q}}^1)(P_n)),$$

where we require that the next censoring mechanism estimator ĝ(Q̂¹)(P_n) is obtained with the same algorithm as presented in above subsection, but now maximizing over candidate estimators that are more nonparametric than the previously obtained ĝ(Q̂)(P_n).

In general, we define the k-th step of this targeted maximum likelihood estimator as

$${\widehat{Q}}^k(P_n)={\widehat{Q}}^{k-1}(P_n)+{\epsilon }_h^{k}h(\widehat{g}({\widehat{Q}}^{k-1})(P_n)),$$

where ĝ(Q̂^k−1)(P_n) involves maximizing over more nonparametric candidate estimators than ĝ(Q̂^k–2)(P_n).

This algorithm results in a sequence of k-th step collaborative targeted maximum likelihood estimators Ψ(Q̂^k(P_n)) of ψ₀, and corresponding increasingly nonparametric censoring mechanism estimators ĝ^k(P_n) (i.e., ĝ(Q̂^k–1)(P_n) in above notation), k = 1, . . . , K.

We could also have defined candidate targeted maximum likelihood estimators using a forward selection algorithm each time finding the best next term to add in the treatment mechanism, so that k denotes the number of terms included in ĝ^k. In that case, k corresponds with the size of the model for ĝ^k, and the targeted MLE step would be carried out when needed in order to guarantee an increase in either the penalized or non-penalized log-likelihood fit of Q̂^k, as described in our general template for collaborative targeted maximum likelihood estimation in Section 2.

6.4. Collaborative TMLEs

If the initial estimator Q̂ is indexed by a choice δ₁ and the choice of algorithm ĝ(Q̂) is indexed by a δ₂, then, for each δ₁, δ₂, this results in candidate k-th step collaborative targeted maximum likelihood estimators $P_n\to {\widehat{Q}}_{{\delta }_1,{\delta }_2}^k(P_n)$, corresponding treatment mechanism estimators $P_n\to {\widehat{g}}_{{\delta }_2}^k(P_n)$, and corresponding $P_n\to \Psi ({\widehat{Q}}_{{\delta }_1,{\delta }_2}^k(P_n))$ targeted maximum likelihood estimators of ψ₀, indexed by k.

For each δ₁, δ₂, in order to select among these candidate targeted maximum likelihood estimators indexed by k, we use the cross-validated penalized log-likelihood defined as:

$$\begin{array}{l}L(k,{\delta }_1,{\delta }_2)=E_{B_n}{P}_{n,B_n}^1{\left(Y-{\widehat{Q}}_{{\delta }_1,{\delta }_2}^k(P_{n,B_n}^0)(W,A)\right)}^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\widehat{MSE}}_{CV}(P_n)({\widehat{Q}}_{{\delta }_1,{\delta }_2,}^k{\widehat{g}}_{{\delta }_2}^k).\end{array}$$

This results now in candidate (δ₁, δ₂)-specific collaborative targeted maximum likelihood estimators ${\widehat{Q}}_{{\delta }_1,{\delta }_2}^{*}$, with corresponding initial estimator Q̂_δ1 and collaborative treatment mechanism estimator ĝ_δ1,δ2 (note the choice of k is now a function of δ₁, δ₂ so that also the collaborative estimator ĝ is indexed by these choices).

6.5. Selection among candidate collaborative targeted maximum likelihood estimators

We could select δ₁, δ₂ by minimizing the same cross-validated penalized log-likelihood, e.g., by simply simultaneously minimizing the above criterion over the triplets (k, δ₁, δ₂). Alternatively, we could employ empirical efficiency maximization for all these candidate collaborative targeted maximum likelihood estimators that are assumed to be asymptotically linear with influence curve the efficient influence curve plus a contribution from the collaborative estimator of g₀, as stated in our asymptotic linearity theorem. Thus, by ignoring this latter contribution to the influence curve, we could also select δ₁, δ₂ as the minimizer of the sum of the variances of the components of the efficient influence curve of ψ₀: (with δ = (δ₁, δ₂))

$${\delta }_n=\text{arg}\underset{\delta }{\text{min}}\sum _{j=1}^d{P}_n{D}_j^{*}{({\widehat{Q}}_{\delta }^{*},{\widehat{g}}_{\delta })}^2.$$

Other criteria based on the vector-efficient influence curve could be considered as well.

6.6. Statistical inference based on CLT

The resulting collaborative targeted maximum likelihood estimator Q_n = Q̂^*(P_n) and corresponding g_n = ĝ(P_n) solve the efficient influence curve equation 0 = P_nD^*(Ψ(Q_n), g_n, Q_n), so that ψ_n = Ψ(Q_n) can be analyzed with our asymptotics theorem, and inference can be based on the influence curve. So we could estimate the covariance matrix as

$${\Sigma }_n=E_{B_n}{P}_{n,B_n}^{1}D*{(\widehat{Q}*(P_{n,B_n}^0),\widehat{g}*(P_{n,B_n}^0))}^2,$$

where one should include the g_n-component to obtain more accurate inference. Statistical inference would be based on the normal working model ψ_n ∼ N(ψ₀, Σ_n) to construct confidence intervals, confidence bands, p-values, and possible multiple testing adjusted p-values.

7. Discussion

For most data sets little to no knowledge is available about the data generating distribution. Consequently, the true model is a large infinite dimensional semi-parametric model. In such models many data adaptive approaches can be considered for fitting the true distribution of the data, based on different approximation function spaces, different searching strategies for maximizing an empirical criterion (such as the empirical log-likelihood) over these spaces, and different methods for selecting the fine tuning parameters indexing the function spaces and search strategies. Depending on the true data generating distribution, these algorithms will have very different levels of performance in approximating the true data generating distribution. As a consequence, cross-validation based super learning should be employed to find the best weighted combination among a large user supplied set of candidate estimators of the true data generating distribution. The user has an option to select the wished loss function. The oracle property of the cross-validation selector (van der Vaart et al. (2006), van der Laan et al. (2006)) teaches us that the super learner will asymptotically perform exactly as well, w.r.t. the loss-based (e.g., Kullback-Leibler) dissimilarity measure, as the best weighted combination of the candidate algorithms optimized for each data set. A crucial assumption is that the loss function used in this super learning methodology is uniformly bounded in all the candidate estimators. This could be viewed as a semi-parametric model assumption, and it is essential for robustness of the resulting estimator against outliers. It can be arranged by bounding the candidate estimators so that the loss function remains bounded.

The super learner fit represents a best fit for the purpose of estimation of the whole distribution of the data w.r.t. the loss-function specific dissimilarity, so that the bias-variance trade-off is not targeted (enough) w.r.t. the parameter of interest. Overall, the resulting estimate it overly biased for the smooth target parameter.

Therefore, our methodology involves a second targeted modification of the first stage super learner fit that aims to reduce the bias w.r.t the target parameter, while simultaneously increasing the likelihood fit. A single fluctuation function that would yield asymptotic optimal bias reduction as defined by the efficient influence curve of the target parameter is determined. This fluctuation function needs to have a score-vector at zero fluctuation whose linear span includes the efficient influence curve of the target parameter. This fluctuation function depends on an unknown nuisance parameter of the data generating distribution, such as a censoring mechanism.

In one particular embodiment of our C-TMLE, we define an iterative sequence of subsequent fluctuations, starting with the initial super learner fit, where the subsequent fluctuation functions are estimated with increasingly nonparametric estimates of the nuisance parameter, including a final fully non-parametrically estimated fluctuation function. In addition, by construction, we make sure that for each fluctuation function the nuisance parameter estimator that results in maximal increase in likelihood (or preferred loss function) fit is selected, among the candidate nuisance parameter estimators that are more nonparametric than the one selected at previous fluctuation function. In this way, we arrange that most of the targeted bias reduction occurs in the first few fluctuations. The actual number of times we carry out the subsequent update is selected with likelihood based cross-validation.

Essentially, we try to move towards the asymptotically optimal bias reduction (identified by the true nuisance parameter/censoring mechanism used in the data generating distribution) along a sequence of targeted bias reduction steps, but we stop moving towards this asymptotically optimal bias reduction when it results in a loss of likelihood fit as measured by the cross-validated log-likelihood. In general, our template for C-TMLE allow a fine sequence of nested targeted bias reduction steps (i.e., a fine sequence of candidate second stage estimators indexed by increasingly nonparametric nuisance parameter estimators) whose fits contain this set of candidate-fits as a subsequence, thereby potentially providing an additional improvement in practical performance of the resulting C-TMLE.

Theoretical results teach us that this push towards the asymptotically optimal bias reduction takes into account how well the initial estimator approximates the true distribution, by giving preference to targeted bias reduction steps that improve the log-likelihood fit using the initial estimator as off-set. As a consequence, the C-TMLE is able to avoid selecting irrelevant or harmful (w.r.t. relevant factor of density) fits of the nuisance parameter, even though such fits might improve the overall fit of the nuisance parameter. That is, the fit of the nuisance parameter is targeted towards our primary goal, the parameter of interest.

Specifically, we establish a general asymptotic linearity theorem for collaborative targeted maximum likelihood estimators, which provides us with the influence curve of our estimator, and thereby statistical inference. Fortunately, the influence curve happens to be equal to the efficient influence curve at the collaborative nuisance parameter estimator (its limit) plus a contribution of the nuisance parameter estimator as an estimator of its limit, providing immediate variance estimates. Gains in efficiency, resulting in possible super efficiency, are obtained by estimating the nuisance parameter collaboratively, in relation to the initial estimator. An inspection of the efficient influence curve allows us to precisely define the sufficient and minimal term H(g₀, Q–Q₀) one needs to adjust for in g₀ to achieve the wished full bias reduction. We propose to estimate this term and force adjustment by this term in the candidate censoring mechanism estimators within the C-TMLE procedure, without relying on its correct specification, thereby preserving and only enhancing the double robustness of the C-TMLE.

The targeted maximum likelihood estimator relies itself on maximizing an empirical mean of a loss function over a fluctuation function, and the derivative of this empirical criterion at zero fluctuation needs to be the empirical mean of the efficient influence curve at the estimator to be fluctuated. We refer to this loss as the log-likelihood loss, but it needs to be understood that this choice can already be targeted (e.g,. van der Laan (2008b)) in the sense that it is typically implied by the efficient influence curve of the target parameter (e.g, one would not use a likelihood based on factors that are not needed to evaluate the target parameter). In addition, we propose to replace this log-likelihood by a penalized log-likelihood, where the penalty is scaled appropriately, has negligible contribution for nicely identifiable target parameters, but blows up for fits that result in extremely variable or biased estimators of the parameter of interest. Even though the penalty’s effect on the Kullback-Leibler dissimilarity is asymptotically negligible for identifiable parameters, for parameters that are borderline identifiable, this penalty can yield dramatic additional finite sample improvements to the C-TMLE. In essence, it builds in a sensible robustness of the resulting C-TMLE as an estimator of the target parameter.

Given the initial estimator, the candidate censoring mechanism estimators, and the corresponding sequence of targeted MLE indexed by these increasingly nonparametric estimators of the censoring mechanism, the log-likelihood or penalized log-likelihood is used for cross-validation selection of the depth of the bias reduction (i.e, for selection among these candidate targeted MLEs) in the C-TMLE algorithm. However, a preferred loss function can be used to build the initial estimator, to build the candidate censoring mechanism estimators, and to select among different collaborative C-TMLEs. In particular, one could use the penalized log-likelihood as preferred loss function.

We propose as a possibly more targeted selection criterion the cross-validated variance of the square of the efficient influence curve (e.g., if target parameter is one-dimensional), where a collaborative estimator is used for the nuisance parameter (censoring mechanism) in the efficient influence curve: i.e. we propose as loss function for a candidate Q the square of the efficient influence curve at its targeted version, using a collaborative estimator of g₀. Indeed, $E_0{D}^{*2}(Q_{g_0}^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}\Psi (Q_{g_0}^{*})=E_0{D}^{*2}(Q_{g_0}^{*},\hspace{0.17em}{g}_0,\hspace{0.17em}{\psi }_0)$ is a variance of a collaborative double robust estimator of ψ₀, indexed by initial estimator Q, using known g₀, and is thereby a valid and sensible loss function. In order to also take into account that g₀ is estimated, one could also minimize the variance of the actual influence curve of the collaborative double robust targeted MLE using Q as initial and using g_n as collaborative estimator. This would imply the same square of influence curve, but now the influence curve equals D^* plus an contribution from estimation of g₀.

Finally, we are also able to select a targeted loss function for g₀ in the CTMLE template, by making its loss-based dissimilarity a measure of goodness of fit of the g₀-specific fluctuation function in which the estimator of g₀ is used.

The collaborative double robust maximum likelihood estimator utilizes 1) loss-based super learning to obtain the best initial estimator of Q₀ (grounded by theory for cross-validation selector), 2) loss-based super learning to generate best estimators of candidate censoring mechanisms adjusting for increasingly large adjustment sets (grounded by theory for cross-validation selector), 3) specification of loss functions that target the needed Q₀, g₀ for identification of the efficient influence curve, 4) targeted maximum likelihood estimation along a fluctuation function using such a censoring mechanism estimator to remove bias for target parameter (grounded by theory for targeted maximum likelihood estimation), 4) Q₀-(penalized)-likelihood based cross-validation to select among such candidate censoring mechanism estimators, and thereby obtain the collaborative estimator of the censoring mechanism for the fluctuation function that removes the bias, while avoids unnecessary loss in variance (grounded by oracle results for cross-validation, collaborative double robustness, and our asymptotic linearity theorem), 5) efficient influence curve based dimension reductions (the minimal sufficient covariate) to be included in the censoring mechanism estimators that allow for effective bias reduction in the T-MLE, if correctly specified, (and will not harm the collaborative double robustness if not) (grounded by theory on efficient influence curve representation and our collaborative double robustness theorem), 6) efficient influence curve based loss function for Q₀ to build more targeted candidate censoring mechanism estimators 7) efficient influence curve based loss functions for Q₀ to make the initial estimator more targeted, to make the selection among candidate C-TMLE more targeted, resulting in smaller asymptotic variance of the resulting C-TML estimator of the target parameter (grounded by empirical efficiency maximization theory, and our asymptotic linearity theorem for C-TMLE).

To summarize, this article provides a template for loss-based adaptive (super) efficient estimators in semiparametric models that are targeted towards a particular target feature of the distribution of the data, and for which statistical inference is available.