Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution

Abstract

We demonstrate lensfree holographic microscopy on a chip to achieve ~0.6 µm spatial resolution corresponding to a numerical aperture of ~0.5 over a large field-of-view of ~24 mm². By using partially coherent illumination from a large aperture (~50 µm), we acquire lower resolution lensfree in-line holograms of the objects with unit fringe magnification. For each lensfree hologram, the pixel size at the sensor chip limits the spatial resolution of the reconstructed image. To circumvent this limitation, we implement a sub-pixel shifting based super-resolution algorithm to effectively recover much higher resolution digital holograms of the objects, permitting sub-micron spatial resolution to be achieved across the entire sensor chip active area, which is also equivalent to the imaging field-of-view (24 mm²) due to unit magnification. We demonstrate the success of this pixel super-resolution approach by imaging patterned transparent substrates, blood smear samples, as well as Caenoharbditis Elegans.

1. Introduction

Digital holography has been experiencing a rapid growth over the last few years, together with the availability of cheaper and better digital components as well as more robust and faster reconstruction algorithms, to provide new microscopy modalities that improve various aspects of conventional optical microscopes [1–16]. Among many other holographic approaches, Digital In-Line Holographic Microscopy (DIHM) provides a simple but robust lensfree imaging approach that can achieve a high spatial resolution with e.g., a numerical aperture (NA) of ~0.5 [13]. To achieve such a high numerical aperture in their reconstructed images, conventional DIHM systems utilize a coherent source (e.g., a laser) that is filtered by a small aperture (e.g., <1-2 µm); and typically operate at a fringe magnification of F > 5-10, where F = (z₁+z₂)/z₁; z₁ and z₂ define the aperture-to-object and object-to-detector vertical distances, respectively. This relatively large fringe magnification reduces the available imaging field-of-view (FOV) proportional to F ².

In an effort to achieve wide-field on-chip microscopy, our group has recently demonstrated the use of unit fringe magnification (F~1) in lensfree in-line digital holography to claim an FOV of ~24 mm² with a spatial resolution of < 2 µm and an NA of ~0.1-0.2 [15,16]. This recent work used a spatially incoherent light source that is filtered by an unusually large aperture (~50-100µm diameter); and unlike most other lensless in-line holography approaches, the sample plane was placed much closer to the detector chip rather than the aperture plane, i.e., z₁>>z₂. This unique hologram recording geometry enables the entire active area of the sensor to act as the imaging FOV of the holographic microscope since F~1. More importantly, there is no longer a direct Fourier transform relationship between the sample and the detector planes since the spatial coherence diameter at the object plane is much smaller than the imaging FOV. At the same time, the large aperture of the illumination source is now geometrically de-magnified by a factor that is proportional to M=z₁/z₂ which is typically 100-200. Together with a large FOV, these unique features also bring simplification to the set-up since a large aperture (~50µm) is much easier to couple light to and align [15,16].

On the other hand, a significant trade-off is also made in this recent approach: the pixel size now starts to be a limiting factor for spatial resolution since the recorded holographic fringes are no longer magnified. Because the object plane is now much closer to the detector plane (e.g., z₂ ~1mm), the detection NA approaches ~1. However, the finite pixel size at the sensor chip can unfortunately record holographic oscillations corresponding to only an effective NA of ~0.1-0.2, which limits the spatial resolution to <2µm.

In this work, we remove this limitation due to the pixel size to report lensfree holographic reconstruction of microscopic objects on a chip with a numerical aperture of ~0.5 achieving ~0.6 µm spatial resolution at 600 nm wavelength over an imaging FOV of ~24 mm². We should emphasize that this large FOV can scale up without a trade-off in spatial resolution by using a larger format sensor chip since in our scheme the FOV equals to the active area of the detector array. To achieve such a performance jump while still using a partially coherent illumination from a large aperture (~50 µm) with unit fringe magnification, we capture multiple lower-resolution (LR) holograms while the aperture is scanned with a step size of ~0.1mm (see Fig. 1 ). The knowledge of this scanning step size is not required at all since we numerically determine the shift amount without any external input, using solely the recorded raw holograms, which makes our approach quite convenient and robust as it automatically calibrates itself in each digital reconstruction process. Because of the effective demagnification in our hologram recording geometry (z₁/z₂ >100), such discrete steps in the aperture plane result in sub-pixel shifts of the object holograms at the sensor plane. Therefore, by using a sub-pixel shifting based super-resolution algorithm we effectively recover much higher resolution digital holograms of the objects that are no longer limited by the finite pixel size at the detector array. Due to the low spatial and temporal coherence of the illumination source, together with its large aperture diameter, speckle noise and the undesired multiple reflection interference effects are also significantly reduced in this approach when compared to conventional high-resolution DIHM systems providing another important advantage.

Fig. 1.

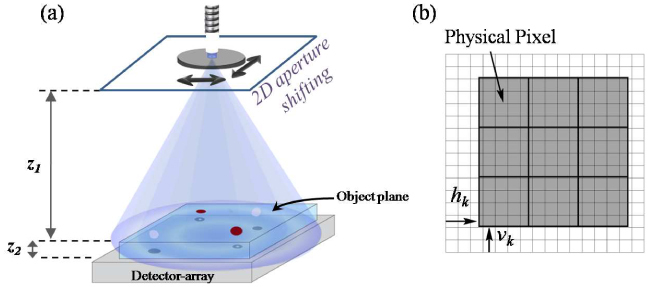
(a) Schematic diagram of our experimental setup. The aperture to object distance is much larger than the object to detector distance (z₁~10 cm, z₂<1mm). A shift of the aperture causes a demagnified shift of the object hologram formed at the detector plane, allowing sub-pixel hologram shifting. (b) Physical pixels captured in a single frame, here marked by bold borders, over imposed on the high-resolution pixel grid. This frame is shifted a distance of h_k horizontally and v_k vertically with respect to a reference frame.

2. Pixel super-resolution in lensfree digital in-line holography by sub-pixel shifting

As discussed in the introduction, with unit fringe magnification and low coherence illumination, our spatial resolution is limited by the pixel size, rather than the detection NA. Therefore, a higher spatial density of pixels is desirable to represent each hologram for reconstruction of higher resolution images. This can in principle be achieved by physically reducing the pixel size at the sensor to e.g., <1µm, which has obvious technological challenges to claim a large FOV. Therefore, in this manuscript we demonstrate the use of a pixel super-resolution approach to digitally claim 6 fold smaller pixel size for representation of each object hologram to significantly improve our spatial resolution over a large FOV achieving an NA of ~0.5.

Specifically, here we increase the spatial sampling rate of the lensfree holograms, and hence improve our spatial resolution by capturing and processing multiple lower-resolution holograms, that are spatially shifted with respect to each other by sub-pixel pitch distances. As an example, we take a 5Mpixel imager that is used to record lensfree digital holograms with a pixel size of ~2.2µm, and effectively convert that to a 180Mpixel imager with a 6 fold smaller pixel size (~0.37µm), that essentially has the same active area (i.e., the same imaging FOV). As will be demonstrated experimentally, this improvement enables a spatial resolution of~0.6 µm, corresponding to a numerical aperture of ~0.5 over a large field-of-view of ~24 mm². We refer to this technique as Pixel Super-Resolution (Pixel SR), to avoid confusion with the recent use of the term “super-resolution” describing imaging techniques capable of overcoming the diffraction limit [17–19]. Various Pixel SR approaches have been previously used in the image processing community to digitally convert low-resolution imaging systems into higher resolution ones, including magnetic resonance imaging (MRI), satellite and other remote sensing platforms, and even X-Ray computed tomography [20–22].

The idea behind Pixel SR is to use multiple lower-resolution images, which are shifted with respect to each other by fractions of the low-resolution grid constant, to better approximate the image sampling on a higher resolution grid. In Fig. 1(b), the physical pixels are shown, bordered by thick lines, as well as the virtual higher resolution grid. For each horizontal shift h_k and vertical shift v_k of the lower-resolution image, the output of each physical pixel is simply a linear combination of the underlying high-resolution pixel values.

To better formulate Pixel SR, let us denote the lower-resolution (LR) images by X_k(n₁,n₂), k = 1,…,p, each with horizontal and vertical shifts h_k and v_k, respectively, and each of size M = N₁×N₂. The high-resolution (HR) image Y(n₁,n₂) is of the size N = LN₁×LN₂, where L is a positive integer. The goal of the Pixel SR algorithm is to find the HR image Y(n₁,n₂) which best recovers all the measured frames X_k(n₁,n₂). The metric for the quality of this recovery is described below. For brevity in our notation, we order all the measured pixels of a captured frame in a single vector X_k = [x_k,1, x_k,2,…, x_k,M], and all the HR pixels in a vector Y = [y₁,y₂,…,y_N]. A given HR image Y implies a set of LR pixel values determined by a weighted super-position of the appropriate HR pixels, such that:

$${\tilde{x}}_{k,i}={\displaystyle \sum _{j=1,\mathrm{...},N}{W}_{k,i,j}(h_k,v_k)\cdot y_j}$$ (1)

where ${\tilde{x}}_{k,i}$ denotes the calculated LR pixel value for a given Y, i = 1,…,M; k = 1,…p and $W_{k,i,j}$ is a physical weighting coefficient. We round all the frame shifts (h_k and v_k) to the nearest multiple of the HR pixel size. Therefore, a given LR pixel value can be determined from a linear combination of L² HR pixels (see Fig. 1). We further assume that the weighting coefficients $W_{k,i,j}$ (for a given k and i) are determined by the 2D light sensitivity map of the sensor chip active area and can be approximated by a Gaussian distribution over the area corresponding to the L ² HR pixels. We should also note here that the spectral nulls of this weighting function can potentially cause aberrations in our imaging scheme for cases in which the object has a high spectral weight near those nulls. This is a well known problem in pixel super-resolution approaches, which could be addressed by multiple measurements as further discussed in [23].

In our Pixel SR implementation, the high-resolution image (Y) is recovered/reconstructed by minimizing the following cost function, C(Y):

$$C(Y)=\frac{1}{2}{\displaystyle \sum _{\begin{array}{l}k=1,\mathrm{...},p\\ i=1,\mathrm{...},M\end{array}}{(x_{k,i}-{\tilde{x}}_{k,i})}^2+\frac{\alpha }{2}(Y_{fil}^T•Y_{fil}^{})}$$ (2)

The first term on the right hand side of Eq. (2) is simply the squared error between the measured low-resolution pixel values and the ones recovered from the virtual high-resolution image (see Eq. (1). Minimizing this term by itself is equivalent to the maximum-likelihood estimation under the assumption of uniform Gaussian noise [20]. This optimization problem is known to be ill-defined and susceptible to high frequency noise. The last term of Eq. (2) is meant to regularize the optimization problem by penalizing high frequency components of the high-resolution image, where Y _fil is a high-pass filtration of the high-resolution image Y, and α is the weight given to those high frequencies. For large α, the final high-resolution image would be smoother and more blurred, while for small α, the resulting image would contain fine details in addition to high frequency noise. In this work, we used α = 1 and a Laplacian kernel for high-pass filtering of Y [21].

As will be detailed in the following sections, our experimental setup handles sub-pixel shifting of lensfree holograms and the above described super-resolution hologram recovery algorithm over a large imaging FOV with ease and robustness due to the large demagnification inherent in its recording geometry.

3. Experimental setup

A schematic diagram of our setup is shown in Fig. 1. We use a spatially incoherent light source (Xenon lamp attached to a monochromator, wavelength: 500-600 nm, spectral bandwidth: ~5nm) coupled to an optical fiber with a core size of ~50μm, which also acts as a large pinhole/aperture. The distance between the fiber end and the object plane (z₁ ~10cm) is much larger than the distance between the object and the detector planes (z₂ ~ 0.75mm). Our detector is a CMOS sensor with 2.2μm×2.2μm pixel size, and a total active area of ~24.4 mm².

The large z₁/z₂ ratio, which enables wide-field lensfree holography and the use of a large aperture size, also makes sub-pixel hologram shifting possible without the need for sub-micron resolution mechanical movement. In other words, the requirements on the precision and accuracy of the mechanical scanning stage are greatly reduced in our scheme. Simple geometrical optics approximations can show that the object hologram at the detector plane can be shifted sub-pixel by translating the illumination aperture parallel to the detector plane. The ratio between the shift of the hologram at the detector plane and the shift of the aperture can be approximated as:

$$\frac{S_{\text{hologram}}}{S_{aperture}}=\frac{z_2}{z_1}\times \frac{n_1}{n_2},$$ (3)

where n₁ = 1 is the refractive index of air, and n₂ = 1.5 is the refractive index of the cover glass before the detector array. For z₁ = 10cm and z₂ = 0.75mm, the ratio between these two shifts become S_hologram/S_aperture ~1/200, which implies that to achieve e.g., 0.5μm shift of the object hologram at the detector plane, the source aperture can be shifted by 200×0.5 = 100μm. In the experiments reported here, we have used an automated mechanical-scanning stage to shift the fiber aperture; and captured multiple holograms of the same objects with sub pixel hologram shifts. In principle, multiple sources separated by ~0.1 mm from each other that can be switched on-off sequentially could also be used to avoid mechanical scanning.

Using Eq. (3), the required aperture shift for a desired sub-pixel hologram shift can be calculated. Since the parameters in Eq. (3) may not be exactly known, and as a consistency check, we independently compute the hologram shifts directly from the captured lower-resolution holograms, using an iterative gradient algorithm (see [21], for example). Therefore, quite importantly hologram shifts to be used in Eq. (2) and Eq. (3) are computed from the raw data, and are not externally input, which makes our approach quite convenient and robust as it automatically calibrates itself in each digital reconstruction process, without relying on the precision or accuracy of the mechanical scanning stage.

4. Experimental results

To quantify the spatial resolution improvement due to Pixel SR, we have fabricated a calibration object consisting of 1μm wide lines etched into a glass cover slide (using focused ion beam milling), with 1μm separation between the lines (see Fig. 3(a) ). This object is a finite size grating, and ideally it is a phase-only object, except the scattering at the walls of the etched regions.

Fig. 3.

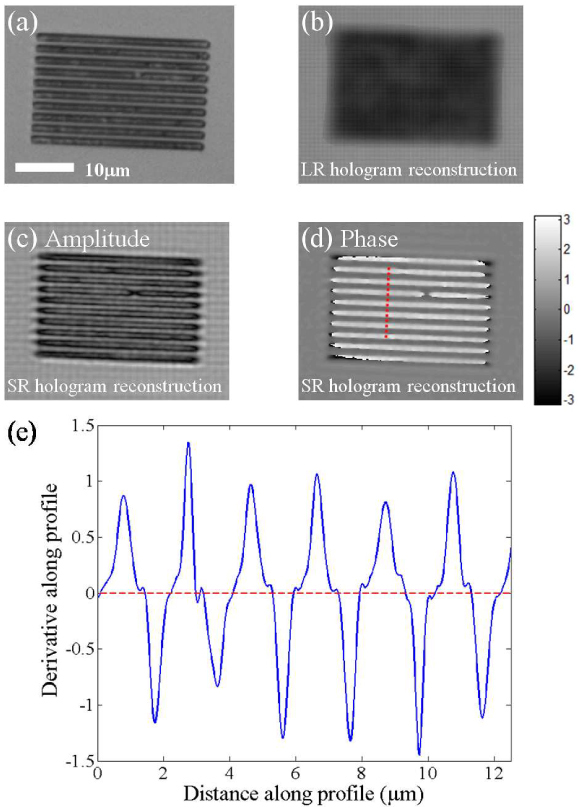
(a) Microscope image of the object captured with a 40X objective lens (NA=0.65). (b) Amplitude reconstruction of the object using a single low-resolution hologram (see Fig. 2(a)). (c) Object amplitude reconstruction using the high-resolution hologram (see Fig. 2(c)) obtained from Pixel SR using 36 LR images. (d) Object phase reconstruction obtained from the same high-resolution hologram using Pixel SR. The object phase appears mostly positive due to phase wrapping. (e) The spatial derivative of the phase profile along the dashed line in pane (d). As explained in the text, this spatial derivative operation yields a train of delta functions with alternating signs, broadened by the PSF, which sets the resolution.

Initially we used L = 6, i.e., we shifted the object holograms by one sixth of a pixel in each direction, for a total of 36 lensfree holograms. Figure 2(a) shows one of these LR holograms captured at the detector. The sub-pixel shift amount of each LR hologram with respect to the first LR hologram is calculated from the raw data without any additional input as shown in Fig. 2(b). The super-resolution hologram (see Fig. 2(c)) is generated by minimizing Eq. (2) using the Conjugate Gradient method [24], incorporating all the captured 36 LR holograms. It is evident that the computed high-resolution hologram now captures the interference fringes which could not be normally recorded with a 2.2μm pixel size. Next, we demonstrate how this super-resolution hologram translates to a high-resolution object reconstruction.

Fig. 2.

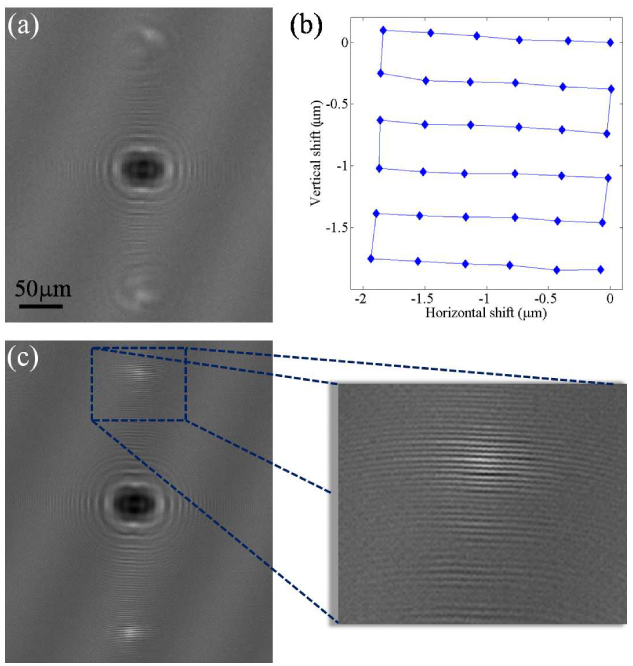
Multiple sub-pixel shifted lower-resolution holograms of the grating object are captured. One such lower-resolution hologram is shown in (a). The sub-pixel shifts between different holograms are automatically computed from the raw data using an iterative gradient method, the results of which are shown in (b). The Pixel SR algorithm recovers the high-resolution hologram of the object as shown in (c). The magnified portion of this super-resolution hologram shows high frequency fringes which were not captured in the lower-resolution holograms.

Given a lensfree hologram (whether one of the lower-resolution holograms or the super-resolution one), we reconstruct the image of the object, in both amplitude and phase, using an iterative, object-support constrained, phase recovery algorithm [15,16,25,26]. Accordingly, Fig. 3(b) shows the amplitude image that we obtain using a single lower-resolution hologram (shown in Fig. 2(a)). The inner features of the object are lost, which is expected due to the limited NA of the raw hologram (i.e., <0.2). Figure 3(c) and 3(d) illustrate the amplitude and the phase images, respectively, recovered from the high-resolution hologram obtained from the Pixel SR algorithm (already shown in Fig. 2(c)). With the SR hologram, fine features of the object are clearly visible, and the object distinctly resembles the 40X microscope image shown in Fig. 3(a).

This grating object was made from indentations filled with air in glass, and therefore should have a negative phase. At the wavelength used in recording the raw holograms (600nm), the object has a phase that is greater than π. This leads to phase wrapping, and the object’s recovered phase appears to be mostly positive. Assuming that this grating object was fabricated with a rather fine resolution (which is a valid assumption since we used focused ion beam milling with a spot size of <50 nm), in an ideal image reconstruction, the phase jumps on each line’s edges would be infinitely sharp and impossible to unwrap. Therefore, we can use the reconstructed phase image at the edges of the fabricated lines to quantify the resolution limit of our Pixel SR scheme. Note that the recovered phase profile of the grating in a direction perpendicular to the lines, e.g., the dashed line in Fig. 3(d), should have sharp jumps with alternating signs. As a result, the spatial derivative of such a profile would consist of delta function with alternating signs. Our limited spatial resolution would broaden these delta functions by our point spread function (PSF). Therefore, if we were to examine the spatial derivative of the phase profile of our images, we would expect to see a series of the PSF with alternating signs. In Fig. 3(e) we show the spatial derivative of the phase profile along the dashed line indicated in panel (d), interpolated for smoothness. The 1/e width of all the peaks shown in Fig. 3(e) is ≤ 0.6μm, which leads to the conclusion that our resolution is ~0.6μm with an NA of ~0.5.

It is rather interesting to note that a similar performance could also be achieved with much less than 36 lower-resolution holograms (see Fig. 4 ). The pixel SR algorithm that we have implemented is an optimization algorithm, which may also work for underdetermined data sets, i.e., we can attempt to optimize the cost function (Eq. (2) to recover the best high-resolution hologram (with the same grid size) using less than L² = 36 LR holograms. Figure 4 shows a comparison of the reconstructed high-resolution object images obtained by processing 5, 12, and 36 LR holograms. These LR holograms were selected from the full set of 36 sub-pixel shifted holograms as shown in Fig. 4(d). We slightly constrict the randomness of this selection process by enforcing that each sub-set of holograms used by the Pixel SR algorithm would contain both the least shifted and the maximum shifted one in order to have well aligned images for accurate comparison. The super-resolution algorithm would perform equally well with complete randomness, but the comparison between different cases would then be less educative. As shown in Fig. 4, the reconstructed HR images are qualitatively the same for different numbers of LR holograms used, though the contrast is enhanced and the distortions are reduced as more LR holograms are used. We have also repeated the process of plotting the spatial derivatives of the recovered phase images perpendicular to the grating lines as shown in Fig. 4(e). The width of the derivative peaks (indicative of the spatial resolution in each recovery) does not appear to differ much as fewer number of LR holograms are used, which is quite encouraging since it implies that a small number of LR holograms, with random shifts, can be assigned to an appropriate HR grid to permit high-resolution lensfree image recovery over a large FOV. This should allow for great flexibility in the physical shifting and hologram acquisition process.

Fig. 4.

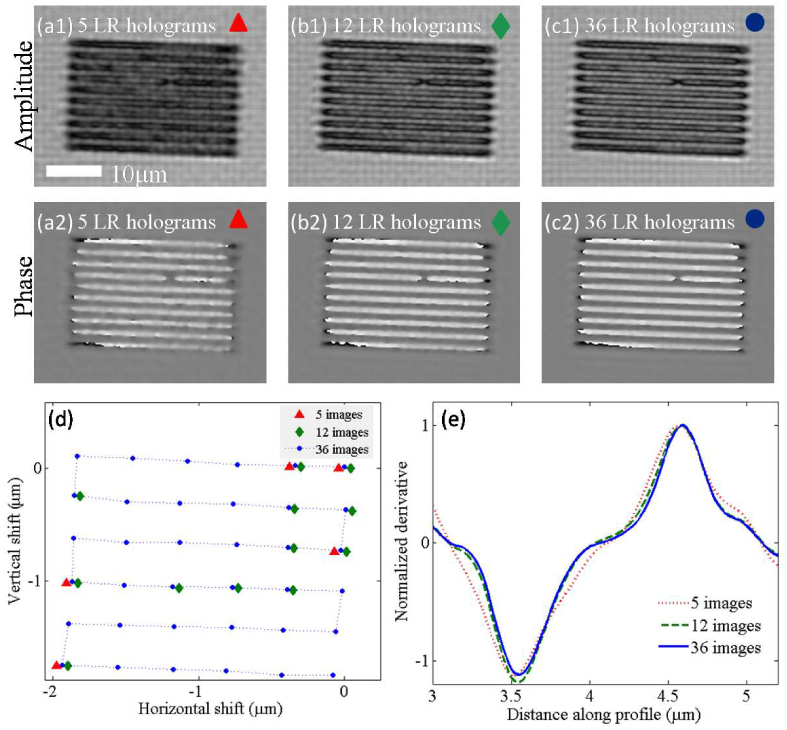
Comparison of pixel SR results using different number of LR holograms. Panes (a1-a2), (b1-b2), and (c1-c2) show the reconstructed amplitude and phase images of the same object using 5, 12, and 36 LR holograms, respectively. In (d), the sub-pixel shifts of the randomly chosen subsets of LR holograms are shown. In (e), the normalized spatial derivative profiles of the recovered phase images for each case (a2, b2 and c2) are shown, similar to Fig. 3(e).

Next, to demonstrate the wide-field imaging capability of our system, we applied the Pixel SR scheme to image a whole blood smear sample. In this experiment, a blood smear was created by smearing a droplet of whole blood on a cover glass to form a single layer of cells. The entire field-of-view (~24mm²) is shown in Fig. 5 top image. We have used a source wavelength of λ = 500nm, and captured 36 sub-pixel shifted holograms. Different regions of the field-of-view are digitally cropped (see Fig. 5 - Regions A, B and C) to show the image improvement due to Pixel SR. The top row of Regions A-B-C is reconstructed using a single LR hologram. The middle row is obtained from processing 36 sub-pixel shifted holograms using our pixel-SR scheme. The images in the bottom row are obtained with a 40X microscope objective (0.65 NA) for comparison purposes. From Fig. 5, it is clear that Pixel SR allows resolving cell clusters which would be difficult to resolve from processing a single LR hologram. Also, the sub-cellular features of white blood cells are visibly enhanced as shown in Fig. 5, Region B.

Fig. 5.

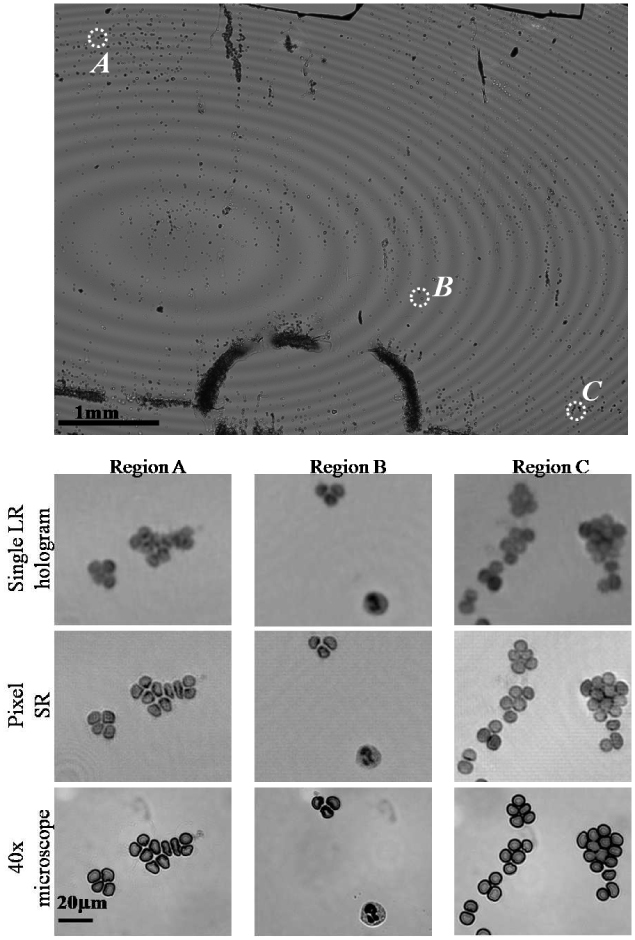
Wide-field (FOV~24 mm²) high-resolution imaging of a whole blood smear sample using Pixel SR. A comparison among the image recovered using a single LR hologram (NA<0.2), the image recovered using Pixel SR (NA~0.5), and a 40X microscope image (NA=0.65) is provided for three regions of interest at different positions within the imaging FOV. Regions (A) and (C) show red blood cell clusters that are difficult to resolve using a single LR hologram, which are now clearly resolved using Pixel SR. In region (B) the sub-cellular features of a white blood cell are also resolved.

Similar to Fig. 4 we have also investigated the image quality that is achieved by the pixel SR algorithm as a function of the number of LR holograms used in the reconstruction. As demonstrated in Fig. 6 , almost the same reconstruction quality for red blood cell clusters can be achieved by feeding a sub-set of LR holograms to the pixel SR algorithm, further supporting our conclusions in Fig. 4.

Fig. 6.

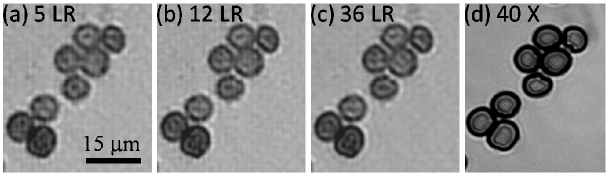
Similar to Fig. 4, we illustrate the pixel SR results of a red blood cell cluster achieved by using (a) 5 LR, (b) 12 LR and (c) 36 LR holograms. Following the same trend as in Fig. 4, almost the same reconstruction quality (especially in terms of the physical gaps among the cells) is achieved by feeding a sub-set of LR holograms to the pixel SR algorithm. (d) shows a 40X objective lens image of the same field of view acquired with NA=0.65.

Finally, Fig. 7 shows Pixel SR results for imaging of Caenorhabditis elegans (C. elegans). These images were obtained by processing 16 sub-pixel shifted LR holograms captured at an illumination wavelength of λ = 500nm. Once again, the resolution improvement due to Pixel SR is clearly visible. Our imaging system has a poorer axial resolution than a 40X microscope objective (NA=0.65), and therefore compared to the microscope image, the Pixel SR image effectively shows a thicker z-slice of the C. elegans 3D body, which is almost a cylinder of ~25 µm diameter.

Fig. 7.

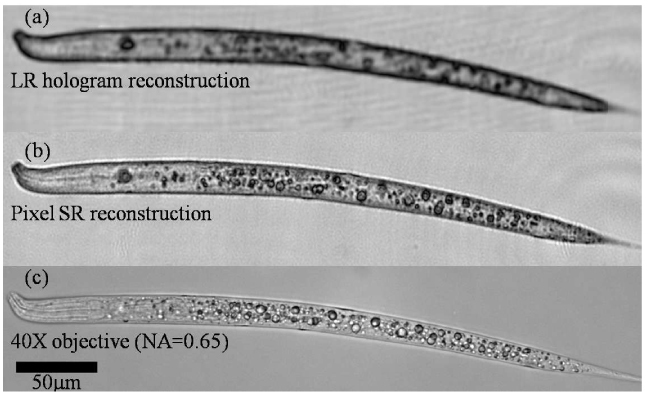
Pixel super-resolution applied to imaging of C. elegans. (a) Recovered amplitude image from a single LR hologram. (b) Pixel SR image recovered using 16 sub-pixel shifted holograms. (c) Microscope image of the same worm captured with a 40X objective-lens (NA=0.65).

5. Conclusions

In conclusion, we demonstrated lensfree holographic microscopy on a chip to achieve ~0.6 µm spatial resolution corresponding to a numerical aperture of ~0.5 over a large field-of-view of ~24 mm². By using partially coherent illumination from a large aperture (~50 μm), we acquired lower resolution lensfree in-line holograms of the objects with unit fringe magnification. For each lensfree hologram, the pixel size at the sensor chip limits the spatial resolution of the reconstructed image. To bypass this limitation, we implemented a sub-pixel shifting based super-resolution algorithm to effectively recover much higher resolution digital holograms of the objects, permitting sub-micron spatial resolution to be achieved across the entire sensor chip active area, corresponding to an imaging field-of-view of ~24 mm². We demonstrated the success of this pixel super-resolution approach by imaging patterned transparent substrates, blood smear samples, as well as C. Elegans.