Abstract
In this work, a first-of-its-kind fully integrated tri-modality system that combines fluorescence, diffuse optical and x-ray tomography (FT/DOT/XCT) into the same setting is presented. The purpose of this system is to perform quantitative fluorescence tomography using multi-modality imaging approach. XCT anatomical information is used as structural priori while optical background heterogeneity information obtained by DOT measurements is used as functional priori. The performance of the hybrid system is evaluated using multi-modality phantoms. In particular, we show that a 2.4 mm diameter fluorescence inclusion located in a heterogeneous medium can be localized accurately with the functional a priori information, although the fluorophore concentration is recovered with 70% error. On the other hand, the fluorophore concentration can be accurately recovered within 8% error only when both DOT optical background functional and XCT structural a priori information are utilized to guide and constrain the FT reconstruction algorithm.
OCIS codes: (170.0170) Medical optics and biotechnology, (170.0110) Imaging Systems, (110.6955) Tomographic imaging, (170.7440) X-ray Imaging, (110.4190) Multiple imaging
1. Introduction
Fluorescence imaging has become an essential in vivo small animal imaging tool in recent years [1–5]. Both commercial availability and relative ease of use has enabled widespread adoption of this technique. Most commercial fluorescence imaging systems utilize a planar imaging approach. However, the location, size and concentration of fluorescence inclusions buried deep in tissue cannot be obtained accurately from a two-dimensional projection image. This is due to the highly diffusive nature of light propagation in tissue. Fluorescence tomography (FT), on the other hand, is capable of generating cross-sectional fluorophore distribution map. In the last decade, researchers from various institutions have developed small animal fluorescence tomography systems for many applications [6–10]. Despite rapid and promising development, the quantitative accuracy of FT technique is limited due to the ill-posed nature of the FT inverse problem.
In order to improve the quantitative accuracy of FT techniques, several attempts have been made to combine FT with other anatomic imaging modalities such as magnetic resonance imaging (MRI) and x-ray computed tomography (XCT). In fact, the idea of combining a functional/molecular imaging modality with a high spatial resolution anatomical imaging modality has been applied previously to optical and nuclear imaging. Examples of this approach can be found in combined positron emission tomography (PET) and XCT systems and combined single photon computed tomography (SPECT) and MRI [11–16]. The advantage of such multi-modality approach is two-fold. First, functional information provided by nuclear imaging is perfectly co-registered with high-resolution anatomical images hence improves visualization of nuclear activity. Second, the structural a priori information can improve quantitative accuracy of the nuclear imaging by guiding and constraining the reconstruction algorithm. Another example of multi-modality approach is combining DOT with MRI and X-ray mammography [17–19]. Like PET, DOT is a low-resolution functional imaging modality, but uses near-infrared light to investigate the optical absorption and scattering properties of tissue. Up to date, extensive effort has been made to integrate DOT with other imaging modalities to obtain accurate optical property maps of the tissue under investigation [17, 20–24]. This approach again aims for obtaining more accurate functional and molecular information with the guidance of the high-resolution anatomical priors.
Similarly, several studies have demonstrated importance of using structural information in fluorescence tomography. Simulation studies have shown that recovered fluorescence parameters can be improved when structural a priori information is used [25, 26]. There are two experimental approaches for obtaining structural a priori information along with FT. The first approach is to acquire FT and anatomical images in separate settings. The anatomical information is then co-registered and used to improve FT reconstruction. We have previously demonstrated that MR structural a priori information drastically improves the quantitative accuracy with a bench-top FT system [27]. Kepshire et al has also developed a PMT based FT system and obtained the structural information using a XCT system [28]. Meanwhile, the second approach is to build integrated systems that can acquire both FT and anatomical images in the same setting. The key advantage of this approach is guaranteed accurate co-registration of the optical and anatomical images. For instance, Davis et al has developed a hybrid FT/MRI system [29]. Anabela de Silva et al have developed an integrated XCT-FT bench-top system. They demonstrated enhanced visualization of the fluorescence activity due to co-localization of FT and XCT images even without utilizing anatomical priors [30, 31]. Besides, Schulz et al have also presented that the fluorophore localization improves with XCT anatomical information using their integrated FT and XCT system [32].
Besides utilization of structural a priori information, FT quantitative accuracy can be improved further if the tissue optical heterogeneity is taken into account. The most common technique is to treat the tissue as a homogeneous medium after normalizing fluorescence measurements with respect to intrinsic excitation measurements [33]. A more elaborate method is to obtain and use background optical property map to accurately model photon migration in both excitation and excitation wavelengths. In FT, excitation light propagation is modeled from the boundary to the fluorophore located inside the tissue first. Afterwards, emission light propagation is modeled from the fluorophore to the detectors located at the boundary of the tissue. Hence, optical properties at both excitation and emission wavelengths that are obtained by DOT can be used as functional a priori information prior to the reconstruction of FT parameters. It has already been demonstrated that the fluorophore concentration is recovered more accurately when the background optical property map is provided [27, 29, 34–36].
To be able to improve the performance of FT by utilizing both structural and functional a priori information, we built a first-of-its-kind gantry-based multi-modality system that combines FT, DOT and XCT in the same setting. As a counterpart of this tri-modality system, the XCT offers anatomical information while the DOT provides optical background heterogeneity to improve the FT images further.
The performance of the system was evaluated using multi-modality phantoms. We first assessed the linearity of the system response using fluorescence inclusions with various concentrations located in a homogeneous, tissue-mimicking phantom. Next, size and location dependence of the recovered fluorophore concentration was investigated. For both studies, the fluorophore concentration maps reconstructed with and without XCT structural a priori information were compared. Finally, we investigated the recovery of the fluorophore concentration of the inclusion in the presence of background heterogeneity. We demonstrated that fluorophore concentration could be accurately recovered only when both functional (DOT) and structural (XCT) co-registered a priori information is available.
2. Materials and methods
2.1 Instrumentation
The XCT system was developed by DxRay, Inc (Northridge, CA) and transferred to UC-Irvine. Afterwards, the XCT gantry was expanded to install the optical imaging components for the tri-modality imaging system. The picture of the combined system from side and front views are shown in Fig. 2a and b .
Fig. 2.

(a) The picture of the system from the side view showing the XCT counterpart. The x-ray source (top) and the flat panel detector (bottom) are positioned on a rotating gantry. All the electrical connections transferred to the gantry using wire harness belts. (b) The picture of the system from the front view showing the FT/DOT components.
2.1.1 Optical Tomographic Imaging
Both absorption and fluorescence measurements were carried out using the same optical instrumentation. Two different lasers were used in the system, 785 nm (75 mW, Thorlabs) and 830 nm (150 mW, Intelite.Inc). The selection of the laser wavelengths was based on the optical property of the fluorophore used in the experiment, Indocyanine Green (ICG), which has the excitation and emission wavelength at 785 nm and 830 nm, respectively. Laser diode mounts and drivers were installed on the gantry. The drivers were operated at constant power mode to ensure the output stability during the experiments. The schematic of the laser delivery path is shown in Fig. 1b . An optical (on/off) switch (Dicon Fiberoptics) was utilized at the end of each laser source prior to combining their outputs. Both laser outputs were combined using a 50/50 fiber optic coupler whose output was connected to a 1 x 3 fiber optic switch. The fiber optic switch allowed sequential activation of each source position. This configuration allowed us to illuminate the sample with a collimated beam at either 785 nm or 830 nm from three different angles (−45°, 0°, 45°). A cooled CCD camera (Perkin Elmer, Cold Blue) was also positioned on the gantry across the three fiber optic collimators and used to capture the images of the phantom. A sigma MACRO 50 mm F2.8 lens was coupled to the CCD camera. A computer controlled filter wheel (Tofra, Inc.) was installed between the CCD camera body and the lens. One 830 nm band-pass filter (MK Photonics) and one long pass edge filter (Semrock, Inc) were stacked and used to eliminate excitation light at 785 nm. This filter combination minimizes the strong excitation leakage with maximum transmission rate at fluorophore emission wavelength.
Fig. 1.
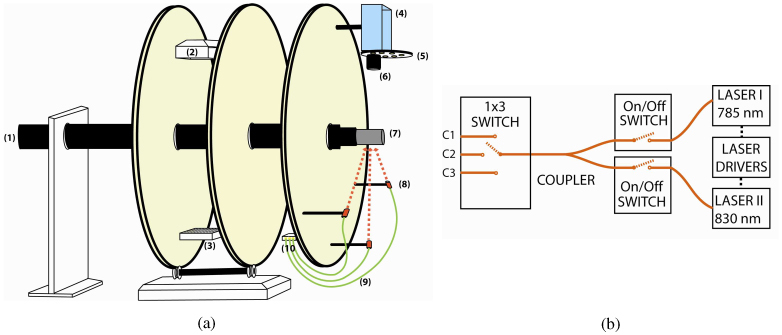
(a) The schematic of the multi-modality gantry-based system. The XCT gantry was expanded and optical imaging components were installed. A sample holder was designed to translate the sample between XCT and optical imaging systems. The components that are seen in the diagram: (1) the sample holder, (2) x-ray source, (3) x-ray detector, (4) CCD camera, (5) filter wheel, (6) lens, (7) phantom, (8) fiber optic collimator, (9) optical fibers, (10) fiber optic switch. (b) The light delivery components. On-off switches were used to select the desired illumination wavelength. A 50/50 fiber optic coupler was used to combine both laser output. A 1 x 3 fiber optic switch allowed the sequential activation of any one the three source sites.
Labview Software (National Instruments, Austin, TX) was used to control each component and perform automatic data acquisition. A data acquisition card (NI-6550) was used to control the on/off switches. In addition to this, a motion controller (NI-7330) and a step motor driver (NI-7604) were used to control the filter wheel. The gantry rotation and the 1 x 3 fiber optic switch were controlled via serial ports while the CCD camera was connected to the computer via a USB port. All electronic connections between the computer and the components of the optical imaging system were transferred through a wire harness belt. A graphical user interface was designed to rotate the gantry, activate the desired source position, and acquire the CCD images with or without excitation filters.
2.1.2 X-ray computed tomography
The XCT system had its own dedicated computer for data acquisition and analysis. The only common component between optical and XCT imaging systems was the gantry control mechanism. Hence, the corresponding serial port connector was switched to the XCT computer prior to the XCT acquisition. The schematic of the system is shown in Fig. 1.a. Again, the electrical connections between the XCT computer and the components on the gantry were transferred through a separate wire harness belt. These components were the following: x-ray tube, flat panel sensor and step motors that control the gantry rotation as well as the source-detector distance. The x-ray tube was operated at 50kVp and 0.5mA. The flat panel sensor had an active area of 12 cm x 12 cm and pixel size of 50 µm (C7942GP, Hamamatsu Photonics). A picture of the XCT counterpart is shown in Fig. 2.a. Planar images were acquired from 256 projections over 360° degree rotation in a set and shoot mode. Trans-axial images were reconstructed using a Feldcamp cone beam filtered back projection algorithm. A standard box-car filter was used.
2.2 Mathematical framework for optical image reconstruction
A coupled diffusion equation is used to model the excitation and emission fluorescence light propagation in tissue:
| (1) |
| (2) |
where Φx(r) and Φm(r) (W·mm−2) are the photon density for the excitation and emission light, respectively. The diffusion coefficient, Dx,m(r) (mm−1), is defined by Dx,m=1/3(µax,m +µs ’ x,m). The reduced scattering and the absorption coefficients of the medium are represented as µs ’ x,m (mm−1) and µax,m (mm−1), respectively. The absorption coefficients are expected to be different at excitation and emission wavelengths due to the diverse spectral dependence of the absorption of each individual tissue chromophore [37]. Meanwhile, absorption coefficient due to fluorophore, µaf(r), is directly related to the ICG concentration by the formula µaf =2.3εC, where ε is the extinction coefficient of the fluorophore with the unit of Molar−1·mm−1 and C is the concentration of the fluorophore. The total absorption coefficient at excitation wavelength (µax) includes the contribution from the fluorescence absorption µaf(r). Quantum yield, η, is the intrinsic property of the fluorophore and defined as the ratio of the number of photons emitted to the number of photons absorbed. The coupled diffusion equation is solved with the finite element method (FEM). The details have been described previously [27].
The inverse problem was solved by minimizing the difference between the measured and calculated data according to the following error function:
| (3) |
| (4) |
for DOT and FT measurements, respectively. Here, i represents the number of sources and j represents the number of detectors. is the measurement. Pij(µa) and Pij(µaf) are the flux on the measured point calculated by the forward solver from the spatial distribution of µax,m and µaf. We iteratively updated the unknown µa and µaf with Levenberg-Marquardt method by
| (5) |
where and X represents the unknown matrix of µax,m and µaf. The dimension of X is N and it represents the number of nodes in the FEM mesh. The Jacobian matrix J is calculated with adjoint method [38].
The data analysis has been divided into the following steps,
-
a)
For optical background heterogeneity correction, we first reconstruct μax,m from the DOT data.
-
b)
Following that, μaf is reconstructed using Φx,m and μax,m that are obtained from the DOT. A homogeneous µaf distribution is assumed as the initial guess in the reconstruction process. These values are found by minimizing the difference between the forward solver solution and the measurements.
-
c)
When the structural a priori information is available, ‘Laplacian-type a priori’ developed by Yalavarthy et. al. is used to find the fluorophore concentration for the inclusion and the background [40]. The L-matrix can be written as
(6)
where Nr represents the number of nodes included in one region. Then the update equation can be expressed as:
| (7) |
Dual mesh is used for reducing the computational time. A fine mesh (4225 nodes and 8192 elements) is used for the forward solver, while a coarse mesh (1089 nodes and 2048 elements) is used for the inverse problem for both DOT and FT.
2.3 Tissue simulating phantom studies
Several phantom studies were carried out to evaluate the performance of the tri-modality system. Optical images were acquired from 8 views (45 degrees apart) for each source position. For DOT measurements, one-second CCD integration time was enough. However, FT measurements were obtained with sixty-second integration time for each source position. For each view, a set of 21 virtual detectors were placed uniformly on the corresponding boundary segment and mapped to the CCD as described in previous work [27].
The phantoms were prepared using agarose powder. Intralipid and Indian ink were added as optical scatterer and absorber, respectively. ICG (IC-Green, Akorn, Inc) was used as the fluorophore in this study. According to the literature, the ICG extinction coefficient at 785 nm and 830 nm is 130,000 Molar−1·mm−1 and 22,000 Molar−1·mm−1, respectively [39]. Meanwhile, the quantum efficiency of ICG is 0.016. The clinical CT contrast agent Omnipaque (GE healthcare) was also added to different compartments of the phantom so that the structure of the phantom could be obtained from XCT scan and used as structural a priori information.
Mainly, three phantoms studies were undertaken. The first study was designed to evaluate the linearity of the system response. The second study was designed to assess the size and location dependence of the reconstruction results without and with the structural a priori information. The third case was designed to investigate the effect of both the functional and structural a priori information on the FT reconstruction. ICG inclusions were embedded in a homogeneous background for the first two studies, and in a heterogeneous optical background for the third study.
A full set of data was acquired using homogeneous DOT and FT calibration phantoms at the end of each study. The optical properties of the DOT calibration phantom were set to μa = 0.01 mm−1 and μs ´ = 0.8 mm−1. The optical properties of the FT calibration phantom were similar. However, ICG (34 nM) was added for the latter case, which set the absorption due to this fluorophore to μaf = 0.001 mm−1. A complete set of FT and DOT measurements were taken using the homogeneous FT and DOT calibration phantom. Then the experimental data (Fmeasured) is calibrated using the calibration phantom measurements (Fhomo_measured) and
where the Fhomo_forw is calculated by the forward solver. The calibrated data Fhete_calibrated is then fed into the inverse solver. This step takes into account for the data/model mismatch. More details are given in our previous work [27].
3. Results
3.1 Phantom study I: response linearity
A 2.4 mm inner diameter glass tube filled with ICG and Intralipid is inserted in a 25 mm diameter phantom. The optical properties of the homogeneous background are set to μa=0.01 mm−1 and μs ´=0.8 mm−1. The inclusion is 6 mm away from the center of the phantom. Figure 3a shows the trans-axial XCT image of the phantom. The ICG concentration in the inclusion was varied in a broad range, from 34 nM to 830 nM, to evaluate the linearity of the system. The reconstructed ICG concentration maps without and with the structural a priori information are shown in the first and second columns in Fig. 4 , respectively. The plot of the recovered ICG concentration with and without the structural a priori with respect to the true ICG concentration is shown in Fig. 3b.
Fig. 3.

a) The trans-axial XCT image of the phantom. The ICG inclusion is held in the glass tube that is seen as a bright circle in the image. b) The plot of the recovered ICG concentration with respect to true ICG concentration. The blue and purple dots represent the recovered values with and without the structural a priori information, respectively. The least squares lines of best fit are the red dashed ones. The recovered ICG concentration shows a linear response with respect to true ICG concentration both with and without the structural a priori information. However, the right values are recovered only when structural a priori information is available.
Fig. 4.

The reconstructed ICG concentration maps without (left column) and with (right column) structural a priori information from XCT for the first phantom study. The color bars all have units of nM.
Results: As shown in Fig. 3b, the recovered fluorophore concentration is linear respect to the true concentration both with and without structural a priori information. The correlation coefficient is 0.998 for both fitted curves. However, the recovered ICG concentration is underestimated without the structural a priori information. On the other hand, the accuracy of the recovered ICG concentration is improved considerably for all the cases when the structural a priori information from XCT is used.
3.2 Phantom study II: size and depth dependence
This study evaluates the effect of inclusion size and location on the recovered ICG concentration using four cases. The XCT images for the four cases are shown in the first column of Fig. 5 . The first two cases both had a 2.4 mm ICG inclusion. The inclusions were positioned 7 mm and 2.5 mm off the center for the first and second case, respectively. Similarly, the third and fourth cases both have a 4.2 mm ICG inclusion. This time, inclusions were placed 6 mm and 2.5 mm away from the center. The background optical properties are kept the same as the first study. The ICG concentration in the inclusion was 334 nM for all four cases. Again, ICG concentration maps were reconstructed with and without the structural a priori information.
Fig. 5.

The results for the second phantom study. The first column is the XCT trans-axial images of the phantoms. The size and location of the inclusion are different for each case. The second the third columns are the reconstructed ICG concentration maps without and with the XCT structural a priori information, respectively. As seen in the images, the recovered ICG concentration value depends drastically on the size and location of the inclusion. However, the true value can be recovered for all four cases when XCT structural a priori information is used. The color bars all have the units of nM.
Results: The recovered ICG concentration with and without the structural a priori information for all the four phantoms are listed in Table 1 . For the small object (∅: 2.4 mm), the ICG concentration is recovered with 80% and 70% error when the inclusion is located 7 mm and 2.5 mm away from the center, respectively. For the 4.2 mm inclusion, on the other hand, the recovered ICG concentration has 50% error when it is located 2.5 mm off the center. The error was reduced to 30% when it was located 6 mm off the center. As expected, these results show that the recovered ICG concentration is more accurate when the inclusion is closer to the surface and its size larger. They also confirm that the recovered ICG concentration is highly dependent on the size and position of the inclusions, without structural a priori information. When structural a priori information from XCT is used to guide the reconstruction, however, the ICG concentration is recovered within 10% error for all cases, Table 1.
Table 1. The recovered ICG concentrations for phantom study 2.
| Case # | Inclusion size (mm) | Offset (mm) | True ICG concentration (nM) | Recovered ICG concentration (nM) without XCT info | Recovered ICG concentration (nM) with XCT info | Error (%) |
| 1 | 2.4 | 7 | 334 | 96 | 326 | 2.4 |
| 2 | 2.4 | 2.5 | 334 | 70 | 328 | 1.8 |
| 3 | 4.2 | 6 | 334 | 232 | 302 | 9.6 |
| 4 | 4.2 | 2.5 | 334 | 157 | 357 | 6.9 |
3.3 Phantom study III: in the presence of heterogeneity
In this case, the ICG inclusion was embedded in a heterogeneous background. The background optical properties were μa=0.01mm−1 and μs´=0.8 mm−1. The heterogeneous optical background was created by adding a 14 mm diameter object with the optical properties of μa=0.025 mm−1 and μs´=0.8mm−1. This heterogeneous object was more absorptive than the background. The clinical available CT contrast agent Omnipaque was also added to the highly absorptive region to make it visible in the XCT image. In this study, a 2.4 mm diameter ICG inclusion was located 6 mm away from the center of the phantom. The absorption map of the phantom was reconstructed using diffuse optical tomography measurements and used as the functional a priori information. The ICG concentration map was reconstructed with three combinations of a priori information as follows:
-
1.
The optical background heterogeneity was neglected, and ICG concentration map was reconstructed without functional and structural a priori information,
-
2.
The optical background was reconstructed with the DOT measurements and used as the functional a priori information. However, the structural a priori information was not used,
-
3.
Both the functional and structural a priori information were used during the reconstruction of ICG concentration map.
When the DOT functional a priori information was available, we first reconstructed μx,m from the DOT data. Then Φx was calculated using μx and used in the second equation. Following that, μaf was reconstructed using Φx and μm that were obtained from the DOT. A homogeneous µax,m or µaf distribution was assumed as the initial guess in the reconstruction process. These values were found by minimizing the difference between the forward solver solution and the measurements.
Result: When the optical background heterogeneity is neglected, the shape of the reconstructed ICG object is distorted as shown in Fig. 6c . When functional a priori information from reconstructed DOT absorption map (Fig. 6b) is used, the ICG inclusion can be located accurately, Fig. 6d. However, the recovered ICG concentration shows 70% error. This is consistent with our second phantom study case 1. Please note that the mean recovered value of the absorptive region is 0.024 mm−1, within 5% of its actual value. On the other hand, when both functional a priori information obtained from DOT and structural a priori information obtained from XCT are utilized, ICG concentration in the ICG inclusion can be recovered with only 8% error, Fig. 6e. The profile plot along the x-axis across the reconstructed fluorescence object for each case is superimposed and shown in Fig. 6f.
Fig. 6.

(a) The XCT trans-axial image of the heterogeneous phantom. b) The reconstructed absorption map at 785 nm using DOT measurements. The reconstructed ICG concentration maps without any a priori information (c), with functional a priori information alone (d), and with both functional and structural a priori information (e). The profile plot along the x-axis across the reconstructed fluorescence object (indicated by the dashed white line) for each case is superimposed and shown in (f). The profile plot along the x-axis across the glass tube (indicated by yellow dashed line in the XCT image) is also shown in (g).
XCT is a high spatial resolution imaging modality. XCT spatial resolution is affected by many factors such as detector resolution (50 μm per pixel), x-ray source focal spot size (50 μm for our setting) and position of the object (magnification). To provide an estimate of the spatial resolution of the XCT system, we used the wall of the thin glass tube (300 μm) that was utilized as an inclusion in the phantom. For our XCT system, each pixel in the reconstructed cross-sectional XCT image corresponded to 150 μm, Fig. 6a. The full with half maximum (FWHM) of the curve (Fig. 6f) revealed that the resolution of the system was approximately 400 μm.
3.4 Phantom study IV: in the presence of background fluorescence
One important aspect in fluorescence tomography studies is the contrast to background ratio (C/B), as in an in vivo setting there is likely to be residual fluorescence and/or auto-fluorescence from the tissues surrounding the fluorescent target. The reconstruction of fluorescence inclusion in the presence of background fluorescence is investigated using similar setting as the first phantom study. The optical properties of the 25 mm diameter homogeneous phantom are set to μa=0.01 mm−1 and μs ´=0.8 mm−1. 34 nM ICG was also added to the background setting the absorption coefficient due to the fluorophore to be μaf=0.001 mm−1. Again, a 2.4 mm inner diameter glass tube filled with 334 nM ICG and Intralipid is inserted in the phantom. The XCT image of the phantom is the same as the one presented in Fig. 3a due to the use of the same phantom mold. The reconstructed ICG concentration maps without and with the structural a priori information are shown in the first and second columns in Fig. 7 , respectively.
Fig. 7.

The reconstructed ICG concentration maps without (a) and with (b) XCT structural a priori information. The profile plot along the x-axis across the reconstructed fluorescence object (indicated by the dashed white line) for each case is superimposed and shown in (c).
Results: The inclusion can be localized in the presence of the background fluorescence even without XCT structural a priori information, as shown in Fig. 7a. Without any a priori info, the recovered ICG concentration for the target and the background is 84 nM (with 75% error) and 15 nM (with 55% error), respectively. On the other hand, when the XCT structural a prior information is used, the recovered ICG concentration for the target and the background is 341 nM (with 2% error) and 29 nM (with 14% error), Fig. 7b. The plot of intensity profiles along x axis across the reconstructed ICG inclusions is shown in Fig. 7c. The ability of this hybrid system to recover accurate ICG concentrations of multiple inclusions in the presence of the background is demonstrated in this study.
3.5 Phantom study V: reconstruction of multiple fluorescence inclusions in the presence of background fluorescence
In the last phantom study, the reconstruction of multiple fluorescence inclusions in the presence of background fluorescence was investigated. The phantom had two 2.4 mm diameter ICG inclusions located 6.5 mm and 9 mm away from the center of the phantom as shown in XCT image (Fig. 8d ), respectively. The background optical properties were μa = 0.01 mm−1, µs ’ = 0.8 mm−1 and μaf=0.001 mm−1 (34 nM ICG). Both inclusions have 500 nM ICG, making the contrast to background ratio 15. The reconstructed ICG concentration maps without and with the structural priori information are shown in the second and third columns in Fig. 8, respectively.
Fig. 8.

(a) The XCT trans-axial image of the phantom with two ICG inclusions. (b) and (c) The reconstructed ICG concentration maps without and with XCT structural a priori information. Without XCT structural a priori information, the object closer to the surface dominates in the image. On the other hand, both ICG inclusions can be accurately recovered when XCT structural a priori information is used.
Results: The two ICG inclusions are positioned at different depth; hence the recovered concentration values differ without XCT a priori information. The ICG concentration of the inclusions located 6.5 mm and 9 mm away from the center were recovered as 93 nM (with 81% error) and 167 nM (with 67% error), respectively. This is consistent with our second phantom study, in which we demonstrate that the recovered fluorophore concentration is highly dependent on the size and depth of the inclusion. In contrary, the error reduces down to 2% (508 nM) and 3% (513 nM) for the two inclusions when the XCT structural a priori information is utilized.
6. Discussion
An ideal FT system should not only allow visualization of the fluorophore distribution in tissue but also provide quantitatively accurate concentration values in a heterogeneous medium. Quantitative accuracy is a pivotal factor for many practical applications of FT. For instance, MMPsense, which is an activatible fluorescence probe, accumulates three times higher in malignant tumors than benign ones in vivo [41]. To be able to differentiate malignant and benign lesions, the reconstructed fluorophore concentration value should be independent of the size and location of the lesion. A stand-alone FT system, unfortunately, would not correctly differentiate a small malignant lesion buried deep in tissue and a large benign lesion located at subsurface lesion.
In order to address the need for quantitative FT imaging, we built a fully integrated FT/DOT/XCT system. There are two main objectives for developing this system. First, the XCT structural a priori information is used to guide and constrain the FT inverse problem, thus fluorophore concentration map can be recovered more accurately. Additionally, DOT provides an effective way of correcting the effect of optical background heterogeneity, thus improves the FT accuracy further.
Recently, Kepshire et al has particularly investigated the depth dependence of a subsurface FT technique with simulation and phantom studies [44, 45]. They concluded that the fluorescence object could be localized but recovered image sensitivity was nonlinear with depth. Our second phantom study also confirms that the recovered fluorescence concentration is highly dependent on not only the depth but also the size of the fluorescence inclusions. On the other hand, the fluorophore concentration in the inclusions can be recovered within 10% error using the XCT structural a priori information independent of their size and location.
Another factor that affects the FT reconstruction results is the background optical property distribution. Without proper modeling of emission and excitation light propagation between boundary of the medium and fluorophores, it is difficult to obtain accurate results. As an alternative, Born normalization method has been commonly used for heterogeneity correction, and applied to localize the fluorescence object robustly in vivo [42, 46]. For instance, Graves et al have recovered a subcutaneously implanted fluorescence inclusion in nude mice with less than 30% error using slab geometry and matching fluid [41]. However, the quantitative accuracy of Born normalization method has not been discussed especially for inclusions deeply embedded in the turbid medium [33, 42, 43]. Furthermore, Herve et al particularly compared Born normalization and a heterogeneity correction method, which used reconstructed optical property for modeling purposes. The results showed that the later was more accurate [47]. Our results also confirmed that significant improvement can be achieved when DOT functional a priori information is utilized during the FT reconstruction process. However, neither functional nor structural a priori by itself is enough to obtain accurate FT maps. In essence, the strength of the tri-modality system described here comes from its ability to offer both XCT structural and DOT functional a priori information that can be utilized to reconstruct quantitatively accurate fluorophore concentration images.
In our study, only absorption heterogeneity was considered and homogeneous scattering coefficient distribution was assumed. However, the scattering coefficient can also be very heterogeneous in reality. Time-dependent DOT measurements, which can be achieved using frequency- or a time-domain DOT system, are required in order to effectively separate the absorption and scattering coefficients. Nevertheless, the effect of the scattering error was evaluated using simulation studies. For example, when the scattering coefficient was chosen to be +/− 25% of the actual value, the recovered absorption coefficient from DOT gives +/− 28% for the absorptive object. In turn, when this absorption map is fed into the fluorescence reconstruction, the fluorescence concentration gives +/− 30% error.
A perquisite for any such multimodality approach is that the region of interest should be detected by each individual modality. This may not be true all the time and even if it is, the boundary of the ROI detected by different modalities may vary. As a solution for the latter case, soft a priori approach is used [48] to reduce the effect of erroneous a priori information on the reconstruction results. For the former case, XCT structural information can at least improve the optical property of the background medium obtained by DOT, which in turn will improve the FT results further. All the XCT images shown in this study is to provide phantom structure for FT reconstruction and demonstrate the importance of such multi-modality imaging system using proof-of-principle experiments. However, the limitation and optimized contrast and geometry for acquiring XCT image need to be addressed and investigated using contrast-detail analysis method in the future. Furthermore, various strategies such as utilization of XCT contrast agents or dual energy XCT technique can be potentially used to improve the vascular or soft tissue contrast [31]. The most favorable case for such multi-modality imaging system is to use dual modality contrast agent where the location of the agent can be seen from the structural imaging modality and the amount of the agent can be quantified by the fluorescence imaging. This is possible with the advances of dual contrast agent development, such as dual MRI-fluorescence, dual XCT-fluorescence contrast agent [49]. Meanwhile, extensive effort is being spent to develop new x-ray detector technology to improve XCT soft tissue contrast further.
Acknowledgments
We would like to thank Dr. Brad Patt from Gamma Medica Ideas Inc. for contributing the X-ray tube and CT gantry for the fabrication of the combined FT/CT system. This work was supported in part by the National Institutes of Health grant number R44 EB007873, #R01EB008716 and #R21/33 CA120175.
References and links
- 1.Weissleder R., Tung C. H., Mahmood U., Bogdanov A., Jr, “In vivo imaging of tumors with protease-activated near-infrared fluorescent probes,” Nat. Biotechnol. 17(4), 375–378 (1999). 10.1038/7933 [DOI] [PubMed] [Google Scholar]
- 2.Tung C. H., Bredow S., Mahmood U., Weissleder R., “Preparation of a cathepsin D sensitive near-infrared fluorescence probe for imaging,” Bioconjug. Chem. 10(5), 892–896 (1999). 10.1021/bc990052h [DOI] [PubMed] [Google Scholar]
- 3.Chen X., Conti P. S., Moats R. A., “In vivo near-infrared fluorescence imaging of integrin alphavbeta3 in brain tumor xenografts,” Cancer Res. 64(21), 8009–8014 (2004). 10.1158/0008-5472.CAN-04-1956 [DOI] [PubMed] [Google Scholar]
- 4.Cheng Z., Wu Y., Xiong Z., Gambhir S. S., Chen X., “Near-infrared fluorescent RGD peptides for optical imaging of integrin alphavbeta3 expression in living mice,” Bioconjug. Chem. 16(6), 1433–1441 (2005). 10.1021/bc0501698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Koenig A., Hervé L., Josserand V., Berger M., Boutet J., Da Silva A., Dinten J. M., Peltié P., Coll J. L., Rizo P., “In vivo mice lung tumor follow-up with fluorescence diffuse optical tomography,” J. Biomed. Opt. 13(1), 011008 (2008). 10.1117/1.2884505 [DOI] [PubMed] [Google Scholar]
- 6.Milstein A. B., Oh S., Webb K. J., Bouman C. A., Zhang Q., Boas D. A., Millane R. P., “Fluorescence optical diffusion tomography,” Appl. Opt. 42(16), 3081–3094 (2003). 10.1364/AO.42.003081 [DOI] [PubMed] [Google Scholar]
- 7.Graves E. E., Ripoll J., Weissleder R., Ntziachristos V., “A submillimeter resolution fluorescence molecular imaging system for small animal imaging,” Med. Phys. 30(5), 901–911 (2003). 10.1118/1.1568977 [DOI] [PubMed] [Google Scholar]
- 8.Ntziachristos V., “Fluorescence molecular imaging,” Annu. Rev. Biomed. Eng. 8(1), 1–33 (2006). 10.1146/annurev.bioeng.8.061505.095831 [DOI] [PubMed] [Google Scholar]
- 9.Deliolanis N., Lasser T., Hyde D., Soubret A., Ripoll J., Ntziachristos V., “Free-space fluorescence molecular tomography utilizing 360°geometry projections,” Opt. Lett. 32(4), 382–384 (2007). 10.1364/OL.32.000382 [DOI] [PubMed] [Google Scholar]
- 10.X. Zhang, C. Badea, M. Jacob, and G. A. Johnson, “Development of a noncontact 3-D fluorescence tomography system for small animal in vivo imaging,” Proc. Soc. Photo Opt. Instrum. Eng. 7 191, nihpa106691 (2009). [DOI] [PMC free article] [PubMed]
- 11.S. Azman, J. Gjaerum, D. Meier, L. T. Muftuler, G. Maehlum, O. Nalcioglu, B. E. Patt, B. Sundal, M. Szawlowski, B. M. W. Tsui, D. J. Wagenaar, and Y. Wang, “A nuclear radiation detector system with integrated readout for SPECT/MR small animal imaging, ” in Proceedings of IEEE Nuclear Science Symposium and Medical Imaging Conference (IEEE, 2007), pp. 2311–17. [Google Scholar]
- 12.O. Nalcioglu, T. Muftuler, D. Wagenaar, M. Szawlowski, M. Kapusta, N. Pawlov, G. Maehlum, and P. Patt, “Development of MR-Compatible SPECT System: A Feasibility Study,” presented at Annual Meeting of the ISMRM, Berlin, Germany, 19–25 May 2007. [Google Scholar]
- 13.Nalcioglu O., Roeck W., Hamamura M., Ha S.-H., Muftuler T., Wagenaar D., Meier D., Patt B., “Development of An MR-Compatible SPECT System (MRSPECT): A Feasibility Study,” J. Nucl. Med. submitted [DOI] [PubMed] [Google Scholar]
- 14.D. Wagenaar, O. Nalcioglu, L. Muftuler, M. Szawlowski, M. Kapusta, N. Pawlov, D. Meier, G. Maehlum, and B. Patt, “Development of MRI-Compatible Nuclear Medicine Imaging Detectors,” in IEEE Nuclear Science Symposium and Medical Imaging Conference (IEEE, 2006), pp. 1825–28. [Google Scholar]
- 15.Di Carli M. F., “Hybrid imaging: integration of nuclear imaging and cardiac CT,” Cardiol. Clin. 27(2), 257–263 (2009). 10.1016/j.ccl.2008.12.001 [DOI] [PubMed] [Google Scholar]
- 16.Basu S., Alavi A., “Revolutionary impact of PET and PET-CT on the day-to-day practice of medicine and its great potential for improving future health care,” Nucl. Med. Rev. Cent. East. Eur. 12(1), 1–13 (2009). [PubMed] [Google Scholar]
- 17.Brooksby B., Pogue B. W., Jiang S., Dehghani H., Srinivasan S., Kogel C., Tosteson T. D., Weaver J., Poplack S. P., Paulsen K. D., “Imaging breast adipose and fibroglandular tissue molecular signatures by using hybrid MRI-guided near-infrared spectral tomography,” Proc. Natl. Acad. Sci. U.S.A. 103(23), 8828–8833 (2006). 10.1073/pnas.0509636103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yuan Z., Zhang Q., Sobel E. S., Jiang H., “Tomographic x-ray-guided three-dimensional diffuse optical tomography of osteoarthritis in the finger joints,” J. Biomed. Opt. 13(4), 044006 (2008). 10.1117/1.2965547 [DOI] [PubMed] [Google Scholar]
- 19.Fang Q., Carp S. A., Selb J., Boverman G., Zhang Q., Kopans D. B., Moore R. H., Miller E. L., Brooks D. H., Boas D. A., “Combined optical imaging and mammography of the healthy breast: optical contrast derived from breast structure and compression,” IEEE Trans. Med. Imaging 28(1), 30–42 (2009). 10.1109/TMI.2008.925082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brooksby B., Jiang S., Dehghani H., Pogue B. W., Paulsen K. D., Kogel C., Doyley M., Weaver J. B., Poplack S. P., “Magnetic resonance-guided near-infrared tomography of the breast,” Rev. Sci. Instrum. 75(12), 5262–5270 (2004). 10.1063/1.1819634 [DOI] [Google Scholar]
- 21.Xu H., Springett R., Dehghani H., Pogue B. W., Paulsen K. D., Dunn J. F., “Magnetic-resonance-imaging-coupled broadband near-infrared tomography system for small animal brain studies,” Appl. Opt. 44(11), 2177–2188 (2005). 10.1364/AO.44.002177 [DOI] [PubMed] [Google Scholar]
- 22.G. Gulsen, M. B. Unlu, O. Birgul, and O. Nalcioglu, “Simultaneous monitoring of multiple contrast agents using a hybrid MR-DOT system,” Proc. SPIE 6431, (2007). [Google Scholar]
- 23.Gulsen G., Birgul O., Unlu M. B., Shafiiha R., Nalcioglu O., “Combined Diffuse Optical Tomography (DOT) and MRI system for cancer imaging in small animals,” Technol. Cancer Res. Treat. 5(4), 351–363 (2006). [DOI] [PubMed] [Google Scholar]
- 24.O. Birgul, G. Gulsen, R. Shafiiha, M. B. Unlu, and O. Nalcioglu, “In vivo Small Animal Imaging using Combined MR-DOT System,” in Biomedical Optics Topical Meeting, Technical Digest (Optical Society of America, 2006), paper TuG1. [Google Scholar]
- 25.Davis S. C., Dehghani H., Wang J., Jiang S., Pogue B. W., Paulsen K. D., “Image-guided diffuse optical fluorescence tomography implemented with Laplacian-type regularization,” Opt. Express 15(7), 4066–4082 (2007). 10.1364/OE.15.004066 [DOI] [PubMed] [Google Scholar]
- 26.Lin Y., Gao H., Nalcioglu O., Gulsen G., “Fluorescence diffuse optical tomography with functional and anatomical a priori information: feasibility study,” Phys. Med. Biol. 52(18), 5569–5585 (2007). 10.1088/0031-9155/52/18/007 [DOI] [PubMed] [Google Scholar]
- 27.Lin Y., Yan H., Nalcioglu O., Gulsen G., “Quantitative fluorescence tomography with functional and structural a priori information,” Appl. Opt. 48(7), 1328–1336 (2009). 10.1364/AO.48.001328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kepshire D., Mincu N., Hutchins M., Gruber J., Dehghani H., Hypnarowski J., Leblond F., Khayat M., Pogue B. W., “A microcomputed tomography guided fluorescence tomography system for small animal molecular imaging,” Rev. Sci. Instrum. 80(4), 043701 (2009). 10.1063/1.3109903 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Davis S. C., Pogue B. W., Springett R., Leussler C., Mazurkewitz P., Tuttle S. B., Gibbs-Strauss S. L., Jiang S. S., Dehghani H., Paulsen K. D., “Magnetic resonance-coupled fluorescence tomography scanner for molecular imaging of tissue,” Rev. Sci. Instrum. 79(6), 064302 (2008). 10.1063/1.2919131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.A. da Silva, T. Bordy, M. Debourdeau, J. M. Dinten, P. Peltie, and P. Rizo, “Coupling X-ray and optical tomography systems for in vivo examination of small animals,” in Proceedings of IEEE Conference on Engineering in Medicine and Biology Society (IEEE, 2007), pp. 3335–3338. [DOI] [PubMed] [Google Scholar]
- 31.Da Silva A., Leabad M., Driol C., Bordy T., Debourdeau M., Dinten J. M., Peltié P., Rizo P., “Optical calibration protocol for an x-ray and optical multimodality tomography system dedicated to small-animal examination,” Appl. Opt. 48(10), D151–D162 (2009). 10.1364/AO.48.00D151 [DOI] [PubMed] [Google Scholar]
- 32.R. B. Schulz, A. Ale, A. Sarantopoulos, M. Freyer, R. Söhngen, M. Zientkowska, and V. Ntziachristos, “Hybrid fluorescence tomography/x-ray tomography improves reconstruction quality,” in Proc. SPIE 7370 (2009). [Google Scholar]
- 33.Ntziachristos V., Weissleder R., “Experimental three-dimensional fluorescence reconstruction of diffuse media by use of a normalized Born approximation,” Opt. Lett. 26(12), 893–895 (2001). 10.1364/OL.26.000893 [DOI] [PubMed] [Google Scholar]
- 34.Hervé L., Koenig A., Da Silva A., Berger M., Boutet J., Dinten J. M., Peltié P., Rizo P., “Noncontact fluorescence diffuse optical tomography of heterogeneous media,” Appl. Opt. 46(22), 4896–4906 (2007). 10.1364/AO.46.004896 [DOI] [PubMed] [Google Scholar]
- 35.Tan Y., Jiang H., “Diffuse optical tomography guided quantitative fluorescence molecular tomography,” Appl. Opt. 47(12), 2011–2016 (2008). 10.1364/AO.47.002011 [DOI] [PubMed] [Google Scholar]
- 36.Y. Lin, H. Yan, G. Gulsen, and O. Nalcioglu, “Dual-modality molecular imaging for small animals using fluorescence and x-ray computed tomography,” in Proc. SPIE 7370 (2009). [Google Scholar]
- 37.Peters V. G., Wyman D. R., Patterson M. S., Frank G. L., “Optical properties of normal and diseased human breast tissues in the visible and near infrared,” Phys. Med. Biol. 35(9), 1317–1334 (1990). 10.1088/0031-9155/35/9/010 [DOI] [PubMed] [Google Scholar]
- 38.Arridge S. R., Hebden J. C., “Optical imaging in medicine: II. Modelling and reconstruction,” Phys. Med. Biol. 42(5), 841–853 (1997). 10.1088/0031-9155/42/5/008 [DOI] [PubMed] [Google Scholar]
- 39.Godavarty A., Sevick-Muraca E. M., Eppstein M. J., “Three-dimensional fluorescence lifetime tomography,” Med. Phys. 32(4), 992–1000 (2005). 10.1118/1.1861160 [DOI] [PubMed] [Google Scholar]
- 40.Yalavarthy P. K., Pogue B. W., Dehghani H., Carpenter C. M., Jiang S., Paulsen K. D., “Structural information within regularization matrices improves near infrared diffuse optical tomography,” Opt. Express 15(13), 8043–8058 (2007). 10.1364/OE.15.008043 [DOI] [PubMed] [Google Scholar]
- 41.Bremer C., Bredow S., Mahmood U., Weissleder R., Tung C. H., “Optical imaging of matrix metalloproteinase-2 activity in tumors: feasibility study in a mouse model,” Radiology 221(2), 523–529 (2001). 10.1148/radiol.2212010368 [DOI] [PubMed] [Google Scholar]
- 42.Soubret A., Ripoll J., Ntziachristos V., “Accuracy of fluorescent tomography in the presence of heterogeneities: study of the normalized Born ratio,” IEEE Trans. Med. Imaging 24(10), 1377–1386 (2005). 10.1109/TMI.2005.857213 [DOI] [PubMed] [Google Scholar]
- 43.Ntziachristos V., Weissleder R., “Charge-coupled-device based scanner for tomography of fluorescent near-infrared probes in turbid media,” Med. Phys. 29(5), 803–809 (2002). 10.1118/1.1470209 [DOI] [PubMed] [Google Scholar]
- 44.Kepshire D. S., Davis S. C., Dehghani H., Paulsen K. D., Pogue B. W., “Subsurface diffuse optical tomography can localize absorber and fluorescent objects but recovered image sensitivity is nonlinear with depth,” Appl. Opt. 46(10), 1669–1678 (2007). 10.1364/AO.46.001669 [DOI] [PubMed] [Google Scholar]
- 45.Kepshire D., Davis S. C., Dehghani H., Paulsen K. D., Pogue B. W., “Fluorescence tomography characterization for sub-surface imaging with protoporphyrin IX,” Opt. Express 16(12), 8581–8593 (2008). 10.1364/OE.16.008581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Graves E. E., Yessayan D., Turner G., Weissleder R., Ntziachristos V., “Validation of in vivo fluorochrome concentrations measured using fluorescence molecular tomography,” J. Biomed. Opt. 10(4), 44019 (2005). 10.1117/1.1993427 [DOI] [PubMed] [Google Scholar]
- 47.Hervé L., Koenig A., Da Silva A., Berger M., Boutet J., Dinten J. M., Peltié P., Rizo P., “Noncontact fluorescence diffuse optical tomography of heterogeneous media,” Appl. Opt. 46(22), 4896–4906 (2007). 10.1364/AO.46.004896 [DOI] [PubMed] [Google Scholar]
- 48.Brooksby B., Jiang S., Dehghani H., Pogue B. W., Paulsen K. D., Weaver J., Kogel C., Poplack S. P., “Combining near-infrared tomography and magnetic resonance imaging to study in vivo breast tissue: implementation of a Laplacian-type regularization to incorporate magnetic resonance structure,” J. Biomed. Opt. 10(5), 051504 (2005). 10.1117/1.2098627 [DOI] [PubMed] [Google Scholar]
- 49.D. P. Cormode, P. A. Jarzyna, W. J. M. Mulder, and Z. A. Fayad, “Modified natural nanoparticles as contrast agents for medical imaging,” Adv. Drug Deliv. Rev. (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]


