Detecting the onset of the lateralized readiness potential: A comparison of available methods and procedures

Abstract

Studies that measure the onset of the lateralized readiness potential (LRP) could well provide researchers with important new data concerning the information-processing locus of experimental effects of interest. However, detecting the onset of the LRP has proved difficult. The present study used computer simulations involving both human and artificial data, and both stimulus- and response-locked effects, to compare a wide variety of techniques for detecting and estimating differences in the onset latency of the LRP. Across the two sets of simulations, different techniques were found to be the most accurate and reliable for the analysis of stimulus- and response-locked data. On the basis of these results, it is recommended that regression-based methods be used to analyze most LRP data.

One of the advantages of using event-related brain potentials (ERPs) in addition to the traditional measures of response time (RT) and accuracy is that ERPs can provide online, temporal markers for various mental processes of interest (see, e.g., Coles, 1989; Kutas & Van Petten, 1994). RT and accuracy indicate only the total amount of time required to do some task and whether the task was performed correctly. Furthermore, for those trials on which no overt response is made(e.g., on “no-go” trials), no direct data concerning the timing of mental events can be collected using traditional measures. In contrast, ERPs can provide detailed time-course information about the processes that intervene between stimulus and response, as well as information about the behavior of processes that are active on “no-go” trials. For these reasons, many questions that have proved difficult to answer using traditional measures are now being addressed using ERPs.

A powerful application of ERPs is illustrated by studies that attempt to assign a processing locus to some known effect (see, e.g., Coles, Gratton, Bashore, Eriksen, & Donchin, 1985; Hillyard & Münte, 1984). Assume, for example, that some manipulation has been shown to have an effect on RT or accuracy, but that there is also some debate as to whether this effect arises within perceptual or subsequent processes. On the assumption that an ERP component related to perception has been identified, a critical study can be conducted. The perceptual model predicts that the manipulation will affect the perceptual ERP component; for example, the component will occur later in the condition with longer RTs. In contrast, models that place the locus of the effect after perception predict no differences in any ERP component that is related to perceptual processing.

Stimulus- Versus Response-Locked Logic

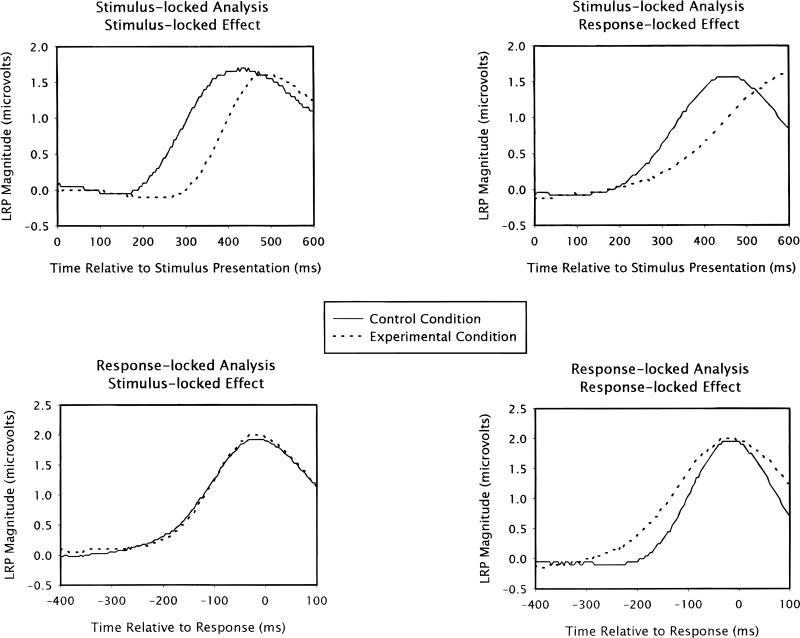
This above type of logic can also be applied to motor-related processes, and becomes especially compelling when both stimulus-and response-locked waveforms are examined (see, e.g., Hackley & Valle-Inclán, 1999; Leuthold, Sommer, & Ulrich, 1996; Mordkoff, Miller, & Roch, 1996; Osman, Moore, & Ulrich, 1995).¹ To illustrate this form of stimulus- versus response-locked logic, consider the lateralized readiness potential (LRP), which is an online marker of response preparation (for an introduction and review, see Coles, 1989, or Miller & Hackley, 1992). As an initial example, assume that a given experimental manipulation affects only some process that precedes response preparation (see left-side panels of Figure 1). In this case, the stimulus-locked LRP will begin later in the slower conditions, because the processes that precede the one that produces the LRP are being prolonged. At the same time, the response-locked LRPs from all conditions will be the same, because the manipulation does not affect the motor-related process that actually produces the LRP. In general, any manipulation that affects only premotor processes will cause a delay in the onset of the stimulus-locked LRP, but no change in the onset of the response-locked LRP. In what follows, this pattern of results will be referred to as a “stimulus-locked effect,” because a difference in LRP onset appears only in the stimulus-locked analysis. Alternative names for this same pattern would be “pre-onset effect” or “premotor effect.”

Figure 1.

Grand-average stimulus-locked lateralized readiness potential (LRP) waveforms (upper panels) and grand-average response-locked LRP waveforms (lower panels) exhibiting either a stimulus-locked effect (left-side panels) or a response-locked effect (right-side panels).

Now assume that the manipulation affects some motor process, instead, such that response preparation has a longer duration (see right-side panels of Figure 1). In this case, the stimulus-locked LRPs from all conditions will have the same onset, because the processes that precede response preparation are unaffected by the manipulation. At the same time, the response-locked LRPs will be “stretched” in the slower conditions, because response preparation is being prolonged. Put differently: the time required for the LRP to rise from onset to the level required to activate an overt response will be extended, because (for example) the accrual of activation within motor processes is being slowed by the experimental manipulation. In general, any manipulation that affects the preparation of responses will cause a change in the onset of the response-locked LRP, but no change in the onset of the stimulus-locked LRP. This phenomenon will be referred to as a “response-locked effect,” because a difference in LRP onset appears only in the response-locked analysis. The alternative labels in this case would be “postonset effect” or “motoric effect.”

According to stimulus- versus response-locked logic, if an effect is observed in the onset of the stimulus-locked LRP, but not in the response-locked LRP, then the manipulation must have affected some process that occurs prior to response preparation. Conversely, if an effect is observed in the onset of the response-locked LRP, but not in the stimulus-locked LRP, then the manipulation must have affected some process involved in response preparation or response execution. Within the cognitive literature, several unresolved debates exist concerning the loci of certain effects (e.g., early vs. late selection; the locus of inhibition-of-return; the locus of response competition) that might be addressed using stimulus- versus response-locked logic. The one obstacle to applying this logic is that detecting the onset of the LRP can be difficult due to the low signal-to-noise ratio of electroencephalographic (EEG) signals. The goal of the present report was to evaluate the various methods and procedures for detecting the onset of the LRP.

Methods and Procedures for Estimating LRP Onsets

A variety of methods for identifying the onset of the LRP in average waveforms have been proposed. The popular methods can be grouped as three general types. In addition, there are two different procedures for averaging LRPs and calculating the variability of onset values across subjects.²

Criterion-based methods

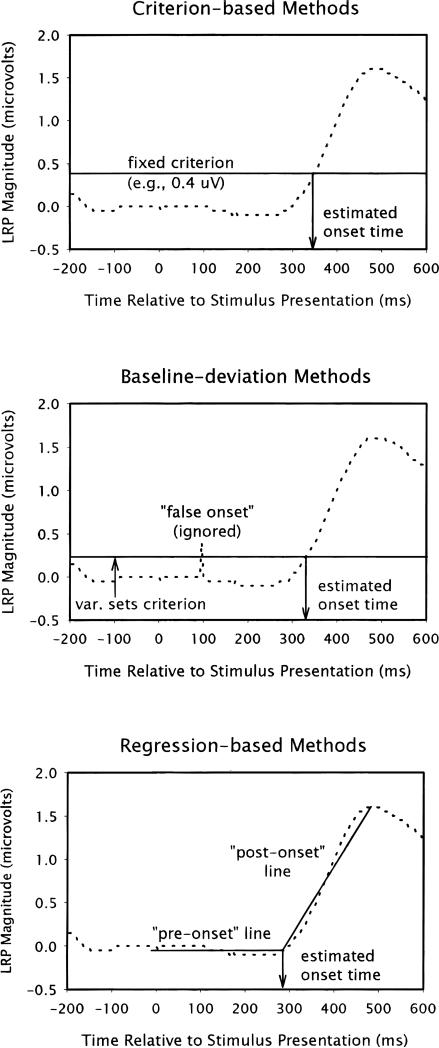
identify the onset of the LRP as the first point in time that the LRP exceeds some arbitrary value (see, e.g., Osman & Moore, 1993; Smulders, Kenemans, & Kok, 1996). The criterion is defined in one of two ways: as a certain proportion of the maximum value of the LRP observed in the condition (i.e., “relative-criterion” methods; e.g., 30% of the height of the peak), or as a certain fixed value used for all conditions (i.e., “fixed-criterion” methods; e.g., 0.6 μV). These methods are the easiest to use and appear to be the most popular (see upper panel of Figure 2 for an example).

Figure 2.

Schematic examples of a criterion-based method of lateralized readiness potential (LRP) onset detection (upper panel), a baseline-deviation method (middle panel), and a regression-based method (lower panel).

Baseline-deviation methods

define the onset of the LRP as the first point in time that the LRP consistently exceeds some value that is equal to the mean plus a multiple of the standard deviation of the LRP during some baseline period (e.g., 2.5 SDs above the mean of the baseline, which is usually reset to zero before the analysis). Another label for this method—which helps to capture the logic involved—is “emergence-from-noise”: the onset of the LRP is defined as the time when the LRP “rises up” out of the noise that is observed during the prestimulus period. Baseline-deviation methods are similar to criterion-based methods in that both define onset as the time when the LRP exceeds some arbitrary value; the two methods may at first appear to differ only in terms of how the criterion is calculated. However, they usually differ in another important respect, which is why they are listed here separately: baseline-deviation methods have also required that the LRP consistently exceed the criterion (see Osman, Bashore, Coles, Donchin, & Meyer, 1992). This is done, for example, by verifying that the mean of the LRP continues to be higher than the noise-based criterion within both of two, 50-ms windows following the point of possible onset; if this two-window rule is not obeyed, then the “false onset” is ignored and the search for the actual onset continues (see middle panel of Figure 2 for an example). Although the “consistently exceed” element is not inherent to the baseline-deviation method (and could be added to any of the criterion-based methods reviewed above), it was always used here because this method appears to be standard practice in the literature.

Regression-based methods

are the most recent development and operate in a different manner to both of the methods already mentioned above. These new methods define the onset of the LRP as the “break-point” between two intersecting straight lines that are fit to the LRP waveform (see, e.g., Schwarzenau, Falkenstein, Hoorman, & Hohsbein, 1998). In general, one of the lines is fit to the putative preonset segment of the LRP, whereas another line is fit to the segment that rises to the peak (see lower panel of Figure 2 for an example). The subtypes of this method differ in terms of the degrees of freedom (DF) that are afforded the two lines during the fitting procedure: 1df, the preonset line starts at the time of stimulus presentation and is forced to be flat at a height of zero, while the terminus of the rising line is locked at the time and the height of the peak, such that only the time of the intersection can vary; 2Rdf, as above, except the preonset line is allowed to have a slope, but is restricted to negative slopes (as might be observed when the LRP shows an early “dip”; see, e.g., Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988), such that the time and height of the intersection both vary, but the height must be equal to or less than zero; 2Udf, as above, except the pre-onset line is allowed to have any slope (unrestricted), such that the time and height of intersection both vary; and 4df, the origin of the preonset line is locked at the time of stimulus presentation and the terminus of the rising line is locked at the time of the peak, but no other restrictions are made, such that the height of the origin of the preonset line, the height of terminus of the rising line, and the time and height of the intersection are all allowed to vary. (Another name for the 4df method is “segmented regression.”) In all subtypes of the regression-based method, the two lines are found using least-squares techniques— minimizing the root mean squared difference between the fitted lines and the LRP—and the time of the intersection is taken as the estimated onset of the LRP.

Turning now to the ways in which the data from different subjects can be combined for statistical purposes, there are two different statistical procedures.

Single-subject procedures

apply a given method of onset detection to the average LRP waveform from each condition for each subject (separately) and use the variability of these values across conditions and subjects to conduct the hypothesis test. Thus, this procedure corresponds closely (but not exactly) to how response time and accuracy data are usually analyzed. The appropriate statistical test also parallels that used for traditional dependent measures, with an error term that represents the residual (unexplained) variance within the conditions.

Jack-knife procedures

first apply a given method of onset detection to the grand-average LRP waveform from each condition to estimate the time of LRP onset. (The grand-average waveform for a condition is the average of all of the subject averages for that condition.) Second, the same method is applied to N different “jack-knifed” subsample grand-averages; in each case, the data from one subject is omitted from the grand-average to create the subsample grand-average. The values of the onset times across the N subsamples are then used to calculate the standard error of onset time (s _O̵ using the following formula:

$$s_{\stackrel{‒}{O}}=\sqrt{\{(N-1)\cdot \Sigma {(O_{-i}-\stackrel{‒}{O})}^2∕N\}},$$ (1)

where N is the number of subjects, O_–i is the onset found using the subsample grand-average that omitted subject i, and O̵ is the mean of the estimated onsets across all N subsamples.³

In theory, with three different methods of detecting the onset of the LRP and two different procedures for combining the data across subjects, there exist six general ways to analyze the results from any given study. Some of these combinations have not been used, but the present study tested them all (and each method has multiple subtypes), which created the need for a shorthand coding scheme. In what follows, each method/procedure combination will be called a “technique” and will be denoted by a two-part label. The first two letters of each label indicate the statistical procedure: SS for single-subject and JK for jack-knife. The remaining characters indicate the specific onset-detecting method: X% (e.g., 30%) or XμV (e.g., 0.4μV) for criterion-based methods; Xsd (e.g., 2.0sd) for baseline-deviation methods; or Xdf (e.g., 2Rdf) for regression-based methods.

Detecting Onsets Versus Estimating Differences in Onset Times

To this point, the discussion has focused on detecting the onset of the LRP in a given condition. However, what researchers are usually concerned with are the differences in the LRP- onset latencies between conditions. Furthermore, as Miller et al. (1998) argued, for most applications, the only requirement of a useful onset-detecting technique is that it produce the correct difference between conditions. With regard to the use of stimulus- versus response-locked logic, for example, a stimulus-locked effect should produce a significant difference only in the analysis of stimulus-locked data, whereas a response-locked effect should evoke a significant difference only in the response-locked analysis. To be consistent with Miller et al., the present study also reports the data in terms of differences in LRP onsets between conditions. However, in contrast to the previous study, the issue of detecting the actual onset of the LRP in a single condition is also addressed.

Overview

To evaluate the relative merits of the various techniques for estimating a difference in LRP onsets, Miller et al. (1998) conducted a simulation study and compared the values produced by many techniques. Using the labels introduced above, Miller et al. recommended the use of JK50% to analyze stimulus-locked data, and the use of JK90% to analyze response-locked data. It should be noted, however, that Miller et al. did not examine any regression-based methods, as none had yet appeared in the literature. Miller et al. also omitted a few specific combinations of method and procedure. One goal of the present study, therefore, was to extend the study of Miller et al. to include a wider range of possible techniques.

Another reason for conducting a new set of stimulations was to establish the ability of the various techniques to discriminate between stimulus- and response-locked effects. Previous studies reported on the ability of various techniques to accurately measure differences in LRP onsets (Miller et al., 1998), or on the ability of various methods to detect a certain type of effect in either stimulus-or response-locked data (Smulders et al., 1996), but none have considered how well a given technique can measure both stimulus-and response-locked effects when either is possible. As noted above, to apply stimulus- versus response-locked logic, one must be able to discriminate between stimulus- and response-locked effects. A secondary goal of the present study was, therefore, to come to some conclusion as to which techniques are the most accurate and reliable when both stimulus- and response-locked effects are considered simultaneously.

Finally, in the simulation study of Miller et al. (1998), two different routines were used to create the LRP waveforms that embodied a response-locked effect. Many techniques produced accurate and reliable estimates of the onset differences when the data were created using the primary routine. (This routine simulated a response-locked effect by shifting the point of the response, while leaving the LRP unchanged.) However, this routine was based on assumptions that the authors acknowledged would seldom be true. In particular, according to the primary routine, manipulations of motor-related processes do not change the onset, size, or shape of the LRP, but only act to increase the delay between the time when the LRP reaches some arbitrary level and when an overt response is observed. This assumption is contradicted by the empirical results of Gratton et al. (1988), Hackley and Valle-Inclán (1999), and Osman et al. (1995). Unfortunately, the secondary routine—which enjoyed much higher face validity because it altered the growth of the LRP and the time of the response (described in detail below)—produced data for which none of the considered techniques could produce an accurate estimate of the difference in onsets between conditions. Therefore, it seemed particularly important that a new set of simulations be conducted and a wider range of techniques be considered.

Random-Sample Simulations

All of the possible methods for detecting the onset of the LRP have at least some face validity. The purpose of simulation studies is to determine which techniques are the most accurate and reliable. To make this determination, what is required are data for which it is known what size and what type of effect is involved, so that the estimated value of the onset difference can be compared with the true value. At the same time, the data need to be realistic, in that they must resemble the LRPs produced by humans. The simulation study conducted by Miller et al. (1998) met both of these criteria by randomly sampling from actual (human) data and artificially manipulating the LRPs and RTs to induce each of the two types of effect. The first study to be reported here not only used the same general approach to LRP simulation, but also used the same data.⁴

The process of simulation involved several steps. For each simulated experiment, 8 subjects were selected without replacement from the entire set of 20. For each subject within an experiment, 100 right- and 100 left-hand-response trials were selected at random without replacement. Half of these data were assigned to the control condition and half were assigned to the experimental condition. For each trial within the control condition, the data were left unchanged and the mean RT and the average stimulus- and response-locked LRPs were calculated in the usual manner. For each trial within the experimental condition, the LRPs were adjusted to simulate the desired type of effect (details below) and the RT was increased by 100 ms. Following these adjustments, the mean RT and the stimulus- and response-locked LRPs were calculated in the same manner as in the control condition. Finally, the data from all 8 subjects were analyzed using each of 36 different techniques. This entire process was repeated 200 times, simulating 100 experiments involving a stimulus-locked effect and 100 experiments involving a response-locked effect.

Simulation of Stimulus- and Response-Locked Effects

As stated above, within the control condition, no adjustments were made to the sampled data. Within the experimental condition, the LRPs were altered to simulate either a 100-ms, stimulus-locked effect, or a 100-ms, response-locked effect, and each RT was also increased by 100 ms. To simulate a 100-ms, stimulus-locked effect, the entire LRP waveform was shifted by 100 ms, such that the initial segment of the poststimulus LRP was a “repeat” of the prestimulus, baseline LRP. In summary, all of the data from the trial were delayed by 100 ms, as would be the case if premotor processes were extended by 100 ms. The left-side panels of Figure 1 display the stimulus- and response-locked, grand-average LRPsãcross all 20 subjects) that were produced in one “run” using this method of simulating a stimulus-locked effect.

To simulate a 100-ms, response-locked effect, the 250 ms of the LRP immediately preceding the response was “stretched” by 100 ms and the sampled RT was also increased by 100 ms. This adjustment was done using the second routine developed by Miller et al. (1998; see pp. 110–111). First, a “correction” waveform was calculated for each subject separately. This waveform was the difference between the average, stimulus-locked LRPûsing all of the data from the subject) and the same waveform after the 250 ms immediately preceding the response had been resampled to extend over a 350-ms period.⁵ Then, on each trial within the experimental condition, the correction waveform was added to the sampled LRP and 100 ms were added to RT. This process extended the “rise time” of the stimulus- and response-locked LRP by 100 ms, as would be the case if motor processes were extended by 100 ms. The right-side panels of Figure 1 display the stimulus- and response-locked, grand-average LRPs produced using this method of simulating a response-locked effect.

Estimation of 100-ms Stimulus- and Response-Locked Effects

Table 1 summarizes the results from the 200 simulated experiments. The left four columns provide the mean estimates (M ) and standard deviations of the estimates (SD) when the experimental and control conditions differed in terms of a 100-ms, stimulus-locked effect. As can be seen, nearly all techniques produced the “correct” mean estimates of 100 ms in the stimulus-locked analysis and 0 ms in the response-locked analysis. The main difference across techniques was in the standard deviations. Replicating and extending the findings of Miller et al. (1998), the least variable techniques were those that used a criterion-based method of onset detection, coupled with a jack-knife procedure for combining data across subjects.

Table 1.

Mean (M) and Standard Deviation (SD) of the Estimated Difference in LRP Onset From the Stimulus-Locked (S-L) Analysis and the Response-Locked R-L) Analysis of Data Involving Either a 100-ms, S-L Effect or a 100-ms, R-L Effect for Each of 36 Different Techniques

	100-ms, Stimulus-locked effect				100-ms, Response-locked effect
	S-L analysis		R-L analysis		S-L analysis		R-L analysis
Technique	M	SD	M	SD	M	SD	M	SD
Single-subject procedure, baseline-deviation method
SS 2.0sd	77.7	54.5	12.8	44.8	35.7	46.4	71.5	40.6
SS 2.5sd	83.3	42.6	7.5	43.1	39.3	45.8	69.0	39.7
SS 3.0sd	94.4	47.4	8.1	39.6	42.5	49.5	65.6	34.4
Jack-knife procedure, baseline-deviation method
JK 2.0sd	103.9	100.7	–2.6	109.5	32.6	78.2	97.4	87.3
JK 2.5sd	100.3	94.3	3.8	111.9	30.1	68.9	79.4	67.0
JK 3.0sd	103.4	82.5	–0.2	92.5	32.3	74.9	75.3	65.0
JK 4.0sd	101.6	54.9	13.4	51.7	37.6	43.5	62.6	48.4
JK 5.0sd	84.9	52.4	9.3	39.9	50.3	44.6	64.3	44.9
JK 6.0sd	101.1	51.6	3.6	40.5	47.3	44.1	59.8	47.5
JK 7.0sd	105.7	38.6	0.8	36.7	50.2	56.4	55.4	44.8
JK 8.0sd	90.3	87.6	20.3	85.1	75.4	92.1	58.3	67.8
JK 9.0sd	98.2	73.4	21.1	74.3	70.9	85.0	59.4	59.3
JK 10.0sd	104.0	60.7	22.4	68.2	63.8	78.3	57.4	55.8
Single-subject procedure, relative-criterion method
SS 10%	61.4	68.8	35.1	57.6	34.2	62.7	72.8	59.0
SS 30%	90.6	42.0	3.3	27.1	42.2	41.0	61.0	32.9
SS 50%	91.7	29.0	0.3	13.6	48.3	35.1	48.7	19.7
SS 70%	95.9	21.3	0.1	11.6	55.4	27.6	38.1	18.6
SS 90%	97.8	16.7	–0.7	12.4	68.1	23.1	23.7	16.7
Jack-knife procedure, relative-criterion method
JK 10%	98.9	78.8	–3.2	53.7	42.9	64.0	78.7	67.5
JK 30%	102.4	17.5	–1.3	19.1	47.3	19.4	59.2	22.3
JK 50%	101.4	13.2	–1.4	11.9	52.1	17.1	46.6	15.3
JK 70%	100.5	13.5	–1.0	8.9	59.2	17.5	34.6	11.2
JK 90%	98.4	15.4	–0.6	7.6	72.6	19.8	20.4	10.7
Jack-knife procedure, fixed-criterion method
JK 0.2μV	100.1	49.1	–3.5	49.7	40.9	51.9	79.8	62.4
JK 0.4μV	103.5	20.0	–3.0	26.7	40.4	22.8	66.7	30.3
JK 0.6μV	103.3	18.7	–3.2	18.9	42.1	21.5	55.2	22.0
JK 0.8μV	104.7	18.7	–3.4	17.3	43.3	23.7	48.7	19.5
JK 1.0μV	100.4	18.7	–3.8	16.5	47.8	24.5	40.8	17.6
Single-subject procedure, regression-based method
SS 1df	92.8	32.3	–0.9	27.7	25.9	33.3	68.6	31.0
SS 2Rdf	93.3	31.8	–2.2	25.6	21.9	32.2	70.3	29.1
SS 2Udf	96.5	30.8	–1.8	26.0	20.2	33.2	78.4	27.5
SS 4df	93.1	27.2	2.3	25.8	25.6	28.2	66.0	27.6
Jack-knife procedure, regression-based method
JK 1df	104.0	29.1	–3.6	28.6	29.7	29.3	86.8	33.2
JK 2Rdf	103.1	22.4	1.1	24.1	24.0	25.6	78.6	30.6
JK 2Udf	104.6	22.5	–0.8	25.9	25.5	25.7	87.0	28.9
JK 4df	102.0	19.8	7.1	25.6	26.8	22.4	72.2	32.5

Note: SS = single-subject procedure; JK = jack-knife procedure; xsd = baseline-deviation method; x% = relative-criterion method; xμV = fixed-criterion method; and xdf = regression-based method.

The right four columns of Table 1 provide the means and standard deviations when the experimental and control conditions differed in terms of a 100-ms, response-locked effect. In contrast to what was found for the stimulus-locked effect, very few techniques produced means close to 0 ms in the stimulus-locked analysis and 100 ms in the response-locked analysis. (This finding also confirms the observations of Miller et al., 1998.) For the methods that use arbitrary criteria to detect the onset of the LRP, this finding is not particularly surprising; nor is it surprising that these methods become less accurate as higher criteria are used. When the slope of the LRP differs between conditions, the “detection lag” between the moment when the LRP actually begins and when it exceeds the criterion will increase moreŵith increasing criterion) in the condition with the lower slope. In contrast, methods that attempt to identify the actual start of the LRP appear to be much less affected by changes in slope. Consistent with this, the only techniques that were consistently within 30 ms of the “correct” values were those that used a regression-based method of detecting the onset of the LRP.

Discriminating Between Stimulus- and Response-Locked Effects

As explained above, to apply stimulus- versus response-locked logic to a set of LRP data, a technique is needed that is capable of discriminating between stimulus- and response-locked effects. Different techniques can be used to analyze stimulus- and response-locked data, but the same technique must be used for both types of effect, because the type of effect is not known in advance. Therefore, in what follows, stimulus- and response-locked analyses are considered separately, but each of the techniques is used simultaneously to estimate the sizes of stimulus- and response-locked effects. To be clear: a “good” technique for the analysis of stimulus-locked LRPs should find a significant difference between LRP onsets when the data include a stimulus-locked effect, but should detect no difference when the data include (only) a response-locked effect. Similarly, a “good” technique for analyzing response-locked LRPs should find a significant difference when the data include a response-locked effect, but should detect no difference when there is (only) a stimulus-locked effect.

Tables 2 and 3 provide various measures of how well each of the techniques could discriminate between a stimulus- and response-locked effect when applied to stimulus-locked data (Table 2) and response-locked data (Table 3). These measures are expressed in terms that describe the decision that would be made by a researcher who set aãlpha) at .05. The first two columns provide the hit and false-alarm rates. A hit is here defined as the finding of a significant difference from zero (by t test) in the analysis that “should” have produced an estimate of 100 ms; the left-most columns in Tables 2 and 3 provide the proportion of simulated experiments that produced this result. A false-alarm is defined as the finding of a significant difference from zero in the analysis that “should” have produced an estimate of 0 ms; the second column in each table reports the proportion of simulated experiments that produced this result.

Table 2.

Proportions of Hits and False Alarms (FA); Measures of Sensitivity (A′) and Bias (B″); Experimental Error Rate (EER); Root Mean Squared Error (RMSE) of the Estimated Difference; and Partition Score (PS) for Each of 36 Techniques When Applied to Stimulus-Locked Data

	Ability to discriminate between types of effect					Accuracy
Technique	Hits	FA	A′	B″	EER	RMSE	PS
Single-subject procedure, baseline-deviation method
SS 2.0sd	0.26	0.10	0.70	0.36	0.42	33.66	0.69
SS 2.5sd	0.33	0.14	0.70	0.29	0.40	32.39	0.68
SS 3.0sd	0.42	0.16	0.73	0.29	0.37	30.56	0.69
Jack-knife procedure baseline-deviation method
JK 2.0sd	0.28	0.02	0.80	0.82	0.37	23.39	0.76
JK 2.5sd	0.29	0.06	0.76	0.57	0.38	21.31	0.77
JK 3.0sd	0.43	0.04	0.83	0.73	0.30	23.11	0.76
JK 4.0sd	0.23	0.00	0.79	0.89	0.38	26.66	0.73
JK 5.0sd	0.40	0.12	0.75	0.39	0.36	38.65	0.63
JK 6.0sd	0.58	0.14	0.82	0.34	0.28	33.49	0.68
JK 7.0sd	0.66	0.22	0.81	0.13	0.28	35.93	0.68
JK 8.0sd	0.29	0.14	0.67	0.26	0.42	54.15	0.55
JK 9.0sd	0.38	0.18	0.69	0.23	0.40	50.19	0.58
JK 10.0sd	0.44	0.12	0.77	0.40	0.34	45.26	0.62
Single-subject procedure, relative-criterion method
SS 10%	0.08	0.07	0.53	0.06	0.50	45.53	0.64
SS 30%	0.55	0.25	0.74	0.14	0.35	31.26	0.68
SS 50%	0.69	0.48	0.68	–0.08	0.40	35.16	0.65
SS 70%	0.91	0.68	0.74	–0.45	0.38	39.37	0.63
SS 90%	0.97	0.81	0.75	–0.68	0.42	48.18	0.59
Jack-knife procedure, relative-criterion method
JK 10%	0.48	0.19	0.74	0.24	0.36	30.37	0.70
JK 30%	0.97	0.60	0.83	–0.78	0.32	33.55	0.68
JK 50%	1.00	0.73	0.81	–0.95	0.36	36.85	0.66
JK 70%	1.00	0.80	0.79	–0.94	0.40	41.86	0.63
JK 90%	0.92	0.74	0.72	–0.45	0.41	51.39	0.58
Jack-knife procedure, fixed-criterion method
JK 0.2μV	0.73	0.23	0.83	0.05	0.25	28.91	0.71
JK 0.4μV	0.95	0.39	0.88	–0.67	0.22	28.81	0.72
JK 0.6μV	0.97	0.50	0.86	–0.79	0.26	29.94	0.71
JK 0.8μV	0.99	0.42	0.89	–0.92	0.22	30.98	0.71
JK 1.0μV	0.97	0.44	0.87	–0.79	0.24	33.77	0.68
Single-subject procedure, regression-based method
SS 1df	0.67	0.09	0.88	0.46	0.21	19.68	0.78
SS 2Rdf	0.67	0.12	0.86	0.35	0.22	16.84	0.81
SS 2Udf	0.74	0.17	0.86	0.15	0.22	14.70	0.83
SS 4df	0.71	0.19	0.84	0.14	0.24	19.35	0.78
Jack-knife procedure, regression-based method
JK 1df	0.80	0.12	0.91	0.20	0.16	21.40	0.78
JK 2Rdf	0.82	0.08	0.93	0.33	0.13	17.28	0.81
JK 2Udf	0.86	0.04	0.95	0.52	0.09	18.60	0.80
JK 4df	0.92	0.10	0.95	–0.10	0.09	19.03	0.79

Note: SS = single-subject procedure; JK = jack-knife procedure; xsd = baseline-deviation method; x% = relative-criterion method; xμV = fixed-criterion method; and xdf = regression-based method.

Table 3.

Proportions of Hits and False Alarms (FA); Measures of Sensitivity (A′) and Bias (B″); Experimental Error Rate (EER); Root Mean Squared Error (RMSE) of the Estimated Difference; and Partition Score (PS) for Each of 36 Techniques When Applied to Response-Locked Data

	Ability to discriminate between types of effect					Accuracy
Technique	Hits	FA	A′	B″	EER	RMSE	PS
Single-subject procedure, baseline-deviation method
SS 2.0sd	0.34	0.02	0.82	0.84	0.34	29.95	0.85
SS 2.5sd	0.38	0.02	0.83	0.85	0.32	31.48	0.90
SS 3.0sd	0.38	0.02	0.83	0.85	0.32	34.83	0.89
Jack-knife procedure, baseline-deviation method
JK 2.0sd	0.08	0.00	0.73	0.75	0.46	03.20	1.03
JK 2.5sd	0.10	0.00	0.75	0.80	0.45	20.73	0.95
JK 3.0sd	0.08	0.00	0.74	0.76	0.46	24.72	1.00
JK 4.0sd	0.10	0.02	0.72	0.64	0.46	38.61	0.82
JK 5.0sd	0.26	0.00	0.80	0.90	0.37	36.32	0.87
JK 6.0sd	0.22	0.00	0.79	0.89	0.39	40.29	0.94
JK 7.0sd	0.22	0.00	0.79	0.89	0.39	44.62	0.99
JK 8.0sd	0.10	0.02	0.72	0.64	0.46	44.14	0.74
JK 9.0sd	0.13	0.02	0.74	0.70	0.44	43.25	0.74
JK 10.0sd	0.06	0.02	0.68	0.48	0.48	45.42	0.72
Single-subject procedure, relative-criterion method
SS 10%	0.32	0.03	0.80	0.76	0.36	36.83	0.67
SS 30%	0.65	0.01	0.91	0.92	0.18	39.07	0.95
SS 50%	0.74	0.02	0.93	0.82	0.14	51.32	0.99
SS 70%	0.65	0.02	0.90	0.84	0.18	61.91	1.00
SS 90%	0.30	0.02	0.80	0.83	0.36	76.26	1.03
Jack-knife procedure, relative-criterion method
JK 10%	0.18	0.01	0.78	0.87	0.42	21.40	1.04
JK 30%	0.59	0.01	0.89	0.92	0.21	40.77	1.02
JK 50%	0.70	0.00	0.92	0.95	0.15	53.45	1.03
JK 70%	0.58	0.01	0.89	0.92	0.22	65.44	1.03
JK 90%	0.18	0.00	0.79	0.93	0.41	79.56	1.03
Jack-knife procedure, fixed-criterion method
JK 0.2μV	0.17	0.02	0.76	0.76	0.42	20.35	1.05
JK 0.4μV	0.36	0.00	0.84	0.96	0.32	33.39	1.05
JK 0.6μV	0.52	0.00	0.88	0.96	0.24	44.86	1.06
JK 0.8μV	0.53	0.01	0.88	0.92	0.24	51.38	1.08
JK 1.0μV	0.44	0.01	0.85	0.92	0.28	59.26	1.10
Single-subject procedure, regression-based method
SS 1df	0.59	0.02	0.89	0.85	0.22	31.42	1.01
SS 2Rdf	0.61	0.01	0.90	0.92	0.20	29.72	1.03
SS 2Udf	0.69	0.01	0.92	0.91	0.16	21.61	1.02
SS 4df	0.54	0.00	0.88	0.96	0.23	34.06	0.97
Jack-knife procedure, regression-based method
JK 1df	0.41	0.00	0.85	0.96	0.30	13.48	1.04
JK 2Rdf	0.43	0.00	0.85	0.96	0.28	21.45	0.99
JK 2Udf	0.40	0.00	0.85	0.96	0.30	13.05	1.01
JK 4df	0.43	0.01	0.85	0.92	0.29	28.25	0.91

Note: SS = single-subject procedure; JK = jack-knife procedure; xsd = baseline-deviation method; x% = relative-criterion method; xμV = fixed-criterion method; and xdf = regression-based method.

To facilitate the process of deciding which techniques are capable of discriminating between stimulus- and response-locked effects, three combined measures of each technique were calculated. The columns labeled A′ and B′ provide the nonparametric combination of the hit and false-alarm rates. (A′ is an estimate of sensitivity and B′ is an estimate of bias; see Aaronson & Watts, 1987.) A value of A′ near 1.00 indicates a very sensitive technique, with zero indicating “chance”; a value of B0 above or below zero indicates a technique with a bias against or in favor of rejecting the null hypothesis, respectively. Finally, the experimental error rate (EER) is here defined as:

$$\mathrm{EER}=\{(1-\text{hit rate})+\text{false-alarm rate}\}∕2,$$ (2)

which is an estimate of the probability that a researcher will come to the wrong conclusion concerning the locus of an experimental effect (on the assumption that stimulus- and response-locked effects are equally likely). On this measure, “chance” is an EER of 0.50.

As can be seen, the ability of the various techniques to discriminate between stimulus- and response-locked effects varied extensively. The criterion-based methods coupled with jack-knife procedures produced the highest hit rates in the stimulus-locked analyses, but these techniques had high false-alarm rates, as well (see Table 2). This pattern becomes understandable when one notes that criterion-based methods operate by detecting the first point that the LRP exceeds some arbitrary proportion of the maximum height (as opposed to locating the actual onset). As this proportion is increased, the point of detection moves farther from the true onset of the LRP and closer to the peak. Therefore, any manipulation that acts to alter the slope of the LRP will cause criterion-based methods to make false-alarm errors (i.e., differences will be detected in the stimulus-locked analysis). To emphasize: criterion-based methods will make false-alarm errors at a rate that is proportional to the criterion used (see Table 2). Although it is possible that prior analyses of the slope could be used to reduce this problem (see Hackley & Valle-Inclán, 1998), specific methods are not yet available and are beyond the scope of the present paper.

In contrast, regression-based methods are capable of adjusting to changes in slope and, therefore, do not suffer from the above limitation. While the power of these methods is often lower than that shown by criterion-based methods, the false-alarm rates are notably lower. Overall, the techniques that produced the best estimates from the stimulus-locked data, when both hit and false-alarm rates are considered together (i.e., when A′ or EER is the measure of quality) were those that used a regression-based method. The quality of these methods was enhanced slightly by the use of a jack-knife procedure.

For the analysis of the response-locked data, a variety of techniques produced good estimates of the type of effect (see the A9′ and EER columns in Table 3). In this case, the use of a criterion-based method with a moderate setting (i.e., 30%, 50%, or 70% of the peak) or a regression-based method worked well. In contrast to the above, however, single-subject procedures were slightly more accurate than jack-knife procedures.

Estimation Accuracy

The last set of analyses concerned the ability of the various techniques to accurately estimate the specific size of the effect being simulated. This analysis was carried out in two ways. First, the root mean squared error (RMSE) was calculated for each technique. This analysis was based on the assumptions that 100-ms differences should have been found in the stimulus-locked analyses of a stimulus-locked effect and the response-locked analyses of a response-locked effect, and that null differences should have been found in the stimulus-locked analyses of a response-locked effect and the response-locked analyses of a stimulus-locked effect. The optimal value of RMSE is zero. Second, the proportion of the two effects (summed) that was observed in the “appropriate” analysis was calculated. For example, if a certain technique produced a difference estimate of 85 ms in the stimulus-locked analysis of a stimulus-locked effect, and an estimate of 20 ms in the stimulus-locked analysis of a response-locked effect, then the partition score (PS) for that technique was 0.81 (i.e., 85 ÷ [85 + 20]). The optimal value of PS is 1.00.

The RMSE and PS results for the stimulus- and response-locked analyses are provided in the last two columns of Tables 2 and 3, respectively. In general, these results parallel those found for A9′ and EER. One noticeable difference is that whereas several of the criterion-based methods (e.g., JK50%) and regression-based methods (e.g., SS2Udf) produced relatively low levels of EER when applied to response-locked data, the regression-based methods were almost always more accurate in terms of RMSE and PS. In other words, whereas criterion- and regression-based methods have comparable accuracies when being used to make the binary decision between a stimulus- and a response-locked effect, the regression-based methods are usually more accurate at measuring the specific size of these same differences in LRP onset.

Interim Summary

Taking all the available data into account—including the results from Miller et al. (1998) and Smulders et al. (1996)—at this point we have no firm recommendations. Several of the regression-based techniques (e.g., JK2Rdf and SS1df) performed well in the stimulus-locked analysis and several techniques (e.g., JK50%, SS2Rdf, and SS1df) performed well in the response-locked analysis. Furthermore, these tentative suggestion are based almost entirely on the results that were observed in the two random-sample simulation studies, which happen to have used the same underlying data and the same, relatively large effects. Therefore, to come to more forceful conclusions, we next present the results from a second set of simulations that involved a completely different set of data and much smaller effects. These new simulations also explored whether the relative accuracies of a subset of the available techniques would be differentially affected by within-trial noise and between-subject variability.

Sine-Wave Simulations

As stated above, to perform a simulation study, the data to be analyzed must involve effects of known size and type, and the waveforms must be realistic in their timing and shape. The first set of simulations met these criteria by randomly sampling from an existing set of human data and adjusting the LRPs to include either a stimulus- or a response-locked effect. The second set of simulations used a different method: realistic LRP waveforms were generated de novo by adding noise to one cycle of a sine wave (see Smulders et al., 1996). In this case, the experimental condition differed from the control condition in terms of either a 50-ms, stimulus-locked effect, or a 50-ms, response-locked effect.

This second set of simulations had two main goals. First, we aimed to extend the first study by using different data and smaller effects. This second set can be thought of as a test for external validity. Second, we wanted to explore whether changes in either within-trial noiseãdded to LRP amplitude) or between-subject variability (in processing speed) would alter the results. Conversely, if changes in the levels of noise and variability have no noticeable influence on the pattern of resultsîn terms of which techniques are the most accurate and reliable), then this finding can only serve to increase our confidence in our final recommendations.

Simulation of Stimulus- and Response-Locked Effects

As before, the process of simulation involved several steps. For each of the eight subjects in each simulated experiment, the “targeted” mean RT for the control condition was selected independently at random from a Gaussian distribution with a mean of 400 ms and a standard deviation of δ_S (see Variability and Noise section below). This mean RT was then divided by two, providing the approximate LRP onset time for the control condition. The first interval is referred to as the “targeted pre-onset time” and the second, as the “targeted postonset time.” To simulate a stimulus-locked effect, 50 ms was added to the targeted pre-onset time; to simulate a response-locked effect, 50 ms was added to the targeted postonset time.

In the second step, 100 trials were simulated for each subject; 50 trials in the control condition and 50 trials in the experimental condition. (In contrast to the previous set of simulations, separate right- and left-hand-response trials were not required because the LRP was created directly, as opposed to be calculated as a difference between right- and left-hand trials.) Each individual trial was simulated in the following manner: First, a specific pre-onset time was created by summing four independent samples from an exponential distribution with a mean (and variance) equal to one-fourth of the “targeted” pre-onset time. Second, a specific postonset time was created by summing four independent samples from an exponential distribution with a mean equal to one-fourth of the “targeted” postonset time.⁶ The RT for the trial was the sum of the preand postonset times. Finally, the LRP for the trial was created using the same procedure as used by Smulders et al. (1996). Gaussian noise of various levels (see Variability and Noise section below) was used to simulate background EEG and smoothed using a second-order autoregression such that:

$$\mathrm{EEG}\left(t\right)=\{0.75\cdot \mathrm{EEG}(t-1)\}-\{0.50\cdot \mathrm{EEG}(t-2)\}+N(0,{\delta }_N),$$ (3)

where EEG(t) is the background EEG at timepoint t, etc., and N(0, δ_N) is a random sample from a Gaussian distribution with mean zero and standard deviation δ_N. The LRP was then added to the background EEG by aligning the onset of one cycle of a sine wave (starting at $-\frac{1}{2}\pi$) with the pre-onset time. The period of the sine wave was adjusted such that it peaked at the time of the response (i.e., the period of the sine wave was equal to twice the value of the postonset time), and the height of the sine wave was first increased by one (to eliminate negative values) and then multiplied by 125 (to set the peak at 250 units). To match the previous set of simulations, the sampling frequency was set to 250 Hz.

Once the 50 control and 50 experimental trials for a given subject had been simulated, stimulus- and response-locked LRPs and mean RT were all found in the usual manner. The entire process was repeated for each of the eight subjects in the experiment and then 14 different LRP-onset techniques were applied to the data. (These techniques were selected on the basis of their performance in the previous set of simulations.) A total of 200 different experiments were simulated at each level of within-subject noise and between-subject variability. Half of these experiments involved a stimulus-locked effect; half involved a response-locked effect.

Variability and Noise

The levels of between-subject variability and within-trial noise were manipulated across sets of simulations by altering the value of δ_S (used to select the “targeted” mean RT for each subject) and the value of δ_N (used to create the background EEG). To simulate experimental situations with low and high levels of between-subject variability, the values of 25 and 50 ms were used for δ_S. The value of 25 ms caused most subjects to have a mean RT in the control condition somewhere within a range of 350–450 ms; the value of 50 ms caused control mean RTs to range from 300 to 500 ms. Following Smulders et al. (1996), the values of δ_N were 26 and 59 (where 250 is the maximum height of the sine function), which creates signal-to-noise ratios of 0.5 and 0.1, respectively. These two ratios surround the empirical median of 0.18 reported by Möcks, Gasser, and Köhler (1988).

Estimation of 50-ms Stimulus- and Response-Locked Effects

Table 4 summarizes the results from the 800 simulated experiments that were conducted using the sine-wave methodology. Three points from these results seem noteworthy. First, paralleling what was found in the previous simulations using random samples from human data, nearly all of the techniques produced the “correct” estimates of about 50 and 0 ms, respectively, in the stimulus- and response-locked analyses of the data that involved a stimulus-locked effect (see first and second sections of Table 4). Second, again replicating the previous simulations, the criterion-based methods did not do as well as the regression-based methods when the data involved a response-locked effect (see third and fourth sections of Table 4). As before, as the relative criterion is increased (from 10% to 90% of the peak), the criterion-based methods tend to make larger and larger errors due to their inability to adjust to changes in the slope of the LRP.

Table 4.

Mean (M) and Standard Deviation (SD) of the Estimated Difference for Each of 14 Techniques From the Stimulus- and Response-Locked Analyses of a 50-ms Stimulus- and a 50-ms Response-Locked Effect, as a Function of Within-Trial Noise and Between-Subject Variability

	Low noise and low variability		Low noise and high variability		High noise and low variability		High noise and high variability
Technique	M	SD	M	SD	M	SD	M	SD
Stimulus-locked analysis of a 50-ms stimulus-locked effect
SS 10%	46.19	15.33	43.80	16.96	6.57	30.36	5.88	26.01
SS 30%	48.42	8.37	49.46	7.82	50.32	10.29	49.13	9.30
SS 50%	48.98	9.33	49.63	9.02	51.21	11.30	49.21	8.99
SS 70%	48.64	10.58	50.82	11.00	50.16	12.28	49.16	9.53
SS 90%	49.03	12.45	51.66	12.21	50.93	17.02	51.47	15.08
JK 10%	48.24	9.15	48.88	8.34	49.44	15.03	47.12	13.16
JK 30%	48.81	9.27	49.92	8.70	51.32	11.34	50.20	8.68
JK 50%	48.93	10.09	50.36	10.40	50.76	12.78	48.00	10.54
JK 70%	49.33	11.75	51.68	11.66	49.84	12.51	48.40	13.54
JK 90%	49.45	14.10	52.12	14.69	51.00	17.37	46.84	18.49
SS 1df	48.70	8.95	48.30	9.38	49.46	11.44	48.81	9.17
SS 2Rdf	48.77	9.11	48.09	9.50	49.42	12.14	48.93	9.84
JK 1df	49.17	14.99	46.08	13.69	51.88	19.07	50.04	16.69
JK 2Rdf	49.33	15.17	45.88	14.05	51.80	19.57	50.04	17.12
Response-locked analysis of a 50-ms stimulus-locked effect
SS 10%	–0.26	7.17	–0.19	7.34	18.63	34.98	19.14	37.44
SS 30%	–0.06	3.53	0.09	4.12	–0.30	5.01	–0.73	5.66
SS 50%	–0.60	3.06	–0.08	3.11	–0.24	3.83	–0.46	4.17
SS 70%	–0.11	2.43	–0.15	2.74	0.08	3.83	–0.23	3.41
SS 90%	–0.35	2.53	–0.26	2.76	0.24	4.60	–0.55	4.52
JK 10%	0.44	7.10	–0.16	7.50	1.60	12.16	0.12	12.98
JK 30%	0.00	4.02	0.20	4.43	0.84	5.67	–0.60	6.23
JK 50%	–0.16	3.36	–0.04	3.51	–0.28	4.09	–0.64	4.79
JK 70%	0.00	2.90	–0.16	3.15	–0.04	4.29	0.08	4.23
JK 90%	–0.24	2.94	–0.48	3.01	–0.40	4.82	–0.56	5.03
SS 1df	–0.08	5.15	0.58	5.37	0.20	6.49	–0.31	6.18
SS 2Rdf	–0.08	5.15	0.58	5.37	0.20	6.49	–0.30	6.18
JK 1df	0.57	5.77	0.60	6.89	0.08	7.80	–0.40	8.05
JK 2Rdf	0.57	5.77	0.60	6.89	0.08	7.80	–0.40	8.05
Stimulus-locked analysis of a 50-ms response-locked effect
SS 10%	21.43	12.07	21.55	14.39	22.20	29.21	22.29	29.24
SS 30%	26.68	7.06	25.65	7.87	28.00	8.84	26.77	9.40
SS 50%	31.11	7.47	30.02	8.46	31.63	8.91	30.39	8.18
SS 70%	34.79	9.39	34.10	9.08	33.52	9.74	34.97	10.31
SS 90%	39.77	11.58	37.96	11.08	39.12	14.82	39.99	14.82
JK 10%	18.24	7.53	18.00	9.66	23.28	18.12	20.76	16.78
JK 30%	26.76	7.50	27.28	8.68	26.28	9.07	28.28	9.77
JK 50%	31.68	8.90	31.36	9.20	31.72	9.14	31.32	11.47
JK 70%	35.20	10.40	34.92	10.82	35.04	12.20	33.96	11.24
JK 90%	40.44	12.37	38.64	13.88	38.08	15.59	37.44	16.02
SS 1df	14.90	9.19	14.62	10.02	15.99	9.16	14.52	9.91
SS 2Rdf	15.12	9.45	14.85	10.23	16.70	9.93	14.75	10.30
JK 1df	16.96	12.68	15.52	12.12	18.28	15.74	15.88	15.99
JK 2Rdf	17.28	13.07	15.44	12.37	18.88	16.12	16.20	16.50
Response-locked analysis of a 50-ms response-locked effect
SS 10%	35.02	9.24	35.89	6.91	46.09	30.80	35.74	36.23
SS 30%	30.29	4.18	29.65	4.57	30.33	5.31	30.44	6.12
SS 50%	25.34	3.09	25.08	3.41	25.49	3.78	25.34	4.34
SS 70%	19.63	2.85	19.39	2.72	19.37	3.55	19.87	3.90
SS 90%	11.02	2.72	11.08	2.72	10.98	4.28	10.72	4.55
JK 10%	34.52	8.29	34.44	8.08	35.24	10.44	35.76	14.55
JK 30%	30.28	4.32	29.80	4.94	29.80	5.75	29.96	6.51
JK 50%	25.52	3.14	25.00	3.64	26.24	3.97	25.44	4.22
JK 70%	20.20	2.96	20.08	3.20	19.36	4.18	20.64	4.44
JK 90%	12.04	2.86	11.88	3.55	10.56	6.11	12.08	5.45
SS 1df	44.17	5.99	44.09	5.66	43.31	5.98	42.40	6.28
SS 2Rdf	44.17	5.99	44.09	5.66	43.32	5.98	42.40	6.28
JK 1df	45.24	6.59	44.64	6.69	45.32	7.27	43.88	8.25
JK 2Rdf	45.24	6.59	44.64	6.69	45.32	7.27	43.88	8.25

Note: SS = single-subject procedure; JK = jack-knife procedure; x% = relative-criterion method; and xdf = regression-based method.

The third point to make with regard to the results shown in Table 4 concerns the influence (or noninfluence) of the changes in within-trial noise and between-subject variability. As can be seen by scanning across each row in the table, neither of the manipulations had much of an effect. The only exceptions to this occurred when the analysis used a criterion-based method of onset detection with an extreme setting (i.e., 10% or 90% of the peak). In these cases, the standard deviation of the estimated difference was often increased by increases in either noise or variability. In general, however, the effects of noise and variability were negligible. This pattern of null findings should be seen as encouraging, as it suggest that even large differences in either of these hard-to-control factors will not adversely affect the external validity of any given study.⁷

Discriminating Between Types of Effect and Estimation Accuracy

Tables 5 and 6 report the results from the sine-wave simulations in a manner that allows one to assess the ability of the various techniques to discriminate between a stimulus- and a response-locked effect (in terms of A′ and EER). This assessment is accomplished as a function of within-trial noise and between-subject variability (however, only the two extreme cells of the simulation design are included for reasons of economy; the other two cells produced intermediate results). These tables also report the accuracies of the 14 different techniques (in terms of RMSE and PS). As above, the series of analyses performed on the stimulus-locked data (Table 5) showed little influence of either noise or variability. More important for present purposes, however, in every case, the techniques with the lowest EER and lowest measurement error (RMSE) were the regression-based methods that used a single-subject procedure. In only one case, for example, did a criterion-based technique (using either procedure) produce an EER below 20%, whereas the single-subject, regression-based techniques never had an EER above 16%. Also important: In contrast to the previous simulations, which used randomly sampled data, in this case the use of a jack-knife procedure increased errors and lowered accuracy when combined with a regression-based method.

Table 5.

Proportions of Hits and False Alarms (FA); Measures of Sensitivity (A′) and Bias (B″); Experimental Error Rate (EER); Root Mean Squared Error (RMSE) of the Estimated Difference; and Partition Score (PS) for Each of 14 Techniques When Applied to Stimulus-Locked Data, as a Function of Within-Trial Noise and Between-Subject Variability

	Ability to discriminate between types of effect					Accuracy
Technique	Hits	FA	A′	B″	EER	RMSE	PS
Low within-trial noise and low between-subject variability
SS 10%	0.82	0.46	0.78	–0.25	0.32	15.62	0.68
SS 30%	1.00	0.89	0.76	–0.90	0.45	18.93	0.64
SS 50%	1.00	0.87	0.77	–0.91	0.44	22.02	0.61
SS 70%	0.99	0.86	0.76	–0.85	0.43	24.64	0.58
SS 90%	0.90	0.89	0.53	–0.04	0.50	28.14	0.55
JK 10%	0.89	0.35	0.86	–0.40	0.23	13.02	0.73
JK 30%	0.96	0.63	0.81	–0.72	0.34	18.96	0.65
JK 50%	0.97	0.71	0.79	–0.75	0.37	22.43	0.61
JK 70%	0.87	0.71	0.68	–0.29	0.42	24.90	0.58
JK 90%	0.71	0.61	0.60	–0.07	0.45	28.60	0.55
SS 1df	0.97	0.30	0.91	–0.76	0.16	10.62	0.77
SS 2Rdf	0.97	0.28	0.92	–0.75	0.15	10.76	0.76
JK 1df	0.49	0.05	0.84	0.68	0.28	12.02	0.74
JK 2Rdf	0.49	0.05	0.84	0.68	0.28	12.24	0.74
High within-trial noise and high between-subject variability
SS 10%	0.02	0.12	–0.78	–0.69	0.55	46.85	0.21
SS 30%	0.99	0.66	0.83	–0.92	0.34	18.95	0.65
SS 50%	1.00	0.80	0.79	–0.94	0.40	21.64	0.62
SS 70%	0.98	0.79	0.77	–0.79	0.41	24.74	0.58
SS 90%	0.86	0.61	0.73	–0.33	0.38	28.32	0.56
JK 10%	0.42	0.13	0.76	0.37	0.35	14.96	0.69
JK 30%	0.84	0.36	0.83	–0.26	0.26	20.00	0.64
JK 50%	0.75	0.43	0.75	–0.13	0.34	22.24	0.61
JK 70%	0.61	0.36	0.70	0.02	0.38	24.07	0.59
JK 90%	0.31	0.27	0.55	0.04	0.48	26.66	0.56
SS 1df	1.00	0.20	0.95	–0.94	0.10	10.34	0.77
SS 2Rdf	0.98	0.17	0.95	–0.76	0.10	10.49	0.77
JK 1df	0.33	0.03	0.80	0.77	0.35	11.23	0.76
JK 2Rdf	0.30	0.02	0.80	0.83	0.36	11.46	0.76

Note: SS = single-subject procedure; JK = jack-knife procedure; x% = relative-criterion method; and xdf = regression-based method.

Table 6.

Proportions of Hits and False Alarms (FA); Measures of Sensitivity (A′) and Bias (B″); Experimental Error Rate (EER); Root Mean Squared Error (RMSE) of the Estimated Difference; and Partition Score (PS) for Each of 14 Techniques When Applied to Response-Locked Data, as a Function of Within-Trial Noise and Between-Subject Variability

	Ability to discriminate between types of effect					Accuracy
Technique	Hits	FA	A′	B″	EER	RMSE	PS
Low within-trial noise and low between-subject variability
SS 10%	0.92	0.01	0.98	0.76	0.04	14.98	1.01
SS 30%	1.00	0.00	1.00	0.00	0.01	19.71	1.00
SS 50%	1.00	0.01	1.00	–0.33	0.01	24.66	1.02
SS 70%	1.00	0.01	1.00	–0.33	0.01	30.37	1.01
SS 90%	0.95	0.03	0.98	0.24	0.04	38.98	1.03
JK 10%	0.76	0.01	0.94	0.90	0.12	15.48	0.99
JK 30%	0.98	0.05	0.98	–0.42	0.04	19.72	1.00
JK 50%	1.00	0.09	0.98	–0.89	0.05	24.48	1.01
JK 70%	0.97	0.14	0.96	–0.61	0.09	29.80	1.00
JK 90%	0.48	0.22	0.72	0.19	0.37	37.96	1.02
SS 1df	1.00	0.00	1.00	0.00	0.01	5.83	1.00
SS 2Rdf	1.00	0.00	1.00	0.00	0.01	5.83	1.00
JK 1df	0.98	0.00	0.99	0.59	0.01	4.78	0.99
JK 2Rdf	0.98	0.00	0.99	0.59	0.01	4.78	0.99
High within-trial noise and high between-subject variability
SS 10%	0.14	0.07	0.64	0.30	0.46	19.66	0.65
SS 30%	1.00	0.02	0.99	–0.60	0.01	19.57	1.02
SS 50%	1.00	0.03	0.99	–0.71	0.02	24.66	1.02
SS 70%	0.99	0.03	0.99	–0.49	0.02	30.13	1.01
SS 90%	0.53	0.02	0.87	0.85	0.25	39.28	1.05
JK 10%	0.29	0.01	0.81	0.91	0.36	14.24	1.00
JK 30%	0.71	0.03	0.91	0.75	0.16	20.04	1.02
JK 50%	0.89	0.01	0.97	0.82	0.06	24.56	1.03
JK 70%	0.77	0.01	0.94	0.89	0.12	29.36	1.00
JK 90%	0.22	0.02	0.78	0.79	0.40	37.92	1.05
SS 1df	1.00	0.03	0.99	–0.71	0.02	7.60	1.01
SS 2Rdf	1.00	0.03	0.99	–0.71	0.02	7.60	1.01
JK 1df	0.94	0.02	0.98	0.48	0.04	6.13	0.99
JK 2Rdf	0.94	0.02	0.98	0.48	0.04	6.13	0.99

Note: SS = single-subject procedure; JK = jack-knife procedure; x% = relative-criterion method; and xdf = regression-based method.

A similar, but less dramatic picture emerged in the analyses of the response-locked data (Table 6). In this case, the advantage of regression- over criterion-based methods was much smaller, and the advantage of single-subject over jack-knife proceduresŵhen combined with regression-based methods) was negligible. However, similar to what was found in the random-sample simulations, regression-based methods were always more accurate (in terms of RMSE) than criterion-based methods.

Recommendations

If the purpose of a given study is to use stimulus- versus response-locked logic to discriminate between pre-motor and motoric effects (see Osman et al., 1995), then the choice of data-analytic technique is crucial. Certain combinations of onset-detection method with statistical procedure are much more accurate than others. Based on the results reported here (and those reported by Miller et al., 1998, and Smulders et al., 1996), coupled with a consideration of technique complexity, our recommendation is that researchers use a regression-based method to analyze stimulus-locked LRP data. In particular, we recommend the use of the SS1df technique. This method involves fitting two intersecting lines to each LRP waveform: the “pre-onset” line begins at the time of stimulus presentation with zero height and remains flat, whereas the “postonset” line ends at the time and height of the peak in the LRP. The time of the intersection between the two lines is the only free parameter and is taken as the estimate of LRP onset. This method should be applied to each subject individually, as opposed to jack-knifed grandaverages.

For the analysis of response-locked LRP data, our recommendation is the same, although the JK50% technique may also be used if the specific sizes of the stimulus- and response-locked effects are not of primary interest. This latter technique uses an onset criterion that is half the height of the peak and combines data across subjects by jack-knifing.

These recommendations are based on two factors. First, these particular techniques have low EERs when used for the type of analysis for which they are suggested. In other words, these techniques have a low probability of leading the user to an erroneous conclusion as to the actual locus of an experimental manipulation. Second, we have argued against the unrestricted versions of the regression-based method because of the inherent ambiguity of these techniques. For example, the 2Udf and 4df methods allow the pre-onset line to have a positive slope (i.e., rising toward the peak), which raises the question as to which point is the actual onset. Some might argue, for example, that when the pre-onset line has a positive slope, the actual onset of the LRP must be the origin of this same line, even though this would place the estimated onset of the LRP at the time of stimulus presentation. To avoid this ambiguity, we suggest that the 2Udf and 4df methods be avoided (cf. Schwarzenau et al., 1998). Another argument against the use of the 2Udf and 4df methods is that these are, by far, the most complicated and time consuming. For example, the SS4df and JK4df techniques required two orders of magnitude more CPU time to conduct than all of the other 34 techniques combined.⁸

In contrast, if the purpose of a given study is to estimate the actual size of a stimulus- or response-locked effect, or if the study requires the identification of the onset of the LRP in a single condition, then we recommend the use of the SS1df technique to analyze stimulus-locked data and the use of the JK1df technique to analyze response-locked data. Our reasons complement those given above. In particular, these techniques have the lowest errors of estimation (RMSE), combined with partition scores that are very close to 1.00.

If the reader would prefer a single recommendation for all types of analysis, then we suggest the use of the SS1df technique. Not only did this technique perform well in all of our simulations, it is also one of the easiest to implement. A good name for this technique that we have found ourselves using is “Catch-21”—this is shorthand for “the best technique to catch the onset of the LRP using two straight lines with one degree of freedom.”