Gravitational forces and sagittal shape of the spine

Abstract

The sagittal morphology of the pelvis determines the amount of lordosis needed for each individual. The proper harmony of the sagittal spinal curves allows a stable balance, economical in terms of mechanical effects and muscular energy. A previous barycentremetrical laboratory study allowed us to demonstrate that the axis of gravity of the upper body segment was located behind the lumbar vertebrae and the femoral heads, thus ensuring economy and stability. The determination of the anatomical connection of the individual gravity is thus of primary importance for the evaluation of sagittal balance. Data for 42 patients without spinal pathology, previously evaluated by barycentremetry, were used to establish a predictive equation for the application point of the gravity at the level of the third lumbar vertebra (L3). This equation, using anthropometric and radiographic pelvic and spinal parameters, was integrated into a software program called Similibary. It was applied to the same 42 subjects. These results were compared in order to validate the method. No significant difference was observed between the two techniques. This easy-to-use tool allows a personalised evaluation of the sagittal balance of the spine, both through the evaluation of the harmonious relationship between the spinal curves and the pelvis, and through the location of gravity supported by the vertebral structures in L3.

Introduction

The surgical treatment of scoliosis with modern procedures permits considerable improvement of the coronal component of the deformity. For some cases, in spite of a durable frontal correction, the functional improvements do not last, as a result of insufficient restitution, or even of a worsening of the sagittal shape [12, 13]. Until now, the purpose in terms of sagittal shape was to restore curves to close to the mean published values, without knowing what is really suitable for an individual case.

The standing posture results from an accurate sagittal arrangement of the various body segments with respect to gravitational forces [4, 5, 7, 10]. Thus the mechanical condition of each vertebral joint is the outcome of the balance between upper body weight and the ligament and muscle’s reactive strength [1, 2]. At the lumbar spine levels, where upper body weight increases, the load supported by the disk and vertebral joints is especially dependant on the proper location of gravity behind or in front of the lumbar vertebrae [2, 16]. A maladapted location may induce a worsening of the imbalance and pain.

The latest studies demonstrate that the wide range of sagittal shapes of the spine was correlated with a similarly wide range of pelvic anatomical shapes. The sacrum is involved in this relationship. Its more or less curved shape, more or less tilted upper plate and more or less high insertion between the two iliac bones were correlated to the more or less strongly marked sagittal curves of the spine (Fig. 1) [2, 3, 21]. A single anatomical pelvic parameter called “pelvic incidence” summarises these distinctive anatomical properties [3, 6, 17, 20, 21, 23]. A strict relation was described between the pelvic incidence and the sagittal tilt of the superior sacral plate, and between this sacral tilt and the amount of lumbar lordosis. When sacral slope and sagittal spine curves are correctly fitted to pelvic incidence, the loads remained positioned behind and near the lumbar spine, closely behind the middle of the sacral plate and behind the coxo-femoral axis. In this case, standing is the most economical position in terms of gravity load and muscle strength forces [5, 6, 18, 19]. These hypotheses were supported by the barycentremetrical studies conducted by G. Duval-Beaupère’s team [1, 2, 4, 5, 19]. These hypotheses were also validated for pathological conditions [4–6]. All disorders associated with a deregulation (an excessive or insufficient sacral tilt, an insufficient lumbar lordosis) produce a forward movement of gravitational forces, which leads to fatigue and pain [19, 20] (Fig. 2). The value of the pelvic incidence is invariable for the adult since the sacral bone attains maturity. It cannot be affected by spine surgery [22, 23]. This anatomical individual parameter gives evidence of the multiple individual sagittal curve configurations. Its measurement is essential for the sagittal spinal balance assessment. Also to be investigated is the adequacy of the relationships between the values of the sacral tilt and of the lordosis. A maladjusted sacral slope or lordotic curve leads to questioning about the location of gravitational force.

Fig. 1.

Normal individual variations in the harmony of the sagittal shape of the spine (theoretical draws). a A large pelvic incidence associated with a greatly tilted upper sacral plate and a pronounced lordosis. b A low pelvic incidence associated with a more horizontal upper sacral plate and flatter sagittal curves

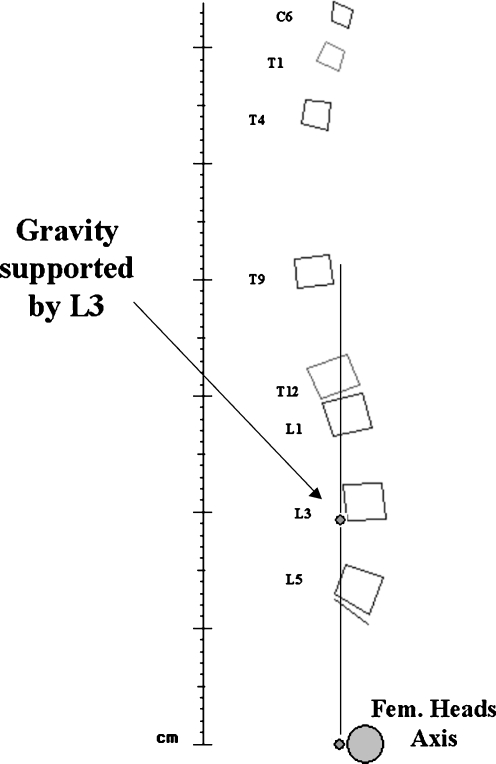
Fig. 2.

Barycentremetrical diagrams expressing the sagittal shape of the spine and the application points of the gravity supported by each vertebral segment. a Economically steady sagittal shape: the gravity is projecting behind the lumbar vertebral structures and the femoral heads. b A non-economical sagittal shape: the gravity is projecting in front of the lumbar structures and the femoral heads

The barycentremetrical measurements were performed with an experimental prototype gamma-ray scanner, which cannot be applied in clinical practice because it is time consuming and because of patient exposure to radiation. It was the only instrument allowing access to in vivo data on the centre of gravity of human torso cross-sections with very high accuracy. It was observed that these centres of segmental weights were located in a vertical cylinder (1 cm diameter). The force platforms, which are more open, cannot produce such segmental information [9, 10, 25], but only vertical projection of the full-body centre of gravity. This value may be affected by all the asymmetrical anatomical shapes of the lower body and by the forward positioning of the femoral head in relation to the sacrum and spine. Taking these facts into account, the barycentermeter’s sagittal values of gravitational line were in accordance with the results of During and Gangnet [7, 10].

Fortunately, the analysis of the numerous anatomical, radiological, gravitational and anthropometrical parameters produced by the barycentremetrical studies demonstrated numerous strong correlations. So, a predictive equation of the location of gravitational forces relative to the lumbar spine could be established. This equation is applicable in daily practice. An easy-to-use software allows a quick recording of spinal and pelvic anatomical X-ray points without any laboratory equipment. The purpose of the this work is, on one hand, to validate the accuracy of the measurement of the anatomical X-ray points to produce the parameters included in the equation, and on the other hand to test the predictive equation itself.

Materials and methods

A cohort of 42 healthy young adults, free of spinal disease, was previously studied with the barycentremeter and the software called Rachis 91. The relation of the gravity line to the spine was analysed using a same referring system for the barycentremetrical data and the X-ray measurements. The origin of this global coordinate system was the centre of the bi-coxo-femoral axis (the middle point between the two centres of each femoral heads). These studies were performed on orthogonal plain radiographs in standing position, the arms lying on a support, the knees in extension. For each, a scaling was incorporated allowing the correction of the radiographic distortion.

There were 19 women (mean age: 24.5 years, SD 6.4; mean height: 170 cm, SD 7; mean weight: 60.5 kg, SD 7.4; mean corpulence index 2.05, SD 0.13) and 23 men (mean age: 24.3 years, SD 5; mean height: 171.7 cm, SD 31; mean weight 70.9 kg, SD 8.5; mean corpulence index 2.24, SD 0.20).

The anthropometric and sagittal X-ray variables used for the establishment of the predictive equation of the location of gravitational forces related to the lumbar spine are described in Table 1 and Fig. 3. The co-ordinates were expressed according to the centre of the bi-coxo-femoral axis. The sagittal y-axis was forward oriented and the vertical h-axis was upward oriented. The “tilt” angles were backward positive.

Table 1.

The anthropometric and sagittal pelvic and spinal variables used for the analysis and the establishment of the predictive equation

The anthropometric variables
Age		Months
Sex
Height	Standing total height	Centimetres
Weight	Total weight	Grams
Corpulence index	Weight/height2	g/cm2
The sagittal X-ray variables
The pelvic variables (Fig. 3a)
Pelvic incidence	Angle between the line perpendicular to the upper plate of S1 in its middle, and the line linking this point and the bi-coxo-femoral axis	Degrees (°)
Sacral slope	Angle between the upper sacral plate and the horizontal	Degrees (°)
Overhang of S1	Geometrical range between the inter-coxo-femoral axis and the projection of the middle of the sacral plate. It was positive when the hip was in front of the sacral plate and negative when it was behind it	Millimetres
The spinal variables (Fig. 3b)
The sagittal co-ordinate of the middle of the L3 lower plate related to the bi-coxo-femoral axis		Millimetres
The oriented sagittal distances between L3 and T1, T4, T9, T12, L1, L5	Measured between the middle of the each lower plates to the middle of the L3 lower plate	Millimetres
The “oriented sum”	Sum of the sagittal distance between L3 and T9 vertebrae and between T4 and T9 vertebrae. It was related to the sagittal length of the L5 vertebra divided by 32.53	Millimetres
Lordosis angle	Angle between the sacral plate and the more posteriorly tilted plate of another lumbar or thoracic vertebra	Degrees (°)
Number of vertebrae involved in the lordotic curve
L1 tilt	Tilting of the line between the middle of the sacral plate and the middle part of the upper L1 plate. It was positive when it was tilted behind	Degrees (°)
T9 tilt	Tilting of the line between the centre of the T9 vertebra and the bi-coxo-femoral axis (since the centre of the weight supported by the hip joints is in mean located in front of the T9 vertebra [15]). It was positive when it was tilted behind	Degrees (°)
T1 tilt	Tilting of the line between the middle of the sacral plate and the centroïd of the T1 vertebra. It was positive when it was tilted behind	Degrees (°)

Fig. 3.

The variables used for the analysis and the establishment of the predictive equation. a The pelvic variables: the pelvic incidence, the sacral slope, the overhang of S1 on the femoral heads. b The spinal variables: the L1 tilt, the T9 tilt, the T1 tilt

The predictive equation

These X-ray variables were selected among the data of our previous barycentremetrical study [5, 6, 19, 20]. They were combined using statistical techniques to the anthropometrical and gravitational data to set up the predictive equation of the sagittal co-ordinate of the centre of gravity supported by the lower plate of L3. It was expressed using the same global referential. This equation takes into account the 21 parameters described, ensuring a high correlation between the predicted and the measured values (r=0.9912).

On the same radiographs, the sagittal and height co-ordinates of the anatomical points were measured. They were: the bi-coxo-femoral axis, the two corners of the sacral plate, the four corners of the L5, L3, L1, T12, T9, T4, T1 and C6 vertebral bodies, as well as those of the transitional vertebra (between kyphosis and lordosis) and of the upper kyphosis vertebra. The precision of the measurements was 1 mm.

Two observers obtained these measures successively, but independently: one was a surgeon living in Belgium, the other a physician living in Paris.

The software Similibary using the predictive equation then computed the anthropometric and the spine and pelvic variables, providing the sagittal co-ordinate of the centre of gravity supported by L3. These two panels of variables were compared successively between themselves and with those of the previous barycentremetrical study in order to validate the reliability of the recording method and the predictive procedure of the sagittal co-ordinate of the centre of gravity. Paired t-tests were used to examine mean differences in the measurements for each parameter derived from the use of the Similibary from each observer’s and from the previous barycentremetrical study. Significance was accepted at the 5% level. The intraclass correlation coefficient (ICC), standard error of measurement, each with 95% confidence intervals, was used to characterise reliability. It has been suggested that, to be acceptable, a measurement should have had an ICC >0.6.

Results

The values of the pelvic and spinal variables issuing from each observer’s measurement using the Similibary software were reported in Table 2a, as those issuing from the previous barycentremetrical study (Rachis 91). We pointed out the similarity between the values, whatever the method or the observers. The few significant differences were very low. They affected the lordosis value, the overhang of S1 and the number of vertebrae involved in the lordotic curve. Only for this last parameter, the ICC was very low; the others were greater than 0.87 (mean =0.92) and showed a high reliability.

Table 2.

The spine and pelvic variables used for the predictive equation

	Rachis 91	Obs. 1	Obs. 2	R91/obs. 1		R91/obs. 2		Obs 1/obs 2
A.
Lordosis
Mean	63.54	61.58	60.32	1.96		3.22		1.26
SD	11.26	11.89	11.90	5.70		5.37		5.44
Test				2.23	S*	3.89	S***	1.50	NS
ICC				0.88		0.88		0.89
Sacral slope
Mean	−40.82	−40.70	−39.96	−0.12		−0.86		−0.74
SD	8.87	10.24	9.95	4.94		4.10		5.31
Test				−0.16	NS	−1.37	NS	−0.91	NS
ICC				0.91		0.88		0.87
Incidence
Mean	51.96	52.12	51.67	−0.16		0.30		0.45
SD	10.89	13.39	13.04	7.15		6.71		6.33
Test				−0.14	NS	0.29	NS	0.46	NS
ICC				0.86		0.85		0.89
T9 tilt
Mean	10.30	10.30	10.29	0.00		0.01		0.02
SD	3.14	2.89	2.89	0.96		0.99		0.64
Test				−0.03	NS	0.09	NS	0.17	NS
ICC				0.95		0.96		0.98
L1 tilt
Mean	7.42	7.20	7.17	0.22		0.25		0.03
SD	4.60	4.57	4.59	0.63		1.14		1.35
Test				2.24	S*	1.43	NS	0.15	NS
ICC				0.97		0.99		0.96
T1 tilt
Mean	2.79	2.90	2.76	−0.11		0.03		0.14
SD	3.55	3.44	3.52	0.40		0.40		0.36
Test				−1.70	NS	0.57	NS	2.53	S
ICC				0.99		0.99		1.00
S1 overhang
Mean	20.93	23.35	23.22	−2.42		−2.29		0.14
SD	11.96	12.74	12.84	6.89		6.17		4.28
Test				−2.28	S*	−2.40	S*	0.20	NS
ICC				0.88		0.85		0.95
Oriented sum
Mean	61.26	61.29	59.03	−0.03		2.23		2.26
SD	15.04	14.72	17.21	3.41		7.76		8.50
Test				−0.06	NS	1.86	NS	1.72	NS
ICC				0.90		0.97		0.87
N vert lordosis
Mean	11.46	11.49	12.32	−0.03		−0.86		−0.84
SD	1.73	1.28	1.31	1.77		1.89		1.32
Test				0.10	NS	2.97	S**	4.10	S***
ICC				0.19		0.36		0.42
B.
T1/L3
Mean	−43.94	−45.01	−43.86	1.07		−0.08		−1.15
SD	32.28	28.76	29.01	12.39		12.24		2.87
Test				0.57	NS	0.04	NS	2.83	S**
ICC				0.93		0.93		0.99
T4/L3
Mean	−66.17	−67.39	−66.82	1.22		0.65		−0.57
SD	29.62	24.31	24.40	15.56		15.69		1.45
Test				0.51	NS	0.27	NS	2.55	S*
ICC				0.85		0.85		0.99
T9/L3
Mean	−61.84	−62.89	−62.67	1.05		0.83		−0.23
SD	21.19	15.24	15.05	14.30		14.06		1.22
Test				0.48	NS	0.38	NS	1.20	NS
ICC				0.75		0.75		0.99
T12/L3
Mean	−34.41	−34.43	−34.40	0.02		0.00		−0.02
SD	14.50	9.25	8.73	9.10		9.12		1.18
Test				0.02	NS	0.00	NS	0.13	NS
ICC				0.80		0.79		0.99
L1/L3
Mean	−21.82	−21.69	−21.93	−0.13		0.11		0.24
SD	10.37	7.14	6.59	6.43		6.42		1.56
Test				0.13	NS	0.11	NS	0.99	NS
ICC				0.79		0.73		0.99
L5/L3
Mean	−6.10	−7.20	−6.67	1.10		0.57		−0.54
SD	8.53	9.04	8.76	3.12		1.88		2.63
Test				2.30	S	1.97	NS	1.32	NS
ICC				0.94		0.98		0.96
L3/Fem
Mean	−46.65	−52.50	−51.04	−5.84		−4.38		−1.46
SD	43.07	27.64	27.68	31.25		31.52		6.15
Test				1.64	NS	1.35	NS	1.54	NS
ICC				0.70		0.70		0.97

For each variable, horizontally, from the left to the right: values produced by the previous barycentremetrical study called Rachis 91 and those provided by the present study using Similibary for observer 1 and for observer 2; the paired differences between each observer and Rachis 91’s data, and the paired differences between the two observers

For each variable, vertically downward: the mean value, the standard deviation, the t-test, its significance for a 5% risk*, 1% risk**, 0.1% risk***; the intra class correlation (ICC)

A: the spine and pelvic parameters, and the sagittal coordinates of the L3 vertebrae

B: the sagittal distance (mm) between the middle of the lower plate of each vertebra

The vertebrae’s sagittal co-ordinates, expressed related to L3, were shown in Table 2b. They were compared according to the same method. The few significant differences were very low. For these variables the mean ICC was 0.89 and showed a high reliability.

The predicted sagittal co-ordinates of the centre of weight supported by L3 were reported in Table 3, expressed according to the middle of the inferior plate, as the lever arm of the gravity loads. The same comparisons were performed between the two observers' recordings and between the results of the barycentremetrical study. These values did not differ between the two observers, and the mean ICC (0.97) showed a very high reliability. They did not differ from those provided by the previous barycentremetrical study, but the mean ICC (0.69) showed a slightly lower reliability.

Table 3.

The sagittal co-ordinate (mm) of the centre of weight supported by L3 related to the middle of the lower plate of the L3 vertebra

Sag. coord. of the centreof weight on L3	Rachis 91	Obs 1	Obs 2	R1/obs1		R1/obs1		Obs1/obs2
Mean	26.11	22.17	23.26	−3.94		−2.85		1.09
SD	21.82	14.23	14.25	5.24		16.66		5.05
Test				−1.68	NS	−1.11	NS	1.40	NS
ICC				0.72		0.65		0.94

For each variable, horizontally, from the left to the right: values produced by the previous barycentremetrical study called Rachis 91, and those provided by this study using Similibary for observer 1 and for observer 2; the paired differences between each observer and Rachis 91’s data, and the paired differences between the two observers

For each variable, vertically downward: the mean value, the standard deviation, the t-test, its significance for a 5% risk*, 1% risk**, 0.1% risk***; the intra-class correlation (ICC)

Discussion

The very high accuracy of the barycentremetrical measurements was specified previously [4, 5]. It provided the same results compared to other methods for determination of the centre of total body weight. For the elementary thoracic cross sections, the centres of weight were located in front of the vertebrae, as described by King Liu [16], but for the lumbar cross sections these elementary centres of weight were backward, probably on account of the greater thickness of the lumbar muscles, which increases with the weight supported by the corresponding vertebrae. On these anatomical levels our co-ordinates differed from those used in the models by Kiefer and Keller [13,14,–15]. The mean accuracy of the sagittal co-ordinate of the centre of the segmental weights expressed by the barycentremeter was 2.44 mm (for the specific L3 level, it was 0.7 mm). Such accuracy cannot be expected using a predictive equation. The values of the ICC of the computed co-ordinates of the centres of weight and those of the SD of the mean paired differences give evidence of this (from 5.25 to 16.6 mm). However such accuracy seems to be adequate as an aid in a spinal examination daily practice.

In the Similibary software, the results are expressed both through a drawing of the sagittal curves of the spine that shows the downward projection of the centre of weight supported by L3 and also through a table displaying the values of the spinal and pelvic parameters (Fig. 4).

Fig. 4.

Graphical expression of the result of the Similibary for a normal subject: down projection of gravity supported by L3 facing this vertebral level

The software also produces other information, provided by several precious findings of the preceding barycentremetrical study:

1. A vertical line in front of T9 showing the mean position of the centre of gravity supported by the hips [since the centre of the weight supported by the hip joints was demonstrated located normally in front of the T9 vertebra [4, 5] (mean 28 mm, SD 20) in front of the middle of the vertebra]. Thus, its close connection with the computed centre of weight supported by L3 can be verified.

2. The theoretical values of the sacral slope and of the lumbar lordosis curve required by the pelvic incidence for an economical standing position. Such data are useful to estimate the amount of lordosis necessary for an economical balance.

3. When the gravity had jumped over the middle of the L3 body, several parameters have together reached specific threshold values. These values were observed for subjects with unfavourable sagittal spinal balance to give evidence of the forward movement of the upper segmental loads relative to the lumbar spine. These cutoff values testifying to a large risk of an anterior location of the gravity loads are:

• a sagittal distance between T9 and L3 inferior to 40 mm

• a sagittal distance between T9 and L3 between 40 to 60 mm associated with insufficient values of the sagittal tilt parameters (T1 tilt <0.5°, T9 tilt <11°, L1 tilt <9.5°).

We have previously described important relationships between pelvic and spinal parameters in order to appreciate the sagittal balance adapted for each individual. These investigations allow to characterise a sagittal shape as a dynamic balance, including the disc, the ligaments and the muscular synergies. It determines an economical position in terms of muscular effort and of loads on the structures. The electromyography of the posterior spinal muscles attests to this: silent when the relation between sacral slope and pelvic incidence is harmonious, but muscular compensatory activity is detected when these relationships are disturbed [5, 6]. These facts are in agreement with the conclusions of Harrison about the load-bearing potential of the spine ligaments in compression related to the T1 sagittal position and the rotation of the pelvis [11]. An anterior slant of the trunk projects forward the gravity supported by the lumbar and pelvic structures. The mechanical loads are therefore increased at the same time by the anterior increase of the lever arm of the gravity and by the excess of loads bound to the posterior muscular compensatory efforts. In these cases, the sagittal position could be qualified as uneconomical or pathological. The three tilt variables give information on the sagittal position of the respective body segmental weight, cephalic, thoracic and lumbar. It is therefore advisable to understand the analysis of the sagittal spinal plane as a balance between gravity and muscular effort. Such theory was raised by the results of our barycentremetrical measures and was corroborated by past as well as by recent publications [7–11, 14, 15, 24, 25].

We have limited our investigation to the sagittal co-ordinate of gravitational forces. We have not provided the coronal co-ordinate, because the frontal effect of the gravity is identical to the line of frontal middle points of the body coronal outline. This is true for scoliotic as well as for “normal” people. The barycentremeter demonstrated this [4–6]. When scoliosis occurs, the apical vertebrae move out of the centre line, but the line of gravity still stays in the centre of the body. This median position of gravity explains the instability of the scoliotic spine.

The clinical application of this software is obvious considering the sagittal shape of the spine as a balance between gravity and muscular compensatory strengths. Studies using plate-form of force have demonstrated that [10, 25].

Conclusion

We have a reliable tool for a functional evaluation of the individual sagittal morphology of the pelvi-spinal unit. Its use is easy and fast. More than a simple tool of evaluation of a static situation in current practice, it is an invaluable help for the planning of correct posture taking into account the constant relationship between muscles’ efficiency, balance and gravity. Nevertheless, it cannot take the place of a good clinical examination, including position and mobility of the spine and of the adjacent joints, in particular the hips and the knees.