The effect of different design concepts in lumbar total disc arthroplasty on the range of motion, facet joint forces and instantaneous center of rotation of a L4-5 segment

Abstract

Although both unconstrained and constrained core lumbar artificial disc designs are in clinical use, the effect of their design on the range of motion, center of rotations, and facet joint forces is not well understood. It is assumed that the constrained configuration causes a fixed center of rotation with high facet forces, while the unconstrained configuration leads to a moving center of rotation with lower loaded facets. The authors disagree with both assumptions and hypothesized that the two different designs do not lead to substantial differences in the results. For the different implant designs, a three-dimensional finite element model was created and subsequently inserted into a validated model of a L4-5 lumbar spinal segment. The unconstrained design was represented by two implants, the Charité^® disc and a newly developed disc prosthesis: Slide-Disc^®. The constrained design was obtained by a modification of the Slide-Disc^® whereby the inner core was rigidly connected to the lower metallic endplate. The models were exposed to an axial compression preload of 1,000 N. Pure unconstrained moments of 7.5 Nm were subsequently applied to the three anatomical main planes. Except for extension, the models predicted only small and moderate inter-implant differences. The calculated values were close to those of the intact segment. For extension, a large difference of about 45% was calculated between both Slide-Disc designs and the Charité^® disc. The models predicted higher facet forces for the implants with an unconstrained core compared to an implant with a constrained core. All implants caused a moving center of rotation. Except for axial rotation, the unconstrained and constrained configurations mimicked the intact situation. In axial rotation, only the Slide-Disc^® with mobile core reproduced the intact behavior. Results partially support our hypothesis and imply that different implant designs do not lead to strong differences in the range of motion and the location of center of rotations. In contrast, facet forces appeared to be strongly dependent on the implant design. However, due to the great variability in facet forces reported in the literature, together with our results, we could speculate that these forces may be more dependent on the individual spine geometry rather than a specific implant design.

Introduction

Lumbar total disc arthroplasty devices have been introduced to clinics as an alternative to fusion with the aim of preserving spinal motion. This should also alleviate back pain, decrease the incidence of adjacent segment degeneration, avoid complications related to fusion, and allow early return to function [3, 14, 15, 26, 33]. Due to these advantages, a large number of different arthroplasty devices have been developed and are currently available and in clinical use. The first successful arthroplasty device was the SB Charité^® disc (Depuy Spine; Raynham, MA, USA). Other concepts followed such as Prodisc^® (Synthes; Paoli, USA), Maverick^TM (Medtronic; Minneapolis, MN, USA), Flexicore^® (Stryker; Kalamazoo, MA, USA), Mobidisc^® (LDR médical; Troyes, France), and Activ L (Aesculap AG; Tuttlingen, Germany).

Most artificial discs consist of two metallic endplates and a polyethylene core. The core is either separated between both endplates (=unconstrained design), partially or intrinsically connected with the lower endplate (=semi-constrained or constrained design). The Charité^® disc is representative of an unconstrained and the Prodisc^® prothesis of a constrained design.

The unconstrained design allows the adjacent vertebrae to translate relatively to each other without any accompanying rotation [11]. This behavior leads to a moving instantaneous center of rotation (ICR) and therefore, mimics the “physiological behavior of a functional spinal unit”, as supposed by Cunningham et al. [3]. In contrast, it is stated that the constrained configuration causes a fixed ICR. This assumption is explained in the way that the segmental translation occurs concurrently with rotation given by the radius of the inner core. We disagree with this assumption, because the kinematical behavior of an implanted spinal segment is not only dependent on the implant itself. The articulating facet joints, which also play a major role for spinal load transmission, the remaining soft disc tissue, and the elastic behavior of the adjacent bony structures also influence the spinal motion behavior and therefore, control the location of the ICRs.

We therefore proposed the hypothesis that different design concepts do not lead to substantial differences in the location of the ICRs. We furthermore hypothesized that the different implant designs lead to a similar range of motion (RoM) and to similar facet joint forces. We investigated our hypotheses in a finite element (FE) analysis.

Materials and methods

Implants

In the current study, we used three different implant designs: The first design was the SB Charité^® III disc—a three piece construct comprised of a biconvex core sandwiched between two concave endplates—representing an unconstrained design. The second implant, also representing an unconstrained design, was a newly developed disc prosthesis: Slide-Disc^® (Weber Instrumente GmbH; Emmingen-Liptingen, Germany) (Fig. 1). Similar to the Charité^® disc, the Slide-Disc^® consists of two endplates and a mobile sliding core. This core is articulated with the upper endplate by a spherical fully congruent surface. In contrast to the Charité^® disc, the articulation between the core and the lower endplate is realized by a slightly curved contact surface. This allows the core to move almost freely within the transversal plane. The developers assume that the Slide-Disc^® is able to better reproduce the ICRs of a healthy intact spinal segment, in particular for axial rotation than the Charité^®, as a result of the freely sliding core. For axial rotation it has been found from in vitro and FE studies that the ICR migrates outside the disc close to the facet joints under higher load conditions [9, 27, 34]. The third implant design was a modification of the Slide-Disc^®. Here, the inner core was rigidly connected to the lower endplate representing a constrained design.

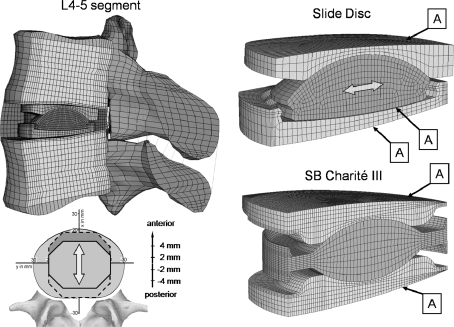
Fig. 1.

Left Finite element mesh of the L4-5 lumbar spinal motion segment with the implanted Slide-Disc. Right Detail view of both investigated dynamic disc implants: Slide-Disc^® (above) and SB Charité^® III (below). The location of both implants was varied by 4 mm in both an anterior and posterior direction. Label A indicates the contact areas which were varied between standard unilateral contact (normal pressure equals zero if separation occurs) and bonded (contact surface is always attached to the target surface along the normal and tangent directions)

Finite element modeling

A three-dimensional, non-linear FE-model of an intact L4-5 ligamentous human lumbar motion segment was used in this study (Fig. 1). This FE-model has been used previously to investigate a number of clinically relevant issues [28–32]. The model validation has been extensively documented in these studies. In the following is given a brief description of this FE-model.

The commercial software ANSYS 11.0 (ANSYS INC., Canonsburg, PA, USA) was utilized to perform the FE analysis. The model consists of two vertebrae, the intervertebral disc, and the seven main ligaments. The intervertebral disc considers the nucleus pulposus and the surrounding annulus fibrosus. The annulus was modeled as a composite of solid matrix with embedded fibers, which are organized in seven concentric rings around the nucleus. Fibers and ligaments were represented by unidirectional spring elements with a non-linear force-deflection curve and no compression capabilities. The articulating facet surfaces were modeled using surface-to-surface contact elements in combination with the penalty algorithm with a normal contact stiffness of 200 N/mm and a friction coefficient of zero. The facet cartilage layer was assumed to yield a thickness of 0.2 mm. The initial gap between the cartilage layers was assumed to be 0.4 mm. The capsular ligament was simulated by using spring elements with a non-linear force-deflection curve forming a ring around the articular contact; they linked the borders of the inferior vertebra superior articular process to the borders of the superior vertebra inferior articular process.

Implant modeling

Both implants were meshed using eight-node isoparametric solid elements. The spiked endplate surfaces of both implants were simplified to a flat surface. The Slide-Disc^® and the Charité^® disc are available in different sizes. For our simulations, we used the Slide-Disc^® type III with a height of 11 mm and a lordotic angle of 4° and the Charité III^® with an approximate height of 13 mm and a lordotic angle of 5°.

A standard unilateral contact was assumed at the articular surface between the core and the concave metallic endplates. A friction coefficient of 0.02 was chosen for both implants [7]. For the Charité^® endplates, a chrome-cobalt alloy was assumed with a Young’s modulus of 300 GPa and a Poisson’s ratio of 0.27 [7]. The inlays were represented by a polyethylene core (ultra high molecular weight polyethylene (UHMWPE)) with a Young’s modulus of 2 GPa and a Poisson’s ratio of 0.3 [7]. A titanium alloy (Ti6Al4 V) with a Young’s modulus of 113.8 GPa and a Poisson ratio of 0.3 was assigned to the Slide-Disc^® endplates. For the inlay a Young’s modulus of 2 GPa and a Poisson’s ratio of 0.3 were similarly chosen. All the values for the SlideDisc^® were provided by Weber Instrumente.

Two cases were simulated for the Slide-Disc^®. In the first case, the inner core was assumed to be movable (Slide-Disc mobile core: SD-MC), as it is intended by the company. In the second case, the inner core was rigidly fixed (bonded) at the lower metallic endplate of the implant, simulating a constrained design (Slide-Disc immobile core: SD-IMC), as it is realized by the ProDisc^®.

Implantation

Disc placement procedure for both implants requires an anterior surgery for implantation. The protocol involves the stepwise removal of the anterior longitudinal ligament, the anterior portion of the annulus, and the entire nucleus pulposus. Only the posterior and lateral portion of the annulus remains in place. To mimic this surgical procedure, the elements representing these structures were removed in the FE-model (Fig. 1).

Investigation of different implantation situations

First, both implants were integrated in the intervertebral space in a geometrically central position. Subsequently, the locations of both implants were varied by 4 mm in both an anterior and posterior directions (Fig. 1).

The contact condition between the metallic endplates and the adjacent bony structures was verified between perfect bond and standard unilateral contact (indicated by the label A in Fig. 1) with a friction coefficient of 1. While a bonded contact represents a perfect bone osteo-integration between the metallic endplates and the adjacent vertebrae, the standard contact investigates the treated segment right after the surgical procedures. The latter additionally represents the poorest osteo-integration, which implies that a gap between implant and adjacent bony endplates may exist under certain loads.

Loading and boundary conditions

The inferior endplate of the lower vertebral body was rigidly fixed. An axial compression preload of 1,000 N was applied simulating upper body weight plus muscle forces. This load was applied using the follower load technique [19], which is thought to have a similar stabilization effect as that of the local muscles [23]. The load follows the curvature of the spine through the proximities of the ICRs and therefore, avoids the generation of additional “larger” moments. This was realized by using connector elements which were spanned between the centers of both vertebral bodies. Subsequently, the spinal segment was loaded with unconstrained moments of 7.5 Nm in the sagittal, lateral, and axial directions simulating flexion, extension, lateral bending, and axial rotation.

Data analysis

1. Range of motion

2. Facet joint force and pressure distribution in the facet surfaces

The resulting forces for each contact element in one facet joint were added together to give a total facet force (F_F). In each facet surface the pressure distribution was displayed independent of the calculated maximum value and divided into a pressure area greater than 70%, greater than 40%, and less than 40% of the maximum value.

1. Center of rotation

The ICR was calculated according to the Reuleaux method [21]. This was performed by intersecting the perpendicular vectors from the midpoint of the translation vectors for two nodes in the upper vertebral body. The applied moments were incrementally increased from zero to the predetermined maximum value of 7.5 Nm, which were attained in ten equally sized incremental steps. The ICRs were evaluated between two consecutive steps. In the corresponding figures, the ICRs were only shown for three different load magnitudes: 1.5, 3.75, and 7.5 Nm in relation to their previous step, i.e., load magnitudes of: 0.75, 3.00, and 6.75 Nm, respectively.

Model verification

Before undertaking the present study we performed mesh convergency tests with both disc prostheses. In previous investigations we also conducted convergency tests with the facet joints. As critical result parameters for both cases we used the RoM and the ICRs, and for the facet joints we additionally used the contact pressure, the pressure distribution, and the contact forces. The element edge length was reduced until the percentage difference of these critical results between two consecutive mesh densities was less than 2%.

Results

In order to better interpret the differences between the individual implant designs and between the implanted and intact situation, we defined a standard evaluation scale for all result parameters. This scale was defined as follows: A difference between 0 and 15% indicated a slight difference, between 16 and 30% indicated a moderate difference, and from 31% to higher values indicated a large difference. All results were adapted according to this scale.

Range of motion

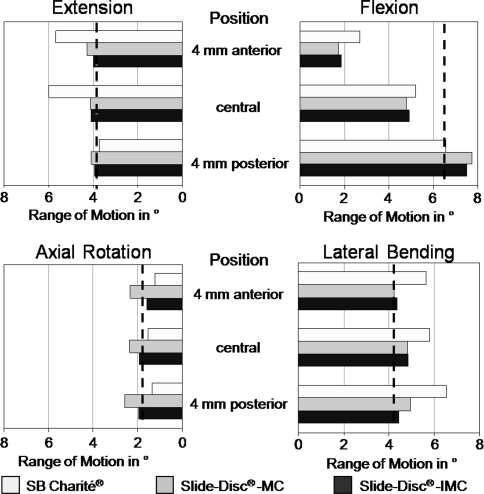
Except for extension, the models predicted only small and moderate inter-implant differences, particularly for both Slide-Disc designs, where the maximal percentage difference was 15% (Fig. 2). For extension, a large difference of about 45% was calculated between both Slide-Disc^® designs and the Charité^®.

Fig. 2.

Influence of implant position in an antero-posterior direction on range of motion in flexion, extension, lateral bending, and axial rotation. The dashed line indicates the range of motion of the intact model. MC Slide disc with mobile core and IMC Slide disc with immobile core

In flexion, all implants led to an averaged decreased RoM of 22% compared to the intact state when the artificial discs are centrally placed. In extension, only the Charité^® caused a strong increase of 52%, while both Slide-Disc^® designs showed a good representation of the intact state. In lateral bending, the different Slide-Disc^® designs led to a slight increase of the RoM. The RoM predicted by the Charité^® is 36% higher than for the intact segment. In axial rotation, all three implant designs restored almost to the intact state.

In flexion, placing the implants more posteriorly led to an increased RoM and a better representation of the intact state. In extension only the Charité^® was influenced by the implant position. Similar to flexion, a more posteriorly placed implant led to a better representation of the RoM calculated for the intact state. A similar behavior was seen for lateral bending. While both Slide-Disc^® designs showed only a slight influence on the implant position, the Charité^® predicted a strong influence. In axial rotation, the implant position did not greatly influence the RoM.

Facet joint forces

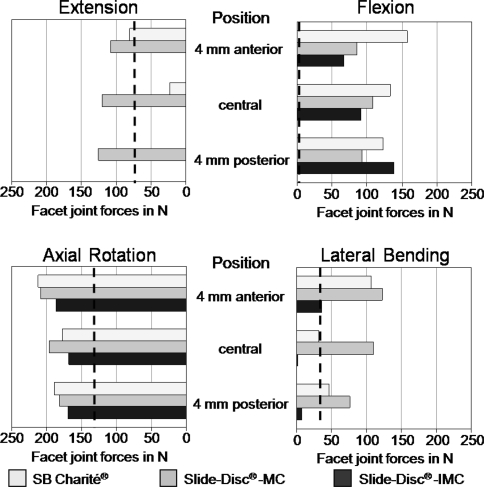
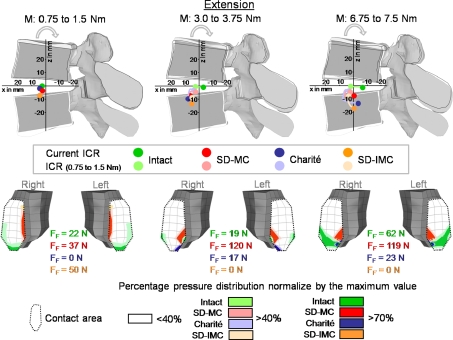
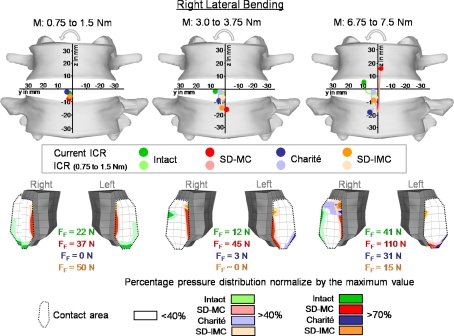
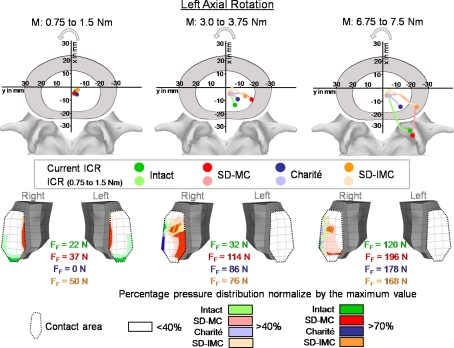
In flexion, the facet joints remained unloaded for the intact model (Fig. 3). In contrast, the presence of any of the disc prostheses led to high facet forces, especially for the Charité^®. Here, the calculated force was 138 N when the implant is centrally placed. Up to 32% inter-implant differences were calculated. In extension, much larger inter-implant differences were found than was indicated under flexion. The models predicted strongly increased forces for the SD-MC (60%) and a strong decrease of 70% for the Charité^® compared to the intact state. Totally unloaded facet joints were predicted for the SD-IMC. In lateral bending, strong inter-implant differences were also calculated. Compared to the intact situation the force decreased by 4% for the Charité^® and 83% for the SD-IMC. In contrast, the facet joint forces strongly increased by 214% for the SD-MC prosthesis. In axial rotation, only small inter-implant differences up to 15% were calculated. The artificial disc models caused an increase of 46% for the SD-MC, 32% for the Charité^®, and 27% for the SD-IMC compared to the intact state.

Fig. 3.

Influence of implant position in an antero-posterior direction on acting forces in the facet joints in flexion, extension, lateral bending, and axial rotation. The dashed line indicates the facet joint forces of the intact model. In flexion, the facets remained unloaded. MC Slide disc with mobile core and IMC Slide disc with immobile core

Changing the position of the artificial discs affected the facet joint forces for all investigated loading cases differently. The SD-MC showed a slight effect for flexion, extension, and axial rotation. In lateral bending, strong differences up to 36% of the resulting forces were calculated. Here, the forces decreased when shifting the implant posteriorly.

The influence of different implant positions was still stronger emphasized by the Charité^® and the SD-IMC, especially in extension. For the Charité^® we calculated completely unloaded facets when shifting the implant posteriorly, whereas, a more anterior position increased the facet forces by 240%. The SD-IMC showed the largest effect in flexion. Here the implant led to a force increase of 110% when shifting the disc from the most anterior to the most posterior position.

Pressure distribution in the facet surfaces

In flexion and in extension, both the left and the right facet joints were equally loaded: in flexion more in the central region (Fig. 4) and in extension more in the inferior tip of the facet (Fig. 5). In lateral bending, the facet joint was loaded on the ipsilateral side of bending for the intact model. The contralateral side remained almost unloaded (Fig. 6). The different artificial discs also caused loaded facets on the contralateral side. However, the calculated forces were always smaller compared to the ipsilateral side. For the intact situation and for all disc implants, left axial rotation led to an increase of contact forces on the right facet joint, while the left facet remained nearly unloaded (Fig. 7). Only for small torsional moments, forces for the left facet were calculated. These forces were mainly produced by the applied preload.

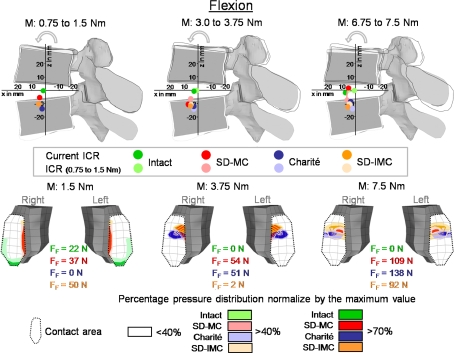
Fig. 4.

Predicted location of the center of rotations (ICR) (above) and the resulting pressure distribution in the inferior facet of L4 (below) with increasing flexion. The ICRs are shown for three different moments (M): 1.5, 3.75, and 7.5 Nm in relation to the moment resulting from the previous sub-step: 0.75, 3.00, and 6.75 Nm, respectively. The dark points show the current ICR for each of the three moment intervals and the light points show the ICR always for the first moment interval (0.75–1.5) to illustrate how the ICRs migrate with increasing load. The maximum forces for each facet joint and the pressure distribution are shown for moments of 1.5, 3.75, and 7.5 Nm. MC Slide disc with mobile core and IMC Slide disc with immobile core

Fig. 5.

Predicted locations of the center of rotations (ICR) and the resulting pressure distribution in the inferior facet of L4 with increasing extension. Explanations for the ICRs see Fig. 4. The maximum forces for each facet joint and the pressure distribution are shown for moments of 1.5, 3.75, and 7.5 Nm. MC Slide disc with mobile core and IMC Slide disc with immobile core, F_F Facet joint forces

Fig. 6.

Predicted locations of the center of rotations (ICR) and the resulting pressure distribution in the inferior facet of L4 with increasing right lateral bending. Explanations for the ICRs see Fig. 4. The maximum forces for each facet joint and the pressure distribution are shown for moments of 1.5, 3.75, and 7.5 Nm. MC Slide disc with mobile core and IMC Slide disc with immobile core, F_F Facet joint forces

Fig. 7.

Predicted locations of the center of rotations (ICR) and the resulting pressure distribution in the inferior facet of L4 with increasing left axial rotation. Explanations for the ICRs see Fig. 4. The maximum forces for each facet joint and the pressure distribution are shown for moments of 1.5, 3.75, and 7.5 Nm. MC Slide disc with mobile core and IMC Slide disc with immobile core, F_F Facet joint forces

Center of rotation

In flexion, the intact model predicted ICRs in the mid-height of the disc (Fig. 4). The ICR was located in the center of the disc for small moments (up to 1.5 Nm). With increasing moment (up to 7.5 Nm) the ICR moved slightly toward the anterior direction. The location of the ICR is only slightly affected by the presence of any of the investigated disc prostheses. For small moments they are shifted slightly caudally close to the superior endplate of the lower vertebral body and slightly altered their positions with increasing flexion, except for the SD-MC model where it moves somewhat cranially close to the inferior endplate of the upper vertebral body.

In extension, the ICRs of the intact model were also located in the center of the disc for small moments of 1.5 Nm (Fig. 5). With increasing moment, the ICR migrated slightly posteriorly. Under the maximum moment of 7.5 Nm the ICR was calculated as being in the posterior nucleus. Similar to flexion, the differences in ICR locations between the investigated prostheses are small. The ICRs were located almost in the center of the disc for small moments. With ongoing extension moment, the ICRs migrated towards the lower vertebral body and moved slightly in the posterior direction.

In lateral bending, the ICRs of the intact spinal model were calculated as being almost in the center of the disc for small moments and migrated towards the side of the bending with increasing moment (Fig. 6). Under the maximum moment of 7.5 Nm, the ICR was located on the right side of the disc, near the inferior endplate of L4. For small moments, the artificial disc models predicted ICRs also almost in the center of the disc. With increasing moment, the SD-MC showed a larger upward movement towards the center of the L4 vertebral body. The Charité^® and the SD-IMC altered slightly their locations in the direction of the lower vertebral body.

In axial rotation, the ICRs were found close to the center of the disc for small moments (Fig. 7). With increasing moment, the ICR migrated to the posterior direction. With a moment of 7.5 Nm the model predicted an ICR location outside of the disc, close to the compressed facet joint. Up to a moment of approximately 5 Nm all three artificial discs showed similar tendencies: with increasing moment, the location of ICRs migrated to the postero-lateral direction of the disc. However, for the maximum moment of 7.5 Nm, only the SD-MC prosthesis led to an ICR location outside the disc, close to the compressed facet joint.

In flexion and extension, placing the implant ventrally showed a shift of the ICR in the anterior location, while a more posterior implant position caused the ICR to migrate slightly posteriorly. For both load directions, the SD-IMC led to ICRs which were located in the region of the adjacent lower vertebral body. In lateral bending, the ICRs were calculated to be more in the adjacent lower bony structures when shifting the implant anteriorly as well as posteriorly. The ICR pattern caused by the SD-IMC was spread over a much larger area compared to the intact situation. Axial rotation led to a shift of the ICR slightly in the anterior location.

Perfect bond and standard unilateral contact

Changing the contact condition between the metallic endplates and the adjacent bony endplates did not strongly affect the results, neither for the central nor for the different implant positions. A maximum difference of 2% for the facet joint forces was calculated.

Discussion

The biomechanical behavior of dynamic non-fusion implant systems were often tested in experimental in vitro studies [10, 12, 13, 17, 18] and evaluated by analyzing clinical radiographs [1–4]. These studies were principally focused on the estimation of remarkable changes in RoM at the treated and adjacent segments. The authors of these studies showed that the various disc prostheses generally preserve the mobility at near physiological level, for both constrained and unconstrained designs, which was confirmed by our FE simulations. However, the RoM alone is not sufficient to evaluate the spinal stability. Therefore, authors used the ICR as an additional parameter to analyze the motion behavior of the treated segment [5, 6, 20]. In a FE analysis, we estimated the measurement error, which is always given when ICRs are experimentally determined [27]. In this study we showed that a small domain of input data led to severe changes on the position of the ICR. This implies that simply alignment of two X-rays generated in different postures, as done in clinical practice, is not sufficient to determine the ICR. Indeed, a high accuracy is needed because of small movements which in particular occur when the spine is exposed to axial rotation. Data evaluations using FE models with a high validity and predictability are a suitable tool for evaluating ICR locations, since there are no further measurement errors.

The results of our FE study supported our hypothesis in that the different mobile implants do not lead to substantial differences in the location of the ICRs. Except in axial rotation, the ICRs of all three implant designs mimicked almost the non-treated intact situation. The implant with the constrained core did not cause a fixed ICR. This result can be explained as follows: The artificial disc should not be considered separately but with the surrounding elastic structure. Our FE results showed that the adjacent bony endplates may strongly deform under certain loads. At the same time high forces in the facet joints occurred, especially in axial rotation (Fig. 3). These high facet forces in combination with the endplate deformation allow the adjacent vertebrae to translate relatively to each other and therefore, lead to a moving ICR.

In axial rotation, the different implant designs showed a slightly different behavior. While the Charité^® and SD-IMC prostheses predicted ICRs inside the disc, the SD-MC prosthesis caused an ICR location outside the disc, close to the compressed facet joint and therefore, better mimicked the intact situation. This is caused by the sliding core. Under small moments no differences in ICRs were calculated between SD-MC and SD-IMC (Fig. 7). Under these small moments, the inner core of the SD-MC prosthesis moved only marginally within the implant (less than 0.1 mm). From approximately 5 Nm upward to 7.5 Nm, the SD-MC led to a sudden change of the resulting ICR locations. This moment increase caused the inner core to migrate 0.8 mm to the ipsi-lateral direction. The movement of the core is the crucial factor, which caused an ICR migration to the compressed facet joint.

In flexion, extension, and lateral bending we calculated a cranial-caudal migration of the ICRs for the SD-MC. In the first instance such a result would seem unexpected, because an implant which is restricted to a transversal movement of the inner core should only allow the migration of the ICRs in same direction. The cranial-caudal migration can, however, be induced by two different parameters. One point is that the lower metallic endplate is slightly concavely curved allowing the core to move slightly vertically during transverse motion. A second point is that the adjacent bony structures are deformed during loading so that the relative distance of the core in relation to the bony structures is altered.

Both results, a posterior migration of the ICRs towards the facet joints as well as the constrained core did not lead to a fixed ICR, seem to be caused by a lift-off of the metallic endplate from the core. However, this phenomenon did not occur in all load situations. The pressure distribution of the core and the metallic endplates was analyzed by the authors and both parts were always found to be under stress, which is an indication that this lift-off would not occur. Such a lift-off was found in a previous study by us (unpublished data), however, for only one specific load direction: pure moment in extension without an axial compression preload. In this case, the facet joints led to an opening of the implant. We made additional investigations in which we defined a ‘no separation’ contact condition between the metallic endplates and the inner core. The results were the same as that found in our study. In addition, no tensile stresses between the metallic endplates and the inner core were calculated, which would indicate a separation between both contact pairs.

In contrast to the RoM and ICRs, the facet joint force strongly depends on the implant design. For all load cases, our model predicted higher facet joint forces for the implants with an unconstrained core (Charité^® and SD-MC) compared to an implant with a constrained core (SD-IMC). This result can be explained by the resulting forces passing through the implant itself. An unconstrained design transfers only normal forces from the upper to the lower vertebral body. In contrast, a constrained design additionally transfers shear forces through the implant and therefore, is stronger loaded than the unconstrained design. Our FE model predicted implant forces in flexion, extension, lateral bending, and axial rotation of 623, 1,013, 785, and 852 N for the SD-MC, and forces of 985, 1,130, 945, and 963 N for the SD-IMC model, respectively. On average, the constrained implant is 19% higher loaded than an unconstrained implant. This force difference is compensated by the articulating facet joints meaning that higher implant forces resulted in lower facet forces.

The resulting forces in the facet joints have been discussed at length in the literature. While Zander et al. [35] calculated a strong increase of the acting forces in the facets in extension for the Charité^®, Grauer et al. [8], Goel et al. [7], and Moumene and Geisler [16] found a slight to moderate decrease in these forces for the same implant. These opposing findings were intensified by our results. For the Charité^® we predicted even less forces, down to unloaded conditions. Whereas, with the Slide-Disc^®-MC we determined a moderate increase in the resulting forces. In the case of the ProDisc^® (which corresponds to the Slide-Disc^®-IMC in our study) these inconsistencies were similarly found. For this implant, both Moumene and Geisler [16], and Zander et al. [35] predicted a slight decrease in the acting forces, whereas, the study results of Rundell et al. [25] as well as our results indicated either almost or completely unloaded facets. In flexion, Zander et al. [35] found no forces in the facets for intact as well as for all the investigated implants. In contrast, Grauer et al. (2006) indicated that the Charité^® led to a slight force in flexion, although more details were not provided. The study results of Rundell et al. [25] for the ProDisc^® together with our results for all three implant designs predicted strong facet forces. The same inconsistencies can be seen for lateral bending and axial rotation.

One reason for such a large variation in the results may have arisen through the use of FE models based on different geometries. Consequently, slight changes in the gap distance, the degree of curvature or the facet orientation can lead to completely different results. In our investigations the gap size was set at 0.4 mm. An increase in the gap of only 0.1 mm led to an average decrease of 45% for all the three implants. A probabilistic FE analysis by Rohlmann et al. [22] confirmed our supposition. The authors investigated how, for example, the facet forces are influenced by parameters such as the implant position, the presence of scar tissue or the gap size in the facet joints when implanting the ProDisc^®. In extension, Rohlmann et al. reported a zero force for the instrumented segment in 70% of all investigated cases (1,000 randomly generated FE models), which is in agreement with our predictions. Rohlmann et al. suggested that the resulting forces are strongly dependent on the gap size. Furthermore, the authors found that in flexion the ProDisc^® caused facet forces in 37% in the instrumented segment, which is also confirmed by our predictions.

The described methodology has some assumptions and limitations. In the current study, we decided on a follower load magnitude of 1,000 N, which contrasts with our previous studies in which we only simulated a follower load of 500 N. The reason for this is that Rohlmann et al. [24] suggested in a FE study that a load of 500 N was not sufficient for simulating flexion, since it did not take into account the global muscle forces. However, when the authors increased the load up to 1,175 N, they obtained results that were comparable with in vivo data. In comparison to 500 N, this increase had only a minor influence on the RoM and a neglectable effect on the resulting facet forces. For extension when they simulate a follower load of 500 N they were already able to calculate an acceptable intradiscal pressure. However, the calculated facet joint forces under this 500 N were much lower in comparison to the simulation when the global muscle forces were considered, which Rohlmann et al. indicated as being a more physiological load application. A ‘more realistic’ facet joint force was much more important in our study than the intradiscal pressure, because the facet joint forces have a stronger influence on our results than the disc pressure, which are moreover absent in our different implant models.

The follower load was applied to the spinal segment by using connector elements which passed almost the ICRs (center of the disc) found for small moment applications and therefore, avoid the generation of additional ‘larger’ moments. However, the ICRs are not fixed in space and changed with motion. This may produce additional moments when further bending or torsional moments are applied. The current study showed that the ICRs are mostly located in the center of the disc, except for axial rotation. Axial rotation produced the largest changes in the ICRs during loading, meaning that the ICRs migrate from the disc center to the corresponding compressed facet joint. This larger distance generates additional moments for the motion segment, which cannot be neglected.

We used a fixed combination of material properties for the different artificial disc implants as used in a prior FE study of Goel et al. [7] and defined by Weber Instrumente. The exact values of the Young’s modulus and of the Poisson’s ratio of the titanium alloy and the UHMWPE were neither published by the company Depuy Spine nor known by Weber Instrumente and therefore, may slightly differ from the values used in the current study. Different values might have a small influence on our findings.

The form, such as the radius and the size of the inlay, of an actual fixed core design was not considered in the current study and therefore a specific functional goal of this design is lacking. The advantage of this approach lies in the fact that the actual functional difference between a fixed and a mobile core can be determined independently of other inter-implant differences. In our study the only difference between mobile and immobile core design was a single condition in the contact definition (standard vs. bonded). If we had used the ProDisc^® prosthesis as an example of a fixed-core design, other parameters would have had an influence on our results and therefore would have obscured the differences that we found.

Our controversial findings in facet forces raise the question of the reliability of deterministic FE studies, which are characterized by a fixed configuration of material and geometrical properties. The results generated by this type of model should always be interpreted with caution, and certain results, such as specific pressure values at the facet surfaces should not be interpreted in a clinical context; they simply provide a trend. Deterministic models are, however, legitimate when directly comparing the biomechanical outcome of two different disc prosthesis, with the qualification that a small modification of the geometry could produce the opposite results.

Conclusions

Total disc arthroplasty inherently alters the kinematics at implant level for all clinical used prostheses. Compared to these alterations, our finite element model predicted that inter-implant differences are small regarding the RoM and ICR. In contrast, facet joint forces are strongly dependent on the implant design. In contrast, facet forces appeared to be strongly dependent on the implant design. However, due to the great variability in facet forces reported in the literature, together with our results, we could speculate that these forces may be more dependent on the individual spine geometry rather than a specific implant design. In order to be able to make a suggestion, it is necessary to know which load directions of the spine and which parameter is most significant. If it is, for example, flexion and the RoM, it does not make any difference which implant design is used. If it is in contrast axial rotation and the ICR, our results suggest the need of a mobile core design.