Untangling complex networks: risk minimization in financial markets through accessible spin glass ground states

Abstract

Recurrent international financial crises inflict significant damage to societies and stress the need for mechanisms or strategies to control risk and tamper market uncertainties. Unfortunately, the complex network of market interactions often confounds rational approaches to optimize financial risks. Here we show that investors can overcome this complexity and globally minimize risk in portfolio models for any given expected return, provided the relative margin requirement remains below a critical, empirically measurable value. In practice, for markets with centrally regulated margin requirements, a rational stabilization strategy would be keeping margins small enough. This result follows from ground states of the random field spin glass Ising model that can be calculated exactly through convex optimization when relative spin coupling is limited by the norm of the network's Laplacian matrix. In that regime, this novel approach is robust to noise in empirical data and may be also broadly relevant to complex networks with frustrated interactions that are studied throughout scientific fields.

1. Introduction

Large and abnormal fluctuations in financial markets can spread into other parts of the global economy with untoward and often incalculable effects—as observed to dramatic consequences in recent times. Therefore a key priority is to minimize risks and contain their propagation in spite of the tendencies of current financial markets to the contrary [1, 2]. Important examples of such market places include exchanges where stocks, commodities, futures and other financial products can be bought and sold short by using leverage on margin accounts held by investors. A central financial decision problem in these markets is, for a given expected return r_P, to distribute the available capital among multiple assets, which comprise a portfolio P of size n, so to minimize the overall risk.

In portfolio selection models this goal can be mathematically formulated as finding the global minimum of a risk function [4-7], $R=1/2{\sum }_{i,k=1}^n{C}_{\mathit{\text{ik}}}{p}_i{p}_k-{\sum }_{i=1}^n{p}_i{r}_i-\mathit{\gamma }{\sum }_{i=1}^n{p}_i{s}_i$, where p_i is the positive or negative amount of capital invested in asset i, and s_i = sign (p_i) ∈ {−1, 1} are binary spin variables; r_i is the expected return of asset i such that $r_p={\sum }_{i=1}^n{r}_i{p}_i;{\text{C}}_{\mathit{\text{ik}}}$ is the covariance between assets i and k; and γ is the margin account requirement which sets the fraction of capital that the investor must deposit in a margin account before buying or selling short assets. With the inverse C⁻¹ of the covariance matrix C the minimum risk distribution p = (p₁,…, p_n) becomes $p_i={\sum }_k{C}_{\mathit{\text{ik}}}^{-1}{r}_k+\mathit{\gamma }{\sum }_k{C}_{\mathit{\text{ik}}}^{-1}{s}_k$. It is known that finding the absolute risk minimum is computationally equivalent to the ground state problem of the random field Ising model [4, 6]. This is evident after inserting p into the risk function while neglecting fixed terms that do not depend on spin variables which gives $R=-1/2{{\sum }_{i,k=1}^n\text{J}}_{\mathit{\text{ik}}}{s}_i{s}_k-{\sum }_{i=1}^n{h}_i{s}_i$, and where we introduced an interaction term $J_{\mathit{\text{ik}}}=\mathit{\gamma }{C}_{\mathit{\text{ik}}}^{-1}$ and a random local field h = (h₁,…, h_n) with $h_i={\sum }_{k=1}^n{C}_{\mathit{\text{ik}}}^{-1}{r}_k$. Covariance among assets can be both positive and negative (see, for example, inset in Fig. 1 A), and globally minimizing risk means finding a ground state of the random field Ising model with random spin glass interactions, which in general belongs to the class of NP-complete decision problems [8, 9] and for which efficient algorithms are not known. This computational intractability arises from the non-convexity of the cost function R; non-convex problems are much harder to solve computationally than convex optimization problems for which efficient algorithms do exist [10]. In the context of financial markets, the non-convexity of the spin glass model prevents equilibration into an optimum ground state and is viewed as an inherent source of risk [3, 4].

Figure 1.

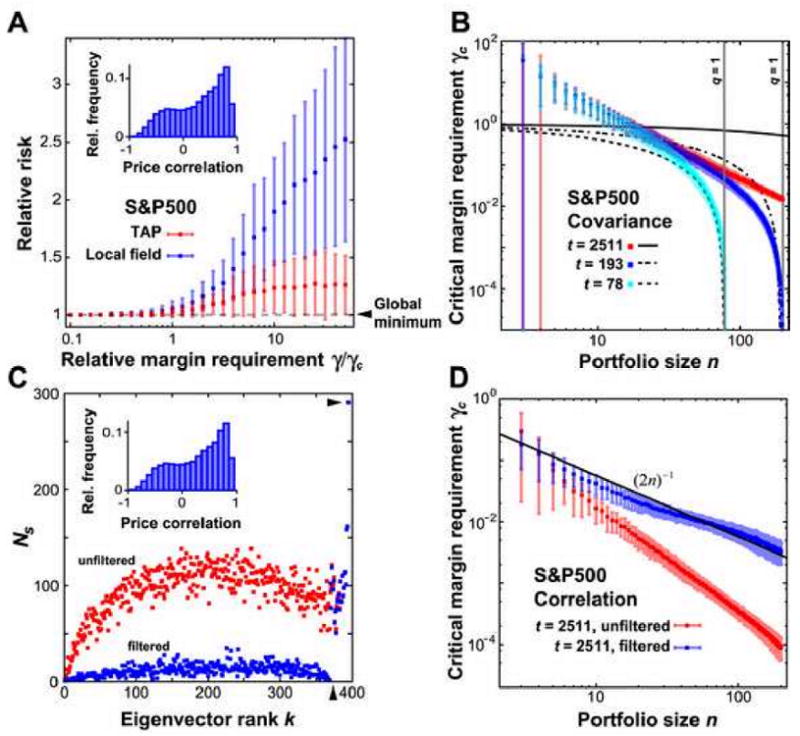
(A) Portfolio risk can be globally and rationally minimized if the relative margin requirement satisfies γ / y_c < 1. In contrast, for γ / γ_c > 1 the estimated risk undergoes large fluctuations above the optimum. Red data points (“TAP”) give the risk from solutions of the TAP equation for n = 16 with randomly selected assets from the S&P500 price data, and with a random field h = (h₁,…, h_n) with |h_i| ≤ 1. Blue data points (“Local field”) depict the risk obtained by taking the sign of local field h. Error bars represent standard deviations after 128 random trials. Inset shows the distribution of all price correlations between all pairs in the m = 395 assets taken from the S&P500 index. (B) Estimated critical margin requirement as a function of portfolio size n ≤ m and for three different choices of price samples, t = {2511, 193, 78}, where stock prices were selected every {1, 13, 32} days, respectively. Error bars represent standard deviations from 128 random selections in the S&P500 price data. Black solid and dashed graphs represent the function ${\left(1-\sqrt{n/t}\right)}^2$. (C) The inverse partition ratio $N_s={\sum }_{l=1}^m{(u_l^k)}^4$ for each normalized eigenvector u^k of the m × m correlation matrix C̃ ranked by its increasing eigenvalues [13]. Red dots represent the unfiltered correlation matrix which, up to a rank of k = 372, follow a semicircle distribution; blue dots represent the filtered correlation matrix after setting all eigenvalues with lower rank to zero, i.e. those in size smaller than λ_max. Inset shows the resulting histogram of pairwise price correlations after filtering. (D) Estimated critical margin requirement γ_c from the S&P500 correlation matrix C̃ before (red) and after (blue) eigenvalue filtering. Black solid line represents the graph (2n)^-1.

2. Accessible ground states in the spin glass Ising model with random field

Here we demonstrate that ground states are efficiently accessible in the random field spin glass Ising model provided the margin requirement γ remains below a critical value, which we define as ${\mathit{\gamma }}_c={\Vert L\Vert }^{-1}={\left[{\text{max}}_i\left({\sum }_{k=1}^n|L_{\mathit{\text{ik}}}|\right)\right]}^{-1}$, where L = D−C⁻¹ is the network's Laplacian matrix, with $D=\text{diag}\left({\sum }_{i=1}^n{\text{C}}_{\mathit{\text{ik}}}^{-1}\right)$ and ‖L‖ is its maximum norm. This upper bound on the margin requirement ensures that there exists a related but convex risk function $R_c=1/2{\sum }_{i,k=1}^n{J}_{\mathit{\text{ik}}}{\left(s_i-s_k\right)}^2+{\sum }_{i=1}^n{\left(h_i-s_i\right)}^2$, which in matrix form reads R_c=(s − h)^T (s − h) + γs^T L s. We note that in the special and simpler case with non-negative interactions J_ik ≥ 0 similar objective functions have been studied in semi-supervised machine learning [11]. In the more challenging spin glass case, our prerequisite γ < γ_c makes the Hessian matrix H_c =1 + γL positive definite such that R_c remains convex with one global minimum even if the interaction is described by a random mix of positive and negative numbers. Let s denote the minimum configuration in R_c obtained after convex optimization, then s also depicts the ground state s* of the spin glass Ising model with a random field because assuming the contrary, R(s) > R(s*), leads to a contradiction. To see this we choose a discrete path of single spin flips that leads from s to s*. At the beginning R_c(s) is a global minimum and nowhere on the path the cost in R_c can be lower. Concurrently, for any spin flip at site i the resulting change in R_c equals twice the risk change in R, viz. $\Delta R_{c,i}=R_c(-s_i)-R_c(s_i)=2\Delta R_i\text{with}\Delta R_i=2s_i\left(h_i+1/2{\sum }_{k=1}^n{J}_{\mathit{\text{ik}}}{s}_k\right)$, and so nowhere along the path–including its end–the risk in R can be lower than at the beginning. Therefore, in contradiction to the assumption, it is R(s*) ≥ R(s) which proves that s is a global minimum of the Ising model. Note that this argument is valid only for the Ising model with non-zero external field h; without a random field the cost function R_c cannot be made convex by reducing the parameter γ.

This result directly implies that once γ < γ_c is satisfied any feasible algorithm that converges to a local minimum of the random field Ising model will, due to the underlying convexity of R_c, reach the absolute minimum in R; for example, this may be achieved by solving for all s_i the local stability condition through fixed points of the TAP (Thouless-Anderson-Palmer) equation [12], $s_i=\text{sign}\left[h_i+{\sum }_k{J}_{\mathit{\text{ik}}}{s}_k\right]$ for i ∈ {1,…, n}. It also shows that the critical margin requirement separates two distinct regimes: a disordered regime for γ > γ_c with an exponential number ∼2ⁿ of equivalent local minima in the risk function [4, 7], each one giving a different selection of the portfolio; and, for γ < γ_c, an ordered regime with only one distinguished minimum. Thus in the latter case the portfolio risk model significantly loses complexity and a computationally efficient, rational access to the optimum is opened.

3. Application to stock price data

To illustrate this general result with a numerical example we compared risk values from actual stock price data evaluated below and above the critical margin requirement. For the calculation of the covariance matrix C we used end-of-day (EOD) stock prices of m = 395 companies included in the Standard and Poor's 500 (S&P500) index over ten years, recorded from February 1999 to February 2009 in t = 2511 time points, which after centralization defined an m×t matrix M with zero mean. From this portfolios of any size n ≤ m were randomly selected defined through a reduced n×t matrix M_n where only n rows out of m were retained. Given the selected portfolio's n×n covariance matrix $C=\left(M_n{M}_n^{\text{T}}\right)/t$ and a random input distribution of the local field h, the portfolio risk was optimized efficiently by solving the TAP equation through iteration until a fixed point was reached. Relative risk is the lowest possible risk value (which was a negative number in our example) divided by the estimated risk after optimization. The lowest risk was found through exhaustive search in all spin states; this was computationally feasible due to our choice of a small portfolio size (n = 16) even though solving the TAP equation by iteration is computationally efficient for any network size n. Consistent with the theoretical prediction Fig. 1A shows that with margin requirements below γ_c the relative risk settled at its global minimum, i.e. at the spin glass Ising model ground state. The picture changes for γ > γ_c, where strong fluctuations significantly elevate the risk above the ground state; for instance, at γ ≫ γ_c, the average relative risk from the TAP solutions leveled out at ∼25% above the optimum.

The price data further allowed us to follow the critical margin requirement as a function of portfolio size n. Figure 1B shows that (a) γ_c is a decreasing function of n, indicating that in larger portfolios efficient risk minimization imposes stricter limitations on margins, and (b) γ_c vanishes for q ≡ n / t → 1, which means that for a given number of observed prices t efficient risk minimization can only occur up to a maximum portfolio size n = t. This behavior can be understood by assuming that C is a random Wishart matrix where the bulk of eigenvalues follows a Marcenko-Pastur distribution [13] with a minimum eigenvalue ${\mathit{\lambda }}_{\text{min}}={\mathit{\sigma }}^2{(1-\sqrt{q})}^2$ and a maximum ${\mathit{\lambda }}_{\text{max}}={\mathit{\sigma }}^2{(1+\sqrt{q})}^2$; here, without loss of generality, σ² ≥ 1 denotes the variance of the elements in M. Therefore—by duality—the spectral radius ρ(C⁻¹), defined as the largest eigenvalue of C⁻¹, equals ${\mathit{\lambda }}_{min}^{-1}$. Since ${(1-\sqrt{q})}^{-2}\le \mathit{\rho }(C^{-1})\le \Vert C^{-1}\Vert \le \Vert L\Vert +\Vert D\Vert$ it follows that in the limit q →1 the norm ‖L‖ diverges and hence γ_c must vanish.

Random matrix theory can be further applied to analyze the influence of noise on the critical margin requirement. For that we normalized C by the variance to obtain the price correlation matrix C̃ with a small parameter q = 395 / 2511 ≈ 0.16; we then filtered C̃ by setting all its eigenvalues below λ_max to zero because these are expected to contribute only uninformative noise [13, 14]. Even though this procedure discarded all but the highest 23 eigenvalues (Fig. 1C) the resulting distribution of price correlations remained practically unaffected (compare inset in Fig. 1C with inset in Fig. 1A), which indicates that spin glass interactions from these data are genuine and not mere noise artifacts [14, 15]. However, filtering significantly lifted the critical margin requirement estimates (Fig. 1D) which suggests that this number is systematically underestimated when computed from unfiltered correlations. In this filtered case, the critical margin requirement is expected to scale inversely proportional to 2n, which directly follows from the definition of γ_c and from the fact that the underlying pairwise correlations form a totally connected graph. Indeed, Fig. 1D shows that this simple scaling, γ_c ∼ (2n)⁻¹, is an accurate approximation to the critical margin requirement graph obtained from actual price data. Thus, in this example, noise filtering becomes a stabilizer that can extend the parameter range for efficient risk optimization.

4. Conclusions

Risk minimization in portfolio selection models with short selling is equivalent to the ground state problem of the random field Ising model with spin glass interactions. Because calculating its ground state is computationally hard in general, globally minimizing the risk has been regarded as unfeasible with a computationally efficient and rational approach [3, 4]. Our result shows that, under realistic conditions, finding the ground state and thus efficient risk minimization is rationally possible. As a direct consequence in financial markets, this may provide an instrument for curbing volatility if financial products are traded below the critical margin requirement, and if investors and traders rationally optimize their portfolios. The second condition is both desirable and realistic in today's highly computerized markets, although it may have been less realistic in the past when computers were not widespread and therefore complex financial decisions were to a lesser degree rational. But the first condition seems to be in conflict with interests of traders and lenders who, in individual contracts, seek to reduce default risk by increasing margins. From a collective market perspective, however, higher margin requirements may have a destabilizing effect through higher transaction costs, which can drive traders from the market place; this may lead to a lower overall liquidity thus making the market more susceptible to volatility [16, 17]. Hence, in financial markets where minimum margin requirements are regulated a reduction of risk by lowering margins is conceivable. Historically, the possibility of such a regulatory approach is indirectly supported by the fact that both the 1987 and the 1929 financial market crashes were accompanied by an increase in margin requirements which exacerbated liquidity problems and which might have contributed to rapid downfall [18, 19]. Of practical relevance may be the observation that for portfolio sizes above n ≈ 10 our estimates on the critical margin requirement from the recent American stock market fall below one (Fig. 1B), thus potentially imposing realistic upper limits on margins requirements.

The efficient access to an optimum is not restricted to portfolio risk models; in general, an efficient computation of a ground state is possible in any spin glass Ising model with a random field if the relative coupling strength between spins falls below the critical value. Further applications may follow in frustrated systems that routinely occur in artificial [20, 21] and in biological [22, 23] networks and where the goal is to find a ground state.