Abstract
Constrained local models (CLMs) have recently demonstrated good performance in non-rigid object alignment/tracking in comparison to leading holistic approaches (e.g., AAMs). A major problem hindering the development of CLMs further, for non-rigid object alignment/tracking, is how to jointly optimize the global warp update across all local search responses. Previous methods have either used general purpose optimizers (e.g., simplex methods) or graph based optimization techniques. Unfortunately, problems exist with both these approaches when applied to CLMs. In this paper, we propose a new approach for optimizing the global warp update in an efficient manner by enforcing convexity at each local patch response surface. Furthermore, we show that the classic Lucas-Kanade approach to gradient descent image alignment can be viewed as a special case of our proposed framework. Finally, we demonstrate that our approach receives improved performance for the task of non-rigid face alignment/tracking on the MultiPIE database and the UNBC-McMaster archive.
1. Introduction
In this paper we propose a new discriminative approach for non-rigid object registration based on the constrained local model (CLM) [7] framework first proposed by Cristinacce and Cootes. A CLM is able to register a non-rigid object through the application of an ensemble of patch/region experts to local search regions within the source image. Given an appropriate non-rigid shape prior for the object, the response surfaces from these local regions are then employed within a joint optimization process to estimate the global non-rigid shape of the object. A major advantage of CLMs over conventional methods for non-rigid registration such as active appearance models (AAMs) [6] lies in their ability to: (i) be discriminative and generalize well to unseen appearance variation; (ii) offer greater invariance to global illumination variation and occlusion; (iii) model the non-rigid object as an ensemble of low dimensional independent patch experts; and (iv) not employ complicated piece-wise affine texture warp operations that might introduce unwanted noise.
In our paper we address an important problem still hindering CLM performance. Specifically, how should we jointly optimize the response surfaces when estimating the global non-rigid shape of the object? Current methods [7] for joint optimization within a CLM are problematic as they: (i) rely on computationally expensive generic optimizers such as the Nelder-Mead simplex [7] method, or (ii) attempt to find a local maximum in each patch response surface and then simply constrain these local maximums to be consistent with the global shape prior [19]. Our work proposes a number of extensions and improvements to these current approaches:-
We show that a specific form of the classic Lucas-Kanade [15] approach to gradient-descent image alignment can be viewed as a CLM where each local response surface is indirectly approximated through a convex quadratic function. Since each of the approximated response surfaces are convex an explicit solution to the approximate joint minima can be found (since it too is convex). This process can be iterated until some convergence towards the actual joint minima is obtained. Unfortunately, this approach is restricted to patch experts that employ a sum of squared differences (SSD) similarity measure and as a result is not directly applicable within the generic CLM frame-work. (Section 4.1)
To circumvent this limitation we propose an approach that is able to directly fit a convex quadratic to the local response surface of any type of patch-expert. As a result we are able to apply a similar optimization as employed in the Lucas-Kanade algorithm without the problems associated with employing a SSD similarity measure at each patch expert. (Section 4.2)
Finally, we demonstrate improved non-rigid alignment performance on the MultiPIE [10] and UNBC McMaster [1] archive facial databases. Our convex quadratic approach exhibits superior performance to the exhaustive local search (ELS) approach [19] and leading holistic AAM [6] approaches to non-rigid object alignment. (Section 5)
Related Work
Robust and accurate non-rigid alignment has been studied intensively in the last two decades [3, 6, 22, 21, 7, 11, 13, 8, 9, 2, 20, 14]. Recently, a number of registration methods have been developed based on local region descriptors and a non-rigid shape prior. Apart from the work of Cristinacce and Cootes [7], which is of central focus in this paper, there have been a number of notable works in the area. Gu and Kanade recently formulated non-rigid alignment fitting as a Bayesian inference problem [11] and then as a graph learning and searching problem [12]. Liang et al. [13] constructed a sophisticated Markov network using image parts and integrated the global shape prior to optimize the face alignment. Liu [14] proposed a generic face alignment method by combining a conventional point distribution model (PDM) and a boosted appearance model (BAM) to maximize a classification score.
2. Learning Constrained Local Models
The notation employed in this paper shall depart slightly from canonical methods in order to easily allow the inclusion of patches of intensity at each coordinate rather than just pixels. When a template T is indexed by the coordinate vector x = [x, y]T it not only refers to the pixel intensity at that position, but the local support region (patch) around that position. For additional robustness the P × P support region1 is extracted after the image has been suitably normalized for scale and rotation to a base template of the non-rigid object. T(xk) and Y(xk) refer to the vector concatenation of image intensity values within the kth region (patch) of the template image T and the source image Y, respectively.
Estimating Patch Experts
The choice of classifier employed to learn patch experts within a CLM can be considered to be largely arbitrary allowing the use of a variety of methods such as boosting schemes [4, 14] (e.g., AdaBoost, GentleBoost, etc.) or relevance vector machine (RVMs) [4] to mention just a few. A linear SVM was chosen in our work over other classifiers due to its computational advantages in that,
| (1) |
where f̂(Δx) is the match-score for the patch-expert at coordinate displacement Δx from the current patch coordinate center x. Y is the source image, Ti is the ith support vector, αi is the corresponding support weight, γi ∈ {not aligned (−1), aligned (+1)} is the corresponding support label, and NS is the number of support vectors. Employing a linear SVM is advantageous as it allows for to be pre-computed rather than evaluated at every Δx. The support images Ti are obtained from an offline training set of positive and negative images. Positive patch examples were obtained for patches centered at the fiduciary points of our training images, while negative examples were obtained by sampling patches shifted away from the ground truth.
An approximate probabilistic output was then obtained by fitting a logistic regression function [4] to the output f̂ of the support vector machine and the labels y = {not aligned (−1), aligned (+1)}
| (2) |
where a and b are learned through a cross-validation process.
Obtaining Local Responses
Once the patch expert has been trained we can obtain a local response for an individual patch expert by performing an exhaustive search in the neighboring region of that patch’s current position within the source image. In our experiments, we found a search window size of 25 × 25 pixels for each patch gave good results for a face object with an inter-ocular distance of 50 pixels.
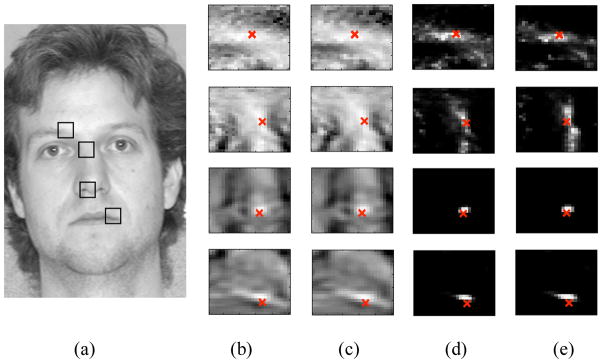
Example response surfaces are shown in Figure 1. To illustrate the effectiveness of our patch experts we placed the center of the searching window randomly away from the ground truth position. From the top row to the bottom in Figure 1(b–e), it shows the local responses for patch experts describing the left eyebrow, the nose bridge, the nose end, and the right mouth corner, respectively. As one can see, the estimated responses perform a good job of finding the ground truth location. All response surfaces were obtained from a linear SVM.
Figure 1.
Examples of local search responses: (a) is the source image to be aligned. (b) shows the local search responses using patch experts trained by 125 positive examples and 15k negative examples. (c) shows the local search responses trained by 125 positive examples and 8k negative examples. (d) and (e) show the estimated logistic regression weight values of (b) and (c), respectively. A high intensity value indicates a small matching error between the template and the source image patch. Each row in (b–e) shows the responses and weights within a 25 × 25 local search window. The location of each search window is illustrated in the source image (a) as a black box, while the red cross illustrate the ground truth alignment. It is interesting to see that the patch experts learned by a smaller training set (including 8k negative examples) have very similar performance as the ones trained by large training examples (including 15k negative examples).
In Figure 1(b), 125 positive examples and 15k negative examples were used to train each patch expert, while in Figure 1(c), 125 positive examples and 8k negative examples were used. Both positive and negative examples contained 15 × 15 patches extracted from the training images. As we can see, the performance of the patch experts learned by a smaller training set, shown in Figure 1(c) and (e) is almost the same as the performance seen for experts trained on a larger number of training examples in Figure 1(b) and (d). This result demonstrated that our patch-experts had a reasonable amount of training examples for employment within a CLM framework.
Estimating the PDM
A point distribution model (PDM) [6] is used for a parametric representation of the non-rigid shape variation in the CLM. The non-rigid warp function can be described as,
| (3) |
where , p is a parametric vector describing the non-rigid warp, and V is the matrix of concatenated eigenvectors. N is the number of patch-experts. Procrustes analysis [6] is applied to all shape training observations in order remove all similarity. Principal component analysis (PCA) [4] is then employed to obtain shape eigenvectors V that preserved 95% of the similarity normalized shape variation in the train set. In this paper, the first 4 eigenvectors of V are forced to correspond to similarity (i.e., translation, scale and rotation) variation.
3. Constrained Local Model Fitting
Based on the patch experts learned in Section 2 we can pose non-rigid alignment as the following optimization problem,
| (4) |
where Ek() is the inverted classifier score function obtained from applying the kth patch expert to the source image patch intensity Y(xk + Δxk). The displacement Δxk is constrained to be consistent with the PDM defined in Equation 3, where the matrix V can be decomposed into submatrices Vk for each kth patch expert, i.e., .
In general, it is difficult to solve for p in Equation 4 as Ek() is a discrete function due to Δx only taking on integer values and there is no guarantee for Ek() being convex. Previous methods have either used general purpose optimizers (e.g., Nelder-Mead simplex [16]) or attempted to pose the problem as a form of graph optimization [7, 12]. Unfortunately, general purpose optimization techniques, such as Nelder-Mead simplex [16], are often computationally expensive and require good initialization. In order to employ graph optimization techniques like loopy belief propagation it has been shown that the warp function 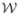 (z; p) needs to be spatially sparse as described in [12].
(z; p) needs to be spatially sparse as described in [12].
Exhaustive Local Search
An efficient approach to solve for p in Equation 4 is to use the exhaustive local search (ELS) method proposed in [19]. Instead of optimizing for the holistic warp update p directly, it optimizes for N local translation updates by exhaustively searching local regions of the object,
| (5) |
where Δxk is the local warp displacement of the kth region/patch (k = 1 … N) within a local search region. Then we enforce the warp update Δp by a weighted least-squares optimization [19]
| (6) |
where V is the Jacobian matrix from the PDM defined in Equation 3. The weighting matrix W is defined as a diagonal matrix 2,
Based on Δp, we update the current warp p by 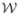 (z; p) ←
(z; p) ← 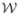 (z; p) ○
(z; p) ○ 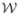 (z; Δp). This algorithm is performed iteratively until ||p|| <= ε or a maximum number of iterations is reached.
(z; Δp). This algorithm is performed iteratively until ||p|| <= ε or a maximum number of iterations is reached.
4. Our Approach
A drawback to the ELS-based approach, however, is that the holistic warp update Δp is not estimated directly, but simply constrains all the local updates Δxk to lie within the subspace spanned by V. A desirable solution is to optimize the objective error function in Equation 4 jointly without checking all possible combinations of discrete local response values. In this section, we propose a new approach to jointly optimize p by convex quadratic fitting.
4.1. Learning from Lucas-Kanade
To gain insight into why convex quadratic fitting is useful it is of interest to briefly review the Lucas-Kanade gradient descent algorithm [15, 6, 3]. Let us assume that we are attempting to solve for N local translation updates as in Equation 5 for the ELS method. The only exception will lie in our employment of a sum of squared differences (SSD) error function instead of the generic Ek() objective error function,
| (7) |
where T is an arbitrarily defined template. When employing a SSD error function we no longer have to exhaustively search a local region around xk. Instead, we can employ a first order Taylor series approximation at Y(xk) to rewrite Equation 7 as,
| (8) |
which can be expressed generically in the form of a quadratic,
| (9) |
given,
| (10) |
where D(xk)= T(xk) − Y(xk), and G(xk) is the 2 × P2 local gradient matrix for each set of P2 intensities centered around xk.
Since Ak is virtually always guaranteed of being positive definite3, this implies the quadratic in Equation 9 is convex and has a unique minima. Since the summation of N convex functions is still a convex function [5] it is possible to solve not only for the local translation updates but the entire warp update Δp explicitly,
| (11) |
where V is the matrix of concatenated eigenvectors describing the PDM in Equation 3, and the matrix A has the form
| (12) |
As we are only using an approximation to the true SSD error surface it is necessary within the Lucas-Kanade algorithm to iterate this operation in a similar manner to the ELS approach and constantly update the warp estimate p until convergence.
4.2. Generic Convex Quadratic Curve Fitting
When assuming Ek () is a SSD classifier it is possible to gain a convex quadratic approximation to the true error responses. A major advantage of these approximations is that it gives a direct method to gain an estimate of the global warp update. In this section we shall elucidate upon how we can generalize this result for any type of objective error function.
Specifically, our approach shall attempt to estimate the parameters Ak, bk and ck, for each patch response surface, through the following optimization
| (13) |
where Ek(Δx) = Ek{Y(xk + Δx)}. We should emphasize that Ek () is now not necessarily a SSD classifier but can be any function that gives a low value for correct alignment. We should note that our proposed approach differs from the standard Lucas-Kanade algorithm in the sense that the actual error response for different translations must be estimated over a local region. In the original Lucas-Kanade approach no such local search responses are required.
For clarity, we list the outline of our convex quadratic curve fitting method in Algorithm 1. Furthermore, for 2D image alignment, we can assume and bk = [b1, b2]. Consequently, Equation 13 can be linearized into the following form
Algorithm 1.
Our convex quadratic curve fitting method.
| Input: | learned patch experts, source image (Y), |
| Jacobian matrix (V) | |
| initial warp guess (p), | |
| index to the template (z), threshold (ε) | |
| Output: | final warp (p) |
| |
| (14) |
where Ek (x, y) = Ek{Y(xk + Δx)} and Δx = [x, y]T. The above optimization is a quadratically constrained quadratic program (QCQP) and in general costly to be solved directly [5]. In the following sections, we will show some simplified versions of this generic quadratic curve fitting optimization.
Quadratic Program Curve Fitting
One way to reduce the complexity of Equation 14 is to enforce Ak to be a diagonal matrix with non-negative diagonal elements. More specifically, , where a11, a22 > 0. As a result, Equation 14 can be simplified as
| (15) |
which can be solved efficiently through quadratic programming [5]. We shall refer to this method of fitting a CLM as convex quadratic fitting (CQF).
When the local search responses from our patch experts have outliers as shown in Figure 1, it might be difficult to have accurate surface fitting. In the following section we will introduce a robust error function to improve the robustness of curve fitting.
Robust Error Function
Robust error functions have been used in many registration approaches [3, 17] to improve robustness for non-rigid image alignment. Although there are many different choices [17], a sigmoid function is selected similar to the weighting function in Equation 2. In particular, we define the robust error function in the following form,
where σ is a scale parameter which can be estimated from ℰ (x). Essentially, this function assigns lower weights to the response values whose fitting error is larger than the scale parameter σ, since they are more likely to be the outliers. As a result, the original curve fitting problem in Equation 13 can be rewritten as
| (16) |
where . By performing a first-order Taylor expansion of ϱ(ℰ(Δx); σ), we can derive the global update Δp explicitly in a similar form to Equation 11
| (17) |
where B is a 2N × 2N diagonal matrix with
where i = 2k and k = 1 … N. We shall refer to this method of fitting a CLM as robust convex quadratic fitting (RCQF).
Example Fits
Examples of local response surface fitting can be found in Figure 2, which illustrates the convex parametric representation of the non-parametric responses of local patch experts. The red cross shows the ground truth location in the search window. The closer the peaks of the local responses are to the red cross indicates the better the performance of the method. We can see that in most cases ELS, CQF, and RCQF methods can all achieve good performance. However, our proposed CQF and RCQF methods in (c) and (d) respectively are less sensitive to local minima than the ELS method in (b). We should note that although the learned patch responses look smooth, they are not generated by a mere smoothing step. Instead, they are continuous convex surfaces achieved by the constrained curve fitting proposed in this paper. The key point of enforcing the convexity of each local patch response is to find a convex local function, which is essential to achieve a fast convergence for the global optimization.
Figure 2.
Examples of fitting local search responses: (a) is the local search responses in Figure 1(d) using patch experts trained by a linear support vector machine (SVM). (b–d) show the surface fitting results. More specifically, (b) picks the local displacement with the minimum response value in the search window, while (c) and (d) fit the local search response surface by a quadratic kernel in Equation 15 and a quadratic kernel with a robust error function in Equation 16, respectively. The brighter intensity means the smaller matching error between the template and the source image patch. In each search window, the red cross illustrates the ground truth location. As we can see, in most cases, the above three methods can all achieve good performance, while the proposed convex quadratic fitting (CQF) (c) and the robust convex quadratic fitting (RCQF) (d) methods are less sensitive to local minima than the exhaustive local search (ELS) method (b).
4.3. Computational Complexity
In this section, we investigate the computation complexity of the our proposed approach and provide a comparison to comparable gradient-descent methods [15,6, 3]. For clarity purposes, we use the following parameters, N, NT, NW and Np, to denote the number of patch experts, the number of pixels within each patch expert, the size of a local search window and the number of shape parameters in the point distribution model (PDM) respectively. In our method we use a square search window and patch expert, so we define α to be the ratio between their size, i.e., NW = α2NT.
It has been demonstrated that the simultaneous and the project out extensions [3] to the Lucas-Kanade algorithm can be employed quite efficiently within an AAM framework. The main difference our proposed CLM approach has with methods exists in steps 2–4 of Algorithm 1. More specifically, at each iteration the computational complexity is for Step 2, O (NNT) for Step 3 and for Step 4 respectively. Furthermore, for the convex quadratic fitting in Section 4.2 there are only 5 parameters in Equation 15 which can be solved in polynomial time through quadratic programming [5]. As a result, the complexity of Step 2 is negligible compared to Steps 1 and 3. (Note that there is a small additional cost with robust error functions in Section 4.2, which will be analyzed further in our future work.) Therefore, in our proposed approach, the overall computational complexity of estimating the warp update in steps 2–4 is
| (18) |
Based on [3], we can also obtain the following computational complexity for the warp estimating steps in the simultaneous method
| (19) |
and
| (20) |
in the project out method, where NB is the number of the appearance parameters in an AAM. We can see that for a small α (whose typical value is 1 – 2 in our experiments), Equation 18 lies between Equation 20 and Equation 19. Therefore, our proposed algorithm has comparable speed performance with existing gradient-descent AAM methods.
5. Experiments
We conducted our experiments on two independent data sets: the MultiPIE face database [10] and the UNBC-McMaster archive [1]. The frontal portion of the MultiPIE database is used in our experiments. Among them 125 subjects were used for learning and the other 125 subjects were used for testing. The UNBC-McMaster archive [1] contains video clips of clinical patients with shoulder injuries. These clips contain a large amount of head motion and facial expression. All the images had 66 fiducial points annotated as the ground truth data.
5.1. Evaluation
In all our experiments the similarity normalized base template had an inter-ocular distance of 50 pixels. To test the robustness of our algorithms, we set the initial warp randomly with 5 – 10 pixels root mean squared point error (RMS-PE) from the ground-truth coordinates. These initial starting points were selected based on our offline experiments with the OpenCV Viola-Jones face detector [18], which regularly gave us an initial starting point between 5 – 10 RMS-PE.
For a fair comparison, we took into account differing face scales between testing images. This is done by first removing the similarity transform between the estimated shape and the base template shape and then computing the RMS-PE between the 66 points. In all our experiments 5 random warps were created for each source image in the testing set. To compare all our algorithms we employed an alignment convergence curve (ACC) [7]. These curves have a threshold distance in RMS-PE on the x-axis and the percentage of trials that achieved convergence (i.e., final alignment RMS-PE below the threshold) on the y-axis. A perfect alignment algorithm would receive an ACC that has 100% convergence for all threshold values.
5.2. Comparison Results
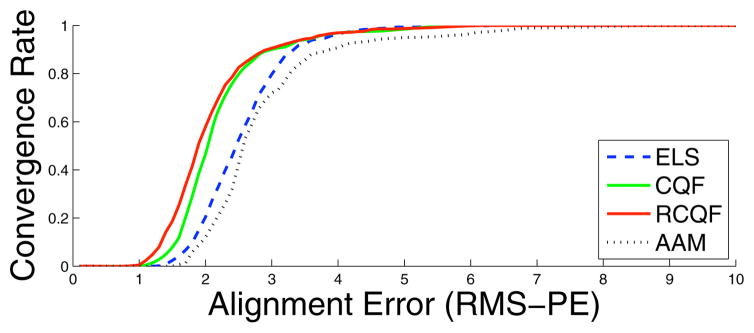
In this section we evaluate the performance of the three CLM algorithms discussed in our paper for non-rigid alignment, specifically, the ELS (Section 3), CQF (Section 4.2) and RCQF (Section 4.2) methods. For completeness, we also included the simultaneous AAM method which is considered one of the leading algorithms for holistic non-rigid alignment [3]. In our results we shall refer to this algorithm simply as the AAM method. Figure 3 shows the results of our comparison.
Figure 3.
A comparison of results using the MultiPIE face database [10]. 125 subjects were included in the training set and the other 125 subjects were used for testing. The initial shape error was between 5 – 10 pixels RMS-PE. The following four methods were included in the comparison: (i) the exhaustive local search (ELS), (ii) the convex quadratic fitting (CQF) method, (iii) the robust convex quadratic fitting (RCQF) and (iv) the active appearance model (AAM) method. As we can see, the CLM methods all outperformed the holistic AAM method by higher alignment accuracy and larger convergence rates. Moreover, the proposed CQF and RCQF methods had further improved the alignment performance of the ELS method. The RCQF method shows the best performance among all alignment methods.
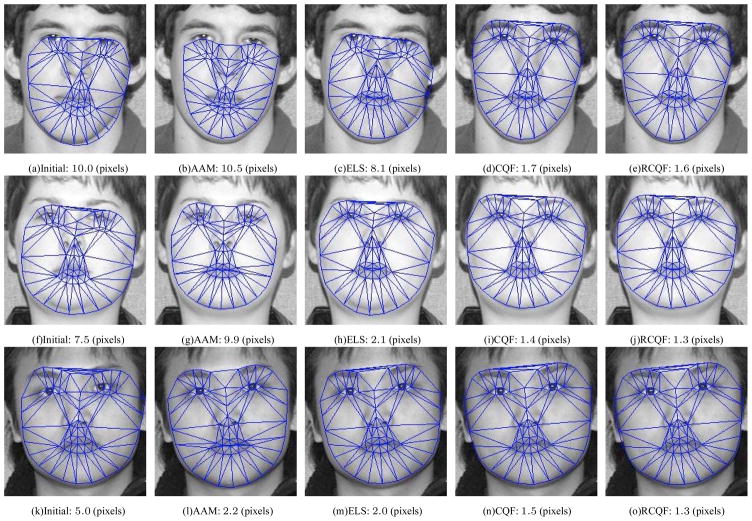
As discussed in Section 2 the CLM methods have several advantages over the holistic AAM method in terms of accuracy and robustness to appearance variation. The results in Figure 3 on the MultiPIE face database further support these claims. We can see in Figure 3 that the CLM algorithms all outperformed the AAM method. Furthermore, the proposed CQF and RCQF methods both received better performance than the ELS method. The RCQF method had the best performance amongst all the alignment methods. Examples of alignment result on different subjects are also shown in Figure 5 to illustrate the performance of the different methods compared in Figure 3.
Figure 5.
Examples of alignment performance on a single subject’s face. Rows 1, 2 and 3 illustrate the alignment for initial warp perturbation of 10, 7.5 and 5 pixels RMS-PE respectively. The first column shows the initial warp, while from the second and fifth column shows the resulting alignment from the holistic active appearance model (AAM), the exhaustive local search (ELS), the convex quadratic fitting (CQF), and the robust convex quadratic fitting (RCQF) methods, respectively. The resulting alignment error listed under each picture is computed in the same way as explained in Section 5.1.
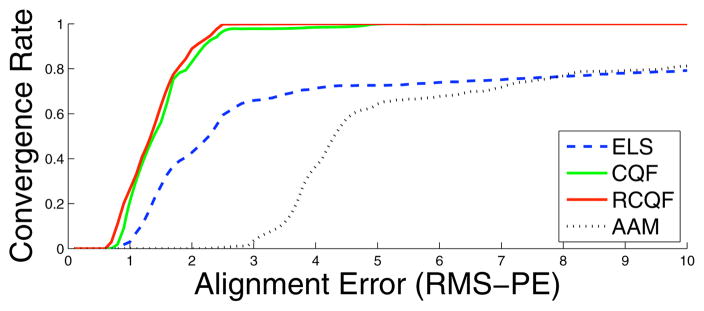
We also evaluated our proposed method to track non-rigid facial motion in video sequences. To evaluate the performance we conducted comparison experiments on a subset of the UNBC-McMaster archive [1] which included video clips of 6 clinical patients with significant head motion and facial expression. There are 200 – 400 frames in each video sequence. To make this task even more challenging we trained all models, including the PDM and the patch experts, separately on the MultiPIE face database [10]. As shown in Figure 4, all CLM methods had much better performance than the AAM method. Furthermore, compared to the ELS method, the proposed CQF and RCQF method were both more robust and accurate on non-rigid motion tracking.
Figure 4.
A comparison of tracking results on a subset of the UNBC-McMaster archive [1] which includes video clips of 6 clinical patients with significant head motion and facial expression. There are 200 – 400 frames in each video sequence. To make this task even more challenging, we trained all models, including the PDM and the patch experts, separately on the MultiPIE face database [10]. The definition of the terms can be found in the caption of Figure 3. As we can see, all CLM methods had much better performance than the holistic AAM method. Furthermore, the proposed CQF and RCQF method outperformed the ELS method by a larger margin in the accuracy and convergence rate compared to Figure 3. One hypothesis is that the patch experts trained in one data set does not perform as well in a new data set. By enforcing the convex constraint, the joint optimization can suppress the outliers and improve the robustness and accuracy of the non-rigid alignment.
6. Conclusion and Future Work
In this paper, we proposed a number of extensions to the canonical constrained local models (CLM) framework of Cristinannce and Cootes [7]. Specifically, we proposed an approach that is able to jointly optimize the local responses in an efficient manner when estimating the global non-rigid shape of an object. Our approach attempted to model each local response using a convex quadratic function. This convex quadratic framework was motivated by the effectiveness of the canonical Lucas-Kanade algorithm when dealing with a similar optimization problem. By enforcing this convexity it was possible, through an iterative method, to solve jointly for the global non-rigid shape of the object. Furthermore, our extension of the Lucas-Kanade algorithm leaded to an efficient and robust implementation of the CLM method.
We evaluated the performance of our proposed method using the CMU MultiPIE face database [10] and the UNBC-McMaster archive [1]. The experimental results demonstrated that our robust convex quadratic CLM has better alignment performance than other evaluated CLMs and leading existing holistic methods for alignment/tracking (i.e., AAMs). In future work, we shall investigate other discriminant classifiers such as boosting schemes [4, 14] or relevance vector machine (RVMs) [4] to further improve the performance of our patch experts. We would also like to explore alternate geometric constraints to handle large deformations and occlusion.
Acknowledgments
This work was partially supported by the NIH Grant R01 MH051435.
Footnotes
A typical patch size is 15 × 15 in our experiments for a face object with an inter-ocular distance of 50 pixels.
In our experiments, we used the patch expert confidences estimated by Equation 2 to define the weighting matrix W.
Actually, Ak is always guaranteed of being positive semidefinite. In the rare occurrence that Ak is positive semidefinite but not positive definite (i.e., singular) we can employ a weighted identity matrix to ensure its rank.
References
- 1.Ashraf AB, Lucey S, Cohn JF, Chen T, Ambadar Z, Prkachin K, Solomon P, Theobald BJ. The painful face: pain expression recognition using active appearance models. ICMI. 2007:9–14. doi: 10.1016/j.imavis.2009.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Avidan S. Support vector tracking. PAMI. 2004 August;26(8):1064–1072. doi: 10.1109/TPAMI.2004.53. [DOI] [PubMed] [Google Scholar]
- 3.Baker S, Matthews I. Lucas-Kanade 20 years on: A unifying framework: Part 1: The quantity approximated, the warp update rule, and the gradient descent approximation. IJCV. 2004 [Google Scholar]
- 4.Bishop CM. Pattern Recognition and Machine Learning. Springer; 2006. [Google Scholar]
- 5.Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- 6.Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. ECCV. 1998;2:484–498. [Google Scholar]
- 7.Cristinacce D, Cootes TF. Feature detection and tracking with constrained local models. BMVC. 2006:929–938. [Google Scholar]
- 8.Dowson N, Bowden R. N-tier simultaneous modelling and tracking for arbitrary warps. BMVC06. :II:569. [Google Scholar]
- 9.Felzenszwalb P, Huttenlocher D. Pictorial structures for object recognition. IJCV. 2005 January;61(1):55–79. [Google Scholar]
- 10.Gross R, Baker IMS, Kanade T. Technical Report CMU-RI-TR-07-08. Robotics Institute; Carnegie Mellon University: 2007. The CMU Multiple pose, illumination and expression (MultiPIE) database. [Google Scholar]
- 11.Gu L, Kanade T. 3D Alignment of face in a single image. CVPR. 2006;1:1305–1312. [Google Scholar]
- 12.Gu L, Xing E, Kanade T. Learning gmrf structures for spatial priors. CVPR. 2007:1–6. [Google Scholar]
- 13.Liang L, Wen F, Xu Y, Tang X, Shum H. Accurate face alignment using shape constrained Markov network. CVPR. 2006:I: 1313–1319. [Google Scholar]
- 14.Liu X. Generic face alignment using boosted appearance model. CVPR. 2007:1–8. [Google Scholar]
- 15.Lucas B, Kanade T. An iterative image registration technique with an application to stereo vision. International Joint Conference on Artificial Intelligence; 1981. pp. 674–679. [Google Scholar]
- 16.Nelder JA, Mead R. A simplex method for function minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
- 17.Theobald B, Matthews I, Baker S. Evaluating error functions for robust active appearance models. FGR06. 2006:149–154. [Google Scholar]
- 18.Viola P, Jones M. Rapid object detection using a boosted cascade of simple features. CVPR. 2001 December;1:511–518. [Google Scholar]
- 19.Wang Y, Lucey S, Cohn J. Non-rigid object alignment with a mismatch template based on exhaustive local search. IEEE Workshop on Non-rigid Registration and Tracking through Learning; 2007. [Google Scholar]
- 20.Williams O, Blake A, Cipolla R. Sparse Bayesian learning for efficient visual tracking. PAMI. 2005 August;27(8):1292–1304. doi: 10.1109/TPAMI.2005.167. [DOI] [PubMed] [Google Scholar]
- 21.Xiao J, Baker S, Matthews I, Kanade T. Real-time combined 2d+3d active appearance models. CVPR. 2004:II:535–542. [Google Scholar]
- 22.Zhou Y, Gu L, Zhang H. Bayesian tangent shape model: Estimating shape and pose parameters via Bayesian inference. CVPR. 2003;1:109–116. [Google Scholar]