Validity and reliability of a computer method to estimate vertebral axial rotation from digital radiographs

Abstract

Axial vertebral rotation, an important parameter in the assessment of scoliosis may be identified on X-ray images. In line with the advances in the field of digital radiography, hospitals have been increasingly using this technique. The objective of the present study was to evaluate the reliability of computer-processed rotation measurements obtained from digital radiographs. A software program was therefore developed, which is able to digitally reproduce the methods of Perdriolle and Raimondi and to calculate semi-automatically the rotation degree of vertebra on digital radiographs. Three independent observers estimated vertebral rotation employing both the digital and the traditional manual methods. Compared to the traditional method, the digital assessment showed a 43% smaller error and a stronger correlation. In conclusion, the digital method seems to be reliable and enhance the accuracy and precision of vertebral rotation measurements.

Introduction

Scoliosis is a tridimensional spine deformity and its severity is traditionally measured by the Cobb angle. However, the method is limited to spinal evaluations on the sagittal and coronal planes. However, axial plane vertebral rotation is an essential parameter to understand scoliosis as a tridimensional deformity. It provides characteristic indicators of scoliotic spines, monitors deformity and predicts the curvature prognosis [1] in addition to supplying important quantitative information about surgical results.

Over the last decades, several techniques have been developed, by different authors, to measure vertebral rotation. By identifying the position of some anatomical vertebral structures and their geometrical relations, these authors were able to estimate the degree of axial rotation using conventional X-ray images. In his study, Cobb [2] utilized the position of the spinous process to evaluate the rotation degree while Nash and Moe [3], Perdriolle and Vidal [4], Derup [5], Stokes [6] and Raimondi [7] utilized the pedicle shadow positions in relation to the spinal body. Computerized tomography has been recently used for this purpose, but it exposes patients to high doses of ionizing radiation, and the supine position required for the procedure alters the real magnitude of spine deformation [8, 9].

Among the methods previously quoted as estimating vertebral axial rotation, we focused on the methods of Raimondi and Perdriolle. The Perdriolle method uses a template (known as Perdriolle torsiometer) graded in 5° intervals. The observer marks the vertebral pedicle shadow and the edges of the vertebral bodies and then measures with the torsiometer the degree of axial rotation. Likewise, the Raimondi method uses a template (known as regolo Raimondi and graded in 2° steps). The vertebral pedicle shadow of the vertebral body and the vertebral waist are measured on this template. As in the Perdriolle procedure, the convex-sided pedicle is bisected longitudinally. The distance from this bisecting line to the convex-sided waist is measured, corresponding to the pedicle offset. After the measurements, the width of the vertebra and the pedicle offset are used to estimate on the regolo Raimondi the degree of vertebral axial rotation.

The creation of digital radiographs and the digitalization of conventional X-ray films have been recently made possible by the use of digital technology in radiology. Some advantages over conventional procedures are the shorter exposure of patients to radiation [10], variable contrast scales, efficient image transfers and comparisons and easy storage. Such advantages have encouraged some researchers [11, 12] to develop new computer-based methods to assess vertebral axial rotation.

In this context, the objective of this study was to evaluate the influence of digital methods on the accuracy of vertebral axial rotation measurements and the reliability of the digital technique. A computer program was developed to analyze images on digital X-rays. The classical methods of Perdriolle and Raimondi reproduced in this software provide the basis for the measurements of vertebral rotation angles on digital images. Three independent observers compared the variability of digital measurements to that of manual methods used with traditional radiographs and analyzed the relative precision of the two methods.

Methods

Data acquisition procedure

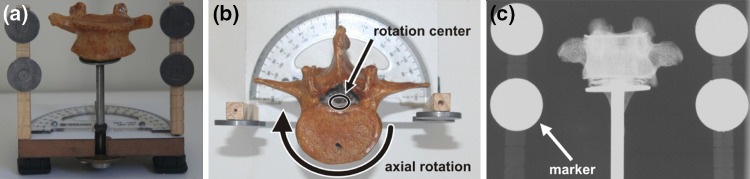
Two human vertebrae (T3 and L4) and a rotating device were used in a lab experiment designed to evaluate the reliability of the digital method in measuring vertebral axial rotation from X-ray images (Fig. 1a). Isolated vertebrae were placed on the device and manually rotated on the axial plane around a fixed shaft. A goniometer placed as a background scale on the device identified the rotation degrees and a dented roller assured a precisely controlled rotation. During the procedure, the vertebrae were rotated from 0° to 60°, at 5° increments, comprising 13 rotation stages. As recommended by Molnar et al. [13], the vertebra rotation axis was positioned on the anterior portion of the spinal canal (Fig. 1b). The rotation movement was performed only on the axial plane and, as emphasized by Drerup [5], the measurement of vertebral rotation was independent from lateral tilting and forward–backward inclination.

Fig. 1.

Device used in the experimental rotation of vertebra on the axial plane. a Coronal and b axial views of the device showing a lumbar vertebra in neutral rotation. c Sample of a vertebra radiograph fixed on the device. The four markers appear as white circles

The vertebrae were radiographed in the 13 rotation stages in anterior–posterior view resulting in a total of 26 samples, subsequently digitalized by scanning (Vidar Systems, Diagnostic Pro, Herndon, USA) at a resolution of 1,000 × 450 pixels (300 dpi), and used to digitally calculate the axial rotation with the computer program. Figure 1c shows a digitalized sample. The experiment was previously approved by the local Research Ethics Committee. The two vertebras used in this research were gently supplied by the Anatomy Studies Center of the University of São Paulo Medical School.

Acquired and digitalized X-ray images commonly show alterations and distorted dimensions modifying the real size of the vertebrae. To avoid this problem, four radio-opaque markers were fixed on the rotation device at known and exact distances. The distances will eventually permit the recovery of the real object size by the software, thus minimizing image perspective distortions by calibration [14].

Axial rotation measurement

Vertebral axial rotation was evaluated using the Perdriolle and Raimondi methods both by manual and digital measurements. The methods developed by these authors are well validated and suitable for development into computer programs. Three observers, orthopedic surgeons familiar with the methods, independently analyzed the 26 vertebral images from each of the 6 trials conducted at 1 week intervals. Manual measurements were performed and analyzed in the first three trials and digital measurements were used in the last three procedures. The observers were blind to their own previous measurements.

For the manual measurements, the observers received 26 radiographs of vertebrae T3 and L4, the Perdriolle torsiometer, the Raimondi table and a ruler. The same objects were used by all observers, who were instructed to measure vertebral width, the distance of the pedicles to the convex vertebral side and to calculate the rotation in each sample using the available torsiometer and table. No marks were made by the observers on the films. For the digital measurements, the observers received the digitalized X-ray images and the software developed in this study reproducing the Perdriolle and Raimondi methods. In this procedure, observers were instructed to use the mouse to select the position of the pedicle center and the vertebra width on each image. A single mouse click marks the pedicle position while the width of the vertebra is determined at the narrowest part of the vertebra body, i.e. the vertebral waist, by a straight line drawn by the observer on the computer screen. This basic information is sufficient for the computer program to provide automatic projection of the pedicle distances to the convex vertebral side, an estimation of the actual vertebra width and the rotation corresponding to the relation between these two measurements according to the values defined by the Perdriolle and Raimondi methods. Internally, the computer program has a data set—based on the values determined by Perdriolle and Raimondi—that automatically converts the relation between the projections of the pedicles and the vertebral width into an axial rotation angle. Prior to the digital measurements, observers were given time to familiarize with the methodology, the zooming tools, border enhancement, increased image brightness and contrast. The program was automatically calibrated by the four markers on the images, the distances between these markers being entered by the observer at the start of the procedure. As pointed out by Kushner et al. [10] the calibration process is fundamental in the extraction of radiographed measurements, recovery of the suppressed geometrical scale and compensation of image perspective distortions. Fifty-two measurements were performed by each observer during each trial. The three observers made a total of 468 manual and 468 digital measurements during the 6 trials.

Statistical analysis

To analyze the reliability of the digital method, the accuracy (degree of veracity) and precision (degree of reproducibility) of the data obtained by observers were calculated. The root mean square (RMS) error indicated measurement accuracy and the standard deviation (SD) of measurements, the precision. Additionally, the intraclass correlation coefficient (ICC) and the 95% confidence interval (CI) were also calculated. The analysis of variance (ANOVA) was used to assess for differences in the mean variability of trials of each observer using manual and digital measures. The mean values were calculated by the bootstrap method. Statistical calculations and graphs were made using the Matlab software (MathWorks, Massachusetts, USA).

Results

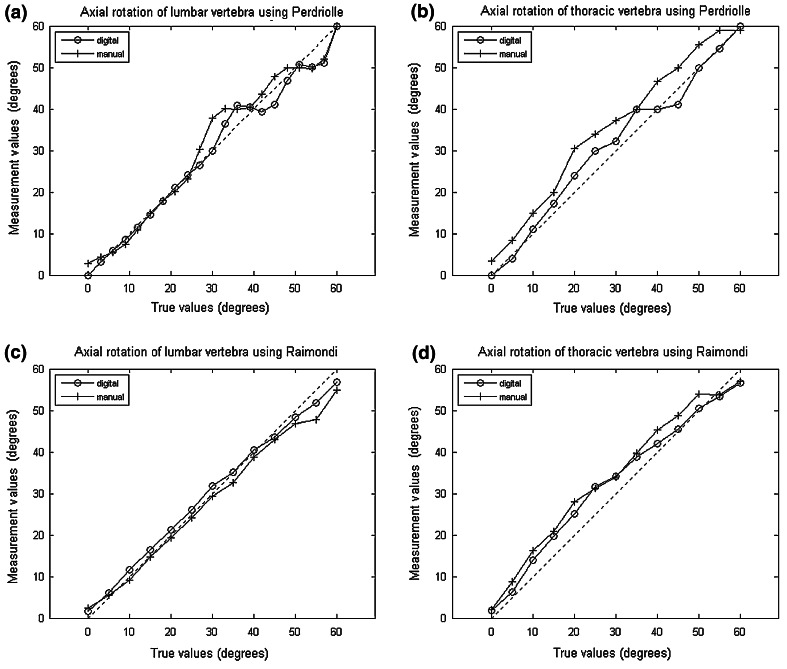
Manual measurements showed an RMS error of 5.0° (±4.9 SD) and an ICC of 0.96 (CI 0.89, 0.99) by the Raimondi technique, and the Perdriolle values were RMS error of 5.7° (±4.9 SD) with an ICC of 0.95 (CI 0.86, 0.98). For the digital measurements, the RMS error was 3.1° (±2.7 SD), the ICC, 0.99 (CI 0.97, 0.99) by the Raimondi method, and RMS error of 3.1° (±3.0 SD), ICC, 0.98 (CI 0.94, 0.99) by the Perdriolle method. Figure 2 shows digital and manual axial rotation values of T3 and L4 vertebrae as determined by the Perdriolle and Raimondi methods. The mean time spent by the observers to calculate the rotation for each sample was about 1 min using the digital method and 2.5 min with the manual method.

Fig. 2.

Mean measurement values using manual and digital methods. Mean measured values and actual values of rotation are represented on the Y and X axes, respectively. a, c Lumbar vertebra rotation by the Perdriolle and Raimondi methods, respectively; b, d Thoracic vertebra rotation by the Perdriolle and Raimondi methods, respectively. Graphs generated by bootstrap statistical technique

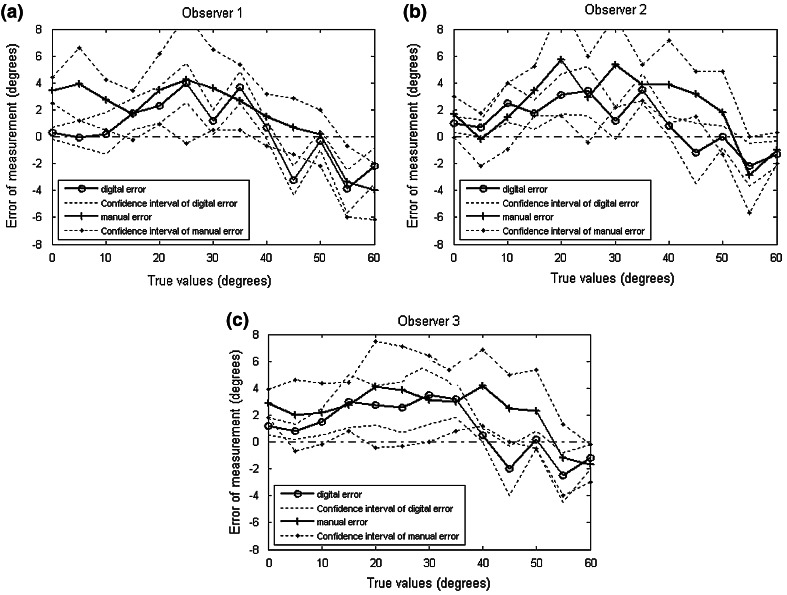
Irrespective of the technique used for rotation measurements (Raimondi vs. Perdriolle), the RMS error of the manual method was 5.4° (±5.0° SD) and the ICC was 0.96 (CI 0.88, 0.98) whereas the digital method exhibited an RMS error of 3.1° (±2.9° SD) and an ICC of 0.98 (CI 0.96, 0.99). Values related to the inter- and intra-observer analysis are shown on Fig. 3 and Tables 1 and 2.

Fig. 3.

RMS errors of rotational values and their 95% confidence intervals (upper and lower limits) measured by the manual and digital methods. The parameters were individually calculated for each observer

Table 1.

Interobserver reliability of data acquisition using manual and digital methods

	RMS error		SD		ICC		CI
	RAI	PER	RAI	PER	RAI	PER	RAI	PER
Manual
Trial 1	5.2°	5.6°	5.0°	5.0°	0.96	0.95	0.88, 0.98	0.86, 0.98
Trial 2	5.2°	6.2°	5.2°	5.0°	0.97	0.95	0.90, 0.99	0.85, 0.98
Trial 3	4.5°	5.4°	4.5°	4.7°	0.96	0.94	0.89, 0.99	0.83, 0.98
Digital
Trial 1	3.0°	3.0°	2.5°	2.9°	0.99	0.98	0.97, 0.99	0.96, 0.99
Trial 2	3.2°	3.0°	2.8°	3.0°	0.99	0.98	0.98, 0.99	0.94, 0.99
Trial 3	3.0°	3.2°	2.8°	3.2°	0.99	0.98	0.96, 0.99	0.94, 0.99

Axial vertebrae rotations were assessed in both methods by the Raimondi (RAI) and Perdriolle (PER) techniques in three trials each. The root mean square (RMS) error, standard deviation (SD), intraclass correlation coefficient (ICC) and 95% confidence interval (CI) were calculated for each method and technique

Table 2.

Intraobserver reliability of data acquisition using manual and digital methods

	RMS error		SD		ICC		CI
	RAI	PER	RAI	PER	RAI	PER	RAI	PER
Manual
Observer 1	5.3°	5.1°	5.3°	4.5°	0.95	0.95	0.83, 0.98	0.85, 0.98
Observer 2	4.9°	6.1°	4.8°	5.2°	0.97	0.97	0.90, 0.99	0.89, 0.99
Observer 3	4.8°	6.0°	4.7°	5.0°	0.98	0.95	0.93, 0.99	0.84, 0.98
Digital
Observer 1	3.0°	3.0°	2.8°	3.0°	0.99	0.98	0.98, 0.99	0.95, 0.99
Observer 2	3.0°	2.9°	2.4°	2.7°	0.99	0.98	0.97, 0.99	0.95, 0.99
Observer 3	3.2°	3.4°	2.9°	3.3°	0.99	0.98	0.96, 0.99	0.93, 0.99

Axial vertebrae rotations were assessed by each of the three observers in both methods by the Raimondi (RAI) and Perdriolle (PER) techniques. The root mean square (RMS) error, standard deviation (SD), intraclass correlation coefficient (ICC) and 95% confidence interval (CI) were calculated for each method and technique

Error analysis of measurements as a function of vertebra type, irrespective of the technique employed (Raimondi vs. Perdriolle) reveals that the lumbar vertebra shows an RMS error of 4.0° (±3.9° SD) in the manual method and 2.4° (±2.3° SD) in the digital method while the thoracic vertebra shows values of 6.5° (±4.7° SD) and 3.7° (±3.0° SD), respectively.

The ANOVA analysis evaluates the difference between trials. This function returns the P value (probability) under the null hypothesis that all trials are drawn from populations with the same mean. For the trials using the manual method, the P value was 0.84 whereas for the trials using the digital method the P value was 0.99.

Discussion

The reported results suggest a good reliability in the measurements performed by both manual and digital methods. The error values obtained with the manual method confirm published data showing mean values between 5° and 6° [15–17]. However, better accuracy (smaller RMS error) and precision (smaller SD) were provided by the digital method. In fact, the digital RMS error is 43% smaller than the manual error. Both methods show good correlation coefficients and confidence intervals indicating data consistency. But the digital data correlation coefficients and confidence intervals are better than their manual counterparts, probably reflecting the smaller number of observer operations, with less interference in the calculation. Some resources of the digital technique, such as the exact calculation of distance projections, more precise scales, image distortion compensation (as a result of calibration), border emphasis (through image processing techniques), increased contrast and zoom, which offer sharper views of anatomical structures, may explain the results. According to Lam et al. [18], a 2 mm error in the determination of pedicle position on the convex side may lead to an error of up to 5° in estimating vertebral rotation.

The analysis of data from Tables 1 and 2 showed less inter- and intra-observer variation with the digital versus manual method. In general, confidence limits in ICC were similar for all samples and close to 1, suggesting an excellent correlation between measurements. However, the CIs with the digital method showed less variation within limits and higher consistency.

The results obtained by the Perdriolle and Raimondi methods were not significantly different, in contrast with reports by Weiss [7]. However, this author worked with spine X-rays from scoliotic patients with different rotation degrees and unknown actual values, which was not the case in this study, where known rotation values were used, at 5° increments, following the Perdriolle torsiometer scale. Future studies using the digital method in scoliotic patients should help clarify the differences between the two techniques.

Additional analyses taking into account the type of vertebra revealed that the lumbar vertebra showed a 42% smaller error than the thoracic vertebra, probably because the former is better visualized on X-rays, allowing for better selection of the pedicle shadow position on the image.

Besides being more precise and accurate, the digital method has other significant advantages, such as an immediate comparison between radiological images, distances and angles easily measured and efficient storage and transmission. Furthermore, the scant individual intervention with the use of the software may help less experienced observers estimate vertebra rotation as accurately as more experienced professionals. Computer aided diagnosis systems [19] may also be combined with the digital method providing inputs for the treatment and follow-up of scoliosis. However, it is important to remember that digital images frequently show altered and distorted dimensions and therefore should always include reference markers.

Conclusion

A computer method is considered valid if it is both accurate and precise. Based on these criteria, the digital method (computational) may be validated, since its accuracy and precision were substantially better as compared to the manual method. The digital method was able to increase the reliability of vertebral rotation measurements on the axial plane and should be recommended for use in clinical practice.