Determination of axial vertebral rotation in MR images: comparison of four manual and a computerized method

Abstract

Axial vertebral rotation (AVR) of 14 normal and 14 scoliotic vertebrae from magnetic resonance (MR) images was determined by three observers using four manual methods and a computerized method, which were based on the evaluation of vertebral symmetry in two dimensions (2D) and in three dimensions (3D). The method of Aaro and Dahlborn proved to be the manual method with the highest intra-observer (1.7° SD) and inter-observer (1.2° SD) reliabilities, and was also most in agreement with the computerized method (1.3° SD, 1.0° MAD). The computerized method yielded higher intra-observer (1.3° SD) and inter-observer (1.4° SD) reliabilities than the manual methods, indicating it to be an efficient alternative for repeatable and reliable AVR measurements.

Introduction

Measurement of axial vertebral rotation (AVR) from two-dimensional (2D) and three-dimensional (3D) images has long been a major research topic in clinical orthopedics and medical imaging [21]. When compared to manual methods, computerized methods were reported to increase the accuracy and precision of the measurements [5, 10, 12, 17, 20], although still requiring some observer interaction. To the best of our knowledge, the intra- and inter-observer reliabilities of manual and/or computerized methods for measuring AVR in images acquired by magnetic resonance (MR) imaging have not been investigated yet. This study therefore aims to analyze the AVR values obtained by four manual [1, 9, 11, 13] and a computerized method [20], obtained from MR images of normal and scoliotic vertebrae.

Materials and methods

Images

Vertebral levels between T4 and L5 from one normal (subject sex, male; age, 28 years; T6–L3 Cobb angle around 1°) and one scoliotic (subject sex, male; age, 25 years; T6–L3 Cobb angle around 14°) MR spine image were included in this study, i.e. a total of 28 vertebrae. The images were T2-weighted axial MR scans (mean repetition time T_R = 4,560 ms, echo time T_E = 102 ms, matrix size 512 × 512, field of view 200 × 200 mm², slice thickness 3 mm), acquired by a spine array coil with a 1.5-Tesla scanner (Signa Excite, GE Healthcare, Milwaukee WI, USA). The original DICOM files were completely anonymized before use and the axial scans were automatically joined into 3D images according to the recorded co-ordinate locations.

Observers

Three observers with different experience in medical imaging and orthopedic surgery were included in this study, i.e. a postgraduate biomedical engineering student (D.S., observer 1), a medical imaging researcher (T.V., observer 2) and a spine surgeon (R.V., observer 3). Using each method, two series of AVR measurements were performed by each of the three observers, resulting in six (n = 6) measurements for each vertebra. The second series of measurements was performed 2 weeks after the first series.

Manual methods

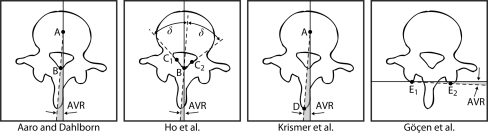
The manual methods of Aaro and Dahlborn [1], Ho et al. [11], Krismer et al. [13] and Göçen et al. [9] (Fig. 1) were used to measure the AVR in 3D MR images. Although these methods were originally developed for orthogonal axial computed tomography (CT) cross sections, their application to MR cross sections is straightforward, as they are based on specific anatomical landmarks that can be identified in both CT and MR images [4, 5]. As the sagittal and/or coronal vertebral tilt may introduce errors in the determination of AVR [13, 18], the manual measurements were not performed in orthogonal, but in oblique, 2D axial MR cross sections. Each oblique axial cross section was obtained by oblique planar image reformation, which extracts image intensities along a plane that passes through the vertebral centroid in 3D and is inclined for the sagittal and coronal vertebral tilts against the corresponding orthogonal axial cross section. For each vertebra, the observers used a dedicated computer program to manually identify the vertebral centroids in 3D, the sagittal and coronal vertebral tilts required to extract oblique axial cross sections and the specific anatomical landmarks required to measure AVR by the four manual methods (Fig. 1).

Fig. 1.

Four manual methods for measuring axial vertebral rotation (AVR). Specific anatomical landmarks: A vertebral centroid, B posterior junction of the two laminae of the vertebral arch, C1/C2 junction of the left/right lamina with the left/right pedicle, D tip of the spinous process, E1/E2 most posterior point of the left/right pedicle

Computerized method

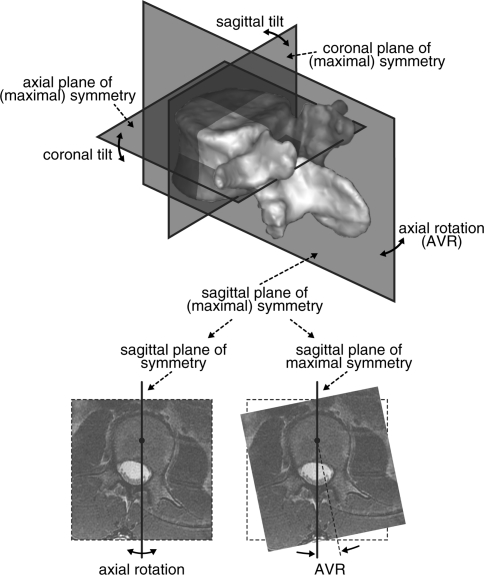
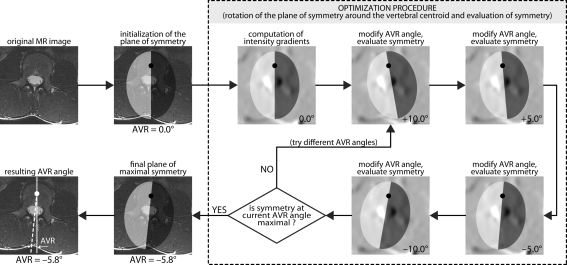
The computerized method for measuring vertebral rotation in 3D images was recently proposed by Vrtovec et al. [20]. By considering the natural biological property that the anatomical structures are relatively symmetrical, the method is based on the assumption that the sagittal and coronal vertebral tilts and the AVR angle can be simultaneously determined from the planes of maximal symmetry, which divide the vertebral body into symmetrical anterior/posterior halves and cephalic/caudal halves, and the whole vertebra into symmetrical left/right halves (Fig. 2). For each vertebra, the sagittal, coronal, and axial planes of symmetry are first initialized so that they are parallel to the axes of the MR image (i.e. zero rotation) and intersect in the vertebral centroid in 3D, which represents the center of rotation for the planes (manually identified twice by each observer). By rotating these planes in 3D, the symmetry of the vertebral anatomical structures is evaluated for the current combination of the three rotation angles that are obtained from the inclination of the three planes. The estimation of symmetry is yielded by mirroring the edges of anatomical structures (i.e. image intensity gradients) over each plane and comparing them with the corresponding edges on the opposite side of that plane. To ensure that such estimation is performed on edges that belong to the vertebral structures, the comparison is performed in regions that are larger than the average size of vertebral anatomy [14–16], i.e. up to 30, 50, and 25 mm away from the sagittal, coronal, and axial plane of symmetry, respectively. An optimization procedure is then applied to search for the maximal symmetry, which is achieved when the planes of symmetry are aligned with the vertebra in the MR image and therefore represent the planes of maximal symmetry (Fig. 3). As the procedure does not search for a perfect, but maximal, symmetry of vertebral anatomical structures, the angles of vertebral rotation can be obtained from the inclination of the planes of maximal symmetry. Two variations of the computerized method were applied to each vertebra:

1. 2D: the sagittal and coronal vertebral tilts were determined manually when extracting the oblique MR axial cross section from the 3D image, while the AVR angle was determined automatically in the extracted oblique 2D axial MR cross section using the inclination of the sagittal plane of maximal symmetry (Fig. 3).

2. 3D: the sagittal and coronal vertebral tilts and the AVR angle were determined automatically in the 3D MR image using the inclination of the sagittal, coronal, and axial planes of maximal symmetry (Fig. 2).

Fig. 2.

The planes of (maximal) symmetry in 3D and the determination of axial vertebral rotation (AVR) from the inclination of the sagittal plane of maximal symmetry

Fig. 3.

An illustration of the computerized search for the plane of maximal symmetry (left/right) in a 2D oblique axial MR cross section of the L3 vertebra

Statistical analysis

The intra-observer reliability (test–retest repeatability), inter-observer reliability (agreement between observers) and inter-method variability (agreement between methods) were computed using the Bland–Altman analysis [6]. The Bland–Altman difference plots show the mean of the two measurements as the abscissa value and the difference between the two measurements as the ordinate value. Additional horizontal lines represent the mean difference and the limits of agreement, i.e. the 95% confidence intervals of the measurements (mean ± 1.96 × standard deviation). The absolute variability of AVR measurements was estimated as standard deviations (SD) from the mean of individual variances and as the mean absolute differences (MAD) between the mean of individual values. Relative variability of AVR measurements was obtained by computing the coefficients of variation (CV = SD/MAD).

Results

For each of the 28 vertebrae, six AVR measurements (n = 6, 3 observers × 2 series) were obtained using each of the four manual methods and the two variations of the computerized method. The largest mean positive and mean negative angle was +3.4° (normal T10, method of Ho et al.) and −11.8° (scoliotic L2, method of Krismer et al.), respectively. Detailed analysis of the obtained AVR measurements for each vertebral level is presented in Table 1.

Table 1.

Mean standard deviation (SD, absolute variability; top row values in degrees) and mean coefficient of variation (CV, relative variability; bottom row values) of all measurements reported separately for each vertebral level (T4–L5)

Method	T4	T5	T6	T7	T8	T9	T10	T11	T12	L1	L2	L3	L4	L5
Normal vertebrae
Aaro and Dahlborn	1.2° 1.24	1.0° 1.29	0.5° 1.30	1.1° 1.56	1.4° 1.51	1.0° 1.17	1.3° 1.16	1.6° 1.31	1.0° 1.28	1.3° 1.17	0.4° 1.30	1.1° 1.46	1.4° 1.60	1.6° 1.35
Ho et al.	4.0° 1.37	3.5° 1.33	1.2° 1.38	2.0° 1.23	2.8° 1.24	1.9° 1.46	1.9° 1.29	2.8° 1.40	2.5° 1.33	1.2° 1.24	2.0° 1.42	4.5° 1.28	1.6° 1.21	3.6° 1.28
Krismer et al.	1.3° 1.28	1.2° 1.31	2.2° 1.22	1.2° 1.29	1.6° 1.19	2.6° 1.39	2.5° 1.24	2.0° 1.37	1.0° 1.34	3.0° 1.28	1.2° 1.25	1.6° 1.14	2.6° 1.37	2.7° 1.23
Göçen et al.	1.1° 1.50	1.9° 1.49	1.3° 1.20	1.5° 1.33	1.3° 1.31	2.0° 1.17	1.0° 1.21	1.2° 1.23	1.5° 1.34	1.4° 1.41	2.6° 1.38	1.7° 1.42	1.7° 1.20	0.7° 1.26
Computerized (2D)	0.9° 1.25	0.9° 1.28	0.5° 1.18	0.3° 1.20	1.5° 1.21	0.6° 1.27	0.7° 1.13	0.8° 1.18	1.3° 1.17	1.6° 1.28	1.5° 1.48	0.9° 1.25	1.3° 1.27	1.0° 1.18
Computerized (3D)	0.5° 1.31	0.7° 1.31	0.6° 1.20	0.4° 1.30	1.7° 1.19	1.7° 1.46	0.5° 1.29	0.6° 1.24	1.5° 1.17	1.8° 1.32	1.4° 1.48	0.7° 1.19	1.3° 1.26	0.7° 1.26
Mean	1.9° 1.72	1.8° 1.62	1.2° 1.42	1.2° 1.50	1.8° 1.31	1.8° 1.44	1.5° 1.39	1.7° 1.46	1.6° 1.35	1.8° 1.37	1.7° 1.55	2.2° 1.63	1.7° 1.37	2.0° 1.50
Scoliotic vertebrae
Aaro and Dahlborn	1.1° 1.20	1.0° 1.47	1.3° 1.39	0.7° 1.23	1.0° 1.45	1.2° 1.40	1.7° 1.31	0.9° 1.21	1.2° 1.25	1.1° 1.17	1.5° 1.25	1.1° 1.50	2.1° 1.38	1.5° 1.21
Ho et al.	3.2° 1.29	1.7° 1.45	3.4° 1.23	2.9° 1.25	1.1° 1.23	4.4° 1.33	2.4° 1.32	2.9° 1.25	1.4° 1.27	2.4° 1.30	2.3° 1.25	2.3° 1.27	3.3° 1.49	3.5° 1.54
Krismer et al.	2.4° 1.28	1.7° 1.17	2.0° 1.25	3.3° 1.16	2.3° 1.22	1.7° 1.22	2.5° 1.35	1.4° 1.39	2.8° 1.24	1.6° 1.31	2.2° 1.28	1.8° 1.42	1.3° 1.43	2.2° 1.19
Göçen et al.	1.0° 1.15	1.9° 1.22	1.6° 1.19	1.7° 1.35	2.6° 1.44	1.1° 1.25	2.8° 1.19	2.4° 1.38	2.0° 1.30	3.1° 1.30	2.0° 1.24	1.4° 1.38	2.0° 1.31	1.9° 1.28
Computerized (2D)	1.3° 1.41	0.8° 1.49	0.7° 1.44	1.0° 1.21	0.7° 1.40	0.4° 1.26	0.8° 1.21	0.2° 1.48	2.0° 1.49	2.6° 1.32	2.2° 1.22	0.7° 1.28	1.7° 1.30	1.2° 1.22
Computerized (3D)	1.6° 1.48	1.1° 1.52	0.6° 1.26	1.3° 1.29	0.9° 1.44	0.7° 1.41	1.1° 1.22	0.4° 1.31	0.4° 1.43	2.8° 1.17	1.8° 1.22	0.3° 1.27	1.2° 1.25	1.1° 1.31
Mean	1.9° 1.41	1.4° 1.43	1.9° 1.49	2.1° 1.39	1.6° 1.50	2.1° 1.67	2.0° 1.37	1.7° 1.61	1.8° 1.48	2.4° 1.33	2.0° 1.26	1.4° 1.54	2.1° 1.49	2.1° 1.45

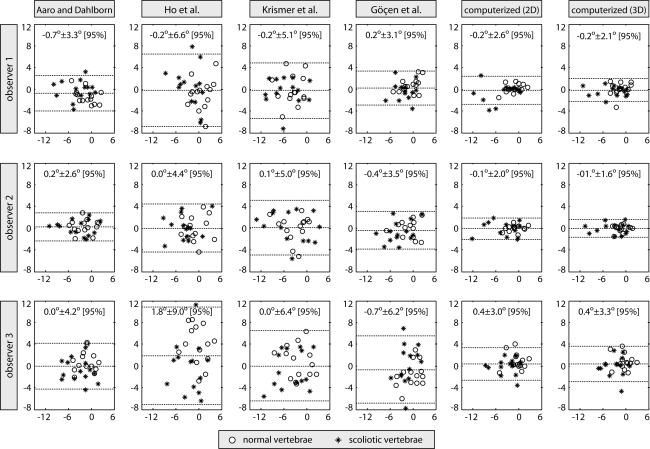
Intra-observer reliability

The intra-observer reliability (SD [CV]) of observers 1, 2, and 3 was 2.4° [2.68], 2.1° [2.48], and 3.4° [1.42], respectively, for manual measurements and 1.2° [2.93], 0.9° [1.60], and 1.6° [1.57], respectively, for computerized measurements (Fig. 4). The overall intra-observer reliability was therefore estimated to be 2.7° [2.56] for manual methods and 1.3° [1.90] for the computerized method. In general, the measurements were more repeatable for normal than for scoliotic vertebrae (mean SD difference of 0.6° for all three observers).

Fig. 4.

Bland–Altman analysis of intra-observer reliability for each observer and method. The horizontal and vertical axes represent the mean and the difference between the two measurements of each observer, respectively. The dotted horizontal lines represent the mean difference and the 95% confidence intervals (mean ± 1.96 × standard deviation)

Inter-observer reliability

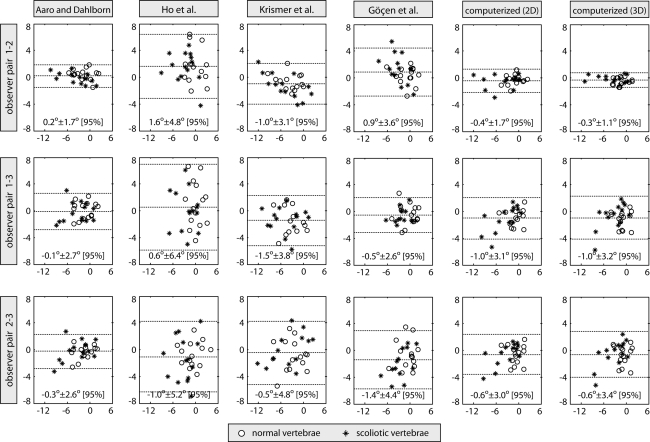
The inter-observer reliability (SD [CV]) of observer pairs 1–2, 1–3, and 2–3 was 1.8° [1.17], 2.1° [1.22], and 2.2° [1.17], respectively, for manual measurements and 0.8° [1.27], 1.6° [1.19], and 1.6° [1.24], respectively, for computerized measurements (Fig. 5). The total inter-observer reliability was therefore estimated at 2.1° [1.19] for manual methods and 1.4° [1.28] for the computerized method. In general, the measurements were more reliable for normal than for scoliotic vertebrae (mean SD difference of 1.2° for all three observer pairs).

Fig. 5.

Bland–Altman analysis of inter-observer reliability for each observer pair and method. The horizontal and vertical axes represent the mean and the difference between the mean measurements of each observer pair, respectively. The dotted horizontal lines represent the mean difference and the 95% confidence intervals (mean ± 1.96 × standard deviation)

Comparison of the methods

The comparison of the methods for AVR measurement is presented in Table 2 in terms of the difference and agreement of each method pair.

Table 2.

The inter-method difference, shown in the lower left part of the table as the mean absolute differences and coefficients of variations (MAD [CV]), and the inter-method reliability, shown in the upper right part of the table as the mean differences ±1.96 × standard deviation (95% confidence intervals)

Method	Aaro and Dahlborn	Ho et al.	Krismer et al.	Göçen et al.	Computerized (2D)	Computerized (3D)
Aaro and Dahlborn	·	–1.0° ± 3.6°	1.3° ± 2.9°	–0.9° ± 2.6°	–0.2° ± 2.6°	–0.3° ± 2.5°
Ho et al.	1.7° [1.08]	·	2.3° ± 5.4°	0.1° ± 3.0°	0.8° ± 3.3°	0.7° ± 3.0°
Krismer et al.	1.6° [0.92]	2.9° [0.95]	·	–2.2° ± 3.1°	–1.5° ± 3.9°	–1.6° ± 3.9°
Göçen et al.	1.2° [1.11]	1.1° [1.39]	2.5° [0.63]	·	0.7° ± 3.1°	0.6° ± 3.0°
Computerized (2D)	1.0° [1.33]	1.5° [1.12]	1.9° [1.05]	1.3° [1.22]	·	–0.1° ± 1.4°
Computerized (3D)	1.0° [1.28]	1.3° [1.18]	1.9° [1.05]	1.2° [1.28]	0.6° [1.19]	·

Discussion

AVR has been identified as a valuable parameter for the evaluation of spinal deformities [19] and its measurement from CT images proved to be most accurate [13]. On the other hand, MR has become the modality of choice for follow-up examinations and longitudinal studies, providing high-quality 3D images of soft tissues and bone structures, without exposing the patients to ionizing radiation [3, 7]. Methods for measuring AVR that were originally developed for CT images have already been successfully applied to MR images. Birchall et al. [4] manually identified the landmarks according to the method of Ho et al. and reported surprisingly low intra- and inter-observer variability of 0.4° SD (2.6° MAD) and 0.3° SD (3.0° MAD), respectively. In a later study [5], a total variability of 1.3° SD (0.8° MAD) was reported for the rotation of vertebral endplates. To obtain the rotation between two neighboring lumbar vertebrae, Haughton et al. [10] matched two axial MR cross sections with a precision of around 0.5°. A similar study from the same authors reported a precision of up to 1.5° SD [17]. Kouwenhoven et al. [12] segmented the vertebrae in axial MR cross sections of normal spines to obtain vertebral centroids and centers of vertebral canal, which were used for measuring AVR with intra-class correlation coefficient (ICC) of 0.91 and 0.87 for intra- and inter-observer reliability, respectively. The concept of vertebral symmetry was, for measuring AVR, first used by Adam and Askin [2] in orthogonal CT cross sections, reporting variability of 3.3° SD and 3.4° SD between their symmetry-based method and the method of Aaro and Dahlborn and Ho et al., respectively. The computerized method used in this study was recently proposed by Vrtovec et al. [20]. By evaluating AVR from the vertebral symmetry and comparing each value to a single manually identified line that best described the vertebral symmetry, an accuracy of 0.5° and a precision of 0.3° were reported for both CT and MR images. As the method does not search for a perfect, but the maximal, symmetry of vertebral anatomical structures, it is suitable for both normal and scoliotic vertebrae.

Vertebral levels

By observing the absolute (standard deviation, SD) and relative (coefficient of variation, CV) variability of AVR measurements on different vertebral levels (from T4 to L5, Table 1), we can conclude that, in general, the computerized method resulted in lower variability than any of the manual methods, and that no considerable differences exist between the results obtained for normal and scoliotic vertebrae using different methods. This may indicate that the extent of AVR does not reduce the variability of AVR measurement, which can be therefore performed with consistent reliability on normal as well as scoliotic vertebrae.

Manual methods

In this study, each of the three observers was approximately equally able to repeat the measurements using a specific manual method (Fig. 4). The intra-observer reliability was, however, constantly lower for observer 3 (i.e. the spine surgeon), which indicated that medical background may not be indispensable for achieving highly repeatable measurements of AVR. The method of Aaro and Dahlborn proved to be the most repeatable manual method (SD [CV] = 1.7° [2.40]), followed by the methods of Göçen et al. (2.3° [2.57]) and Krismer et al. (2.9° [2.42]), while the method of Ho et al. proved to be the least repeatable manual method (3.6° [2.55]). In terms of inter-observer reliability (Fig. 5), the method of Aaro and Dahlborn also proved to be the most reliable manual method (SD [CV] = 1.2° [1.24]), followed by the methods of Göçen et al. (1.9° [1.09]), Krismer et al. (2.0° [1.08]) and Ho et al. (2.8° [1.18]). Such results may be related to the remark of the observers that the ability to detect the anatomical landmarks required by the method of Aaro and Dahlborn (i.e. the vertebral centroid and the posterior junction of the two laminae) was in general stronger than that required by the other manual methods. On the other hand, the obtained results were not in accordance with the study of Göçen et al. [8], where the method of Ho et al. proved to be among the methods with the highest intra- and inter-observer reliability. However, all of the existing comparison studies [2, 8, 9] were performed on CT spine images (Table 3).

Table 3.

Comparison of intra-observer and inter-observer reliabilities as reported by different studies [2, 8, 9]. The values represent the standard deviations (SD) of the measurements

Method	Intra-observer reliability			Inter-observer reliability
	MR	CT		MR	CT
	this	[8, 9]	[2]	this	[8, 9]	[2]
Aaro and Dahlborn	1.7°	1.8°	2.8°	1.2°	4.7°	2.6°
Ho et al.	3.6°	1.2°	3.3°	2.8°	2.4°	2.4°
Krismer et al.	2.9°	3.3°		2.0°	6.1°
Göçen et al.	2.3°	1.1°		1.9°	1.8°
Computerized (2D)	1.3°			1.4°
Computerized (3D)	1.2°			1.4°

Computerized method

The computerized measurements in 3D are more computationally demanding and error-prone than those in 2D, as three rotation angles are simultaneously evaluated from the vertebral symmetry in 3D inside an optimization framework. However, no considerable differences in intra-observer (SD [CV] = 1.3° [2.84] for 2D and 1.2° [2.86] for 3D, Fig. 4) or inter-observer reliability (SD [CV] = 1.4° [1.26] for 2D and 1.4° [1.30] for 3D, Fig. 5) were discovered. On the other hand, the measurements in 2D required to be initialized in the manually identified vertebral centroids in 3D with known coronal and sagittal vertebral tilts, while the measurements in 3D required only the vertebral centroid in 3D. Avoiding manual identification of the sagittal and coronal tilts represents a considerable reduction in the observer’s effort. Both intra- and inter-observer reliabilities of the computerized method were higher than or as high as those of manual methods, which may be related to the fact that for each vertebra, only the vertebral centroid in 3D was required for AVR determination, i.e. a single anatomical landmark. The intra- and inter-observer variability of manually localizing the vertebral centroids in 3D were on average equal to 0.7 mm SD and 1.1 mm SD, respectively. For a vertebra of around 50 mm in size, a change in AVR of up to 1° can be caused by a difference in vertebral centroid location of around 0.9 mm. We can therefore conclude that manual localization of vertebral centroids in 3D represents the major source of variability for the computerized method.

Comparison of the methods

Among the manual methods, the highest agreement (Table 2) was found between the methods of Aaro and Dahlborn and Göçen et al. (1.3° SD, 1.2° MAD). This is a very interesting observation, since the methods are defined on two completely different sets of anatomical landmarks (Fig. 1). When comparing the manual with the computerized method, the strongest agreement was observed between the manual method of Aaro and Dahlborn and the computerized measurements in 2D (1.3° SD, 1.0° MAD) and in 3D (1.3° SD, 1.0° MAD). This indicates that among all lines that define AVR according to different manual methods (Fig. 1), the line between the vertebral centroid and the posterior junction of the two laminae divides the vertebra into most symmetrical halves. The measured angles were, however, not necessarily of equal magnitude, as the computerized method was designed to evaluate the vertebral symmetry and not the relative rotation of specific anatomical landmarks. The computerized method was in general relatively consistent with all manual methods, since the weakest agreement was observed for the method of Krismer et al. (2.0° SD and 1.9° MAD).

Conclusion

In this study, AVRs of normal and scoliotic vertebrae from MR images were evaluated using four different manual and a computerized method. The method of Aaro and Dahlborn proved to be the manual method with the highest intra- and inter-observer reliabilities. The computerized method, based on the evaluation of vertebral symmetry, yielded even higher reliabilities of AVR measurements and was most consistent with the manual method of Aaro and Dahlborn. The computerized method is also faster and requires less effort from the observers; therefore, it seems to be an efficient alternative to manual methods.