Characterizing the surface charge of synthetic nanomembranes by the streaming potential method

Abstract

The inference of the surface charge of polyethylene glycol (PEG)-coated and uncoated silicon membranes with nanoscale pore sizes from streaming potential measurements in the presence of finite electric double layer (EDL) effects is studied theoretically and experimentally. The developed theoretical model for inferring the pore wall surface charge density from streaming potential measurements is applicable to arbitrary pore cross-sectional shapes and accounts for the effect of finite salt concentration on the ionic mobilities and the thickness of the deposited layer of PEG. Theoretical interpretation of the streaming potential data collected from silicon membranes having nanoscale pore sizes, with/without pore wall surface modification with PEG, indicates that finite electric double layer (EDL) effects in the pore-confined electrolyte significantly affect the interpretation of the membrane charge and that surface modification with PEG leads to a reduction in the pore wall surface charge density. The theoretical model is also used to study the relative significance of the following uniquely nanoscale factors affecting the interpretation of streaming potential in moderate to strongly charged pores: altered net charge convection by applied pressure differentials, surface-charge effects on ionic conduction, and electroosmotic convection of charges.

1 Introduction

Streaming potential measurements have often been used in membranes (Fievet et al., 2000) and separation devices (Gusev and Horváth, 2002) to infer the charge on the pore or channel surface and to confirm the attachment of surface modification agents that lead to an alteration of surface charge (Erickson et al., 2004; Norde et al., 1990). Characterizing the surface charge of a membrane is useful for the development of high selectivity nanoporous membranes for applications such as extracorporeal and implantable hemofilters (Fissell et al., 2007), because a negative charge on the membrane can improve its selectivity toward albumin and other negatively charged proteins in blood (Conlisk et al., 2009). This is one motivation for the reported work.

Further, in such applications of nanoporous membranes, polyethylene glycol (PEG) based coatings are often used for improving the hemocompatibility of silicon/silica surfaces (Papra et al., 2001; Meagher et al., 2004). However, the practice of silane-mediated attachment of polyethylene glycol (PEG) groups on silicon/silica surfaces (Papra et al., 2001; Meagher et al., 2004) leads to a reduction in the fraction of otherwise ionizable surface silanol groups. This implies that the pore walls of a PEG coated membrane will have an effectively smaller negative surface charge density than the walls of an uncoated membrane (Meagher et al., 2004). The fact that this reduction in the magnitude of surface charge density can be treated as a sign of attachment of the PEG groups provides another motivation for the theoretical and experimental characterization of membrane charge using the streaming potential method that is to be studied in the current work.

The inference of surface charge in the case of membranes and separation devices with microscale pores (∼ 1 μm pore width) is relatively straightforward and reliable compared to nanoscale pores owing to the absence of the phenomenon of overlapped electric double layers (EDL) at ordinary electrolyte concentrations of 1–100 mM. Under these conditions, there is a linear relationship between the zeta potential (ζ) of the membrane and the measured streaming potential (Hasselbrink et al., 2001; Lyklema, 1995). The situation is much more complex when the thickness of the electrical double layer is comparable to or larger than the characteristic dimension of the pore (Pujar and Zydney, 1994).

In this work, streaming potential measurements were obtained with membranes (Figure 1) of varying nanoscale pore widths (6–30 nm) and surface conditions (PEG coated/uncoated). Overlapped electrical double layers, as used in this work, refers to a situation where the characteristic thickness of the electrical double layer as measured by the Debye length $\lambda =\sqrt{({\epsilon }_e\mathit{\text{RT}})/(2{\mathit{\text{IF}}}^2)}$ (Lyklema, 1995) is a significant fraction of the channel width. Here, ε_e, R, T, I and F are the permittivity, universal gas constant, absolute temperature, ionic strength of the solution, and Faraday's constant, respectively. The ionic strength is defined for a solution containing N ionic species each of valence z_i and molar concentration c_i as $I=\frac{1}{2}\text{∑}_{i=1}^N{z}_i^2{c}_i$.

Figure 1.

Nanopore membrane. Top left: Cross-sectional view showing schematically the various structural layers of the membrane (not to scale). Top right: Scanning Electron Micrograph (SEM) of the membrane showing a uniformly-spaced array of slit pores. Bottom left: SEM showing membrane cross-section and a pore. Bottom right: SEM showing the close-up of a 9 nm slit pore. For details on fabrication, consult Fissell et al., 2009. Reproduced from Fissell et al., 2009 by permission from Elsevier Science Inc.

The principal objectives for interpretation of surface charge density from streaming potential measurements in this work are: (a) to confirm the attachment of PEG groups on coated membranes, and (b) to anticipate the extent of electrostatic effects which can influence the retention of charged molecules. In particular, an inference procedure is developed that can be used to evaluate the surface charge characteristics of PEG-coated hemofiltration membranes. Unlike previous experimental-theoretical studies (Fievet et al., 2000; Tang et al., 2007), the streaming potential data are obtained from membranes that simultaneously differ in nanopore size and surface characteristics. Either solution conductivity or ionic strength, but not both, are used as an input in the developed model, consistent with the utilization of Onsager Fuoss theory (Onsager and Fuoss, 1932; Fuoss et al., 1965) of current conduction in electrolytes.

2 The streaming potential in arbitrarily-shaped nanopores with overlapped double layers

If an ionic solution of electrical permittivity ε_e, viscosity μ, and bulk conductivity Λ is transported by a pressure difference ΔP in an appropriately designed streaming potential experiment, then an apparent zeta potential ζ_app (Hasselbrink et al., 2001) can be inferred from the measured voltage difference, ΔV_SP, known as the streaming potential (SP), that appears across the membrane, according to:

$${\zeta }_{\mathit{\text{app}}}=\frac{\mu \Lambda }{{\epsilon }_e\Delta P}\Delta V_{SP}$$ (1)

In the above and subsequent discussions, the term bulk conductivity symbolized by Λ refers to the conductivity of an unconfined electrolyte.

In the case when the electric double layers on the pore walls inside the membrane are significantly smaller than the pore width, the apparent zeta potential, thus inferred, is virtually the same as the ‘true’ zeta potential ζ. This situation prevails in microscale channels/pores under solution ionic compositions of practical interest. At a given electrolyte concentration, the electric double layers may occupy a significantly larger fraction of the channel width in a nanopore than in a micropore. This situation of a finite (rather than infinitesimal) ratio of EDL to channel width will be termed ‘overlapped EDL’ in the current work and is indicative of the absence of the central charge-neutral core region within the nanopore (Lyklema, 1995). As discussed below, the overlapped EDL situation leads to ζ_app ≠ ζ.

The observed streaming potential ΔV_SP can be converted to ζ using Equation (1) if the electric double layers do not overlap. However, when the EDLs overlap, the following three factors become significant (Lyklema, 1995) and affect the interpretation of Equation (1) leading to ζ_app ≠ ζ:

1. The pressure-driven flow convects a different (less compact) distribution of charges.

2. The electrical conductivity Λ_p of the solution confined within the pore changes from its bulk (free-solution) value Λ as the ionic distributions are affected by the charge on the pore walls.

3. Convection of ions by the electroosmotic flow generated by the streaming potential ΔV_SP produces a finite contribution to the current opposing the pressure-driven flow (and adding to the current due to electromigration of ions under ΔV_SP); this effect is especially important for surfaces with large zeta potential (Van der Heyden et al., 2005).

From the condition of zero net current in an open-circuited nanopore, it can be shown (derived in the Appendix for a straight pore of arbitrary cross-sectional shape) that

$$\Delta V_{SP}=\frac{{\epsilon }_e\zeta \Delta P}{\mu \Lambda }\left[\frac{1-\langle \phi \rangle }{\frac{{\Lambda }_p}{\Lambda }+\alpha \langle \nabla \phi \cdot \nabla \phi \rangle }\right]$$ (2)

where ϕ is the dimensionless electrostatic potential (made dimensionless by the zeta potential, ζ) and α = ε_e²ζ²/(μΛ h²) is a dimensionless number defined for a pore of characteristic width h. Here, Λ_p is the conductivity of the solution confined within the pore and Λ is the conductivity of the unconfined solution (bulk conductivity). The angular brackets indicate average over the pore cross section and the dimensionless gradient operator ∇ is scaled by h. In the limit of a very thin double layer, ϕ is zero over the bulk of the pore cross-section and 〈ϕ〉 → 0. As indicated in the Appendix, Equation (2) can be used to evaluate the zeta potential, regardless of the specific form of the ionic concentration distributions prevailing in the EDL, although the latter are usually taken to be of Boltzmann form (Lyklema, 1995). For a related derivation of Equation (2) specialized to slit shaped pores see Hildreth (1970). A similar expression for ΔV_SP as a function of the volumetric charge density, ρ_e, and ϕ (rather than ϕ alone) can be readily derived from the expressions for electric current and flow rate in pores of arbitrary cross-sections provided by Mortensen et al. (2006).

The numerator and the first and second terms of the denominator of the term enclosed by straight brackets on the right hand side of Equation (2), respectively, correspond to the first, second, and third effects enumerated above. In particular, the last of these quantities can be interpreted as the ratio of current density transported per unit streaming potential (ΔV_SP) through electroosmotic convection of charges to that transported due to the intrinsic ionic conductivity Λ. The dimensionless number α, therefore, quantifies the relative importance of charge convection by the electroosmotic flow in comparison to bulk ionic conduction. From Equation (1), the expression in square brackets on the right hand side of Equation (2) can be interpreted as ζ_app/ζ. Since the potential is scaled on the wall (maximum) potential ζ, it can be noted here that 0 ≤ ϕ ≤ 1. Therefore, the numerator satisfies 0 ≤ 1−〈ϕ〉 ≤ 1. The second term of the denominator represents the cross-sectional average of the square of the magnitude of the vector ∇ϕ and, therefore, is also non-negative.

Under confinement by a charged pore, there is a higher density of charge carriers; this usually leads to Λ_p greater than Λ, as discussed below. For an aqueous KCl solution (an aqueous buffered KCl solution is used in the experiments described in Section 3) dissociating into K⁺ and Cl^- ions, if I is the ionic strength of the unconfined solution and if ν denotes the ionic mobilities, then the pore-confined conductivity is given by (Hildreth, 1970)

$${\Lambda }_p=({\nu }_{K^{+}}+{\nu }_{C{l}^{-}})IF\langle cosh(\beta \phi )\rangle +({\nu }_{C{l}^{-}}-{\nu }_{K^{+}})IF\langle sinh(\beta \phi )\rangle =\Lambda \langle cosh(\beta \phi )\rangle +({\nu }_{C{l}^{-}}-{\nu }_{K^{+}})IF\langle sinh(\beta \phi )\rangle$$ (3)

where β = −ζF/(RT), R is the universal gas constant, F is Faraday's constant and T is the temperature. Equation (3) for Λ_p assumes that the dominant effect of the confinement of a solution to a charged nanopore is a change in the distribution of ions and not the change in ionic mobilities (Ho et al. 2005). Note, however, that the ionic mobilities and the bulk solution conductivity Λ appearing in Equation (3) are dependent on the ionic strength I, as discussed below in relation to Equations (4a) and (4b).

In Equation (3), since |sinh(βϕ)| ≤ |cosh(βϕ)|, the absolute value of the ratio of the second to the first term cannot exceed its asymptotic value $({\nu }_{{\text{Cl}}^{-}}-{\nu }_{{\text{K}}^{+}})/({\nu }_{{\text{Cl}}^{-}}^{-}+{\nu }_{{\text{K}}^{+}})$ for large zeta potentials. From the values of ionic mobility at infinite dilution (in the limit I→0), viz. ${\nu }_{K^{+}}^{\infty }=7.62\times {10}^{-8}{\text{m}}^2/\text{V}/\text{s}$ and ${\nu }_{C{l}^{-}}^{\infty }=7.91\times {10}^{-8}{\text{ m}}^2/\text{V}/\text{s}$ for K⁺ and Cl^- (Harris, 1997), respectively, it can be anticipated that this ratio is much less than unity and the term Λ〈cosh(βϕ)〉 makes the dominant contribution to Λ_p calculated using Equation (3). Consequently, Λ_p ≥ Λ for infinitely dilute KCl solutions. The relationship Λ_p ≥ Λ happens to be true even for the finite-ionic-strength KCl solutions of interest in this work, as discussed below in relation to Equations (4a) and (4b). The equality in Λ_p ≥ Λ should apply in the limit of infinitely thin EDLs. Overall, from Equations (1) and (2) it can be concluded that ζ_app ≤ ζ for 1:1 electrolytes and the equality occurs in the limit of infinitely thin EDLs.

Although the quantities 〈ϕ〉, 〈∇ϕ · ∇ϕ〉 and Λ_P/Λ on the right hand side of Equation (2) depend on the wall zeta potential ζ, none of these quantities can be specified as closed form functions of ζ when the EDLs on the pore walls overlap and ϕ is governed by the nonlinear Poisson-Boltzmann equation. Therefore, in general, the ΔV_SP(ζ) relationship in Equation (2) cannot be inverted into an explicit ζ(ΔV_SP) relationship that would have offered a direct interpretation of measured streaming potential data. A useful alternative, therefore, is to calculate the streaming potential ΔV_SP for a set of ζ values using numerical/semi-analytical expressions for ϕ, as discussed later in this work for slit shaped pores. The resultant ΔV_SP(ζ) relationship can be inverted graphically or through interpolation to obtain the ζ given value(s) of ΔV_SP or ζ_app.

Experimental methods for measuring the streaming potential of the silicon nanomembranes are discussed in Section 3. The concentration of each ion in the solution is also necessary to obtain the ϕ distribution for a given ζ. One way of inferring the concentration of each ion in an aqueous solution of a 1:1 salt is from the measured conductivity values Λ, as demonstrated in Section 4. Note that measured values of Λ are also needed for use in Equation (3). The calculation of ϕ in slit shaped pores is discussed in Section 5. Results for surface charge density and streaming potential and on the interpretation of experiments with hemofiltration membranes when electric double layers overlap are presented in Section 6.

3 Experimental

Streaming potential measurements were performed with buffered KCl solutions. The phosphate buffer was prepared by dissolving appropriate quantities of sodium phosphate dibasic heptahydrate (Sigma-Aldrich) and potassium phosphate monobasic crystal (J.T. Baker) in deionized water obtained from a NANOpure Diamond water purification system (Barnstead Thermolyne Corporation) with a resistivity greater than 18 MΩ-cm. KCl (BDH) was added to 1 mM phosphate buffer to obtain the desired solution ionic strength. The pH of the solution was measured using a Thermo Orion model 420Aplus pH meter and adjusted by addition of 0.1 M HCl or KOH as required. The conductivity of the solution was measured using Thermo Orion model 105Aplus conductivity meter referenced to 25 °C. All solutions were prefiltered through 0.2 μm pore size Supor-200 membranes (Gelman Sciences, Inc.) to remove any particulates prior to use.

Silicon membranes (Figure 1) with uniform slit-shaped nanopores were fabricated from silicon substrates following the procedure outlined by (Fissell et al., 2006; Lopez et al., 2006). Fabrication of membranes starts with a 400 μm-thick, 100 mm-diameter, double side polished <100>-oriented silicon wafer that is obtained from a commercial vendor. The wafer was coated with a 500 nm-thick layer of low-stress silicon nitride followed by a 5 μm-thick film of polycrystalline silicon (polysilicon). The polysilicon layer was patterned by photolithography and reactive ion etching to create approximately 50 μm-long spaces and lines that are 2-3 μm wide. Thermal oxidation of the patterned polysilicon was performed to grow a thin conformal SiO₂ film that defines the eventual size of the nanopores. The thickness of this conformal SiO₂ film could be readily varied between 5 and 100 nm by adjusting oxidation parameters such as time and temperature. After deposition of another 4 μm-thick polysilicon film, chemical-mechanical polishing was performed to expose the nanopore regions on the front-side of the wafer. Low-stress silicon nitride was deposited on both front- and back-sides of the wafer, with the back-side patterned to define an etch mask. The wafer was subsequently etched in KOH to create suspended membranes. Finally, the masking silicon nitride and SiO₂ films were etched in concentrated hydrofluoric acid to produce nanoporous membranes with slit-shaped pores approximately 45 μm in length and 2.5 – 50 nm in half-width.

The sacrificial oxide film shows <1% mean variation in thickness across 100-mm diameter wafers as judged from 25 separate runs in a thermal oxidation furnace (Fissell et al., 2009). The mean variation between lots was ∼1%. Since the pore size distribution is determined by the variation in the thickness of the sacrificial oxide layer during the fabrication process, these membranes are remarkably monodisperse. Thus, a single pore size rather than a distribution of pore sizes is adequate to accurately characterize a membrane.

Data were also obtained with membranes in which the silicon surface was covalently modified with poly(ethylene glycol) (PEG) using a previously reported solution phase method, modified to omit all sonication steps and continuing the PEG deposition for 12 hours (Papra et al., 2001). The PEG was covalently coupled to the silanol groups (Si-OH) on the silicon surface through a trimethoxysilane group forming a Si-O-Si-PEG moiety.

The surface charge characteristics of the silicon membranes were evaluated from streaming potential measurements using the device described by Burns and Zydney (2000). The silicon membranes were first glued into a square hole cut in the center of a 25 mm disc of latex rubber using a silicone II sealant (GE). The device was assembled with the latex rubber disc sealed between two chambers. The chambers were slowly filled with the desired salt solution while making sure to remove any entrapped air bubbles. A feed reservoir containing the same salt solution was then attached to one of the chambers, with the exit from the second chamber directed to the drain. The system was pressurized using compressed air, with leak testing performed at 55 kPa. The system was allowed to stabilize for approximately 120 minutes at which point the transmembrane voltage (ΔV_SP) was measured using a high impedance Keithley 2000 multimeter connected to the two electrodes. Streaming potential data were obtained with both increasing and decreasing pressure between 5 to 25 kPa at several discrete pressures with the system allowed to equilibrate at each pressure for one minute. Streaming potential data were quite reproducible with error being less than ±0.03 mV during a single experiment. Streaming potential was measured as a function of pressure for each silicon membrane in three separate experiments with the average value of the slope (dV_SP/dP) used to calculate apparent zeta potential.

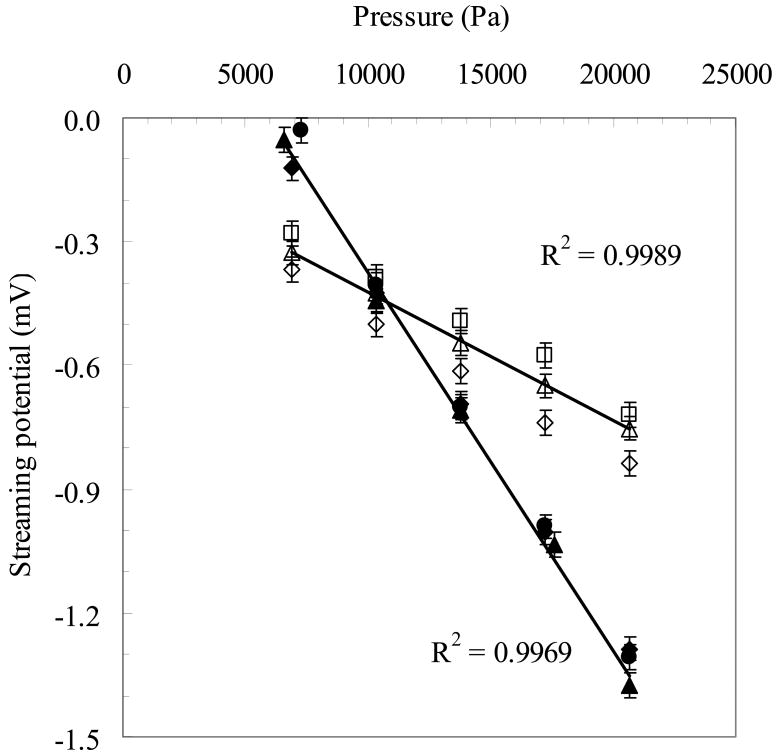
Figure 2 shows typical average streaming potential data as a function of the transmembrane pressure (ΔP) for two silicon membranes collected during six separate experiments. Open symbols are the average streaming potential data collected during three separate experiments for 10 nm pore size silicon membrane with PEG coating while filled symbols are for 30 nm pore size silicon membrane without PEG coating in another set of three experiments. Data were obtained using 10 mM KCl buffered with 1 mM phosphate ions at pH 7.0. The non-zero intercepts in Figure 1 are due to the small asymmetries in the Ag/AgCl electrodes arising during storage and handling and due to the surface chemical reactions during the streaming potential measurements. The membranes examined in Figure 1 were analyzed at different times using electrodes with different asymmetries. However, these asymmetries have no effect on the calculated values of the membrane zeta potential or surface charge. The data were highly reproducible; repeat measurements had slopes that typically differed by less than 10% although there was often a small (but constant) displacement in the measured voltage due to a shift in the zero pressure intercept.

Figure 2.

Streaming potential vs. pressure in typical streaming potential measurement experiments. Open symbols: 10 nm pore size membrane with PEG. Filled symbols: 30 nm pore size membrane without PEG. The shapes index three separate experimental runs with each membrane.

4 Interpretation of experimental measurements

Table 1 shows the pore size of the membranes investigated, presence/absence of PEG coating on the membrane pores, and the measured bulk (unconfined) solution conductivity values in its first, second, and third columns, respectively. This section describes the procedure for obtaining the data in the fourth and fifth columns of Table 1, namely (a) the ζ_app values in the fifth column of Table 1 given ΔV_SP vs. ΔP curves (Figure 2) from experiment, and (b) the ionic strength values I in the fourth column of Table 1, given the conductivity values in the third column of Table 1. This section also provides other related interpretations useful for the Results Section (Section 6). The apparent zeta potential values ζ_app = μ Λ m /ε_e in Table 1 are calculated from the slope m of experimental ΔV_SP vs. ΔP curves (see Equation (1) and Figure 2) for membranes with three different pore sizes (30 nm, 10 nm, and 6 nm). The ratios of the Debye length to channel width are 0.58, 0.35 and 0.1, and the parameter α appearing in Equation (2) are 0.09, 0.033 and 0.003 for the membranes with 6, 10, and 30 nm pore sizes, respectively.

Table 1.

Summary of experimental data on the apparent zeta potential of the membranes. The ionic strengths are inferred from conductivity values as discussed in the text.

Pore size (nm)	Coating	Conductivity (S/m)	Ionic strength (mM)	−ζapp (mV)
30	None	0.1407	9.96	15.84
10	PEG	0.1117	7.76	4.42
6	PEG	0.1117	7.76	2.15

In the experiments, KCl solutions were mixed with small amounts of dibasic sodium phosphate and monobasic potassium phosphate required to buffer the solution at pH=7.4, and these solutions had an approximate ionic strength of 10 mM. However, to obtain simple theoretical estimates, we will treat these electrolytes as solutions of a single salt (KCl). In addition, we infer the ionic strengths not from the more approximate buffer preparation data, but from interpretation of bulk conductivity measurements; a broader significance of this approach is that it can be applied to a solution of unknown composition but known constituents, for which a measured bulk conductivity value is available. The procedure is described below.

Note that (a) the conductivity of a solution is Λ = Συ_i c_i F, where υ_i are the ionic mobility of the constituent ions, and, (b) the mobility of ions are nonlinearly decreasing functions of the ionic strength of the electrolyte calculable by the experimentally validated Onsager-Fuoss theory (Onsager and Fuoss,1932; Fuoss et al., 1965; Fawcett,2004). As a consequence of interionic electrostatic and hydrodynamic interactions, the ionic strength affects ionic mobilities and the bulk solution conductivity. In the solution of a 1:1 symmetric electrolyte such as KCl (Fawcett, 2004):

$$\Lambda =({\nu }_{C{l}^{-}}+{\nu }_{K^{+}})IF=I\left(({\nu }_{C{l}^{-}}^{\infty }+{\nu }_{K^{+}}^{\infty })F-(B_1({\nu }_{C{l}^{-}}^{\infty }+{\nu }_{K^{+}}^{\infty })F+B_2)\frac{I^{1/2}}{1+\kappa a}\right)$$ (4a)

$$({\nu }_{C{l}^{-}}-{\nu }_{K^{+}})=({\nu }_{C{l}^{-}}^{\infty }-{\nu }_{K^{+}}^{\infty })\left(1-B_1\frac{I^{1/2}}{1+\kappa a}\right)$$ (4b)

where B₁ and B₂ are constants from the theory of current conduction in electrolytes (Onsager and Fuoss,1932, Fuoss and Onsager, 1955; Fawcett, 2004). At 25° C, B₁=0.2292 L^1/2 mol^−1/2 and B₂=60.57 cm² L^1/2 Ω⁻¹ mol^−3/2 and the ionic size parameter a=0.35 nm (Fawcett, 2004). In the denominator of the second term, κ is the inverse of the Debye length λ and is proportional to I^1/2. With these values, it was verified that conductivity predictions from Equation (4a) are within 1% of literature values of 0.01 M KCl and 0.1 M KCl standards (Weast et al., 1973). The ratio (ν_Cl⁻ − ν_K⁺)/(ν_Cl⁻ + ν_K⁺) calculated using Equations (4a) and (4b) was less than 2% under the conditions appearing in Table 2. Therefore, as previously anticipated in relation to Equation (3), Λ_p ≥ Λ.

Table 2.

Theoretically calculated zeta potentials and surface charge density of the nanomembranes.

Pore size (nm)	Coating	−ζapp (mV)	−ζ (mV)	−σ (C/m2)
30	None	15.84	20.89	5.0×10−3
10	PEG	4.42	12.19	2.3×10−3
6	PEG	2.15	11.83	1.7×10−3

Use of Equation (4a) and the experimental conductivity values in Table 1 allows the inference of the ionic strength (I) values (also shown in Table 1) for the experimental solutions that correspond to the 1:1 electrolyte theoretical model to be developed. Owing to 1:1 stoichiometry of the salt, I = c_K⁺ = c_Cl⁻. The first term on the right hand side of the last equality in Equation (3) is evaluated from the experimentally measured Λ (Table 1) and the theoretical ϕ distribution obtained from the solution of the Poisson-Boltzmann equation, as described in the next section. The second term in the right hand side of Equation (3) is evaluated using the mobility difference inferred through Equation (4b). Note that the I value inferred from the measured bulk conductivity using Equation (4a) appears explicitly in the second term of Equation (3), and also implicitly affects the ϕ distribution required for evaluating the first term of Equation (3).

Except for the membrane having 30 nm pores, all other membranes were coated with PEG. Since the attachment of PEG leads to neutralization or partial neutralization of surface silanol groups on oxidized silica surfaces, the zeta potential (ζ) of an uncoated pore as well as its ζ_app is expected to be larger than that of a coated pore of the same size. However, the same conclusion is not necessarily valid when comparing coated and uncoated pores of different sizes, since a smaller pore has a higher degree of double layer overlap; this effect alone regardless of the coated/uncoated condition of the pore surface makes both ζ (Probstein, 1999) and ζ_app/ζ (the quantity within square brackets in Equation (2)) significantly pore-size dependent. In comparison, the pore wall surface charge density σ is relatively invariant with variations in the pore size (Van der Heyden et al., 2005) and with the minute variations in ionic strength (Scales et al., 1992;Wang and Revil, 2009) of interest in this work. Therefore, the comparison of the ζ_app values in the first and second rows of Table 1 does not necessarily imply that attachment of PEG has been successful. Instead, if the true zeta potential, ζ can be evaluated by adequately modeling the electric double layers and the corresponding σ can be obtained, an inference on attachment/nonattachment of PEG can be drawn; this is one of the objectives of this work.

The ζ_app values in Table 1 will be converted to the true zeta potential, ζ, and the latter will be converted to surface charge density σ. The values of σ obtained later in the article will not only differentiate the electrostatic behavior of coated and uncoated surfaces, but also serve as an indirect evidence of PEG attachment.

5 Calculation of electric potential distribution and surface charge

From Equation (2), the determination of electric potential is required to calculate the apparent zeta potential. The dimensionless electric potential ϕ(0) at the centerline y=0 of a slit-shaped pore of width h (Figure 3) having overlapped double layers, given ϕ(±h/2)=1 was calculated through iterative solution of the following result (Verwey and Overbeek, 1999) from the theory of the nonlinear Poisson Boltzmann equation in symmetric electrolytes confined to slit-shaped pores (Behrens and Grier, 2001):

Figure 3.

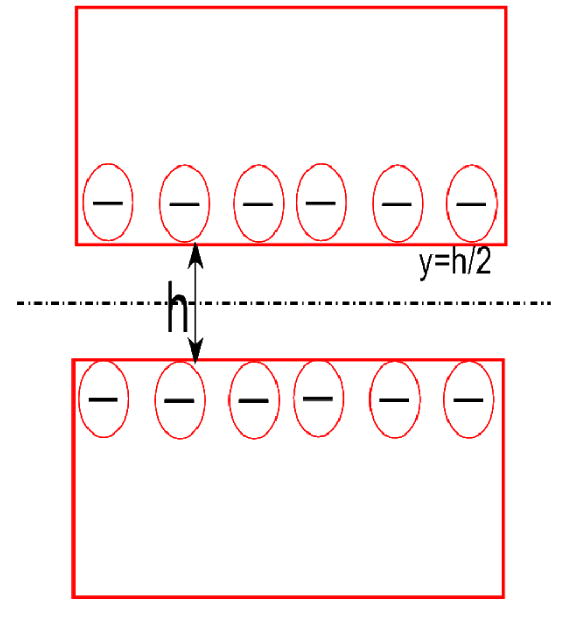
Schematic of a negatively charged membrane pore (not to scale).

$$\phi (0)=1-\frac{1}{\beta }ln\left[\text{cd}\left(\kappa \frac{h}{4}exp\left(-\frac{\beta \phi (0)}{2}\right)|exp(2\beta \phi (0))\right)\right]$$ (5)

where cd (u ∣ m) is a Jacobi elliptic function with argument u and parameter m, κ is the inverse of the Debye length λ and β = Fζ / (RT). The distribution ϕ(y) was then obtained through

$$\phi (y)=\phi (0)+\frac{1}{\beta }ln\left[\text{cd}\left(\kappa \frac{y}{2}exp\left(-\frac{\beta \phi (0)}{2}\right)|exp(2\beta \phi (0))\right)\right]$$ (6)

The averages 〈ϕ〉 and 〈cosh(βϕ) 〉 appearing in Equations (1) and (3) were evaluated through numerical integration by Simpson's rule on a grid fine enough to give five decimal place accuracy. The dimensionless average 〈∇ϕ·∇ϕ〉 in Equation (2) was calculated using the following relationships derived from the Poisson-Boltzmann equation for 1:1 electrolytes (Verwey and Overbeek, 1999)

$$\langle \nabla \phi \cdot \nabla \phi \rangle =2{\left(\frac{\kappa h}{\beta }\right)}^2\left[\langle cosh\left(\beta \phi \right)\rangle -cosh\left(\beta \phi (0)\right)\right]$$ (7)

The surface charge density σ was calculated using

$$\sigma =\frac{{\epsilon }_e\kappa RT}{F}\sqrt{2\left[cosh(\beta )-cosh(\beta \phi (0))\right]}$$ (8)

This solution method involves no numerical differentiation and is accurate and efficient for parametric study of the effect of a wide range of ζ values on ΔV_SP needed to invert the function ΔV_SP(ζ) in the current problem, though it cannot be extended easily to asymmetric electrolytes. The interval between successive ζ values studied in the results described below differ, at most, by RT/(300F); intermediate values of the dependent variable ζ_app, where required, are found by linear interpolation.

6 Results

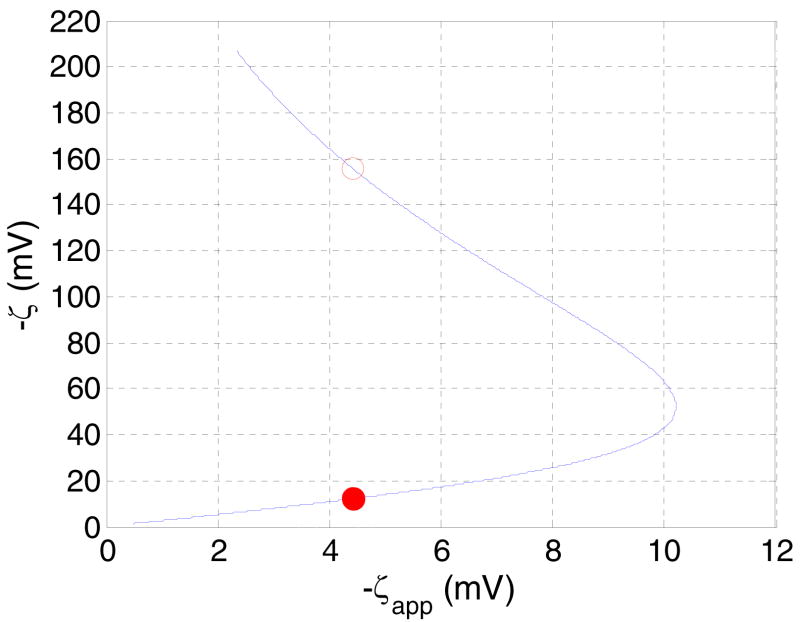
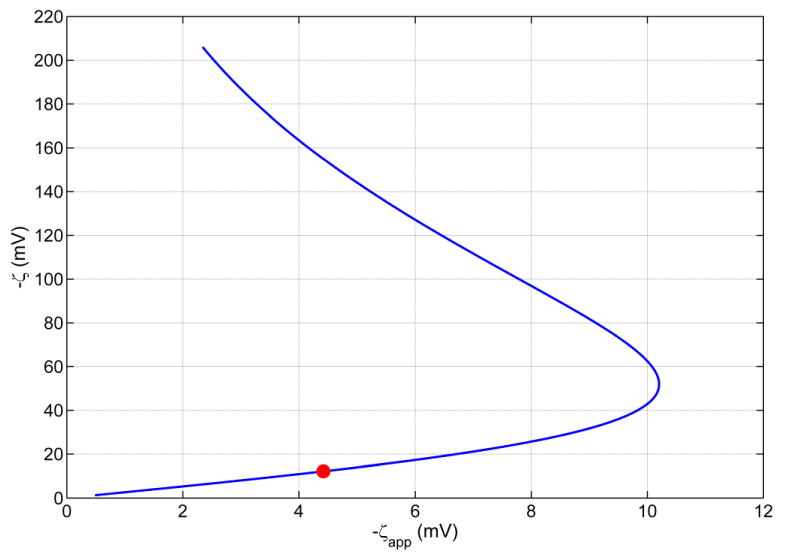
Parametrically studying the dependence of ΔV_SP (or ζ_app given by Equation (1)) as a function of ζ offers a convenient way to solve the inverse problem of finding ζ for a given ΔV_SP defined by Equation (2). For this purpose, in Figure 4, the dependent variable ζ_app of such a study is plotted on the x axis and the independent variable on the y axis. Figure 4 reveals that for a given ζ_app there are two possible ζ values. Although an observed streaming potential ΔV_SP corresponds to a unique ζ_app (Equation (1)), a unique ζ_app leaves two possibilities ζ₁ and ζ₂ (with ζ₂ > ζ₁) for the interpretation of the surface charge condition, except at ζ_app=-10.21 mV, where ζ₁₌ζ₂=-52.07 mV according to Figure 4. This point is an extremum of the function ζ_app(ζ), where dζ_app / dζ = 0. This extremum results from the competing tendencies of increased ionic convection to raise the magnitude of the streaming potential and increased ionic conduction to lower the magnitude of the streaming potential; the former effect being dominant at low absolute values of ζ and the latter effect at large absolute values of ζ.

Figure 4.

Theoretical curve showing the dependence of the true zeta potential (ζ) on the apparent zeta potential ζ_app in PEG coated silicon nanomembranes with slit-shaped pores of 10 nm width (Table 1), calculated using Equations (1), (2), (3), and (4). The ordinates of the filled/hollow circles are the two ζ values on the curve that correspond to the given observed experimental ζ_app =-4.42 mV inputted as the abscissa. The lower ζ value (ζ₁=-12.19 mV) corresponding to the filled circle is taken as the true zeta potential, as discussed in the text. The larger zeta value, ζ₂=-155.50 mV.

For example, the experimental datum ζ_app=−4.42 mV in 10 nm pore corresponds to two possible zeta potential values, ζ₁=−12.19 mV (indicated by a solid symbol) and ζ₂=−155.50 mV (indicated by a hollow symbol). Stated differently, two surfaces with distinctly different surface charge density values (corresponding to true zeta potential values of ζ₁ and ζ₂) may result in the same ΔV_SP (or ζ_app) datum in a streaming potential experiment, as evident from Figure 4. Figure 4 also suggests that −ζ_app ≤ −ζ_c=10.21 mV for a 10 nm pore, regardless of the magnitude of the true ζ potential. Therefore, according to Figure 4, there exist apparent zeta potential values (such as -12 mV), that are not realizable.

Qualitatively different interactions between the three effects of double layer overlap discussed in Section 2 give rise to the above situation. For the surface with potential ζ₁, the primary reason for |ζ_app |< |ζ₁| is the reduction in the ‘effective potential’ (1−〈ϕ〉) (see Equation (2)) in an overlapped EDL situation, the other two factors described in Section 2 are both significantly less influential. For a surface with potential ζ₂, enhancement of the conductivity (Karnik et al., 2005) due to a larger surface charge density, as embodied by the first term in the denominator of Equation (3), and also, enhancement of electroosmotic convection of charges (the second term in the denominator) are the dominant causes for |ζ_app |< |ζ₁|. This will be clearer on studying the large −ζF/(RT) behavior in Figure 5 and from an understanding of the qualitative effects of increasing the pore size. On increasing the pore size, the fact that ζ_app→ ζ for h ≫ 1/κ is reflected in the lower branch of the hairpin shape in Figure 4 progressively approaching (not shown) a straight line with 45° inclination to the horizontal and the point −ζ_c moving toward the right. Thus, for a given ζ_app, ζ₁→ ζ for h ≫ 1/κ. The other root ζ₂ for a given ζ_app corresponding to the upper branch of the curve still exists, but increases progressively with κh to large values unlikely to be observed in practice. However, since surface charge governed current conduction (Λ_p ≫ Λ) (Karnik et al., 2005) has been observed in channels with wall surface charge density σ > I/(hF) and h < 1/κ and electroosmotic convection is expected to be significant in pores with electric double layer overlap (Fievet et al., 2000), the possibility of ζ₂ being the true zeta potential cannot be ruled out if streaming potential measurements are carried out on such channels/pores.

Figure 5.

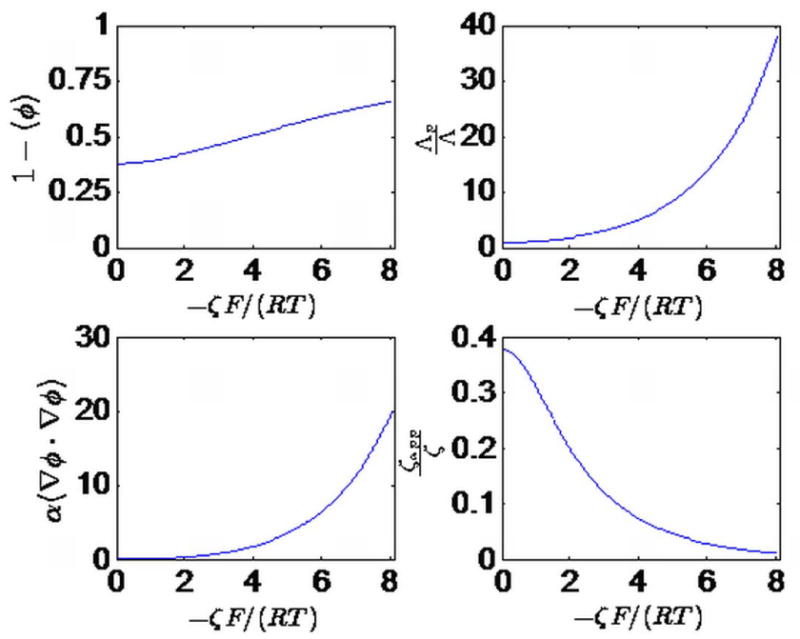
The different components of ζ_app/ζ (see Equation (2)) as a function of the dimensionless zeta potential, -ζF/(RT). The first three subplots (left to right, then top to bottom) plot numerator, the first term in the denominator, the second term in the denominator and the third term in the denominator of the factor enclosed in square brackets in Equation (2), and the last subplot plots ζ_app/ζ, i.e. the factor enclosed in square brackets.

Given the Figure 4 prediction of two permissible ζ potentials per ζ_app value, it may be possible to infer using auxiliary information which one of the above described surface conditions actually prevails in an experiment. Such an approach would involve elimination of the ‘unrealistic’ ζ potential value.

For example, corresponding to the experimentally measured ζ_app= −4.42 mV (Table 1) in the membrane with 10 nm pore size, we note that the absolute values of zeta potential observed in the literature for fused silica surfaces in contact with 10 mM KCl at pH ∼ 7 in situations where the electric double layers do not overlap is around 60 mV or less (Scales et al., 1992; Kosmulski and Mattjevic, 1992; Kirby and Hasselbrink, 2004). Since silicon, used in the nanomembranes studied, when exposed to the ambient, spontaneously develop a thin silica (SiO₂) film on its surface (Kuo, 2004), electrostatic behavior similar to silica surfaces can be expected for silicon. Further, PEG coated silicon/silica is expected to exhibit lower zeta potentials than uncoated silicon/silica (see e.g. Burns et al., 1995). Therefore, 60 mV should qualify as a conservative upper bound on the absolute value of the zeta potential on an isolated PEG coated silicon surface. If the surface charge density is preserved between an isolated silicon surface in contact with an electrolyte and the silicon surface of a pore confining the same electrolyte at the nanoscale (Van der Heyden et al., 2005), utilizing the approximate Debye-Huckel theory of EDL; a conservatively large estimate for the zeta potential of the 10 nm pores is ζ_10nm = −60mV / tanh(κh) = −60.2 mV (Probstein, 1999), for an ionic strength of 9.95 mM (Table 2). Note that, it is well known that the Debye-Huckel theory itself overestimates the zeta potential of strongly charged surfaces in comparison to the predictions from the more accurate Poisson-Boltzmann theory (see for example, Plecis et al., 2005). Clearly, the estimated realistic upper bound of 60.2 mV on the absolute value of the zeta potential of the 10 nm pore is still lower than the absolute value 155.50 mV of ζ₂, the larger of the two permissible ζ potentials in Figure 4. Therefore, a zeta potential as high as -155.50 mV is unlikely to be realizable a 10 nm silicon pore at I=9.95 mM and we conclude that ζ₁=−12.19 mV (shown by a solid circle on Figure 4) is its true zeta potential. If practicable, an experiment can also be performed with a membrane fabricated with sufficiently large pore size (say, of the order of ∼ μm) under otherwise similar conditions, to obtain an estimate of the zeta potential of an isolated silicon surface that is more accurate than the literature-based estimate of -60 mV used in the above calculation.

Another approach to the unambiguous inference of ζ would be based on the experimental measurement of the ratio of the conductivity of the fluid when confined in the pores to the bulk conductivity Λ_p/Λ (see Equation (3)) (Fievet et al., 2000; Zheng, 2003). For a given ζ_app, if ζ₁ is the true zeta potential, experiments should reveal Λ_p ≃ Λ, as will be evident more clearly from the discussion of Figure 5. On the other hand, if ζ₂ is the true zeta potential, experiments should reveal Λ_P ≫ Λ. The measurement process requires specially designed conductivity cells (Fievet et al., 2000) where the membrane can be installed, and isolation of the effect of current conduction through the confined column of liquid in the pore from that of current-conductive liquid and solid regions that are not confined by the pore. A third method is based on the observation, based on a suggestion by (Fievet et al., 2000), that a small increment in pH of the working solution at constant ionic strength (which leads to an increment in −ζ and −σ, see e.g. Scales et al., 1992) near ζ₁ should, in principle, cause an increase in ΔV_SP (or ζ_app, see Figure 4), while the same change in pH near ζ₂ should cause a decrease in ΔV_SP (or ζ_app). From this point onward, for every pore size of interest in the experiments, we will only consider only the smaller of the two permissible ζ potentials (see Figure 2) as ‘realistic’.

Figure 5 plots the different contributions to the apparent zeta potential of the PEG-coated membrane with 10 nm pore width: (a) the numerator of the factor enclosed in straight brackets in Equation (2) (top left), (b) the first term of the denominator (top right) of the same factor, (c) the second term of the numerator (bottom left), and (d) the entire factor in straight brackets (bottom right). As discussed before, the interpretation of these factors are, respectively, the effective zeta potential, the ratio of pore confined ionic conductivity to unconfined ionic conductivity, the ratio of current conduction due to electroosmotic convection to that due to ionic conduction and the ratio ζ_app/ζ. The independent variable is the dimensionless zeta potential −ζF/(RT). At large values of −ζF/(RT), the conductivity of the pore confined liquid increases exponentially (see Equation (3) and the top right pane of Figure 5) due to the strong negative charge on the pores attracting a large concentration of positive ions (K⁺) leading to an increase in conductivity. This factor, coupled with stronger electroosmotic convection of charges (bottom left pane of Figure 5) means that, for strongly charged surfaces, the larger zeta potential ζ = ζ₂ corresponding to the observed ζ_app can indeed be the ‘true zeta potential’. The largest surface charge density studied in Figures 4 and 5 is -0.3 C/m² corresponding to a zeta potential of about -210 mV.

Similar results (not shown) are obtained for the 6 nm and 30 nm uncoated pores with input data given in Table 1. The resultant true zeta potential and the surface charge density calculated by Equation (8) for all three pore sizes, coated or uncoated, are summarized in Table 2. The smaller values of the surface charge density for the PEG coated membranes confirm the attachment of PEG to the pore walls. Note that the calculated zeta potential for the PEG-coated membranes with 6 and 10 nm pores differ by about 3% although the apparent zeta potentials for these membranes differ by more than a factor of two. This is a direct result of the greater overlap of the electrical double layers in the smaller pore size membrane and the resulting shift in ζ. The nonzero surface charge density (and/or nonzero true zeta potential) on the PEG surface could mean all silanol groups have not been attached to the PEG silane. Another possibility is that the PEG chains have acquired anions (hydroxyl groups, as suggested by Chan et al, 2003) which would explain the existence of a residual negative charge even though saturation coverage has been reached (Hu et al., 2002; Chan et al. 2003, Burns et al., 1995). The larger absolute value of σ for the 6 nm pores compared to 10 nm pores is somewhat counterintuitive since it should be more difficult to achieve good coverage on the surfaces of membranes with narrower pores by the solution phase method (Papra et al. 2001). However, we note that so far the PEG layer has been implicitly assumed to have negligible effect on the pore size, which were determined through hydraulic permeability testing (Fissell et al. 2007) of uncoated membranes. Below, we relax this assumption.

Allowing 1 nm for a monolayer of low molecular weight (< 600 kDa) PEG (Papra et al., 2001) will lead to reduced values of 4 nm and 8 nm for the effective thickness (h) of the electrolyte-filled region of the PEG-coated pores studied. The estimates of true zeta potential and surface charge density obtained by using the above h values in Equations (5) and (6) are tabulated in Table 3. Table 3 quotes larger values of −ζ and −σ than Table 2. As before, we may take σ to be a pore-size-independent property of the PEG-coated surface. Given that σ=-0.005 C/m² for an uncoated pore (see Table 2), Table 3 suggests a smaller surface-charge-reducing effect of PEG than Table 2.

Table 3.

Theoretically calculated zeta potentials and surface charge density of the PEG-coated nanomembranes taking into account a 1 nm thick PEG layer deposited on each surface of the pore.

Nominal pore size (nm)	Coating	−ζapp (mV)	−ζ (mV)	−σ (C/m2)
10	PEG	4.42	16.85	2.9×10−3
6	PEG	2.15	31.56	4.0×10−3

Contrary to Table 2 and contrary to the trend in ζ_app, Table 3 suggests a lower value of -σ in the 10 nm membrane than in the 6 nm membrane. Further, if the possibility of anionic adsorption by PEG is discounted, the trend -σ_{10 nm} <-σ_{6 nm} in the PEG-chain-size-adjusted calculations (Table 3) would suggest that the 10 nm channel has a higher surface coverage than the 6 nm channel. Thus, after accounting for the PEG layer thickness, Table 3 (unlike Table 2) reveals surface charge densities that are consistent with the expected difficulty in achieving good surface coverage in the membrane with the smaller pore size. Additional significance of these observations is currently under investigation. It is clear, however, that (a) the reversed trend in σ is an example of the unreliability of ζ_app values alone in characterizing the charge of membranes containing pores with finite EDLs, and (b) both the unadjusted and the PEG-chain-size-adjusted calculations suggest that charge reduction can be considered a sign of PEG attachment.

Quantitative demonstration of the suitability/unsuitability of the surface charge densities inferred in this work for applications such as charge-selective ultrafiltration are beyond the scope of this work. It can be noted, however, that a model developed on the basis of a Derjaguin-Landau-Verway-Overbeek (DLVO) model of solute pore electrostatic interactions in Conlisk et al., (2009) suggests that surface charge density values of the order of −0.04 C/m² can explain observed sieving coefficients for proteins obtained with phosphate buffered saline solutions and PEG-coated nanomembranes of slit-pore widths 9.69, 10.78 and 12.78 nm.

7 Conclusions

The surface charge of three membranes having different pore sizes has been characterized theoretically and experimentally. In addition the relationship between the apparent zeta potential and the true zeta potential has been calculated numerically. The main conclusions from the theoretical interpretation of the streaming potential measurements discussed here are:

1. Silicon nanomembranes are negatively-charged and remain so even after modification with polyethylene glycol.

2. The true zeta potential of a membrane with nanometer-scale pores is higher in magnitude (in this case more negative) than the apparent zeta potential determined from streaming potential measurements and can be predicted from the model of electric double layer overlap and streaming potential discussed in this work.

3. The PEG coated membranes have lower surface charge density than the uncoated membranes, confirming the attachment of PEG groups.

4. PEG coating has the smallest effect on the surface charge density of the smallest pore size investigated, when the constriction of pore cross-section due to the finite thickness of the PEG layer is considered in the theoretical analysis of the experimental data (Table 3).

5. A low measured streaming potential does not necessarily correspond to a low zeta potential, when electric double layers overlap (Table 3).

6. According to the theoretical model, increase in the membrane charge tends simultaneously to increase the streaming potential through enhancement of ionic convection and reduce the streaming potential through the enhancement of ionic conduction. The former effect is dominant at low zeta potentials and the latter effect is dominant at large zeta potentials.

In general, the observed streaming potential will have a non-unique interpretation, in terms of the corresponding ‘true’ surface charge density, in nanopores where the electrical double layers overlap. As discussed in Section 5 (Figure 4), highly charged membranes (−ζF/(RT) ≫ 1) can result in deceptively low streaming potentials, and can thus exhibit streaming potential behavior similar to membranes of much lower surface charge density. Interpretative and experimental suggestions have been provided to circumvent this difficulty, such as measurement of pore confined conductance. The sole use of conductivity measurements to infer the ionic strength of the solution and the use of ionic-strength-dependent mobilities in the calculation of the conductivity of the nanopore-confined electrolyte are unique features of the theoretical development in this work. Although the specific case of KCl solutions has been studied, the developed theory can also be used to predict solution conductivity given the ionic strength (or vice versa) of other 1:1 electrolytes. The derivation of the equation governing the streaming potential in pores of arbitrary cross-sectional shape, as provided in the Appendix, also appears not to have been reported elsewhere.

The effect of mobility of ions in the Stern layer (Lyklema, 1995) has been neglected in this work. If necessitated by further experimental evidence, this effect can be incorporated through the use of a Stern Layer conductance (Lyklema, 1995; Van der Heyden et al., 2005). The pores have been considered to be homogeneously charged and all pores in the membrane are considered to have the same charge density, assumptions which may not necessarily be true, for example, if the PEG-silane solution used for the PEG coating fails to percolate the membrane uniformly. For example, the region near the entrance and exit to the pore could have a larger coverage of PEG groups. For moderately charged surfaces, the zeta potential as inferred in the current work can still be interpreted as a zeta potential averaged over the pore length with the local fractional coverage as the weighing function (Norde et al., 1991). However, the same interpretation may not be accurate for very strongly charged membranes at large degrees of double layer overlap since the conductivity of the pore-confined solution will also become a function of the local coverage fraction under these conditions; further generalization of the current model is necessary to study such situations.

The results from this work can be extrapolated to more concentrated solutions of physiological interest under the assumption that the surface charge density is insensitive to the corresponding change in ionic strength (Van der Heyden et al., 2005); in practice, charge regulation and metal cation complexation effects may invalidate this assumption (Pujar and Zydney, 1994; Scales et al., 1992; Wang and Revil, 2009). A charge regulation model is currently under development to study the simultaneous effects of PEG coating and nanoscale confinement. In this study, the edge of the diffuse part of the electrical double layer on the PEG coated as well as uncoated silicon surface is considered to coincide with the shear surface (Probstein, 1998), which may not necessarily be a good representation of polymer coated surfaces (Burns et al., 1995); this effect will be investigated in the future.

The uniform pore size assumed in this work appears to be a reasonable approximation based on characterization work carried out on membranes of similar design and fabrication history (Fissell et al., 2009). Extension of the current work to membranes with a distribution of pore sizes is possible through an appropriate choice of pore size distribution functions parameterized by appropriate measures of dispersion and central tendency (cf. Saksena and Zydney, 1995). Equation (2) and Equation (16) of the Appendix can also be used as the starting point for studying the current-voltage characteristics of strongly charged membranes of other pore shapes (e.g. circular), such as ion-exchange-membranes. Generalization of the current work on finite EDL effects to asymmetric membranes would require an appropriate definition of the pore size and thickness characteristic of the dense skin layer. For very small pore sizes (∼ 1 nm or less), non-continuum effects not modeled in the current work, such as dielectric saturation of water, may become important, the Poisson-Boltzmann equation-based approach for which requires the use of a smaller near-wall dielectric constant for water (Karimi and Li, 2005). The model and the associated diagnosis of attachment through the alteration of surface charge can also be applied to other polymers such as polyethyleneimide (Burns et al., 1995) attached through the functionalization of silanol groups on silicon/silica-based substrates. The surface charge densities on both coated and uncoated membranes observed in this study appear to be comparable to that inferred from their protein sieving performance utilizing a DLVO model of electrostatic exclusion (Conlisk et al., 2009).

Abbreviations

EDL

Electric Double Layer

PEG

polyethylene glycol

SEM

Scanning Electron Micrograph

SP

streaming potential

Appendix: Streaming potential in a straight nanopore of arbitrary cross-sectional shape

Consider a straight pore of constant but arbitrary cross-sectional shape. An electrolyte solution flows through this pore owing to a pressure difference of ΔP maintained between its entrance and exit. The pore develops a wall zeta potential ζ in contact with the electrolyte. Since length of the pore L is much larger than a characteristic cross-pore dimension h, the flow is fully developed and axial variations in the distribution of ions in the electrolyte can be neglected. The electric potential inside the pore can be split into an equilibrium electric potential ϕ*=ϕζ which is present even in the absence of any fluid motion and a potential Ψ that appears when an external pressure difference ΔP is established between the pore entrance and exit, while establishing no external electrical connectivity. Since the walls of the pore are insulating, the electric field due to the potential Ψ has no component normal to the pore walls, and only a uniform component E= −dΨ/dx =−ΔV_SP/L along the axis of the pore.

The velocity field under a pressure-gradient ΔP and the induced voltage differential ΔV_SP can be calculated by linear superposition of the pressure-driven and electroosmotic components

$$u=-\frac{1}{\mu }\left(u_p\frac{\Delta P}{L}+{\epsilon }_e{u}_e\frac{\Delta V_{SP}}{L}\right)$$ (9)

where u_e=ϕ*−ζ and u_p are quantities with dimensions of potential and length squared, respectively. In order to satisfy the balance of viscous drag forces and forces due to pressure differential, the quantity u_p has to satisfy

$${\nabla }^{{\ast }^2}{u}_p=-1$$ (10)

where ∇*² is the two-dimensional Laplace operator on a given cross-sectional plane, having dimensions of inverse length squared. For the equilibrium potential ϕ*=u_e+ζ to satisfy the Gauss Law of electrostatics, when the volumetric charge density inside the electrolyte solution is ρ_e, the auxiliary function u_e must satisfy

$${\epsilon }_e{\nabla }^{{\ast }^2}{u}_e=-{\rho }_e$$ (11)

The function u_p has units of length squared and u_e has the units of electric potential. The current density vector inside the channel only has a component J perpendicular to the pore cross-section, originating from convection of charges and ionic conduction:

$$J=\langle {\rho }_{e}u\rangle -{\Lambda }_P\frac{\Delta V_{SP}}{L}$$ (12)

Substituting u from Equation (9) and ρ_e from Equation (11):

$$J=-\frac{{\epsilon }_e}{\mu }\left(-\langle u_p{\nabla }^{\ast 2}{u}_e\rangle \frac{\Delta P}{L}-{\epsilon }_e\langle u_e{\nabla }^{\ast 2}{u}_e\rangle \frac{\Delta V_{SP}}{L}\right)-{\Lambda }_P\frac{\Delta V_{SP}}{L}$$ (13)

The identities 〈 u_p∇*²u_e 〉= 〈 u_e ∇*²u_p 〉 and 〈 u_e∇*²u_e 〉= − 〈 (∇*u_e)² 〉 can be deduced by integrating the left hand sides by parts and using u_e=u_p=0 on the pore wall, or more precisely on the “shear surface” (Probstein, 1999). Here, ∇* is the gradient operator with dimensions of inverse length. Therefore, the first two terms in the above equation can be written in a more convenient form:

$$J=\frac{{\epsilon }_e}{\mu }\left(\langle u_e{\nabla }^{{\ast }^2}{u}_p\rangle \frac{\Delta P}{L}-{\epsilon }_e\langle {\nabla }^{\ast }{u}_e\cdot {\nabla }^{\ast }{u}_e\rangle \frac{\Delta V_{SP}}{L}\right)-{\Lambda }_P\frac{\Delta V_{SP}}{L}$$ (14)

Substituting for ∇*²u_p using Equation (10):

$$J=\frac{{\epsilon }_e}{\mu }\left(-\langle u_e\rangle \frac{\Delta P}{L}-{\epsilon }_e\langle {\nabla }^{\ast }{u}_e\cdot {\nabla }^{\ast }{u}_e\rangle \frac{\Delta V_{SP}}{L}\right)-{\Lambda }_P\frac{\Delta V_{SP}}{L}$$ (15)

Using u_e=ϕ*−ζ

$$J=\frac{{\epsilon }_e}{\mu }\left(\left(\zeta -\langle {\phi }^{\ast }\rangle \right)\frac{\Delta P}{L}-{\epsilon }_e\langle {\nabla }^{\ast }{\phi }^{\ast }\cdot {\nabla }^{\ast }{\phi }^{\ast }\rangle \frac{\Delta V_{SP}}{L}\right)-{\Lambda }_P\frac{\Delta V_{SP}}{L}$$ (16)

The condition of zero current through the pore (J=0) gives Equation (2) after reverting to the dimensionless definitions ϕ = ϕ*/ζ and ∇ =∇*/h:

$$\Delta V_{SP}=\frac{{\epsilon }_e\zeta \Delta P}{\mu \Lambda }\left[\frac{1-\langle \phi \rangle }{\frac{{\Lambda }_p}{\Lambda }+\alpha \langle \nabla \phi \cdot \nabla \phi \rangle }\right]$$ (17)

where the bulk conductivity of the electrolyte is Λ. According to Equation (17) (or Equation (2)) knowledge of the local equilibrium electric potential (ϕ) distribution at all points of the cross-section and both the pore confined conductivity and bulk conductivity of the electrolyte either from experiment (Fievet et al., 2000; Fuoss et al., 1965), or from the application of a conductivity model (Lyklema, 1995; Fuoss et al., 1965; Fawcett, 2004) is, in general, necessary for the calculation of streaming potential ΔV_SP. Note that no information on the distribution of ions is necessary to derive Equation (17) (or Equation (2)).

In this work, the Boltzmann distribution of ions has been used in the specification of ρ_e on the right hand side of Equation (11), which means ϕ satisfies the Poisson-Boltzmann equation (Lyklema, 1995), the solution to which is given by Equations (5) and (6) (Behrens and Grier, 2001; Verwey and Overbeek, 1999). The Boltzmann distribution of ions (and equal ionic mobilities for the cations and anions from the 1:1 symmetric electrolyte) has also been used in the calculation of the pore-confined conductivity Λ_p according to Equation (3).

The zeta potential ζ_app apparent from streaming potential measurement and thin electric double layer theory is corrected to the true zeta potential value (circle) using finite-EDL streaming potential theory (curve)

Nomenclature
a	Ionic size parameter in Onsager-Fuoss theory (Equation (4))
B1	Parameter in Onsager-Fuoss theory (Equation (4))
B2	Parameter in Onsager-Fuoss theory (Equation (4))
c	Molar concentration of an ion
h	Pore slit height
F	Faraday's constant
I	Ionic strength
J	Current density through pore
L	Pore length
m	Parameter in Jacobi elliptic function
ΔP	Pressure drop (Pexit - Pinlet)
R	Universal Gas Constant
T	Temperature
u	Flow velocity along pore axis (Appendix)
ue	Parameter characterizing electroosmotic flow (Appendix)
up	Parameter characterizing pressure-driven flow (Appendix)
y	Coordinate along pore slit height measured from pore center (Appendix)
x	Coordinate along pore axis from inlet to exit of the pore (Appendix)
ΔVSP	Voltage drop due to streaming potential (Vexit - Vinlet)
z	Valence of an ion
Greek characters
α	Dimensionless number characterizing electroosmotic convection in Equation (2)
β	short form for the dimensionless number ζF/ (RT)
εe	Electrical permittivity
κ	Debye-Huckel parameter
λ	Debye length
Λ	Conductivity of the unconfined solution
Λp	Conductivity of the pore-confined solution
μ	Viscosity
ν	Ionic mobility
ρe	Volumetric charge density
ϕ	Equilibrium dimensionless electric potential
σ	Surface charge density
Ψ	Induced electric potential due to streaming potential effect
ζ	Zeta potential (apparent or true)
∇	Dimensionless gradient operator
Superscripts
∞	Property defined in unconfined solution
*	Dimensional quantity (Appendix)
Subscripts
app	Apparent
i	index number for identifying a particular ion
p	Property defined in pore-confined state
SP	Streaming Potential
K+	Potassium ion
Cl-	Chloride ion