Model of Transient Oscillatory Synchronization in the Locust Antennal Lobe

Summary

Transient pairwise synchronization of locust antennal lobe (AL) projection neurons (PNs) occurs during odor responses. In a Hodgkin-Huxley-type model of the AL, interactions between excitatory PNs and inhibitory local neurons (LNs) created coherent network oscillations during odor stimulation. GABAergic interconnections between LNs led to competition among them such that different groups of LNs oscillated with periodic Ca²⁺ spikes during different 50–250 ms temporal epochs, similar to those recorded in vivo. During these epochs, LN-evoked IPSPs caused phase-locked, population oscillations in sets of postsynaptic PNs. The model shows how alternations of the inhibitory drive can temporally encode sensory information in networks of neurons without precisely tuned intrinsic oscillatory properties.

Introduction

Stimulus-evoked field potential oscillations have been observed in a variety of neuronal systems (Adrian, 1942, 1950; Hubel and Wiesel, 1965; Gray and Singer, 1989; Gelperin and Tank, 1990). These oscillations are caused by synchronized neural activity in large ensembles of interacting cells. If all activated neurons contribute continuously to population activity during a stimulus presentation (synchronized firing of every participating neuron lasting the full period of stimulation), the ability of the system to process and represent information is then limited to identity coding—different neuronal ensembles oscillate in response to different stimuli. An additional coding dimension emerges if the set of contributing neurons changes in time over the period of stimulation in a stimulus-specific manner. In olfactory systems, slow temporal patterns of excitation and inhibition have long been observed in the olfactory bulbs of amphibians (Kauer, 1974; Kauer and Shepherd, 1977), mammals (Chaput and Holley, 1980; Meredith, 1986, 1992), and in the antennal lobes of insects (Burrows et al., 1982; Christensen and Hildebrand, 1987; Laurent and Davidowitz, 1994; Stopfer et al., 1999). These slow temporal patterns have been shown in the locust olfactory system to be odor specific, reproducible over repeated trials, and superimposed on faster oscillatory patterns (Laurent and Davidowitz, 1994; Laurent et al., 1996; Wehr and Laurent, 1996). Odor encoding or representation in this system thus appears to rely on both the composition and the temporal recruitment of neuronal ensembles.

Intracellular recordings in vivo from locust antennal lobe projection neurons (PNs) revealed that individual PNs phase-lock with population oscillations at times that depend on the stimulus. Thus, there is a fine structure to the timing of PN action potentials within the population response that is stable over trials and different for different PNs (Laurent et al., 1996; Wehr and Laurent, 1996; Laurent, 1996). PNs’ action potentials were usually phase-locked with the field potential for epochs of 1–5 cycles of network oscillations (50–250 ms), followed or preceded by epochs of desynchronized firing or silence. This structure appeared to be independent of slow temporal patterns; epochs with or without spike synchronization could alternate while a neuron fired continuously (Wehr and Laurent, 1996; Laurent, 1996). This fine structure could be eliminated by picrotoxin application, while the slow temporal patterns were not affected (MacLeod and Laurent, 1996).

In this paper, we investigate the mechanisms underlying these transient spatiotemporal patterns of synchronization with a realistic computational model of the antennal lobe network. We explore whether oscillatory synchronization of PNs and local neurons (LNs) requires local reciprocal inhibition to both local and projection neurons and whether realistic network and cellular dynamics can emerge from circuit interactions alone. We also examine the conditions under which transient synchronization of participating neurons occur, as observed in the antennal lobe. Because similar dynamics are observed in larger, analogous circuits in vertebrates (the olfactory bulb), this small system constitutes an ideal model system for studying odor-evoked spatiotemporal activity patterns in early olfaction.

Results

Transient Synchronization of the Antennal Lobe Neurons in Vivo

When activated by odor stimulation to the antenna, the antennal lobe of the locust produces a coherent and distributed population response: sets of PNs begin to fire in oscillatory synchrony. The timing and extent of this organized population activity can be monitored by placing an extracellular field potential electrode in the ipsilateral mushroom body, a target of the PNs. Upon odor stimulation, these recordings show 20–30 Hz oscillations, reflecting the coherent arrival of action potentials from many coactivated PNs. The identity of these activated PNs, however, changes progressively during a response in an odor-specific manner. Consequently, the synchronization between 2 PNs or between 1 PN and the local field potential (LFP) is generally transient, i.e., shorter than the total duration of the population response (Laurent and Davidowitz, 1994). During the odor response, PN action potentials are generally phase-locked with the field potential, although this phase-locking between a PN's spikes and the LFP may occur for only a fraction of the spikes it produces during the odor response. (See, for example, Laurent et al. [1996], Figure 4; in this example, characteristically, action potentials were transiently locked to the population activity at consistent times over consecutive stimuli.) When phase-locking is transient, the periods of transient synchrony are odor specific (Laurent et al., 1996; Wehr and Laurent, 1996). We now explore, using models of increasing size and complexity (see Figure 1), the minimum requirements for evoking such cellular and circuit dynamical behavior.

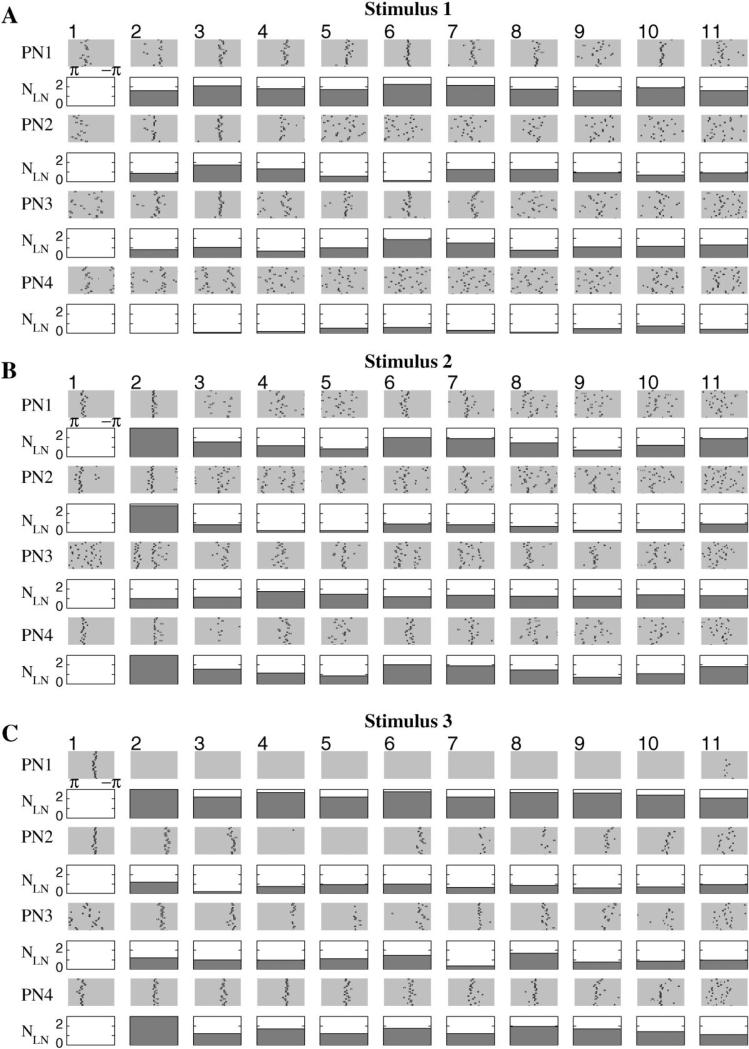
Figure 4. PN Responses for Different Stimuli and Role of the Strength of LN Inhibition.

Four cells (rows) are shown. The response of each cell has been divided into 11 epochs of about 50 ms, each corresponding to oscillatory cycles of activity. In each epoch, the positions (phases) of the action potentials relative to the maximum of the corresponding field potential were calculated and plotted (rows labeled PN1, PN2, etc.). This operation was repeated 20 times for each odor (rasters within each epoch). The number of Ca²⁺ spikes in all presynaptic LNs, averaged over 20 trials, is shown for each cycle (rows labeled N_LN).

(A and B) During stimulation of similar sets of neurons, almost identical subsets of PNs responded, but with different temporal patterns. (C) A different subset of PNs was stimulated during these trials, and different PNs responded.

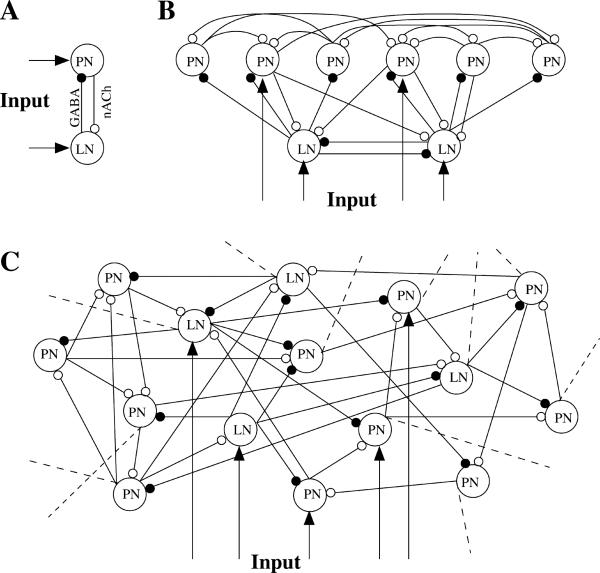
Figure 1. Network Geometries.

(A) Two reciprocally connected neurons.

(B) A simple network model of 6 PNs and 2 LNs. Four neurons were stimulated by current pulses to simulate the effect of odor presentation.

(C) A network model of 90 PNs and 30 LNs. All interconnections were random with probability 0.5. Thirty-three percent of the total population was stimulated by time-modulated current pulses. Dashed lines illustrate connections to the rest of the network.

Oscillations in a Reciprocal LN-PN Pair

One-compartment models of excitatory (cholinergic) PNs and inhibitory (GABAergic) LNs (Laurent, 1996) were first constructed to create a simple network model of the antennal lobe (Figure 1, see Experimental Procedures). Isolated neurons were silent at resting membrane potentials but fired Na⁺ (PN) or Ca²⁺ (LN) action potentials when direct current was applied (Figure 2A). This response increased with the amplitude of the injected current (M.S., unpublished data). Isolated PNs displayed overshooting Na⁺ spikes at a fixed frequency throughout the DC pulse, but isolated LNs generated low-amplitude Ca²⁺ spikes (Laurent, 1996) whose frequency decreased during the first 150–200 ms of stimulation (Laurent et al., 1993). This adaptation depended on a hyperpolarizing Ca²⁺-dependent potassium current in LNs which was activated during the first few Ca²⁺ spikes. Although such a current has not been characterized biophysically in LNs, its existence, or that of a functionally equivalent current, is implied by current-clamp data (M.S. and G.L., unpublished data) in which LN Ca²⁺ spike discharges adapt upon maintained depolarization.

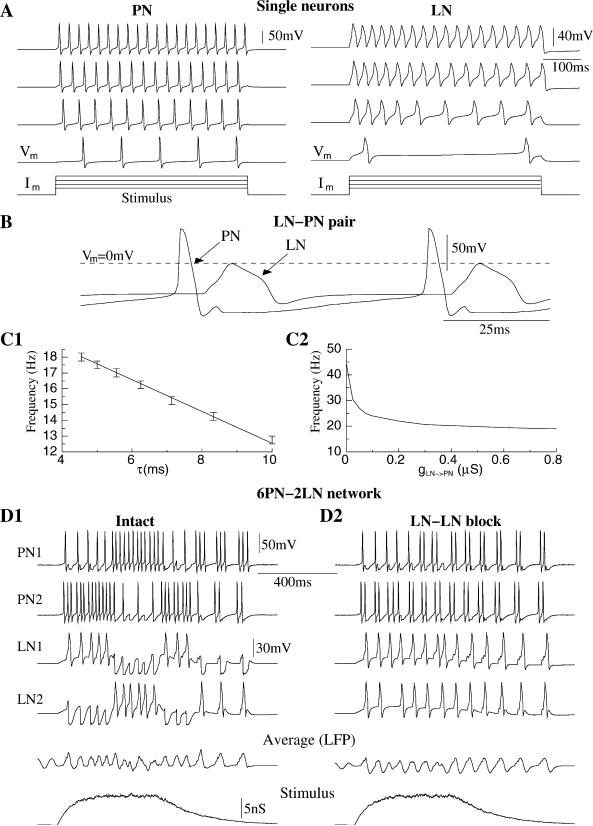
Figure 2. Stimulus-Evoked Oscillations in PN and LN Models.

(A) Responses of isolated PN and LN to current pulses of different amplitude.

(B) A reciprocally connected LN-PN pair oscillated out-of-phase at about 15 Hz.

(C) Frequency of oscillations in reciprocal LN-PN pair versus decay time constant of inhibitory synapse (_{gLN → PN} = 0.8 μS) and versus maximal conductance of inhibitory synapse (τ = ms).

(D) Oscillations in a network of 6 PNs and 2 LNs.

(D1) Lateral inhibition between LNs led to alternations in the temporal patterns of LN oscillation. Variations in LN-evoked fast IPSPs changed the temporal patterns of PN activity.

(D2) Blocking LN-LN reciprocal connections made these cells oscillate regularly thus decreasing the complexity of PN responses.

When reciprocally coupled (as in Figure 1A), the LN and PN oscillated out-of-phase at a frequency of about 20 Hz when direct current was applied (Figure 2B). The first Na⁺ spike in a PN elicited an EPSP followed by a Ca²⁺ spike in the LN, which in turn evoked a fast IPSP in the PN. This IPSP then delayed activation of the next Na⁺ spike in the PN. The frequency of the resulting oscillations was controlled mainly by the duration and the amplitude of the LN-evoked IPSPs (Figure 2C). As the coupling (_{gLN → PN}) increased from zero, the frequency quickly stabilized at a level depending on the decay time constant of inhibition. These results indicate that the fast inhibitory input from a LN can effectively control the oscillatory response of a PN during DC stimulation. In the next sections, we investigate this effect in more realistic and progressively larger network models.

LN-LN “Competition” in a Small LN-PN Network

A network model consisting of 6 PNs and 2 LNs (Figure 1B) was constructed to evaluate the effect of reciprocal inhibitory interconnections between LNs on stimulus-evoked PN responses. We first simulated a network that had intact inhibitory synapses between the 2 LNs and from LNs to PNs. The stimulus, delivered to both LNs and to 2 of the PNs (PN1 and PN2 in Figure 2D), elicited an oscillatory response in the network. Both LNs started to fire synchronously, but the LN-LN inhibition quickly organized the fast periodic synchrony into a slower sequence of out-of-phase patterns (Figure 2D1): each LN produced periodic (20 Hz) Ca²⁺ spikes during 100–200 ms epochs, interrupted by epochs of subthreshold oscillations. These interruptions were caused by inhibitory input from the other LN, which displayed a complementary activity pattern. This slower patterning of LN oscillations and antagonistic activity depended on the rate at which LN responses adapted (see Figure 2A) and also on the input from other neurons and external stimulation. The oscillations in one of the LNs (e.g., LN1) always started at a higher frequency, which dampened the activation of the other LN (LN2). After a few cycles, activation of the Ca²⁺-dependent potassium current in LN1 reduced the frequency of its Ca²⁺ spikes, thus diminishing the inhibitory input to LN2. LN2 then “escaped” from its “silent” state, producing periodic Ca²⁺ spikes which, in turn, damped oscillations in LN1. The timescale of this slower temporal structure was determined by the rate of LN spike adaptation [controlled mainly by the K(Ca) current in LNs] and the strength and time constant of LN-LN interactions. Blocking reciprocal inhibition between LNs eliminated this slow patterning; both neurons then displayed sustained synchronous periodic activity (Figure 2D2).

In the simple network model of 2 LNs and 6 PNs, each LN provided inhibitory input to 3 PNs (see Figure 1B). This input was significant during the epochs of oscillations with Ca²⁺ spikes but was greatly reduced during epochs of subthreshold oscillations in the presynaptic LN. Thus, alternations in patterns of subthreshold/suprathreshold oscillations in LNs significantly affected LN-evoked IPSPs in the PNs and could affect the synchrony of PNs during stimulus-evoked oscillations. Below, we show in a larger network model that patterns of LN-mediated inhibition can effectively control the transient synchrony of PN oscillations.

Oscillations in a Larger LN-PN Network

To examine stimulus-evoked responses in a larger LN-PN population, we simulated a network consisting of 90 PNs and 30 LNs (see Figure 1C and Experimental Procedures). These numbers were selected to match the PN/LN ratio in the locust antennal lobe (about 900 PNs and about 300 LNs; Laurent, 1996) and also to allow practical computation times. Receptors for both excitatory and inhibitory transmission had fast ionotropic-type kinetics. Weak, slow GABAergic synapses, which could be activated by a long train of Ca²⁺ spikes at relatively high frequencies, were introduced between LNs and PNs to limit network activity in those simulations when fast GABAergic synapses were blocked. Maximal conductances for these slow receptors were set low so they did not affect the network oscillations when fast GABAergic connections were intact. External stimulation was delivered to a randomly selected subset of about 30 PNs and 10 LNs (33% of the total population). About 50% of the total PN population was recruited in oscillations through direct external stimulation and PN-PN interaction.

In contrast to the simple networks described in the previous sections, but similar to experimental findings, this model displayed a low level of spontaneous activity even without external stimulation (Figure 3). This was a consequence of distributed coupling bringing the average membrane potential of all neurons closer to the threshold for spike generation and a small-amplitude Gaussian noise current in each cell (see Experimental Procedures). When several PNs occasionally fired together, they caused EPSPs in a set of postsynaptic PNs. Some of these EPSPs occurred at the peak of a depolarization (evoked by the random fluctuations of the membrane potential) and produced Na⁺ spikes in the postsynaptic cells. Spontaneous PN activity, however, was not synchronized; the field potential (averaged PN membrane potential, see Experimental Procedures) was therefore almost flat between stimulus presentations (see Figure 3A).

Figure 3. The Response Properties of a Network of 90 PNs and 30 LNs.

(A) Averaged PN activity (field potential) showed periodic oscillations at about 20 Hz during stimulation.

(B) Network response, spikes indicated with dots. Firing rates of PNs and LNs increased during stimulation. During 1 s intervals between stimulus presentations, the PNs displayed spontaneous activity leading to occasional Na⁺ spikes.

(C) To simulate odor presentations, two 500 ms time-modulated current pulses with added Gaussian noise were introduced to 33% of the PNs and LNs.

(D) Different PNs and LNs participated in the coherent network oscillations during different portions of the stimulus presentation.

(E) Power spectrum of averaged PN activity had a sharp peak near 20Hz.

(F) Typical odor responses recorded in vivo. Odor stimulation evoked oscillations in the local field potential (upper trace, recorded in the mushroom bodies), and action potentials in a PN (lower trace).

When an external stimulus was delivered, the field potential began to oscillate with a frequency of about 20 Hz (Figures 3A and 3D), reflecting the onset of synchrony in a large subset of PNs. LNs tend to fire after PNs; the average phase shift between spikes in LNs and PNs at each cycle of network oscillation was 72° ± 91°. This is in agreement with measurements from recordings made in vivo (Laurent and Davidowitz, 1994). Figure 3D shows examples of these oscillations in 2 randomly selected PNs and 1 LN. The PNs were synchronized with one another and with the field potential during several 100–150 ms epochs. These epochs corresponded to intervals of suprathreshold (Ca²⁺ spike) oscillations in the LN. The timing of these epochs was consistent and reproducible (see below). Results obtained with the model closely resembled those from recordings made in vivo. Figure 3F shows an intracellular recording from a single PN, with a simultaneously recorded field potential from the ipsilateral mushroom body, where PNs send axon collaterals.

These results indicate that, as in the simpler network of 2 LNs and 6 PNs, LN activity in the larger network alternated between intervals of sub- and suprathreshold oscillations. Switching between these modes of LN activity appeared to control transitions between the periods of synchronized and nonsynchronized PN spikes.

Transient Synchronization

To investigate temporal patterns of synchronization among PNs more precisely, we analyzed the fine structure and timing of action potentials during many successive stimulus presentations. The length of each stimulus-evoked oscillatory response was divided into 11 consecutive windows corresponding to the cycles of the field potential oscillation. Then, the timing of all spikes in each window was measured relative to the corresponding peak in the field potential (see Experimental Procedures). Each action potential was thus represented by its phase, where zero corresponded to the positive peak of the field potential and ±π corresponded to the following/preceding trough in the field potential. The phases of all spikes were then plotted (black dots) as rasters (Figure 4), where each row corresponded to a different trial (20 trials in all).

The results of this analysis for 4 PNs and three different stimuli (“odors”) are presented in Figure 4 (shaded rectangles). We first show an example of one set of 20 responses to one stimulation pattern (Figure 4A) and then compare it with the responses to two other stimuli. In stimulus 2 (Figure 4B), we activated the same subset of PNs as in stimulus 1 but a different subset of LNs. We found that the first two stimuli (1 and 2, Figures 4A and 4B) elicited responses in almost identical groups of PNs; the fine temporal structure of the PN responses, however, was different. For stimulus 1, for example, PN1 was clearly synchronized with the field potential during epochs 1–8 and 10, less so during epoch 11, and desynchronized during epoch 9 (although still active). When stimulus 2 was presented, PN1 locked to the field potential during epochs 1, 2, 6, and 7 only. PN4 was desynchronized during almost all epochs for stimulus 1 but displayed very clear synchronization during epochs 2, 6, and 7 in response to the second stimulus.

Figure 4C shows the response to a different stimulus pattern consisting of a subset of PNs and LNs that only partially (about 10%) overlapped with that of stimulus 1 (Figure 4A). Stimulus 3 produced responses in a different group of PNs. Some of the neurons that fired in response to the first two stimuli showed only subthreshold responses when stimulus 3 was presented and vice versa. The average network activity, however, was comparable in all three cases. Other panels (open rectangles) in the Figures 4A–4C will be discussed later.

Figure 5A plots the standard deviation (SD) of spike phase as a function of time (cycle number) for all 90 PNs calculated over 20 trials. Strongly phase-locked activity (low SD of phase, dark bars) appeared during different temporal epochs in each PN and usually persisted for 1–3 cycles of network oscillation and alternated with epochs of weakly or non-phase-locked activity (large SD). Thus, different groups of PNs contributed to the field oscillations during different epochs of the response to the stimulus. These results were independent of stimulus shape. When square-pulse stimuli were presented, a similar alternation of epochs with high and low spike synchronization was found. In this case, however, the offset excitation, otherwise observed in many PNs after stimulus termination (e.g., Figure 3B), was absent.

Figure 5. Standard Deviation of PN Spike Phases Measured over Repeated Stimulus Presentations.

(A) Standard deviation (20 trials) is shown as a function of oscillatory cycle number for 90 PNs. Zero deviation (black) corresponded to precise phase-locking of PN spikes with field oscillations. Maximal deviation (white) corresponded to complete desynchronization of PN spikes with field oscillations. White also indicates silent PNs.

(B) Standard deviation of PN spike phases (shown in Figures 4A and 4B) plotted against the total number of LN spikes in all presynaptic LNs. The data for four PNs and two stimuli are plotted with different symbols. Straight line is linear regression.

In our model, PNs usually displayed active (i.e., including Na⁺ spikes) responses or subthreshold oscillations throughout the period of stimulation. In some cases, however, spikes were skipped during a few cycles. For example, PN2 displayed well-synchronized responses to stimulus 3 (Figure 4C) but no spikes during the fourth and fifth epochs of stimulation. Spikes were here replaced by subthreshold oscillations (data not shown). Such slow temporal patterning results in part from the slow inhibition and will be explored elsewhere (Bazhenov et al., 2001 [this issue of Neuron]).

The results presented in Figures 4 and 5A indicate that different PNs phase-lock during different epochs of a response to a stimulus. This fine structure in PN responses was stable and reproducible (see Figure 4). To examine the mechanisms underlying this transient oscillatory synchronization of PNs, we analyzed the activity of sets of presynaptic LNs. For each of the PNs shown in Figures 4A–4C, we first identified the set of presynaptic LNs (a 0.5 probability for LN-PN interconnections yielded about 15 presynaptic LNs for each PN in our simulated network). Then, for each cycle of oscillation, we measured the number of Ca²⁺ spikes produced by the presynaptic LNs over the interval between the two nearest peaks of the field potential. The number of Ca²⁺ spikes thus represented the total inhibitory input to the selected PN during each cycle of the stimulus-evoked response. The average number of spikes (over 20 trials) in all presynaptic LNs, N_LN, is plotted as a function of oscillation cycle number for each one of the 4 PNs (open rectangles in Figure 4). There was a clear correlation between N_LN and the tightness of firing in PNs; PN action potentials phase-locked with the field potential when N_LN was 2 or higher and desynchronized when N_LN was <1. The SD of PN spike phases was calculated for all 11 consecutive oscillation cycles (Figure 5B). This SD decreased as N_LN increased. Thus, the alternation of LN-mediated GABAergic input provides a potential mechanism for PN synchronization and the transient nature of PN synchronization is linked to variations in inhibitory drive from LNs over the duration of a response.

Roles of Fast GABA-Mediated Inhibition

To separate the potentially different influences of LN-LN and LN-PN inhibitory synapses over PN synchronization during odor responses, we selectively blocked the fast GABA receptors on LNs. Figure 6A1 shows the average activity of such a partially “disinhibited” network (configuration in Figure 1C). Similarly to the simple network of 6 PNs and 2 LNs (Figure 2D), the partially disinhibited large network oscillated at a lower frequency (about 15 Hz) when LN-LN synapses were blocked, a result of higher activity levels in LNs. LNs now showed weaker temporal clustering and produced Ca²⁺ spikes more regularly during almost every cycle of the collective network oscillation (data not shown).

Figure 6. Effect of Fast Inhibition and LN Spike Adaptation for PN Responses.

(A) Blocking LN-LN GABA_A inhibition.

(A1) Average PN activity (field potential).

(A2) PN responses for the two different stimuli presented in Figures 4A and 4B. Most of the PNs were now phase-locked with the field potential during the whole trial, reducing the discriminability of PN responses for similar stimuli.

(B) Blocking Ca²⁺-dependent K⁺ current in LNs.

(B1) Average PN activity shows oscillations at higher frequency (about 30 Hz).

(B2) PN responses for the two different stimuli presented in Figures 4A and 4B. Now PN synchronization (or its absence) usually endured throughout the whole stimulus duration.

We analyzed PN oscillatory synchrony in this partially “disinhibited” network using the approach used previously for the intact network (Figure 4). Figure 6A2 shows the phases of PN action potentials in the disinhibited network for the same neurons as in Figures 4A–4B. The increase in LN activity could lead to more tightly synchronized PN responses. This synchrony was typically reduced by the end of stimulation, possibly a result of the increased number of PN action potentials per oscillation cycle. Even in such cases, PN spike structure could be highly reproducible, with action potentials that were phase-locked to the field potential. Their average phases, however, varied widely between –π and +π (Figure 6A2). In general, the number of desynchronized PNs was reduced when LN-LN connections were selectively blocked. As a result, the responses of this partially disinhibited network to different stimuli were more similar to each other than in the intact network.

When both LN-LN and LN-PN fast GABAergic connections were blocked, the synchronization of PN spikes was completely lost (data not shown), reproducing the observation made in picrotoxin application experiments (MacLeod and Laurent, 1996; Stopfer et al., 1997; Mac-Leod et al., 1998). This is explored in greater detail in a companion paper (Bazhenov et al., 2001).

Effects of LN Spike Adaptation

Computer simulations of the small 2 LNs-6 PNs network demonstrated the essential role of LN spike adaptation for transient PN synchronization. When the rate of Ca²⁺ spikes in 1 LN decreased as a result of I_K(Ca) activation, another LN was released from inhibition and produced periodic Ca²⁺ spikes, which, in turn, dampened activation of the first LN (Figure 2D). These switches caused temporal changes in the inhibitory input to postsynaptic PNs, hence controlling transient PN spike synchronization.

To explore the effects of LN spike adaptation in a large network, we blocked I_K(Ca) in all the LNs in the network in Figures 3 and 4. One immediate consequence was a frequency increase in the stimulus-evoked network oscillations (about 30 Hz; Figure 6B1). Figure 6B2 shows the phases of selected PNs’ action potentials (same neurons as in Figures 4A, 4B, and 6A2), illustrating these general findings: fewer PNs showed transient synchronization; PNs were generally either phase-locked during the entire stimulus duration (e.g., PNs 1–3, stimulus 1) or fired desynchronized spikes all or most of the time. We analyzed the number of presynaptic LN spikes over the stimulus duration (as in Figure 4A and 4B) and found that while the average number of presynaptic spikes (characterizing strength of the inhibitory input) was different for different PNs, the variability in LN spike number from one cycle of field oscillations to another was less after I_K(Ca) blockade (data not shown). This result suggests that transient PN synchronization can be caused by I_K(Ca)-mediated adaptation of LN firing.

Stimulus Discrimination

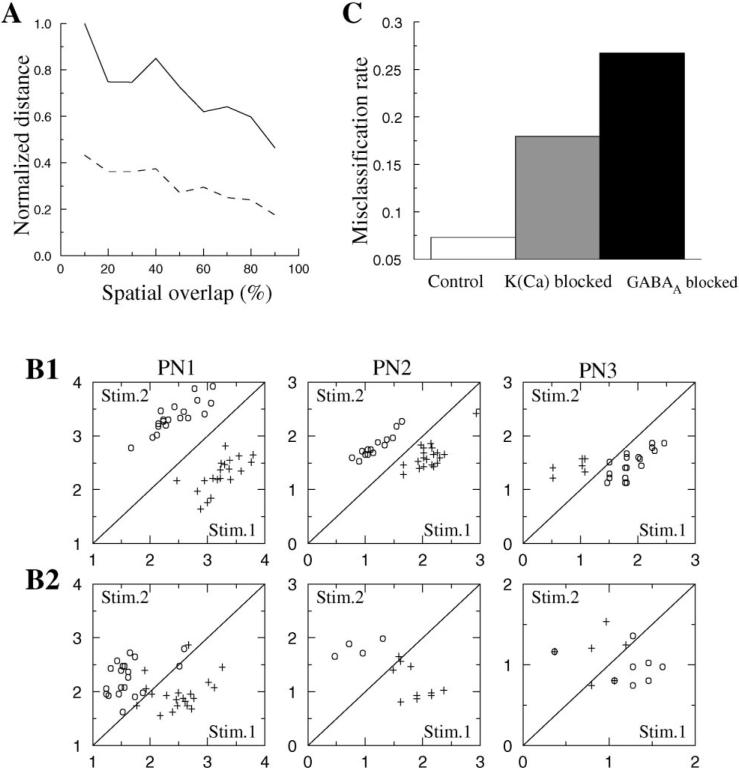
To test the ability of the 120-neuron network to discriminate between different stimuli, we first calculated the distance between the trajectories corresponding to different responses in “standard deviation space” (see Experimental Procedures) for both intact and partially disinhibited (only LN-LN GABA_A connections were blocked; LN-PN synapses were intact) networks. This analysis permitted us to assess variability in spike position on a cycle-by-cycle basis. Each point in the 90-dimensional standard deviation space represented a vector of PN spike deviations calculated from all PNs for a given cycle of network oscillation (see Experimental Procedures). The oscillatory cycle number provided a common time reference, against which the network evolution could be represented by a sequence of points in the standard deviation space. The distance between different responses in this space would be zero if the network responded identically to all stimuli. We found that blocking the fast LN-LN synapses reduced the average interrepresentation distance by a factor of about 2.5. Thus, at each oscillation cycle, the SDs of PN spike timings evoked by presentations of different stimuli were much more similar in the disinhibited network than in the intact one. Consequently, the ability of the network to discriminate among different stimuli, based on sequences of synchronized/desynchronized epochs, was significantly reduced after LN-LN disinhibition.

We also calculated the average distance between network responses for two different stimuli as a function of the spatial overlap between the sets of activated neurons. We used the stimulus used in Figure 4A as a control and then randomly selected a second set of LNs and PNs that overlapped, to a varying extent, with the control set. The amount of overlap varied between 0% and 97.5%. The average distance presented in Figure 7A was calculated by averaging the distances over five sequential cycles (third to seventh) for both intact (solid line) and disinhibited (dashed line) networks. The following conclusions can be drawn. First, the distance between network responses was always about 2.5 times greater for intact networks than for partially disinhibited networks. Second, even when the stimulated sets of neurons overlapped by >90%, the distance between evoked dynamical network responses was only reduced by about 50% in either intact or partially disinhibited networks. This indicates that the intrinsic antennal lobe mechanisms underlying temporal patterning of responses can dramatically increase an observer's ability to discriminate between overlapping stimuli.

Figure 7. Effect of LN-LN Inhibition and LN Spike Adaptation on Spike Time Variability and Stimulus Discrimination.

(A) Average (over cycles 3–7) distance between two different responses (see Experimental Procedures) versus the percentage of overlap of activated sets of neurons.

(B) A clustering algorithm (τ = 100 ms) was applied to spike trains in 3 PNs to illustrate discrimination between two stimuli presented in Figures 4A and 4B. Each trial was characterized by the distances to the centers of two clusters corresponding to stimuli 1 and 2 (see Experimental Procedures); these distances are plotted on axes x and y.

(B1) Intact network.

(B2) Fast LN-LN inhibitory synapses blocked.

(C) Misclassification rate calculated for all PNs for intact and disinhibited networks and for the network where Ca²⁺-dependent K⁺ channels in all LNs were blocked.

To further analyze the ability of this model to discriminate among different stimuli, we employed a clustering algorithm previously applied to experimental data from locust PNs (MacLeod et al., 1998) (see also Experimental Procedures). In contrast to the spike deviation analysis, which characterizes how reliably individual PNs fire spikes at different cycles of the network oscillation, the clustering algorithm characterizes the reproducibility of spike counts on a slower timescale to examine odor-specific differences in slower modulations. Figure 7B presents the results of this analysis for 3 PNs from intact and partially disinhibited networks. The ability of the intact network to discriminate between pairs of odors (Figure 7B1) was reduced when fast LN-LN inhibition was blocked, as shown by the increase in misclassifications (Figure 7B2). The histogram in Figure 7C shows the rate of misclassified responses (responses in which the cluster algorithm matched the network response with the wrong stimulus) calculated for the full network (all 90 PNs) in intact and disinhibited models and in the model where I_K(Ca) in all LNs was blocked, thus eliminating spike adaptation. This error rate was relatively small (about 7%) for the intact network but increased to about 18% after blocking I_K(Ca) and increased to about 26% when fast GABA-mediated connections between LNs were blocked. Note, however, that most of the stimuli were identified correctly even in the absence of fast LN-LN inhibition, probably because the cluster algorithm takes into account not only the specificity of the fine temporal structure of PN responses (which was reduced after blocking LN-LN inhibition) but also variations in spike rate that are determined by other mechanisms. These mechanisms include the activation of slow inhibitory receptors between LNs and PNs, which can significantly contribute to the discrimination of the network responses for different stimuli (Bazhenov et al., 2001). In the next paper (Bazhenov et al., 2001), we will show that the presence of potentially strong slow inhibitory synapses between LNs and PNs can explain the slow temporal patterns observed experimentally (Laurent and Davidowitz, 1994) and improve stimulus discriminability after fast inhibition blockade.

Discussion

In vivo recordings from the locust antennal lobe have revealed that individual PNs respond with complex temporal patterns when the antenna is presented with airborne odors. The antennal lobe network of LNs and PNs produces coherent oscillations at about 20 Hz; however, individual PNs are synchronized with and participate in this ensemble activity during relatively brief epochs of a response. These epochs of phase-locked activity are different for different PNs. Hence, the ensemble of PNs contributing to coherent network oscillations evolves within a single odor stimulation. When a new odor is presented, some of the same PNs may respond, but usually with different temporal patterns (Laurent and Davidowitz, 1994; Laurent et al., 1996; Wehr and Laurent, 1996).

To explore the mechanisms underlying the transient oscillatory synchronization of PNs, we constructed a network model of the antennal lobe consisting of two kinds of neurons: excitatory (cholinergic) PNs and inhibitory (GABAergic) LNs. Upon stimulation, some PNs started to fire; PN-evoked EPSPs induced Ca²⁺ spikes in postsynaptic LNs, which in turn evoked a fast IPSP, hyperpolarizing PNs and delaying activation of the next Na⁺ spikes. In a model of 90 PNs and 30 LNs, PNs and LNs oscillated with an average phase shift of 72° ± 91°. This mechanism has been previously described in computational models of the olfactory bulb (Rall et al., 1966; Rall and Shepherd, 1968). Similar but more reliable phase shifts (84° ± 4°) between excitatory and inhibitory units was observed also in linear model of the olfactory bulb (Freeman, 1979). In our model, variability in the phase between oscillations in the excitatory and inhibitory cells was a consequence of the transient properties of neuronal synchronization. PN synchronization started when the total number of Ca²⁺ spikes in all LNs presynaptic to each PN during one cycle exceeded a threshold of about 2. This number depended on the strength of the inhibitory synapses. More simultaneous LN spikes were required to synchronize PNs when the peak conductance of inhibitory synapses between LNs and PNs was reduced. Stimulus-evoked synchronization of olfactory neurons, also dependent upon input from inhibitory interneurons, was previously employed in a model of the Limax olfactory lobe (Ermentrout et al., 1998). However, in that model, synchronization always endured throughout the stimulus presentation and did not display the transient properties described here and in experiments with insects (Laurent et al., 1996).

If GABA-mediated synapses were placed only between LNs and PNs (but not between LNs), many PNs showed sustained synchronized oscillations, unlike the transient synchronization observed in vivo and in the intact model. Inhibition between LNs (Leitch and Laurent, 1996) appears to provide an important source of complexity in the PN responses. Random synaptic interconnections between LNs created clusters of synchronously firing neurons. The LNs in each of these clusters generated periodic Ca²⁺ spikes during specific epochs only, during which the fast IPSPs synchronized sets of postsynaptic PNs, thus generating strong field potential oscillations. These IPSPs also dampened the periodic depolarization of other LNs, causing their postsynaptic PNs to quickly desynchronize with the field potential and with each other.

Spatiotemporal clustering of network oscillations has been observed in models of other systems. It was described in network models of the thalamic reticular nucleus with localized GABA_A interconnections between neurons (Destexhe et al., 1994a; Golomb et al., 1994) and in models of sparse inhibitory networks (Golomb and Hansel, 2000) whose geometry is close to that of the LN population in the model of the antennal lobe presented here. Excitatory/inhibitory connections between LNs and PNs and inhibitory connections between LNs were found to be essential for maintaining coherent network oscillations and creating transient synchrony of PN responses, but the role of excitatory PN-PN connections was less obvious. We blocked all PN-PN connections and found little difference in the spatiotemporal dynamics of the AL network; however, fewer PNs were recruited into network oscillations. Increasing PN-PN coupling by 100% slightly increased the frequency of coherent network oscillations, and a larger subset of PNs displayed active responses during stimuli presentations. The role of PN-PN interaction might become more significant if smaller subsets of PNs were activated directly by the stimulus. In this case, specific patterns of PN-PN interconnections could be an additional factor for increasing the complexity of PN responses.

We analyzed the ability of our model LN-PN network to discriminate between different stimuli that evoked responses in almost identical, overlapping sets of PNs. Although discriminations were robust in the intact network, performance was significantly reduced when LN-LN inhibition was blocked. Discrimination was at almost chance level when fast GABAergic input to PNs was blocked. These results suggest that local inhibitory control of precise spike timing in excitatory relay cells can provide a specific mechanism for information coding in sensory systems. Stimulus encoding in this model depends on stimulus-specific alternations of the fast GABAergic input. In other systems, different intrinsic and network mechanisms could control these alternations. Individual GABAergic interneurons in the hippocampus, for example, can effectively control the spontaneous firing and subthreshold oscillations of pyramidal cells. The efficiency of this control depends on an interaction between GABAergic IPSPs and intrinsic oscillatory mechanisms in pyramidal cells (Cobb et al., 1995). Precise control of the timing of individual spikes by inhibitory input has also been described in cerebellar nucleus neurons in the context of fine temporal control of movement via inhibitory output from cerebellar cortex (Gauck and Jaeger, 2000). The vertebrate thalamus appears to be another example of a system where the necessary inhibitory circuits are present (Steriade et al., 1990, 1993). Sensory information passes to the cortex through thalamic relay cells whose spike timing can be controlled by GABAergic thalamic reticular neurons and inhibitory interneurons. As one reticular cell inhibits many relay neurons, its inhibitory input could synchronize firing in stimulus-specific groups of relay neurons, thus affecting responses at the cortical level.

In the present model, when distinct, nonoverlapping sets of PNs were stimulated, they evoked dynamic, evolving responses in distinct populations of PNs. By contrast, when stimuli were delivered to overlapping sets of PNs, the responses were distributed to overlapping PN sets which, however, showed subtle differences in the temporal sequences of the epochs with/without spike synchronization, enabling a high level of discrimination. Our simulations thus support the idea that odor identity is contained both in the identities of the active PNs and in the relative timing of spikes in those PNs. While temporal patterning may be unnecessary for the discrimination of nonoverlapping ensembles (activated, generally, by chemically different odorants), such features become important when activated PN ensembles overlap significantly (Stopfer et al., 1997; MacLeod et al., 1998).

Results with blocking fast inhibition in the AL model appear to contradict data recorded in vivo showing that picrotoxin application, which blocks inhibitory synapses onto PNs and onto LNs, causes no loss of information in the odor-evoked spike patterns of individual PNs (MacLeod et al., 1998). This discrepancy can be explained by the presence of additional temporal struc ture—slow temporal patterns—in the locust AL. Such slow patterns are, at least in part, a result of the activation of additional slow inhibitory receptors between LNs and PNs (MacLeod and Laurent, 1996), which contribute to the ability of the disinhibited network to discriminate between different stimuli (Bazhenov et al., 2001). The slow inhibitory receptors in the present model were too weak to serve this purpose even though they were able to control total network activity when the fast GABAergic synapses were blocked. Activation of these receptors required relatively long trains of Ca²⁺ spikes at high frequencies. They were thus unable to organize slow temporal structure in the network with intact fast inhibition. This suggests that the slow inhibition needed for slow temporal patterning should be activated by relatively short sequences of LN depolarizing potentials, as typically observed in the intact antennal lobe.

These results lead to several conclusions. First, consistent with physiological evidence (MacLeod and Laurent, 1996), our model shows that epoch-specific synchrony of PN oscillations depends on LN-evoked fast GABA-mediated IPSPs. Reducing the inhibitory input during certain epochs of stimulus-evoked oscillation led to desynchronization of the PNs. Conversely, enhancing the GABAergic synapses between LNs and PNs led to stereotyped PN responses that were always synchronized with network oscillations. The strength of these inhibitory synapses must therefore fall within a certain range to enable the fine temporal structure characteris tic of PN spike synchronization. Second, the odor-specific fine temporal structure of the PN responses results in part from odor-specific spatiotemporal patterning of LN activity, controlled by the fast inhibitory synapses between LNs. Blocking LN-LN connections selectively reduced the differences between PN responses to like stimuli but did not affect the coherence of the network oscillations. Enhancing LN-LN inhibition can shorten the epochs when PN spikes are phase-locked with network activity. Third, adaptation of LN Ca²⁺ spikes contributes significantly to the temporal variations in inhibitory input to target PNs. In the absence of spike adaptation, the transient character of PN spike synchronization is essentially eliminated. Modulation of a Ca²⁺-dependent K¹ current in LNs by Ca²⁺ entry during Ca²⁺ spikes is sufficient to account for the experimentally observed transient PN synchronization. Fourth, slow, inhibitory receptors between LNs and PNs appear to be necessary to account for realistic slow temporal patterns in PN spike trains; omitting these receptors makes it impossible to model accurately the temporal patterns of PNs described experimentally. Fifth, the fine temporal structure of PN responses is necessary to discriminate similar stimuli, while distinct stimuli can be separated based on activated PN identity alone (consistent with behavioral and physiological results; Stopfer et al., 1997; Laurent, 1999). Thus, the importance of temporal coding for stimulus discrimination increases with the spatial overlap between ensembles of activated glomeruli.

The present model provides, for the first time, a mechanism for generating the stimulus-specific temporal patterns created during olfactory stimulus encoding. Remarkably, this was accomplished using only basic and realistic parameters and without making assumptions about complex intrinsic properties of the AL neurons. The model is simple, and it was constructed to study mechanisms underlying transient synchronization; nevertheless, this model was also able to reproduce many important details of AL dynamics qualitatively and, in some cases, quantitatively. The fact that unusual neural properties were not required by our model suggests that the principles and the mechanisms of spatiotemporal coding implemented here may obtain elsewhere, too. Vertebrate olfactory bulb, for example, has many features which, as we describe here, appear to be important for spatiotemporal coding (such as lateral inhibitory connections between periglomerular cells and excitatory-inhibitory loops including periglomerular [or granule] and mitral cells [Shepherd and Greer, 1998]). This analogy leads us to suggest that the vertebrate olfactory bulb may use the temporal dimension to encode olfactory stimuli also, as shown experimentally in zebrafish (Friedrich and Laurent, 2001).

Experimental Procedures

Intrinsic Currents

Each PN and LN was modeled by a single compartment that included voltage- and Ca²⁺-dependent currents described by Hodgkin-Huxley kinetics (Hodgkin and Huxley, 1952). Because no data exist as yet on the biophysical properties of locust antennal lobe LNs and PNs, we used general descriptions borrowed from other cell types with two guiding principles: (1) minimize the number and complexity of ionic currents in each cell type (LN and PN); (2) generate realistic (though simplified) firing profiles. The expressions for voltage- and Ca²⁺-dependent transition rates for all currents are given in the Appendix (below). No attempt was made to produce intrinsic resonant oscillations (pacemaker properties) in LNs or PNs because such properties have never been observed in locust LNs or PNs (Laurent and Davidowitz, 1994; Laurent, 1996).

Synaptic Currents

Fast GABA and nicotinic cholinergic synaptic currents (Laurent, 1996) were modeled by first-order activation schemes (see review in Destexhe et al., 1994b). We found that an additional inhibitory synaptic current was required to accurately model physiological results. Slow GABAergic synapses with a time constant of a few hundred milliseconds were introduced to diminish synchronous high-frequency oscillations in the model network in the tests where fast GABAergic synapses were blocked. Such oscillations have never been observed in vivo when fast GABA currents were blocked, and thus we predict that activation of slow inhibitory receptors contributes to the appearance of slow temporal patterns and also controls network activity when fast inhibition is blocked (MacLeod and Laurent, 1996; Stopfer et al., 1997; MacLeod et al., 1998). In our model, these slow inhibitory receptors could be activated by a long train of LN Ca²⁺ spikes at relatively high frequencies only; their maximal conductances were low so that these receptors did not affect the network oscillations controlled by intact fast GABAergic connections. The rate constants for all synaptic kinetic equations are given in the Appendix.

Network Geometry

In the locust antennal lobe, LNs are synaptically connected to other LNs and to PNs (Leitch and Laurent, 1996). Both LNs and PNs receive direct synaptic input from olfactory receptor neurons (Laurent, 1996).

We simulated three network models: (1) a reciprocal LN-PN pair (Figure 1A); (2) a network of 6 PNs and 2 LNs (Figure 1B); and (3) a network of 90 PNs and 30 LNs (Figure 1C). In the second model, we assumed random (with 0.5 probability) interconnections between PNs (nicotinic), random (with 0.5 probability) connections from PNs to LNs (nicotinic), and reciprocal connections between two LNs (fast GABA) and from LNs to PNs (fast GABA) (each LN was connected with 3 different PNs). In the third model, all interconnections were random with 0.5 probability. This probability is higher than that estimated from experimental data (G.L., unpublished data). However, connection probability should be scaled with the total number of neurons so that the average number of synapses on each neuron does not depend on the size of the network. In a network with a number of neurons close to that of the actual antennal lobe (about 10 times more than in model 3), the probabilities of all interconnections would be reduced by a factor of 10. Note that these estimations are in agreement with the scaling law derived by Golomb and Hansel (2000) for sparse networks. Assuming probability of connections 0.05–0.1 for locust AL (total number of LNs 300 and PNs 900), the probability scaled for our network model (30 LNs and 90 PNs) will be 0.3–0.5. In addition to the fast GABAergic synapses, slow inhibitory receptors were introduced for connections between LNs and PNs (MacLeod and Laurent, 1996). Some of the intrinsic parameters of the neurons in the network were initialized with random variability to ensure robust results. Also, small-amplitude current in the form of Gaussian noise (σ ≈ 10%) was introduced to each cell to achieve random and independent membrane potential fluctuations. We tested different noise levels (σ ≈ 0%–10%) and generally found no difference in the network dynamics. Temporal patterns of the individual neurons, however, were slightly different in simulations with different noise level.

The local field potential (LFP) was calculated in the model as the average membrane potential of all PNs. In experiments with locusts, the LFP was measured in the ipsilateral mushroom body; its oscillations during odor presentations indicated synchrony of PN spiking (Laurent, 1996; Laurent et al., 1996). Thus, the LFP measured in vivo reflected only the action potentials of PNs but did not reflect subthreshold membrane potential fluctuations. Because we used the LFP only as an indicator of synchrony in the network and as a common time reference, its specific shape was not important to our results.

Stimulation

To simulate odor stimulation, 33% of the LNs and PNs, randomly selected, were activated by current pulses. In the antennal lobe, the actual number of LNs and PNs activated by an odor is estimated to be smaller (10%–20%) (Laurent, 1996) but distributed over a network of about 900 PNs and 300 LNs. These simulations, therefore, could be thought to concern a small fraction of the actual network, explaining the relatively high rate of activation. The stimuli were modeled by current pulses with a rise time constant of 100 ms and decay time constant of 200 ms. The current used for each pulse was calculated as the total synaptic current produced by N Poisson distributed spike trains (each with average spike rate μ) arriving at N-independent excitatory synapses. Each glomerulus in the locust AL receives between 100 and 200 axons from olfactory receptors neurons (Laurent, 1996); thus N was set to 200 and μ was varied between 50 and 150 Hz. In this case, random current fluctuations were 5%–10% of its amplitude; lower μ produced slightly higher current fluctuations and vice versa. We used μ = 100 Hz for the simulations presented here to match the membrane potential fluctuations observed in postsynaptic PNs in vivo (see, e.g., Figure 2 in Wehr and Laurent, 1999).

Computational Experimental Procedures

All simulations described in the paper were performed using a fourth-order Runge-Kutta [RK(4)] integration method and, in some cases, an embedded Runge-Kutta [RK6(5)] method (Enright et al., 1995). The time step was 0.04 ms. Source C++ code was compiled on an Intel PC using a GCC compiler (ver. 2.7.2.1). A simulation of 1 s of network activity among 90 PNs and 30 LNs took about 14 min of CPU time.

Phase Analysis

PN voltages were averaged and low-pass filtered with frequency cutoffs at 50 Hz (second-order, Butterworth) to simulate local field potentials (LFPs). PN spike times were converted to phases with respect to the LFP. The positive peaks of the field potential were assigned a phase 0 or 2π, and following or preceding nearest minima were assigned a phase +π or –π, respectively. The phase of each PN spike was calculated relative to the nearest peak of the field potential according to the equation (Laurent et al., 1996):

$${\varphi }_{PNspike}=\left(\frac{t_{PNspike}-t_{lastFPpeak}}{t_{nextFPpeak}-t_{lastFPpeak}}\right)2\pi .$$ (1)

Standard Deviation Calculation

PN spikes times were converted to phases as described above. Standard deviations of spike phases during 20 trials, D_i(k), were calculated for each PN with number i (i = 1,...,N) at each cycle of oscillations k (k = 1,...,K), where N is number of PNs in the network and K is total number of oscillation cycles, depending on the duration of the stimulus. At each oscillation cycle, k, the state of the network was represented by the vector D(k) = D_i(k), i∈[1,N]. A network response for stimulus S was represented by the sequence of points D(k) (k = 1,...,K) in the N dimensional vector space. A Euclidean distance between responses for two different stimuli S1 and S2 at each moment k was calculated as dist(D1(k),D2(k)) = ‖ D1(k) – D2(k) ‖, where $\Vert \mathrm{D}\Vert =\sqrt{(}{\sum }_{i=1}^N{D}_i^2)$.

Cluster Analysis

PN spike train with duration T was divided into nonoverlapping bins of duration τ, and the number of spikes in each bin was counted. This trial was then represented by a vector in n = T/τ dimensional vector space. Repetitive presentations of the same stimulus to the same selected PN produced a set of points in this space and the centroid of this set was calculated. Two different stimuli were used to produce different clusters, each defining a centroid. The Euclidean distances from each trial to the two centroids were then calculated and plotted against each other (as in MacLeod et al., 1998), thus characterizing the effectiveness of a single PN spike train to represent different stimuli. This procedure was repeated for different PNs. Bins between 50 and 200 ms were tested to ensure the results were not dependent on the bin size.

Appendix

The membrane potentials of PN and LN are governed by the equations

$$\begin{array}{cc}\hfill C_m\frac{d{V}_{PN}}{dt}& =-g_L(V_{PN}-E_L)-I_{Na}-I_K-I_A-g_{KL}(V_{PN}-E_{KL})-I_{GAB{A}_A}-I_{slow\text{-}inh}-I_{nACh}-I_{stim}\hfill \\ \hfill C_m\frac{d{V}_{LN}}{dt}& =-g_L(V_{LN}-E_L)-I_{Ca}-I_{K\left(Ca\right)}-I_K-g_{KL}(V_{LN}-E_{KL})-I_{GAB{A}_A}-I_{nACh}-I_{stim}.\hfill \end{array}$$ (2)

The passive parameters are C_m = 1.43 · 10^–4 μF, g_L = 0.021 μS, E_L = –50 mV for LNs and C_m = 1.43 ·10^–4 μF, g_L = 0.021 μS, E_L = –55 mV for PNs.

The leak potassium current is I_KL = g_KL(V – E_KL), where E_KL = –95 mV, g_KL = 1.43 · 10^–3 μS for LNs and g_KL = 5.72 · 10^–3 μS for PNs.

Intrinsic Currents

A fast sodium current, I_Na, a fast potassium current, I_K, a transient Ca²⁺ current, I_Ca, a calcium-dependent potassium current, I_K(Ca), and a transient potassium A current, I_A, are described by the equation

$$I_j^{int}=g_j{m}^M{h}^N(V-E_j),$$ (3)

where the maximal conductances are g_Na = 7.15 μS, g_K = 1.43 μS, g_A = 1.43 μS for PNs and g_Ca = 0.286 μS, g_K(Ca) = 3.58 · 10^–2 μS, g_K = 10 μS, for LNs. For all cells, E_Na = 50 mV, E_K = –95 mV, E_Ca = 140 mV.

The gating variables 0 ≤ m(t), h(t) ≤ 1 satisfy

$$\stackrel{.}{m}=(m_{\infty }\left(V\right)-m)∕{\tau }_m\left(V\right),\stackrel{.}{h}=(h_{\infty }\left(V\right)-h)∕{\tau }_h\left(V\right),$$ (4)

where m_∞(V), h_∞(V), τ_m(V), τ_h(V) are nonlinear functions of V derived from experimental recordings of ionic currents. I_Na, I_K are described in Traub and Miles (1991).

The I_Ca current used for LNs has (Laurent et al., 1993) M = 2, N = 1, m_∞ = 1/(1 + exp(–(V + 20)/6.5)), τ_m = 1 + (V + 30)0.014, h_∞ = 1/(1 + exp((V + 25)/12)), τ_h = 0.3exp((V – 40)/13) + 0.002exp(–(V – 60)/29).

The I_K(Ca) current used for LNs cell has (Sloper and Powell, 1978) M = 1, N = 0, m_∞ = [Ca]/([Ca] + 2), τ_m = 100/([Ca] + 2).

The I_A current used for PNs has (Huguenard et al., 1991) M = 4, N = 1, m_∞ = 1/(1+exp(–(V + 60)/8.5)); τ_m = (0.27/(exp((V + 35.8)/19.7) + exp(–(V + 79.7)/12.7)) + 0.1); h_∞ = 1.0/(1 + exp((V + 78)/6)); τ_h = 0.27/(exp((V + 46)/5) + exp(–(V + 238)/37.5)) if V < –63 mV and τ_h = 5.1 if V > –63 mV.

For all cells Ca²⁺ dynamics is described by a simple first-order model:

$$\frac{d\left[Ca\right]}{dt}=-A{I}_T-(\left[Ca\right]-{\left[Ca\right]}_{\infty })∕\tau ,$$ (5)

where [Ca]_∞ = 2.4 · 10^–4 mM is the equilibrium intracellular Ca²⁺ concentration, A = 2 · 10^–4 mM · cm²/(ms · μA) and τ = 150 ms.

Synaptic Currents

Fast GABA and cholinergic synaptic currents are given by

$$I_{syn}=g_{\text{syn}}\left[O\right](V-E_{syn}),$$ (6)

where the reversal potential is E_nACh = 0 mV for cholinergic receptors and E_GABA = –70 mV for fast GABA receptors. The fraction of open channels [O] is calculated according to the equation

$$\frac{d\left[O\right]}{dt}=\alpha (1-\left[O\right])\left[T\right]-\beta \left[O\right].$$ (7)

For cholinergic synapses

$$\left[T\right]=A\theta (t_0+t_{\text{max}}-t)\theta (t-t_0),$$

and for GABAergic synapses

$$\left[T\right]=1∕(1+exp(-(V\left(t\right)-V_0)∕\sigma )),$$

where θ(x) is the Heaviside (step-) function (Korn and Korn, 1968), t₀ is the time instant of receptor activation, A = 0.5, t_max = 0.3 ms, V₀ = –20 mV, and σ = 1.5. The rate constants, α and β, were α = 10 ms^–1 and β = 0.16 ms^–1 for GABA synapses and α = 10 ms^–1 and β = 0.2 ms^–1 for cholinergic synapses.

The slow inhibitory synaptic current (presumptive metabotropic GABA mediated; see MacLeod and Laurent, 1996) is given by equation (Destexhe et al., 1996; Bazhenov et al., 1998)

$$\begin{array}{cc}\hfill I_{slow-inh}& =g_{slow-inh}\frac{{\left[G\right]}^4}{{\left[G\right]}^4+K}(V-E_K),\hfill \\ \hfill \frac{d\left[R\right]}{dt}& =r_1(1-\left[R\right])\left[T\right]-r_2\left[R\right],\hfill \\ \hfill \frac{d\left[G\right]}{dt}& =r_3\left[R\right]-r_4\left[G\right],\hfill \end{array}$$ (8)

where [R] is the fraction of activated receptors, [G] is the concentration of G proteins, E_K = –95 mV is the potassium reversal potential. The rate constants were r₁ = 0.5 mM^–1ms^–1, r₂ = 0.0013 ms^–1, r₃ = 0.1 ms^–1, r₄ = 0.033 ms^–1, and K = 100 μM⁴.

Peak synaptic conductances were g_GABAA = 0.4 μS between LNs; g_GABAA = 0.8 μS between LNs and PNs; g_slow-inh = 0.015 μS between LNs and PNs; g_nACh = 0.3 μS between PNs and LNs; g_nACh = 0.35 μS between PNs.