Abstract
The only established technique for intracranial pressure (ICP) measurement is an invasive procedure requiring surgically penetrating the skull for placing pressure sensors. However, there are many clinical scenarios where a noninvasive assessment of ICP is highly desirable. With an assumption of a linear relationship among arterial blood pressure (ABP), ICP and flow velocity (FV) of major cerebral arteries, an approach has been previously developed to estimate ICP non-invasively, the core of which is the linear estimation of the coefficients f between ABP and ICP from the coefficients w calculated between ABP and FV. In this paper, motivated by the fact that the relationships among these three signals are so complex that simple linear models may be not adequate to depict the relationship between these two coefficients, i.e., f and w, we investigate the adoption of several nonlinear kernel regression approaches including kernel spectral regression (KSR) and support vector machine (SVM) to improve the original linear ICP estimation approach. The ICP estimation results on a dataset consisting of 446 entries from 23 patients show that the mean ICP error by the nonlinear approaches can be reduced to below 6.0 mmHg compared to 6.7 mmHg of the original approach. The statistical test also demonstrates that the ICP error by the proposed nonlinear kernel approaches is statistically smaller than that estimated with the original linear model (p<0.05). The current result confirms the potential of using nonlinear regression to achieve more accurate non-invasive ICP assessment.
Index Terms: Intracranial pressure, cerebral blood flow velocity, arterial blood pressure, noninvasive, nonlinear kernel regression
I. Introdution
Intracranial pressure (ICP) is a critical physiological variable for managing brain injury patients because acute cerebral diseases frequently lead to a change in ICP [1-4]. It, however, can be only measured by surgically penetrating the rigid skull for pressure sensors placement in either brain tissues or the ventricles. Associated with this invasive procedure are risks of infection and brain tissue damage, which make the measurement infeasible for some patients [5, 6]. It thus remains highly desirable to have a noninvasive ICP (nICP) assessment technique as exemplified by several existing attempts to estimate ICP non-invasively [7, 8]. The early trial for non-invasive ICP estimation is exclusively implemented to monitor ICP for infants having open fontanelles [9], and obviously this approach is not feasible for the elder children or adults. The dynamic magnetic resonance imaging (MRI) technique may be a promising tool for non-invasive ICP estimation, which non-invasively estimates ICP based on the relationship between intracranial elastance and pressure [10, 11]. However, the current MRI scanner is rather complicated and expensive if used for this purpose. Ragauskas proposed a method to estimate ICP using two depth TCDs to monitor blood flow information of eye arteries, and this method does not need the calibration [9]. Communication of the CSF space through the inner ear has also provided another basis and technique for further attempts to measure ICP non-invasively [12]. Because various studies have shown that the change of ICP is not only associated with changes of flow velocity (FV) in the major cerebral arteries but also tightly associated with arterial blood pressure (ABP) waveforms [7, 13-15], the estimation of ICP using ICP related ABP and FV time series is another promising solution. This kind of work includes the data-mining based approach proposed by Hu and the Schmidt's method, which is based on a series of parametric input/output linearly modeling of ABP and FV, and that of ABP and ICP [7, 8].
In the data-mining approach, a simultaneously recorded segment of ABP, FV and invasive ICP is organized as an entry of a signal database containing large number of such entries. Each database entry is used to identify an input/output model for estimating ICP from ABP and CBFV in an offline training phase. In the online running stage, one of those models is then selected to estimate ICP based on the characteristic feature extracted from the input ABP and CBFV. Given this operation, this approach is of local nature in the sense that an optimal input/output model is discovered for different realizations of ABP and CBFV inputted signals on a case-by-case basis. This data-mining framework is highly flexible and complex. Therefore, it needs a large amount of data to achieve good performance but at an enormous computational cost in training the models.
In contrary to this complex data-mining based approach, the other approach developed by Schmidt [7, 8] is of global nature where only one model will result from the training and be applied to all future input signals. In this procedure, two linear models are firstly established to depict the relationship between ABP and ICP and that between ABP and FV, which will result in two vectors of model coefficients f and w, respectively. Then another linear model is learned to map w to f. Utilizing this linear mapping function, non-invasive ICP estimation can be performed by first estimating f from the coefficients w that can be readily obtained from ABP and CBFV. An estimate of ICP can then be derived from ABP using this calculated f. Even though this approach is less flexible than the data mining approach, it has less complexity and received quite amount of clinical attentions [7, 8, 16]. Therefore, it is still meaningful to further improve this approach. In particular, this approach assumes that intracranial pressure dynamic system and cerebral hemodynamic system are coupled so that hemodynamic information as embodied in the coefficient w can be used to infer ICP. However, intracranial pressure dynamics and cerebral hemodynamics are very complex and their coupling is most likely to be nonlinear. Therefore, a linear model of the relationship between w and f may not be adequate [17-20]. Based on the accumulating evidence that non-linear regressions such as support vector machines [21-23], kernel spectral regression [24] have been proved to be more powerful for the prediction problem than the linear ones [25-27], we propose to use the nonlinear approaches to model the relationship between coefficients f and w, which will consequently be helpful to improve the non-invasive ICP estimation.
We describe the nonlinear regression based ICP estimation in Section II, and the patient data set is introduced in Section III. In Section IV, the comparison results among different estimation approaches are given. Section V gives the discussion and conclusion for this paper.
II. Methods
A. Linear approach based non-invasive ICP estimation
In [7, 8], the ICP value at time k can be obtained by n ABP values before k as
| (1) |
where ti (0 ≤ i ≤ n − 1) is time for the ith selected point prior to current time k. Its matrix form is,
| (2) |
where ABP = [ABP(t0), ABP(t1),⋯ABP(tn_1)] and f = [f(0), f(1),⋯f(n − 1)]. Those n points are equally spread over three cardiac cycles before time point k, which means that in this model the current ICP value is determined by ABP over a period of three heart cycles [7, 8]. Apparently, when ABP and ICP have enough samples, the n coefficients can be calculated by solving a linear equation. Considering that each patient's hemodynamic state may be better represented by a linear model in a relatively short time period, data from 14 cardiac cycles was used to estimate this linear model. The linear model within 14 cardiac cycles has a form as the follows [7, 8],
| (3) |
And the least square solution of this equation is,
| (4) |
where is the K ICP values in 14 heart cycles, and with ABPk (0 ≤ k ≤ K) being a vector having n points evenly spread over the three cardiac cycles before time k.
Similar to the linear model between ABP and ICP, a linear model is established to describe the relationship between ABP and FV, where the linear coefficients (w) are called Transcranial doppler (TCD) coefficients [7, 8]. The ABP value at k can be modeled by the m FV values after time point k as,
| (5) |
where ti (0 ≤ i ≤ m − 1) is the selected ith time point after current time k, and this equation implicitly accounts for the physiological fact that blood pressure causes blood flow [7, 8]. These m FV points are evenly distributed within one heart cycle following time point k. The matrix form of this relationship between ABP and FV is,
| (6) |
where FV = [FV(t0), FV(t1), ⋯ FV(tm−1)] and w = [w(0), w(1), ⋯ w(m − 1)]. Consistent with calculation of coefficients between ICP and ABP, TCD coefficients are estimated within 14 heart cycles, too. The least square solution of this model is,
| (7) |
where is the K ABP values within 14 heart cycles, and with FVk(0 ≤ k ≤ K) being a vector with m points evenly spread over one cardiac cycle following time k.
After the above two kinds of coefficients have been calculated, a linear regression is used to model the relationship between f and w as,
| (8) |
With J pairs of {f, w} calculated for different recordings (patients), we can rewrite the above formula as,
| (9) |
where and are the coefficient matrices for ICP and ABP, ABP and FV, respectively. A with dimension of n × m and B with dimension of n × J are the linear coefficients to be estimated from those coefficients W and F, both of which are known from training set. Apparently, A and B can be easily estimated using a least square approach [28].
In this paper, we adopted n=25 and m=6 as those recommended by authors in [8]. To estimate the transform matrices A and B, a training dataset including many recordings of simultaneous ABP, ICP and FV is needed prior to the estimation. With A and B estimated by solving equation (9), after the TCD coefficients w is calculated from non-invasively recorded ABP and FV, the coefficients f between ABP and ICP can be estimated by equation (8) and therefore ICP values can be non-invasively estimated with formula (2).
B. Non-linear regression based approach to estimate coefficients between ICP and ABP
B. 1. Motivation to use non-linear approach
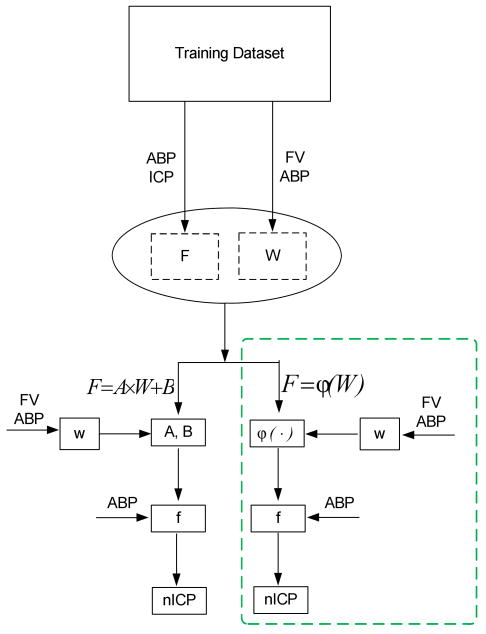
As shown in Section II-A, the key to estimate ICP non-invasively using this approach is the indirect estimation of the coefficients f between ABP and ICP from the TCD coefficients w calculated from ABP and FV by equation (8), which means that the ICP estimation is largely dependent on whether the coefficients f are accurately estimated. In the original approach, the author assumed that the relationship between the TCD coefficients w and coefficients f are linear. However, the physiological association between these two kinds of coefficients may be very complex so that a nonlinear model is more appropriate [17-19]. Accordingly, we propose to use more sophisticated models to estimate the f coefficients from the w coefficients, which may be helpful to improve the quality of estimated ICP. The difference in ICP estimation procedure between using linear model and using non-linear regression model can be succinctly depicted in Fig. 1.
Fig.1.
Block diagrams for the linear/nonlinear noninvasive ICP estimation approaches. The nonlinear approach is highlighted by a green dotted square in the diagram where ϕ(·) is used as a general nonlinear function form.
As seen from Fig.1, the basic flow chart of these two approaches are the same except for the different functions used to estimate the coefficients between ABP and ICP based on the TCD coefficients calculated from ABP and FV.
B.2. Non-linear kernel based regression approaches
Generally, the regression problem can be denoted with this equation [22, 26],
| (10) |
where f(·) is the map function and θ is the noise. If f(·) is linear, it is a linear regression, otherwise the regression problem will be extended to a nonlinear sense. The nonlinear function can be assumed to have different forms, among which the Gaussian function is one of the useful nonlinear realizations [22, 26, 27, 29]. The Gaussian function usually has form as,
| (11) |
After the form of nonlinear function is determined, such kernel regression methods as kernel spectral regression [24], support vector regression [22, 23, 30] can be used to establish non-linear function f(·) to map TCD coefficients w to the coefficients f between ABP and ICP. In this work, we used the KSR and two versions of support vector regressions, i.e., SVM-eplison and SVM-nu, to estimate the possible non-linear function. In the following subsections, we will briefly introduce these nonlinear regression approaches.
B.2.1. Kernel spectral regression
Kernel spectral regression is an extension of original spectral regression. The spectral regression is a recent method for regression or dimension reduction combined with spectral graph analysis and standard linear regression [24]. The main idea of spectral regression is to find a regression model, which has similar predictions yˆi ∈ Y for those inputs xˆi ∈ X that are close to each other. With optimal predictions y = [yˆ1, yˆ)2 ⋯, yˆn], the objective function is [24],
| (12) |
where .
With some mathematical transformation, solution of the objective function (12) can be found by solving this eigen problem [24],
| (13) |
where D is a diagonal matrix with . After solving the eigen-problem in equation (13) to get y, the following norm-2 problem is solved to find the transformation f(·),
| (14) |
When f(·) is linear, it is just the original linear spectral regression, and when f(·) is some non-linear forms, the procedure is the kernel spectral regression. In this work, we adopt the Gaussian (Radial basis function) kernel.
B.2.2. Support vector machine regression
SVM is a supervised approach usually used for classification and regression problems [22, 29]. For nonlinear regression problem, SVM approach performs first a mapping from the input space onto a high-dimensional feature space, and then performs linear regression in the high-dimensional feature space using ε -insensitive loss. SVM approach enables efficient model complexity control using a special structure on a set of high-dimensional linear models in the feature space. For the regression problem denoted by formula (10), dependent on the definition of objective function, the SVM has two implementations, one is the SVM-nu [30] and another is SVM-eplison [21, 22]. The SVM-eplison approach has the following objective function,
| (15) |
where ϕ(xi) is the kernel function, w is the linear hyper plane parameters, ε is the tolerated parameter, ζi, 1 ≤ i ≤ N are the slack variables introduced in SVM to account for those observations having deviation larger than tolerance ε, and C is the regularization parameter to determine the trade-off between the flatness and the amount of deviations larger than tolerance ε. C and ε are two important tunable parameters to be decided before regression for SVM-eplison regression [22, 29].
The objective function for SVM-nu is,
| (16) |
where ν is a parameter correlated with the number of support vector and other parameters including w, ε, ζi, and C are same as those in above SVM-eplison. C and ν are two important tunable parameters and need to be decided before regression when using this kind of SVM for regression [30].
In this work, Gaussian (Radial basis function) kernel was used in both forms of SVM regression as implemented in the LIBSVM toolkit [31].
III. Patient Dataset and Evaluation Protocol
The database used in this work contains data from 9 hydrocephalic and 14 brain injury patients. Each patient had a 5-25 minutes long recording of ABP, ICP and FV. FV was obtained at the right middle cerebral artery, ipsilateral to the ICP measurement location, with ultrasonography transducers fixed to a headband to prevent motion artifacts. ABP was measured through radial arterial-lines while ICP was measured using ventricular catheter connected to an external strain gauge for brain injury patients. A noninvasive tonometric ABP device (Colin Medical Instruments Corp, Model 7000) was used to measure ABP at the radial artery and ICP was invasively measured using the Codman intraparenchymal pressure monitor. The recording of these signals were conducted after IRB approved consents were signed by either the patients or their next-of-kins. All three signals were obtained in analog form from the corresponding monitoring devices and were then simultaneously sampled at 400 Hz using the Powerlab data acquisition system. Each recording was decomposed into short segments of 100 heart beats long, each of which is saved as a database entry. Because the lengths of recordings are different for those 23 patients, the different patient may contribute different number of entries to dataset. The total number of database entries is 446. The value information of ABP, FV and ICP for those patients is listed in Table I.
TABLE I.
The values of ABP, ICP and CBFV included in the database
| NPH(n=9) | SAH(n=14) | n=23 | |
|---|---|---|---|
| ABP [mm Hg] | 105.6±22.1 | 97.2±23.5 | 100.5±22.9 |
| ICP [mm Hg] | 14.8±5.6 | 12.8± 8.3 | 13.6±7.3 |
| CBFV [cm/s] | 64.4±33.7 | 68.2±36.9 | 66.7±34.9 |
In this paper, as the main aim in the following sections is to compare the differences between linear approach and non-linear approaches, we used the same original parameters proposed by authors in [8] to implement non-invasive ICP estimation. The used setup for those parameters have been defined in Section II-A, and the detail about those parameters could refer to [8]. We evaluate the performance of different approaches using leave-one-out strategy. The leave-one-out strategy consists of 23 separate runs for the 23 patients. During every run the samples from the same patient will be regarded as the testing set and the samples from the remaining 22 patients will be used to train the model. For 23 patients, the similar approach will be run for 23 times with different testing and training sets in every run. The parameters of three non-linear approaches as denoted in Section II are simply decided by 80 short segments from the first 4 patients, where the number of entries is 20 for each patient. In this algorithm tuning phase, we still used the leave-one-out strategy to find the optimal parameters. The ‘optimal’ parameters are determined within the predefined searching range to achieve the minimum ICP estimation error for this small tuning dataset with 80 entries. To ensure a relatively optimal parameter, we precisely search the parameters in a relatively local range after the parameters are roughly searched in a relatively wide coarse range, which is the usually adopted strategy in machine learning [29]. Table II lists the parameters used for each nonlinear approach in this paper. After ICP is estimated, nICP was quantitatively compared with original ICP using mean absolute errors,
TABLE II.
Optimal parameters found in the tuning stage for various nonlinear approaches
| Approach | Optimal Parameters | |
|---|---|---|
| SVM-eplison | C | 0.003 |
| ε | 0.003 | |
| SVM-nu | C | 0.001 |
| ν | 0.8 | |
| KSR | T | 15 |
| α | 520 | |
| (17) |
where N is the number of samples.
IV. Results
Table III gives the overall mean EICP for each estimation approach. The paired t test was used to test the null hypothesis that the ICP error as assessed using linear approach is not significantly different from that achieved with the corresponding nonlinear regression based approach. An asterisk is used in Table III to indicate that that the null hypothesis can be rejected at a significance level of 0.05. The statistical results show that the kernel regression based approaches can statistically lower the ICP errors. Table IV lists the EICP corresponding to 25%, 50%, 75% and 90% percentiles, respectively.
TABLE III.
Mean ICP estimation errors for different approaches
| Approach | Linear | SVM-eplison | SVM-Nu | KSR |
|---|---|---|---|---|
| EICP (mean±std) |
6.76±5.39 | 5.98±5.61* | 5.97±5.73* | 5.99±5.49* |
TABLE IV.
ICP estimation errors at different percentiles of different approaches
| 25% (mmHg) |
50% (mmHg) |
75% (mmHg) |
90% (mmHg) |
|
|---|---|---|---|---|
| Linear | 2.83 | 5.56 | 10.02 | 14.44 |
| SVM-eplison | 1.74 | 4.03 | 8.56 | 14.42 |
| SVM-Nu | 1.90 | 4.48 | 8.10 | 14.13 |
| KSR | 1.88 | 4.93 | 7.81 | 13.86 |
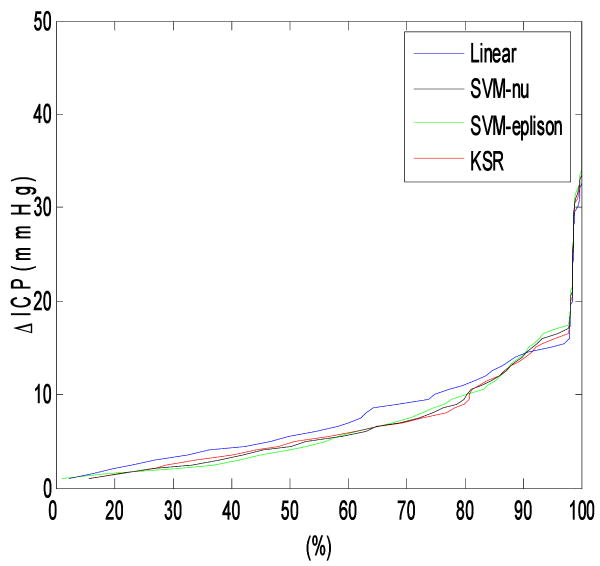
Fig.2 shows the continuous EICP vs ratio curves for these four approaches, and we can see that approximately 90% of results estimated with non-linear approaches have smaller EICP than that of linear approach.
Fig.2.
Percentiles curves for different approaches. The point on the curve means that the x axis defined percent of estimated entries have ICP errors below the value defined by the y component of point. Approximately 90% of the tested database entries have smaller estimation error if nonlinear regression approaches were used to estimate noninvasive ICP.
The 95% confidence limits for the ICP errors are shown in Table V for the four approaches.
TABLE V.
The 95% confidence limit of ICP errors
| Linear | SVM-eplison | SVM-Nu | KSR | |
|---|---|---|---|---|
| 95% confidence limit (mmHg) |
8.38 | 7.68 | 7.59 | 7.61 |
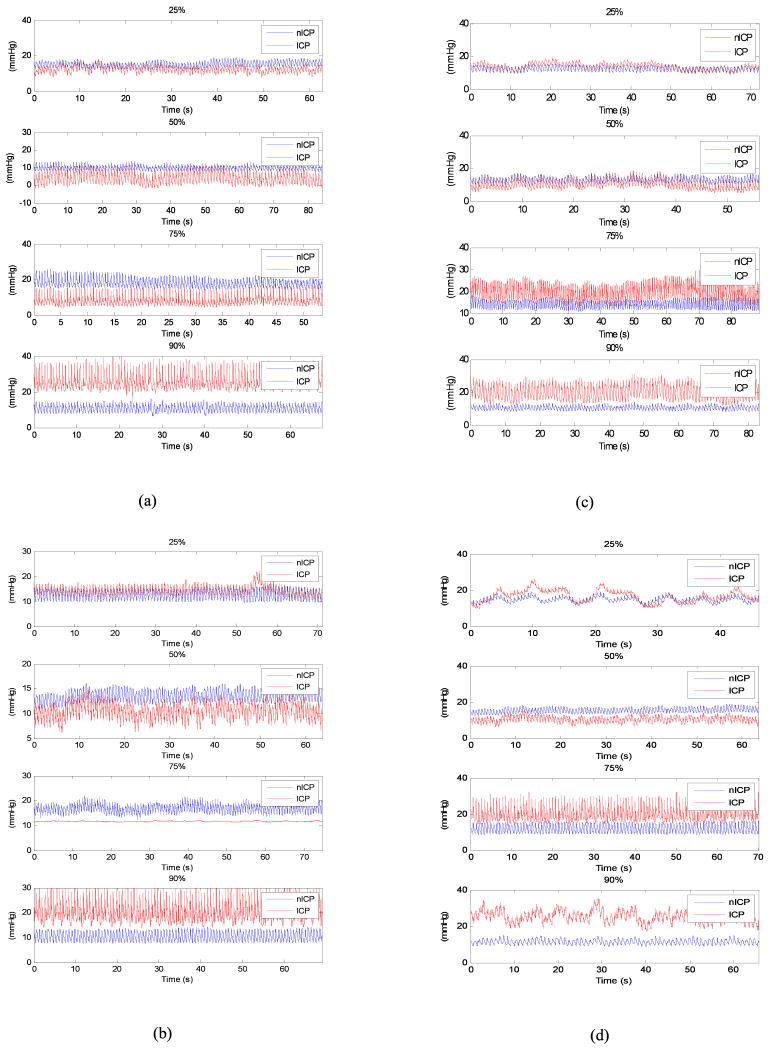
The exemplary ICP waveforms having the error corresponding to different error percentiles in Table IV for different approaches are shown in Fig.3.
Fig.3.
Representative ICP and noninvasive ICP waveforms at different estimation error percentiles in Table IV. The waveform in each subplot denotes the estimation having error mostly close to the corresponding error value in Table IV. (a) linear approach; (b) SVM-eplison regression; (c) SVM-nu regression; (d) KSR regression
V. Discussion
As shown in Table III, the mean absolute ICP errors (<6.00 mmHg) when using non-linear regression approaches are smaller than that (6.76 mmHg) calculated with linear approach in a statistically significant sense (p<0.05). Table IV shows that EICP is smaller than 8.56 mmHg, 8.10 mmHg and 7.81 mmHg for SVM-eplison, SVM-nu, and KSR in 75% of the evaluated recordings, which for the linear approach is 10.02 mmHg. The curves in Fig.2 also indicate that 90% of the recordings have smaller EICP than the original linear approach. Table V consistently revealed that the 95% confidence limits for the three non-linear approaches are smaller than that for the linear approach. The above results did not show too much difference among those three different non-linear approaches, and the reason may be that the non-linear kernel functions for these three regression methods were all realized in Gaussian forms.
The non-invasive ICP estimation procedure in Section II includes three linear models, i.e., the first one to model the relationship between ICP and ABP with coefficients f, the second one to calculate TCD coefficients w to model the relationship between ABP and FV, and the third one to describe the relationship between coefficients f and w. The third model plays a role to map the TCD coefficients w that is non-invasively calculated with ABP and FV to the coefficients f, which is finally used to estimate ICP from ABP non-invasively. Apparently, the quality of f estimated from w directly affects the ICP estimation. The simple linear model may be incapable of adequately capturing the relationship between w and f, and therefore a nonlinear model was proposed as a more accurate alternative in this paper. The results reported in Section IV indeed confirm the feasibility of non-linear regression based approach for a better ICP estimation.
In [7], the author improved the original linear-model-based ICP estimation approach using additional information about the state of cerebral blood flow autoregulation. The enhanced approach in [7] divides the training dataset into two groups: one with good autoregulation and the other with relatively poor autoregulation. These two data sets are then used to obtain two separate copies of matrices A and B. Then during the online running stage, after the efficiency of CBF autoregulation is first quantified by processing ABP and CBFV signals, this autoregulation information is taken into account to estimate a more accurate coefficients f by combining individual f coefficients that are separately obtained from the two sets of A and B matrices. A more accurate estimation of ICP has been confirmed with this enhanced approach. As reported in [7], this enhanced approach can decrease error by an approximate 0.7 mmHg as compared to the original approach, where EICP were 7.6 mmHg and 6.9 mmHg for original linear estimation approach and the enhanced one, respectively. In our results, the nonlinear approach reduced error by 0.8 mmHg, which is similar to what was achieved in [7]. However, this comparison should be treated cautiously because the two approaches were tested on two different datasets.
Among three possible undertakings of non-linearizing the original non-invasive ICP approaches, we only partially chose to build a nonlinear model between f and w. This effort has already been demonstrated effective for improving non-invasive ICP estimation. This result may indicate that the other two linear models used to account for the relationship between ABP and ICP and that between ABP and FV can be potentially replaced with some similar nonlinear models. This future effort is supported by recent findings that the hemodynamic relations among ICP, ABP and FV are more than linear and need more complicated nonlinear methods for their characterization [17-19]. Therefore, utility of nonlinear models to account for the relationships among ABP, ICP and FV may be a choice to further improve the ICP estimation performance. In current work, the nonlinear function is realized in the Gaussian version. Solving the non-linear model is more difficult than the linear cases, and we used the mature kernel regression approaches like SVM and KSR to solve this non-linear problem. Certainly, other nonlinear functions and solving methods can be considered in future.
Compared to the linear model, the training procedure of nonlinear model consumes more computational time. However, the obtainment of this nonlinear model needs to be done only once at the training stage. It will not influence the online running where the computational speed is of a major concern.
It should be emphasized that noninvasive ICP assessment approach is still at an early development stage. The minimum 90% error achieved in this enhanced approach as reported in Table IV is 13.86 mmHg offering a statistically significant improvement over the original linear approach. However, the improvement is not clinically significant and neither of the original and the improved approaches can be recommended for clinical use as a 10% error in terms of mean ICP usually exists in the current invasive ICP devices, which amounts to a tolerable error of 2 mmHg for mean ICP of 20 mmHg. Given that 20 mmHg is usually a threshold for starting treatment of elevated ICP, as far as we know, none of the existing techniques can reliably establish this threshold non-invasively yet. Therefore, the contribution by the improved method proposed in the present work should be appreciated in a relative sense, and the current work shows that the nonlinear regressions are promising for the estimation problem of biomedical signals. However, common to both the original approach and this improved approach is that they are all data-driven. Hence, adequate amount of data is critical. Considering that data from a small set of 23 patients are used in the present work, for those patients having different dynamics far from those patients included in current dataset, it may be difficult to estimate their ICPs accurately. Herein, we expect that a larger and more diverse data set can help significantly improve the absolute performance of noninvasive ICP assessment for both approaches. Because ICP fluctuations for hydrocephalus and TBI patients are due to different physiological origins, CSF circulation for hydrocephalus patients and vasogenic for TBI patients, it needs to point out that it may be a more reasonable manner to treat these two kinds of patients separately, which may give better results. In current work, due to the lack of the corresponding patients to construct the training database, we didn't specifically compare the difference existing between these two kinds of patients. With accumulation of data, we are able to build different databases to deal with the patients under the different pathological conditions such as TBI, hydrocephalus, stroke, etc.
It is still a challenge to monitor ABP and FV accurately, and the uncertainty of ABP and FV data will definitely influence the non-invasive estimation of ICP, which may be part of the reason that current reported non-invasive ICPs are still not clinically accepted. Actually, about 4 mmHg errors will be induced in the current non-invasive ICP recordings [32]. Due to lacking of the gold standard, the invasive ICPs recorded in a clinically established way are still regarded as the referenced signals in this paper and other published works [2, 7, 9, 13, 16]. However, it needs to point out that the use of inaccurate ICPs as the reference signals to evaluate non-invasive approach may be unreasonable. The uncertainties derived from the inaccurate ABP, FV and ICP measurements can be somewhat reduced with the rapid development of the bio-sensors in the near future.
Acknowledgments
The authors would like to thank the anonymous reviewers for their helpful comments to improve this work, and thanks are given to Shaozhi Wu for his help to collect data.
The present work is partially supported by NINDS R21 awards (NS055998, NS055045 and NS059797), a R01 award (NS054881), and NSFC awards (#60701015 and #60736029).
Biographies

Peng Xu received the B.S and Ph.D. degrees in biomedical engineering from the University of Electronic Science and Technology of China (UESTC), Chengdu, China in 2000 and 2006, respectively. He was a postdoctoral at Neural Systems and Dynamics Laboratory, University of California, Los Angeles form 2007.4 to 2009.2. Currently, he works in school of life science and technology, UESTC.
His research interest includes biomedical signal processing, biomedical models, EEG inverse problem and medical image analysis.

Magdalena Kasprowicz was born in Jelenia Gora in Poland in 1976. She received the M.S. and Ph.D. degrees in biomedical engineering from the Wroclaw University of Technology, Poland in 2000 and from Warsaw University of Technology, Poland in 2005, respectively. She is currently on leave from Wroclaw University of Technology in Poland working as a post-doc researcher at UCLA Neurosurgery Neural Systems and Dynamics Laboratory (NSDL).
Her research interests include monitoring, modeling and analysis of intracranial pressure (ICP), arterial blood pressure (ABP) and cerebral blood flow velocity (FV) in patients with hydrocephalus.

Marvin Bergsneider received the B.S. degree in electrical engineering from the University of Arizona, Tucson, in 1983, and the M.D. degree from the University of Arizona College of Medicine, Phoenix, in 1987.
He obtained his neurosurgical residency training at the University of California, Los Angeles (UCLA), where he joined the faculty in 1994, and is currently a Professor of neurosurgery and a faculty member of the UCLA Biomedical Engineering Interdepartmental Program. His current research interests include modeling of intracranial fluid biomechanics and hydrocephalus, and biomicroelectromechanical system (MEMS) development.

Xiao Hu (S'03–M'04) received the B.S. and M.S. degrees from the University of Electronic Science and Technology of China, Chengdu, China, in 1996 and 1999, respectively, and the Ph.D. degree in biomedical engineering from the University of California, Los Angeles, in 2004.
He joined the Division of Neurosurgery, University of California, Los Angeles (UCLA) Medical Center as an Assistant Researcher in 2004 and then as an Assistant Professor in December 2006, where he is currently the Director of the Neural Systems and Dynamics Laboratory (NSDL). His current research interests include biomedical modeling, signal processing, and biomedical informatics.
Contributor Information
Peng Xu, Neural Systems and Dynamics Laboratory, department of Neurosurgery, the David Geffen School of Medicine, University of California, Los Angeles; Key Laboratory for NeuroInformation of Ministry of Education, school of Life Science and Technology, University of Electronic Science and Technology of China, China, 610054.
Magdalena Kasprowicz, Neural Systems and Dynamics Laboratory, department of Neurosurgery, the David Geffen School of Medicine, University of California, Los Angeles; Department of Biomedical Engineering and Instrumentation, Faculty of Fundamental Problems of Technology, Wroclaw University of Technology, Wroclaw, Poland.
Marvin Bergsneider, Neural Systems and Dynamics Laboratory, department of Neurosurgery, the David Geffen School of Medicine, University of California, Los Angeles; Biomedical Engineering Graduate Program, Henry Samueli School of Engineering and Applied Science, University of California, Los Angeles.
Xiao Hu, Neural Systems and Dynamics Laboratory, department of Neurosurgery, the David Geffen School of Medicine, University of California, Los Angeles; Biomedical Engineering Graduate Program, Henry Samueli School of Engineering and Applied Science, University of California, Los Angeles.
References
- 1.Jennett B, Bond M. Assessment of outcome after severe brain damage. Lancet. 1975;1:480–484. doi: 10.1016/s0140-6736(75)92830-5. [DOI] [PubMed] [Google Scholar]
- 2.Czosnyka M, Matta BF, Smielewski P, Kirkpatrick PJ, Pickard JD. Cerebral perfusion pressure in head-injured patients: a noninvasive assessment using transcranial Doppler ultrasonography. J Neurosurg. 1998;88:802–808. doi: 10.3171/jns.1998.88.5.0802. [DOI] [PubMed] [Google Scholar]
- 3.Czosnyka M, Smielewski P, Kirkpatrick P, Laing RJ, Menon D, Pickard JD. Continuous assessment of the cerebral vasomotor reactivity in head injury. Neurosurgery. 1997;41:11–17. doi: 10.1097/00006123-199707000-00005. [DOI] [PubMed] [Google Scholar]
- 4.Oertel M, Kelly DF, Lee JH, McArthur DL, Glenn TC, Vespa P, Boscardin WJ, Hovda DA, Martin NA. Efficacy of hyperventilation, blood pressure elevation, and metabolic suppression therapy in controlling intracranial pressure after head injury. J Neurosurg. 2002;97:1045–1053. doi: 10.3171/jns.2002.97.5.1045. [DOI] [PubMed] [Google Scholar]
- 5.Sherman RW, Bowie RA, Henfrey MME, Mahajan RP, Bogod D. Cerebral haemodynamics in pregnancy and pre-eclampsia as assessed by transcranial Doppler ultrasonography. British Journal of Anaesthesia. 2002;89:687–692. [PubMed] [Google Scholar]
- 6.Kaups KL, Parks SN, Morris CL. Intracranial pressure monitor placement by midlevel practitioners. Journal of Trauma-Injury Infection and Critical Care. 1998;45:884–886. doi: 10.1097/00005373-199811000-00007. [DOI] [PubMed] [Google Scholar]
- 7.Schmidt B, Czosnyka M, Raabe A, Yahya H, Schwarze JJ, Sackerer D, Sander D, Klingelhofer J. Adaptive noninvasive assessment of intracranial pressure and cerebral autoregulation. Stroke. 2003;34:84–89. doi: 10.1161/01.str.0000047849.01376.ae. [DOI] [PubMed] [Google Scholar]
- 8.Schmidt B, Klingelhöfer J, Schwarze JJ, Sander D, Wittich I. Noninvasive prediction of intracranial pressure curves using transcranial Doppler ultrasonography and blood pressure curves. Stroke. 1997;28:2465–2472. doi: 10.1161/01.str.28.12.2465. [DOI] [PubMed] [Google Scholar]
- 9.Ragauskas A, Daubaris G, Dziugys A, Azelis V, Gedrimas V. Innovative non-invasive method for absolute intracranial pressure measurement without calibration. Acta Neurochir. 2005;95:357–361. doi: 10.1007/3-211-32318-x_73. [DOI] [PubMed] [Google Scholar]
- 10.Alperin N. MR-Intracranial Compliance and Pressure: A Method for Noninvasive Measurement of Important Neurophysiological Parameters. Methods in Enzymology. 2004;386:323–349. doi: 10.1016/S0076-6879(04)86016-6. [DOI] [PubMed] [Google Scholar]
- 11.Miyati T, Mase M, Kasai H, Hara M, Yamada K, Shibamoto Y, Soellinger M, Baltes C, Luechinger R. Noninvasive MRI Assessment of Intracranial Compliance in Idiopathic Normal Pressure Hydrocephalus. Journal of Magnetic Resonace Imaging. 2007;26:274–278. doi: 10.1002/jmri.20999. [DOI] [PubMed] [Google Scholar]
- 12.Marchbanks RJ, Reid A, Martin AM, Brightwell AP, Bateman DE. The effect of raised intracranial pressure on intracochlear fluid pressure: three case studies. British Journal of Audiology. 1987;21:127–130. doi: 10.3109/03005368709077785. [DOI] [PubMed] [Google Scholar]
- 13.Hu X, Nenov V, Glenn TC, Bergsneider M, Martin N. A Framework of Noninvasive Intracranial Pressure Assessment via Data Mining of Cerebral Hemodynamic Signals. Biomedical Signal Processing & Control. 2006;1:64–77. [Google Scholar]
- 14.Sidi A, Mahla ME. Noninvasive monitoring of cerebral perfusion by transcranial Doppler during fulminant hepatic failure and liver transplantation. Anesth Analg. 1995;80:194–200. doi: 10.1097/00000539-199501000-00032. [DOI] [PubMed] [Google Scholar]
- 15.Homburg AM, Jakobsen M, Enevoldsen E. Transcranial Doppler recordings in raised intracranial pressure. Acta Neurol Scand. 1993;87:488–93. doi: 10.1111/j.1600-0404.1993.tb04142.x. [DOI] [PubMed] [Google Scholar]
- 16.Schmidt B, Czosnyka M, Schwarze JJ, Sander D, Gerstner W, Lumenta CB, Klingelhofer J. Evaluation of a method for noninvasive intracranial pressure assessment during infusion studies in patients with hydrocephalus. J Neurosurg. 2000;92:793–800. doi: 10.3171/jns.2000.92.5.0793. [DOI] [PubMed] [Google Scholar]
- 17.Hu K, Peng CK, Huang NE, Wu Z, Lipsitz LA, Cavallerano J, Novak V. Altered phase interactions between spontaneous blood pressure and flow fluctuations in type 2 diabetes mellitus: Nonlinear assessment of cerebral autoregulation. Physica a-Statistical Mechanics and Its Applications. 2008;387:2279–2292. doi: 10.1016/j.physa.2007.11.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hu X, Nenov V, Glenn TC, Steiner LA, Czosnyka M, Bergsneider M, Martin N. Nonlinear analysis of cerebral hemodynamic and intracranial pressure signals for characterization of autoregulation. IEEE Transactions on Biomedical Engineering. 2006;53:195–209. doi: 10.1109/TBME.2005.862546. [DOI] [PubMed] [Google Scholar]
- 19.Hu K, Peng CK, Czosnyka M, Zhao P, Novak V. Nonlinear assessment of cerebral autoregulation from spontaneous blood pressure and cerebral blood flow fluctuations. Cardiovascular Engineering. 2008;8:60–71. doi: 10.1007/s10558-007-9045-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ursino M, Lodi CA. A simple mathematical model of the interaction between intracranial pressure and cerebral hemodynamics. Journal of Applied Physiology. 1997;82:1256–1269. doi: 10.1152/jappl.1997.82.4.1256. [DOI] [PubMed] [Google Scholar]
- 21.Lin CJ. Formulations of support vector machines: A note from an optimization point of view. Neural Computation. 2001;13:307–317. [Google Scholar]
- 22.Vapnik VN. Statistical learning theory. New York: Wiley; 1998. [Google Scholar]
- 23.Vapnik VN. An overview of statistical learning theory. IEEE Transactions on Neural Networks. 1999;10:988–999. doi: 10.1109/72.788640. [DOI] [PubMed] [Google Scholar]
- 24.Cai D, He X, Han J. Spectral Regression for Efficient Regularized Subspace Learning. presented at Computer Vision, 2007 ICCV 2007 IEEE 11th International Conference; Rio de Janeiro, Brazil. 2007. [Google Scholar]
- 25.Melgani F, Bazi Y. Classification of electrocardiogram signals with support vector machines and particle swarm optimization. IEEE Transactions on Information Technology in Biomedicine. 2008;12:667–677. doi: 10.1109/TITB.2008.923147. [DOI] [PubMed] [Google Scholar]
- 26.Bates DM, Watts DG. Nonlinear regression analysis and its applications. New York; Chichester: Wiley; 2007. [Google Scholar]
- 27.Yobbi DK, Tampa Bay Water (Fla.) Southwest Florida Water Management District (Fla.) Geological Survey (U.S.) Application of nonlinear least-squares regression to ground-water flow modeling, west-central Florida. Tallahassee, Fla Denver, CO: U.S Dept of the Interior U.S Geological Survey, Branch of Information Services; 2000. distributor. [Google Scholar]
- 28.Kailath T, Sayed AH, Hassibi B. Linear estimation. Upper Saddle River, N.J.: Prentice Hall; 2000. [Google Scholar]
- 29.Smola AJ, Scholkopf B. A tutorial on support vector regression. Statistics and Computing. 2004;14:199–222. [Google Scholar]
- 30.Scholkopf B, Smola AJ, Williamson RC, Bartlett PL. New support vector algorithms. Neural Computation. 2000;12:1207–1245. doi: 10.1162/089976600300015565. [DOI] [PubMed] [Google Scholar]
- 31.Chang CC, Lin CJ. LIBSVM-A library for support vector machines. Available: http://www.csie.ntu.edu.tw/∼cjlin/libsvm/index.html.
- 32.Citerio G, Piper I, Chambers IR, Galli D, Enblad P, Kiening K, Ragauskas A, Sahuquillo J, Gregson B. Multicenter clinical assessment of the Raumedic Neurovent-P intracranial pressure sensor: a report by the BrainIT group. NeuroSurgery. 2008;63:1152–1158. doi: 10.1227/01.NEU.0000335148.87042.D7. [DOI] [PubMed] [Google Scholar]