Voxelwise genome-wide association study (vGWAS)

Abstract

The structure of the human brain is highly heritable, and is thought to be influenced by many common genetic variants, many of which are currently unknown. Recent advances in neuroimaging and genetics have allowed collection of both highly detailed structural brain scans and genome-wide genotype information. This wealth of information presents a new opportunity to find the genes influencing brain structure. Here we explore the relation between 448,293 single nucleotide polymorphisms in each of 31,622 voxels of the entire brain across 740 elderly subjects (mean age±s.d.: 75.52±6.82 years; 438 male) including subjects with Alzheimer's disease, Mild Cognitive Impairment, and healthy elderly controls from the Alzheimer's Disease Neuroimaging Initiative (ADNI). We used tensor-based morphometry to measure individual differences in brain structure at the voxel level relative to a study-specific template based on healthy elderly subjects. We then conducted a genome-wide association at each voxel to identify genetic variants of interest. By studying only the most associated variant at each voxel, we developed a novel method to address the multiple comparisons problem and computational burden associated with the unprecedented amount of data. No variant survived the strict significance criterion, but several genes worthy of further exploration were identified, including CSMD2 and CADPS2. These genes have high relevance to brain structure. This is the first voxelwise genome wide association study to our knowledge, and offers a novel method to discover genetic influences on brain structure.

Introduction

A key goal in imaging neuroscience is to discover specific genetic variants that influence brain structure and function (Glahn et al., 2007a; Glahn et al., 2007b). The dynamic trajectory of brain development and aging throughout life is strongly influenced by genetic factors, and genetic variants have been discovered that increase risk the for Alzheimer's disease (Corder et al., 1993), other mental illness, (Gottesman and Gould, 2003; Meyer-Lindenberg and Weinberger, 2006; Purcell et al., 2009) and even obesity (Frayling et al., 2007; Ho et al., submitted for publication). The goals are both scientific and practical: by selecting those at genetic risk for early treatment, drug trials will be better powered to detect treatment effects (Frisoni et al., in press). A more mechanistic understanding of mental illness will be achieved if gene variants over-represented in patients are studied both at the molecular level and in terms of their effects on brain structure.

Early neuroimaging studies of twins found that several aspects of brain structure are under strong genetic control (Thompson et al., 2001; Posthuma et al., 2002) and that common sets of genes may influence brain structure and cognition (Posthuma et al., 2002). These “first-generation” studies estimated the relative influence of genetic contributions from relatives or family members, based on the expected genetic similarity among different types of relatives. Studies of identical and fraternal twins, and their siblings, have consistently identified heritable aspects of brain structure (Thompson et al., 2001; Styner et al., 2005; Hulshoff Pol et al., 2006; Peper et al., 2007; Schmitt et al., 2008; Brun et al., 2009; Chou et al., 2009). Except for the genotyping necessary to confirm the zygosity of twins in these studies, specific variations at the DNA level are not used in these analyses.

Early studies that use more detailed genotype information focus on specific candidate gene effects on brain structure. Several studies of candidate genes such as APOE, COMT, and BDNF have divided populations into carriers and non-carriers of risk polymorphisms within these genes, and detected systematic differences in brain structure using a standard statistical comparison of two groups (Egan et al., 2001; Pezawas et al., 2004; Hua et al., 2008; Chiang et al., 2009).

More recently, the second generation of studies has used genome-wide scans to search the entire genome for genetic polymorphisms that influence brain structure. In Stein et al. (submitted for publication), a common variant in the GRIN2B glutamate receptor gene was found to be over-represented in Alzheimer's disease and was associated with ~1.5% lower temporal lobe volume per risk allele in the elderly (N=742 subjects; P<5×10⁻⁷). Genome-wide searches have not generally been the most efficient or feasible approach in imaging genetics, as they require large samples of subjects to discover gene effects that survive stringent multiple comparisons corrections for searching over the entire genome. However, several international efforts are now underway to scan genotyped healthy and diseased subjects with the goal of discovering which genetic variants contribute to brain architecture (Thompson and Martin, 2010).

Perhaps surprisingly, no genome-wide study of brain images has used the armory of statistical methods that are now standard in human brain mapping, such as statistical parametric mapping (Friston et al., 1994; Frackowiak, 2004). One study has looked at statistical power for statistical parametric mapping with simulated genome-wide data (Hayasaka, 2009), but no experimental whole-brain whole-genome approach has been implemented to our knowledge. Most twin morphometric studies still break up the brain into subvolumes (Schmitt et al., 2007) and run genetic analysis on the numerical summaries (subvolumes).

By contrast, voxel-based morphometric approaches can make detailed 3D images of volume differences throughout the brain, without the need to specify a priori regions of interest or time consuming manual tracing of anatomy in brain images. These maps of individual differences in brain morphometry make it possible to create detailed maps of gene and environmental effects on the brain, identifying spatially-varying patterns of genetic control that may not be evident if the images were summarized using a few summary indices. Maps of genetic influences on cortical anatomy reveal strong genetic control of frontal anatomy (Thompson et al., 2001), and regionally-varying gene effects (Panizzon et al., 2009). Genetic maps based on tensor-based morphometry suggest that there may be some gradients in the degree of genetic influence, with earlier developing occipital lobe structures showing stronger genetic control than frontal brain regions that mature over a more protracted developmental time-course (Brun et al., 2009; Lee et al., submitted for publication).

Here we extend the notion of statistical parametric mapping, using voxel-based methods, to include genome-wide association (GWAS) data in large populations. The result may be termed voxelwise GWAS (or vGWAS). GWAS is usually applied to study a single trait, such as IQ or the diagnosis of a specific disease, but here it is applied at each location in a brain image. The result is a 3D map of the specific genetic variants that have the greatest statistical effect in accounting for volume variations in each part of the brain, and a method to assess their statistical significance.

Recent advances in neuroimaging and genetics have made it possible, and financially feasible, to scan populations with multi-modality brain imaging and collect genome-wide data (Toga, 2002; McCarthy et al., 2008). The Alzheimer's Disease Neuroimaging Initiative (ADNI) has recently acquired genome-wide genotype data as well as structural MRI scans of 740 subjects (Mueller et al., 2005). This wealth of data is a blessing and a burden: 448,293 genotypes and 31,622 voxels in the brain in each of 740 subjects present powerful and previously unknown spatial and genetic resolution to detect specific variants that influence the brain. However, this vast amount of data requires new ways to deal with the computational load and account statistically for multiple comparisons. A genetic association is usually conducted by performing a linear regression of a phenotype on each genotype of interest, controlling for other confounding variables of no interest. Generally, a genome-wide association study examines only a few phenotypes of interest (Wellcome Trust Case Control Consortium, 2007; Sabatti et al., 2009). When conducting a voxelwise genome-wide association study, each voxel represents a phenotype, so a regression must be run at each voxel and at each SNP (~1.4×10¹⁰ tests), which requires large amounts of computation time (years) if run serially on one computer. Parallelizing this process across a computing cluster can ease the computational burden, giving results in a reasonable amount of time (days). Additionally, by conducting many statistical tests (in this case ~1.4×10¹⁰) on the same dataset, we are highly prone to false-positive findings (Curran-Everett, 2000). Finding a method to determine only those genetic hits that are interesting to pursue without overlooking those with potentially important effects is a difficult question explored further here.

For the first time, we conducted a voxelwise genome-wide association study (vGWAS) in 740 subjects to discover genes influencing brain structure across the entire brain. Each genetic variant identified is a potential candidate with the ability to effect brain structure. If these brain traits lie on the path from genes to disorders that involve the brain (Gottesman and Gould, 2003), they could represent candidates for further study in neurological and psychiatric diseases.

Materials and methods

Sample

Neuroimaging and genetic data were acquired from 818 subjects as part of the Alzheimer's Disease Neuroimaging Initiative (ADNI), a large 5-year study launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies, and non-profit organizations, as a $60 million, public-private partnership. The goal of the ADNI study is to determine biological markers of Alzheimer's disease through neuroimaging, genetics, neuropsychological tests and other measures in order to develop new treatments, monitor their effectiveness, and lessen the time of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, M.D., VA Medical Center and University of California – San Francisco. Subjects were recruited from 58 sites in the United States. The study was conducted according to the Good Clinical Practice guidelines, the Declaration of Helsinki, and U.S. 21 CFR Part 50—Protection of Human Subjects, and Part 56—Institutional Review Boards. Written informed consent was obtained from all participants before protocol-specific procedures were performed. All data acquired as part of this study are publicly available (http://www.loni.ucla.edu/ADNI/).

All subjects underwent thorough clinical and cognitive assessment at the time of scan acquisition to determine diagnosis. The mini-mental state exam (MMSE) was administered to provide a global measure of mental status (Cockrell and Folstein, 1988). The clinical dementia rating (CDR) was used to assess dementia severity (Morris, 1993). Healthy volunteer status was determined through MMSE scores between 24 and 30 (inclusive), a CDR of 0, non-depressed, non-MCI, and non-demented. MCI diagnosis was determined by MMSE scores between 24 and 30 (inclusive), a memory complaint, objective memory loss measured by education adjusted scores on the Wechsler Memory Scale Logical Memory II, a CDR of 0.5, absence of significant levels of impairment in other cognitive domains, essentially preserved activities of daily living, and an absence of dementia. Diagnosis of AD was made according to NINCDS-ADRDA criteria for probable AD (McKhann et al., 1984), MMSE scores between 20 and 26 (inclusive), and CDR of 0.5 or 1.0.

Population stratification is a known problem in genetic association analyses, which can produce false-positive or false-negative results (McCarthy et al., 2008). When multiple subpopulations are present in the data (population stratification), spurious associations (or lack of associations) can result from allele frequency differences between populations rather than associations with the phenotype (Lander and Schork, 1994). 818 subjects were genotyped as part of the ADNI study. However, only unrelated Caucasian subjects (non-Hispanic; N=740) identified by self-report and confirmed by MDS analysis (see Stein et al., submitted for publication) were included to reduce population stratification effects. Volumetric brain differences were assessed in 173 AD patients (78 female/95 male; mean age±standard deviation=75.54±7.66), 361 MCI subjects (130 female/231 male; 75.16±7.29), and 206 healthy elderly subjects (112 male/94 female; 76.13±4.94). The genome-wide analyses were not split into diagnostic groups as the goal was to present as broad a phenotypic continuum (Petersen, 2000) as possible, to provide the highest power to detect genetic associations.

MRI analysis methods

3D T₁-weighted baseline brain MRI scans were analyzed using tensor-based morphometry (TBM) as detailed in a previous study (Hua et al., 2008). Briefly, high-resolution structural brain MRI scans were acquired at 58 ADNI sites with 1.5 T MRI scanners using a sagittal 3D MP-RAGE sequence developed for consistency across sites (Jack et al., 2008) (TR=2400 ms, TE=1000 ms, flip angle=8°, field of view=24 cm, final reconstructed voxel resolution=0.9375× 0.9375×1.2 mm³). Images were calibrated with phantom-based geometric corrections to ensure consistency across scanners. Additional image corrections included (Jack et al., 2008): (1) correction of geometric distortions due to gradient non-linearity, (2) adjustment for image intensity inhomogeneity due to B1 field non-uniformity using calibration scans, (3) reducing residual intensity inhomogeneity, and (4) geometric scaling according to a phantom scan acquired for each subject to adjust for scanner- and session-specific calibration errors. Images were linearly registered with 9 parameters to the International Consortium for Brain Imaging template (ICBM-53) (Mazziotta et al., 2001) to adjust for differences in brain position and scaling.

For TBM analysis, the protocol was identical to that of a prior study analyzing the clinical correlates of temporal lobe atrophy (Hua et al., 2008) in a smaller population; since then, genome-wide genotype data was collected. First, a minimal deformation template (MDT) was created for the healthy elderly group to serve as an unbiased average template image to which all other images were warped using a nonlinear inverse-consistent elastic intensity-based registration algorithm (Leow et al., 2005). Volumetric tissue differences were assessed at each voxel in all individuals by calculating the determinant of the Jacobian matrix of the deformation, which encodes local volume excess or deficit relative to the mean template image. The map of volumetric tissue differences were then down-sampled using trilinear interpolation to 4×4×4 mm³ isotropic voxel resolution for computational efficiency. This percentage volumetric difference relative to a population-based brain template at each voxel served as a quantitative measure of brain tissue volume difference for genome-wide association.

DNA isolation and SNP genotyping methods

DNA was isolated from B lymphocytes cells taken from blood (Neitzel, 1986) and extracted (Lahiri et al., 1992) using standard procedures. 7 ml of EDTA blood was extracted using the QIAamp DNA Blood Maxi Kit (Qiagen, Inc., Valencia, CA). Samples were processed according to the manufacturer's protocol. Genomic DNA samples were analyzed on the Human610-Quad BeadChip (Illumina, Inc. San Diego, CA) according to the manufacturer's protocols (Infinium HD Assay; Super Protocol Guide; Rev. A, May 2008). Before initiation of the assay, 50 ng of genomic DNA from each sample was examined qualitatively on a 1% Tris-acetate-EDTA agarose gel for visual signs of degradation. Any degraded DNA samples were excluded from further analysis. Samples were quantitated in triplicate with PicoGreen® reagent (Invitrogen, Carlsbad, CA) and diluted to 50 ng/µl in Tris-EDTA buffer (10 mM Tris, 1 mM EDTA, pH 8.0). 200 ng of DNA was then denatured, neutralized, and amplified for 22 h at 37 °C (this is termed the MSA1 plate). The MSA1 plate was then fragmented with FMS reagent (Illumina) at 37 °C for 1 h and then precipitated with 2-propanol and incubated at 4 °C for 30 min. The resulting blue precipitate was then resuspended in RA1 reagent (Illumina) at 48 °C for 1 h. The samples were then denatured (95 °C for 20 min) and immediately hybridized onto BeadChips at 48 °C for 20 h. BeadChips were then washed and subjected to single base extension and staining. Finally, the BeadChips were coated with XC4 reagent (Illumina), dessicated, and imaged on the BeadArray Reader (Illumina).

Genetic analysis

Genome-wide genotype information was collected at 620,901 markers. Multiple types of genetic variants were genotyped, but only Single Nucleotide Polymorphisms (SNPs) were included in this analysis. Alleles on the forward strand are reported. Individual markers were excluded from the analysis that did not satisfy the following quality criteria based on previous genome-wide association studies (Wellcome Trust Case Control Consortium, 2007): genotype call rate <95% (42,670 SNPs removed), significant deviation from Hardy–Weinberg equilibrium P<5.7×10⁻⁷ (871 markers removed), minor allele frequency <0.10 (161,354 SNPs removed), and a platform-specific recommended quality control score of <0.15 (variable number of SNPs removed across subjects). A minor allele frequency cut-off of 0.10 (10%) was used to ensure that sufficient numbers of subjects would be found in our sample in each genotypic group (homozygous major allele, heterozygous, homozygous minor allele) using an additive genetic model. If alleles are in Hardy–Weinberg equilibrium, a minor allele frequency cut off of 0.10 ensures that at least 7 subjects are in the smallest genotypic category. If this cut-off is not imposed, there is a risk of findings being driven by a small number of subjects in the sample, which may be less robust to sampling effects. 448,293 SNPs remained for analysis after quality control. Missing data still occurs over these remaining SNPs, but after filtering >95% of the subjects must have a successfully genotyped SNP for it to be included.

Association was conducted using a modified version of the Plink software package (Purcell et al., 2007) (version 1.05; http://pngu.mgh.harvard.edu/purcell/plink/) to conduct a genome-wide association at each of 31,622 voxels within a whole-brain mask of the MDT across all 740 subjects. At each voxel, a regression was conducted at each SNP with the number of minor alleles, age, and sex as the independent variables and the quantitative phenotype (percentage volume difference relative to a subject specific template at each voxel) as the dependent variable, assuming an additive genetic model. To simplify and condense the large results (~140 MB) output at each voxel, the open-source Plink software was modified to only output the identifier and P-value of the most associated SNP (21 bytes). Each genome-wide regression required ~9 min of computation time, so the process was split for parallel computing across 300 cluster nodes using the Laboratory of Neuro Imaging (LONI) pipeline (http://pipeline.loni.ucla.edu/). The total computation time was approximately 27 h.

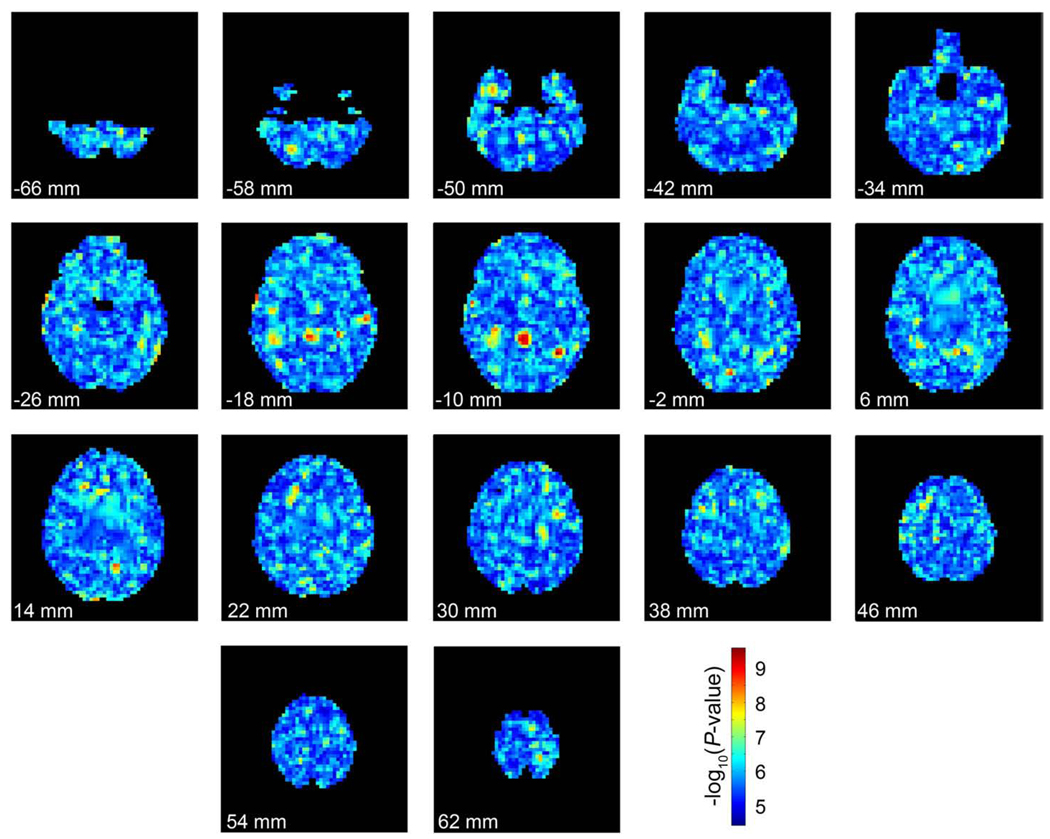
An additional analysis was performed to determine if spatial clustering of P-values occurred in a null map. Though a calculation of an extensive permutation distribution was not feasible, we conducted one permutation to get an idea of how the data on top (most significant) SNPs might look in a null distribution. The genomes, sex, and age were randomly swapped among subjects and the same analysis as above was run again. The output from this analysis is shown in Fig. 5.

Fig. 5.

The significance of the most strongly associated SNP at each voxel in a single permuted dataset. Each image represents slices through the brain at 8 mm intervals from inferior to superior. The top of the page represents anterior of the brain and the bottom of represents posterior. The images are in radiological convention (left of the image is the right side of the subject). Each voxel is colored by the –log₁₀ of the P-value of the genetic association at each point (warmer colors are more strongly associated). The same color scale is used from Fig. 4 for comparisons. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Genes and ESTs (expressed sequence tags) in close proximity to significant SNPs were localized through the UCSC genome browser (Kent et al., 2002) (http://genome.ucsc.edu/) and are reported in Table 2. Additionally, gene functions and known associations with disease were reviewed using the gene ontology information from the Entrez Gene (http://www.ncbi.nlm.nih.gov/sites/entrez?db=gene) database.

Table 2.

The top 20 most associated SNPs organized by minimum P-value at any voxel. The identifier of each SNP is shown with its minor allele frequency (MAF), and the number of subjects in each genotype group (homozygous major allele, Maj; heterozygous, Het; homozygous minor allele, Min). Note that the number of subjects ineach genotype group may not add up to the total number of subjects (740) if data is missing for that SNP in some subjects. The volume of all the voxels where this SNP was the most associated SNP is shown in the Volume (mm³) column. Minimum P-value gives the raw P-value at the most associated voxel where this SNP was a winner. Mean P-value gives the mean P-value of association across all voxels where it is the winning SNP. Additionally, the gene or expressed sequence tag (EST) within 50 kb is shown, where bold typeface indicates that the SNP is located in the gene or EST.

Chr	Base Pair	SNP	MAF	Number of subjects in genotype groups			Volume (mm3)	Minimum P-value	Mean P-value	Gene or EST (± 50 kb)
				Maj	Het	Min
6q16.2	99778735	rs2132683	0.3257	340	318	82	4224	2.56×10−10	1.01×10−6
6q15	91474473	rs713155	0.3966	274	345	121	7296	3.11×10−10	5.08×10−7
1p35.1	34020651	rs476463	0.1203	567	168	5	1472	3.18×10−10	1.27×10−6	CSMD2
7q31.32	121989829	rs2429582	0.3417	319	331	86	2496	4.23×10−10	6.46×10−7	CADPS2
3p21.31	46314816	rs9990343	0.4811	197	374	169	2048	5.34×10−10	4.41×10−7
11q23.3	115803577	rs490592	0.2149	450	255	29	14528	1.39×10−9	1.32×10−6
20q13.12	43557937	rs11696501	0.1935	480	232	27	768	1.41×10−9	8.54×10−7	WFDC2, SPINT3
3p12.1	84563758	rs10511089	0.1095	589	140	11	1664	1.79×10−9	6.57×10−7
8q23.1	108858992	rs4534106	0.3007	367	301	72	1984	2.27×10−9	1.00×10−6	BG436399
6q12	67705937	rs11970254	0.3464	293	358	72	1024	2.29×10−9	6.21×10−7
9p13.1	38030095	rs7025303	0.4061	263	347	124	768	2.30×10−9	1.21×10−6	SHB
1p36.13	19441559	rs710865	0.3824	277	354	103	256	2.65×10−9	1.10×10−7	KIAA0090, MRT04, AKR7L
9p13.1	38031142	rs7873102	0.3821	283	340	109	832	2.96×10−9	6.42×10−7	SHB
20p12.1	12822585	rs2073233	0.4291	234	369	131	2560	3.17×10−9	1.42×10−6	BC036700
2q37.3	242151629	rs12479254	0.4049	255	341	119	1408	3.88×10−9	5.70×10−7	BOK, THAP4
16p12.1	24439219	rs11643520	0.1160	574	146	11	1920	4.39×10−9	6.06×10−7	RBBP6
5p12	44222425	rs4296809	0.1448	539	177	17	12736	4.41×10−9	8.75×10−7	BG334794
13q32.2	97764318	rs688872	0.3804	283	345	106	3392	4.68×10−9	1.06×10−6	FARP1
14q22.1	51080549	rs7140150	0.4566	219	353	160	1856	5.78×10−9	4.77×10−7	FRMD6
6p12.3	49596867	rs9473582	0.3973	274	339	121	4416	5.98×10−9	8.25×10−7	GLYATL3

Determination of statistical threshold

Selecting only the P-value for the most highly associated SNP at each voxel does not give, in the null case, a usual uniform distribution of P-values from which to calculate the corrected significance of the findings. Because we are using only the minimum P-value from a set of tests of each of the genetic markers, we must find the appropriate type of null distribution to use in this situation. If n independent random variables X₁, X₂, …, X_n are uniformly distributed on the unit interval [0,1], the minimum of these variables follows the probability density function (Ewens and Grant, 2001):

$$f_{min}(x)=n{(1-x)}^{n-1}.$$

The PDF derived above f_min(χ) is a Beta distribution with parameters α=1 and β=n. At each voxel then, the null distribution for the P-value of the most strongly associated SNP across n independent genomic markers (the minimum P-value) approximately follows a Beta(1, n) distribution.

It is well known, however, that all genomic markers are not independent (Frazer et al., 2007). Genetic variation is often inherited in contiguous segments of DNA, such that there tends to be correlation between the inheritance of alleles at markers close to each other on the same chromosome. This genetic correlation is called linkage disequilibrium (LD), and, as a result, the effective number of independent tests (M_eff) conducted is less than the total number of markers (M). By effective number of tests, we mean the number of independent tests that would have to be conducted to lead to a null distribution for the minimum P-values that was approximately the same as that obtained when conducting tests that are necessarily correlated due to LD.

To estimate the effective number of tests conducted as part of the study, simpleM (https://dsgweb.wustl.edu/rgao/) was used (Gao et al., 2008; Gao et al., 2010). This program first derives the composite LD structure between SNPs, calculates eigenvalues through principal component analysis on the composite LD matrix, and sets M_eff equal to the number of principal components required to jointly explain 99.5% of the variance in the SNPs. This process has been verified to give M_eff estimates similar to those derived from a gold-standard permutation-based null distribution when applied to several commonly used SNP chips (Gao et al., 2010).

SimpleM requires that there must be no missing genotype information. Therefore, it was necessary to perform imputation of the genetic data prior to M_eff analysis. Imputation was done using Mach (version 1.0; http://www.sph.umich.edu/csg/abecasis/MaCH/index.html) to infer the phase of the haplotype and automatically impute missing genotypes (Li et al., 2009). The parameters of Mach were set to 50 iterations of the Markov Sampler and 200 haplotypes considered when updating each individual. Each chromosome was imputed separately. Imputation was not conducted for sex chromosomes or for mitochondrial DNA. SimpleM was used on the imputed dataset, and the resulting M_eff estimates are presented in Table 1. M_eff was set to be equal to M for sex chromosomes and mitochondrial DNA as the use of simpleM in this context has not been verified (Gao et al., 2008; Gao et al., 2010).

Table 1.

Number of SNPs measured and the effective number of tests (M_eff) on each chromosome. The effective number of tests was not estimated in sex chromosomes or for mitochondrial DNA, where the effective number of tests was set to be equal to the number of SNPs measured in those regions, rather than a smaller number. This is the most conservative estimate. Chromosome XY refers to SNPs on both the X and Y chromosomes.

Chr	Number of SNPs	Meff
1	33,850	20,205
2	36,384	21,747
3	30,765	18,275
4	27,072	15,972
5	27,396	16,245
6	30,054	16,669
7	24,446	14,680
8	24,768	14,710
9	21,283	13,231
10	23,089	13,806
11	21,796	13,066
12	21,461	12,787
13	16,605	9809
14	14,501	8916
15	13,355	8557
16	13,460	9111
17	11,721	7764
18	13,198	8232
19	7,895	5425
20	11,169	7148
21	6,582	4193
22	6,757	4341
X	10,637	10,637
Y	12	12
XY	25	25
Mitochondrial	12	12
Total	448,293	275,575

The effective number of tests was estimated to be 275,575, which is markedly reduced from the 448,293 markers directly measured in this experiment. A comparable reduction was reported by (Gao et al., 2010). We therefore chose to model the null distribution as Beta(1, 275575). Because the inter-SNP correlation depends on the number and density of SNPs examined, this distribution would need to be re-estimated for new types of genomic data, for instance if a chip with a different density were used (e.g., 1 million SNPs). To determine how well the analytic Beta distribution derived above fits the observed data, a histogram of the observed distributions is compared to PDF of the theoretical distribution in Fig. 1. Both distributions are compared directly in a Q–Q plot. The theoretical distribution fits the observed data well for the most part.

Fig. 1.

The theoretical and observed distributions of the minimum P-value across voxels. (a) The normalized histogram of the observed minimum P-values is shown. Lines represent the PDF of the Beta(1, 275575) distribution (solid line) based on M_eff and the Beta(1, 448293) distribution (dashed line) based on the number of measured markers. (b) The Q–Q plot shows the observed P-values plotted against those expected from the Beta(1, 275575) (blue dots). The black line gives a purely null distribution. The observed data matches well with that expected by the M_eff based null distribution. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

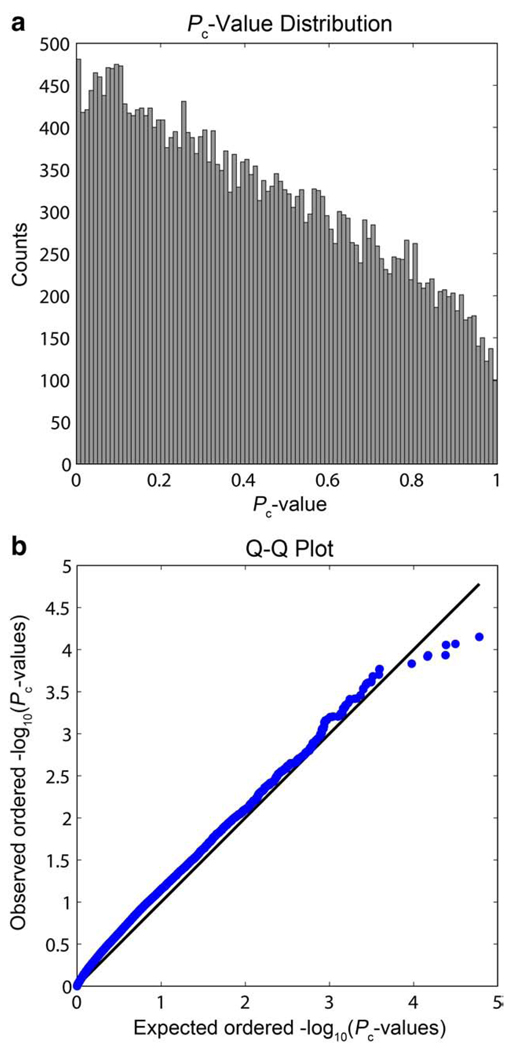
Based on the theoretical distribution of the minimum P-value from all genetic markers, the P-values from the empirical studies were then “corrected” through the cumulative distribution function (CDF) of the derived beta distribution. By adjusting the data using the CDF of the theoretical distribution, common corrections for multiple comparisons may be used on the “corrected” P-values (P_c-values). The False Discovery Rate (FDR) correction for multiple comparisons (Benjamini and Hochberg, 1995) is reliant on receiving data that has a null P-value distribution that is uniform on the interval [0,1] (Dabney and Storey, 2006). The minimum P-value distribution above clearly does not meet that criterion, but the P_c-value data at least approximately does, as shown in the histogram and quantile–quantile plot of the P_c-value distribution (Fig. 2).

Fig. 2.

A histogram and quantile–quantile plot for the “corrected” P-values (P_c-values). (a) The histogram shows the P_c-values approximately follow a uniform distribution. (b) The Q–Q plot shows the expected ordered −log₁₀(P_c-values) as drawn from a uniform distribution plotted against the observed ordered −log₁₀(P_c-values) as blue dots. The black line shows the null distribution. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

False discovery rate correction for multiple comparisons

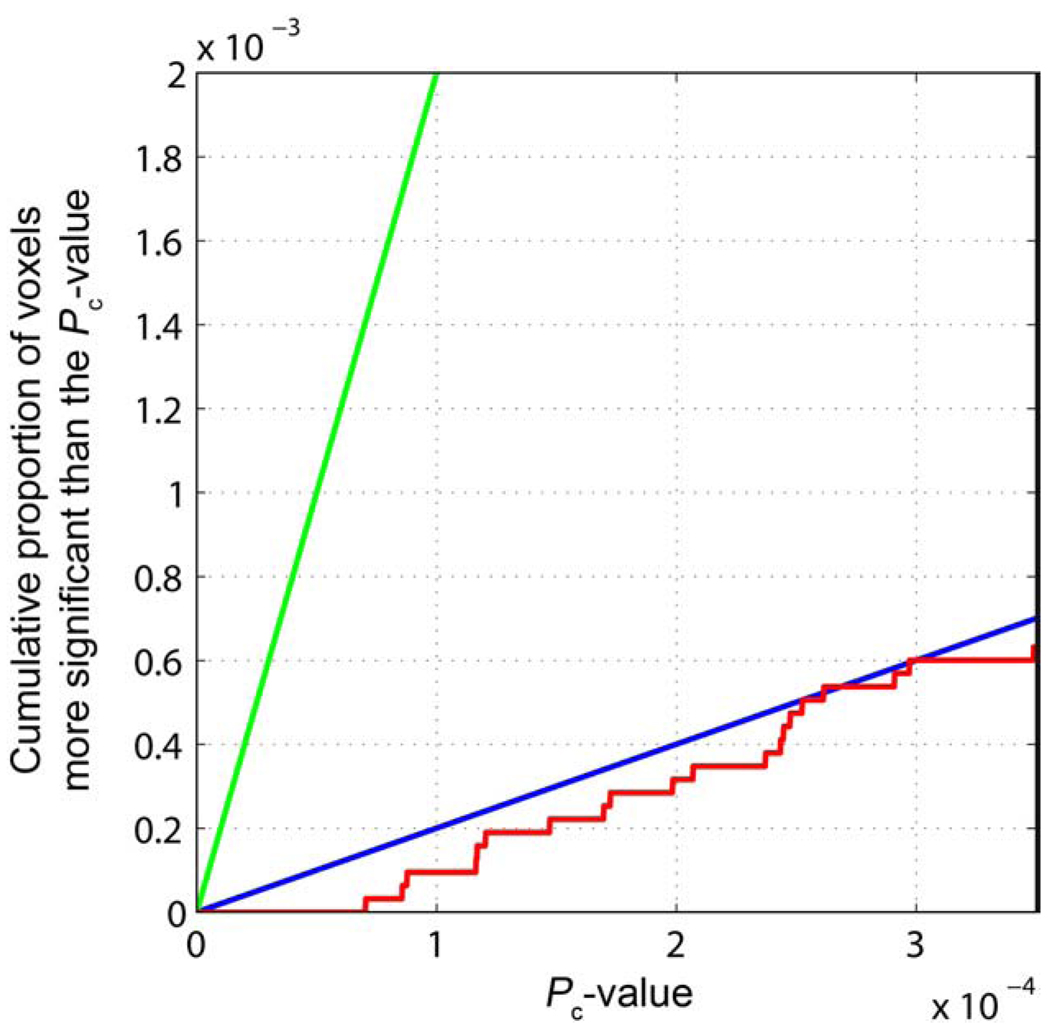
Following correction of the raw P-values, a False Discovery Rate (FDR) correction for multiple comparisons may be used to estimate if there is a statistical threshold that can be applied to the maps that controls the expected rate of false-positives at a nominal rate (usually 5%) among all rejected hypotheses (Benjamini and Hochberg, 1995; Genovese et al., 2002). The FDR method for multiple comparisons correction is especially suitable for exploratory analyses like those presented here where we search for genes affecting brain structure (Storey, 2003). Here we set the FDR to q=0.05, so that, on average, 95% of voxels declared significant are true positives. The maps show that our data can only be thresholded at a level that gives a false discovery rate of roughly 50%, and no statistical threshold controls the FDR at the conventional q=0.05 level (Fig. 3).

Fig. 3.

The cumulative distribution function of corrected P-values. The cumulative distribution function of P_c-values is shown (red) with two lines representing thresholds of q=0.50 (blue), and q=0.05 (green). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The original FDR method (Benjamini and Hochberg, 1995) assumes that the data for each test is statistically independent and the P-values are sampled from a uniform [0,1] distribution (Dabney and Storey, 2006). The data are not statistically independent as the genomic structure has linkage disequilibrium, or correlation between markers, and the neuroimaging data also has spatial smoothness. If the data have a “positive regression dependency”, i.e., the test statistics of the regression are positively correlated, the Benjamini– Hochberg procedure controls the FDR successfully (Benjamini and Yekutieli, 2001). This is most likely a valid assumption for neuroimaging and genetic data (Genovese et al., 2002; Storey and Tibshirani, 2003).

The original FDR method (Benjamini and Hochberg, 1995) is the most conservative of FDR methods in that it will always control the number offalse-positives among rejected hypothesesat the specified q-level, given independence of the data and sampling from a uniform distribution when null. Given added assumptions, though, several alternative FDR methods may be used to correct for multiple comparisons, and can give less conservative estimates of significance (Pounds, 2006). The positive False Discovery Rate (pFDR) is a modification of FDR, conditioningon one finding positive finding having occurred (i.e., one null hypothesis being rejected) (Storey, 2003). The pFDR method is implemented inthe R statistics program (http://www.r-project.org/; Version 2.8.1) as the “q-value” package (Version 1.20.0), used here to calculate the q-values according to the pFDR method.

Several alternative methods have been proposed to correct empirical data to fit the assumptions of the FDR method (Leek and Storey, 2008), or to correct the FDR assumptions to fit the non-independence of the data (Li and Ji, 2005).

Estimation of sample size needed for replication

To estimate how many subjects would be needed to replicate the finding that these genetic variants are associated with brain structure conditional on the dataset, we used a re-sampling approach. The most associated voxel for each of the 5 most significantly associated SNPs (see Table 2) was used as an example phenotype. For each SNP, three subjects, one from each diagnostic category (AD, MCI, and healthy control), were randomly picked and removed from the analysis and the P-value for each of the significant SNPs was calculated at the most associated voxel. The process was repeated until no more subjects remained in the diagnostic category with the least number of subjects (165AD subjects). Toestimate confidence intervals for this estimate, the resampling was repeated 1000 times. 95% confidence intervals were based on the 2.5th and 97.5th percentiles of the resampled distribution.

Results

Voxelwise GWAS results

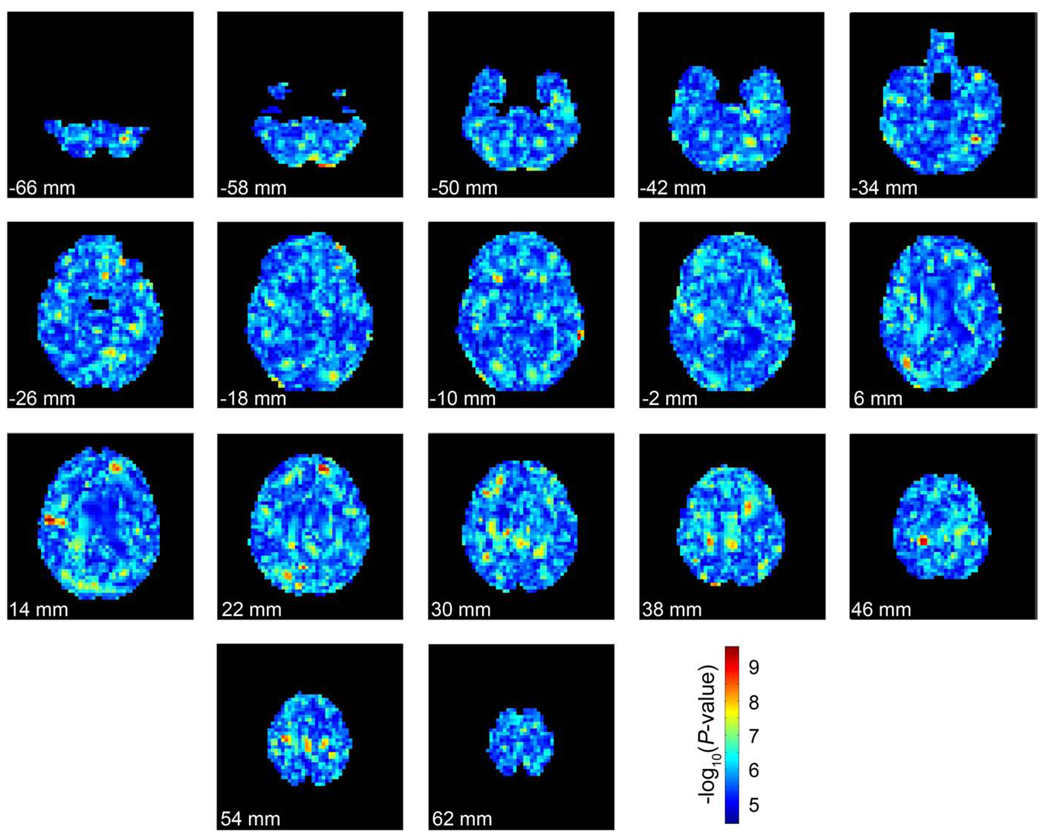
Maps of the significance level at each voxel for the most associated SNP within that voxel were recorded and displayed in Fig. 4. There are spatially contiguous hot spots of significant association, with a “raw” minimum P-value of 2.56×10⁻¹⁰ (P_c-value=7.05×10⁻⁵) across the entire brain. There is a certain amount of spatial clustering because all voxels are not independent so some spatial clustering is expected even if the null hypothesis were true. To get an approximation of how much spatial clustering is expected by chance, Fig. 5 shows the minimum P-values in each voxel after the genomes have been randomly assigned to each subject. A certain amount of clumping is expected when top SNP maps are made from null data. One source of spatial coherence in these maps is that they are based on smooth maps of volumetric differences computed using tensor-based morphometry, which uses nonlinear image registration of each subject's imaging data to a template. These methods generate spatially smooth maps of volume differences, where the level of smoothness is dependent on the form of the regularizer (Laplacian, elastic, fluid, etc.) and also on the spatial resolution of the numerical grid used to solve the differential equations whose solution is the deformation field. In our approach, the elastic regularizer is decomposed into its eigenfunctions so that the warping fields can be computed using a Fast Fourier transform. Because these deformation fields are smooth, so are averages and differences of their Jacobian (gradient) maps, and so are the resulting statistical maps. In the future, it may be interesting to see if there is more latent structure or anatomical coherence in the top SNP maps than would be otherwise expected if the data were completely null. Even so, there may be relevant genes that influence brain structure but are never the top SNP in a map of this kind. If so, their effects might be more spatially distributed (coherent) without ever being represented in a top SNP map. Given this, clearly extensions of vGWAS might be proposed that emphasize the total extent, or cluster size, as well as the peak height of the association P-values, a tactic that can be more powerful than a peak height or maximum statistic (top SNP) test for detecting subtle but distributed effects of weak effect size in statistical parametric maps.

Fig. 4.

The significance of the most associated SNP at each voxel. Each image represents slices through the brain at 8 mm intervals from inferior to superior. The top of the page represents anterior of the brain and the bottom of represents posterior. The images are in radiological convention (left of the image is the right side of the subject). Each voxel is colored by the –log₁₀ of the P-value of the genetic association at each point (warmer colors are more strongly associated). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The voxelwise GWAS showed 8,212 unique SNPs which were most associated at each voxel. In other words, if the “winning SNP” was picked for each voxel, the same SNP was picked over spatially coherent regions. There does not appear to be a great deal of hemispheric symmetry in the spatial distribution of the “winning” SNP at each voxel (Fig. 6). However, the SNPs presented here do have an effect on brain volume beyond the most highly associated voxels shown. The 20 “top” SNPs with the most significant association to any voxel are shown in Table 2. The most significant SNPs were found in several genes.

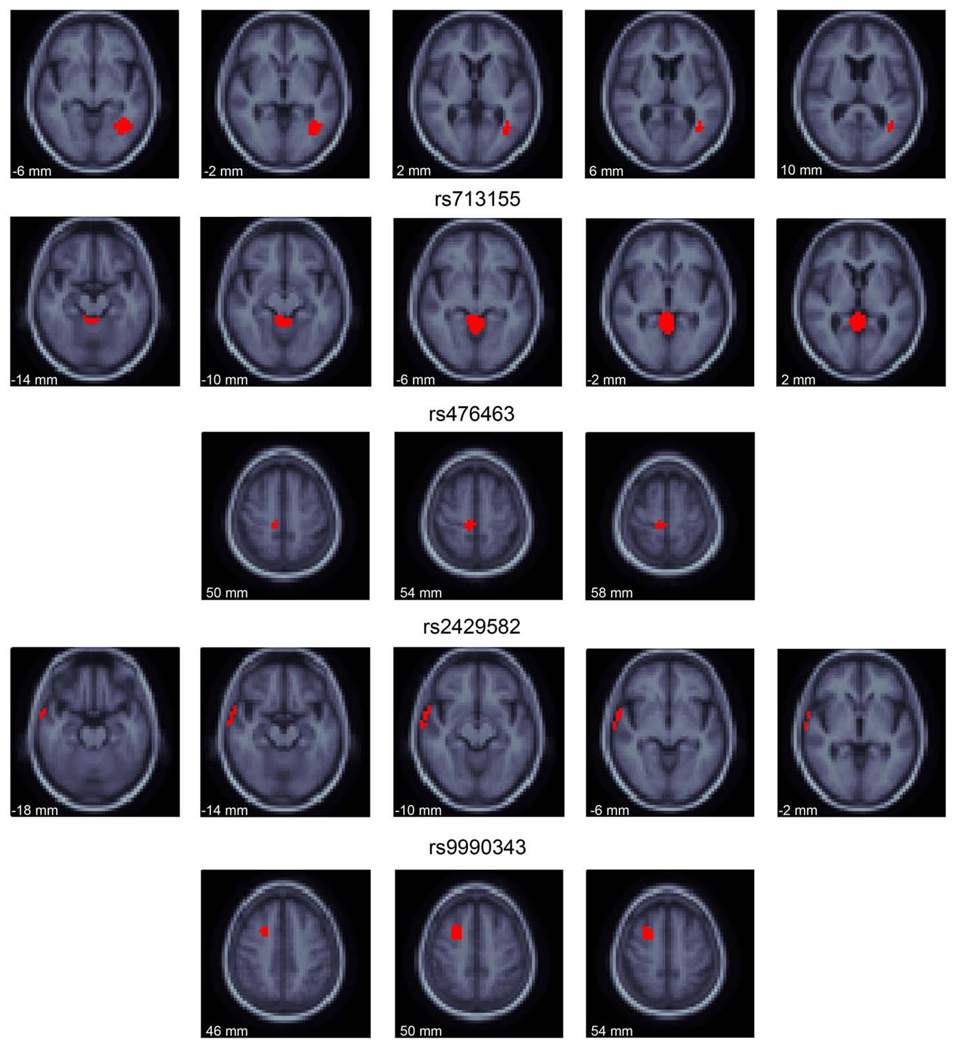
Fig. 6.

The locations of association for the 5 most associated SNPs. Slices through the MDT are shown in regions where the indicated SNP is the most associated at the voxel (red). The SNPs have effects on brain structure beyond the red colored voxels, but these voxels are associated with the labeled SNP more than any other. The slices through the MDT are every 4 mm and go from inferior (left of page) to superior (right of page). The images are in radiological convention (left of the image is the right side of the subject). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The two most significantly associated SNPsin the study, rs2132683 and rs713155, are both found in intergenic regions of chromosome 6. These SNPs are the “winning SNP” at voxels located in the white matter near the left posterior lateral ventricle (rs2132683) and in the cerebral aqueduct and fourth ventricle (rs713155; Fig. 6). The allele frequency of the minor allele at rs2132683 has a trend level difference between diagnostic groups (AD and MCI: 0.339; healthy elderly: 0.291; P=0.0793; OR=1.25) as does rs713155 (AD and MCI: 0.416; healthy elderly: 0.347; P=0.016; OR=1.34).

SNP rs476463 is located within an intronic region of the CSMD2 gene. CSMD2 has highest expression in the brain and may be a oligodendroglioma suppressor (Lau and Scholnick, 2003), though the function of the protein is largely unstudied. Additionally, it has been associated with ADHD (Lesch et al., 2008) and addiction (Liu et al., 2006). The allele frequency of this SNP did not statistically differ between diagnostic groups (AD and MCI: 0.116; healthy elderly: 0.131; P=0.428; OR=0.871).

SNP rs2429582 is located within an intronic region of the CADPS2 gene and is the SNP that associated with brain structure the most in the lateral temporal lobe. This gene regulates synaptic and large dense core vesicle priming in neurons, especially promoting monoamine uptake and storage in neurons (Brunk et al., 2009). CADPS2 is strongly expressed in the brain, specifically in cerebellum, cortex, olfactory bulb, hippocampus, striatum, thalamus, and superior and inferior colliculi (Speidel et al., 2003). The gene is located in an area with known linkage to autism (Cisternas et al., 2003). Splice variants of this gene may also be relevant to autism (Sadakata et al., 2007), though there is some controversy over this finding (Eran et al., 2009). The allele frequency for this SNP had a trend level difference between diagnostic groups (AD and MCI: 0.355; healthy elderly 0.307; χ²=2.989; OR=1.24).

The fifth most associated SNP in this analysis, rs9990343, is in an intergenic region of the genome on chromosome 3. It is the “winning SNP” in voxels of the superior frontal lobe (Fig. 6). The allele frequency for this SNP did not statistically differ between diagnostic groups (AD and MCI: 0.489; healthy elderly 0.461; P=0.341; OR=1.12).

Other genes of interest identified here are WFDC2, expressed in epithelial cells and thought to be involved in ovarian cancers (Bingle et al., 2002); SPINT3, serine peptidase inhibitor, Kunitz type 3 (Lundwall, 2007); SHB, involved in apoptosis, signal transduction (Lindholm, 2002), cell differentiation, and may interact with other proteins to cause neurite growth (Zhang et al., 2006); KIAA0090 which currently has an unknown function; MRTO4 which may be involved in mRNA turnover and ribosome assembly (Lo et al., 2009); AKR7L which is an aldo-keto reductase (Mindnich and Penning, 2009); BOK which is in a family of proteins that act as anti- and pro-apoptotic regulators (Bartholomeusz et al., 2006); THAP4, which does not have a known function (Roussigne et al., 2003); RBBP6, which encodes a retinoblas-toma tumor suppressor (Sakai et al., 1995); FARP1, which promotes dendritic growth (Zhuang et al., 2009); FRMD6 and GLYATL3 have unknown function. Additionally, SNPs were found in ESTs BG436399 and BC036700 (Strausberg et al., 2002) and BG334794.

Statistical threshold

The statistical threshold was calculated using two methods that control the FDR on the P_c-values. The original FDR method (Benjamini and Hochberg, 1995), which is valid in cases of positive regression dependency (Benjamini and Yekutieli, 2001), sets a critical P-value significance threshold for the second-most associated SNP (rs713155), with a false discovery rate of q=0.50 (or ~50%) when the P_c-value threshold is 2.97×10⁻⁴ (Fig. 3). The pFDR threshold gives a q-value of 0.25 for the most associated voxel of SNP rs2132683.

Sample size needed for replication

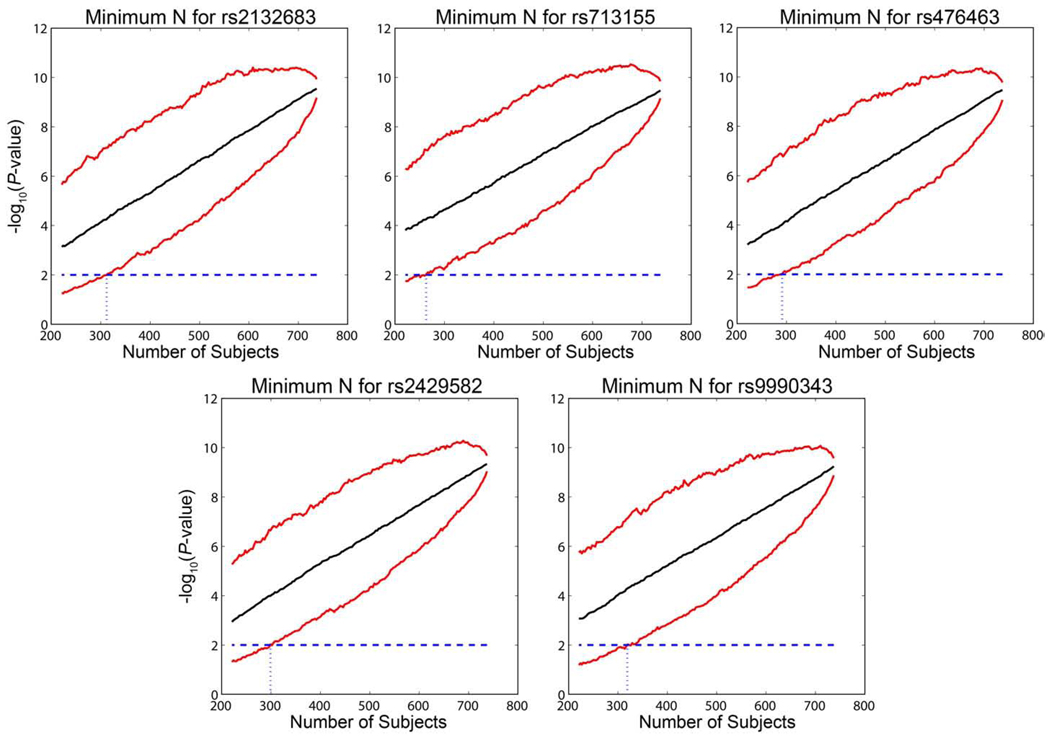
Replication is crucial for any experiment, but especially so in genomic studies that have a high chance for false-positive results because so many tests are conducted. Here, we conducted a resampling approach to determine how many subjects would be needed to replicate our findings with 95% confidence (Fig. 7). This resampling procedure shows that an independent sample of fewer than 312 subjects for rs2132683, 263 subjects for rs713155, 291 subjects for rs476463, 299 subjects for rs2429582, and 319 subjects for rs9990343 would be required to replicate the effects shown here with 95% confidence in a new sample at a significance level of P < 0.01 (a nominal P < 0.05, Bonferroni corrected for five independent tests). We note that the standard P < 0.05 level rather than the genome-wide significance would be applicable to a replication sample, as a prior hypothesis regarding the specific gene variant exists. In general, it seems desirable for imaging genetics studies to estimate the sample size needed to replicate a given finding, and to rank them for different findings, so that promising leads can be followed with maximum efficiency. In the imaging genetics community, it may also be possible to facilitate data sharing through the ENIGMA (Thompson and Martin, 2010) network (http://enigma.loni.ucla.edu/) sufficient to replicate a finding if the sample size required is known. The tables of “top SNPs” may then be shared with useful estimates of the sample sizes needed for replication.

Fig. 7.

The minimum number of subjects needed to replicate the findings for the top 5 most associated SNPs was estimated with a resampling approach. Subjects were randomly removed from each of the diagnostic categories until none was left in a category, and the association P-value of the SNP was calculated. This process was repeated 1000 times, to estimate 95% confidence intervals (red lines). The median P-value of the repetitions for each number of subjects removed is shown as the solid black line. The blue line shows the replication threshold for the first 5 SNPs, a Bonferroni corrected P-value of 0.01. The dotted blue line shows the estimated minimum sample size that would be required to detect a replication of the finding with 95% confidence (N=312 for rs2132683; N=263 for rs713155; N=291 for rs476463; N=299 for rs2429582; N=319 for rs9990343). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Discussion

Methodological overview

Here we present a method to conduct a voxelwise genome-wide association study (vGWAS). In summary: (1) we conducted a genome-wide association analysis using volume differences relative to a mean brain image template at each voxel as a phenotype, after controlling statistically for age and sex; (2) we selected only the most associated voxel, saving its P-value and identifier; (3) the effective number of tests was calculated through determination of the number of principal components that describe 99.5% of the genotypic variance; (4) the P-value was corrected across SNPs through a transformation using the CDF of an analytic Beta distribution with parameter estimated by the effective number of tests; and (5) the P_c-value maps were assessed for how they controlled the false discovery rate, using various implementations of the FDR theory to correct for multiple comparisons.

Overall, no SNPs survived FDR correction at the conventional q=0.05 threshold, but several interesting genes were identified that already have a known mechanistic relation to brain structure or to specific diseases of the brain, making them worthy of attempting replication.

Assumptions of model

This method defined above is equivalent to a “winner-take-all” map for SNPs, where the most associated SNP is represented in each voxel. Our method is losing information by only looking at one SNP per voxel, but even this data reduction technique requires novel analysis methods and extensive computational time. Other methods have been proposed to assess the simultaneous effects of multiple SNPs across multiple voxels, such as multivariate principal or independent component analysis (Liu et al., 2009). In addition, canonical correlation analysis (CCA) (Hotelling, 1935, 1936; Lee et al., submitted for publication), could be used to seek an optimal basis (or linear combination) for two high-dimensional vectors (i.e., the images and the SNP set), to maximize their correlation or mutual information. This basis can then be used to determine the maximum correlations between the two datasets, by diagonalizing the total covariance matrix between the vectors (Fillard et al., 2005). CCA, and its nonlinear variants such as kernel CCA and adaptive boosting, are especially attractive as they could be used to find optimal image projections that maximally correlate with subsets of genes. A region of an image, with specific weights derived from CCA, could then become a candidate phenotype of interest. This multivariate correlation method has been adapted already to seek genetic influences on 6-dimensional diffusion tensors in twins, without throwing away the substantial information in the diffusion tensor by dimension reduction (Lee et al., submitted for publication). Even so, the extension of these multivariate correlation methods to genome-wide data has not been explored and would require a great deal of memory.

Both the Beta transformation and FDR correction for multiple comparisons work under the assumption of independence (or positive dependence in the case of FDR). This assumption of independence is not precisely true for neuroimaging or genetic data. Neuroimaging data has spatial smoothness due to both scan acquisition and analysis parameters. The smoothness of the Jacobian maps that are derived from TBM analysis is partially determined by pre-specified registration parameters that affect the spatial covariance (Green's function) in the 3D deformation vector fields that are used to measure volumetric differences. These Green's functions can be set adaptively, in principle, and can be considered equivalent to spectral or neural network model of neuroanatomical variation that may be estimated from the data rather than specified analytically (Grenander and Miller, 1998; Fillard et al., 2005). Because of this, some spatial autocorrelations (spatial coherences) in the maximum SNP map are expected even when null (Fig. 5). Similarly, because genetic variation is inherited in contiguous segments of DNA due to recombination happening often in specific locations, there is a great deal of correlation between genetic markers recorded here, which is taken into account through calculation of M_eff (Table 1).

A common method to correct for multiple comparisons taking into account non-independence of the data is to calculate exact P-values by shuffling labels, in this case genetic variation and voxels, between subjects. By doing this many times, a true null distribution is developed which automatically accounts for the spatial and genetic correlations in the sample. Unfortunately, with data sets this large it is not computationally feasible to calculate a null distribution through resampling in a reasonable amount of time. Each analysis takes 27 h to complete even when parallelized across 300 computing nodes, so a resampling with only 1000 permutations would take ~3 years.

Permutation tests are the gold standard for calculating significance levels and determining M_eff. As mentioned above, permutation tests are not computationally feasible here, so we used a quick and effective method for determining M_eff. Using a measure of the effective number of independent tests is controversial (Nichols and Hayasaka, 2003; Dudbridge and Koeleman, 2004). Previous work has shown that when calculating the effective number of tests conducted, the calculated distribution was significantly different from a permutation-derived distribution (Dudbridge and Koeleman, 2004). However, a different algorithm is used here for determining the effective number of tests (simpleM) and was found to match very well with the effective number of independent tests fit to a Beta distribution of permuted data in two datasets (Gao et al., 2010). Other work has shown that in neuroimaging data, the effective number of independent tests does not match that of a permuted dataset when there is high spatial smoothness (local autocorrelation) in the residuals of the dataset after statistical model fitting (Nichols and Hayasaka, 2003). However, here we use the effective number of tests to correct across the genetic data, an application where the procedure has been shown to give accurate results in comparison to a gold-standard permuted null dataset (Gao et al., 2010).

Validity of the beta distribution and effects of violations of distributional assumptions

Serious consideration must be given to how violations of the assumptions of the Beta transformation might affect the results of the analyses. In fact, if null data deviates from a Beta distribution (e.g., in the tails) will impact some steps of the analysis (the FDR correction, which is based on significance) but not others (the ranking of the SNPs and the top SNP map). The goal of the Beta(1, M_eff) method of adjusting the raw P-values is “uniformization” of the P_c-values under the null hypothesis. In other words, if the data are truly null, then the P_c-values should approximately follow a uniform distribution on the unit interval [0,1]. In Figs. 1 and 2, the Q–Q plots show the approximate fit to the Beta(1, M_eff) distribution in the bulk regime (i.e. where the effect sizes are lowest), but in the tail, there may be deviations from the fit. True positives would induce such deviations, but an inappropriate fit could also do this. In simulations with correlated Gaussian samples, a Beta(1, M_eff) fit does well in the bulk, but there are deviations from uniformity for small P_c-values (we acknowledge an anonymous reviewer for noting this). Such deviations will not affect the SNP ranking, as any conversion from P to P_c is monotonic. However, they would affect the significance testing. Although FDR applied to the images here did not give a significant finding, so the point does not affect the conclusions drawn, if the P-to-P_c is used as the basis for significance testing, its empirical fit should be tested more thoroughly and perhaps modified based on a partially permuted dataset, where feasible.

Methods to increase power in vGWAS

First, minimal N plots (Fig. 7) estimate, through a resampling procedure, how many subjects might be needed to replicate a finding. These SNPs could be validated by conducting a similar experiment in a new sample, looking at only the SNPs of interest at the voxels or regions found here. By reducing the number of comparisons (fewer voxels and fewer SNPs), a less stringent statistical threshold is needed for comparison because fewer tests are conducted.

This minimal N analysis differs from experiments which do not reject the null hypothesis, and then attempt to determine the experimental power to reject the null. The idea of a post-hoc power calculation has been shown to be fallacious (Hoenig and Heisey, 2001; Levine and Ensom, 2001) and is not the goal here. Instead we look to estimate, approximately, the reduced number of subjects that might be needed to replicate our results in a separate experiment. Using an initial sample to determine the number of subjects needed to replicate a finding in a completely independent sample does not have the same fallacy of the post-hoc power calculation which attempts to calculate the power to achieve significance on the same sample. The goal of the analysis presented is to determine how many subjects are needed to pass a lower replication significance threshold. If the finding is true, and if the sample here is representative of the population, 95% of the time in new experiments the SNP will be significant at a replication threshold.

Notably, because vGWAS does lead to restricted regions of interest for associations, future studies could take advantage of the limited search region to specify a region of interest, increasing power by eliminating false-positive voxels. The selection of statistically-defined regions of interest has been useful in other large voxel-based morphometry studies. For example, in a study of 515 ADNI subjects scanned twice, Hua et al. (2009) found that the sample sizes needed to find drug effects on the rates of brain atrophy were drastically reduced if the analysis focused on voxels that had shown strong effects sizes in a small independent training sample. Summary measures from this statistical region of interest were more powerful than those based on atlas-based anatomic criteria, suggesting the benefit of voxel-based methods, at least in some cases, over anatomical parcellation.

To implement such an approach, one could use two datasets: one for training and one for testing. The training dataset could be trained to specify areas of greatest heritability or areas of greatest genetic association. These areas could then be used as “training” ROIs to search for genetic influence. Using vGWAS, the most associated SNPs at the most associated voxels could be used as “testing” ROIs where we would expect much higher power in the “testing” dataset, as fewer voxels and fewer SNPs are tested for association. The ADNI study has used this method successfully to increase power to detect changes with greatest statistical effect sizes in AD (Hua et al., 2009; Ho et al., in press). Genetics studies have also advocated this multi-stage approach to maximize power with reduced genotyping cost (Skol et al., 2006).

Additionally, machine learning algorithms such as support vector machines (Burges, 1998) or Adaboost (Freund and Schapire, 1997; Morra et al., 2008) could offer a method to identify the most powerful phenotype, that is a set of voxels, and an associated set of weights, with the greatest power to associate with genetic variation. A linear version of this approach is canonical correlation analysis; a nonlinear version might use machine learning methods such as kernel CCA, support vector machines, or boosting (Morra et al., 2009). If the performance of this system were high on new data, one could use the new classifier output as the endophenotype (Sun et al., 2009) and regress it against genetic variation using standard association software, such as Plink.

Conversely, machine learning methods could be used to find gene sets or networks that best predict the image value (Gu et al., 2009). In this way, one would be directly building a genetic model for the data. The gene set could be limited to the best candidates from the training/ screening phase of the data as detailed above. This could motivate a design where one detrends the effects of the top SNPs when looking for others. Adaptive boosting could be applied to this problem, as it could fit a powerful weighted model ranking the top SNPs even if they each had a small effect (similar to “weak learners”, in terminology of machine learning) (Morra et al., 2009).

Biological significance of the findings

Genome-wide association using brain phenotypes in humans has only been started in a few previous studies, to our knowledge (Seshadri et al., 2007; Potkin et al., 2009a; Potkin et al., 2009b). These studies used data reduction techniques by only studying gross phenotypes of interest like total cranial, lobar, ventricular, or hippocampal volumes. Our analysis offers a conceptual advantage as it searches for voxelwise genetic associations in 3D, which should offer much greater anatomical detail about genomic association, with potentially higher statistical power. Using this method, we found several genes with high relevance to brain structure. Specifically, CADPS2 is involved with monoamine uptake in neurons; CSMD2 and CADPS2 have been associated with psychiatric illness; and SHB and FARP1 are associated with neurite growth. Given this prior information on how these genes function on the brain, it is likely that some of the genetic variants found here have important effects on the structure of the brain. Many other genes have not been well-studied or characterized so may well have an effect on brain structure.

In Fig. 6, many of the locations of greatest association beyond any other SNP for the 5 most associated SNPs are near a significant edge in the brain—next to the brain surface, major fissure, or ventricles. It is worth considering whether such a localization may be due to a bias (differential sensitivity) that might arise from the method of image warping followed by using the warp's Jacobian determinant as the dependent variable. If statistical maps based on deformation fields tended to detect effects more frequently at edges than in the rest of the brain, then this would be a possible source of bias, but it appears not to be the case in other empirical studies using TBM (in fact the opposite tends to be the case). Most studies with deformation morphometry tend to show the greatest effect sizes throughout large homogeneous regions, and notably our TBM studies of Alzheimer's disease find greatest effects in broad regions of the brain's white matter, or throughout the lateral ventricles, both at 1.5 T and 3T, and in large samples (Hua et al., 2009; Ho et al., in press). Also, statistical effects are not preferentially detected at edges in images when the effects of single candidate genes on the brain are assessed with TBM (Ho et al., submitted for publication). Although the deformation is driven by a body force (image gradient, or variational derivative of a cost function) that is generally greatest at the edges of structures in the images, the interiors of structures still tend to be better registered than their boundaries once all the data are aligned. In the interiors of structures, coherent patterns (such as atrophy) are more likely to be reinforced across all members of a group than at boundary voxels that may be less well registered across all subjects in the group, even after nonlinear registration. After all, the registration algorithm focuses on improving the alignment of edges as they are always the least well registered parts of the image, and therefore these regions are likely to show low effect sizes in a population study. Even so, some warping methods use regularizers that are designed to make the Jacobian determinant as uniform as possible in regions of homogeneous image intensity (e.g., the sKL-MI method, see Yanovsky et al., (2009)), so the Jacobian determinant will change the most at an image edge. If this is true, and if the “top SNP” is a different SNP for different structures, then it is more likely that the top SNP in a vGWAS map will change at the boundary of a structure. This is speculative, and the spatial coherence of top-SNP maps may depend on the sample size, the true spatial correlation in the “top SNP” maps in an arbitrarily large sample, as well as the methods (maximum statistic vs. cluster size statistic) used to detect them. The spatial correlation for single gene effects on brain structure can be quite large, in TBM studies of candidate genes that influence brain structure (Ho et al., submitted for publication).

As in other ADNI analyses, we did not covary for medication status of the subjects. It cannot be absolutely ruled out that some of the volumetric brain differences between AD, MCI, and normal subjects might arise due to differences in medications, but such effects are likely minimal. The major treatments for AD, including acetylcholine eesterase inhibitors (AChE-I) and NMDA receptor modulators, have effects at the synaptic (neurotransmitter) level that can provide limited symptomatic relief and have not been found to resist the progression of atrophy, despite many efforts to find such effects. In their ADNI study of 269 MCI subjects, Kovacevic et al. (2009) noted that 45% of the MCI subjects were being treated with AchE-Is, but controlling for treatment status in prediction of decline did not change the association between medial temporal lobe volumes on MRI and cognitive decline, not did treatment status affect regional volumes. In addition, some psychiatric medications do have direct effects on brain structure that are not attributable to the illness itself, and these include lithium a treatment for bipolar disorder (Bearden et al., 2007; Bearden et al., 2008), and the antipsychotics haloperidol or olanzapine (Thompson et al., 2009). However, ADNI's exclusion criteria required subjects to be free from major depression, bipolar disorder, or any history of schizophrenia.

Conclusion

In summary, here we presented a novel method for discovering genetic variations associated with brain structure. The resulting method, termed vGWAS, is capable of integrating a large amount of biological information, yet still allows sufficient power to detect significant variants. This method will be useful in any brain maps that have coordinate systems, such as voxel-based morphometry, cortical surface data, and parameterized tracts derived from diffusion tensor imaging. In addition, we have provided a ranked list of new candidate genes with potential effects on brain structure that are worthy of further study.