THE RELATIONSHIP BETWEEN SELF-REPORTED DRINKING AND BAC LEVEL IN EMERGENCY ROOM INJURY CASES: IS IT A STRAIGHT LINE?

Abstract

Background

While the validity of self-reported consumption, based on blood alcohol concentration (BAC) has been found to be high in emergency room (ER) samples, little research exists on the estimated number of drinks consumed given a BAC level. Such data would be useful in establishing a dose-response relationship between drinking and risk (e.g., of injury) in those studies for which the number of drinks consumed is not available but BAC is.

Methods

Several methods were used to estimate the number of drinks consumed in the six hours prior to injury based on BAC obtained at the time of ER admission of n=1,953 patients who self-reported any drinking 6 hours prior to their injury and who arrived to the ER within six hours of the event, from the merged Emergency Room Collaborative Alcohol Analysis Project (ERCAAP) and the World Health Organization Collaborative Study on Alcohol and Injury across 16 countries.

Results

The relationship between self-reported consumption and averaged BAC within each consumption level appeared to be fairly linear up to about 7 drinks and a BAC of approximately 100 mg/dl. Above about 7 reported drinks, BAC appeared to have no relationship with drinking, possibly representing longer consumption periods than only the 6 hours before injury for those reporting higher quantities consumed. Both the volume estimate from the bivariate BAC to self-report relationship as well as from a Widmark calculation using BAC and time from last drink to arrival to the ER indicated a somewhat weak relationship to actual number of self-reported drinks.

Conclusions

Future studies may benefit from investigating the factors suspected to be driving the weak relationships between these measures, including the actual time over which the reported alcohol was consumed and pattern of drinking over the consumption period.

INTRODUCTION

There is now a well-established literature on alcohol use and injury in patients presenting to hospital emergency room (ER) services. Two measures of alcohol use prior to injury that have been primarily used in these ER studies are a measure of blood alcohol concentration (BAC), usually by breath-test, and self-reported questions about drinking in the six hours prior to the event leading to the ER visit. A number of studies have attempted to examine the relationship between BAC and self report with varying success.

One U.S. study found that 3.6% of those who were BAC positive at ER arrival denied any drinking within the six hours prior to the event while 29% of those who reported drinking during this time were negative for BAC (Cherpitel, 1989b). A similar study among injured patients found proportions denying drinking but registering positive for BAC ranging from 3.3% in Mexico, to 1.5% in Spain and .5% in the U.S., while proportions reporting drinking but registering negative for BAC were considerably greater (41% in the U.S., 37% in Spain and 18% in Mexico) (Cherpitel et al., 1992). To explore whether the validity of self-report was positively affected by patient’s being breathalyzed prior to eliciting a report (bogus pipeline effect), one ER study obtained self-report data prior to breathalyzing the patient on part of the sample, and following, on the remainder of the sample, with no effects in self-report validity observed (Cherpitel, 1993).

Prior analysis of ER data reported here across 16 countries found an average of 75% of those who reported drinking in the six hours prior to injury had a positive BAC at ER admission, (ranging from 88% to 44%) (Cherpitel et al., 2007). A substantial proportion of those denying drinking while registering positive for BAC was accounted for by reporting drinking following the injury (38%). Although this same 16-country study found a positive association between BAC and the likelihood of reporting drinking, none of these ER studies have examined the validity of self-reports based on BAC in relation to the number of drinks consumed.

Two studies of motor vehicle injury patients in trauma centers which analyzed the relationship of self-reports of the number of drinks consumed with serum BAC found only moderate correlations, r=0.43 (Sommers et al., 2000) and r=0.26 (Sommers et al., 2002). In each study, self-reported volume underestimated BAC on average indicating that patients either under-reported the number of drinks consumed or overestimated the amount of time spent drinking. Other, non-ED based, studies have also found poor correlation of reported volume of consumption with BAC. A study of college students found a general over-reporting of drinking, with BAC inversely related to the likelihood of over-reporting (Kraus et al., 2005). Another college student drinking study found that while estimated BAC from self-reported volume and BAC estimated from breath analysis were highly correlated (r=.84), at higher breath analysis levels (> 0.08%) the relationship was no longer significant (r=0.23) (Carey and Hustad, 2002).

These mixed findings are indicative of a complex relationship between the two variables. Therefore, before attempting to study the relationship between BAC and self-reported drinks in naturalistic studies, it may help to first consider the hypothetical relationship between these two quantities in an idealistic setting. For example, assume that we knew the actual unbiased number of drinks consumed before the injury over the entire drinking occasion that lead up to the injury (i.e., not just in an arbitrarily defined period such as six hours prior to injury) which will vary across individuals. Call this quantity the self-report “gold standard”. In addition to this quantity, consider information associated with the drinking occasion including the time period over which the drinks were consumed, the actual pattern of drinking (e.g., slow steady drinking vs. concentrated drinking at specific times over the drinking occasion), as well as other characteristics such as the type of beverage consumed (i.e., size, strength, beverage type), whether food was consumed with the alcohol, what other activities the respondent was engaged in as well as other relevant individual demographic and usual drinking characteristics. As an analogy of the self-report gold standard, the BAC “gold standard” measure would be that taken a single time at the exact time of injury (not arrival to the ER) and would be free from any measurement error or other biases.

Given both gold standards but not all of the additional information linking the two (i.e., actual length of time over which the alcohol was consumed, pattern of drinking, food consumption, etc.), there may be considerable variation in the strength of their relationship. This may be especially true if larger quantities consumed are associated with longer (but unknown) time periods and more variable patterns of consumption, as these are two variables that are very influential on the underlying BAC curve over time. That is, the gold standards (either self-report or BAC) must consist of more than just themselves alone for them to actually be considered equivalent (i.e., to be able to move from one to the other).

Estimates of relative risk for injury morbidity at various levels of acute consumption (number of drinks consumed) is important in that they have been used to inform population guidelines for low-risk drinking and have also been used in determining alcohol attributable fraction of injury morbidity to inform comparative risk assessment in the Global Burden of Disease estimates (Rehm et al., 2004). However, studies have been conducted (Taylor et al.) for which self-reported volume was not collected but a measure of BAC was. Therefore, a study of the relationship between volume of consumption and BAC is critical to inform whether such studies can be used together in estimating the Relative Risk of injury due to alcohol use. Although the accurate estimation of volume from BAC for use in Relative Risk estimates is the primary intended purpose of this research, it may apply more generally towards a number of different areas including clinical or forensic settings.

In the present analyses we draw on a 16-country dataset (Cherpitel et al., 2007) to analyze how the patient’s report of quantity of drinking in the six hours preceding an injury compares with the measured BAC at the time of ER admission.

While we are interested in the summary correlation statistics, our attention is also focused on the shape of the relationship between reported volume and BAC. These findings will help inform the prediction of the volume of alcohol consumed at the individual level in the ER and in other settings in which only BAC is available.

METHODS

Samples

Data are analyzed from 44 ER sites in 28 ER studies across 16 countries (Argentina, Australia, Belarus, Brazil, Canada, Cezch Rep, China, India, Mexico, Mozambique, New Zealand, Poland, South Africa, Spain, Sweden, U.S.) comprising the combined Emergency Room Collaborative Alcohol Analysis Project (ERCAAP) (1984–2009) (Cherpitel et al., 2003) and the WHO Collaborative Study on Alcohol and Injuries (2001–2002) (WHO Collaborative Study Group, 2005). See Cherpitel (2005) for a more detailed description of the study sites. The WHO study included only those patients arriving at the ER within 6 hours of the injury event. For comparability, ERCAAP data analyzed here were selected to include only those injured patients meeting this 6-hour criterion.

Both the ERCAAP and WHO studies used a similar methodology (Cherpitel, 1989a) in which probability samples of patients 18 years and older were obtained by sampling consecutive arrivals to each ER in the study, with equal representation of each shift for each day of the week during the study period. Each patient was approached with an informed consent to participate. Completion rates for the ERCAAP studies averaged 72%, while those for the WHO studies averaged 91%. Interviewers trained in each ER setting obtained a BAC estimate, and administered a 25-minute questionnaire that included, among others items, the time of injury occurrence, drinking in the six hours prior to injury, amount consumed, and drinking following injury.

Measures

An estimate of BAC was obtained immediately after ER admission using a breath analyzer (Alco-Sensor III and in New Zealand the Alcotec AR1005) in all but the Canadian (Alberta and Quebec) ERCAAP studies, which has been found to provide estimates that are highly correlated with chemical analysis of blood (Gibb et al., 1984). In Alberta and Quebec, BAC was estimated from urine samples using KDA enzymatic testing and standardized to the unit measure quantifying BAC estimated from breath samples. Self-report data was based on the patient’s report of consuming alcohol during the six hours prior to the injury and the number of drinks consumed during that time. Within each study, detailed questions about the commonly consumed beverages within the country were asked, including size and number of containers consumed as well as beverage concentrations for each beverage type consumed. Drinks in each country were converted to grams of ethanol and the number of standard drinks for each country was calculated based on the U.S. standard of 12 grams equal to one drink.

Analysis

A total of 10,325 of the combined ERCAAP/WHO sample had sufficient data available on BAC, self reported volume of consumption (if drinking 6 hours prior to the event), and who did not report drinking after the injury. Of these, 1,953 patients reported drinking 6 hours prior to injury (and 822 reported to the ER within 3 hours of their last drink).

Two approaches were taken with the goal of estimating self-reported volume of consumption from BAC among these 1,953 patients. The first approach was to estimate self-reported number of drinks empirically from the bivariate relationship between BAC and self reported volume using fractional polynomials in Stata (Stata Corp, 2007). The second approach was to use Widmark’s equation (Brick, 2006), defined as: BAC= [(0.01882816× V_SR ×C)/(W×G)] − L·H where the constant .01882816 is the concentration of alcohol in blood (g/L), V_SR is the self-reported volume of consumption in number of 12 gram drinks, C is the alcohol concentration by volume of the specific beverage type (40% was used for spirits, 12.5% for wine, and 5% for beer), W is the weight of the patient in kg, G is the percentage of water in the body (assumed to be 58% for men and 49% for women), L is the liver clearance rate (assumed to be .017/hour for those reporting a usual quantity of less than 2 drinks/day and .020/hour for reporting 2 or more drinks/day) and H is the number of hours from the last drink to arrival at the ER. As patient weight was not available, average country-specific weight values were used for men and women based on data from the GENACIS (Rahav et al., 2006) collection of survey data from a large number of countries worldwide.

Time of arrival was used instead of time of BAC to calculate the variable H as it allowed the inclusion of additional data (i.e., for some studies/individuals, time of BAC was not available or missing). For those cases with both time of arrival and time of BAC (87% of the total used in this analysis), about 75% of the cases had time between arrival and BAC of less than 30 minutes, 90% less than 1 hour, and 98% less than 2 hours. Therefore, this difference should not significantly affect calculation of BAC using the Widmark method.

Using the empirical relationship between BAC and self-reported volume (V_SR), a continuous empirical volume estimate (V^_E) was produced from each BAC by inverting the empirical relationship. Similarly, for each BAC a Widmark-estimated volume (V^_W) was produced by inverting the Widmark equation for the volume consumed. In order to simplify the display of the results for the various volume measures, volume bins (or grouped continuous ranges of volume) were defined for 1, 2, 3–4, 5–7, 8–9, and 10+ drinks for each of the 3 measures (V_SR, V^_E, and V^_W). For example, the volume bin for 1 drink was the volume range from 0 to 1.5 drinks; for 2 drinks the volume range was 1.51–2.5 drinks, etc. Measures of the agreement between V_SR (the self-reported volume of consumption) and V^_E as well as between V_SR and V^_W were estimated for the continuous underlying measures using Pearson’s correlations. For the corresponding binned volume variables, a weighted Cohen’s κ was estimated.

Sensitivity analyses were also performed by estimating the relationships only for those arriving to the ER within 3 hours of the event. Concordance between self-reported consumption and estimated BAC, for each of the two methods, was also estimated for a hold out sample (a separate sample not used in the estimation of the relationship between self-report and BAC and instead used to simply to assess how well the estimated relationships hold) of data from Ireland and Switzerland.

RESULTS

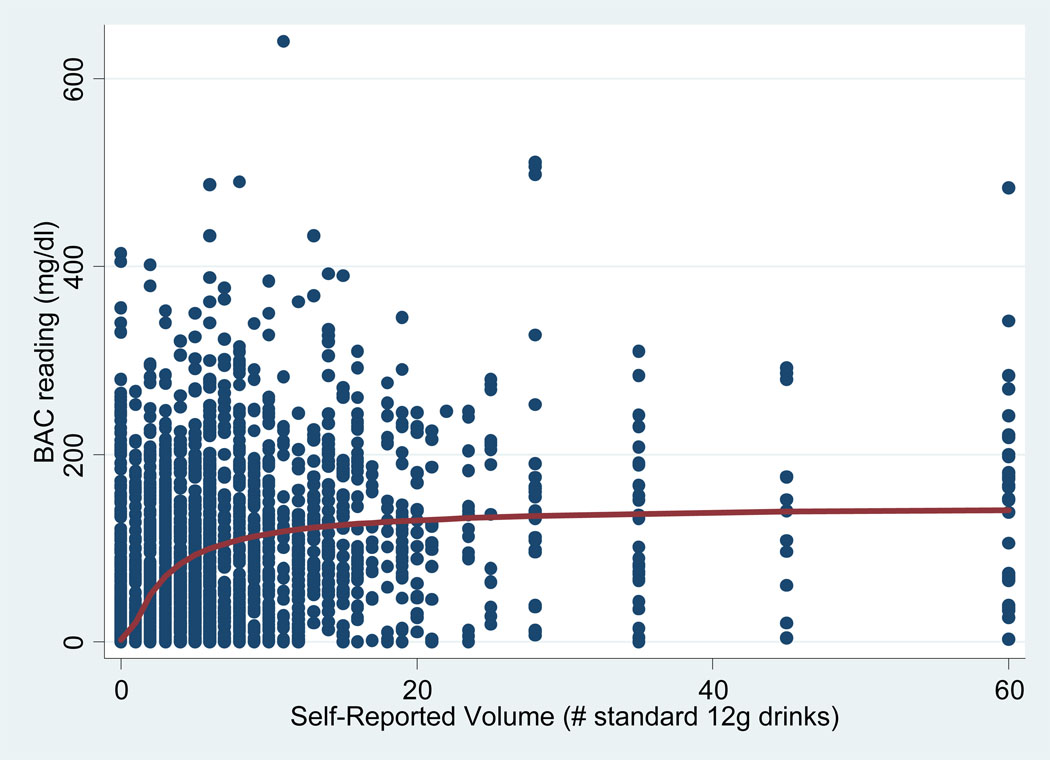
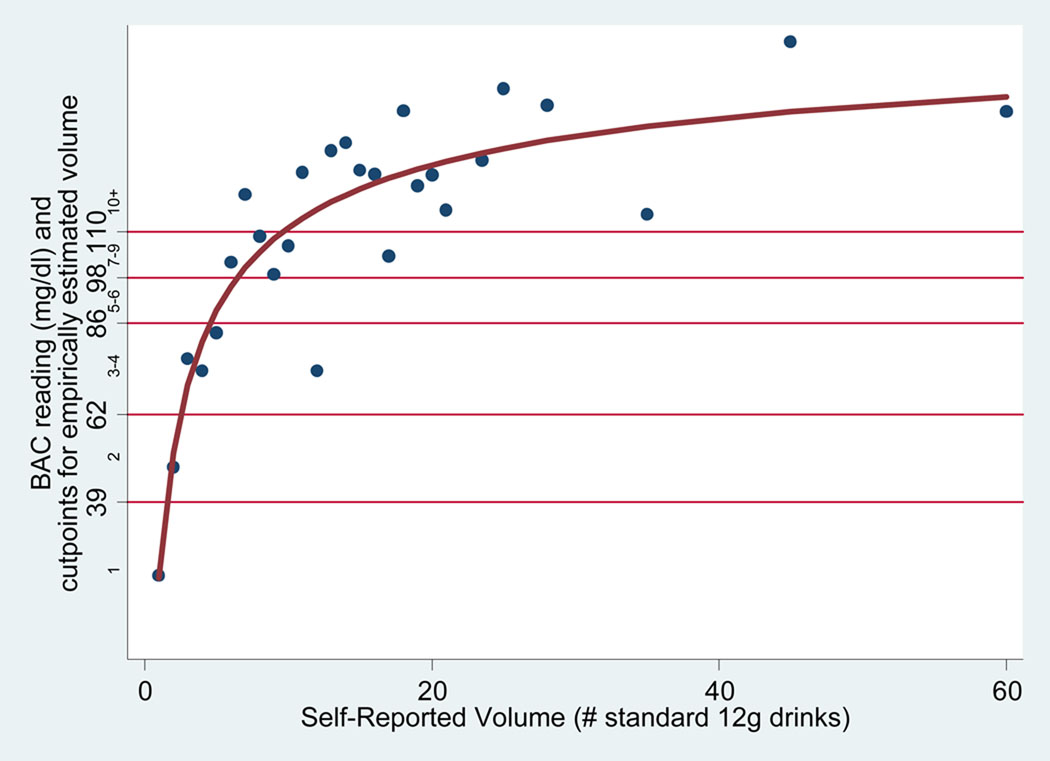
Figure 1 shows the empirical relationship between self-reported volume (x-axis) and BAC (y-axis) for all respondents (the individual-level relationship) and indicates substantial variability between the two measures. Note that BAC is measured in milligrams/deciliter (mg/dl) so that, for example, a BAC concentration of .08%= 80 mg/dl. Figure 2 shows averaged BAC values for each of a number of categorized self-reported volume levels V_SR (the aggregate-level relationship) and indicates a steep initial rise in BAC (up to about 7 self-reported drinks) followed by a leveling off above (starting above about 7 drinks) with increasing variability in the average value.

Figure 1.

Individual-Level Relationship Between Self-reported Volume (V_SR) and BAC and Fractional Polynomial Fit to the Data

Figure 2.

Aggregate-Level Relationship Between Self-Reported Volume (V_SR) and BAC and Fractional Polynomial Fit to the Data

With the goal of estimating the relationship between BAC and V_SR, a number of regression relationships were estimated. As the relationship between BAC and volume flattens out (see Figure 2), models that might estimate V_SR from BAC would produce a curve that could not reproduce the vertical line for the relationship at higher BAC levels. Therefore, BAC (y-axis) was instead estimated from V_SR (x-axis) and the relationship inverted. After examining the bivariate relationship, (more easily seen in the aggregate-level relationship in Figure 2) between BAC and V_SR, several potential regression models (including linear, quadratic, cubic) were considered. Curvature in the bivariate relationship was followed by a flattening out of the average BAC levels at higher volume levels that quadratic models could not possibly capture. Although cubic regression models were estimated, it was decided to choose fractional polynomial regression models over cubic models as they allow for a more flexible estimation of the curve while incurring only slightly more complexity in the estimated functional form. The fractional polynomial model was of the form y = α + β₁x^a + β₂x^b + ε, where a and b are chosen from the set of fractional powers defined as: (−3, −2.5, −2, −1.5, −1, −.5, 0, .5, 1, 1.5, 2, 2.5, 3) and α, β₁, and β₂ are regression parameters. All parameters were chosen simultaneously to maximize explained variance in the outcome. The shape of the prediction equation from the fractional polynomial regression models differed little whether the models were fitted on the raw or the aggregated data.

Figure 2 shows the fitted fractional polynomial curve to the aggregated data. Values of R² (i.e., percent variance in the outcome explained) for the models fitted to the raw data and aggregated data were .47 and .79, respectively. In the fractional polynomial regression model, the dependent variable is aggregated BAC which is modeled as a function of V_SR. Therefore, in order to estimate the volume corresponding to a given BAC level, the regression equation must be solved (i.e., inverted) for volume. Note that the y-axis of the figure indicates actual BAC level but also includes a sub-axis that represents a BAC range corresponding to the estimated number of drinks (obtained from Widmark equation). These estimated drink ranges were computed by inserting the volume bin endpoints described in the analysis section.

Table 1 shows the categorized volume levels, the actual bin endpoints of the continuous volume scale corresponding to each categorized level, and the BAC values that correspond to the volume bin endpoints derived from the inverted empirical regression relationship. For example, the volume level defined as 1 drink corresponds to the continuous volume range of less than 1.5 drinks, while a volume level of 2 drinks corresponds to the continuous volume range of 1.5 to 2.5 drinks. Higher volume levels were categorized similarly.

Table 1.

Volume Bins and Corresponding Cutpoints on the Volume and BAC Continuum

Volume (# drinks)	Volume range	Corresponding BAC
1	<1.5	<0.039
2	≥1.5, <2.5	≥0.039, <0.062
3–4	≥2.5, <4.5	≥0.062, <0.086
5–6	≥4.5, <6.5	≥0.086, <0.098
7–9	≥6.5, <9.5	≥0.098, <0.110
10+	≥9.5	≥0.110

Two predicted continuous volume variables were then created for each patient, one corresponding to the patient’s BAC from the empirical fractional polynomial regression equation, another from inserting the BAC into the Widmark equation. These two relationships were then inverted to obtain V^_E andV^_W. The empirical BAC estimate was used along with Table 1 in order obtain a corresponding estimate of the volume bin. The continuous volume estimate from the inverted Widmark equation was also categorized corresponding to the volume bin cutpoints in Table 1. In this way, the self-reported categorized volume could be compared directly to either the categorized volume from the empirical regression estimation or from Widmark’s equation.

A categorical any drinking compared to no drinking from self-reported was first compared to the empirical volume estimate and can be seen in Table 2. As the first row of the table shows, a total of 1,953 patients self-reported any drinking and 511 (26.2%) of these patients had a value of 0 for BAC. Among the 511 cases, over two-thirds reported less than 2 drinks consumed within 6 hours prior to injury and over 88% reported fewer than 6 drinks (results not shown). Of those 8,372 patients who reported no drinking, a total of 175 (2.1%) had positive values for BAC. Similarly, Table 2 also shows the any vs. no drinking relationship between self-report and from the inverted Widmark equation. Of the 1,953 who reported any drinking, a total of 156 (8.0%) did not report time from last drink to arrival at the ER and therefore the Widmark volume could not be computed. In addition, of the 8,372 who reported no drinking within 6 hours prior to the injury, the time from last drink to arrival to the ER was not available and therefore an estimated volume could not be computed.

Table 2.

Concordance of Self-Report vs. Empirical & Widmark Volume

	Empirically Estimated Volume		Widmark Estimated Volume
Self-reported volume	Any Drinking	No Drinking	Any Drinking	No Drinking	Missing	Total
Any Drinking	1442	511	1286	511	156	1953
No Drinking	175	8197	0	8197	175	8372
Total	1617	8708	1286	8708	331	10325

The relationship between the resulting categorical volume levels, defined as 1, 2, 3–4, 5–6, 7–9, and 10+ drinks for each of self-reported consumption, the empirical regression, and the Widmark approaches can be seen in Table 3 and Table 4. A weighted Cohen’s κ with weights defined as 1, .8, .6, .4, .2 and 0 was used to estimate agreement between self-reported consumption (V_SR) and volume from both the empirical (V^_E) and Widmark (V^_W) approaches. The self-reported and empirical volume relationship is shown in Table 3 and produces κ = .16 (.02) with a correlation of the two quantities of ρ = .26. The relationship between self-reported and Widmark volume is shown in Table 4 and produces κ = .15 (.02) with ρ = .25. When the sample is restricted to only those who arrive to the ER within 3 hours of the last drink, yielding 822 cases with complete data for which all 3 volume variables could be calculated, the corresponding values were κ = .18 (.02) and κ = .19 (.02).

Table 3.

Relationship Between Self-Reported and Empirically Estimated Volume

	Empirically Estimated Volume
Self-Reported Volume	1	2	3–4	5–6	7–9	10+	Total
1	37	7	13	1	3	20	81
2	59	19	20	3	3	38	142
3–4	55	37	32	13	7	97	241
5–6	39	48	29	9	10	101	236
7–9	29	22	26	15	8	90	190
10+	43	39	45	32	34	203	396
Total	262	172	165	73	65	549	1,286

Weighted Choen’s κ = .16 (se = .02), ρ=.26

Table 4.

Relationship Between Self-Reported and Widmark Estimated Volume

	Widmark Estimated Volume
Self-Reported Volume	1	2	3–4	5–6	7–9	10+	Total
1	8	14	23	11	19	6	81
2	7	25	37	31	22	20	142
3–4	8	23	56	65	55	34	241
5–6	5	20	61	49	56	45	236
7–9	2	5	34	54	51	44	190
10+	7	19	57	88	131	94	396
Total	37	106	268	98	334	243	1,286

Weighted Choen’s κ = .15 (se = .02), ρ=.25

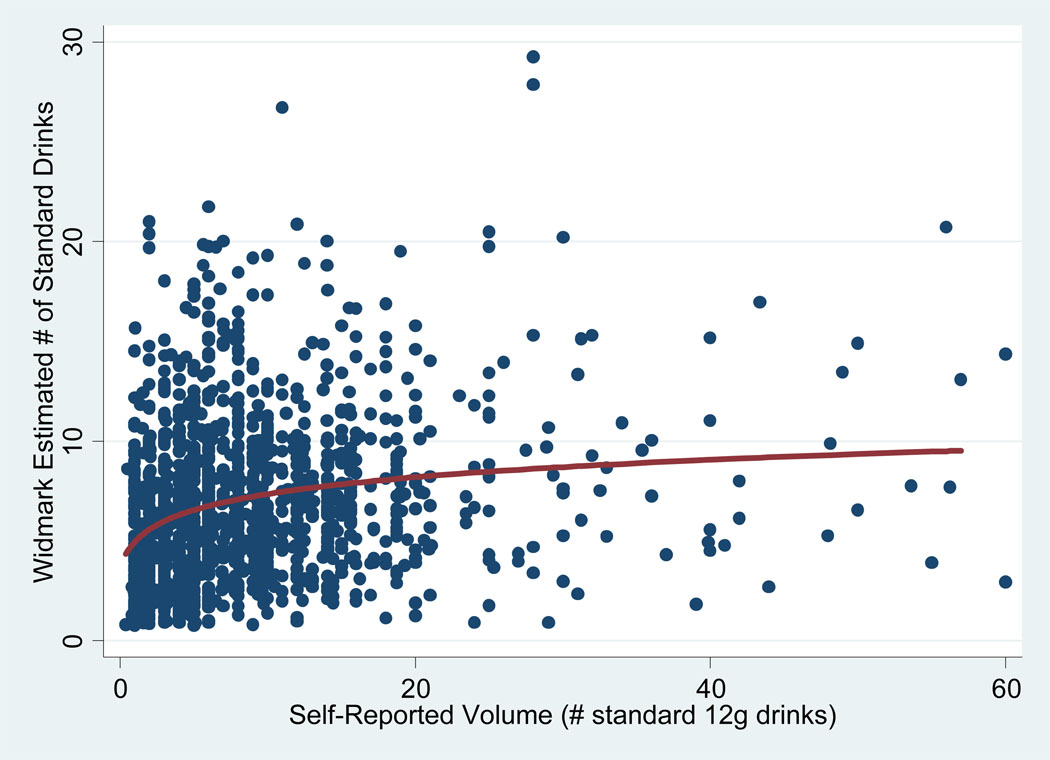
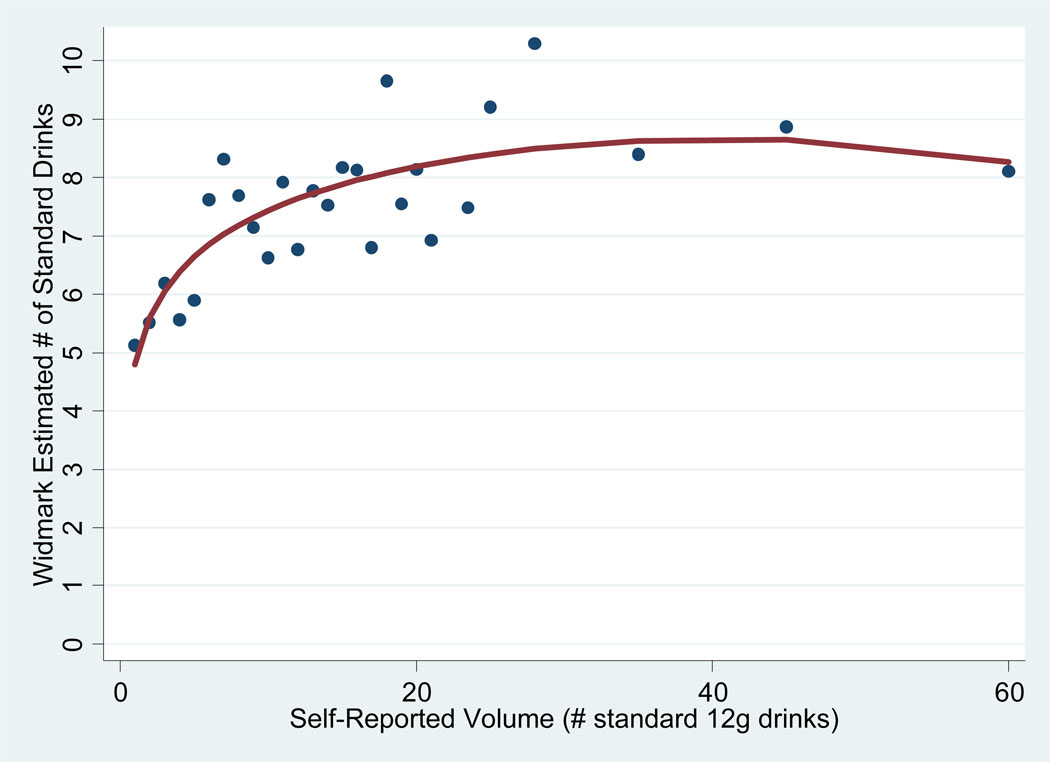
The relationship between self-reported volume (x-axis) and individual (Figure 3) or aggregated (Figure 4) volume estimated from the Widmark equation can be seen in Figure 3 and Figure 4. In addition, the fractional polynomial fit to the data in each graph is shown as the solid line. For the individual and aggregate level data in Figure 3 and Figure 4, the R² for the fractional polynomial fit to the data is .06 and .59, respectively.

Figure 3.

Individual-Level Relationship Between Self-reported Volume (V_SR) and Widmark Estimated Volume (V_W) and Fractional Polynomial Fit to the Data

Figure 4.

Aggregate-Level Relationship Between Self-Reported Volume (V_SR) and Widmark Estimated Volume (V_W) and Fractional Polynomial Fit to the Data

A hold out sample of n=400 fairly heavy drinkers from Ireland and Switzerland ERs with sufficient data to calculate all 3 volume variables was used as a validation sample. Weighted values of κ = .17 (.03) and κ = .09 (.02) reflected similar relationships found for the validation sample as compared to the main sample used to estimate the parameters.

DISCUSSION

Below 7 drinks, the aggregated BAC and self-report appears to show a rather strong relationship. However, above a self-reported volume of about 7 drinks, the empirical plot of BAC vs. volume suggested a weak relationship between the two measures. While this could possibly reflect the (extended) length of time from drinking to BAC measurement, findings were similar when analysis was restricted to those arriving to the ER (and having a BAC estimate) within 3 hours of the injury event. Note that, as seen in Figure 1, a number of individuals reported a very large number of drinks (up to 60). Analyses were also performed removing all individuals who reported consuming from than 30 drinks (results not shown) and very similar results were found for model parameter estimates and resulting estimated volumes.

Overall, a relatively poor level of agreement was found between individual-level self-reported volume and BAC for both the empirical estimates and those derived from the Widmark equation. This was found even when the sample was again restricted to those arriving to the ER within three hours of their injury for which, due to the restriction on elapsed time, it might be argued that factors that may be associated with the heterogeneity of results (e.g., drinking with food vs. not, highly differential physiological processing of ethanol) would be minimized.

In discussing these findings, it may help to identify some differences between the gold standard measures outlined in the introduction and those available here. The parallel measures to the self-report volume and BAC gold standards available in the present study are the respondent’s self-report of the number of drinks consumed six hours before the injury and BAC at time of arrival to the ER (which may perhaps be referred to as the self-report and BAC ‘silver standards’). In addition to the lack of important drinking context information for these studies, shown to be vital to an accurate linkage of even the gold standard measures, silver standard measures may contain additional potential sources of error and bias.

For the self-reported silver standard, the respondent is asked about the number of drinks consumed six hours prior to the injury. This formalized period of inquiry may cause some respondents, as instructed, to attempt to mentally truncate the consumption for the entire drinking occasion to that occurring in the requested period (when, in fact, alcohol consumed prior to six hours before the injury, if in large enough quantities, could also contribute to positive BAC at the time of assessment) while others will report consumption during the entire drinking occasion they deem associated with the period prior to the injury, whether six hours or longer. Other problems with self-reports, including recall bias paired with the consumption of larger quantities of ethanol as well as the possible fear of legal repercussions (e.g., traffic accidents) (Borges et al., 2006) or other liabilities associated with injury of themselves or others due to their own alcohol use, may also bias reports. Alternatively, patients may also overestimate their drinking; for example, those with violence-related injuries may over-report alcohol consumption to excuse behavior that would otherwise be seen as socially unacceptable (MacAndrew and Edgerton, 1969). For respondents consuming large quantities, there bay also be the reality that they simply cannot remember how much they consumed which could lead to substantial measurement error at high quantity levels. In addition, although efforts were made to obtain BAC and self-report data from those presenting to the ER with more serious conditions, this was not possible for all cases. Prior work has found that such cases have relatively high rates of positive BAC (15%) readings and may be more likely to have relatively high BAC levels (Touquet et al., 2008).

The silver standard BAC might be considered less affected by biases, at least in terms of those described above, as an estimate of the gold standard BAC. The accuracy of the breathalyzer has been shown to be quite good and, with accurate assessment of the time between injury and arrival (and excluding those drinking after the injury), an approximation of the BAC at the time of injury can be constructed. However, estimation of the rate of elimination of ethanol from the body using the Widmark zero-order kinetic model would typically assume that the patient was in the descending portion of their BAC curve in order to estimate BAC at time of injury. This may be a very poor estimate of that BAC if the BAC curve is still in ascension at the time of injury, in which case the BAC at time of injury may be even lower than that at the time of assessment. In addition, if the time from last drink until the BAC measure was long enough such that the BAC reading was to fall to 0, the empirical relationship between self-reported volume and BAC would be biased downward. In each of these cases, the period over which the alcohol was consumed and the pattern of consumption can be key in the estimation of the gold standard BAC from that of the silver standard. In fact, due to their effect on BAC, these two factors are likely to be the largest contributors to the lack of agreement between self-report and BAC measures, much moreso than other factors such as demographics or typical drinking characteristics of the patient.

In this aggregated sample of injured persons coming to emergency rooms, the relationship between both the empirically as well as Widmark-estimated and self-reported number of drinks consumed is relatively low (weighted Cohen's κ = 0.16, κ = .15, respectively). The Widmark estimate appears to make the numbers of nonmatches with V_SR more even in each direction moreso than does the empirical estimate; in Table 4, 37%/41% of the cases are on the upper/lower diagonal whereas in Table 3, 33%/43% are on the upper/lower diagonal. On average, the estimates by the two measures are fairly close together in the range of 1–6 drinks. At higher levels, the raw BAC reading tends to be systematically lower than the reported number of drinks consumed (Figure 2). A large part of this discrepancy is due to the fact that time has passed between the consumption of the drinks and the measurement of the BAC.

That VSR and Widmark estimated drinks are roughly in balance implies that there is no systematic correction which should be applied to estimates of risk of injury from self-reports in emergency room studies. On the other hand, the extent of discrepancies from the Widmark estimate means that the estimates of risk are much affected by "noise", perhaps in the direction of dampening the relative risks.

Should ER studies, and the risk estimates derived from them, switch to BAC rather than self-report as the main source of estimation of alcohol consumed? The main problem with this, as has been noted in these studies, is the substantial number of cases who reported drinking but show a zero BAC, presumably because their body had already metabolized drinks they had in fact consumed (and not due to a bogus pipeline effect). Over one-quarter (26.2%, Table 2) of those reporting some drinking showed a zero BAC, while only 2.1% of those who reported no drinking had a positive BAC.

A switch to relying solely on the BAC at ER arrival, even with a Widmark correction, would thus be unwise and would give misleading results. Future studies might, however, consider using some combination of the two measurements. One simple solution would be to use whichever of the two measurements gave a higher implied number of drinks.

This discussion is an attempt to outline the difficulties encountered in trying to predict drinks from BAC in a naturalistic setting. Some of the difficulties that result from a lack of complete information about the drinking event, present even in situations where very accurate and unbiased estimates of quantity consumed and BAC are available, are made worse by the restrictions placed on researchers by the use of standardized survey methods (e.g., measuring consumption over a 6 hour window). Therefore, it is not surprising that a rather weak relationship was found between BAC and self-reported number of drinks. Subsequent studies focusing not only on the overall drink count in a six hour period, but the total drinking that occurred in the entire drinking episode before the injury, as well as the pattern of drinking over this period, may be key in more accurately predicting consumption from BAC readings.