Ensemble Methods for Monitoring Enzyme Translocation along Single Stranded Nucleic Acids

Abstract

We review transient kinetic methods developed to study the mechanism of translocation of nucleic acid motor proteins. One useful stopped-flow fluorescence method monitors arrival of the translocase at the end of a fluorescently labeled nucleic acid. When conducted under single-round conditions the time courses can be analyzed quantitatively using n-step sequential models to determine the kinetic parameters for translocation (rate, kinetic step size and processivity). The assay and analysis discussed here can be used to study enzyme translocation along a linear lattice such as ssDNA or ssRNA. We outline the methods for experimental design and two approaches, along with their limitations, that can be used to analyze the time courses. Analysis of the full time courses using n-step sequential models always yields an accurate estimate of the translocation rate. An alternative semi-quantitative “time to peak” analysis yields accurate estimates of translocation rates only if the enzyme initiates translocation from a unique site on the nucleic acid. However, if initiation occurs at random sites along the nucleic acid, then the “time to peak” analysis can yield inaccurate estimates of even the rates of translocation depending on the values of other kinetic parameters, especially the rate of dissociation of the translocase. Thus, in those cases analysis of the full time course is needed to obtain accurate estimates of translocation rates.

1. Introduction

Many nucleic acid enzymes must translocate processively along a nucleic acid filament in order to function. For example, DNA and RNA helicases are ATPases that can generally translocate along one or both nucleic acid (ssNA) strands that result from unwinding of a double-stranded nucleic acid (dsNA) [1]. Hence, most of these enzymes are also ssNA translocases [2]. In fact, ssNA translocation activity, even in the absence of helicase activity, may be important for some enzymes in their function to displace proteins from the ssNA [3, 4]. As such, studies of the mechanism of ssNA translocation are important to gain insight into these processes. Steady state approaches are generally not useful to obtain information on the rates of translocation because steady state rates are often dominated by other processes such as enzyme assembly, binding, or dissociation, that are much slower than translocation rates. Hence, pre-steady state methods are needed to detect the more rapid kinetic steps involved in translocation. The study of ssNA translocation has been facilitated by the development of fluorescent stopped-flow assays that monitor the arrival of a translocase at a unique site on the ssNA, usually the 3′ or 5′ end [5–7]. First described by Dillingham et al.[6], the assay involves the use of ssDNA labeled with a fluorophore at either the 3′ or 5′ end. When the translocase reaches the fluorophore, its fluorescence intensity is affected (either enhanced or quenched), thus providing a means to monitor arrival of the enzyme at the end of the NA. By comparing time courses performed using ssNA with fluorophores on either the 3′- or 5′-end, one can readily determine the directionality of translocation. In addition to gaining information on translocation directionality, these time courses can be analyzed to determine the kinetic parameters (i.e., translocation rate, processivity, etc) describing translocation. This is accomplished by conducting experiments using ssNA that vary in length, L. The analysis of these time courses is simplified by including a “trap” for free enzyme that prevents dissociated translocase from rebinding the ssNA [8]. The resulting “single-round” translocation time courses can be globally analyzed using non-linear least squares methods to determine the translocation kinetic parameters [5].

Here we outline the use of these methods that have been used to study ssDNA translocation of E. coli UvrD [8, 9], B. stearothermophilus PcrA [10], E. coli Rep [11], S. cerevisiae Srs2 [4] and the helicase domain of the NS3 helicase from hepatitis C virus [12]. We discuss aspects of experimental design and assumptions used in the quantitative analysis of the full time courses using an n-step sequential model. We also compare the analysis of the full time course with a semi-quantitative approach (“time-to-peak” analysis method) and discuss the limitations of these methods for translocases that initiate at random positions along the DNA.

2. Single-round stopped-flow assay for monitoring enzyme arrival at the end of a single-stranded nucleic acid

Information about the elementary kinetic steps involved in enzyme translocation along a linear lattice requires the use of pre-steady state kinetic methods. Here we discuss a pre-steady state fluorescence stopped-flow method to examine enzyme translocation along ssNA [6, 8]. The assay has been used to study ssDNA translocation [4, 6, 8–11, 13] as well as ssRNA translocation [12]. In this assay the ssNA is labeled covalently at either the 3′ or 5′ end with a fluorophore that undergoes a fluorescence intensity change (quenching or enhancement) upon arrival of the translocase at the fluorophore. Through analysis of a series of such experiments performed with ssNA of different lengths, L, one can obtain information about the kinetic steps involved in the translocation process. The assay is performed by pre-incubating the translocase with ssNA in buffer in one syringe of the stopped-flow apparatus, and then mixing rapidly with the contents of the second syringe, containing buffer, ATP, MgCl₂, and a protein trap as depicted in Figure 1A. The protein trap prevents any free translocase or translocase that dissociates during translocation from rebinding to the ssNA, ensuring a single-round of translocation [8, 9]. Below we highlight issues that should be considered in optimizing the experiment for a given translocase and features of the resulting time courses.

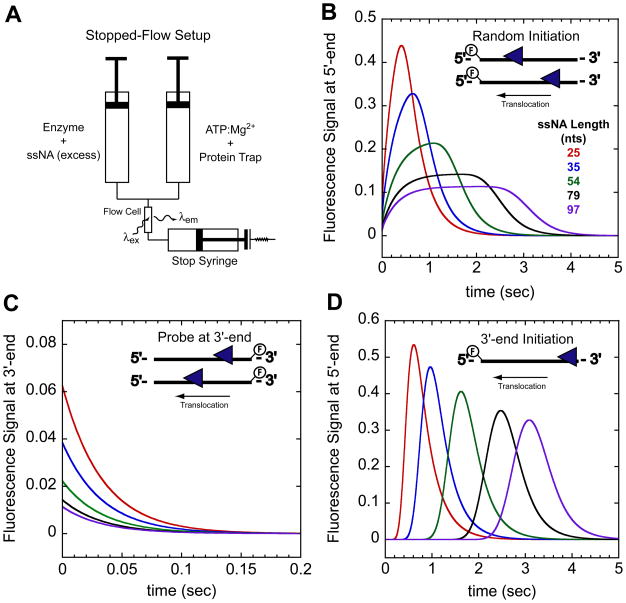
Figure 1.

Stopped-flow experimental setup and expected time courses for monitoring directionally biased translocation. (A)- Schematic of stopped-flow experiment. In one syringe enzyme is pre-incubated with excess ssNA labeled at either the 5′ or 3′end with a fluorophore. The enzyme:ssNA complex is rapidly mixed with ATP, Mg²⁺, and a protein trap to initiate translocation. Detection of changes in the fluorophore fluorescence intensity as the translocase nears the fluorophore indirectly monitors translocation. (B)- Example time courses monitoring arrival of a 3′ to 5′ translocase at the 5′-end of the ssNA when the translocase is initially bound to random sites along the ssNA. (C)- Example time courses monitoring the translocase leaving the 3′-end of the ssNA. In this experiment the ssNA is labeled at the 3′-end. Combing the experiments in (B) and (C) one can directly assess the directionality of translocation. (D)- Example time courses monitoring arrival of 3′ to 5′ translocase at the 5′-end of the ssNA when the translocase is initially bound at the 3′-end. The time courses were simulated with the following parameters described in the text mk_t = 30 nts/sec, k_d = 0 sec⁻¹, k_end = 3 sec⁻¹, and m = 1 nt/step.

2.1 ssNA substrates and fluorophore selection

When designing the ssNA substrates it is important to consider the base composition and the length. When studying ssDNA translocation oligodeoxyribothymidylates ((dT)_L) of defined length, L, have generally been used to eliminate base paired structures that could affect translocation. For similar reasons, oligouridylates ((U)_L) can be used to study ssRNA translocation. Both nucleic acids can be synthesized using standard phosphoramidite chemistry using a DNA synthesizer [14] or can be obtained commercially. We typically prepare 5–8 ssNA with lengths between 16-124 nucleotides (nts), [4, 9–11]. In using oligonucleotides for these studies, one needs to consider whether there are substantial “end-effects” associated with the binding of the translocase to the ssNA. In other words, if the enzyme binds differently to the ends than the interior regions of the nucleic acid then the initial binding distribution can be skewed. In fact, such effects can occur in many systems simply due to differences in the electrostatic properties of the ends of linear nucleic acids [15]. Such effects were observed for the UvrD system and were minimized by using ssNA that are greater than ~40 nucleotides [8].

The selection of the fluorophore is clearly important since its fluorescence intensity must be perturbed upon interaction with the translocase. In general, we have found that Cy3 (enhanced fluorescence) and fluorescein (quenched fluorescence) work well for most of the translocases that we have studied. We have also used Cy5, Rhodamine Red and Oregon Green. Most of these fluorophores are available as phosphoramidite derivatives allowing them to be incorporated directly during synthesis of the ssNA. If a phosphoramidite derivative of a particular fluorophore is unavailable then the ssNA substrate can be labeled post synthesis. This requires incorporation into the ssNA of a carbon linker possessing a primary amine, which can be readily accomplished using commercially available phosphoramidite derivatives. Fluorescent dyes activated with an N-hydroxy-succinimidyl-ester (NHS ester) react with primary amines allowing the ssNA to be labeled.

2.2 Solution conditions

The buffer conditions for these experiments can be varied and are limited only by the particular enzyme under study. One should find conditions under which a single enzyme species (e.g., monomer, dimer, etc.) is initially bound to the ssNA since a mixture of species with different kinetic properties will complicate the analysis. It is also important that no more than one translocase be bound to any ssNA. For some systems this can often be achieved by simply using a molar excess of ssNA over the translocase. However, the stoichiometry of the translocase bound to the ssNA should be verified independently, which can be done using a sedimentation equilibrium experiment [4, 10].

2.3 Selection of protein trap

Analysis of the translocation time courses is considerably simplified if performed under single-round conditions such that no re-binding of the translocase occurs once it dissociates from the ssNA. These conditions are achieved by including a protein trap to sequester enzyme once it dissociates from the ssNA. For the enzymes we have studied, we find that heparin serves as an efficient, inexpensive trap [4, 9–11]. Heparin also has the added benefit of not supporting the ATPase activity of the translocase, which is important when studying ATP hydrolysis during translocation [9]. One drawback of heparin is that in some cases it is able to actively promote dissociation of the translocase from the ssNA, presumably by binding directly to the enzyme while it is translocating. One can detect whether this occurs by examining the effect of heparin concentration on the translocation activity as well as on the dissociation kinetics [8]. However, even for enzymes that can be actively displaced by heparin, this does not influence the translocation kinetics of the enzyme [8, 9]. We have also observed that the ability of heparin to actively displace (strip off) the translocase from the ssNA can vary depending on the commercial source of the heparin. Thus, any new preparation of heparin should be characterized as described below to determine the concentration of heparin that is sufficient to serve as an efficient trap.

After preparation of a heparin stock, it is necessary to determine the minimum amount of heparin needed to serve as an efficient trap for the translocase under study. This is performed in a stopped-flow experiment by rapidly mixing the translocase in buffer with a buffer containing the fluorescently labeled ssNA, ATP, MgCl₂, and different concentrations of trap [8]. In this way one can determine the minimum trap concentration that results in no change in the fluorescent signal indicating that all enzyme is bound to the heparin trap. At this concentration no re-binding will occur to the labeled ssNA.

2.4 Translocation time courses

The qualitative features of the translocation time courses can be used to assess the directionality of enzyme translocation and the initial distribution of enzyme bound to the ssNA. In the discussions to follow, we will consider a translocase that exhibits biased 3′ to 5′ directionality; however, the same qualitative features and trends in the time courses apply to a translocase with 5′ to 3′ directionality. Figure 1B shows a series of simulated time courses monitoring the arrival at the 5′-end of ssNA of a translocase population that is initially bound randomly to sites along the ssNA. In this example, we assume that a fluorescence enhancement occurs upon interaction of the translocase with a fluorophores at the 5′-end. Once the translocation reaction is initiated by the addition of ATP, the time course shows an initial fluorescence increase until a maximum is reached (referred to as the peak). This is followed by a decay of the fluorescence back to the level for free ssNA, reflecting dissociation of the translocase from the 5′-end of the ssNA. As the length of the ssNA increases, the average time required to reach the maximum signal change increases and the time courses become broader consistent with directional translocation [6, 8]. The simulations in Figure 1C show that when the fluorescent probe is at the 3′-end, an exponential decrease in fluorescence occurs reflecting movement of the translocase away from the fluorophore and/or dissociation from the ssNA; the rate of decay is independent of ssNA length, although the amplitude of the signal change is length dependent [8]. The qualitatively different features for the time courses when the ssNA is labeled at the 5′-end or the 3′-end are indicative of an enzyme that translocates with biased 3′ to 5′ directionality.

The qualitative features of the translocation time course also yield information about how the ensemble population of enzyme is distributed when initially bound to the ssDNA (before addition of ATP). The time courses in Figure 1B were simulated for a translocase that initially binds randomly along the ssNA. Such time courses have been observed for monomers of UvrD [8], PcrA[6, 10], Rep [11], and yeast Srs2 [4] translocation. A different translocation time course is expected for a translocase that initiates at a unique site away from the fluorescent probe (e.g., at the 3′-end) as shown in Figure 1D. In this case, a ssNA length dependent lag in the fluorescence signal is observed followed by an increase in fluorescence reflecting the translocation phase followed by a decrease in signal as the translocase dissociates from the 5′-end. Such lag kinetics are similar to those observed in DNA unwinding by helicases that initiate from a unique site [16, 17]. As discussed below, consideration of the initial binding distribution is important when analyzing the translocation time courses.

3. Analysis of the full time course of translocation monitoring arrival of translocase at one end of the ssNA yields accurate estimates of the translocation rate

Time courses, such as those in Figures 1B and 1D, have been analyzed using two approaches. The first is a semi-quantitative approach that uses only the change in the “time to reach the peak” of fluorescence as a function of increasing ssNA length [6, 13]. The second involves a fitting of the full time course to a simple n-step sequential model [7, 8]. As we discuss below, when the translocase initiates from a unique site, the macroscopic translocation rates can be estimated reliably using either approach, although analysis of the full time course can yield additional kinetic information. However, for a translocase that initiates from random sites along the ssNA, a reliable estimate of even the macroscopic translocation rate requires analysis of the full time course. In contrast, the semi-quantitative approach of examining only the “time to peak” as a function of ssNA length can yield unreliable estimates of the translocation rate depending on the values of the rate constants for dissociation of the translocase from the ssNA.

3.1 Fitting algorithms and simulations for the full time course of translocation

Based on the n-step sequential kinetic model, mathematical expressions have been obtained that describe the time dependent arrival of a translocase at the 5′-end of the ssNA [5]. The experimental translocation time courses can be fit to these expressions using non-linear least squares (NLLS) methods using the software Conlin [18] and the IMSL library (Rogue Wave Software, Boulder, CO). The Conlin programs that we use for this purpose are available upon request and IMSL library can be purchased from (www.vni.com).

The translocation time courses, such as those shown in Figure 1, were simulated using MatLab (The MathWorks, Inc. Natick, MA). The simulations were generated by solving the linear differential equations for the translocation scheme described below and plotting the translocase population at either the 5′ or 3′-end as a function of time. Translocation was modeled by assuming the enzyme (translocase) moves along the ssNA in directionally biased one-nucleotide steps with translocation rate, k_trans. After each step the enzyme can either dissociate from the ssNA with rate constant k_d, or take another step. Upon reaching the 5′-end the enzyme dissociates with rate constant k_end. The enzyme does not rebind the ssNA since the experiments are performed under single-round conditions. In these simulations the enzyme binds to the ssNA with a contact size of 10 nts. The initial binding distribution of the enzyme population was either constrained to be random along the ssNA or to occur only at the 3′-end. The values of the kinetic parameters used in the simulations are defined in the figure legends. The MatLab code for simulating ssNA translocation is also available upon request.

3.2 Analysis of complete time courses using n-step sequential models

The preferred method to obtain the most reliable estimates of the kinetic parameters describing enzyme translocation is to analyze the full time course using an n-step sequential kinetic model [7]. This approach is facilitated by having independent estimates of dissociation rate constant of the enzyme from internal sites on the ssNA since this will allow this to be constrained in the analysis and facilitate estimates of other parameters that can be highly correlated [8]. N-step sequential models have been used to describe the kinetics of nucleic acid unwinding by helicases and translocation along nucleic acids [8, 17]. The approaches discussed below have been used to analyze the single-round ssNA translocation kinetics of E. coli UvrD [8, 9], B. stearothermophilus PcrA [10], E. coli Rep [11], S. cerevisiae Srs2 monomer [4] and the helicase domain of hepatitis C viral NS3 [12].

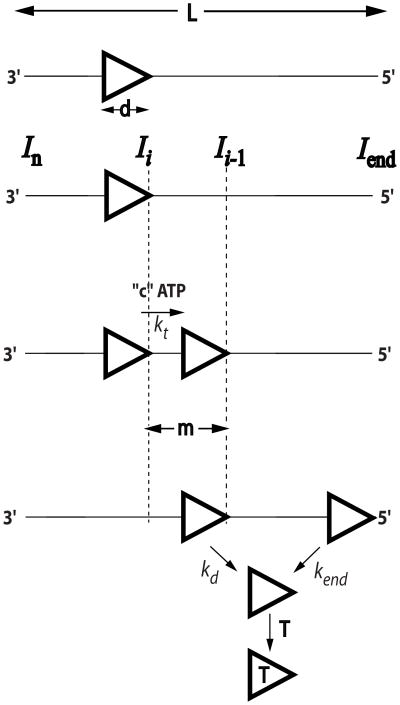
The n-step sequential model is depicted in Figure 2 [5]. In this model a translocase with ssNA contact size, d (nucleotides), binds randomly, but with polarity to a ssNA of length, L (nucleotides). The translocase is assumed to bind with equal probability to any stretch of d nucleotides (i.e., potential end effects are ignored) using its full contact size even when bound to the ends of the DNA (i.e., no dangling protein). The translocase is initially bound i translocation steps away from the 5′-end, with concentration, I_i. The number of translocation steps, i, is constrained (1 ≤ i ≤ n), where n is the maximum number of translocation steps needed for a translocase bound at the 3′ end to move to the 5′ end of the nucleic acid. Upon addition of ATP the translocase moves with directional bias along the ssNA via a series of repeated steps with translocation rate constant, k_t. During each translocation step the translocase moves “m” nucleotides, while hydrolyzing “c” ATP molecules and can dissociate from any internal ssNA site with rate constant, k_d. The ratio “c/m” defines the ATP coupling stoichiometry. When the translocase reaches the end of the ssNA it dissociates with rate constant, k_end. Inclusion of a protein trap with the ATP prevents any free translocase from rebinding ssNA. The average number of nucleotides translocated between two successive rate-limiting steps is defined as the translocation kinetic step-size, m. In order to determine the ATP coupling stoichiometry, the time course and/or quantity of ATP hydrolyzed during translocation needs to be determined along with the time courses of arrival of the translocase at the ssNA end [9]. The product mk_t (nts/sec) is the macroscopic translocation rate and is equivalent to k_trans (nts/sec) used in the simulations.

Figure 2.

Cartoon depicting n-step sequential mechanism for ssNA translocation. Translocase (triangle) bind randomly, but with polarity, to a ssNA of L nucleotides, with contact size d nucleotides and translocate (3′ to 5′) in steps of m nucleotides (kinetic step-size) with rate constant, k_t, hydrolyzing c ATP molecules per m nucleotides. Upon reaching the 5′-end the translocase may futilely turnover ATP with rate constant k_a. Translocase dissociates from internal ssNA sites with rate constant, k_d, and from the 5′-end of the ssNA with rate constant k_end and is prevented from rebinding the DNA by binding to trap molecule such as heparin. The product of mk_t is the macroscopic translocation rate (nts/sec), which is equivalent to k_trans used in the simulations.

The experimental translocation time courses obtained for different ssNA lengths are analyzed by fitting them with the appropriate expression for the time-dependent accumulation of translocase at the 5′-end of the nucleic acid using NLLS methods [7, 8]. Equations (1) and (2) show expressions for f_5′(t), the time-dependent accumulation of translocase at the 5′end for two different initial binding distributions of enzyme along the ssNA [7]. Equation (1) assumes a random initial binding distribution and would be used to analyze time courses such as those shown in Figure 1B; while Equation (2) assumes all enzymes initiate at the 3′-end (unique site) and would be used to analyze time courses such as those shown in Figure 1D. In these equations, ℒ⁻¹ is the inverse Laplace transform operator, s is the Laplace variable, the parameters k_t, k_d, k_end, and n are as defined above, and r is the initial (at time, t = 0) ratio of the probability of translocase binding to any position on the nucleic acid other than the 5′-end and the probability of the translocase binding to the 5′-end.

$$f_{5^{\prime }}(t)=\frac{A}{1+nr}{\mathcal{L}}^{-1}\left[\frac{1}{s+k_{\mathit{end}}}\left(1+\frac{k_{l}r}{s+k_d}\left(1-{\left(\frac{k_t}{s+k_t+k_d}\right)}^n\right)\right)\right]$$ (1)

$$f_{5^{\prime }}(t)=A{\mathcal{L}}^{-1}\left[\frac{1}{k_{\mathit{end}}+s}{\left(\frac{k_t}{k_t+k_d+s}\right)}^n\right]$$ (2)

The scalar A in Equations (1) and (2) allows for conversion of the concentration of protein bound at the 5′ end of the nucleic acid to the fluorescence signal measured in the stopped-flow assay.

When implementing the above equations in a NLLS fitting algorithm the parameters k_t, k_d, k_end, and r are floated as global parameters (i.e., they are the same for each ssNA length), while A and n are allowed to float independently for each ssNA length. A plot of the maximum number of steps, n, as a function of ssNA length will have a linear relationship that can be fit to equation (3) to determine the translocation kinetic step size, m, and the apparent contact size, d, of the translocase on the ssNA [7].

$$n=\frac{L-d}{m}$$ (3)

We have found that the values of some of the kinetic parameters (e.g., k_end, r, n, k_t, and m) determined in the analysis can be fluorophore-dependent; however, the product of m and k_t, the macroscopic translocation rate (equivalent to k_trans in the simulations), is generally independent of the fluorophore [8, 9]. To minimize the influence of the fluorophore on the estimates of r, n, k_t, and m, time courses obtained with ssNA substrates labeled with two different fluorophores can be analyzed simultaneously as described [8, 9].

3.2.1 Application of the n-step sequential model for the analysis of the translocation of E. coli UvrD monomer along ssDNA

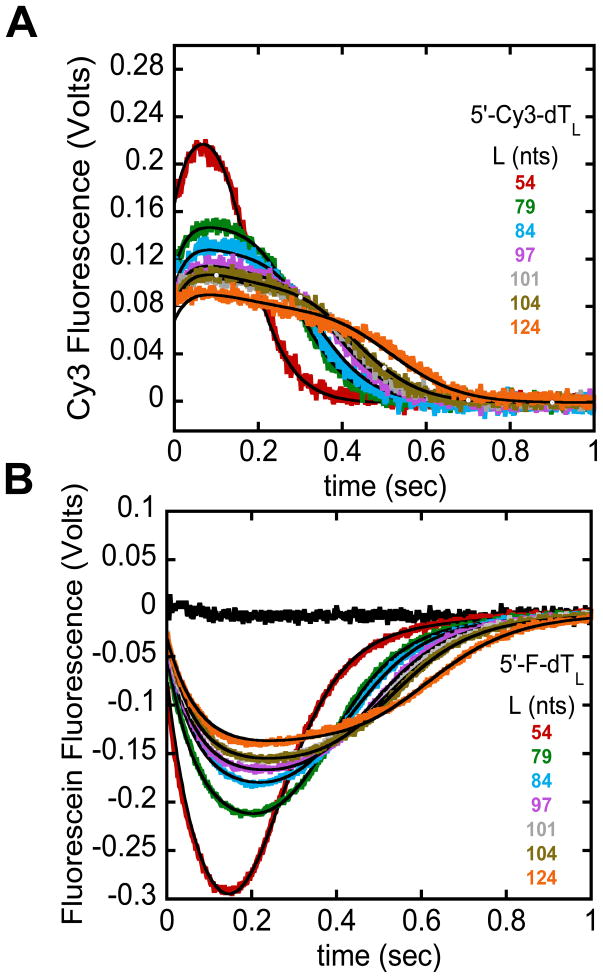
It has been shown that NLLS analysis of a series of time courses using the n-step sequential model (Eqs. (1) and (2)) will yield accurate estimates of the translocation kinetic parameters [5]. Figures 3A and 3B show time courses obtained for the E. coli UvrD monomer translocation along ssDNA (dT_L) labeled at the 5′-end with Cy3 or fluorescein, respectively [9]. The black curves are simulations using the best-fit parameters determined from NLLS analysis of the complete time courses using the n-step sequential model as described [9] (mk_t = 193 ± 1 nts/sec, k_t = 42 ± 2 kinetic steps/sec, m = 4.6 ± 0.2 nts/kinetic step, d = 8 ± 1 nts, k_d = 0.81 ± 0.04 sec⁻¹, r = 1.8 ± 0.8, k_{end, Cy3} = 0.5 ± 0.1 sec⁻¹, k_{c, Cy3} = 30 ± 3 sec⁻¹, k_{end, fluorescein} = 2.5 ± 0.1 sec⁻¹, and k_{c, fluorescein} = 13.7 ± 0.2 sec⁻¹). In this example a modified version of the n-step sequential model depicted in Figure 2 was used to fit the data where UvrD dissociation from the 5′-end occurred through two elementary steps defined by rate constants k_c and k_end [8, 9].

Figure 3.

Example analysis of the full translocation time courses using a n-step sequential model. E. coli UvrD monomer translocation along ssDNA monitored by the arrival of UvrD at the 5′-end of either Cy3 (A) or fluorescein (B) labeled (dT)_L as described [9]. The black time course shows that the amount of heparin (trap) present in the reaction is sufficient to prevent UvrD from rebinding to ssDNA. The smooth black curves are simulations using the n-step sequential model and the best-fit parameters determined from a combined global NLLS analysis of the time courses in (A) and (B) [9].

3.2.2 Interpretation of the apparent translocation kinetic step size

In addition to the macroscopic rate of translocation, mk_t, the analysis of the complete time course also yields an estimate of the translocation kinetic step-size, the average number of nucleotides translocated each translocation cycle. However, for a variety of reasons the translocation kinetic step-size should be viewed as an upper limit to the physical translocation step-size. This is primarily due to the potential presence of pausing, slipping, and static disorder (persistent heterogeneity among the enzyme population, such that different translocase molecules persist with different translocation rates over the course of the experiment) [7]. The presence of these phenomena generally cannot be assessed from ensemble methods alone and require the use of single molecule methods [19–23]. Despite the limitation on the mechanistic interpretation of the kinetic step-size, these phenomena do not hinder the determination of the average macroscopic translocation rate (mk_t) [7].

4. Use of the “time to peak” analysis

4.1 The semi-quantitative “time-to-peak” analysis can yield inaccurate estimates of translocation rates for enzymes that initiate from random sites along the ssNA

The initial description of the fluorescence method used to monitor the kinetics of arrival of the B. stearothermophilis PcrA translocase at the 5′-end of a ssNA introduced a semi-quantitative “time to peak” analysis to estimate the translocation rate [6]. Although this method is simple and straightforward, it can provide inaccurate estimates of translocation rates for enzymes that initiate randomly along ssNA. However, the “time to peak” analysis does provide accurate estimates of translocation rates for enzymes that initiate translocation from a unique site on the ssNA. In contrast, the NLLS analysis of the full time courses using the n-step sequential model discussed above always provides a reliable estimate of the macroscopic rate of translocation regardless of the initial distribution of enzyme.

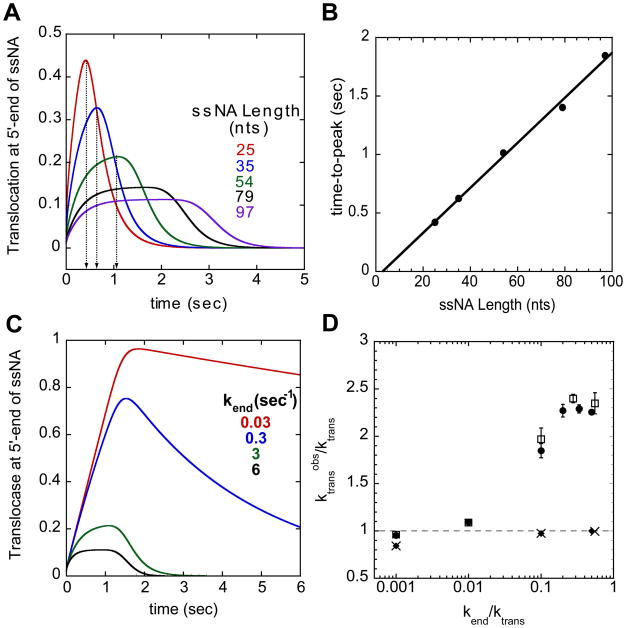
The premise of the time-to-peak analysis is that the time to reach the maximum signal (for fluorescence enhancement) or minimum signal (for fluorescence quenching) reflects the average time needed for the population of translocases to reach the 5′-end of the ssDNA. A plot of the time-to-peak determined from the time course for each ssNA length (see Figure 4A) will generally result in a linear relationship (see Figure 4B) if translocation is directionally biased. The inverse of the slope provides an estimate of the translocation rate (nts/sec) [6]. The first difficulty arises in that it is often difficult to even identify a peak position when the enzyme initiates randomly along the ssNA. This is evident for the longer ssNA lengths (79 and 97 nts) in Figure 4A. However, as we show here, use of the time-to-peak analysis can result in significant overestimates of the translocation rate; in many cases, the translocation rate can be overestimated by more than a factor of two. However, the extent of this overestimation depends on the rate of translocation relative to both the dissociation rate from internal ssNA sites as well as from the 5′-end of the ssNA, as we discuss below. Since the true rate of translocation can only be obtained accurately from an analysis of the full time course for the random binding case, one cannot know the extent of the inaccuracy of an apparent translocation rate estimated from a time-to-peak analysis.

Figure 4.

Time-to-peak analysis and the effect of translocase dissociation from the ssNA end on the estimated translocation rate. (A)- Time-to-peak analysis is done by determining the time of the maximum signal change (peak) in the translocation time courses for each ssNA length. The time courses were simulated with the following parameters k_trans = 30 nts/sec, k_d = 0 sec⁻¹, k_end = 3 sec⁻¹, and m = 1 nt/step. (B)- Plot of the time-to-peak from (A) as a function of ssNA length. The inverse of the slope of the linear fit yields an estimate of the translocation rate, mk_t. (C)- Simulation of translocation time courses on ssNA 54 nts in length with different dissociation rate constants from the 5′-end (k_end). The same simulation parameters as above but at k_end = 0.03 (red), 0.3 (blue), 3 (green), and 6 (black) sec⁻¹. (D)- Effect of k_end on the translocation rate determined using the time-to-peak analysis. Ratio of translocation rate determined by analysis to actual translocation rate plotted versus the ratio of k_end to the actual translocation rate. The analysis results for simulations with two different translocation rates (k_d = 0 sec⁻¹) when the translocase initiates from random sites, 30 nts/sec (circles) and 180 nts/sec (squares) and when the translocase initiates from the 3′-end, 30 nts/sec (diamond) and 180 nts/se (X). The error bars represent the error from the linear regression of the observed time-to-peak as a function of ssNA length.

4.2 The rate of enzyme dissociation from the ssNA end can influence the apparent translocation rate estimated from the “time-to-peak” analysis

To demonstrate that the value of the dissociation rate constant for the translocase from the ssNA end, k_end, can influence the estimate of the apparent translocation rate determined using the time-to-peak analysis, we simulated translocation time courses for the arrival of a translocase at the 5′-end for a series of ssNA lengths and analyzed these time courses using the time-to-peak method. The time courses were simulated using a constant translocation rate (k_trans = 30 nts/sec or 180 nts/sec) and a constant dissociation rate from internal sites of the ssDNA (k_d = 0) while systematically varying the dissociation rate constant from the 5′-end (k_end). Figure 4C shows the effects on the time courses for a ssNA length of 54 nts as k_end is varied. As k_end decreases the time-to-peak increases and the peak becomes broader. These changes were observed for all ssNA lengths examined. Figure 4D plots the ratio of the apparent translocation rate, (k_trans)obs, as determined from the time-to-peak analysis, to the actual translocation rate, k_trans, used to simulate the time course, as a function of the ratio, k_end/k_trans. If k_end is very small relative to k_trans, then the time-to-peak will reflect translocation of all the translocases to the 5′-end, just as it would if all translocases were initially bound at the 3′-end (see below). Under these conditions, the time-to-peak analysis provides an accurate estimate of the translocation rate. However, as k_end increases and approaches the value of the true translocation rate, the apparent translocation rate will be overestimated by as much as 2.3-fold. A similar trend was observed for simulations employing a faster translocation rate (k_trans = 180 nts/sec, Figure 4D, open squares). In contrast, analysis of simulated time courses in which the translocase initiates translocation from a unique site (e.g., the 3′-end) always resulted in an accurate estimate of the true translocation rate regardless of the value of k_end (Figure 4D, diamonds (k_trans = 30 nts/sec), X symbols (k_trans = 180 nts/sec)). Alternatively, if a clear lag phase is observed, as in Figure 1D, the lag time can be used instead of the time-to-peak to estimate the translocation rate. Analysis of the lag times yields an estimate of the translocation rate that is within 5% of the true translocation rate (data not shown). An accurate estimate of the true translocation rate is expected in this case since the time-to-peak (or the lag time) now reflects the average time for all translocases to reach the 5′-end.

4.3 Enzyme processivity can influence the apparent translocation rate estimated from the “time-to-peak” analysis

The translocation rate estimated from a time-to-peak analysis can also be influenced by the processivity of enzyme translocation. Processivity, defined as $P=\frac{k_{\mathit{trans}}}{k_{\mathit{trans}}+k_d}(0\le P\le 1)$, is the probability that the translocase takes a step forward (k_trans) rather than dissociates from the ssNA (k_d). Thus, the degree of processivity will determine whether a translocase reaches the end of the ssNA and is detected in the assay. The effect of processivity on the observed signal change and time-to-peak is more pronounced when the translocase is initially bound randomly along the ssNA. Figure 5A shows a series of simulated time courses for translocase arrival at the 5′-end of a 54-nucleotide long ssNA for varying values of k_d. In these simulations the translocation rate was maintained at 30 nts/sec while k_d was varied from 0 to 5 sec⁻¹. Figure 5A shows that the time-to-peak shifts to earlier times as k_d increases and the peak profile becomes more asymmetric. In fact, the asymmetry causes very little change in the peak position for ssNA lengths greater than 30 nts (Figure 5B), prohibiting use of those lengths for a determination of the translocation rate. The increased asymmetry in the time course is due to the fact that as k_d increases, enzymes initially bound closer to the 5′-end have a higher probability of reaching the 5′-end and thus contributing to the signal, while enzymes initially bound further away never reach the 5′-end.

Figure 5.

Effect of the translocase dissociation rate constant from internal sites of the ssNA on the translocation rate determined using the time-to-peak analysis. (A)- Simulation of translocation time courses on ssNA 54 nts in length for translocase randomly bound along ssNA with different dissociation rate constants from internal sites (k_d). The time courses were simulated with the following parameters k_trans = 30 nts/sec, k_end = 3 sec⁻¹, and m = 1 nt/step with k_d = 0.0 (red), 0.5 (dark blue), 1.0 (green), 2.0 (black), 3.0 (magenta), and 5.0 (light blue) sec⁻¹. (B)- Simulation of translocation time courses on ssNA of different lengths using the same parameters as in (A) with k_d = 1.5 sec⁻¹. Notice for lengths greater than 30 nts, the peak position does not appear to shift to longer times. (C)- Effect of k_d on the translocation rate determined using the time-to-peak analysis. Ratio of translocation rate determined by analysis to actual translocation rate plotted versus the ratio of k_d to actual translocation rate. Analysis results for two different translocation rates (30 nts/sec (filled) and 180 nts/sec (open)) where translocase is initially bound to random sites along the ssNA (circles) or initially bound at the 3′-end (squares). The diamond data points were obtained from simulations using long ssNA (Lengths: 25, 35, 54, 79, and 97 nts) as in figure 1 and 2. All other data was obtained from simulations using short ssNA (Lengths: 15, 20, 25, 30, and 35 nts). The error bars represent the error from the linear regression of the observed time-to-peak as a function of ssNA length. (D)- Simulation of translocation time courses on ssNA 54 nts in length for translocase bound at 3′-end with different dissociation rate constant from internal sites (k_d). Same simulation parameters as in (A).

To demonstrate the effect of k_d on the estimation of the translocation rate using the time-to-peak analysis we simulated time courses for shorter lengths of ssNA (12, 15, 20, 25, and 30 nts) where a clear shift in the peak position is observed as the ssNA length increases. Analysis of the time courses where the translocation rate and k_end were held constant (mk_t = 30 or 180 nts/sec and k_end = 3 or 18 sec⁻¹, respectively) but k_d was varied resulted in apparent translocation rates that were 1.3–2.2-fold larger than the true translocation rate (Figure 5C). In contrast, if the enzyme is initially bound at the 3′-end, the time-to-peak (Figure 5D) is essentially unaffected by increases in k_d or processivity. Only the amplitude is affected, which reflects the amount of translocase reaching the 5′-end. As a result, the apparent translocation rate determined using the time-to-peak analysis for this case provides a more accurate (within 10%) estimate of the true translocation rate regardless of k_d and the ssNA lengths used (Figure 5C, square and diamond symbols).

The effect of k_d on the translocation time courses can be understood by considering the initial binding distribution of translocase along the ssDNA in relation to the observed signal. When the enzyme is initially bound randomly along the ssNA the enzymes closest to the 5′-end have the highest probability of reaching the 5′-end. When k_d increases, the observed signal is biased to reflect the translocases that initiate nearest to the 5′-end. Translocases bound further away have a lower probability of reaching the 5′-end, and thus do not contribute to the observed signal, resulting in the increased asymmetry feature in the time courses as mentioned above. The result is an overestimation of the translocation rate since the time-to-peak reflects translocation over only a fraction of the full ssNA length. When all enzymes are initially bound at the 3′-end any observed signal is due to translocases that reach the 5′-end, thus the time-to-peak will always reflect the average time of translocation for the entire length of the ssNA. An increase in k_d only results in fewer enzymes reaching the 5′-end (decreased amplitude), but with the same average time of translocation. Of course if k_d is too high compared to the translocation rate then no signal change will be observed (see Figure 5D, k_d = 5 sec⁻¹).

5. Concluding Remarks

A useful approach to study the kinetics of enzyme translocation along ssNAs has been a stopped-flow method in which either the 3′ or 5′ end of a ssNA substrate is labeled with a fluorophore [6, 8]. Analysis of the full time courses using n-step sequential models reliably determines the translocation rate without making assumptions about translocation processivity or the dissociation rate constant from the labeled end of the ssNA. We compared this analysis method with a semi-quantitative method that estimates a translocation rate from the length dependent trends observed in the time courses [6, 13]. Our simulations demonstrate that the semi-quantitative time-to-peak analysis can provide a reliable estimate of the true translocation rate, but only when the enzyme initiates translocation from a unique site at a known distance from the fluorescent probe. In contrast, if the enzyme initiates translocation from random sites along the ssNA, the apparent translocation rate estimated from a time to peak analysis can be greatly overestimated.