The Long and the Short of it: On the Nature and Origin of Functional Overlap Between Representations of Space and Time

Abstract

When we describe time, we often use the language of space (The movie was long; The deadline is approaching). Experiments 1–3 asked whether—as patterns in language suggest—a structural similarity between representations of spatial length and temporal duration is easier to access than one between length and other dimensions of experience, such as loudness. Adult participants were shown pairings of lines of different length with tones of different duration (Experiment 1) or tones of different loudness (Experiment 2). The length of the lines and duration or loudness of the tones was either positively or negatively correlated. Participants were better able to bind particular lengths and durations when they were positively correlated than when they were not, a pattern not observed for pairings of lengths and tone amplitudes, even after controlling for the presence of visual cues to duration in Experiment 1 (Experiment 3). This suggests that representations of length and duration may functionally overlap to a greater extent than representations of length and loudness. Experiments 4 and 5 asked whether experience with and mastery of words like long and short—which can flexibly refer to both space and time—itself creates this privileged relationship. Nine-month-old infants, like adults, were better able to bind representations of particular lengths and durations when these were positively correlated (Experiment 4), and failed to show this pattern for pairings of lengths and tone amplitudes (Experiment 5). We conclude that the functional overlap between representations of length and duration does not result from a metaphoric construction processes mediated by learning to flexibly use words such as long and short. We suggest instead that it may reflect an evolutionary recycling of spatial representations for more general purposes.

Introduction

Central to human sophistication is the ability to engage in abstract thought—thought about things that we cannot directly perceive with our senses. Consider the ability to reason about time. The experience of time is fundamental— as Robert Ornstein (1969) has remarked, “…time is one of the continuing, compelling, and universal experiences of our lives, one of the primary threads which combine in the weave of our experience.” Yet there is no bodily organ specialized for temporal representation, nor any physical process in the world that gives rise to its experience. A challenge for cognitive science is to characterize the representations that underlie our experience of time and account for how they arise over evolution and ontogenesis.

The study of the nature and origin of abstract concepts has often taken representations in the domain of time—considered by many to be an example of an abstract domain par excellence—as a test case (e.g., McGlone & Harding, 1998; Gentner, Imai, & Boroditsky, 2002; Boroditsky, 2000, 2001; Casasanto & Boroditsky, 2008; Casasanto, 2008). Some clues to the representation of time come from language. Linguists have noted that when we talk about temporal experience (and our experiences in other abstract domains), we co-opt the language of space, describing time as something we can actually see (Gruber, 1965; Clark, 1973; Lakoff & Johnson, 1980; Jackendoff, 1983; Talmy, 1988; Langacker, 1987). For example, in English, we speak of a ‘long meeting’, the ‘approaching deadline’, and the ‘future that lies ahead’ (see Table 1). The use of spatial language to describe time is also robust across languages (Traugott, 1978; Sweetser, 1991; Alverson, 1994).

Table 1.

Parallels between spatial and temporal language (from Jackendoff, 1983).

Spatial Reference	Temporal Reference
At the corner	At 6:00 P.M.
From Denver to Indianapolis	From Tuesday to Thursday
The bus is fast approaching	Christmas is fast approaching
The train crept by	Tuesday crept by
The border lies ahead of us	Our future lies ahead of us
In Cincinatti	In 1976

These uses of language motivate a provocative proposal: we may use spatial language to describe time because we have adapted our cognitive faculties of spatial reasoning (for which we have richer perceptual experience) to the task of temporal reasoning, resulting in structural similarities and functional overlap among representations in the two domains (Lakoff & Johnson, 1980; Jackendoff, 1983; Pinker, 1997, 2007; Murphy, 1996; Casasanto & Boroditsky, 2008; Casasanto, 2008). Of course, it would be hasty to draw sweeping conclusions about how we think from the presence of metaphorical language (cf. Murphy, 1996, Pinker, 1997). In order to gain new meanings, words were initially extended creatively (e.g., from using long to refer to not only space, but also to time). But over time, the initial motivation for these extensions could have faded, and could no longer be transparent to speakers today. This would suggest that, in these cases, metaphorical language is just an etymological relic (see Keysar, Shen, Glucksberg, & Horton, 2000; but see also Thibodeau & Durgin, 2008).

But while metaphorical language need not reveal relationships among concepts, a compelling body of evidence suggests that spatial and temporal representations are intimately related in the mind (McGlone & Harding, 1998; Gentner, Imai, & Boroditsky, 2002; Boroditsky, 2000, 2001; Xuan et. al., 2007; Casasanto & Boroditsky, 2008; Casasanto, 2008). A first contribution of the present experiments is to add another phenomenon in support of this position, which demonstrates that magnitude representations of space and time more spontaneously engage with and align with one another than do other structurally similar representations. We suggest that spatial and temporal representations functionally overlap to a large extent, perhaps due to a shared neural substrate. A second contribution of these experiments is to elucidate the role of ontogenetic and evolutionary processes in establishing this functional overlap. On the one hand, it is possible that spatial representations have been recycled, over evolutionary time (see Gould & Vrba, 1982), for the purpose of representing time, resulting in an innate, generalized representation for both space and time. Alternatively, functionally overlapping representations of space and time could result from a metaphorical construction process over development that is motivated by learning to use spatial words such as long and short to metaphorically describe temporal experience (see Boroditsky, 2000). We test whether this type of linguistic experience is necessary for the creation of functional overlap among spatial and temporal representations and provide evidence that it is not.

In the present studies, we focus on one aspect of the representation of time: namely, the representation of temporal duration, as invoked in phrases such as “a long tone” or “this tone is longer than that one.” The structurally similar representations of space we consider are representations of spatial length, as invoked in phrases such as “a long line” or “this line is longer than that one.”

Structural Similarity

Two representational systems are structurally similar if they can be relationally aligned as follows: symbols (a, b, c, …) and relations (P, Q, …) in one system are mapped to symbols (a′, b′, c′, …) and relations (P′, Q′, …) in the other such that if a given relation holds among symbols in the first system, a mapped relation among mapped symbols holds in the second, structurally similar system. This is a fairly weak sense of structural similarity and it describes many systems of representation. Under this definition, for example, dimensions in which symbols are serially ordered (e.g., numbers, days of the week, and letters of the alphabet) are structurally similar and can be aligned by virtue of that relation (e.g., 1=Monday, 2=Tuesday, 3=Wednesday, etc.). However, structurally similar representations can have even richer relational mappings. Consider the case of analog magnitude representations, which include representations of numerosity as well as other continuous quantities and intensities such as area, spatial length, duration, brightness, temperature, and loudness (Meck & Church, 1983; Brannon, Suanda, & Libertus, 2007; Feigenson, 2007). The structural similarity among these dimensions goes beyond the fact that each is characterized by a serial order. First, each has an analog format—each dimension of experience is represented by a physical magnitude that is proportional to the quantity it depicts. Second, in virtue of their analog formats, these representations are inherently noisy, such that representations of increasing values are increasingly more variable. This ensures that comparison of different values along a particular dimension is subject to Weber’s law, where discriminability is a function of the ratio of two values, rather than their absolute difference. Third, locating individual values along each of these continua depends upon a contextually defined standard, as evidenced by the semantic congruity effect (Banks, Clark, & Lucy, 1975; Holyoak & Walker, 1976; Petrusic, 1992).

Analog magnitude representations meet the basic conditions of structural similarity: a pair of dimensions can be relationally aligned such that the ratio between a pair of values on a first dimension is the same as that between a pair of mapped values on a second dimension (e.g., 1 = a line one inch long, 2 = a line two inches long, etc.). Classic work in psychophysics on cross-modal matching demonstrates that people can access this structural similarity when they are instructed to do so (Stevens & Guirao, 1963; Stevens & Marks, 1965, Stevens, 1975). Participants are presented with successive pairs of stimuli that differ along some dimension (e.g., tones of different durations). For each stimulus pair presented in this first dimension, participants are asked to adjust the stimuli from a second dimension (e.g., lines of different lengths) until the difference between them seems to match that of those of the first dimension (such that the lengths of lines differ by the same ratio as the lengths of tones). Adults and even young children find this a meaningful task and provide consistent and systematic responses. In particular, one can predict matching responses from the discriminability of each matched dimension on its own. Many dimensions of experience are represented by analog magnitudes, and all participate in cross-modal matching (Stevens, 1975).

The structural similarities among analog magnitude representations are important in explaining how it is that different dimensions could be described using the same language: if metaphorical extensions of words are to be understood, people must be able to align elements and relations between the source and target domains (Gentner, 1983). However, the use of spatial language to describe time across languages suggests a stronger relationship between representations of space and time than the mere possibility of relationally aligning them. That is, although all magnitude representations are alignable with representations of duration in the sense defined here, we do not use the language of loudness, brightness, temperature, or pain to describe duration.

Functional Overlap

Some structural similarities among systems of representation may reflect an even stronger relationship—a functional overlap in processing that allows these representations to automatically engage one another, leading to spontaneous access of their structural similarity (Walsh, 2003; Cantlon, Platt, & Brannon, 2009). Psychological evidence for functional overlap of many of the dimensions discussed above dates back to the ‘congruity’ tasks of Paivio (1975). In these Stroop-like paradigms, participants are shown two stimuli on a computer screen, such as two numerical digits. Participants are told to attend to one dimension of the stimuli (e.g., their cardinal value) and choose which of the two stimuli is larger on this dimension, while ignoring variation in an irrelevant dimension (e.g., physical size). The two dimensions are varied such that the stimuli are either relationally congruent (the numerically larger digit is also physically larger), neutral (the two digits are of the same size), or incongruent (the numerically larger digit is the physically smaller one). These studies find a facilitative effect of congruent pairings (they are responded to faster than neutral pairings), and an inhibitory effect of incongruent pairings (they are responded to slower than neutral pairings) and have been observed in the interactions between number, size, and luminance (Henik & Tzelgov, 1982; Cohen Kadosh & Henik, 2006, but see Pinel et al., (2004), who do not find behavioral interference between number and luminance). Automatic effects of congruence on processing have also been observed in the SNARC effect, in which participants are faster to make judgments about larger numbers on the right side of space and smaller numbers on the left side of space (Dehaene, Bossini, & Giraux, 1993; Fias, 2001). These effects demonstrate a spontaneous, intrinsic mapping between number and space, and similar effects have also been observed for pitch and space (Rusconi et al., 2006).

Studies on the processing of temporal duration also suggest that its representations functionally overlap with spatial representations. For instance, Xuan and colleagues (2007) had participants judge which of two stimuli were presented for a longer duration, and found that participants were affected by variation in irrelevant properties of the stimuli presented (e.g., their numerosity, size, and luminance), such that when these were of a “larger” magnitude, stimuli were judged to last longer. Casasanto and Boroditsky (2008) also suggested that representations of duration are spontaneously aligned with representations of spatial length. Participants were presented a line for some amount of time, and were then asked to reproduce its duration by indicating the beginning and end of the interval with mouse clicks. The spatial length of the line interfered with duration estimates—longer lines were estimated to last for longer periods of time, and shorter lines for shorter periods.

Just as structural similarity is graded, so too is functional overlap—representations of different dimensions may engage with and align with one another to different degrees. For example, Casasanto (2008) found that irrelevant variation in spatial length interfered with estimates of temporal duration for English and not Greek speakers, while irrelevant variation in quantity interfered with estimates of duration for Greek speakers and not English speakers. These effects are consistent with linguistic patterns in English and Greek—while the dominant spatial metaphor for duration in English is length (a long meeting), the dominant metaphor in Greek involves quantity (a big meeting). This result suggests that language learning may play a role in the degree to which representations functionally overlap, an issue to which we will later return.

Functional overlap may in some cases also reflect shared neural substrate. Information processing of many of the different dimensions under discussion here appears to involve the same brain areas, including inferior parietal areas and the intraparietal sulcus (IPS). For example, the level of behavioral interference observed in congruity tasks is correlated with level of activity in the IPS, suggesting that it may be the site of integration of information from different dimensions, including number, size, and luminance into a generalized magnitude system (Fias et al., 2003; Cohen Kadosh, Cohen Kadosh, & Henik, 2008, but see Pinel et. al., 2004, who suggest a different locus for representations of luminance). Neuropsychological data from non-human primates also support this possibility, as individual neurons in posterior parietal areas simultaneously code for both line length and numerical value (Tudusciuc & Nieder, 2007).

There are also indications that the IPS and other inferior parietal areas may include representations of duration, in addition to representations of space, numerosity, luminance, and other magnitudes. First, these areas have been shown to be active during the encoding of temporal intervals (Rao, Meyer, & Harrington, 2001). Second, damage to inferior parietal areas often results in temporal disorientation—and also often results in deficits in spatial and numerical abilities (Critchley, 1953). Finally, application of trans-cranial magnetic stimulation to the IPS can cause deficits in spatial tasks, number comparison, and temporal discrimination (Bjoertomt, Cowey, & Walsh, 2002; Cohen Kadosh, et al., 2007; Rushworth, Ellison, & Walsh, 2001; Walsh & Pascual-Leone, 2003).

Thus, inferior parietal areas and the IPS may be responsible for representations and computations that are general to a variety of quantities and intensities including numerosity, size, length, duration, and brightness (Walsh, 2003; Cantlon, Platt & Brannon, 2009), although these representations could share neural circuitry to different extents (cf. Pinel et al., 2004). This functional and neural overlap could reflect a recycling, over evolutionary time, of representations and processes for more general purposes (e.g., from a system that once computed only spatial length, to one that computed length, duration, numerosity, and other magnitudes) (Cantlon, Platt, & Brannon, 2009). Environmental, cultural, and linguistic experience could also play a role in creating functional overlap among different quantities and intensities over ontogeny (Lakoff & Johnson, 1980, 1999; Berch et al., 1999; Zebian, 2005, Boroditsky, 2000; Casasanto, 2008).

Due to their functional overlap, the representations of different magnitudes could automatically engage with one another, making their relational correspondences transparent. To the extent that functional overlap is graded, those correspondences that are the easiest for people to notice might also be reflected in flexible word use, as the same words (e.g., long, short, big, high, etc.) come to be applied to functionally overlapping dimensions. Thus, while a structural similarity among different representations is necessary to explain how different dimensions could be relationally aligned and described using the same words, a large degree of functional overlap could explain why some dimensions, such as spatial length and temporal duration, receive common expression in many of the world’s languages.

Human Development

Evidence from human infants’ discrimination of values in different domains provides unequivocal evidence that infants deploy analog magnitude representations for a variety of quantities, including temporal duration. Like human adults and non-human animals, human infants discriminate numerosity, length, duration, and other continuous quantities and intensitities according to Weber’s law. For example, 6-month-old infants can discriminate numerosity at a 1:2 ratio (but fail at a 2:3 ratio), independent of whether sets are presented as dots (Xu & Spelke, 2000), sounds (Lipton & Spelke, 2003), or actions (Wood & Spelke, 2005), and independently of the absolute size of the sets (success at 4 versus 8 but not 4 versus 6; success at 16 versus 32 but not 16 vs. 24). Discrimination of duration, area, and length also depend on ratio, and interestingly, at 6 months of age the critical Weber ratio for these dimensions is also 1:2 (vanMarle & Wynn, 2006; Brannon, Lutz, & Cordes, 2006; Huttenlocher, Duffy, & Levine, 2002). Discrimination of numerosity increases in precision by 9 months of age, when infants succeed at a 2:3 ratio (Lipton & Spelke, 2003; Wood & Spelke, 2005). The discrimination of duration also shows increasing precision at the same age (Brannon, Suanda, & Libertus, 2007).

These studies of human infants suggest that numerosity, duration, length, area, and other continuous quantities and intensities have a common representational format, as mental analog magnitudes, and so are structurally similar to each other in the sense defined above. But in addition, the fact that the Weber ratio for numerosity and duration is the same at 6 months, and improves equivalently at 9 months suggests that the representations of these dimensions, and perhaps others (such as area and length, which are also discriminated at a 1:2 ratio at 6 months), may be more intimately related. Rather than merely drawing on a common type of representation, these dimensions may draw on functionally overlapping, generalized representations. However, the common and increasing precision in discrimination seen with numerosity and duration could also reflect an increase in precision of the common magnitude comparison process, which could in principle operate over distinct representations from different domains (Feigenson, 2007; Cantlon, Platt, & Brannon, 2009). In order to establish whether infants, like adults, have functionally overlapping representations of different dimensions, studies are needed to explore whether infant representations of different dimensions can automatically engage with and relationally align with one another.

Given the ubiquity of analog magnitude representations in the animal kingdom as well as their early presence in infancy (e.g., Meck & Church, 1983; Gallistel, 1990; Feigenson, 2007; Cantlon, Platt, & Brannon, 2009), it is unlikely that a metaphorical construction process over ontogeny is necessary for the creation of structurally similar representations of space and time. Nonetheless, it is an open question as to whether such a process plays a role in creating functional overlap between representations of temporal duration and spatial length. Indeed, the results of Casasanto (2008) suggest that experience using the spatial metaphors of one’s language may play an important role in creating or strengthening functional overlap between these dimensions. The present studies begin to explore these issues.

The Present Studies

The experiments reported here make use of a novel paradigm to explore the degree of functional overlap between the representation of spatial length, on the one hand, and other representations—of temporal duration (Experiments 1 and 3) and loudness (Experiment 2)—on the other. Because a form of this paradigm was to be used with pre-linguistic infants (Experiments 4 and 5), it could not, like Paivio’s congruity paradigm, explicitly direct participants to attend to certain dimensions of the stimuli and ignore others. Instead, the task measured participants’ spontaneous tendencies to relationally align the values of two dimensions. The task was simple—participants were asked to attend to a randomly presented array of lines of different lengths. Each line was paired with a tone, the tones differing from one another on a second dimension (duration in Experiments 1 and 3; loudness in Experiment 2). In familiarization, one group of participants saw a relationally congruent set of pairings in which the two magnitudes that constituted the stimuli were related by a positive linear function (e.g., longer lines paired with longer tones). The other group of participants saw an incongruent set of stimuli where the two magnitudes were related by a negative linear function (e.g., longer lines paired with shorter tones). In test, both groups were shown pairings from both the congruent and incongruent sets and were asked whether they remembered seeing each one in familiarization.

Because any given magnitude (e.g., a line or a tone) would appear, during familiarization, in the context of other magnitudes (other lines or tones), each could be encoded in relative terms, as having a certain relative “quantity”. Pairings from the congruent set could consequently be seen to consist of two magnitudes that stand in the same relations to other magnitudes from their respective domains (e.g., a line that is x times longer than the shortest line and y times shorter than the longest line would be paired with a tone that is x times longer than the shortest tone and y times shorter than the longest tone). As previous studies have shown, if participants access a structural similarity among dimensions and recognize relational equivalence in a pairing, it can be encoded and processed more efficiently and precisely (Paivio, 1975; Dehaene, Bossini, & Giraux, 1993). This could then yield an asymmetry whereby participants receiving a congruent familiarization are better able than participants receiving an incongruent familiarization to process those stimuli, and to later differentiate between them and the novel test stimuli. Of interest to us was the degree to which participants receiving a congruent familiarization would spontaneously construct a relational mapping among the stimuli from the paired dimensions, given that they could approach this task without doing so. For instance, participants could instead make arbitrary associations between the lines and tones presented during familiarization, in which case performance would not differ between the two groups of participants. Participants could also formulate an explicit, general rule to describe the pairings they see—the longer the line, the longer the tone, or the longer the line, the shorter the tone—in which case performance would also not differ between the groups.

While a structural similarity between representations is necessary and sufficient for the recognition of relational equivalence in pairings from the congruent set (as shown by cross-modal matching phenomena, Stevens & Guirao, 1963; Stevens & Marks, 1965, Stevens, 1975), a functional overlap between representations could make participants more likely to access that structural similarity and construct a relational mapping between those representations. Thus, conceptually, functional overlap between two dimensions is suggested if those dimensions are more spontaneously and precisely aligned than other, equally alignable pairs of dimensions. Experiments 1–3 present evidence for such a dissociation, demonstrating that, within this task, congruence affects the binding of values of spatial length and temporal duration but not of values of length and loudness.

EXPERIMENT 1

Method

Participants

The participants were 18 Harvard University students: two participants were excluded due to failure of a method check, which showed that these participants were responding randomly. All participants were undergraduate students, and were given course credit or a token gift for their participation.

Materials

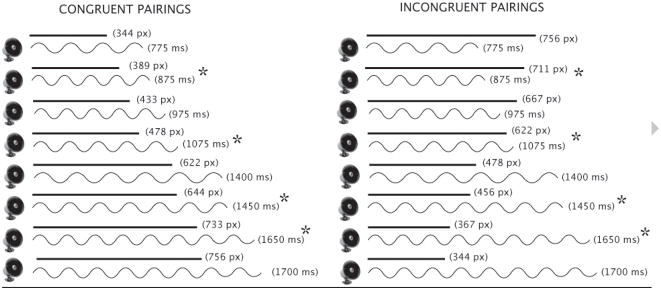
Stimuli consisted of a visual stimulus (a solid line) and an auditory stimulus (a tone) presented simultaneously. In each exposure, the line appeared at the center of a screen with a white background as the tone simultaneously began playing. The visual stimulus appeared on the screen for the duration of the tone, and then was immediately removed and followed by a 500 ms pause during which no images were presented and no sounds played. 16 different lines were used, varying in equal steps of length from the shortest line (344 pixels) to the longest line (756 pixels). All lines were 10 pts thick and blue. The 16 different tones varied in duration in equal steps from the shortest tone (775 ms) to the longest tone (1700 ms). The tones were always in A3 (220.0 Hz). Pairings of lines and tones that fell in the middle range of the presented lengths (between 500 and 600 pixels) and durations (between 1125 and 1350 ms) were omitted, as these pairings offer almost no information with respect to congruence (i.e., they could belong equally to either the congruent or incongruent sets).

In the congruent condition, pairings were positively correlated: longer lines were paired with longer tones. In the incongruent condition, the pairings were negatively correlated: longer lines were paired with shorter tones (See Figure 1). Importantly, however, the relationship between length and duration was equally predictable in the two conditions, such that a function could perfectly describe each set of pairings (Congruent: Length (pixels) = Duration (ms)/2.25; Incongruent: Length = (2475 – Duration)/2.25). Thus, a difference in processing pairings of line length and tone duration could not be attributed to a lack of predictability in the pairings of the incongruent set.

Figure 1.

Congruent and incongruent pairings of line length and tone duration presented in Experiment 1. Asterisked pairings were presented in test to both groups

The lines were generated according to the desired length using Macromedia Flash MX (Adobe Systems Incorporated, San Jose, CA), and were also combined on Flash with tones generated from Audacity, creating two simple films, one with only parings from the congruent set, and one with only pairings from the incongruent set. These films were exported in QuickTime format and embedded in Keynote for presentation.

Procedure

The study had the following structure: participants first were asked to watch and pay attention to a film of some lines and tones that they were told they would be asked questions about. The familiarization stimuli included all 16 line/tone pairings, and were presented in a random order. Half of the participants saw only pairings from the congruent set, and the other half saw only pairings from the incongruent set. Eight test trials followed. On these trials, participants were shown a pairing and asked to provide a rating of whether they had seen that pairing before or not, which they did on a 1 (definitely did not see) – 5 (definitely did see) scale. Four of the test pairings were from the congruent set and four were from the incongruent set. Thus, for each group, half of the test stimuli had been seen during familiarization and half were novel. Each test pairing was shown twice before participants were asked to give their rating. After the first four test trials, there was a method check to make sure participants were paying attention to the task: a pairing was presented that obviously had not been seen before (a red line appeared with a tone of a previously unheard pitch (c4)). Following this, participants were shown the original film again to refresh their memory, after which they were asked about the remaining four test pairings.

Test pairings were designed to vary in difficulty. Four of the pairings were drawn from the extremes of the continua (e.g., relatively long or short lines paired with relatively long or short tones), and four from closer to the middle (moderately long lines paired with moderately long tones) (See Figure 1). Because pairings drawn from the ends of the continua were less ambiguous with respect to which set they were a part of compared to those drawn from the middle, they should be easier to make judgments about. We quantified how much information a pairing gives about which set it belonged to by calculating the ratio difference in length the two functions predict, given the duration of the paired tone. In the more difficult test pairings, lengths for a given duration differed by factors of 1.3 and 1.4, while in the easier pairings, lengths varied by factors of 1.8 and 2.0.

Eight test orders were used, counterbalancing across participants the order of the pairings seen. The different test orders varied in whether pairings from the congruent or incongruent sets appeared first, in how these pairings alternated over the course of the test trials, and in the order of the easy and hard pairings.

Results

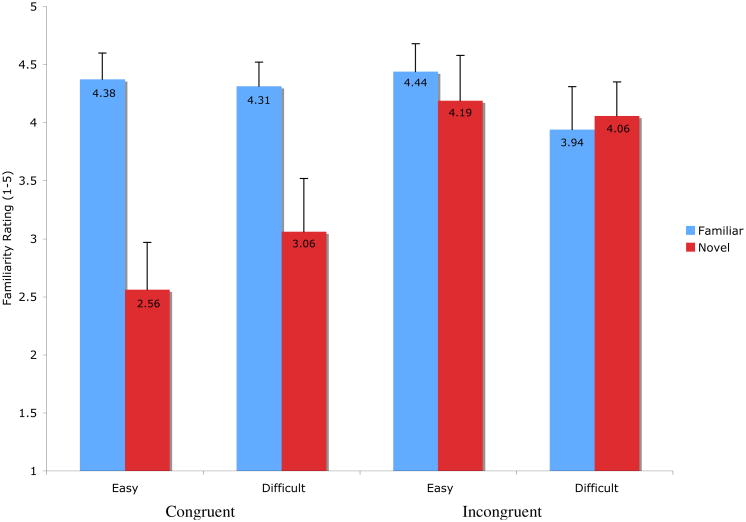
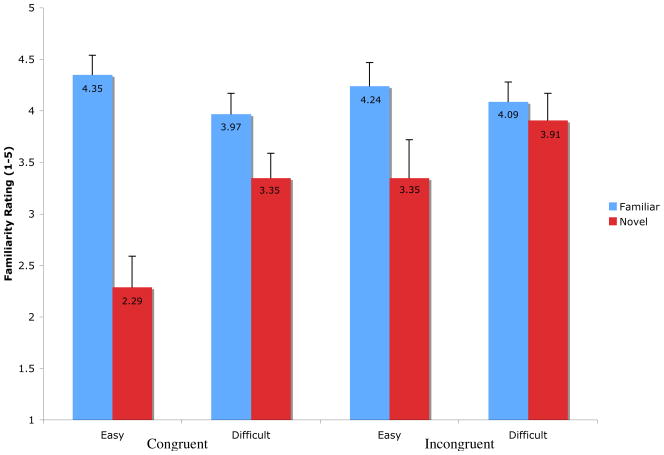
Figure 2 shows how participants in Experiment 1 rated familiar and novel trials, based on whether they had initially seen a film with only pairings from the congruent set, or one with only incongruent pairings, and on whether the test pairings were easy or difficult. Independent of difficulty, participants in the congruent group were able to differentiate the pairings they had seen (M_fam = 4.34, SD_fam = .53) from the ones they had not (M_nov = 2.8, SD_nov = 1.13), while participants in the incongruent group were not able to do this: (M_fam = 4.19, SD_fam = .83; M_nov = 4.13, SD_nov = .89). All participants gave a rating of ‘1’ to the method check trial, in which an entirely differently colored line and differently pitched tone were played.

Figure 2.

Results from Experiment 1, by test trial type, difficulty, and group

A 2 × 2 × 2 mixed-factor repeated-measures ANOVA examined the effects of the between-subjects factor of group (congruent or incongruent), and the within-subjects factors of test trial type (novel or familiar) and difficulty (easy or difficult) on the participants’ familiarity ratings¹. There was a main effect of novelty, F(1, 14) = 9.79, p < .01: participants judged the familiar items (M_fam = 4.27, SD_fam = .68) as more familiar than the novel items (M_nov = 3.47, SD_nov = 1.19). More importantly, there was a group × novelty interaction F(1,14) = 8.32, p < .05, indicating that participants in the congruent group differentiated the familiar trials from the novel trials, t(7) = 4.20, p < .005, while participants in the incongruent group did not. This interaction also receives support from the finding that seven out of eight participants in the congruent group rated familiar pairings higher than novel pairings (Wilcoxon signed ranks test, z = 2.38, p < .05), while only three out of eight did so in the incongruent group (z = .41, p = .69). No main effects or interactions involving difficulty reached significance.

Experiment 1 Discussion

The results from Experiment 1 demonstrate that adults are better able to encode and hold in memory spatial-temporal pairings when variation in length and duration is congruent, compared to when it is incongruent. On one hand, this is a surprising result, given that adults have many mechanisms and strategies for binding the features of these stimuli together, which ought not be vulnerable to whether variations among those features are congruent or not. But, under the conditions of this experiment—with only a limited number of familiarization pairings—participants more often succeeded when the variation in length of lines and duration of tones was congruent. Indeed, it is telling that the participants familiarized to pairings from the incongruent set judged both the familiar and novel pairings as being relatively familiar, and in fact, not much less familiar than the participants familiarized to pairings from the congruent set judged familiar pairings. Both groups definitively judged the control stimuli that included novel colors and pitches as novel. This suggests that participants in the incongruent group were familiarized to the pitch and range of durations of the tones, and the color and range of lengths of the lines, but—unlike participants in the congruent group—not to information on how the tones and lines were paired.

This asymmetry between the groups suggests that participants in the congruent group were not just associating together the particular lines and tones they saw in familiarization, or forming an explicit rule to describe the relationship between them, because these strategies could also have been used by participants in the incongruent group. The asymmetry in performance between the two groups instead suggests that participants in the congruent group spontaneously accessed the structural similarity between representations of length and duration, and recognized relational equivalence in the pairings they were familiarized with. Recognition of this equivalence could have allowed for precise encoding of these pairings, supporting the detection of novelty even on the difficult test trials in which novel pairings deviated minimally from familiar pairings.

Participants in the congruent group could also have induced a function to describe the pairings they saw during familiarization. This function, which would use line length to predict the duration of the tone, could have been calibrated over the course of familiarization, and used later to distinguish familiar from novel pairings. But because representations of length and duration are structurally similar, some functions could be easier to learn than others. In particular, because participants might be biased to expect tone duration to be proportional to line length, it might be easier for them to learn a function describing relationally equivalent pairings, compared to one describing relationally inverse pairings (for a related body of work suggesting this is true, see Brehmer, 1971, 1974; Busemeyer et al., 1997).

It is impossible to decide between these accounts here, because the test pairings did not require participants to interpolate or extrapolate beyond the specific pairings presented in familiarization. What is clear is that both accounts claim that participants in the congruent group spontaneously accessed a structural similarity and constructed a relational mapping between the pairings of length and duration they were familiarized with, which in turn supported the detection of novelty in both the easy and difficult test pairings. But these results do not on their own suggest that representations of length and duration functionally overlap. That is, while functional overlap would facilitate access of structural similarity, the presence of structural similarity among these representations alone may be sufficient to explain the results observed.

Thus, in Experiment 2, we ask whether, in this task, pairings from a congruent set are easier to process than pairings from an incongruent set for any two dimensions that share the structural similarity defined by an analog magnitude format, by taking pairings of lines of different length and tones of different loudness as a test case. The case of length and loudness provides an excellent and stringent comparison to that of length and duration, given that adults and even young children are able to access their structural similarity when instructed to in cross-modal matching tasks. Furthermore, the psychophysical function that equates discriminability in these two dimensions is well established and is confirmed by a number of studies of cross-modal matching (Stevens & Guirao, 1968; Stevens & Marks, 1965; Teghtsoonian, 1980). But despite the fact that representations of length are alignable with representations of loudness, the two dimensions do not receive common expression in language, nor is there evidence in the neuropsychological literature that they share neural substrate. If, as cross-linguistic patterns suggest, the relationship between representations of space and time is a privileged one, participants should be more likely to spontaneously access a structural similarity and construct a relational mapping between representations of length and duration than between representations of length and loudness.

EXPERIMENT 2

Method

Participants

The participants were 18 Harvard University students (a distinct group from Experiment 1): two participants were excluded due to failure of a method check. All participants were undergraduate students, and were given course credit or a token gift for their participation.

Materials

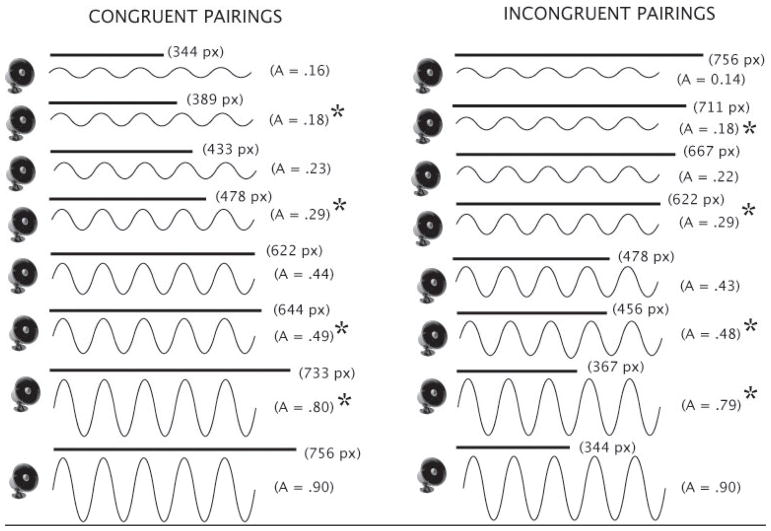
Solid lines and tones were presented simultaneously. The same 16 lines that appeared in Experiment 1 were used. 16 tones in A3 (220.0 Hz) were again used, but instead of varying in duration, they varied in loudness, while their duration was held constant at 1000 ms. The specific amplitudes for the tones were chosen such that the loudness of each tone would be as discriminable from the other tones as the lengths of the lines were. Because previous research has shown that people are less sensitive to changes in loudness than they are to changes in duration or length (Stevens, 1956), amplitude values that were simple linear transformations of lengths could not be chosen (as the durations were, in Experiment 1). Rather, the ratios between tones of different loudness needed to be larger than the ratios between lines of different length to yield comparable levels of discriminability.

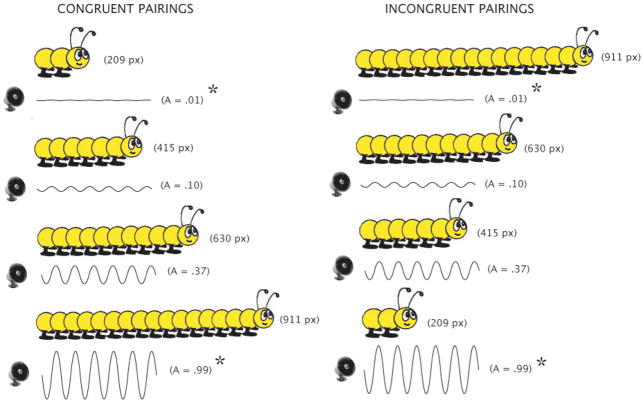
Accordingly, amplitudes were chosen using the following procedure. First, the highest, reference amplitude, which could either be paired with the longest line (in the congruent group) or the shortest line (in the incongruent group), was set to 0.9 (76 dB). To choose the amplitudes for tones paired with other lines, we then calculated the ratio differences in length between those lines and the line that was paired with the reference amplitude. To achieve changes in loudness comparable to the ratio changes in length, we used a function based on Stevens (1975), where ratio change in loudness (decibels) ⁶⁷ = ratio change in length. Having computed the decibel change (d) needed from the reference amplitude (A₀), we could choose the appropriate amplitude (A) by: A = A_0/(10(d/20)). The resulting sixteen tones varied in amplitude from 0.14 (60 dB) to 0.90 (76 dB). In the congruent condition, pairings were positively correlated in magnitude: longer lines were paired with louder tones. Meanwhile, in the incongruent condition, the pairings were negatively correlated: longer lines were paired with softer tones (see Figure 3). Participants listened to the films using closed Sennheiser headphones, with the volume setting on the iMac computer standardized at three-quarter strength.

Figure 3.

Congruent and incongruent pairings of line length and tone loudness presented in Experiment 2. Asterisked pairings were presented in test to both groups

Procedure

As in Experiment 1, participants first watched the film and were then asked questions about the eight pairings. After the first four test trials, there was again a method check to make sure participants were paying attention. The method check trial consisted of the same novel item as did the method check trial of Experiment 1, a red line paired with a pitch not heard before. Difficulty was again varied, and in this case referred to the difference in loudness between tones paired with a given line in the congruent and incongruent conditions. In the more difficult test pairings, amplitudes between conditions for a given spatial length differed by 3.2 and 5.7 decibels, while in the easier pairings they differed by 11.8 and 14.1 decibels (see Figure 3). All other aspects of the procedure were the same as in Experiment 1.

Results

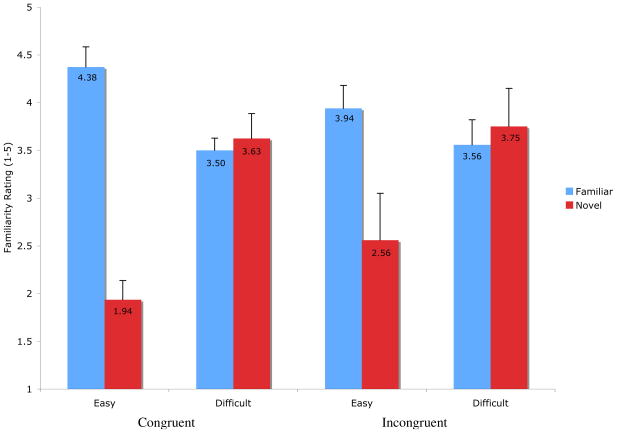
Figure 4 shows how participants in Experiment 2 rated the familiar and novel trials, based on whether they had initially seen a film with only pairings from the congruent set or the incongruent set, and whether the pairings were easy or difficult. In contrast to Experiment 1, the participants in the incongruent condition provided the same pattern of ratings as did those in the congruent condition. Participants in both conditions differentiated between the easy novel and familiar test trials and failed to differentiate between the difficult novel and familiar test trials (Figure 4). All participants in the final sample gave a rating of ‘1’ to the method check trial.

Figure 4.

Results from Experiment 2, by test trial type, difficulty, and group

As in Experiment 1, when participants failed to differentiate the novel and familiar stimuli—on the difficult test trials—they still rated them all as familiar. This suggests that for these more difficult pairings, participants were familiarized to the pitch and range of the loudness of the tones, and the color and range of length of the lines, but not to information on how the tones and lines were paired.

A 2 × 2 × 2 mixed-factor repeated-measures ANOVA examined the effects of the between-subjects factor of group (congruent or incongruent), and the within-subjects factors of test trial type (novel or familiar) and difficulty (easy or difficult) on the participants’ familiarity ratings². There was a main effect of novelty, F(1, 14) = 19.36, p < .001: participants judged the familiar items (M_fam = 3.84, SD_fam = .43) as more familiar than the novel items (M_nov = 2.97, SD_nov = .91). Importantly, however, and unlike Experiment 1, the group × novelty interaction did not reach significance: F(1,14) = 2.0, p = ns. In another analysis, we pooled the data of Experiments 1 and 2 together, and the three-way interaction between experiment (Experiment 1 vs. 2), group, and novelty approached significance, F(1, 28) = 2.69, p = .11, indicating a larger interaction effect in Experiment 1 than in Experiment 2.

Novelty significantly interacted with difficulty: F(1, 14) = 30.31, p < .001: participants in each group distinguished between familiar and novel trials only on the easy trials (Congruent: t(7) = 7.04, p <.001, Incongruent: t(7) = 2.62, p < .05), but not on the difficult trials (Congruent: t(7) = −.447, p = .668, Incongruent: t(7) = .532, p = .61). In line with this, eight out of eight participants in the congruent group and five out of eight in the incongruent group judged the easy familiar trials as more familiar than the easy novel trials (Wilcoxon signed ranks tests, Congruent: z = 2.54, p < .05; Incongruent: z = 1.88, p = .06) but on the difficult trials, only two out of eight in the congruent group and one out of eight in the incongruent group did so (Congruent: z = .32, p = .75; Incongruent: z = .54, p = .59).

Experiment 2 Discussion

Two features of the data from Experiment 1 suggested that the participants in the congruent group spontaneously aligned the pairings of length and duration they were familiarized with: first, these participants outperformed participants receiving an incongruent familiarization, and second, they were able to detect novelty in even the difficult test pairings. The results of Experiment 2 stand in contrast to those of Experiment 1 on both of these grounds: participants in the congruent group of Experiment 2 performed no better than those in the incongruent group, and also did not succeed in detecting the difficult novel test trials. On the easier test trials, participants in both the congruent and the incongruent groups were able to differentiate between the familiar and novel pairings. Success on these trials does require some binding of representations of length and loudness—participants may have formed associations of particular pairings, or may have constructed a general rule that longer lines were paired with louder (congruent group) or softer tones (incongruent group)—but whatever strategy was adopted was available equally to both groups. Participants may have failed on the difficult trials because the strategy they used may not have allowed for a precise enough encoding of the familiarization stimuli.

The presence of an effect of congruence in Experiment 1, but not in Experiment 2, suggests that while the participants of Experiment 1 accessed the structural similarity between representations of length and duration, the participants of Experiment 2 were not able to do so for representations of length and loudness. Access of this structural similarity may have allowed participants in the congruent condition of Experiment 1—but not either group from Experiment 2—to differentiate between even the difficult novel and familiar test trials. This would suggest that representations of length and duration functionally overlap more than do representations of length and loudness, making sense of the use of spatial language to describe time across languages.

However, there are two alternative accounts of the results reported thus far preclude adopting this conclusion. In Experiment 1, stimulus duration varied in two aspects of the stimuli—visually (i.e., in the duration the line remained on-screen) and via audition (i.e., in the duration of the tone), while in Experiment 2, loudness information was accessible only to audition and all lines remained on-screen for the same amount of time. The presence of multiple cues to duration in Experiment 1 raises two problems. First, because there was a visual cue to duration in Experiment 1, but only an auditory cue to loudness in Experiment 2, only participants in Experiment 2 were required to integrate information across modalities, as participants in Experiment 1 could have matched spatial and temporal information using vision alone. Second, in the congruent condition of Experiment 1, the longer lines were visible for a longer time than they were in the incongruent condition. Because the lengths of the lines varied in equal steps, the longer lines differed from one another by smaller, less discriminable ratios than did the shorter lines. This meant that participants in the congruent condition of Experiment 1 had more time available to encode the more difficult-to-discriminate lines than did participants in the incongruent condition, which may account for why there was an effect of congruence in Experiment 1, but not in Experiment 2 (in which all lines were visually presented for the same amount of time). Of course, this account does not explain why participants in the incongruent group of Experiment 1 also failed to differentiate familiar pairings of short lines with long tones (which they would have had ample time to encode) from novel pairings of long lines with long tones or short line with short tones.

To address these concerns, both of which derive from the presence of a visual cue to duration in Experiment 1, in Experiment 3 we repeated Experiment 1, removing the visual cue. All lines were visually presented for the same duration, such that only the duration of their accompanying tones conveyed temporal information. If spontaneous access of the structural similarity between representations of length and duration does not depend on the presence of a visual cue to duration, but instead reflects functional overlap between these representations, the results of Experiment 3 should closely resemble those of Experiment 1.

EXPERIMENT 3

Method

Participants

The participants were 37 Harvard University students (a distinct group from Experiments 1 and 2): three participants were excluded due to failure of a method check. We doubled our sample size from the previous experiments to ensure that we had enough statistical power to detect any differences from the pattern of effects found in Experiment 1. All participants were undergraduate students, and were given course credit or a token gift for their participation.

Materials

As in Experiment 1, stimuli consisted of a paired solid line and tone. In each exposure, the line was displayed on the screen for 2000 ms. The tones were played such that they would be centered within this 2000 ms interval (i.e., the 1400 ms tone began playing 300 ms after the visual onset of its paired line, and ended 300 ms before the offset of that line). All other aspects of the materials and procedure were the same as in Experiment 1.

Results

Figure 5 shows how participants in Experiment 3 rated familiar and novel trials, based on whether they had initially seen a film with only pairings from the congruent set, or one with only incongruent pairings, and on whether the test pairings were easy or difficult. Participants in the congruent group appeared to better differentiate the pairings they had seen from the ones they had not, compared to participants in the incongruent group, on both the easy trials and on the difficult trials. All participants gave a rating of ‘1’ to the method check trial, in which an entirely differently colored line and differently pitched tone were played.

Figure 5.

Results from Experiment 3, by test trial type, difficulty, and group

A 2 × 2 × 2 mixed-factor repeated-measures ANOVA examined the effects of the between-subjects factor of group (congruent or incongruent), and the within-subjects factors of test trial type (novel or familiar) and difficulty (easy or difficult) on the participants’ familiarity ratings³. There was a main effect of novelty, F(1, 32) = 23.37, p < .001: participants judged the familiar items (M_fam = 4.16, SD_fam = .74) as more familiar than the novel items (M_nov = 3.23, SD_nov = 1.10). Just as in Experiment 1, there was also a group × novelty interaction, F(1,32) = 4.38, p < .05, indicating that participants in the congruent group better distinguished the familiar from novel pairings than participants in the incongruent group. Difficulty also significantly interacted with novelty, F(1, 32) = 15.39, p < .001, indicating a larger effect of novelty for both groups on the easy trials compared to on the difficult trials. While participants in the congruent group readily distinguished the easy familiar from novel trials, t(16) = 5.87, p < .001, there was only a trend for participants in the incongruent group to do so, t(16) = 2.07, p = .06, and while participants in the congruent group detected novelty in the difficult test trials, t(16) = 2.70, p < .05, participants in the incongruent group did not, t(16) = .58, ns. Furthermore, while thirteen out of thirteen participants in the congruent group differentiated the easy familiar from novel trials, z = 3.20, p < .001, only eight out of fourteen did so in the incongruent group, z = 1.64, p = .10, and while ten out of twelve participants in the congruent group differentiated the difficult familiar from novel trials, z = 2.3, p < .05, only four out of ten participants in the incongruent group did so, z = .10, ns.

In a final analysis, we pooled the data from Experiment 3 with that of Experiment 1 and entered the data into a mixed-factor repeated-measures ANOVA with the within-subjects factor of test trial type, and the between-subjects factors of group and experiment. While the group × novelty interaction was significant, F(1, 46) = 11.77, p < .001, the three-way experiment (Experiment 1 vs. Experiment 3) × group × novelty interaction was not, F(1, 46) = .99, ns, indicating a similar group × novelty interaction in the two experiments.

Experiment 3 Discussion

The two features of the data that suggested that participants in the congruent group of Experiment 1 had spontaneously constructed a relational mapping across representations of length and duration were both present in Experiment 3: participants receiving a congruent familiarization in Experiment 3 outperformed participants receiving an incongruent familiarization, and were able to detect novelty in even the difficult test pairings. These results demonstrate that participants do not need redundant cues to duration to spontaneously align representations of length and duration when these two dimensions vary congruently. The results of Experiments 1 and 3 stand in contrast to those of Experiment 2, in which participants were not better able to process pairings of lines of different length and tones of different loudness when variation along the two dimensions was congruent.

This pattern of results is especially compelling because adults and even young children are able to access the structural similarity between length and loudness when instructed to do so in cross-modal matching tasks (Stevens & Guirao, 1968; Stevens & Marks, 1965; Teghtsoonian, 1980). Taken together, Experiments 1 through 3 suggest that the access of structural similarity and construction of a relational mapping across representations of length and duration is more spontaneous than it is across representations of length and loudness. The presence of structural similarity among analog magnitude representations—which extends to representations of length, duration, and loudness alike—is thus insufficient to account for the results. This conclusion converges with that of Casasanto (2008) who found that irrelevant variation in spatial length intruded onto estimates of duration for English speakers, suggesting, as in Experiments 1 and 3, that representations of length are spontaneously aligned with representations of duration. But, as in Experiment 2, this effect was not general to all dimensions represented by analog magnitudes—there was no effect of irrelevant variation in quantity of liquid onto estimates of duration.

The present results suggest that the use of spatial language to describe time across languages reveals a privileged relationship between representations in these domains. These representations could functionally overlap, perhaps sharing neural substrate, such that they may spontaneously and precisely align with one another. This conclusion, however, should not be taken to suggest that representations of loudness do not functionally overlap with representations of length or other magnitudes. Although we know of no evidence that representations of length and loudness do overlap, there is evidence that representations of loudness and brightness share processing mechanisms (Marks, 1987) and automatically interact with one another early in infancy (Lewcowicz & Turkewitz, 1980). One possibility, then, is that the representations of different magnitudes functionally overlap to different extents—and that representations of length and duration (and perhaps representations of loudness and brightness) overlap more than do representations of length and loudness (cf. Pinel et al., 2004, for a similar proposal).

The Origin of Functional Overlap between Representations of Length and Duration

How might functional overlap between representations of length and duration (as observed with the adult participants of Experiments 1–3) arise? One possibility is that it is innate, having resulted from a recycling, over evolutionary time, of spatial representations in the service of representing other dimensions. However, environmental, cultural, and linguistic experience could also play a role in creating functional overlap between representations of length and duration over development. This latter possibility has received some support as an account of how spatial and numerical representations come to be linked. For example, it is only in the elementary school years that children begin to show a SNARC effect—an enhanced processing of large numbers on the right side of space, and of small numbers on the left side of space (Berch et al., 1999)—and children who learn to read from right to left show a reversed SNARC effect (Zebian, 2005). This leaves open the possibility that experience with external spatial representations of number (e.g., number lines) and explicit instruction in school could motivate children to construct functional overlap between space and number (but see de Hevia & Spelke, 2009, for evidence of a non-directional mapping between number and space in early childhood).

What types of experience might be relevant for the creation of functional overlap between representations of length and duration? Experience with external spatial representations of time—calendars, timelines, clocks, hourglasses—could play a role. But another possibility is that learning to use words such as long and short, which can refer both to spatial length, as well as to temporal duration, could suggest to children an equivalence between the two dimensions. This possibility has received some attention because of differences in how different languages describe time (Núñez & Sweetser, 2006; Boroditsky, 2001; Casasanto, 2008). For example, while English speakers typically use words like long and short to describe temporal duration, speakers of other languages such as Greek and Spanish more often use quantity terms (much time) (Casasanto, 2008).

This linguistic difference creates a cognitive difference in how duration is represented for speakers of the two languages. As alluded to before, Casasanto (2008) found that while English participants were affected by the length of a line when reproducing the duration for which that line appeared, they were unaffected by irrelevant quantity information, such as how much water filled into a beaker when reproducing the duration of that event. Greek and Spanish speakers, on the other hand, were affected by the irrelevant quantity information but not the length information. That language learning establishes this difference is supported by a training study in which English speakers learned to use quantity expressions for time (e.g., a big party to refer to a party that takes a long time). These participants subsequently showed interference from quantity information onto their estimations of duration, like the Greek and Spanish speakers.

These results suggest that language learning does not just reflect the structure of representations of duration, but is also instrumental to its development (for a related proposal, see Choi et al., 1999; Bowerman & Choi, 2001). On this view, children learning a language may notice that expressions for length or quantity can also be used to describe duration, and accordingly organize their representations of duration to functionally overlap with those of length or quantity. Parallels in language, on this view, may have been set up historically, as conventional spatial expressions for length or quantity were extended to then-novel descriptions of temporal duration. But once these parallels had become entrenched in language, they could affect children’s developing conceptual representations, creating overlap between representations of length, quantity, and duration.

The alternative is that functional overlap among representations of length, quantity, and duration exists prior to experience with the use of words like long and short. Functional overlap among these representations could be innate or could be learned from experienced correlations between distance, quantity and duration (Lakoff & Johnson, 1980, 1999; Casasanto, 2008; Jackendoff, 1983; Pinker, 1997; Walsh, 2003; Cantlon, Platt, & Brannon, 2009). On these alternatives, language learning would not play a role in the construction of cross-dimensional relationships. However, both alternatives could explain why linguistic metaphors can be drawn and comprehended in the first place (Gruber, 1965; Lakoff & Johnson, 1980; Jackendoff, 1983), and why spatial language of some kind (i.e., of length or quantity) is co-opted to describe time in language after language. On both of these alternatives, Casasanto’s (2008) cross-linguistic effects would reflect the influence of linguistic experience on the accessibility and weighting of strong, pre-existing, relationships among different dimensions (spatial length, quantity, temporal duration), but not on their actual creation.

Because understanding of dimensional adjectives such as long and short requires not only an understanding of their compositional semantics but also a consideration of the context in which they are deployed (i.e., to resolve the difference between a ‘long worm’ and a ‘long border’), the acquisition of these adjectives stretches into even the preschool years (e.g., Carey, 1982; Smith, Rattermann & Sera, 1988; see also Barner & Snedeker, 2008). Experiments 4 and 5 therefore provide a test of the competing hypotheses by asking whether 9-month-old infants, who have not yet acquired words like long and short, have functionally overlapping representations of spatial length and temporal duration. We adapted the method of Experiments 1–3 into an infant habituation study (method based on Goldman, 2005). Experiment 4 paired cartoon pictures of caterpillars of different lengths with tones of different durations. Any given exposure would thus consist of a caterpillar of some length appearing on a screen for the duration of its corresponding tone. In habituation, we manipulated whether the spatial and temporal entities were positively or negatively correlated: for the congruent group, we paired relatively long caterpillars with relatively long tones, and relatively short caterpillars with relatively short tones, and for the incongruent group, we presented the opposite pairings. In test, all participants were shown pairings from both sets.

If experience with and mastery of words like long and short is necessary for children to spontaneously construct a relational mapping across representations of length and duration, no advantage would be predicted for infants in the congruent group. Thus, on this view, infants in both groups should either fail to differentiate novel from familiar pairings, or infants in both groups should succeed, due to a general ability to construct associations in habituation. In contrast, if infants can spontaneously access a structural similarity between representations of length and duration, the results of Experiment 4 should mirror those of Experiments 1 and 3: infants in the congruent group, but not infants in the incongruent group, should encode the habituation pairings and show a novelty preference during the test trials. Experiment 5, like Experiment 2, tests whether the recognition of relational correspondences is more spontaneous in the case of length and duration than in the case of length and loudness.

EXPERIMENT 4

Method

Participants

The participants were 34 healthy full-term nine-month-old infants (mean age = 9 months 15 days, range: 9 months 0 days – 10 months 0 days). Families were contacted based on information from birth records and received a token gift for participation. 16 infants formed the congruent group, and 18 infants formed the incongruent group. 21 infants were female. Data from an additional four infants were discarded because of fussiness resulting in failure to complete four test trials.

Apparatus

Infants were seated on a parent’s lap in a chair approximately 70 cm away from a screen onto which stimuli were projected, which rested on a stage surrounded by black fabric, and which could be covered by a retractable black curtain. Speakers (also hidden, located behind the stage) attached to the stimuli presentation computer played the audio component of the stimuli. Parents were instructed to avoid interacting with their infant for the duration of the study. However, if a child became fussy, the experimenter paused between trials, allowing the parent to comfort the child, and then resumed the study. Infants that remain in the final sample reported here did not take breaks longer than one minute, and did not take breaks during the test trials.

Within a small opening on the stage sat a video camera, which recorded participants’ eye movements. Behind where the parent and child sat was another video camera, mounted on a tripod, which recorded the presentation of stimuli. The feeds from both video cameras were sent to another room, where an experienced coder, blind to condition and trial type, measured looking time using a button-box attached to a computer. The second experimenter signaled to the experimenter in the testing room when each trial ended and when the habituation criterion had been reached, using a two-way radio. Reliability between two observers (who were blind to condition) was computed based on agreement or disagreement at each 100-ms interval. All participants were double-coded, and average inter-coder reliability across participants was 92%, with reliability for each individual participant exceeding 90%.

Materials

Stimuli consisted of a visual stimulus (a cartoon caterpillar) and an auditory stimulus (a tone) presented simultaneously. In each such exposure, the caterpillar appeared at the center of a screen with a white background as the tone simultaneously began playing from the speakers. The visual stimulus appeared on the screen for the duration of the tone, and then was immediately removed and followed by a 250 ms pause during which no images were presented and no sounds played.

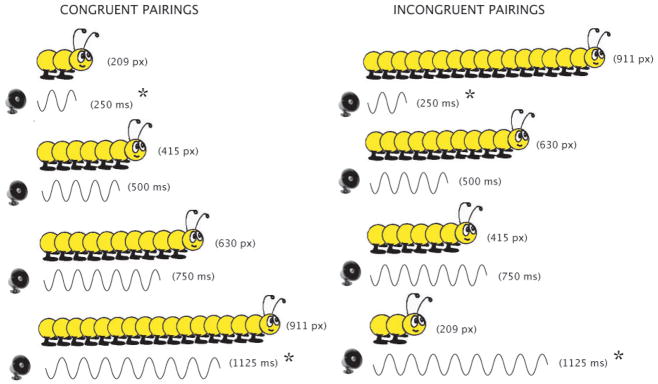
All caterpillars were 175 pixels tall, and length was controlled by trial, in habituation and test, to be either short (209 pixels) or long (911 pixels) (see Figure 6). Two intermediate lengths (415 pixels; 630 pixels) were also seen during familiarization only. The tones were always in E4 (329.63 Hz), and their duration was controlled by trial, in habituation and test, to be either short (250 ms) or long (1125 ms). Two tones with intermediate durations (500 ms; 700 ms) were also heard during familiarization only. Successive spatial lengths and temporal durations were constructed to vary in a 1:2:3:4.5 ratio to ensure their discrimination by nine-month-old infants in the familiarization trials, given that previous studies have shown that infants, at this age, can discriminate number and duration at a 2:3 ratio (Lipton & Spelke, 2003; Wood & Spelke, 2005; Brannon, Suanda, & Libertus, 2007). In the congruent condition, longer lengths were paired with longer tones, but in the incongruent condition, longer lengths were paired with shorter tones (see Figure 6). The stimuli presented during habituation and test were drawn from the extremes of these continua and varied in length and duration by a 1:4.5 ratio. There were thus easily discriminable for infants at this age.

Figure 6.

Congruent and incongruent pairings of caterpillar length and tone duration presented in Experiment 4. Asterisked pairings were presented in test to both groups

The caterpillars were altered and manipulated to vary their length using Adobe Photoshop (Adobe Systems Incorporated, San Jose, CA), and the tones were generated using Audacity. The caterpillars and tones were then combined together into simple films with timing of presentation controlled, using Macromedia Flash MX (Adobe Systems Incorporated, San Jose, CA). These films were exported in QuickTime format and embedded in Keynote for presentation.

Procedure

Informed consent was obtained from the parent before any testing began. The study had the following structure: infants first saw three familiarization trials that introduced the range of length and duration of the stimuli, followed by the habituation phase in which they could see between six and 12 trials (depending on rate of habituation), and finally two blocks of four test trials. At the start of each trial, the experimenter raised a curtain, and said ‘Look, [infant’s name], Look!’ before initiating the exposure.

Familiarization

In each trial of familiarization, infants were shown the full range of spatial and temporal variation that they would see in the study (see Figure 6). This was meant to help participants establish a relative notion of what was ‘long’ and ‘short’, both spatially and temporally, in the context of the experiment. In the congruent group, the familiarization consisted of seeing three cycles of four exposures in which length and duration varied congruently, either beginning with the shortest caterpillar and tone (SS) and ending with the longest caterpillar and tone (LL), or beginning with LL and ending with SS, with order counterbalanced across participants. Each cycle was shown on a separate trial. Participants in the incongruent condition were shown three cycles of four exposures in which length and duration varied incongruently, either beginning with the shortest caterpillar and longest sound (SL) and ending with the longest caterpillar and shortest sound (LS), or beginning with LS and ending with SL, with order counterbalanced across participants. The interval in between each of the pairings in all of the cycles was 500 ms. Looking times were not recorded during any of the familiarization trials.

Habituation

Stimuli in habituation were chosen from the extremes of the continua—SS and LL in the congruent condition, and SL and LS in the incongruent condition. In each habituation trial, exposures were looped over and over (e.g., SS SS SS …) until the infant looked away from the screen for two consecutive seconds. The inter-stimulus interval was again 500 ms. Looking times were measured from the infant’s first look toward the screen after the trial had begun. Infants in the congruent condition were shown alternating trials of SS and LL with order counterbalanced, while infants in the incongruent condition were shown alternating trials of SL and LS with order counterbalanced. Habituation trials continued until the infant met the habituation criterion (when the average looking time for the last three trials was less than half of the average looking time for the first three trials), or had completed 12 trials.

Test

Like the habituation trials, each test trial consisted of repetitions of one of the caterpillar-tone pairings. These trials continued looping until the child looked away for two consecutive seconds (e.g., SS SS SS …). The test phase contained two blocks of four trials each (eight trials overall). Each block contained one each of SS, SL, LL, and LS, with trials from the congruent and incongruent sets alternating. Four test orders were used, counterbalancing for whether a short caterpillar was paired with a congruent or incongruent tone (SS or SL), and for whether the next trial switched to a long caterpillar or not. The second block of test trials repeated the order of the first block.

Results

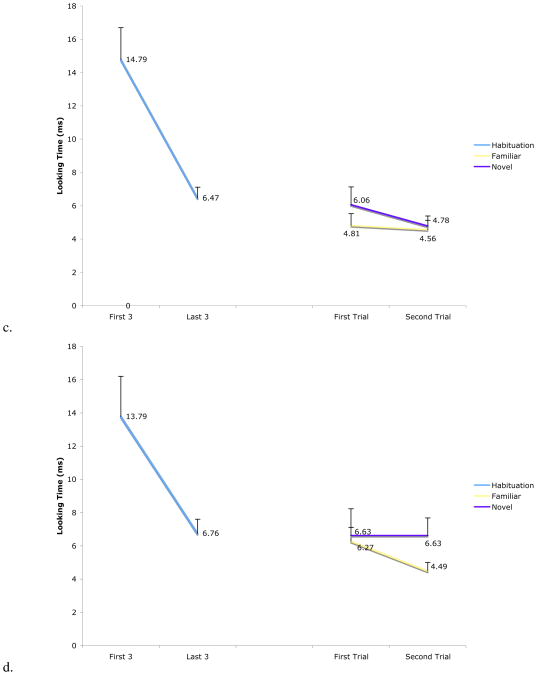
13 out of 16 infants in the congruent condition, and 17 out of 18 infants in the incongruent condition met the habituation criterion. Infants in the congruent condition took an average of 8.1 trials to habituate, and infants in the incongruent condition took an average of 7.7 trials. Infants in both the congruent condition and in the incongruent condition looked significantly longer at the first three habituation trials compared to the last three trials (congruent: t(15) = 6.09, p < .01; incongruent: t(17) = 6.20, p < .01).

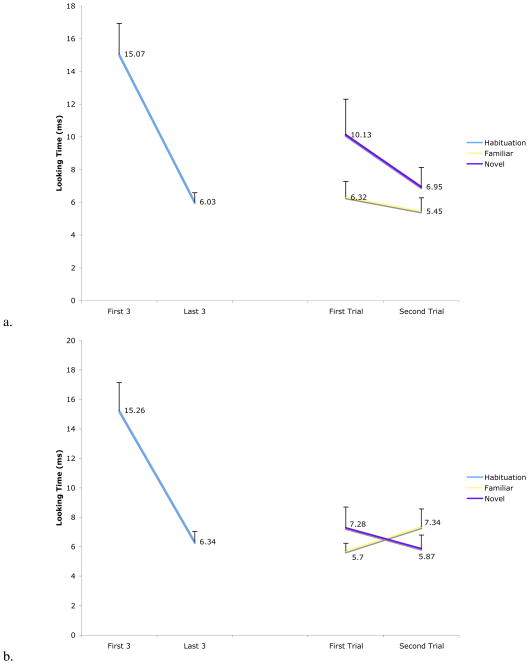
All infants completed the full eight test trials. In both Experiment 4 and Experiment 5, infants were thoroughly bored by the second set of test trials, failing to differentiate familiar from novel stimuli in any condition of either experiment. Accordingly, we present data from the first four test trials only (i.e., 2 familiar and 2 novel pairings; SS, LL, familiar in congruent condition, novel in incongruent condition, and SL, LS; novel in congruent condition, familiar in incongruent condition). Figure 7 shows the average looking time for the first three habituation trials, the last three habituation trials, and the two novel and two familiar test trials. Infants in the congruent condition, but not infants in the incongruent condition, looked longer at the novel test trials. A 2 × 2 mixed-factor repeated-measures ANOVA examined the effects of the between-subjects factor of habituation group (congruent and incongruent), and the within-subjects factor of test trial type (novel or familiar) on infants’ looking time⁴. There was a main effect of novelty, F(1,32) = 4.14, p < .05, as infants looked longer at the novel test trials (M_nov = 7.50, SE_nov = 0.71) than the familiar test trials (M_fam = 6.22, SE_fam = 0.54). There was a nearly significant group × novelty interaction F(1,32) = 3.82, p = .059, significant in a one-tailed test, t(32) = 1.95, p < .05 (one-tailed). The group × novelty interaction was due to the fact that infants in the congruent group looked significantly longer at the novel test trials, t(15) = 2.87, p < .05, whereas those in the incongruent group did not, t(17) = .056, p = .96. Wilcoxon signed ranks tests confirmed this, as 11 out of 16 infants in the congruent group looked longer at the novel test trials (z = 1.99, p < .05), compared to only 8 out of 18 in the incongruent group (z = 0, ns). A final analysis compared the looking times of infants over the last three habituation trials to those of the first two test trials. As would be expected, neither group of infants dishabituated to the first familiar test trial they saw, as this was one of the pairings they had been habituated to. Infants in the congruent condition, however, dishabituated to the first novel (incongruent) trial they saw (t(15) = 2.16, p < .05), while infants in the incongruent condition did not (t(17) = .25, p = .81; see Figure 7).

Figure 7.

Full habituation and test data from Experiment 4 for the a) congruent group and b) the incongruent group.

Experiment 4 Discussion

Previous studies have shown that infants’ representations of number, duration, area, and other continuous quantities are structurally similar in the sense that they are each represented by analog magnitudes. In each of these stimulus dimensions, discrimination follows Weber’s law, and in the specific case of number and duration, there is a common and increasing precision in discrimination of the quantities over development (Brannon, Suanda, & Libertus, 2007). The results from Experiment 4 go beyond previous work in suggesting that infants in the congruent group spontaneously accessed this structural similarity and constructed a relational mapping between the congruent pairings of length and duration they were habituated to. The recognition of relational equivalence in these pairings would have allowed them to be more precisely encoded and held in memory, and subsequently distinguished from the novel pairings shown in test.

In Experiment 4, as in Experiment 1, duration information was provided in two modalities—in the duration of the auditory tones and in the duration that the caterpillars were visually presented. Experiment 3 showed that this redundancy was not necessary for adults to spontaneously construct a relational mapping between representations of length and duration. Of course, we cannot be sure that this is also the case for infants. Nonetheless, the infants in Experiment 4 did spontaneously align representations of length and duration, as shown by their success in detecting the novel test stimuli only when habituated to caterpillars and tones that varied congruently.

That a relational mapping was constructed only in the congruent condition might have had the consequence that infants in this condition would habituate more rapidly than infants in the incongruent condition, due to a relatively greater ease of encoding. Although this prediction was not borne out in the data—infants in the incongruent group habituated as quickly as infants in the congruent group (Incongruent: 7.7, Congruent: 8.0)—it is not a necessary one to make. One could equally argue that infants in the incongruent group may have had less to encode than infants in the congruent group, and so may have quickly become bored. The infants in the incongruent group may have encoded aspects of the spatial stimulus (e.g., the shape, color, and brightness of the caterpillar, and its different lengths), as well as aspects of the tone (e.g., its pitch, loudness, and duration), but not information on how the caterpillars and tones were paired. Infants in the congruent group, on the other hand, because of a sensitivity to relational equivalence, seem to have encoded this additional information about the pairings.

Experiment 4 shows that 9-month-old infants can spontaneously access the structural similarity between representations of length and duration, but they fall short of suggesting that these dimensions overlap functionally, in the sense that this structural similarity is more spontaneously accessed than one between any two dimensions of experience encoded by analog magnitude representations. In Experiment 5, we test whether infants are better able to process pairings of caterpillars of different length and tones of different loudness when variation along those dimensions is congruent.

EXPERIMENT 5

Method

Participants

The participants were 36 healthy full-term nine-month-old infants (a distinct group from Experiment 4; mean age = 9 months 16 days, range: 9 months 0 days – 9 months 29 days). 16 infants formed the congruent group, and 16 infants formed the incongruent group. 16 infants were female. Data from an additional four infants were discarded because of fussiness resulting in failure to complete at least four test trials. Infants were recruited and compensated as in Experiment 4.

Apparatus

All aspects of the apparatus were the same as in Experiment 4. Average inter-coder reliability across participants was 93%, with reliability for each individual participant exceeding 90%.

Materials

Caterpillars and tones were presented simultaneously. The same four caterpillar images that appeared in Experiment 4 were used. Four tones in E4 (329.63 Hz) were again used, but instead of varying in duration, they varied in loudness, while their duration was held constant at 750 ms. The specific amplitudes for the tones were chosen such that the loudness of each tone would be as discriminable from the other tones as the lengths of the caterpillars were. Amplitudes were chosen using the same procedure as in Experiment 2, with the highest reference amplitude set to 0.99. Loudness was controlled by trial, in habituation and test, to either be soft (A = 0.01; 50 db), or loud (A= 0.99; 89 db). Two tones with intermediate loudness (0.10, 70 db; 0.37, 81 db) were also presented during familiarization only. In the congruent condition, pairings were positively correlated in magnitude: longer caterpillars were paired with louder tones. Meanwhile, in the incongruent condition, the pairings were negatively correlated: longer caterpillars were paired with softer tones (see Figure 8). The tones were generated using Audacity, and the sounds were played through Logitech speakers. The speakers were set to three-quarter strength. All other aspects of the materials were the same as in Experiment 4.

Figure 8.

Congruent and incongruent pairings of caterpillar length and tone loudness presented in Experiment 5. Asterisked pairings were presented in test to both groups

The tones that we chose were adequately discriminable in their loudness from each other, as auditory discrimination studies have shown that infants by the age of nine months are able to discriminate tones that differ by between 6–9 decibels (Werner & Marean, 1996; Sinnott & Aslin, 1985), whereas the loudness differences between the tones we presented in habituation and test differed much more than that (i.e., by about 40 decibels). Our softest tones (50 decibels at 329.6 Hz) were also detectable, as studies have shown that by 3 months of age, infants can already detect 500 Hz tones that are 40 decibels (Oisho et al., 1988), and that by six months, infants can detect 250 Hz tones that are 38 decibels (Trehub et al., 1980).

Procedure

All aspects of the procedure were the same as in Experiment 4.

Results

13 out of 16 infants in the congruent condition, and 10 out of 16 infants in the incongruent condition met the habituation criterion. Infants in the congruent condition took an average of 8.1 trials to habituate, and infants in the incongruent condition took an average of 9.1 trials. Infants in both the congruent condition and in the incongruent condition looked significantly longer at the first three habituation trials compared to the last three trials (congruent: t(15) = 4.89, p < .01; incongruent: t(15) = 2.94, p < .05).

All infants in the sample completed the full eight test trials, but as infants had lost interest by the second block of test trials, we analyzed only the first block, as in Experiment 4. Figure 9 shows the average looking time for the first three habituation trials, the last three habituation trials, and the first two pairs of test trials. It appears that both groups of infants looked slightly longer at the novel test trials, but neither group did so more than the other. A 2 × 2 mixed-factor repeated-measures ANOVA examined the effects of the between-subjects factor of habituation group (congruent and incongruent), and the within-subjects factor of test trial type (novel or familiar) on infants’ looking time⁵. This test yielded a marginal effect of novelty, F(1, 30) = 3.1, p = .09, as infants looked longer at the novel test trials (M_nov = 6.02, SE_nov = .66) than the familiar test trials (M_fam = 5.03, SE_fam = .39). Unlike Experiment 4, the group × novelty interaction did not approach significance, F(1,30) = 0.21, p = .65. Infants in the congruent group did not look significantly longer at the novel test trials (t(15) = 1.54, p = .15), and neither did the infants in the incongruent group (t(15) = 1.22, p = .24)⁶. No differences between the groups were seen in the non-parametric statistics either, as 10 out of 16 infants in the congruent group looked longer at the novel test trials (Wilcoxon signed-ranks test, z = 1.63, p = .10), compared to 11 out of 16 in the incongruent group (z = 1.19, p = .23). The three-way interaction between experiment (Experiment 4 vs. 5), group, and novelty approached significance, F(1, 62) = 3.15, p = .08, indicating a larger interaction effect in Experiment 4 than in Experiment 5. A final analysis compared the looking times of infants over the last three habituation trials to those of the first two test trials. As would be expected, neither group of infants dishabituated to the first familiar test trial they saw, as this was one of the pairings they had been habituated to. But infants in both groups also failed to dishabituate to the first novel test trial they saw (Congruent: t(15) = 1.41, p = .18; Incongruent: t(15) = .11, p = .91).

Figure 9.

Full habituation and test data from Experiment 5 for the c) congruent group and d) the incongruent group.

Experiment 5 Discussion

The results from Experiment 5 stand in contrast to those of Experiment 4. In Experiment 4, infants in the congruent, but not the incongruent condition, were able to notice and benefit from the relational equivalence between the length of the caterpillars and duration of the tones they were habituated to. Experiment 5 yielded no such difference between the congruent and incongruent groups, although overall, there was a trend for infants to look longer at the novel stimuli. The results of Experiment 5 parallel the limited success of the congruent and incongruent groups of adults in Experiment 2, who succeeded only on the easier test trials. Thus, the construction of a relational mapping across domains appears to be more spontaneous in the case of length and duration than it is in the case of length and loudness for both adults (Experiment 1–3) and infants (Experiments 4 and 5). This is despite the fact that both adults and young children can access the structural similarity between length and loudness when they are instructed to do so (Stevens & Guirao, 1968; Stevens & Marks, 1965; Teghtsoonian, 1980).

These results show that experience with and mastery of words like long and short does not create a functional overlap between representations of length and duration. Rather, the early presence of functional overlap could itself help explain why it is that spatial language is used to describe time across languages. Those correspondences that young infants most spontaneously notice could be reflected in flexible language use, as the same words (e.g., long, short, big, high, etc.) come to be applied to different, functionally overlapping dimensions. These data, however, should not be taken to suggest that language learning can have no effect on relationships between these representations. Recall that while English participants are affected by irrelevant length information when reproducing the duration for which a line appears on a screen, Greek and Spanish speakers (who more often use quantity terms to describe duration) are more affected by irrelevant quantity information (Casasanto, 2008). Experiments 4 and 5 suggest that in infancy there is already functional overlap between representations of length and duration, and we would predict similar overlap between representations of quantity and duration. Acquisition of a language, such as English, that highlights only one of the relationships among these dimensions, could increase the accessibility of the shared representational units of those dimensions, at the expense of the accessibility of the shared representational units of other dimensions.

General Discussion

The use of spatial language to describe time across languages suggests that representations of space and time are intimately related, a possibility supported by prior research (McGlone & Harding, 1998; Gentner, Imai, & Boroditsky, 2002; Boroditsky, 2000, 2001; Xuan et. al., 2007; Casasanto & Boroditsky, 2008; Casasanto, 2008). The experiments reported here make two additional contributions to this literature. In doing so, they also introduce a new measure to assess overlap among representational systems. Previous work has typically measured overlap through behavioral interference, whereby participants cannot ignore one feature of a stimulus despite being instructed to encode a different one (Paivio, 1975; Henik & Tzelgov, 1982; Cohen Kadosh & Henik, 2006, Pinel et al., 2004; Xuan et al., 2007; Casasanto & Boroditsky, 2008). As many have suggested, these effects are often open to interpretations in terms of response competition, rather than, or in addition to, common representational mechanisms (e.g., Schwarz & Heinze, 1998). The present studies, in contrast, used efficiency of encoding to assess functional overlap. Our logic was as follows: if participants are able to access the structural similarity between two representational systems, it should be easier for them to encode pairings of the two dimensions when variation among these dimensions is congruent, compared to when it is incongruent. And if two structurally similar representations have functional overlap, participants should be able to spontaneously access this structural similarity.

Using this paradigm, the present studies make two empirical contributions. First, they show that the relationship between representations of length and duration goes beyond the structural similarity defined by analog magnitude representations: these representations appear to have a large degree of functional overlap. Experiments 1 and 3 showed that adults are better able to bind together pairings of lines of different length and tones of different duration when they are relationally equivalent than when they are not. Relatively few pairings were required for adults to encode the relations between the lines and tones, and participants were able to detect even small deviations between the pairings that were relationally equivalent and those that were not. Experiment 2 showed that this pattern does not extend to pairings of lengths and loudness, even though the latter representations are as alignable as representations of length and duration under the conditions of cross-modality matching experiments (Stevens & Guirao, 1963; Stevens & Marks, 1965; Stevens, 1975). Second, the present studies show that experience with and mastery of words like long and short does not create the functional overlap between representations of length and duration, as it is also present in 9-month-old infants. Experiment 4, adapting the method of Experiments 1–3 into an infant habituation study, showed that nine-month-old infants, like adults, are better able to bind together pairings of length and duration when they are relationally equivalent. Experiment 5 showed that this result does not hold for pairings of length and loudness.

Taken together, the results suggest that representations of length and duration functionally overlap to a larger degree than do representations of length and loudness, such that the former representations may effortlessly engage with and align with one another. The early presence of this functional overlap in infants may help explain why it is that spatial and temporal language overlap in language after language. One possibility that we have suggested throughout is that this functional overlap may be part of our biological endowment, having resulted from an evolutionary recycling of spatial representations for more general purposes. But a second possibility, which we now turn to, is that sensorimotor experience, over development, motivates the construction of links between the representations of abstract and concrete domains.

Sensorimotor Experience and Conceptual Metaphor Theory

According to Conceptual Metaphor theory (Lakoff & Johnson, 1980, 1999), the use of spatial language in abstract domains, such as time, reflects metaphoric thought: representations of abstract concepts derive their inferential structure from concrete domains such as space. Concepts in concrete domains are directly meaningful and include basic-level concepts and image-schemas (developed abstractions, or re-descriptions, of patterns of sensorimotor interaction with the world; see Mandler, 1992; Johnson, 2005). Because image-schemas capture the inferential structure inherent to these domains, metaphoric links from abstract to concrete domains allow for the use of inferential image-schematic structure that would otherwise be absent. This results in a conceptual system in which all concepts are directly based on—or metaphorically grounded in—sensorimotor experience.

Metaphoric links are established during a lifetime, and are motivated by two kinds of information, each of which indicate to the child similarities between different domains. The first kind, shared language, is not operative in the mapping between length and duration (Experiment 4). The second kind, correlative experience, has not yet been addressed—Lakoff and Johnson (1980, 1999, see also, Casasanto, 2008) argue that metaphoric links are motivated as children notice correlations in their environment between space and more abstract domains. For example, because the accumulation of substances typically results in larger piles, children may come to metaphorically construe the abstract notion of ‘more’ in terms of the more concrete, spatial meaning of ‘up’ (Lakoff & Johnson, 1980). This is thought to be one of a series of mappings that gives the domain of quantity access to image-schematic spatial structure. Note that in order for a correlation between any given abstract domain and a concrete one to be noticed, the child must be equipped with some machinery for representing both domains. The claim from Conceptual Metaphor theory is that such structure, before metaphoric re-structuring, is not inferentially rich (indeed, in the case of temporal reasoning, Lakoff and Johnson (1999) suggest that “…it is virtually impossible for us to conceptualize time without metaphor,” p. 139).

It is difficult to believe that 9-month-old infants have the relevant sensorimotor experience they would need to metaphorically construe duration in terms of length. Conceivably, children could pick up on a correlation between distance and duration: given a constant direction of motion, the longer in time an object travels, the more distance it traverses. But note that this would still leave the child an important step away from a correlation between length and duration, because she would need to abstract away from distance traversed to any kind of length, such as the length of an object. It is exactly the latter kind of correlative experience—of a static, long object being present in experience for a long time—that would be essential for constructing the link exploited by infants in Experiment 4, but which is not present in the environment.

Innate Functional Overlap

In light of the prior discussion, we believe it more likely that there is innate functional overlap between representations of length and duration. Abstract concepts, such as time, need not rely on representations of more ‘concrete’ domains and do not have to be constructed with sensorimotor experience (Murphy, 1996; Jackendoff, 1983; Pinker, 1997, 2007). The idea that we may be biologically endowed with representations from different domains that automatically engage with and align with one another, perhaps sharing neural substrate, converges with recent evidence suggesting that infants are able to spontaneously access a structural similarity between representations of numerosity and length (de Hevia & Spelke, in press). Using methods similar to those in the studies presented here, de Hevia and Spelke (in press) showed that infants were better able to encode pairings of sets of dots of different numerosity and lines of different length, when variation in numerosity and length was congruent, compared to when it was incongruent. As one reviewer suggested, this finding opens another possible interpretation of the infants’ success in Experiment 4—namely that infants may have accessed a structural similarity between representations of numerosity and duration rather than one between representations of length and duration, because caterpillar length was confounded with number of body parts (segments, legs and feet). There is no evidence that infants represent the numerosity of body parts, but this possibility should be addressed with further experiments. On either possibility, the present results show that by 9 months of age, representations of duration functionally overlap with those of length and/or numerosity, which in turn also functionally overlap with each other at these ages. Thus, early on in infancy, magnitude representations in the domains of number, space, and time appear to easily coordinate with one another, joining evidence from cognitive neuroscience suggesting functional overlap and common neural substrate for these representations (Fias et al., 2003; Cohen Kadosh & Henik, 2006; Cohen Kadosh, Cohen Kadosh, & Henik, 2007, Pinel et. al., 2004; Walsh, 2003; Cantlon, Platt & Brannon, 2009).

Such an organization may reflect an evolutionary recycling of magnitude representations from more specific to more general purposes, and may help to explain the cross-referencing of different magnitudes in language (i.e., space to refer to time (Table 1) and space to refer to number (e.g., Which is bigger, 5 or 7?)), a pattern that holds cross-linguistically (Traugott, 1978; Sweetser, 1991; Alverson, 1994; Lakoff & Núñez, 2000). This is not to say that how easily a structural similarity is accessed is the only factor that determines whether that correspondence is expressed with overlapping language. Some strong cross-domain correspondences may not receive common expression in language at all (e.g., one between brightness and loudness, but see Marks (1982), who shows that participants intuitively understand novel extensions of the language of brightness to describe loudness, and vice versa).

The use of spatial language to refer to the abstract goes well beyond descriptions of magnitudes such as numerosity and duration—we also use spatial language to talk about ideas, desires, similarity, possession, and most other abstract notions. Such metaphorical uses of spatial language may be due to an extensive co-option of the representational resources deployed in spatial reasoning for other purposes over evolutionary time. Steven Pinker (1997) articulates this proposal in How the Mind Works (p. 355–356):

Suppose ancestral circuits for reasoning about space and force were copied, the copies’ connections to the eyes and muscles were severed, and references to the physical world were bleached out. The circuits could serve as a scaffolding whose slots are filled with symbols for more abstract concerns like states, possessions, ideas, and desires. The circuits would retain their computational abilities, continuing to reckon about entities being in one state at a time, shifting from state to state, and overcoming entities with opposite valence.

As Pinker suggests, metaphorical uses of language may reveal an evolutionary recycling that has yielded a rich set of innate correspondences across concrete and abstract domains. But it is also possible that in some cases, metaphorical language reveals and contributes to the construction of new representational resources over ontogenesis, as Conceptual Metaphor theory would have it. We endorse such processes in cases of bootstrapping and conceptual change (see Carey, 2009, for several worked examples, both in ontogenesis and in the history of science). It is an open empirical question as to which metaphorical uses of language reflect innate functional overlap and which involve the construction of new representational resources.

Evidence that representations of space organize representations of time and not vice-versa

Although the presence of functional overlap among representations of space and time correctly predicts that spatial and temporal language should overlap, it does not make a directional prediction as to whether spatial words should more often take on temporal senses compared to the opposite. But historical analyses point to a clear asymmetry in which spatial senses are primary (Sweetser, 1991; Alverson, 1994; Haspelmath, 1997; Traugott, 1978). This asymmetry also extends to language processing: spatial primes that lead participants to adopt a certain frame of reference (e.g., imagining oneself moving through space) facilitate interpretations of temporal sentences in the same frame of reference, but not vice versa (Boroditsky, 2000).

The Conceptual Metaphor theory predicts these asymmetries because it predicts that they result from a deeper asymmetry in conceptual representation: if abstract representations borrow structure from spatial representations, an asymmetry should result whereby abstract representations depend on concrete structures, but concrete representations do not depend on abstract structures. Casasanto and Boroditsky (2008) provided non-linguistic evidence for this asymmetry. These authors found that participants were affected by irrelevant spatial information (how long a line grew across a screen) when estimating the duration for which the line appeared, but were not affected by irrelevant temporal information (the duration for which the line appeared) when estimating the distance the line grew.

How can these linguistic and conceptual asymmetries be accounted for and reconciled with the evidence presented here for a presumably symmetric functional overlap among representations of length and duration? One possibility is that concrete domains sometimes structure abstract domains for purposes of communication—explaining the linguistic asymmetry—in cases where they are not responsible for the creation or structure of the abstract representations themselves (Thibodeau & Durgin, 2008; Gerrig & Gibbs, 1988). That is, spatial words may have been extended, historically, to refer to abstract referents—not because of metaphoric thought—but because it may be easiest to refer to something abstract, for which shared reference may be difficult, by analogically referring to something that is structurally similar to it from a concrete domain, in which shared reference is facile.

The demands of language learning could also place constraints on lexical innovations such that innovations that extended spatial words to refer to abstract referents are easier to learn. Imagine first learning the meaning of the word “long”. One must first learn that it is a dimensional adjective, and then must figure out which dimension of experience it applies to. While spatial length is a static property of objects, and objects can easily be ostensively indicated, temporal duration is a property of events, which are fleeting in experience and available mainly in memory representations.

This difference may make it simpler to learn “long” as it applies to spatial length than as it applies to temporal duration (see Clark, 1973), just as it is easier to learn the meanings of nouns than verbs (Gentner & Boroditsky, 2001; Gleitman et al., 2005; Snedeker & Gleitman, 2004). Having first learned that “long” refers to spatial length, the functional overlap between length and duration could help to constrain interpretation of the meaning of “long” as it is applied to temporal intervals. This would predict that children should work out the spatial meanings of words before temporal meanings. Of course, Conceptual Metaphor theory would predict the same: on that view, the acquisition of concrete before abstract language reflects the ongoing construction of metaphoric links in conceptual structure. On the present account, it would merely reflect a strategy for mapping words to pre-existing, abstract concepts.

While the asymmetry observed across languages, on this proposal, is to be explained by its communicative advantages and the demands of language acquisition, the evidence for nonlinguistic, asymmetric interference (reported by Casasanto and Boroditsky (2008)) may be a consequence of the linguistic asymmetry. Some evidence comes from Merritt, Casasanto, and Brannon (under review). These investigators adapted the method of Casasanto & Boroditsky (2008) so that it could be used with rhesus monkeys, and found no evidence of asymmetric interference: monkeys experienced interference from length onto estimates of duration as well as from duration onto estimates of length. This result provides additional supporting evidence for our conclusion that language learning does not create functional overlap between representations of length and duration. But it also suggests that the acquisition of human language may create the asymmetric interference observed by Casasanto & Boroditsky (2008) in human adults. This interference, rather than reflecting an asymmetry in conceptual structure whereby abstract concepts necessarily depend on concrete concepts, may instead result from spatial representations more strongly eliciting the structures they have in common with temporal representations than the reverse.

Conclusion and Future Directions

The studies reported here have provided evidence for a privileged relationship between representations of spatial length and temporal duration—in addition to sharing a common representational format, these representations may have functional overlap such that correspondences are easily and precisely computed (Experiments 1 and 3, contrasted with Experiment 2). This functional overlap is present in nine-month old infants (Experiment 4, contrasted with Experiment 5), and we argue that it is part of our biological endowment and a precursor to language learning.

This conclusion does not imply that processes of metaphoric structuring have no role to play in creating new representational resources for abstract reasoning. In the specific case of time, proponents of Conceptual Metaphor Theory have argued that non-metaphorical temporal representations are too fleeting to support higher-order reasoning of the sort required for comparing temporal intervals, serially ordering events, transitive inference, and so on (Lakoff & Johnson, 1980, 1999; Casasanto, 2008). These claims should be subjected to empirical scrutiny: can young infants see parallels between congruent pairings of spatial relations of objects and temporal relations of events? If higher-order temporal reasoning requires metaphoric structure, we should expect the answer to be no, and if early developing representations of spatial and temporal relations are intimately related, the answer should be yes.