An implicit body representation underlying human position sense

Abstract

Knowing the body's location in external space is a fundamental perceptual task. Perceiving the location of body parts through proprioception requires that information about the angles of each joint (i.e., body posture) be combined with information about the size and shape of the body segments between joints. Although information about body posture is specified by on-line afferent signals, no sensory signals are directly informative about body size and shape. Thus, human position sense must refer to a stored body model of the body's metric properties, such as body part size and shape. The need for such a model has long been recognized; however, the properties of this model have never been systematically investigated. We developed a technique to isolate and measure this body model. Participants judged the location in external space of 10 landmarks on the hand. By analyzing the internal configuration of the locations of these points, we produced implicit maps of the mental representation of hand size and shape. We show that this part of the body model is massively distorted, in a reliable and characteristic fashion, featuring shortened fingers and broadened hands. Intriguingly, these distortions appear to retain several characteristics of primary somatosensory representations, such as the Penfield homunculus.

Perceiving the body's location in external space is essential for interacting with our environment and for constructing a coherent sense of self. Proprioceptive signals from afferents in muscles, joints, and skin provide information about joint flexion or extension (1, 2), contributing to a representation of body posture, the postural schema (3). To perceive the absolute position of body parts in external space, however, this postural information must be combined with information about the size and shape of the body segments connecting the joints (4–8) (Fig. 1A). No sensory signal, however, directly informs the brain about the metric properties of body parts. Thus, localization of the body in external space requires that on-line afferent signals specifying joint angles be informed by a stored body model. Although several researchers have identified the need for such a body model (4, 6, 8), no attempt has been made to measure this model, and its properties are unknown. Here, we systematically investigate the body model mediating position sense of the human hand, showing that it is massively distorted, and appears to retain distortions characteristic of the somatosensory homunculus.

Fig. 1.

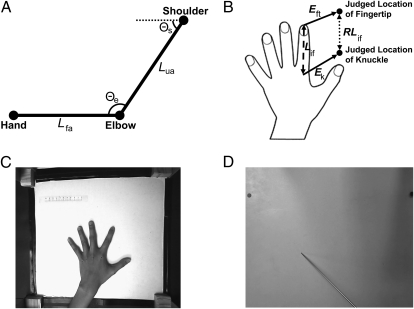
(A) Schematic illustration of the need for a body model to localize the body in external space. Perceiving the elbow's location relative to the shoulder requires information about the length of the upper arm (L_ua), and perceiving the hand's location relative to the elbow requires information about the length of the forearm (L_fa). Perceiving the location of the hand relative to the shoulder clearly requires information not only about joint angles at the shoulder (Θ_s) and elbow (Θ_e), but also about the segment lengths of the upper arm (L_ua) and forearm (L_fa). Information about segment lengths, however, is not specified by on-line afferent signals, implying that they must come from a stored body model. (B) Schematic illustration of how this body model can be isolated from location judgments of distinct landmarks. Traditionally, studies of position sense have measured the error between the judged location of a body part and its actual position in space (i.e., E_ft and E_k). The represented length of a segment, such as the index finger (RL_if), can be determined by comparing the distance between the judged locations of the fingertip and knuckle, without respect to their true locations. RL_if can then be compared with true finger length (L_if). Thus, the size and shape of the body model can be assessed by investigating the internal configuration of localizations of multiple landmarks, without regard to differences in actual and perceived location. (C) Sample image showing the experimental setup and the image of the actual hand taken before and after each block. (D) Sample image showing the occluding board and localization judgment.

The essential contribution of the body model to position sense is specifying the relative locations of body parts. The overall “localization error” for a single landmark (i.e., the distance between actual and judged locations) depends on several factors. In contrast, the distance between the judged locations of two adjacent landmarks (e.g., the tip and knuckle of a single finger) depends only on the represented length of the body segment connecting them. Other sources of error, such as misperceptions of joint angles, will affect localization error for each individual landmark, but will preserve the relative positions of the landmarks. Thus, we isolated and measured the body model by having participants localize ten landmarks on their hand. We analyzed the internal spatial configuration of the hand representation, by comparing the judged position of these landmarks, irrespective of their true positions (Fig. 1B). Crucially, the distances between these judgments are fundamentally distinct from either constant or variable error of localization, and allow us to estimate the internal structural representation of the body model of the hand.

Results

Dissociation of Body Model from Conscious Body Image.

Participants placed their left hand palm down under a board (Fig. 1 C and D), and judged the location of the knuckles and tips of each finger by positioning a baton on the board directly above each landmark. An overhead camera recorded responses. Before and after each block, a picture was taken without the board to record actual hand size and shape and to check that the hand had not moved. Comparing the judged position of different landmarks allowed us to build a spatial map of the body model, which could then be compared with actual hand shape. Figure 1B shows an example: the judged positions of the index fingertip and knuckle are used to calculate represented index finger length (RL_if; dotted line) for comparison with its actual length (L_if; dashed line). Finally, we measured the conscious body image by asking participants to select, from an array of differently shaped hand images, the image most closely resembling their own hand shape (9).

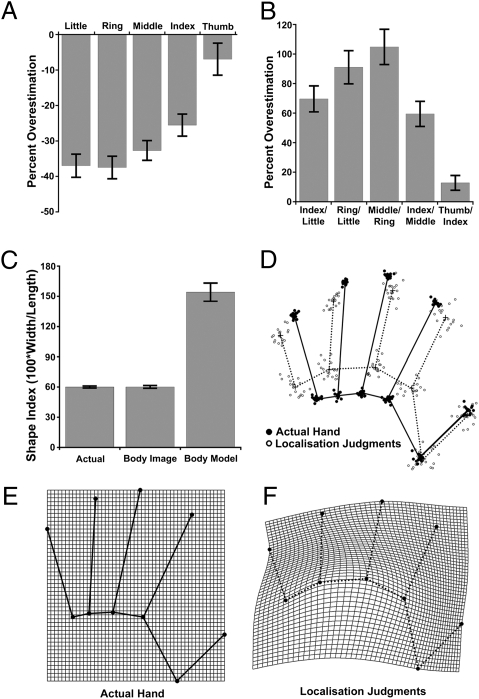
The distance between the average judged locations of each knuckle and fingertip was used to estimate represented finger length, which systematically and strikingly underestimated actual length (Fig. 2A) [M, −27.9%, t(17) = −9.57, P < 0.0001]. The magnitude of this underestimation, furthermore, increased from the thumb to the little finger (Fig. 2A). This radial–ulnar gradient was quantified using least-squares linear regression, in which digit number (i.e., 1 = thumb to 5 = little finger) was used predict underestimation. On average, underestimation increased by 7.2% from one digit to the next [mean β = −7.2%/digit, t(17) = −7.79, P < 0.0001]. Intriguingly, this gradient in finger size mirrors similar gradients of decreasing tactile acuity (10, 11) and somatosensory cortical territory (11) from the radial to the ulnar side of the hand.

Fig. 2.

Results from Exp. 1. (A) Percent overestimation [i.e., (100 × judged length − actual length)/actual length] of finger lengths. Clear underestimation was observed, increasing from the radial (thumb) to the ulnar (little finger) side of the hand. Error bars are 1 SEM. (B) Percent overestimation of spacing between pairs of knuckles. Clear overestimation was observed. (C) Shape indices (100 × width/length) quantifying overall aspect ratio of the hand for the actual hand, the conscious body image measured by template matching, and the body model measured by localization judgments. (D) GPS of landmark positions for actual hands (black dots/black lines) and the body model inferred from localization judgments (white dots/dotted lines). Solid line indicates mean shape of actual hand; dotted line indicates mean shape of body model. (E) Average actual hand shape superposed on a rectangular coordinate grid. (F) Thin-plate spline depicting body model as a deformation of the actual hand.

To assess hand width, the distance between pairs of adjacent knuckles was computed as for finger length. In striking contrast to the underestimation of finger length, strong overestimation of knuckle spacing was observed (Fig. 2B) [M, 67.0%, t(17) = 9.55, P < 0.0001]. Substantial overestimation was observed between knuckles of the fingers, with more modest overestimation of the distance between the index–thumb knuckles. An overall measure of hand width, the distance between the knuckles of the index and little fingers, also showed large overestimation (69.6%) [t(17) = 7.92, P < 0.0001].

To assess overall hand shape, we adapted Napier's shape index (12), which quantifies the aspect ratio (i.e., ratio of width to length) of the hand. For hand length, we used the length of the middle finger, and for width we used the distance between the knuckles of the index and little fingers. The shape index was defined as 100 × (width/length) and was calculated for (i) the participants’ actual hand, (ii) the average template hand image selected, and (iii) the internal model of the hand inferred from localization judgements. Explicit template judgments of hand shape were approximately veridical, not differing significantly from actual hand shape [t(17) = 0.09] and were significantly correlated with actual hand shape across participants [r(17) = 0.498, P < 0.05]. Localization judgments, in contrast, showed massive overestimation of width relative to length [t(17) = 10.15, P < 0.0001] (Fig. 2C). That is, we found dramatic overrepresentation of the medio-lateral over the proximo-distal hand axis. This pattern mirrors the greater tactile acuity on the dorsum medio-laterally than proximo-distally (13, 14). The pattern also echoes known anisotropies in tactile receptive fields of sensory neurons: these are smaller medio-laterally than proximo-distally, particularly on the hairy skin of the forearm and hand dorsum (15, 16).

To assess the shape of the body model in more detail, we used generalized Procrustes superposition (GPS) (17) to compare the actual configuration of landmarks from each participant's hand with the internal representation based on localization judgments (Fig. 2D). GPS removes differences in location, rotation, and scale, thus highlighting differences in shape (17, 18). Analysis of this data revealed a highly significant difference in mean shape between the actual hand and the body model [Goodall's F(16, 544) = 70.52, P < 0.0001]. The shape of the body model can be depicted as a transformation of the actual shape of the hand, following D'Arcy Thompson (19). Figure 2F therefore shows the shape of the body model, averaged across participants, as a transformation of mean actual hand shape using a thin-plate spline (18).

Effects Are Not Caused by Motor Biases or Foreshortening.

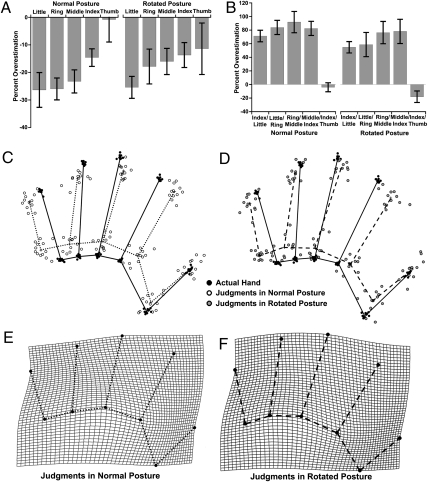
The biases described above could potentially reflect either motor biases in a torso-centric reference frame for the pointing responses, or a general foreshortening of perspective in the near–far axis. To address these issues, we conducted a second experiment, measuring the body model with participants’ hands in both a standard posture, the fingers pointing away from the torso (as in Exp. 1), and with the hand rotated 90°, the fingers pointing to the right. Any biases independent of the body model should reverse in the rotated relative to the standard posture. In fact, results were almost identical in the two postures (Fig. 3), demonstrating that these biases reflect representation of the hand, rather than biases in retina- or torso-centered coordinates or in motor control. Overall underestimation of finger length was observed both in the standard posture [mean (M), −18.2%, t(11) = −4.03, P < 0.005] and in the rotated posture [M, −16.9%, t(11) = −3.31, P < 0.01], and was correlated across conditions [r(11) = 0.685, P < 0.01]. As in Exp. 1, these underestimations increased from the thumb to the little finger, both in the normal posture [mean β = −6.2%/digit, t(11) = −4.38, P < 0.005] and the rotated posture [mean β = −3.2%/digit, t(11) = −2.01, P = 0.07]. Similar overall overestimations of the spacing between adjacent knuckles were observed both for the standard posture [M, 63.5%, t(11) = 8.77, P < 0.0001] and the rotated posture [M, 48.8%, t(11) = 5.05, P < 0.0005], correlated across conditions [r(11) = 0.719, P < 0.01].

Fig. 3.

Results from Exp. 2. (A) Percent overestimation of finger lengths in “normal” and “rotated” postures. (B) Percent overestimation of knuckle spacings in the two postures. (C) GPS of actual hands (black dots/black lines) and body model in normal posture (white dots/dotted lines). (D) GPS of actual hands (black dots/black lines) and body model in rotated posture (gray dots/dashed lines). (E) Thin-plate spline depicting shape of body model in normal posture as a deformation of actual hand shape. (F) Comparable thin-plate spline for rotated posture.

Analysis of GPS superposed data revealed highly significant differences in mean shape between the actual hand and the shape of the body model in the normal posture [Goodall's F(16, 352) = 30.21, P < 0.0001] and the rotated posture [Goodall's F(16, 352) = 18.72, P < 0.0001]. There was no significant difference between mean shape of the body model in the two postures [Goodall's F(16, 352) = 1.61, P = 0.064].

Effects Generalize Across Hands.

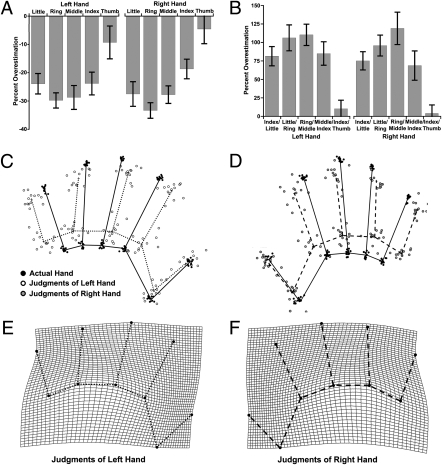
Although we interpreted the increasing underestimation of finger length from the thumb to the little finger as a radial–ulnar gradient, a general right–left gradient could also explain our results. To resolve this issue, we ran a third experiment in which we asked participants to judge either their right or left hand in separate blocks (Fig. 4). Represented hand shape was very similar for both hands, with similar radial–ulnar gradients. Overall underestimation of finger length was found both for the left hand [M, −22.4%, t(12) = −9.61, P < 0.0001] and the right hand [M, −23.1%, t(12) = −10.23, P < 0.0001], and was correlated across the two hands [r(12) = 0.666, P < 0.01]. Crucially, significant gradients in this underestimation from the thumb to little finger were observed for both the left hand [mean β = −6.1%/digit, t(12) = −4.93, P < 0.0005] and the right hand [mean β = −3.5%/digit, t(12) = −2.40, P < 0.05], demonstrating that this shift reflects a radial–ulnar, rather than a left–right, shift across the hand. Overall overestimation of knuckle widths, similar to the previous experiments, was also found both for the left hand [M, 71.2%, t(12) = 5.56, P < 0.0001] and the right hand [M, 78.0%, t(12) = 6.60, P < 0.0001], correlated across the two hands [r(12) = 0.927, P < 0.0001].

Fig. 4.

Results from Exp. 3. (A) Percent overestimation of finger lengths for left and right hands. (B) Percent overestimation of knuckle spacings for the two hands. (C) GPS of actual left hands (black dots/black lines) and left hand body model (white dots/dotted lines). (D) GPS of actual right hands (black dots/black lines) and right hand body model (gray dots/dashed lines). (E) Thin-plate spline depicting shape of left hand body model as a deformation of actual hand shape. (F) Comparable thin-plate spline for right hand body model.

Analysis of GPS superposed data revealed significant differences in mean shape between the actual hand and the body model for both the left [Goodall's F(16, 384) = 30.12, P < 0.0001] and right [Goodall's F(16, 384) = 29.85, P < 0.0001] hands. As Goodall's test treats reflection as a difference in shape, the Procrustes coordinates for the right hand were mirror reflected around the medio-lateral hand axis, so that the shape of the body model could be compared between the two hands. No significant difference in the mean shape of the body model was found between the left and right hands [Goodall's F(16, 384) = 0.64, not significant].

Clustering of Finger Representations.

Finally, to investigate individual differences in the body model, we used principal components analysis to analyze underestimations of finger lengths in 67 participants. Principal components analysis with varimax orthogonal rotation was used to investigate the relation between underestimation of finger length of the five digits. Analysis of scree plot and eigenvalues led to the extraction of three components, which together accounted for 86.66% of variance in the data (Table S1). Component 1 appeared to represent the index and middle fingers, component 2 the ring and little fingers, and component 3 the thumb. Intriguingly, this grouping of fingers mirrors the organization of sensory afferents from the hand into three separate groups corresponding to sixth – eighth cervical dermatomes (20). This clustering of fingers, furthermore, is maintained both in the human (21) and monkey (22) somatosensory cortex.

Consistent with the previous experiments, there was significant overall underestimation of finger length [M, −27.8%, t(66) = −12.74, P < 0.0001] (Fig. S1A), as well as a significant radial–ulnar gradient in the magnitude of this effect [mean β = −3.5%/digit, t(66) = −3.68, P < 0.001]. Similarly, there was overall overestimation of knuckle spacings [M, 75.5%, t(66) = 15.70, P < 0.0001] (Fig. S1). Also as before, analysis of GPS superposed data revealed a highly significant difference in shape between the actual hand and the body model [Goodall's F(16, 2112) = 103.70, P < 0.0001].

Discussion

The postural (or body) schema has been the focus of a large research literature for more than a century (3, 23, 24). Although many researchers have noted that position sense requires a stored model of the body's metric properties (4, 6, 8), we believe that our systematic investigation of this body model is unique. Many models of position sense have simply assumed that the true metric properties of the body are known (5, 7). In contrast, we show that the body model is massively distorted, at least in the case of the hand. These distortions, furthermore, are not idiosyncratic or random, but are highly stereotyped across individuals and appear to retain vestigial traces of the primary somatosensory homunculus of Penfield (25), including (i) a radial–ulnar gradient of magnification of the digits (10, 11), (ii) accentuation of the medio-lateral over the proximo-distal axis (13–16), and (iii) clustering of digit 2 with digit 3 and of digit 4 with digit 5 (21, 22). Although the homunculus is defined as the cortical map of tactile stimuli on the skin, our results suggest it may also provide the mental map of the body itself. Nevertheless, the exact relation between the body model and the homunculus remains unclear; this is an important topic for future research.

In contrast to these distortions, however, explicit judgments of body shape assessed with a template-matching task were approximately veridical. Thus, in addition to being distinct from the postural schema, the body model is also distinct from the conscious body image. Although the distinction between the postural schema (or body schema) and body image is well established (3, 23, 24), our results demonstrate the existence of an additional, highly distorted, representation of body form. Although the brain has access to a veridical representation of hand shape in the form of the body image, the highly distorted body model is nevertheless used to localize the body in space. This suggests that the process of localization and the associated body model are, at least in part, cognitively impenetrable (26).

Effective control over everyday actions clearly requires accurate information about body structure as well as posture. How can the highly distorted representation of the hand in our data be compatible with skilled manual action? One view suggests that the motor system avoids explicit representation of initial limb location by simply coding the desired end point of a movement (27, 28). Alternatively, the motor system could use a different model of the body from those involved in perception and cognition. Clearly, position sense does not rely on proprioceptive information alone, but supplements this with vision (29, 30) and efferent copies of motor commands (31). Motor learning might involve correcting a distorted underlying model with these additional inputs, analogous to adaptive changes following exposure to visually distorting prisms (32) or surgical elongation of limbs (33). Our experiments removed these two potentially enriching inputs to the represented body. Indeed, studies isolating localization following passive movement find remarkably poor performance (34), to which the distortions reported here presumably contribute.

The study of shape has a long history in organismic biology (19). Morphometric analyses of landmark data (18) have provided rich insight into the nature of biological forms. We applied an analogous logic to investigate not a biological form, as such, but the mental representation of such a form. This psychomorphometric approach offers a powerful, quantitative method for studying a fundamental form of self-awareness in the brain. Although the need for a stored body model mediating human position sense has long been recognized (4, 6, 8), we have rendered this representation observable.

Materials and Methods

Participants.

Eighteen individuals (15 female and three male) between 18 and 33 y of age participated in Exp. 1. All but three were right-handed as assessed by the Edinburgh Inventory (35) (M, 54.94; range, −100 to +100]. Twelve individuals (eight female and four male) between 19 and 68 y of age participated in Exp. 2. All but three were right-handed [M, 41.62; range, −78.95 to +100]. Thirteen individuals (eight female and five male) between 19 and 27 y of age participated in Exp. 3. All were right-handed [M, 78.39; range, 33.33–100]. Sixty-seven individuals (50 female and 17 male) between 19 and 76 y of age participated in Exp. 4. All but seven were right-handed by self-report. Data from an additional eight participants was excluded because of hand movement (n = 5) and experimenter error (n = 3).

Measures.

Localization task.

Participants sat with their left hand on a table aligned with their body midline. An occluding board (40 × 40 cm) was placed over the hand, resting on four posts (6 cm in height). A camera (Creative Live Cam Voice) was suspended on a tripod directly above the center of the board (27 cm high), pointing straight down. The camera was controlled by a custom MATLAB (Mathworks) script, which captured still JPEG images (1,280 × 960 pixels) and saved them for offline coding. A 10-cm ruler was placed on the table near the hand, which appeared in the photographs of the participant's hand and allowed conversion between pixel units and centimeters.

Participants used a long metal baton (35-cm length and 2-mm diameter), which tapered to a point at the end, to indicate with their right hand the perceived location of landmarks on their occluded left hand. Ten landmarks were used: the knuckle at the base of each finger and the tip of each finger (i.e., the center of the fingernail). On each trial, the experimenter verbally cued the participant as to which landmark to judge. Participants were instructed to take their time, to be precise in their judgments, and to avoid ballistic points. They were explicitly told to judge each landmark individually and to avoid strategies such as tracing the outline of the hand. To avoid hysteresis effects, participants moved the tip of the baton to a blue dot at the edge of the occluding board before the start of each trial. To avoid ambiguities in the coding of knuckle location from the photos, a small black mark was made on the center of each of the participant's knuckles with a nonpermanent felt-tip pen at the beginning of the session.

Template matching task.

To measure the conscious body image, we adapted the template matching task of Gandevia and Phegan (9). The logic of this task is to present participants with an array of images of a body part that differ systematically in size or shape, and to ask them to pick the one that most closely matches what it feels like the size or shape of their own body is. Whereas Gandevia and Phegan used this task to obtain measures of perceived hand size, here we used it to measures perceived hand shape (i.e., aspect ratio). Our approach here is identical to the one that we recently used (36), except that here we tested the left rather the right hand. On each trial, 15 hand images were presented on a sheet of A4 paper (210 × 297 mm). One image was of an average-looking hand; the other images were distortions of this image, stretched in length or in width by 5–35% in steps of 5%. Thus, seven stimuli were progressively wider (“fatter”) than the template hand, whereas seven stimuli were progressively more slender. Each sheet showed all 15 hands in a 5 × 3 grid, with the letters A–O in sequence beneath each image. Participants in Exp. 1 made a total of 16 judgments of hand shape, four before and four after each of the two blocks. Sixteen sheets with different random positions of the 15 hand images were created. Participants verbally reported the letter corresponding to the image that they selected.

Procedures.

In Exp. 1, there were two blocks of 100 trials each. Each block was composed of 10 miniblocks of 10 trials, one of each landmark, in random order. Just before and after each block, a photo was taken without the occluder so that the actual size, shape, and location of the hand could be determined and also to check that the hand had not moved during the block. Exp. 2 was identical except that in half the blocks participants rotated their left hand 90° clockwise relative to their torso such that the fingers were pointing toward the right. There were four blocks of 20 trials, each composed of two miniblocks of 10 trials, each containing each landmark in random order. Blocks were counterbalanced in ABBA fashion (initial condition counterbalanced across participants). Exp. 3 was identical to Exp. 2 except that participants made judgments about either their left or their right hand in different blocks (in “normal” posture). Responses were made with the hand not being judged. Exp. 4 was the same as Exp. 1 except that there was only a single block of 20 trials (two miniblocks of each landmark).

Analysis.

Image processing.

Fisheye distortion in the photographs was corrected using the Panotools plug-in (http://www.panotools.org/) for Adobe Photoshop CS2. The x–y pixel coordinates of each landmark on the images of the actual hand and the corresponding judged locations were coded using ImageJ (37). From these, mean coordinates were computed for each landmark. The set of these coordinates in a block constitutes two hand maps, one reflecting actual hand shape, the other reflecting the shape of the hand as represented by the body model. Distances between the tips and knuckles of each finger and between pairs of knuckles were computed and converted into centimeters.

Shape index.

We quantified hand aspect ratio using a modifid form of Napier's (12) shape index, defined as SI = 100 × (width/length), where hand width was operationalized as the distance between the knuckles of the index and little fingers, and length as the distance between the knuckle and tip of the middle finger. For each participant's actual hand and the body model, these values were straightforward to code. For the template matching task, the responses on the 16 trials were averaged, and the shape index of this average response was calculated by determining how much the average response was stretched, either vertically or horizontally, compared with the undistorted hand.

GPS.

As articulated structures, the fingers can rotate independently of the hand. Thus, the exact posture of each finger will differ slightly among participants. Although this will not affect analyses of distances between adjacent landmarks, it will affect analyses of whole-hand shape, such as GPS (38). Thus, to isolate information about hand shape, we rotated the fingers of each hand to a common posture, defined for each finger as the angle formed by the intersection of the line running through the knuckles of the index and little fingers and the line running between the tip and knuckle of a particular finger. First, we computed these angles for each of the five fingers of the actual hand map for each participant. The average angle for each finger was then used as the template posture. These angles were 44.4°, 64.4°, 77.4°, 86.8°, and 106.1°, for digits 1–5, respectively. For each hand map, the tip of each finger was rotated such that the finger was at the template posture while maintaining the same distance between the knuckle and fingertip. This results in hand maps that all have the same posture, allowing shape comparison (38).

Once differences in posture were removed, shapes were compared using GPS, which removes differences resulting from location, size, and orientation (17, 18). GPS analyses were conducted with CoordGen software, part of the Integrated Morphometrics Program (IMP; H. David Sheets, Canisius College, http://www.canisius.edu/~sheets/morphsoft.html). As there were two experimental blocks in Exps. 1–3, maps from each were placed in GPS alignment and mean shape coordinates were computed separately for the actual hand and localization judgments. Then a second, group-level GPS analysis was run, including the two averages from each participant. Goodall's F-statistic (39), which uses the GPS superposed data to test for difference in the average shape between two conditions, was computed using TwoGroup6h software, also from the IMP package.

This analysis also allows computation of grand-mean coordinates for both the body model and actual hand. To depict the body model as a deformation of actual hand shape using a thin-plate spline (Fig. 2F), we used tpsSplin 1.2 (F. James Rholf, SUNY Stony Brook, http://life.bio.sunysb.edu/morph/index.html).