Double dissociation of two cognitive control networks in patients with focal brain lesions

Abstract

Neuroimaging studies of cognitive control have identified two distinct networks with dissociable resting state connectivity patterns. This study, in patients with heterogeneous damage to these networks, demonstrates network independence through a double dissociation of lesion location on two different measures of network integrity: functional correlations among network nodes and within-node graph theory network properties. The degree of network damage correlates with a decrease in functional connectivity within that network while sparing the nonlesioned network. Graph theory properties of intact nodes within the damaged network show evidence of dysfunction compared with the undamaged network. The effect of anatomical damage thus extends beyond the lesioned area, but remains within the bounds of the existing network connections. Together this evidence suggests that networks defined by their role in cognitive control processes exhibit independence in resting data.

Cognitive control is required in everyday life to coordinate our thoughts and actions to achieve internal goals while still allowing the flexibility to adjust these goals with changing task demands. Although previous studies have attributed cognitive control to various prefrontal cortical regions (1, 2), recently it has been proposed that a dual-network architecture exists in the human brain in which cognitive control depends on regions that extend beyond the frontal cortex (3). In a recent cross-task analysis, Dosenbach et al. (4) identified a number of regions active during different stages of cognitive control tasks. Given the difficulty in isolating cognitive control networks that are simultaneously active during task performance, the investigators took advantage of the recent advent of resting state functional MRI (rs-fMRI) for detecting spontaneous fluctuations between coherent brain regions. In a follow-up study, these predefined regions of interest (ROIs) obtained from the task data served as seeds in a correlation analysis of rs-fMRI data (3) in which graph theory and hierarchical clustering were applied to the correlation matrices. These analyses identified two distinct networks labeled as fronto-parietal (FP) and cingulo-opercular (CO) (Fig. 1A). Based on their role in cognitive tasks, the FP network consists of nodes proposed to provide signals that act on a rapid time scale to initiate and adjust control, whereas the CO network nodes act to provide signals that allow set maintenance over a longer time scale (3, 5).

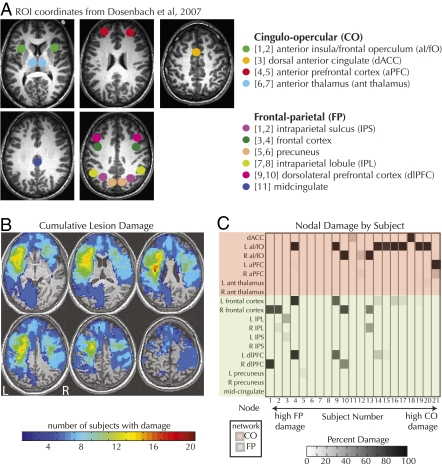
Fig. 1.

(A) FP and CO ROI locations from Dosenbach et al. (3) (B) Degree of lesion overlap across all patients. (C) Amount of damage sustained at each node by each subject. Subjects 5–8, despite having lesions elsewhere, sustained no damage to either network.

Numerous studies using rs-fMRI have shown that neuronal activity is characterized by temporal correlations in blood oxygen level-dependent signal across disparate brain regions (6, 7). These fluctuations seem highly consistent over time and reflect the presence of intrinsic functional (8) and structural (9) connectivity. Among these fluctuations, different networks can be distinguished, many of which show remarkable resemblance to task-related networks (10). Using rs-fMRI, there are a number of different methods for assessing network properties, from measuring the magnitude of correlations between single nodes (11) to calculating mean correlation values across predefined network nodes (12). Here we use the latter method to compare mean correlations within and between the FP and CO networks.

Although correlations between brain regions can reveal global network properties, they do not provide information about the relationship between nodes within those networks or about the small-scale regional organization within network nodes. Graph theory is a mathematical tool that has recently been applied to rs-fMRI data with the goal of quantifying the organization of network nodes at both the whole-brain and local levels (13–16). One graph theory property that distinguishes brain networks from other nonbiological networks is its characteristic small-world architecture (13) that is hypothesized to be scale-free in that it exists at both local and global levels (17). In both structural and functional MRI data (14, 15), brain networks have been found to be optimized for high local and global information transfer while maintaining low wiring costs. This organization is so consistent that disruptions in small-worldness can be used as a biomarker for distinguishing young healthy subjects from those with Alzheimer's disease (18), schizophrenia (19), and even normal aging (20).

Examining the correlation structure of resting state networks in patients with focal lesions offers the opportunity to test the hypothesized functional independence of the FP and CO cognitive control networks. Furthermore, the incorporation of graph theory analyses allows detection of small-scale changes in regional organization that may underlie more global network changes. In the current study, we scanned patients with heterogeneous focal brain damage in an rs-fMRI session. We computed time-series correlations among the ROIs in the FP and CO network as well as among voxels within each ROI. At the global network level, we found higher within-network than between-network correlations across all patients, and a negative relationship between within-network functional connectivity and the amount of damage sustained by the network. Simulating lesions in data from healthy control subjects resulted in less severe decreases in functional connectivity than found in our patients. Thus, it is likely that the functional disruption captured by the decrease in connectivity extends beyond the site of anatomical damage to the remaining nondamaged nodes of the network. Indeed, the small-worldness of these nodes was lower than those of the undamaged network, supporting the notion that global network connectivity changes can be accounted for by disruptions in local network organization. We can thus conclude that anatomical damage to portions of two networks shown previously to be differentially engaged during different cognitive control processes specifically affects only the damaged network. This finding points toward the functional independence of these networks at rest and presumably under conditions requiring cognitive control.

Results

In this study, 21 patients with heterogeneous focal damage (Fig. 1B) underwent 10 min of rs-fMRI followed by high-resolution anatomical scans to enable accurate lesion mapping. All patient lesion masks can be seen superimposed on normalized T1 axial slices in Fig. 2. Time-series correlations were assessed among 18 predefined ROIs (3) after standard preprocessing (6). The amount of damage sustained by each patient was quantified as the number of voxels in each ROI that overlapped with the lesion mask divided by the total number of voxels across all ROIs in that network to account for the differing network sizes. Some patients (Fig. 1C) sustained significant damage to both networks, so we used a damage-difference score to represent the relative amount of damage to the networks. This measure allowed us to examine how the amount of relative damage affected the difference in connectivity between the two networks. As noted in Fig. 1C, the lesions in subjects 5–8 did not overlap with either the FP or CO network. The inclusion of these subjects in this study can be considered a control to examine the functional connectivity among anatomically intact network nodes in patients who have sustained brain damage elsewhere.

Fig. 2.

Lesion masks in normalized space for all 21 subjects.

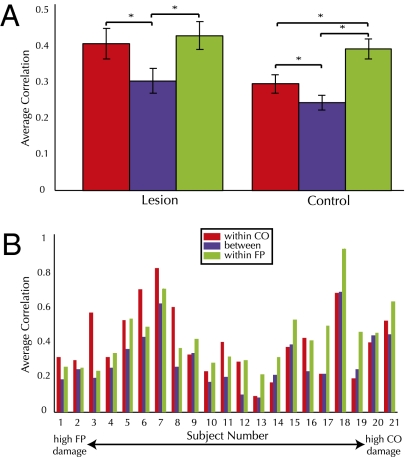
In addition to this anatomical measure of network integrity, we obtained a measure of functional connectivity within and between the CO and FP networks by averaging over the correlations among network nodes in each patient, a method that has been used elsewhere (12). Paired t-tests (Fig. 3A) revealed significantly higher average correlations within the CO network and within the FP network compared with average between-networks correlations, in the patient group [t(20) = 3.55; P < 0.005 and t(20) = 5.94; P < 0.0001, respectively] and in a group of age-matched control subjects [t (20) = 3.4; P < 0.005 and t(20) = 9.25; P < 0.0001, respectively]. Individual patient mean correlation values are shown in Fig. 3B. In previous studies of healthy populations (3), the FP and CO networks exhibited higher within-network than between-network correlations. This is also true here with both lesion patients and age-matched control subjects, an observation that lends support to the dissociability of these networks in the resting state. Importantly, however, it is only by capitalizing on the extent of damage to these networks that we can address the question of whether the within-network connectivity of the FP and CO networks is independently affected by this selective damage.

Fig. 3.

(A) Average FP and CO connectivity across subjects in lesion and control groups. (B) Average FP and CO network connectivity within each lesion patient sorted from high FP to high CO damage.

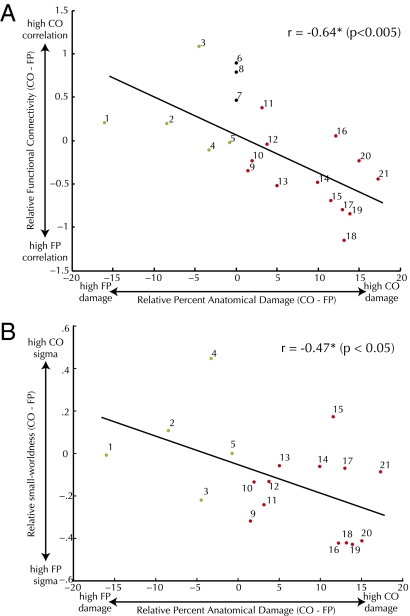
To assess the extent to which the networks are independent, we correlated relative network damage with relative strength of functional connectivity within each network. Relatively more damage to a network was negatively correlated (r = −0.64, P < 0.001; Fig. 4A) with relatively poorer connectivity within that network. When the size of the lesion was taken into account, this negative relationship remained significant (r = −0.73, P < 0.001). The method that we used of averaging correlation values introduces the potential confound of combining negative and positive values. However, performing the correlation analyses in Fig. 4A with r² values did not change this relationship (r = −0.44, P < 0.05).

Fig. 4.

(A) Relative functional connectivity of CO and FP networks versus relative CO and FP anatomical damage. (B) Relative small-worldness (sigma) of CO and FP network nodes versus relative CO and FP anatomical damage.

A potential confound to our relative measure of functional connectivity is that the functional data from damaged nodes is allowed to contribute to the mean network correlation values. Because of the small number of nodes in both the CO and FP networks and the variability in the number of damaged nodes per subject, removing the damaged nodes entirely was not a viable option, as this would negatively affect the signal-to-noise ratio in the individual subject estimates. Instead, we used the percent node overlap (Fig. 1C) to conduct a weighted-average, lesion-masking analysis, in which each node was weighted by the degree of lesion overlap. Correlation values from those nodes overlapping with the patients’ lesions thus contributed to the network averages in proportion to our best estimate of their integrity. Repeating the correlation analysis in Fig. 4A with this method yielded the same result obtained without weighted averaging (r = −0.45, P < 0.05). In addition, we performed a simulation analysis (SI Materials and Methods), which argues against the possibility that it is the damaged nodes themselves driving this negative relationship. In this simulation, the functional correlations of those nodes overlapping with regions of network damage were substituted into the correlation matrix of corresponding undamaged regions in healthy subjects. If it were the case that the low correlations from the damaged nodes were driving the negative relationship between damage and connectivity, this same relationship should have been observed in the simulated patients. However, this was not the case. Thus, we conclude that the decrease in network correlations in these patients must be due to the dysfunctional organization of the anatomically intact nodes within the damaged network.

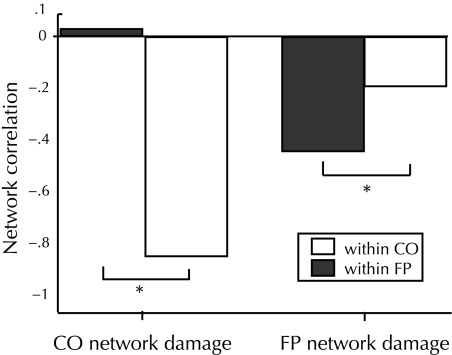
The correlation between lesion location and functional connectivity used relative differences and as such, could be due to increased connectivity in the undamaged network rather than decreased connectivity in the damaged network. However, examining connectivity as a function of absolute damage in each network separately rejects this claim (Fig. 5). Across patients, CO damage is negatively correlated with CO (r = −0.8, P < 0.0001) and unrelated to FP connectivity (r = 0.03, P < 0.90), and FP damage is negatively correlated with FP (r = −0.44, P < 0.05) and unrelated to CO connectivity (r = −0.19, P < 0.41). Partial correlations taking into account the amount of damage to the opposite network strengthens these relationships. For CO damage, controlling for FP damage, the partial correlation with the CO network remained significant (partial r = −0.83, P < 0.0001) and remained nonsignificant for the FP network (partial r = 0.2, P = 0.388). For FP damage, controlling for CO damage did not change the significance of the relationship with the FP network (partial r = −0.47, P < 0.05) and the correlation with the CO network remained nonsignificant (partial r = −0.14, P = 0.559). Together, these data support our assertion that increasing damage to one network is correlated with increasingly disrupted connectivity within that network, but does not affect the other network or the connectivity between networks.

Fig. 5.

Mean correlation values within the CO or FP networks in either patients with relatively more CO network damage or patients with relatively more FP network damage. *Significant differences between within-FP and within-CO network correlations (P < 0.05).

In a parallel analysis to the ROI-to-ROI functional correlations shown in Fig. 4A, we calculated within-ROI voxel-by-voxel time-series correlations to capture the local changes to undamaged FP and CO network nodes. Importantly, these voxelwise correlations were computed on unsmoothed functional data. For each ROI, we assessed graph theory metrics (clustering and path length) over these within-ROI-correlation matrices as well as for equivalent sized random networks yielding a metric of small-worldness (sigma). The average sigma values across network nodes showed a similar relationship to the ROI-to-ROI functional correlations; that is, the average small-worldness of the small-scale networks contained in each individual node in the large-scale cognitive control network was decreased only within the damaged network, leaving the undamaged network relatively intact. This relationship were significant (cost = 0.1, r = −0.47, P < 0.05) within a range of cost values. A single cost value and the best-fitting regression line is shown in Fig. 4B.

In summary, results from both the functional correlations across network nodes and graph theory measures within nodes indicate that anatomical damage to one network has a specific detrimental effect on the remaining undamaged nodes in that network but no effect on the other network. Simulating brain lesions in healthy control subjects also supports this claim (SI Materials and Methods and Fig. S1).

Discussion

Whether in a controlled experimental environment or in a real-life situation, humans are adept at maintaining a task-relevant goal while simultaneously making moment-to-moment adjustments in behavior to achieve that goal. Such cognitive control, we and others (5, 21) argue, is supported by multiple independent neural systems. Here we assess network structure using multinodal network functional correlations and within-node graph theory metrics to provide converging evidence in support of the putative independence of two proposed cognitive control networks (3). We have demonstrated that damage to two networks thought to support different components of cognitive control alters connectivity within the damaged network but leaves the other network preserved. Within the damaged network, it is not only the portion of the network subjected to anatomical damage that exhibits dysfunction; rather, as we have demonstrated by within-node graph theory measurements, it is also the remote, interconnected regions that seem to be affected by this damage.

Our findings are consistent with the concept of diaschisis, which was originally formulated to describe temporary clinical deficits related to areas remote from the area of damage (22). The concept of diaschisis has since been expanded to include neurophysiological observations of depression of activity in remote, undamaged brain sites that are functionally connected to lesion areas. The prevailing hypothesis for the underlying mechanism responsible for this phenomenon is the withdrawal of excitatory influences from anatomically connected brain regions (23), but evidence for this mechanism from neuroimaging data in stroke patients has been mixed. Some investigators have demonstrated significant reductions in resting activity in structurally intact regions homologous to the site of damage using positron emission tomography (24) and magnetoencephalography (25), as well as decreases in EEG coherence throughout the lesion hemisphere (26) and across the entire brain (27). One study, however, found that whereas resting PET activity showed significant decreases at a distance from the lesioned site, task-evoked BOLD signal was minimally affected (24).

Although the aforementioned studies are largely consistent in their observation that functional disruptions extend beyond the region of anatomical damage, none have examined the specific effects of damage on functional networks. Perhaps the disparate results from these studies can be explained by our hypothesis that damage remains localized to the particular network affected. This has been examined in an fMRI study of patients with right hemisphere strokes who exhibited spatial neglect (11). In this study, functional connectivity of nodes in two attention networks was assessed at both the acute and chronic stage of recovery. Functional correlations between pairs of network nodes in both the anatomically damaged ventral attention system and intact dorsal attention system were decreased at the acute stage compared with age-matched control subjects. Over time, the dorsal system recovered its functional connectivity, but the ventral system remained impaired. The investigators posited that although only one system had sustained physical damage, because the ventral and dorsal attention systems normally interact, anatomical damage to the ventral system carried over into the dorsal system and manifested as a disruption in functional connectivity. That is, the dorsal system normally relies on the operation of the ventral system to maintain some aspects of spatial attention, so anatomical damage to the ventral system has functional consequences for the distal parts of the network even though they are remote from the damage.

Another recent study from the same group (28) examined the behavioral significance of intra- versus interhemispheric interactions following ischemic stroke. Subjects’ levels of behavioral impairment were correlated with the strength of functional connectivity both within the damaged hemisphere and across to the intact hemisphere nodes. Interhemispheric interactions most strongly predicted the level of impairment in behavior, adding to the collection of evidence that anatomical damage produces network dysfunction in nonlesioned regions of the same network. However, in the current study, rather than assessing the damage to a single functional network, we used patients with damage to nodes throughout two different, predefined cognitive control networks. This disparate pattern of damage allowed comparisons of network correlations within subject rather than with a control group and, more importantly, has allowed us to assess the degree of independence of these two multinodal networks. Damage to the FP network degraded the functional connectivity of nodes only within the FP network, and damage to the CO network impaired connectivity only within CO nodes. Applying graph theory to individual nodes in these two networks provides a potential explanation for this decrement in connectivity. The small-scale organization of these brain regions only within the damaged network exhibited disruptions in small-worldness compared with the organization of nodes within the nondamaged network.

Other investigators have used graph theory to examine the effects of brain lesions on the organization of large-scale brain networks; however, to our knowledge, none of these investigators have had the advantage of using real data from patients with brain lesions. In a recent study, Alstott et al. (29) simulated the effects of brain lesions on network properties derived using graph theory and found that the degree of disruption in network organization depends on the location of the lesion. When nodes were classified based on properties pertaining to their role in the network as a whole, removing nodes that were considered “hubs” was most detrimental. This approach treats the entire brain as a single network without considering the effect of lesions on individual subnetworks. The difficulty with using graph theory on smaller subnetworks is that many of the metrics are sensitive to the number of nodes in a graph, necessitating networks that are larger that the number of nodes in each of the networks examined here. Using graph theory at a local level as we do in the current study is one way of addressing the question of the organization of subnetworks with and without a lesion.

The observed double dissociation between the FP and CO networks using both multinodal functional correlations and within-node graph theory suggests a parallel organization whereby the function of one network may not be necessary for the other network to function adequately. Consistent with clinical observations (30), the existence of independent, distributed networks supporting cognitive control may render the brain less susceptible to persistent behavioral deficits as a result of focal cortical damage. However, the finding that these networks are distinct functional units does not preclude the possibility that they flexibly interact to carry out complex cognitive control (31). That is, in a healthy individual with functionally and structurally intact cognitive control networks, either system or both could contribute toward accomplishing the goal at hand. Understanding how these parallel systems coordinate their activities to carry out complex cognitive control represents an important next step. Moreover, given the important role of these networks in a wide variety of cognitive processes, it will also be critical to relate the strength of functional connectivity to behavior in both intact and damaged networks.

Materials and Methods

Participants.

Twenty-one patients (age: mean ± SE, 58 ± 14 y; range, 19–83 y) with focal lesions due to ischemic stroke (n = 16), cerebral hemorrhage (n = 1), tumor resection (n = 2), or traumatic brain injury (n = 2), and 21 healthy subjects (age: mean ± SE, 61 ± 17 y; range, 19–83 y) were studied. All patients were at least 5 mo poststroke or postinjury (mean, 8.3 y; range, 5.8 mo to 32 y). All participants were prescreened to exclude individuals with a history of other neurologic or psychiatric conditions. Informed consent was obtained from subjects in accordance with procedures approved by the Committees for Protection of Human Subjects at the University of California, Berkeley.

MRI Acquisition Procedures.

T2*-weighted echo planar images (EPI) were collected on a whole body 3-T Siemens MAGNETOM Trio MRI scanner using a 12-channel head coil. Structural images were acquired using an axial MP-RAGE 3D T1-weighted sequence (TR = 2,300 ms, TE = 2.98 ms, FA = 9°, 1 × 1 × 1-mm voxels) for patients and controls, and an additional FLAIR image was collected for each patient to better visualize the lesion. For patients, 10 min of EPI data were analyzed (300 time points, TR = 2,000 ms, TE = 30 ms, 28 3.30-mm-thick axial slices). For controls, 10 min of EPI data were analyzed in seven subjects (435 time points, TR = 1,370 ms, TE = 26 ms, 24 3.85-mm-thick axial slices), and 4 min 20 s of EPI data in 14 subjects (250 time points, TR = 1,000 ms, TE = 50 ms, 24 4.025-mm-thick axial slices). All participants were instructed to stay awake with their eyes open; no other task instruction was provided.

MRI Preprocessing.

Image preprocessing was carried out with AFNI (32). The following prestatistics processing was applied: slice-time correction and removal of nonbrain structures from the EPI volumes. Spatial smoothing using a 5-mm Gaussian kernel was applied to all functional data except for those used in the within-ROI graph theory analysis. Following Fox et al. (6), signal from movement, white matter, and ventricles was regressed out, although we did not subject the data to global mean scaling. The high-resolution T1-weighted image was coregistered to the mean functional data and subsequently segmented using SPM5 (Wellcome Department of Cognitive Neurology, London, United Kingdom). The template used for segmentation was derived from 152 normal subjects (MNI152; Montreal Neurological Institute, Montreal, QC, Canada). Parameters obtained from segmenting the brain were later used to normalize each individual's T1-weighted brain, but all analyses of functional data were performed in the subjects’ native space. This extra segmentation step was necessary for accurate registration, which is often confounded by structural brain damage.

Lesion Mapping.

Lesion masks were manually traced by EN and CG in native patient space according to visible damage on a T1-weighted anatomical scan and guided by damage and hyperintensities on a T2-weighted FLAIR image. All lesion masks were examined by MD for anatomical specificity. Individual patient masks in normalized space are shown in Fig. 2.

Percent Network Damage.

To answer the question regarding how lesions differentially affect two predefined networks (3), the extent of the brain lesion for each individual was quantified by counting the percentage of voxels in each ROI that overlapped with the lesion. These percentages were then averaged over all of the nodes within a network, resulting in one number for each network; a percentage of damage to that particular network. By subtracting these “damage scores” from one another, a number between −100 and + 100 was obtained, indicating relative damage to one network compared with the other, for each individual separately.

Functional Connectivity.

Eighteen 6-mm spheres centered on coordinates from fMRI data reported in Dosenbach et al. (3) were transformed from Talairach to MNI space and then reverse-normalized to each subject's native space. The reverse-normalization procedure used the normalization parameters obtained from the SPM5 segmentation tool to go from atlas space to the individual's native space. For between-ROI correlations, voxel time-series were averaged within each ROI, and these averages were bandpass filtered (0.005–0.08 Hz) to remove physiological noise such as cardiac and respiratory artifact (1). Functional connectivity was assessed in each subject by correlating average time-series across seeds, resulting in an 18 × 18 matrix for each subject. It should be noted that pairwise correlation values derived from this type of analysis reflect only the synchronized activations and deactivations in different regions and will not detect similar time courses that are phase shifted (i.e., these will result in low correlations). Because of the low frequency of the filtered signal and the nature of the resting state activity, we assumed that such phase-shifted patterns would not represent the presence of healthy interactions. For within-ROI correlations, all ROIs were matched for minimum number of voxels (74) across subjects and regions. Functional connectivity was assessed in each subject by correlating time-series across single voxels within each ROI.

Average strength of connectivity within a network was calculated by adding all Fisher-transformed correlation values within a network and dividing this by the number of nodes within that network, as in He et al. (11) and Van Dijk et al. (12). Apart from that average within-network strength, between-network strength was calculated by adding all of the values obtained from the between-network interactions and dividing this by the total number of between-network interactions. This resulted in three values for each individual. We did not assess average strength of connectivity within each ROI, as this would be highly subject to autocorrelations among neighboring voxels.

Partial Correlations.

A partial correlation removes the effect of a third variable from the relationship between the two variables of interest. The number of voxels in the lesion mask was calculated per patient and entered as a controlling variable in both the relative (network Fig. 4A) and individual network (Fig. 5) correlation analyses.

Removing the Contribution of Damaged Nodes from Average Correlations.

The percent overlap between the lesion mask and individual ROIs (Fig. 1C) was used to construct a weighted-average that might more accurately reflect the contribution of each damaged node to the total network average. In this method, the correlation value from each node was multiplied by the percent damage of that node (as damage increased, the weighting coefficient decreased from 1 to 0) and summed across nodes in either the FP or CO network. This sum was then divided by the sum of the percent damage values for all nodes in the network.

Graph Theory.

Voxel-by-voxel correlation matrices were derived for each node (ROI) as described above. We did not compute classical metrics based on graph-theoretic ideas at the FP/CO network level, because such measures are difficult to interpret on small networks (with only 18 nodes). Instead, these binarized 74 × 74 correlation matrices served as adjacency matrices defining graphs over which various metrics were assessed. The threshold used to binarize the correlation matrices was chosen so as to produce graphs with comparable cost, defined as the total number of edges between nodes in the graph divided by the maximum possible number of edges. Rather than restricting our analysis to a set of graphs obtained by applying a single threshold value to the correlation matrices, we systematically explored the properties of graphs over a range of cost values to ensure that all comparisons between subjects equated the number of edges in the graph. Although the following computations were performed at a range of cost values (0.01–1), the main results are reported at cost = 0.1, which is within the range of “ideal costs” (0.01–0.34) (25).

The graph metrics of interest here were the clustering coefficient (C) and the minimum path length (L) defined for each of the nodes in the network. For any node i, C is the ratio between the number of edges that exist among the nearest neighbors of i and the maximum possible number of edges that could exist among them; high values of C imply that most of the neighbors are also neighbors of each other. For any pair of nodes (i, j), the path length L is defined as the minimum number of edges that must be traversed to form a direct connection between i and j. From these local definitions, graph averages of C and L were computed. For comparison, random networks were constructed that contained the same number of nodes and edges. In a random graph, the average minimum path length is typically short and the average clustering coefficient is small. A well-accepted characterization of a network that incorporates these properties is the small-worldness coefficient sigma. Sigma is the ratio of local connectedness (C, clustering coefficient) to global integration (L, path length) of a network; when this ratio is greater than 1, a network is said to demonstrate “small-worldness” (13). Damaged nodes were not included in this analysis and as such, any subjects without overlap to either the FP or CO network were not included, leaving 18 subjects in the analysis reported in Fig. 4B. The same analysis including all subjects is described in SI Materials and Methods.