Abstract
Accurate tracking of tumor movement in fluoroscopic video sequences is a clinically significant and challenging problem. This is due to blurred appearance, unclear deforming shape, complicate intra- and inter- fractional motion, and other facts. Current offline tracking approaches are not adequate because they lack adaptivity and often require a large amount of manual labeling. In this paper, we present a collaborative tracking algorithm using asymmetric online boosting and adaptive appearance model. The method was applied to track the motion of lung tumors in fluoroscopic sequences provided by radiation oncologists. Our experimental results demonstrate the advantages of the method.
Index Terms: Online Learning, Contour Tracking, Fluoroscopy
1. INTRODUCTION
Accurate tracking of tumor movement in fluoroscopic video sequences is a clinically significant and challenging problem. The issue of precise target positioning of tumors in lung cancer is complicated by intra-fraction target motion. It has been well demonstrated that tumors located in the thorax may exhibit significant respiratory induced motions [1]. These physiologically related motions may increase the target positioning uncertainty and have a two-fold of impact on radiation treatment. First, the motions will blur the images and increase the localization uncertainty of the target at the planning stage. On the other hand, this increased uncertainty may unnecessarily include some normal tissues, which may lead to higher than expected normal tissue damage.
Recent computer-aided methods for tracking the tumor can be categorized into three groups: (1) Finding the tumor positions based on the external surrogates [2]; (2) Tumor tracking with the help of fiducial markers inside or near the tumor [3]; (3) Tumor tracking without implanted fiducial markers. The optical flow [4] produce promising tracking results when there is relatively small motion between adjacent frames. Respiration motion also complicates accurate tracking of tumors making it necessary to apply adaptive trackers. Shape models of individual annotated tumors at different phases of respiration were learned offline to achieve good tracking results [5]. A motion model and one step forward prediction were applied to reliably track the left ventricle in 3D ultrasound [6]. However, these methods require a lot of expensive annotations and can only track tumors by utilizing learned shape priors or motion priors.
In this paper, we present an adaptive tracking algorithm of lung tumors in fluoroscopic image sequences using online learned collaborative trackers. Through the use of online updating, our method does not require large number of manual annotations and can adjust to appearance changes adaptively. Adaptive classifiers are “taught” to discriminate landmark points in the contour from others. They are incrementally updated during the whole tracking process. Appearance of the local window centered in each landmark point is modeled in a low dimensional subspace. The algorithm was evaluated using two fluoroscopic sequences of lung cancer provided by radiation oncologists.
2. ONLINE CONTOUR TRACKING
The tumor contour is represented as a list of landmark points in clockwise. We denote the contour as C = {c1, c2, …, cn}, where ci is the i-th landmark point. Let Z = {z1, z2, …, zn} as the observation of the contour, and Λ = {χ1, χ2, …, χn} as the states of the contour. The χi = {x, y} is the coordinates of landmark point ci. The tracking problem can be represented as the estimation of a state probability p(Λt|Z1:t), where Zt is the observation at the t-th frame.
| (1) |
is the estimation of the contour tracking result.
Assuming each landmark point is independent to each other, let χti and zti serve as the state and observation of the i-th landmark point in the t-th frame. Then (1) is equivalent to:
| (2) |
Tracking results for all landmark points with a maximum p(χti|zti) yield the optimal solution of (2). For convenience, we present the contour tracking as the estimation of p(χt|zt) for each point. Bayesian importance sampling estimates and propagates the probability by recursively performing prediction:
| (3) |
and updating
| (4) |
The transition model p(χt|χt−1) is constrained by assuming a Gaussian distribution  ;(χt|χt−1, σ). The observation model p(zt|χt) represents the likelihood of zt being generated from state χt. In our algorithm, it is measured with two independent models collaboratively. One is a discriminative model using an asymmetric online updated classifier. The other is based on a generative model, which represents the appearance of each small region around the landmark point in an incrementally learned low dimensional subspace. For point observation zt in the current frame, the observation model is
;(χt|χt−1, σ). The observation model p(zt|χt) represents the likelihood of zt being generated from state χt. In our algorithm, it is measured with two independent models collaboratively. One is a discriminative model using an asymmetric online updated classifier. The other is based on a generative model, which represents the appearance of each small region around the landmark point in an incrementally learned low dimensional subspace. For point observation zt in the current frame, the observation model is
| (5) |
where pD(zt|χt) and pG(zt|χt) are the likelihood calculated from the discriminative and generative models, respectively. Substituting (5) into (4), the point tracking result χt = argmaxχtp(χt|z1:t).
3. ASYMMETRIC ONLINE BOOSTING
We define training samples and their labels , where y = 1 denotes a landmark point and y = −1 is a background point. A function f(x) : Rd → R can be learned as the confidence of labeling sample x. x is classified to be the object if f(x) > 0 or background otherwise. The pD(zt|χt) in (5) is measured by f (x), where x is the sample generated with state χt. Because the training samples are unbalanced and provided incrementally, the discriminative model is trained using asymmetric online boosting. This method provides a more robust classifier and converges faster for unbalanced training sets [7].
Boosting constructs a strong classifier as a linear combination of T weak classifiers hi(x) ∈ {−1, 1} where i = 1, 2, …, T:
| (6) |
| (7) |
The weight αi of hi(x) is correlated to its classification accuracy on the training data. However, good performance of the standard Adaboost requires a large and balanced training set. We have a limited amount of labeled training samples, and the number of positive samples is much lower than the number of negative samples. Instead of weighting positive and negative samples evenly, we force the penalty of a false negative to be k times larger than a false positive. Compared with the standard loss function exp(−yi * Ht(xi)) defined in Adaboost, the loss function in our algorithm is:
| (8) |
where
| (9) |
which is proven to be effective in [7]. This asymmetric loss function can be integrated into an online boosting algorithm by multiplying the original weights exp(−yi * Ht(xi)) with . For an online boosting algorithm with iterations, samples are weighted by times at each iteration to avoid the asymmetric weights to be absorbed by the first selected weak learner.
The asymmetric online boosting method used in our algorithm is summarized in Algorithm (1). The strong classifier H(x) is updated incrementally using tracking results in the current frame. Each weak learner hi(x) and its corresponding weight αi are updated with learning rate γ (shown in Algorithm (1)). This online updating schema enabled the incrementally trained classifier to be more adaptive to gradual appearance changes.
Algorithm 1.
Asymmetric online boosting
|
Define: Let
represent the dataset, xi = {xi1, …, xid}is d dimensional feature vector and yi ∈ {−1, 1} is its label. The γ is the learning rate. ω = {ω1, ω2, …, ωN} is the samples’ weight. The Ht(x) is the strong classifier in the t-th iteration, the weighted accuracy and error are denoted as
and
, m = 1, …, M, where M is number of weak classifiers in the pool. The I is the indicator function. | |
| 1. | ωi = 1, i = 1, …, N |
| 2. | for t = 1, 2, …, T do |
| 3. | |
| 4. | |
| 5. | for m = 1, 2, …, M do |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | end for |
| 11. | m* = argminmεm |
| 12. | |
| 13. | Ht(x) = Ht−1(x) + αthm*(x) |
| 14. | ωi = ωiexp(−yi* Ht(xi)) |
| 15. | end for |
4. DYNAMIC APPEARANCE MODEL AND SUBSPACE LEARNING
The online boosting classifier utilizes a limited number of online selected weak learners with best discriminative power. However, it is still challenging to discriminate landmarks with similar appearance, which are very common in fluoroscopic images. Dynamic appearance model handles this challenge by learning the target incrementally.
Without losing generality, we define I = (I1, I2, …, In) as n observations of one landmark point in n consecutive frames, I can be modeled as a space spanned by low dimensional orthogonal subspace Uq*k centered at μ, where q is the length of the vectorized model and k is the dimension of the subspace. The U is the low dimension eigenvectors of the samples’ covariance matrix , and is the moving average.
Let Ω = {μ, U, Σ} serves as the appearance model for I, Σ is a diagonal matrix contains k largest ordered singular values of I and λ1 > λ2 > … > λk. For a given sample Iχt extracted in state χt, the likelihood of Iχt generated from the model Ω can be decomposed into the probabilities of distance-within-subspace,
| (10) |
and distance-to-subspace,
| (11) |
The generative model pG in (5) is estimated as
| (12) |
Let A denote the observations in the previous n frames and B represent the most recent m frames. Incremental subspace learning [8] is performed to merge the new frames into the original subspace learned from A. With A = UΣVT by singular value decomposition (SVD), and B̃ as the components of B orthogonal to U, the concatenated matrix of A and B then can be written as
| (13) |
where After we calculate the SVD of R = ŨΣ̃ṼT, the new subspace is updated as U′ = [U B̃]Ũ and Σ′ = Σ̃. The mean is updated with a forgetting factor γ to decrease the weight of the older appearance models.
5. EXPERIMENTAL RESULTS
Two sets of fluoroscopic video sequences on a patient were collected to test our algorithm. The fluoroscopic images were acquired for a consented lung cancer patient who had right lilar T2 stage non-small cell lung cancer and was undergoing radiotherapy. These fluoroscopic images were saved in digital format and readily available for video display and analysis. Each sequence lasts for about 10 seconds and covers two to three respiration cycles. The first set is a posterior-anterior (PA) fluoroscopic video sequence, and the second one is a lateral sequence. As discussed previously, the quantified moving information is extremely important in radiotherapy management of lung cancers. Using the prescribed algorithm, an optimal plan and treatment strategy can be designed to provide a desired conformal dose coverage to a tumor target while sparing as much surrounding normal tissues as possible.
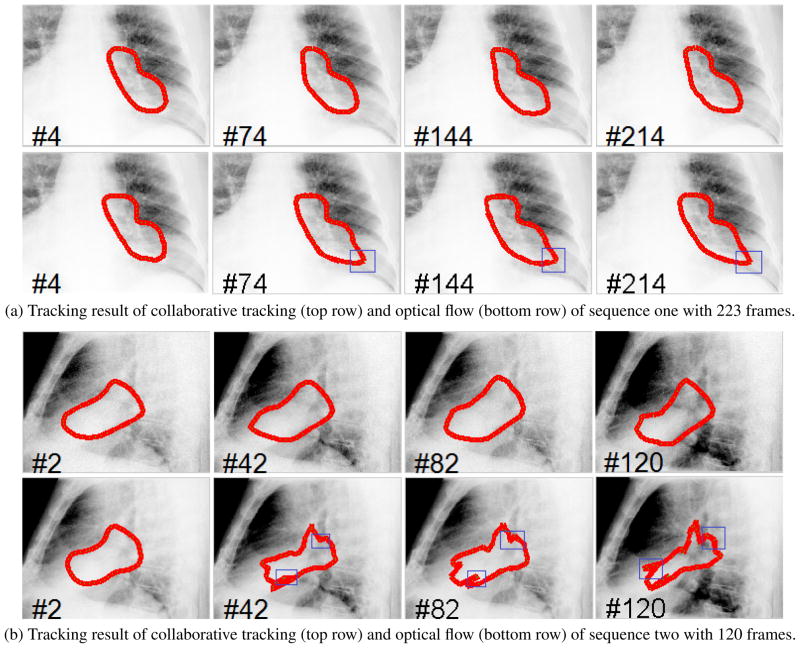
The experiments of the developed algorithm were conducted as follows. The initial contours for these sequences were labeled in a 3D CT by an experienced radiation oncologist. On the 3D CT images, the target (cancer tumor) could be clearly identified and delineated. Digitally reconstructed radiograph, along with the delineated contours, were projected along the PA and lateral directions. Based on the digitally reconstructed radiograph and projected target, an experienced radiation oncologist manually identified and delineated the target in the first frame of each of the fluoroscopic video sequence. The tracking procedure was then started automatically. The results are shown in Figure 1. Sequence 1 contains 223 frames and the results of frame (4, 74, 144, 214) are displayed in Figure 1a. Sequence 2 contains 120 frames and the results of frame (2, 42, 82, 120) are displayed Figure 1b. The tracking results were compared with optical flow using a 40 × 40 window. The results show that although each sequence exhibits different illumination and contrast changes due to different acquisition directions, the algorithm we presented can provide a reasonably accurate tracking result of the tumors.
Fig. 1.
The tracking results for two fluoroscopic sequences, where the frame index is marked on the left bottom of each image. The template drifting errors in the optical flow based tracking are marked in blue rectangles.
6. CONCLUSION
We have proposed an adaptive tracking algorithm for lung tumors in fluoroscopy using online learned collaborative trackers. No shape or motion priors are required for this tracking algorithm. This saves many expensive expert annotations. The experimental results demonstrate the effectiveness of our method. Instead of building a specific model, all the major steps in our algorithm are based on online updating. This adaptive online learning algorithm is therefore general to be extended to other medical tracking applications.
References
- 1.Giraud P, De Rycke Y, Dubray B, Helfre S, Voican D, Guo L, Rosenwald JC, Keraudy K, Housset M, Touboul E, Cosset JM. Conformal radiotherapy (CRT) planning for lung cancer: Analysis of intrathoracic organ motion during extreme phases of breathing. International Journal of Radiation Oncology Biology Physics. 2001;51:1081–1092. doi: 10.1016/s0360-3016(01)01766-7. [DOI] [PubMed] [Google Scholar]
- 2.Jiang SB. Radiotherapy of mobile tumors. Seminars in radiation oncology. 2006;16:239–248. doi: 10.1016/j.semradonc.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 3.Tang X, Sharp GC, Jiang SB. Fluoroscopic tracking of multiple implanted fiducial markers using multiple object tracking. Physics in Medicine and Biology. 2007;52(14):4081–98. doi: 10.1088/0031-9155/52/14/005. [DOI] [PubMed] [Google Scholar]
- 4.Xu Q, Hamilton RJ, Schowengerdt RA, Alexander B, Jiang SB. Lung tumor tracking in fluoroscopic video based on optical flow. Medical Physics. 2008;35(12):5351–5359. doi: 10.1118/1.3002323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Xu Q, Hamilton RJ, Schowengerdt RA, Jiang SB. A deformable lung tumor tracking method in fluoroscopic video using active shape models: A feasibility study. Physics in Medicine and Biology. 2007;52(17):5277–5293. doi: 10.1088/0031-9155/52/17/012. [DOI] [PubMed] [Google Scholar]
- 6.Yang L, Georgescu B, Zheng Y, Foran DJ, Comaniciu D. A fast and accurate tracking algorithm of left ventricles in 3D echocardiography. International Symposium on Biomedical Imaging. 2008:221–224. doi: 10.1109/ISBI.2008.4540972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Viola P, Jones M. Fast and robust classification using asymmetric adaboost and a detector cascade. Advances in Neural Information Processing System. 2002;14:1311–1318. [Google Scholar]
- 8.Ross D, Lim J, Lin RS, Yang MH. Incremental learning for robust visual tracking. International Journal of Computer Vision. 2008;77(1):125–141. [Google Scholar]