Reconstruction of dynamic contrast enhanced magnetic resonance imaging of the breast with temporal constraints

Abstract

A number of methods using temporal and spatial constraints have been proposed for reconstruction of undersampled dynamic magnetic resonance imaging (MRI) data. The complex data can be constrained or regularized in a number of different ways, for example, the time derivative of the magnitude and phase image voxels can be constrained separately or jointly. Intuitively, the performance of different regularizations will depend on both the data and the chosen temporal constraints. Here, a complex temporal total variation (TV) constraint was compared to the use of separate real and imaginary constraints, and to a magnitude constraint alone. Projection onto Convex Sets (POCS) with a gradient descent method was used to implement the diverse temporal constraints in reconstructions of DCE MRI data. For breast DCE data, serial POCS with separate real and imaginary TV constraints was found to give relatively poor results while serial/parallel POCS with a complex temporal TV constraint and serial POCS with a magnitude-only temporal TV constraint performed well with an acceleration factor as large as R=6. In the tumor area, the best method was found to be parallel POCS with complex temporal TV constraint. This method resulted in estimates for the pharmacokinetic parameters that were linearly correlated to those estimated from the fully-sampled data, with K^trans,R=6=0.97 K^trans,R=1+0.00 with correlation coefficient r=0.98, k_ep,R=6=0.95 k_ep,R=1+0.00 (r=0.85). These results suggest that it is possible to acquire highly undersampled breast DCE-MRI data with improved spatial and/or temporal resolution with minimal loss of image quality.

1. Introduction

Dynamic MRI plays an important role in a number of clinical magnetic resonance imaging applications, such as in dynamic contrast-enhanced MRI and functional MRI. For such applications, a common strategy used to balance tradeoffs between spatial resolution and temporal resolution is to reduce sampling of k-space data at each time frame. A variety of reduced k-space data acquisition and reconstruction techniques have been proposed to do this. Examples include sliding window, UNFOLD [1], keyhole [2], RIGR [3], k-t BLAST/k-t SENSE [4], k-t FOCUSS [5], compressed sensing [6,7] and HYPR [8]. Most of these methods use constraints (also known as “prior information”) to compensate for the information loss from reduced sampling. Sophisticated methods are typically needed to reconstruct the images with the constraints. For dynamic MRI applications, the images of adjacent time frames are often assumed to be similar, especially when motion is minimal, in which case temporal TV is a reasonable regularization term [9,10]. In this article, two tools were applied to the implementation of constrained reconstruction. One powerful tool is the Projection onto Convex Sets (POCS) formalism which can include prior information flexibly and has been extensively used in MRI reconstruction applications [11–14]. Another tool is the gradient descent method, which is regularly used for the minimization of an objective function, and can be considered as a type of projection to be included in the POCS framework.

For constrained MRI image reconstruction, the regularization term is typically used in its complex form [4,5,15]. However, separate real and imaginary TV regularization, and separate magnitude and phase regularization terms have also been investigated by several investigators. Fessler et al. [16] reported that the L2 norm of the spatial derivative in separate magnitude and phase form worked better than that in complex form on simulated phantom data. He et al. [17] reported that separate real and imaginary constraints produced results similar to the use of the complex form of regularization on phantom data. In this paper, different forms of temporal TV terms are compared for reconstruction of undersampled dynamic contrast-enhanced (DCE) MRI data acquired in breast cancer patients.

The article is organized as follows: in the first section, we present the form of the fidelity term and of various temporal TV terms including: complex TV, real and imaginary TV, and magnitude TV. Next, specific implementation details for the serial and parallel POCS methods are presented. Finally, we present and discuss results of undersampled breast DCE-MRI reconstructed using the different POCS methods.

2. Methodology

Two types of POCS, serial POCS (also known as sequential POCS) and parallel POCS, as summarized in [12], are used in this paper. For serial POCS, different projections are sequentially applied to update the data term at each iteration, while for parallel POCS, different projections are weighted to update the data term each iteration. Both the L2 norm of the fidelity term and the temporal TV term are convex functions. The gradient descent forms of both can be viewed as projections.

The fidelity term is defined as the L2 norm:

$$\delta (\stackrel{\sim }{m})={\left|\right|WF\stackrel{\sim }{m}-d\left|\right|}_2^2,$$ (1)

where m̃ is the vectorized 2D image estimate including all time frames, F is the (2D) spatial Fourier transform applied on each time frame in the dynamic sequence, W is a binary undersampling pattern (W is diagonal matrix, and it is identity if no undersampling), that changes each time frame and matches the undersampling pattern of the acquired k-space, and d is the undersampled data in k-space of one image slice over time (see acquisition section). The projection corresponding to the fidelity constraint term can be denoted as m̃_n+1=m̃_n−αθ_n with the updating term θ_n given by

$${\theta }_n=\frac{d\delta ({\stackrel{\sim }{m}}_n)}{d{\stackrel{\sim }{m}}_n}={(WF)}^H(WF{\stackrel{\sim }{m}}_n-d)=F^{H}WF{\stackrel{\sim }{m}}_n-F^{H}Wd,$$ (2)

where H is the Hermitian transpose operator and F^H is the 2D inverse Fourier transform applied on each time frame.

Besides the mandatory data fidelity convex set described above, any other convex sets can be used to regularize the solution. Three different forms of the temporal TV constraint are considered here. The first and most widely used form is the complex temporal TV term:

$$\psi (\stackrel{\sim }{m})={\Vert \frac{d\stackrel{\sim }{m}}{dt}\Vert }_1\approx \sqrt{{\left|\frac{d\stackrel{\sim }{m}}{dt}\right|}^2+\epsilon }$$ (3)

where ε is a small positive constant to avoid singularities in the derivative of the functional as shown by Acar et al. [18]. The gradient descent method gives $\frac{d\psi }{d\stackrel{\sim }{m}}=\frac{d^2\stackrel{\sim }{m}}{d{t}^2}/\sqrt{{\left|\frac{d\stackrel{\sim }{m}}{dt}\right|}^2+\epsilon }$ with its discrete implementation, denoted here as S, as

$$S=\frac{{\stackrel{\sim }{m}}^{t-1}-{\stackrel{\sim }{m}}^t}{\sqrt{{\mid {\stackrel{\sim }{m}}^{t-1}-{\stackrel{\sim }{m}}^t\mid }^2+\epsilon }}+\frac{{\stackrel{\sim }{m}}^{t+1}-{\stackrel{\sim }{m}}^t}{\sqrt{{\mid {\stackrel{\sim }{m}}^{t+1}-{\stackrel{\sim }{m}}^t\mid }^2+\epsilon }}$$

The projection corresponding to the complex temporal TV term can be written as m̃_n+1=m̃_n−α_nS_n, where α_n can be set to a constant step size.

The second form of TV constraint is to use separate real and imaginary temporal TV terms, defined as:

$$\begin{array}{l}\varphi (\stackrel{\sim }{m})={\Vert \frac{dR(\stackrel{\sim }{m})}{dt}\Vert }_1\\ \approx \sqrt{{\left(\frac{dR(\stackrel{\sim }{m})}{dt}\right)}^2+\epsilon }\text{where}R(\stackrel{\sim }{m})\text{is}\text{the}\text{real}\text{part}\text{of}\stackrel{\sim }{m}\end{array}$$ (4)

$$\begin{array}{l}\phi (\stackrel{\sim }{m})={\Vert \frac{dI(\stackrel{\sim }{m})}{dt}\Vert }_1\\ \approx \sqrt{{\left(\frac{dI(\stackrel{\sim }{m})}{dt}\right)}^2+\epsilon }\text{where}I(\stackrel{\sim }{m})\text{is}\text{the}\text{imaginary}\text{part}\text{of}\stackrel{\sim }{m}\end{array}$$ (5)

The gradient descent projection gives ${\stackrel{\sim }{m}}_{n+1}={\stackrel{\sim }{m}}_n-{\alpha }_n^{\prime }{S}_n^{\prime }$ and ${\stackrel{\sim }{m}}_{n+1}={\stackrel{\sim }{m}}_n-i{{\alpha }_n}^{″}{S_n}^{″}$ where $S_n^{\prime }=\frac{d\varphi ({\stackrel{\sim }{m}}_n)}{d{\stackrel{\sim }{m}}_n}{S}_n^{″}=\frac{d\phi ({\stackrel{\sim }{m}}_n)}{d{\stackrel{\sim }{m}}_n}$ and ${\alpha }_n^{\prime }$ and ${\alpha }_n^{″}$ can be Polyak’s step size [19]

$${\alpha }_n^{\prime }=\frac{\varphi ({\stackrel{\sim }{m}}_n)}{{\left|\right|S_n^{\prime }\left|\right|}^2}\text{and}{\alpha }_n^{″}=\frac{\phi ({\stackrel{\sim }{m}}_n)}{{\left|\right|S_n^{″}\left|\right|}^2}$$ (6)

that make it unnecessary to fit the step size or can be useful to provide a reference for step size selection.

The third form of temporal TV constraint is to use separate magnitude and phase terms. It was found that use of temporal magnitude and phase TV terms gave only slightly better reconstructions than temporal magnitude temporal TV alone (see Fig. 3 and the Discussion section), and so a magnitude only method was also evaluated in this work:

$$\mu (\stackrel{\sim }{m})={\Vert \frac{dM(\stackrel{\sim }{m})}{dt}\Vert }_1\approx \sqrt{{\left(\frac{dM(\stackrel{\sim }{m})}{dt}\right)}^2+\epsilon }$$ (7)

where M(m̃) is the magnitude part of m̃.

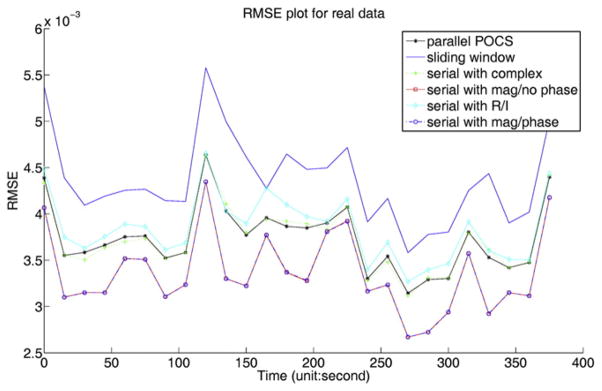
Fig. 3.

RMSE plot for each time frame computed for different methods with one data set of all coils.

The gradient descent projection gives $M({\stackrel{\sim }{m}}_{n+1})=M({\stackrel{\sim }{m}}_n)-{\alpha }_n^{‴}{S}_n^{‴}$ where $S_n^{‴}=\frac{d\mu (\stackrel{\sim }{m}n)}{d{\stackrel{\sim }{m}}_n}$ and ${\alpha }_n^{‴}$ can be Polyak’s step size [19]

$${\alpha }_n^{‴}=\frac{\mu ({\stackrel{\sim }{m}}_n)}{{\left|\right|S_n^{‴}\left|\right|}^2}.$$ (8)

3. Materials and methods

3.1. Data acquisition and simulation

Breast DCE-MRI data were acquired using a 3D spoiled gradient echo pulse sequence with the following imaging parameters: TR=2.35–3.16 ms, TE=0.99–1.24 ms, flip angle=10–15° using a seven-channel dedicated breast coil. Omniscan of dose 0.1 ml/kg was injected at 4 ml/s followed by 20 ml saline flush injected at 2 ml/s. Temporal resolution per frame was 12–15 s with data acquired with 6/8 reduced Fourier space in the phase and slice directions and elliptical acquisition in the kx-ky plane. The acquisition matrix for the breast data varied between 256×(80–104)×80 of 42–60 time frames. The acquisition was bilateral, with the read direction left to right. The fast inverse Fourier transform (IFT) was performed in the read (kx) direction, and the ky-kz datasets were extracted from each slice in the x dimension. Four datasets from three study participants with histopathologically-confirmed breast cancer were obtained under an institutional review board–approved protocol. One subject was imaged on two separate occasions.

Undersampled k-space data were simulated by deleting a portion of the acquired phase encodes in the ky and kz directions. In the outer areas in the ky direction, one in every two points was sampled; while in the kz direction, one in every three points was sampled. An example of the sampling pattern over a series of time frames is shown on Fig. 1A. In the k-space center, a 6×6 window of ky-kz phase encodes were fully sampled for every time frame, as shown in Fig. 1B. The net acceleration was R=6 (17% of the k-space data were used). The elliptical partial Fourier acquisition of the original data further increased the undersampling to an acceleration factor of R=10, though note that the “true” data used to compare with the constrained reconstruction methods had only 6 times as many samples as the undersampled version, so our results are reported as using an acceleration of R=6.

Fig. 1.

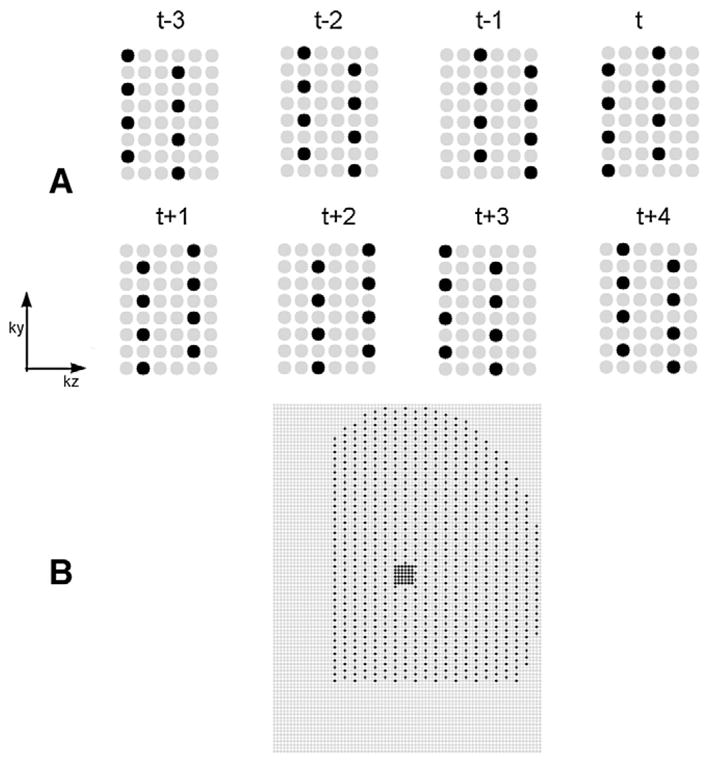
Undersampling pattern for breast DCE data. The gray circles were not sampled, and the black circles were sampled. (A) The outer k-space sampling of eight adjacent time frames. (B) A typical k-space sampling pattern of one time frame.

3.2. Implementations

Four reconstruction methods were implemented: parallel POCS with complex temporal TV term, serial POCS with complex temporal TV term, serial POCS with separate real/imaginary temporal TV term, and serial POCS with magnitude TV alone. These were denoted as parallel +complex, serial+complex, serial+real/imaginary, and serial+magnitude, respectively. Reconstruction using a simple “sliding window” method was presented for comparison and for algorithm initialization. Sliding window was implemented by inverse Fourier transformation of k-space data after filling missing measurements in k-space using the corresponding measurement from the most recent time frame in which it was acquired. This is not technically a “sliding window,” but this method gave better results than interpolating based on all of the data within a window.

Parallel POCS requires weighting factors to be chosen, and serial POCS accomplishes similar weighting by the number of iterations each convex set is performed before going on to the next convex set. For parallel POCS, 150 iterations were used and the fidelity weighting was set to be 1, and temporal TV weighting was set by trying a range of different parameters from 0.01 to 1.2 on the data set of each coil, and the weighting factor of 0.1 was selected based on minimizing the root-mean-squared error (RMSE) in a test dataset. This weighting was then used for all of the coils and all of the datasets. The RMSE value was calculated by square root of the mean square difference between the reconstructed images and the true images that were reconstructed by inverse Fourier transform of the elliptical partial k-space data.

For serial POCS, the weighting of different terms are affected by both the step size of the projection term and the iteration number ratios among different convex set projections. For simplicity, the iteration ratio of 1:1:1 or 1:1 was applied for all serial POCS methods. For the fidelity term, the step size was set to be 1, and could be viewed as replacing the measured k-space data into the corresponding k-space points of the current estimate. For the temporal TV term, Polyak’s step size (Eq. 6) was used for the initial estimation of the constant step size. There were two reasons for not using Polyak’s step size to adapt the step size at each iteration: one was that from our tests, the constant step size converges faster; the other is that computation of Polyak’s step size takes some time during each iteration.

The POCS methods were applied independently to sparse data obtained from each of the seven coils. The reconstructions from each coil were then combined using the square root of the sum of squares.

3.3. Kinetic parameters from breast data

After dynamic images were reconstructed and the baseline pre-contrast signal subtracted, the signal intensity difference curve of every pixel was fitted to the extended Tofts-Kety two-compartment model for tissue contrast agent (CA) concentration:

$$C_t(t)=K^{\mathit{trans}}{C}_p(t)\otimes e^{-k_{ep}t}+v_p{C}_p(t)$$

where K^trans and k_ep are the transfer constant and rate constant respectively, ⊗ is the convolution operator, v_p is the blood plasma volume fraction, and C_p(t) is the concentration of CA in the blood plasma [20]. The linearized regression method described in [21] was used to perform curve fitting, and a population-averaged arterial input function (AIF) was used for C_p(t) [22].

To quantify the linear relationship between the kinetic parameters generated from constrained methods and that generated from the true data, L1 regression, where the sum of absolute difference is minimized, was used. This type of analysis was used due to its robustness to outliers, rather than least square regression that minimizes the sum of squares difference.

4. Results

4.1. Comparison of different methods

The images reconstructed from undersampled data of one subject with two tumors using the undersampling pattern described in Fig. 1 are shown in Fig. 2. Fig. 2A shows a time frame in a typical DCE sequence obtained from full k-space data using IFT. Fig. 2B shows the corresponding time frame reconstructed using IFT on the undersampled data. Figs. 2C–F show the corresponding time frame reconstructed using the parallel+complex, serial+complex, serial+magnitude, and sliding window (SW) method, respectively. The RMSE plots of images reconstructed from this subject with the simulated undersampling using the different POCS methods are shown in Fig. 3. The separate real and imaginary TV does not work as well as complex TV and magnitude TV in terms of RMSE. Fig. 3 shows that for all time frames, serial+complex, parallel+complex, and serial+magnitude constrained reconstructions had reduced RMSE as compared to the SW method. The serial+magnitude method consistently had the lowest RMSE.

Fig. 2.

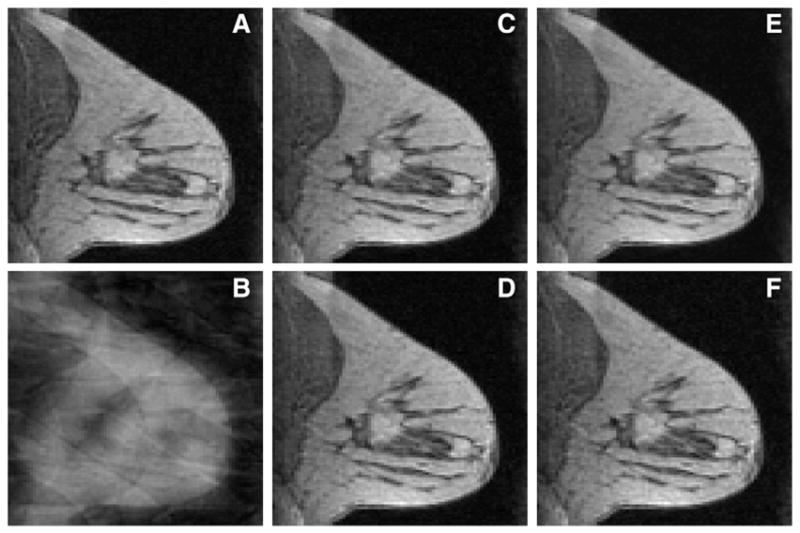
Comparison of reconstructions from full data and R=6 (using pattern shown in Fig. 1) data using different methods with all coils. (A) The 22nd time frame reconstructed from full k-space data using IFT. The corresponding time frame reconstructed from undersampled data using IFT method is shown in panel (B), the parallel+complex in (C), serial+complex in (D), serial+magnitude in (E), and the sliding window method in (F).

POCS methods were applied independently to the sparse R=6 data obtained from each of the seven coils. The reconstructions from each coil were then combined using the square root of the sum of squares and the results are shown in Fig. 4. Fig. 4A shows the images reconstructed from full k-space data using IFT. Figs. 4B–E shows the images reconstructed from parallel+complex, serial+complex, serial+magnitude, SW, respectively. Figs. 4F–I show the difference images with full-sampled image (a) of corresponding time frame. The residual errors of images reconstructed using the complex constraint (Figs. F–G) were smaller than that of the other methods.

Fig. 4.

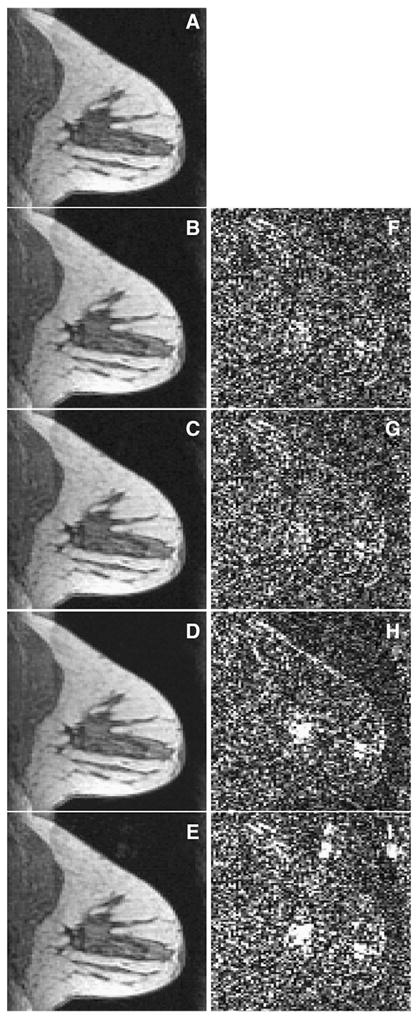
Reconstructions results from all coils. a–e (left column): the 12th time frame of reconstructed images (from top to bottom, the left column is full sampled image, parallel+complex, serial+complex, serial+magnitude, sliding window). f–i (right column): the difference image between the corresponding left image and (A). Larger residual errors of the images reconstructed with the serial+magnitude and SW methods are evident in the bottom two rows of the right column. The left column images are scaled to [0,30]; and the right column images are scaled to [0,2].

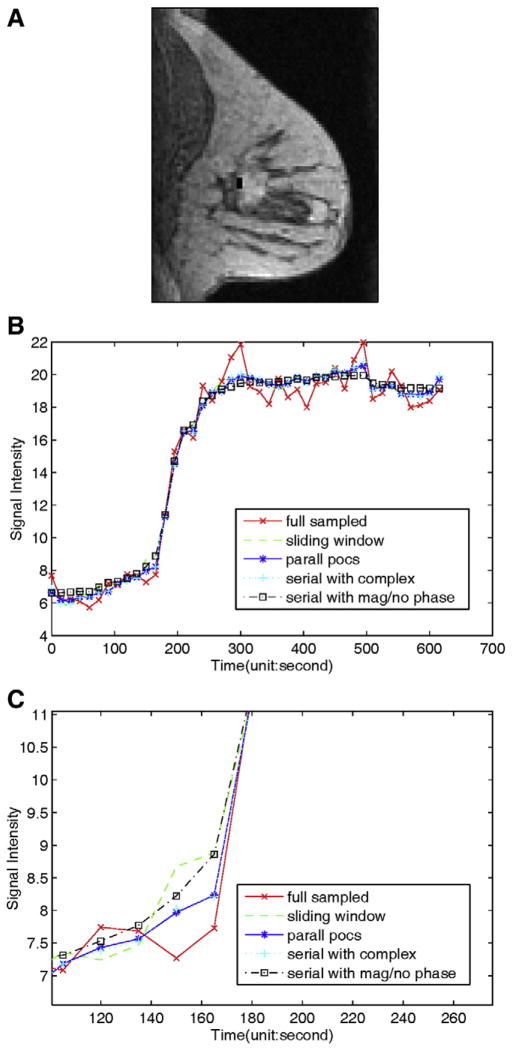
Fig. 5 compares the mean signal intensity time curves from one breast lesion region using different methods. Fig. 5A shows the region of interest (ROI) in the breast. Figs. 5B–C compares the mean signal intensity curves for the region. The time curves obtained from POCS methods matched with the full data reconstructions closely.

Fig. 5.

Comparison of dynamics of reconstructions from undersampled data (R=6) in two different breast lesion regions using different methods. (A) Images showing the one ROI in the breast lesion, indicated by the small black rectangle. (B) Comparison of mean signal intensity time curves for the lesion region shown in (A), and (C) is the magnified images of (B). The magnified image shows the signal intensity curve of SW methods have a larger deviation from that of the true images.

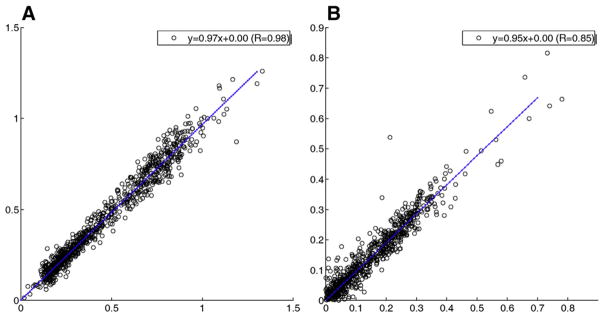
The relationship of kinetic parameters from the reconstruction of the R=6 data and that from full-sampled data are shown in Fig. 6 for parallel POCS with complex temporal TV, the reconstruction method that correlated with full data best in the tumor area. Pharmacokinetic parameters determined from the images reconstructed using this method showed strong linear correlation with those determined from the fully-sampled data. The results are summarized in Table 1, with the exception of v_p. The values of v_p determined from all methods are close to zero (v_p=0.014±0.033 for parallel+complex, v_p=0.027±0.051 for fully sampled data).

Fig. 6.

The correlation plots between kinetic parameters (K^trans, k_ep) generated from images using parallel+complex and that using IFT of full-sampled k-space data, with K^trans plot shown in (A), k_ep plot shown in (B). The kinetic parameters data sets came from all four datasets’ lesion areas.

Table 1.

The linear relationship between pharmacokinetic parameters determined from the images reconstructed using different methods and those determined from the fully sampled data. The data in the bracket are the correlation coefficients

	Ktrans	kep
Parallel+complex	Y=0.97X+0.00 (0.98)	Y=0.95X+0.00 (0.85)
Serial+complex	Y=0.97X+0.00 (0.98)	Y=0.96X+0.00 (0.84)
Serial+magnitude	Y=0.93X+0.00 (0.98)	Y=0.90X+0.00 (0.92)
Sliding window	Y=0.97X+0.00 (0.97)	Y=0.94X+0.00 (0.80)

5. Discussion

Three types of temporal TV terms were used for reconstruction of undersampled breast data. A POCS method with gradient descent method was used for implementation. From difference images (Fig. 4), signal intensity curves (Fig. 5) and kinetic parameters (Fig. 6), it can be seen that parallel+complex, serial+complex, and serial+magnitude are capable of accurately reproducing the measured signal intensity curves and pharmacokinetic parameters.

In Fessler’s work [16], it was demonstrated that the L2 norm of the spatial derivative of separate magnitude and phase performed better than that of the complex form in one set of simulated data. It is known that most MRI data has relatively smooth phase in the spatial dimension, and that the spatial phase L2 is a strong constraint. In the breast DCE MRI data used here, serial+magnitude/phase worked approximately the same as serial+magnitude without the temporal phase TV term. The phase TV term did not help significantly to get better images (see Fig. 3), possibly due to the good initialization of the phase images.

Keyhole techniques have been used for quantitative dynamic contrast-enhanced breast MRI [23], and it was reported that the minimum keyhole size should be restricted by the approximate minimum size of the expected lesions. Parallel imaging and generalized series model have been combined to accelerate dynamic contrast-enhanced breast cancer imaging with an acceleration factor of 3–4 for the 2D case [24]. The techniques used here enabled an acceleration factor of 6 for 3D acquisitions while maintaining good correlation with the kinetic parameters in the tumor.

Polyak’s step size is useful to adjust the step size range, which is necessary for L1 norm minimization. However, it was found that the optimal step size, in terms of efficiently reaching images that gave minimum RMS errors compared to the full data reconstruction, was not close to Polyak’s step size. However, all of the POCS methods performed robustly to perturbations (±0.5α) in the optimal step size of α [9], which implies relatively few trial step sizes are needed to get the optimal step size. As well, the same step size performed well for different data sets, indicating that it is likely not a parameter that needs to be found for each dataset.

The parallel POCS methods used here can also be termed temporally constrained reconstruction (TCR) [9]. TCR was performed by iteratively minimizing a cost function of a data fidelity term and constraint terms. The cost function was defined as

$$C=argmin\{\delta (\stackrel{\sim }{m})+\lambda \psi (\stackrel{\sim }{m})\}$$

The gradient descent method gives

$${\stackrel{\sim }{m}}_{n+1}={\stackrel{\sim }{m}}_n-\tau C^{\prime }({\stackrel{\sim }{m}}_n)={\stackrel{\sim }{m}}_n+\alpha F^T(Wd-WF{\stackrel{\sim }{m}}_n)+\beta S_n$$

Interestingly, this gradient descent implementation of TCR is the same as parallel POCS with complex temporal TV constraints used here. A spatial TV term can also be added to the parallel (or serial) POCS methods [10].

Compared to parallel POCS, serial POCS makes it easier to add other constraints. In [12], several convex sets and associated projection operators pertinent to MRI data reconstruction were defined, such as fixed phase and limited object support. Other types of convex functionals can also be included in the POCS framework, such as a prior image constraint [25].

For the kinetic parameter analysis, the signal intensity curves were not converted to the contrast agent concentration, as is sometimes done [26]. Most of the signal intensity difference curves were expected to remain linear with the contrast agent concentration, and since the truth was computed in the same manner, it was not essential to perform this extra step. The extra step of conversion to concentration would have made the comparison less direct.

The sliding window method also worked reasonably well. This can be explained in part through Fig. 7: although the sliding window method is often biased more than the temporally constrained method when the intensity increases sharply, the fitted line is not so sensitive to this area because of sharp onset of the population AIF. Thus similar kinetic parameters similar to truth can be found even when the curves from the undersampled reconstructions have a slower onset.

Fig. 7.

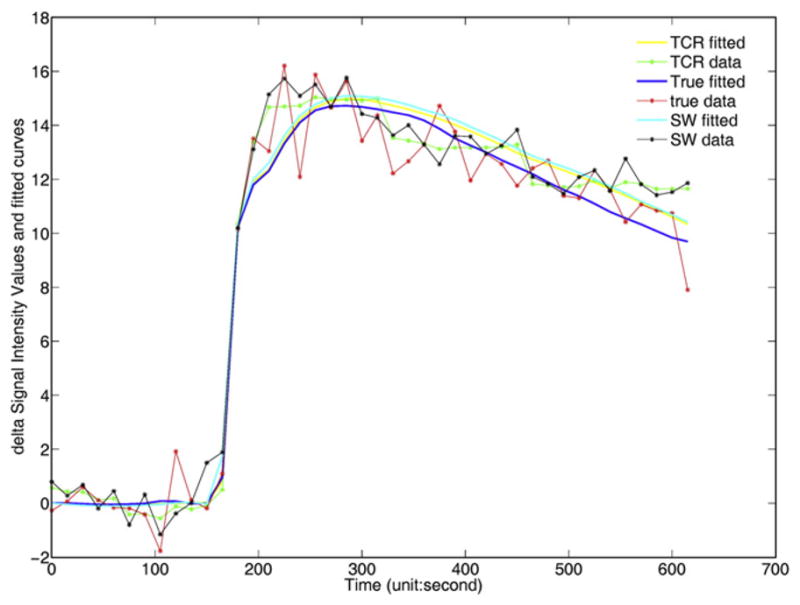
The delta signal intensity values and model fits for images reconstructed from parallel+complex, sliding window and full-sampled data (denoted as “TCR,” “SW,” “True,” respectively). The delta signal intensity value is the intensity value with the mean value of the first ten time frames subtracted off. The plot demonstrates that in particular for the sliding window curve, the fit is much closer to the fully sampled data when the tissue curves increases sharply. This is because the sharp onset of the AIF used does not permit an exact fit to the curve.

Another limitation of this study is that the signal intensity curves of two of the data sets show relatively slow and steady uptake in the lesions, and this is particularly amenable to undersampling. Also, v_p can be difficult to analyze with voxelwise curves in general, and did not correlate well here (r=0.55 for parallel POCS with complex TV).

The results here were based on simulated undersampling, in order to have a measure of truth. The simulated undersampling may not have as high temporal resolution as actual undersampled acquisitions. Actual undersampled data will likely be more robust since temporal and/or spatial resolution can be increased, and the effective rate of change of the contrast will be slower and easier to reconstruct. It is also possible that the current acquisitions were undersampled temporally and that the time curve will vary more rapidly when temporal resolution is improved. In this case, there may be greater differences between the reconstruction methods.

Spatial and temporal resolution are crucial for MRI breast cancer detection and characterization [27]. The proposed method can be used to increase temporal resolution without compromising spatial resolution. High spatial resolution is required for detection of small lesions and for assessment of lesion morphology. Thus, this approach may increase the detectability of small lesions. It is also possible that the high temporal resolution can increase specificity for diagnosing malignancy [28].

The computation time is demanding, especially when the dataset size is large. In a Matlab (The Mathworks, Natick, MA, USA) implementation on a desktop PC, it takes approximately 40 s to reconstruct one slice. Considering that 20–40 slices of 5–12 coils will have to be reconstructed in a clinically-acceptable time span of 30–60 seconds, the computation time will have to be improved by a factor of between 60 and 640. An efficient C++ implementation on a more powerful computer will provide improvement in computation time. Recently published papers have shown that computationally intensive medical imaging tasks can be processed on a graphics processing unit to increase computation speed by a factor of 85–100 [29,30]. Taking advantage of these techniques, clinical implementation would be feasible.

In conclusion, we have demonstrated that temporal TV could be successfully employed for dynamic MRI breast perfusion applications. Complex TV or magnitude TV constraints could be used to give good results at an acceleration factor R of 6, which can translate into improved spatial and temporal resolution for DCE breast scans without a cost to image quality. In the tumor area, the best method, parallel POCS with complex temporal TV, gave kinetic parameter K^trans,R=6=0.97 K^trans,R=1+0.00 with correlation coefficient r=0.98, k_ep,R=6=0.95 k_ep,R=1+0.00 (r=0.85). These promising methods warrant further study to determine how increasing spatial or temporal resolution affects clinical assessment and management of breast cancer and other cancers.