Pixel-based Comparison of Spinal Cord MR Diffusion Anisotropy with Axon Packing Parameters

Abstract

Water diffusion in nerve fibers is strongly influenced by axon architecture. In this study, fractional diffusion anisotropy (FA) and transverse and longitudinal diffusion coefficients (tADC and lADC) were measured in excised human cervical spinal cord with MR line scan diffusion imaging, at 625 μm in-plane resolution and 3 mm slice thickness. A pixel-based comparison of FA, tADC, and lADC data with axon packing parameters derived from corresponding stained histological sections, was performed for four slices. The axon packing parameters, axon density (AD), axon area-fraction (AAF), and average axon size (AAS), for entire specimen cross-sections were calculated by computerized segmentation of optical microscopy data obtained at 0.53 μm resolution. Salient features could be recognized on FA, tADC, AD, AAF, and AAS maps. For white matter regions only, the average correlation coefficients for FA compared to histology-based parameters AD and AAF were 0.37 and 0.21, respectively. For tADC compared to AD and AAF, they were –0.40 and –0.36, and for lADC compared to AD and AAF, –0.14 and –0.30. All average correlation coefficients for AAS were low. Correlation coefficients for collectively analyzed white and gray matter regions, were significantly higher than correlation coefficients derived from analysis of white matter regions only.

Introduction

Diffusion-weighted magnetic resonance imaging has been widely used to probe the diffusion of water molecules in biological tissues. In nerve fibers, water diffusion is strongly influenced by the presence of axonal membranes and myelin sheaths [1–3]. It is believed that the observed diffusion anisotropy is primarily the result of directionally dependent diffusion restrictions exerted by the huge number of densely packed axonal membranes, whereas the contribution of myelin sheaths to the observed diffusion anisotropy is thought to be minor [4, 5]. Although diffusion anisotropy has been demonstrated at the resolution level of individual axons [1], the quantitative connection between anisotropy observed with MRI and axon caliber, axon density, and myelination, has not been well established. A more quantitative understanding would be immensely helpful in the interpretation of subtle changes in diffusion anisotropy that occur in the white matter tracts of patients with certain diseases [6,7]. The current study was designed to develop computerized methodology to compare fiber architecture and diffusion measures on a pixel-by-pixel basis across an entire tissue sample.

Despite the fact that MR diffusion imaging can probe structures at the micrometer level, the parameters measured represent averages over the macroscopic scales of image voxels with volumes on the order of several cubic millimeters. In order to achieve any meaningful understanding of the measured diffusion anisotropy, correlation between fiber architecture and diffusion anisotropy should be studied in nerve fiber tissues where the fiber orientation is largely uniform. There are several areas in the brain that fulfill this condition.

The spinal cord is another nerve fiber structure that is sufficiently large, and where the majority of fibers are uniformly oriented. In the current study, diffusion-weighted image data of entire cross-sections of a human cervical spinal cord specimen was used, along with subsequently obtained axon histology. Comparisons were then made between fractional anisotropy (FA) [8], as well as transverse and longitudinal apparent diffusion coefficients (tADC and lADC), measured in axial sections of the spinal cord, and the following axon packing parameters at corresponding locations in the histological sections: axon density, axon area-fraction, and average axon size. All axon measures were derived through automatic pixel-by-pixel segmentation of the histological image data. For this purpose, image processing tools were developed to automatically segment axons in high-resolution histology data and to register the findings at a much lower resolution in the MR image space.

In an earlier report by Schwartz et al. [9], diffusion parameters measured at high field strength in rat spinal cord, were compared with axon morphometry derived from histology images. Although this comparison was only performed for selected regions of interest (ROIs), the authors concluded that the diffusion measured transverse to the dominant fiber direction correlates negatively with axon density. Similarly, Mottershead et al. [3] compared axon density in selected ROIs in the spinal cord of multiple sclerosis patients with diffusion and other MR parameters. In the current study, the goal was to make similar comparisons, but employing both the FA index, as well as the tADC and lADC indices used in the previous studies, and, instead of only using manually-selected ROIs, carry out the comparisons on entire images of whole spinal cord cross sections, on a pixel-by-pixel basis. We note that this is a rather difficult task because there is a significant difference between the feasible resolution for MR imaging and the required resolution for histological imaging, in turn implying a large data volume, which requires a significant level of automation. Since the tissue sample size is relatively large compared to the histological resolution, it is difficult to achieve consistent focusing and illumination across the entire image. This inconsistency in turn causes difficulties for image processing algorithms. At the same time those algorithms need to recognize features that are relatively small, i.e., on the order of a few histology image pixels. Moreover, from the diffusion imaging point of view the sample is relatively small, exacerbating the effect of any registration inconsistencies along the tissue borders as well as partial volume effects. Thus, the goal here is to establish feasibility of conducting such a study on a pixel basis, to illustrate that indeed reasonable comparison results can be obtained, and to point the way towards future work along this path.

Materials and Methods

A human cervical specimen was excised at the C1-C2 level of a female 34 year old deceased patient with no known spinal cord abnormality. Specimen MR scans were performed within 24 h after death. The study was conducted within the guidelines of the institutional internal review board (IRB). Other aspects of this human spinal cord data have been reported in an earlier article [10].

Magnetic Resonance Imaging

Diffusion tensor scans were performed with line scan diffusion imaging (LSDI) [11] on a 1.5 Tesla, whole-body LX Horizon Echospeed MR system (General Electric Medical Systems, Milwaukee, WI) with 40 mT/m magnetic field gradients. A standard 3-inch surface receiver coil was employed for optimal SNR. The imaging protocol included T₁-weighted spin echo localizing scans and axial LSDI tensor scans with the following parameters: TE, 76 ms; TR between column excitations, 111 ms; TR, 2442 ms; FOV, 80×40 mm; scan matrix size, 128×64 (frequency × column); in-plane resolution, 625×625 μm; slice thickness, 3.0 mm with 0.5 mm gap; receiver bandwidth, ±3.91 kHz; magnitude signal averages, 16; diffusion encoding times Δ and δ, 37 ms and 26 ms; b-factors, 5 and 2000 s/mm²; scan time, 16 minutes per slice. A total of four sections were scanned. The specimen was suspended in physiological saline solution at approximately 22 Celsius. Since diffusion in the post-mortem tissue sample at this temperature was much lower than under normal vital conditions, a very high b-factor of 2000 s/mm² was used. Diffusion weighting was applied along six non-collinear and non-coplanar directions. For more accurate image registration, fast spin echo (FSE) T₂-weighted images (TR 5000 ms, TE 105 ms) with the same slice geometry, but two-fold in-plane spatial resolution, were acquired concurrently. Effects of Rician noise on magnitude signal averaging and associated errors in the FA estimation were also considered [12]. Correction was deemed unnecessary because the SNR in the unaveraged diffusion-weighted images was already quite high, i.e., varying from 8:1 to 20:1, depending on fiber and diffusion encoding directions.

Histology Image Acquisition

Shortly after the MR scan, the specimen was fixed in formaldehyde. Four axial histology sections at locations corresponding to the imaging planes of the MRI experiment, were obtained. For microscopic visualization of individual axons, the specimen sections were stained according to Bielschowsky's method of silver impregnation. Between 160 and 188 slightly overlapping digital microscopy images at 0.53 μm resolution were acquired per section. For imaging details refer to [10]. For each section, images were then combined into a mosaic slice by registering each image to its neighbors using a phase correlation technique with sub-pixel resolution [13, 14]. A slight lens-related distortion was evident and resulted in a negligible mismatch in some overlapping areas. An example of a complete histology cross-section assembled from overlapping subimages is shown in Fig. 1.

1.

Composite histology image of Slice 1 from assembly of overlapping sub-images. The central, butterfly shaped and more brown-colored area, shows the gray matter. The peripheral, surrounding area, shows the white matter. The blockiness in the image are visual artifacts due to differences in illumination across the cross section, as explained in the text.

Image Registration

The diffusion-weighted MR images suffered from minor spatial deformations due to eddy-currents, which appear as mismatches among the six diffusion-weighted images. Moreover, specimen fixation resulted in shrinkage and non-uniform warping of the histology data. To enable the desired comparisons, both types of data had to be registered into a common space. For this purpose, the FSE T₂-weighted image was selected as the reference, as it was assumed to suffer the least from distortion. First, for each section, histology images and all images obtained with LSDI were registered to the corresponding FSE T₂-weighted image. Then, diffusion tensor components and FA maps were computed. For all registrations, the outer boundary of the visualized specimen was manually drawn as a polygonal outline in each image and the corresponding set of vertices was used as the landmark feature. Polygonal outlines of the distorted image data were then registered to the polygonal outlines of the reference image data via a global affine transformation allowing translation, scaling, rotation, and shear. In a first step, the outlines underwent an optimal whitening transformation [15], so that they shared the same first and second order moments. In a second step, the registration was optimized further by minimizing the Hausdorff distance between the polygon vertices point sets, defined as the maximum Euclidean distance between one set of points and the nearest points in another set [16]. Finally, after co-registering all image data, the histology was divided into regions corresponding to FA image pixels for further image processing analysis.

Computerized Identification of Axons

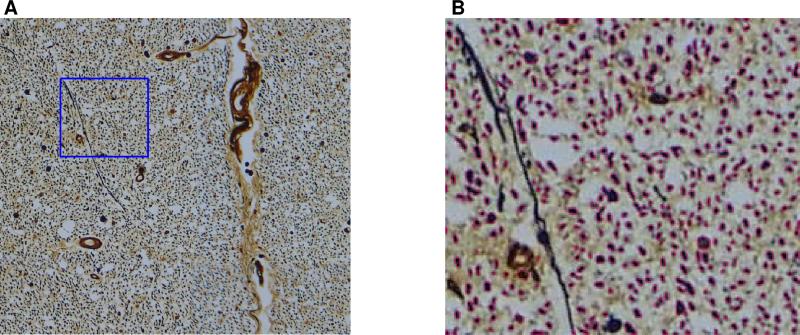
Through-plane axon identification was performed automatically using a pipeline assembled from standard image processing techniques in the MATLAB (Mathworks, Natick, MA) Image Processing Toolbox. With Bielschowsky's silver stain process, through-plane axons appear as dark roundish objects. Since the myelin is dissolved, the axons are typically surrounded by a bright halo (see Fig. 2A). The segmentation algorithm located through-plane axons by identifying instances of dark roundish objects in the image, with appropriate constraints on shape and intensity. The basic processing steps for each region of the histology image corresponding to one FA image pixel are summarized below:

1. Images were converted from 24 bit color scale to 8 bit gray scale to reduce sensitivity to the type of stain used and the wide color spectrum of individual components in the histology images.

2. To enhance the contrast between axons and background, a morphological top hat filter [17], was applied. The filter disk radius was 5.3 μm, i.e., ten times the size of a histology image pixel and much larger than the radius of the largest through-plane axons.

3. A binary map, separating axon areas from the other tissue components, was generated by thresholding the filtered image using a local threshold selected by Otsu's method [18] for each one-fourth of an MR pixel.

4. The combination of filtering and thresholding resulted in some candidate axons being merged. Boundaries separating merged axons were detected by watershed segmentation of the filtered images [19]. Only those watershed boundaries were retained, which divided candidate axons identified by the thresholding into two or more candidate axons.

5. After normalizing image intensity over each one-fourth of an MR pixel, candidate axons where a) the average axon intensity exceeded 70% of the overall intensity, or b) the minimum intensity found within an axon exceeded 50% of the overall intensity, were excluded.

6. Finally, shape-based filtering was used to exclude candidate axons with the following criteria: a) area less than 0.56 μm² or greater than 16.8 μm², b) length of the major axis of an enclosing ellipse greater than 9 μm, c) ratio of the major axis to minor axis of the ellipse greater than 5, d) perimeter greater than 17 μm, and e) ratio of their perimeter to radius greater than 9.

2.

(A) A white matter histology region, corresponding to an area of 625 × 625 μm², i.e., the area of one MR pixel. With Bielschowsky's silver stain, through-plane axons appear as dark round objects, surrounded by a bright halo of dissolved myelin. (B) Automatically identified axons within the blue outlined region shown in (A) are marked by pink boundaries.

The parameter values in the last two steps were chosen heuristically based on physical resolution and darkness of histological components in the histology data images. Fig. 2B shows an example of automatically segmented axons in a white matter region. The axon count derived from the automatic segmentation process was compared to manual axon counting, in small selected white and gray matter regions. The manual axon counting was done by experts to verify the performance of the algorithm, utilizing an interactive graphical user interface written in MATLAB. An axon was considered selected by both human expert and computer algorithm, if the human-expert-determined axon position (a single pixel), resided within an axon boundary identified by the algorithm. Further to that, a similar comparison was performed in the posterior funiculus area (a 0.88 mm² region) in Slices 1 and 2, and in the anterior funiculus area (an aggregate area of 0.10 mm²) in Slices 1 and 4 (see Fig. 3). In this comparison, the manual axon counting was done by one expert only, since it was done over much larger regions.

3.

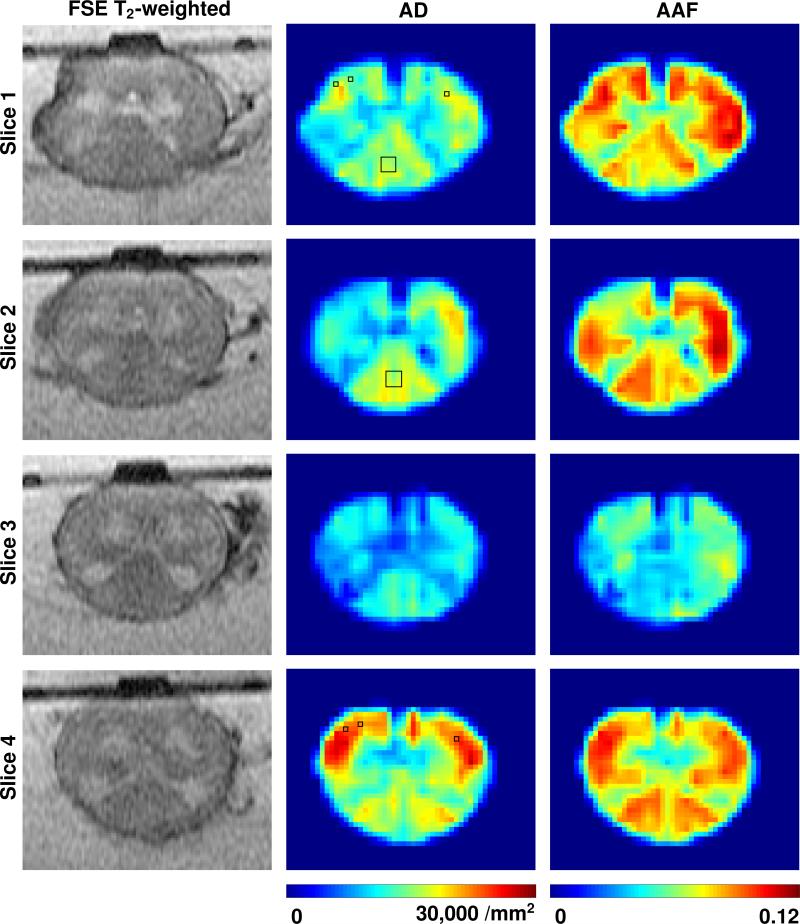
Fast spin echo (FSE) T₂-weighted images (105 ms TE), axon density (AD), and axon area-fraction (AAF) maps for four slices of the spinal cord specimen. Bottom of images corresponds to dorsal. Posterior funiculus regions selected in Slices 1 and 2 and anterior funiculus regions selected in Slices 1 and 4, for comparison with manual axon count, are indicated with rectangles on the AD maps. AD and AAF maps are interpolated for better visualization and scaled to have equal intensity range as identified by the color bar at the bottom of each column of maps.

After the automated axon segmentation, the number of axons, N, and the axon size, a_i, of each axon was determined within all areas corresponding to the individual pixels of the MR image. For each MR image pixel of size s², the following values were then computed: a) the axon density (AD) (N/s²), i.e., the number of axons per square millimeter, b) the axon area-fraction (AAF) (${\sum }_{i=1}^N{a}_i∕s^2$), i.e., the area-fraction occupied by all identified axons, and c) the average axon size (AAS) (${\sum }_{i=1}^N{a}_i∕N$). These parameters evidently obey the relationship AD=AAF/AAS. In a subsequent statistical analysis, the Pearson correlation coefficient between the FA, tADC, and lADC values, and each of the three histology-based computed values was calculated for each slice.

MR pixels without axons in the histology were automatically excluded. Pixels with partial volume effect, i.e., pixels occupied by both saline solution and specimen, were also automatically removed. The selection of such pixels was based on thresholding the tADC and lADC values of MR pixels located on and next to the co-registered histology boundary. The thresholds were derived from the overall histogram distribution of tADC and lADC values. Since the difference between diffusion coefficients in the specimen and water is very large, the partial volume effect of border pixels is much greater in the tADC and lADC maps than in the FA maps, which represent normalized anisotropy measures. Two pixels close to the tissue border were excluded, since the corresponding histology area contained little tissue due to mis-registration. Pixels with high artifactual FA values located along the fissure were excluded. Moreover, in one slice only, four pixels with very high FA values in the lateral funiculus were excluded. In another slice, one pixel, located in an area with a microtome cut imperfection, was also excluded. It should be emphasized that the selection of these pixels was based on MR diffusion values and histology information, rather than outlier rejection in the correlation analysis. The total number of MR pixels analyzed, ranged between 170 and 194, and the percentage of pixels excluded, ranged between 3% and 7%. For further comparison, image pixels were divided into white and gray matter pixels by using manually delineated boundaries of the dorsal and ventral horns. Correlation analysis was then repeated for white and gray matter regions separately. Statistical test of significance was performed for the correlation coefficients using the MATLAB Statistical Toolbox.

Results

The results of the comparison between the manual axon count of two experts and computerized axon segmentation, for both white and gray matter regions, are summarized in Table 1a. The findings of the comparison between computerized and manual axon count, performed by one expert in the posterior and the anterior funiculus regions of different sections, are shown in Table 1b. The total computer-based axon count for Slices 1, 2, 3, and 4 were 1,096,308, 967,973, 718,981, and 1,338,072, respectively.

Table 1.

(a) Results from computerized axon identification (Algorithm) vs. manual axon identification (Human Expert 1 and 2) in white and gray matter regions, and (b) comparison between computerized axon identification (Algorithm) vs. manual axon identification (Human Expert 1) in regions of the posterior funiculus in Slices 1 and 2, and the anterior funiculus in Slices 1 and 4. The locations of the regions on the axon density maps are shown in Fig. 3.

(a) Axon Identification: Algorithm vs. Two Human Experts for One Slice
	Axon Count
	Algorithm	Human Expert 1	Human Expert 2
	Total	Total (% thereof selected by algorithm)
White Matter (0.215 mm2 aggregate area)
Slice 2	3739	3470 (91%)	3503 (95%)
Gray Matter (0.215 mm2 aggregate area)
Slice 2	1662	464 (84%)	515 (86%)

(b) Axon Identification: Algorithm vs. one Human Expert for Multiple Slices
	Axon Count
	Algorithm	Human Expert 1	-
	Total	Total (% thereof selected by algorithm)
Posterior Funiculus (0.88 mm2)
Slice 1	13,909	13,801 (84%)	-
Slice 2	14,191	13,416 (93%)	-
Anterior Funiculus (0.10 mm2 aggregate area)
Slice 1	1,811	1,514 (78%)	-
Slice 4	2,610	2,466 (81%)	-

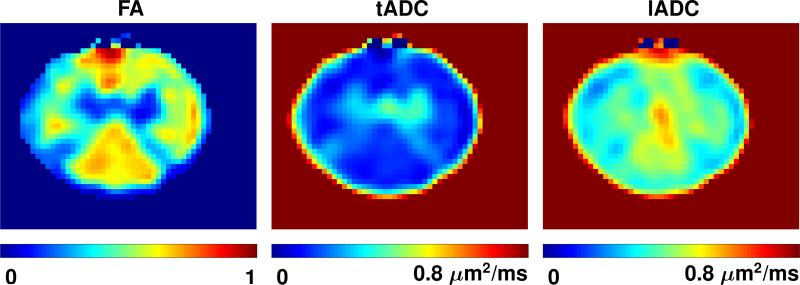
White and gray matter, as well as individual fascicles within the white matter, can be discerned on the FA maps. The same structures have similar appearances on the computed AD and AAF maps. The complete set of FSE T₂-weighted images and maps of AD and AAF parameters are shown in Fig. 3. Maps of FA, tADC and lADC parameters for Slice 2 are shown in Fig. 4.

4.

Computed fractional anisotropy (FA), transverse and longitudinal apparent diffusion coefficient (tADC and lADC) maps for Slice 2 of the spinal cord specimen. Bottom of images corresponds to dorsal. Maps are interpolated for better visualization and scaled to have equal intensity range as identified by the color bar at the bottom of each map. The diffusion coefficients in the tADC and lADC maps have been clipped at 0.8 μm²/ms for better visual contrast.

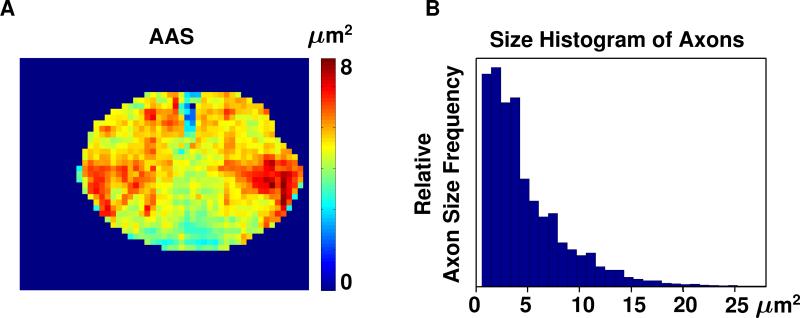
Maps showing the AAS were also constructed, but exhibited less obvious correlation with the diffusion parameter maps. An example of such a map is shown in Fig. 5, together with the histogram of the distribution of axon sizes over an entire histology section.

5.

(A) Average axon size (AAS) map of Slice 1 of the spinal cord specimen and (B) histogram of axon sizes for the same slice.

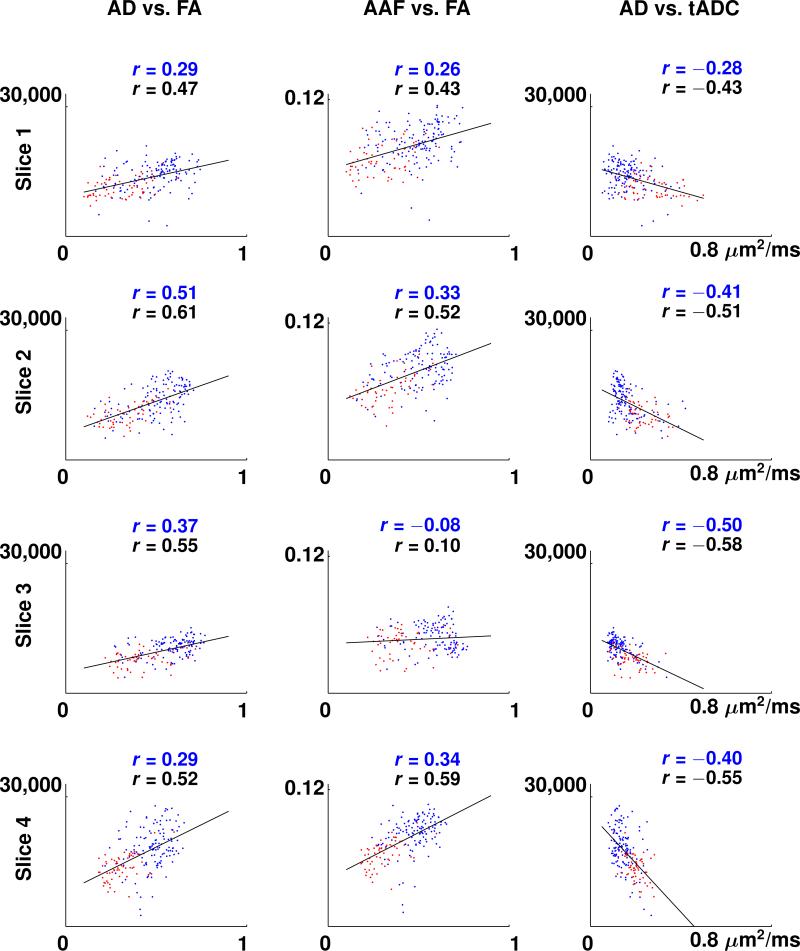
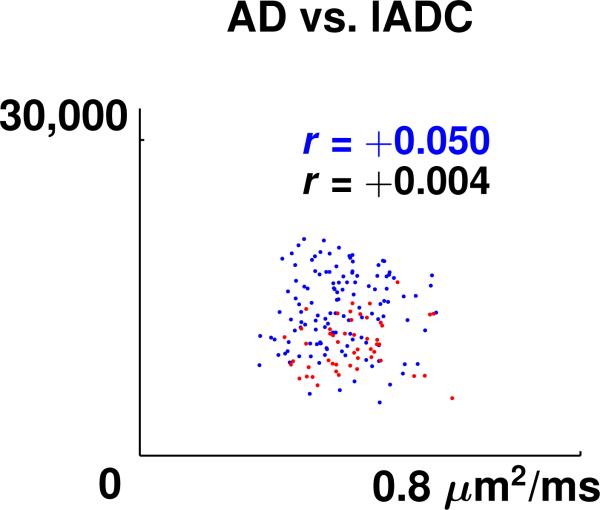
Scatter plots showing the linear correlation between AD and FA data, AAF and FA data, and AD and tADC data, for all four slices, are presented in Fig. 6. The scatter plots for AAF vs. tADC looked similar and therefore are not shown. For all the scatter plots shown in Fig. 6, except AAF vs. FA of slice 3, the p-value for the null hypothesis of no correlation is less than 0.004, which suggests that the correlation of these measures is highly significant. A non-linear relationship between MR diffusion values and axon packing parameters was contemplated. The various model fits tested, however, reduced the sum of residuals by only up to 4 %. For lADC data, which exhibited low correlation with all axon packing parameters, only one representative scatter plot (AD vs. lADC of Slice 2) is displayed in Fig. 7. Pearson's correlation coefficients between the axon packing parameters AD and AAF and the MR diffusion parameters FA, tADC, and lADC, for white matter regions only, in each of the four slices, are presented in Table 2. Pearson's correlation coefficients for the white and gray matter regions combined are shown in Table 3. The average value of the Pearson correlation coefficients between AAS and FA, AAS and tADC, and AAS and lADC, for white matter regions only, are –0.28, 0.14, and –0.15. The respective values for white and gray matter regions combined are –0.28, 0.16, and –0.14. In all scatter plots, blue colored dots represent white matter pixels and red colored dots refer to gray matter pixels. Maps of the residuals, i.e., the errors between AD and AAF measurements and the predicted AD and AAF values on the regression line, did not present any agreement with any anatomical features of the spinal cord tissue.

6.

Scatter plots of axon density (AD) vs. fractional anisotropy (FA), axon area-fraction (AAF) vs. FA, and AD vs. transverse apparent diffusion coefficient (tADC) for the four slices of the spinal cord specimen. Solid lines show linear regression lines for collectively analyzed white and gray matter regions. The separation of gray matter pixels (red dots) and white matter pixels (blue dots) was achieved by manual segmentation. Pearson correlation coefficients in each plot are denoted by r. A blue r refers to the correlation coefficient of white matter only and a black r refers to the correlation coefficient of the combined white and gray matter regions.

7.

Scatter plot of axon density (AD) vs. longitudinal apparent diffusion coefficient (lADC) for the Slice 2 of the spinal cord specimen. The separation of gray matter pixels (red dots) and white matter pixels (blue dots) was achieved by manual segmentation. Pearson correlation coefficient in the plot is denoted by r. A blue r refers to the correlation coefficient of white matter only and a black r refers to the correlation coefficient of the combined white and gray matter regions.

Table 2.

Pearson correlation coefficients (r), between axon density (AD) and fractional anisotropy (FA), axon area-fraction (AAF) and FA, AD and transverse apparent diffusion coefficient (tADC), AAF and tADC, AD and longitudinal apparent diffusion coefficient (lADC), and AAF and lADC for the white matter region only. The last two rows show the average value and the standard deviation (Std Dev) of this data over all four slices.

Correlation Coefficients for Axon Packing vs. Diffusion Measurements for White Matter Only
	AD vs. FA	AAF vs. FA	AD vs. tADC	AAF vs. tADC	AD vs. lADC	AAF vs. lADC
	r	r	r	r	r	r
Slice 1	0.29	0.26	–0.28	–0.41	–0.07	–0.34
Slice 2	0.51	0.33	–0.41	–0.39	0.05	–0.14
Slice 3	0.37	–0.08	–0.50	–0.16	–0.23	–0.33
Slice 4	0.29	0.34	–0.40	–0.49	–0.30	–0.38
Average	0.37	0.21	–0.40	–0.36	–0.14	–0.30
Std Dev	0.11	0.20	0.09	0.14	0.16	0.11

Table 3.

Pearson correlation coefficients (r), between axon density (AD) and fractional anisotropy (FA), axon area-fraction (AAF) and FA, AD and transverse apparent diffusion coefficient (tADC), AAF and tADC, AD and longitudinal apparent diffusion coefficient (lADC), and AAF and lADC for the combined white and gray matter regions. The last two rows show the average value and the standard deviation (Std Dev) of this data over all four slices.

Correlation Coefficients for Axon Packing vs. Diffusion Measurements for White and Gray Matter
	AD vs. FA	AAF vs. FA	AD vs. tADC	AAF vs. tADC	AD vs. lADC	AAF vs. lADC
	r	r	r	r	r	r
Slice 1	0.47	0.43	–0.43	–0.50	–0.14	–0.34
Slice 2	0.61	0.52	–0.51	–0.54	0.004	–0.17
Slice 3	0.55	0.10	–0.58	–0.25	–0.19	–0.30
Slice 4	0.52	0.59	–0.55	–0.63	–0.23	–0.28
Average	0.54	0.41	–0.52	–0.48	–0.14	–0.27
Std Dev	0.06	0.22	0.07	0.17	0.10	0.07

Discussion

In summary, results show that there is high positive linear correlation between the FA values and two of the three axon packing parameters studied, i.e., AD and AAF. For tADC correlation with these axon packing parameters is negative linear and for lADC values, there is almost no correlation. One concern is the integrity of the sample before it underwent fixation. Microscopy analysis of the present sample did not reveal any obvious tissue damage. For rodent brain tissue it has been shown by D'Arceuil and Crespigny [20] that the elapsed time between death and tissue fixation correlates with increasing tissue decomposition and changes of the tissue diffusion properties. In particular they found that the absolute values of all three diffusion eigenvalues in gray and white matter decreased during brain decomposition. Gray matter eigenvalues E1, E2 and E3 all showed a comparable decline over time. Whereas, the white matter E1 showed a much greater decline than white matter E2 and E3 (or gray matter E1, E2, E3). Although, according the results of this rodent study, changes are relatively small in the first 24 hours after death, the more rapid decline of longitudinal diffusion E1 or lADC may have contributed to the low correlation of axon packing parameters with lADC. Indeed, in the current study, lADC in white matter was similar or slightly lower than the lADC of gray matter, whereas LSDI measurements performed in the spinal cord of normal subjects [10] revealed white matter lADC values that were higher than gray matter lADC values.

Schwartz et al. [9] compared the directional (transverse and parallel) apparent diffusion coefficient (ADC) values acquired with diffusion-weighted imaging with the morphometry of axons in histology images of rat spinal cord in selected ROIs. The authors concluded that the directional ADC values correlated with axon density and may reflect distinct histological parameters such as extra-cellular space and axon spacing. Mottershead et al. [3] performed post-mortem diffusion imaging studies of the spinal cord of multiple sclerosis patients. They, also compared axon density with MR parameters in selected ROIs and also concluded that axon density strongly correlates with diffusion anisotropy. The current work complements both previous reports, since diffusion anisotropy, as measured by FA, as well as tADC and lADC, were compared with three axon packing parameters. However, a major improvement in this work is the pixel-wise comparison of the entire spinal cord slices, which is distinct from a limited comparison of selected ROIs. It is reasonable to hypothesize that the correlation explored here might be valid for other white matter structures in the brain. However, this would need to be verified, since different white matter structures exhibit different axon sizes and degrees of myelination.

In all four sections, the dorsal running posterior funiculus with epicritic and proprioceptive sensation fibers was clearly visible as a posterior triangular-shaped high amplitude area in corresponding locations on the FA, AD, and AAF maps. The only exception, was the AAF map in Slice 3, which unlike the other slices, did not show high AAF values in the posterior funiculus region. This appeared to be the result of axon segmentation errors due to poor histology image quality. The lateral and anterior funiculus with sensory and motor nerves also exhibited high values on all of these maps. In contrast, the gray matter regions were consistently characterized by low values.

On the AAS maps, the dorsal running funiculus exhibited the lowest values, i.e., the smallest axons, whereas the gray matter showed higher values, i.e., larger axons. In general, however, a consistent correlation of AAS with FA, tADC, lADC, AD, or AAF, was not observed. This was not only evident from the uniformly lower correlation coefficients, but also from the fact that different areas with high FA, AD, and AAF did not exhibit consistently high or low AAS values. For example, the lateral and anterior funiculus presented the largest axons, whereas axons in the dorsal running funiculus were uniformly small. From the relationship AD=AAF/AAS and the observation that AD and AAF correlate similarly well with FA, it can also be concluded that the correlation between AAS and FA must be inferior. Assaf et al. [21], who used advanced analysis of highly diffusion-weighted data to estimate average axon size, also found the largest axon diameters in the lateral and anterior funiculus. The analysis of Assaf et al. was performed in porcine sciatic and optic nerves and a porcine spinal cord specimen. Acquisition on a high field system with very high diffusion weighting and over a long scan time, permitted the separation of the non-monoexponential diffusion signal decay [22] into a fast and a slow diffusion component. Examination of the diffusion encoding time dependence of each diffusion component revealed solely for the slow diffusion component a clear correlation with average axon size. While a relatively high diffusion weighting of 2000 s/mm² was employed for the current study, it is still within a range, where the fast diffusion component dominates the signal. Moreover, the lack of measurements at multiple b-factors definitely precludes a multi-component analysis. Another fundamental difference is that the inferior gradient performance of the clinical systems used for the current study does not permit any meaningful variation of the diffusion encoding time. Thus, the absence of a strong correlation with axon size for current diffusion data, which is considered to mainly represent the fast diffusion component, is in full agreement with the findings of the study by Assaf et al. In the study by Assaf et al., histological comparison was performed with electron microscopy. Electron microscopy permitted very accurate determination of the size of individual axons, but was limited to selected regions of interest. For the current study, light microscopy yielded less accurate axon dimension values, however, for virtually each axon of the spinal cord specimen. Despite the clear resolution limitations of light microscopy, axon size values presented in Fig. 5 seem to largely agree with the measurements reported by Assaf et al.

A right-left asymmetry, which was most obvious on FA, AD, and AAF maps (see Figs. 3 and 4), can most likely be attributed to the segmented nature of the spinal cord and a slight oblique placement of the histology and/or MR image sections.

The correlations presented in Table 3 are for the aggregate area of white and gray matter. In the scatter plots of Figs. 6 and 7, the contribution by white and gray matter values can be appreciated from the different colors used to plot individual data points. The fact that spinal cord gray matter, unlike cortical gray matter, not predominantly consists of neurons and neuropil, but also contains a large number of long axons that form part of many functional connections within the spinal cord, supports the approach of analyzing the aggregate area. The strong presence of axons is also reflected in the relative high FA value of spinal cord gray matter in comparison to the low FA of cortical gray matter [23].

The correlation statistics for separately analyzed white and gray matter regions were much lower. Probably the most important reason for this decrease was that in this approach the range of the data over which the comparison was performed was greatly reduced, and therefore the average relative variation of the data from the regression line was much higher compared to the average overall variation. A second reason was that a small mismatch in the registration had a larger effect on the overall results, because the number of data points being correlated was significantly lower. A third reason was that the criterion used to label MR pixels as white and gray matter pixels, was based on using manually delineated boundaries around the gray matter dorsal and ventral horn areas of the histology, after the histology images were registered into the FSE T₂-weighted images. Therefore, this labeling may not be completely accurate, because the registration of histology images into FSE T₂-weighted images was performed using a global transformation and did not take into account the internal features of the histology, such as the dorsal and ventral horns. Selection of smaller regions, which are entirely within white or gray matter would improve the objectivity of the tissue selection, but at the same time reduce the data range and number of data points further, thus most likely diminishing correlation.

There were several other factors that contributed to errors of systematic and random nature, as described in detail in the following sections.

Histology Image Quality

In all histology sections, there were some minor local discontinuities due to the presence of fasciae, particularly close to the edge of the specimen, the posterior median septum, and vessels, as well as imperfections of the microtome cut. Moreover, uniformity of illumination and sharpness of the histology image data was not equal for all sections. The best illumination and sharpness was achieved for Slice 2, which also demonstrated the overall best correlation. In contrast, inferior focusing and uneven illumination in Slice 3 produced inferior segmentation results and the overall worst correlation. For each region corresponding to individual MR pixels, image statistics such as first and second order moments, percentages of cumulative density function, and Otsu's gray level threshold, as well as the histogram distribution of image intensities were evaluated for image quality analysis. From this analysis, it was concluded that the intensity normalization resulted in the best image quality.

Axon Segmentation Errors

In white matter regions, the results obtained from computerized axon segmentation and counting were in good agreement with the results from manual axon counting performed by experts (Table 1). Collateral axons, which run approximately orthogonal to the cranio-caudal axons [10], were present in both white and gray matter regions of our samples. The segmentation process described in the Methods section, readily excluded such axons. In gray matter regions, while most of the axons selected by the two experts were also selected by the algorithm, there were a large number of additional axons found by the algorithm. Indeed, in gray matter regions it was evidently more difficult to distinguish true through-plane axons from main branches of dendrites, and even from cell bodies and nuclei. This difficulty could presumably be avoided by using different stains and/or higher resolution for the histology scan. It can be expected that cell bodies, nuclei, dendrite main branches, and even the neuropil, exert considerable diffusion restriction. However, due to the largely randomized arrangement of these structures, these diffusion restrictions do not increase diffusion anisotropy. In the comparison between the segmentation algorithm and the human experts (Table 1a), even with a large number of potentially false gray matter axons found by the computer algorithm, the axon count per unit area, i.e., the AD, is still much lower in gray matter than in white matter. This is also evident in the AD maps of Fig. 3. The differences in total axon count among different slices deserves attention. These differences can also be appreciated on the AD maps, particularly in the anterior funiculus. A manual axon count was performed for larger regions (indicated by rectangles in Fig. 3) in the posterior and anterior funiculus to study a potential error of the automated axon count. Both computer and human expert determined higher regional axon counts in Slice 4 than in Slice 1 (see Table 1b). This is consistent with the higher full-slice axon counts in Slice 4, compared to Slice 1, as reported in the Results section. In contrast, Slices 1 and 2 show similar computerized and manual axon count in the posterior funiculus region, as well as similar total axon counts across the entire slice.

Romero et al. [24], identified through-plane axons automatically in microscopic images by detecting the myelin around the nerve fibers. Schwartz et al. [9] and Mottershead et al. [3], as well as Romero et al. [24] all relied on the myelin as the key feature in the histology for their automatic axon identification algorithm. In the present study, the histology images required a different segmentation approach, because the staining process dissolved the myelin. Therefore, axons were segmented in the images directly, regardless of the presence of myelin.

MR Image Quality

The FA measurements reflect the diffusion anisotropy across 3 mm of the specimen, whereas the histology sections, which are about 3 μm thick, represent only a minute fraction of the MR slice thickness. Therefore, due to the clustered neuron architecture in the spinal cord, axon packing parameters could be different if analyzed across the entire MR slice section. With MR imaging, the Sinc-shaped point spread function also needs to be considered. In contrast, the value of the automated histology axon count is the result of uniform weighting within the area determined by the MR pixel geometry and without contributions from outside the pixel of interest.

Errors of the Registration Algorithm

The registration algorithm utilized here only relied on matching the specimen outer boundaries, using a global affine transformation. This registration resulted in reasonably good matching of the exterior specimen boundaries. Nevertheless, minor registration mismatches among the diffusion-weighted images produced a few artifactual high FA values along the specimen borders or the dorsal fissure. It was speculated that, in addition to the exterior specimen boundary, it might be possible to use boundaries of internal features, such as the boundary between white and gray matter, to guide the registration. A registration algorithm applied to the manually delineated boundaries of the dorsal and ventral horns, matched the central region of the specimen reasonably well, but the exterior specimen boundaries only poorly. Accurate registration of the specimen exterior boundaries was considered critical, since a mismatch of the exterior boundaries resulted in more artifactual high FA values, whereas a mismatch of the interior boundaries, due to the smaller differences between adjacent white and gray matter MR signals, had a less significant effect.

Summary

In conclusion, the correlation between diffusion and axon packing parameters was studied over entire spinal cord specimen sections. Although there was a clear linear correlation, there is good reason to believe the relation between diffusion parameters and axon packing parameters may not be linear. Future research directions may include comparison of other MR diffusion parameters, use of different histological stains and axon architecture parameters, and study of other white matter tissue regions among multiple subjects. With the selection of other white matter regions, the confounding contribution of dendrite main branches and crossing fibers may be avoided. On the other hand, very uniform appearing white matter regions may exhibit only small variations in axon count and other axon architecture parameters, and therefore, may not necessarily result in the establishment of better correlation results.