Impact of Blood Glucose Self-Monitoring Errors on Glucose Variability, Risk for Hypoglycemia, and Average Glucose Control in Type 1 Diabetes: An In Silico Study

Abstract

Background

Clinical trials assessing the impact of errors in self-monitoring of blood glucose (SMBG) on the quality of glycemic control in diabetes are inherently difficult to execute. Consequently, the objectives of this study were to employ realistic computer simulation based on a validated model of the human metabolic system and to provide potentially valuable information about the relationships among SMBG errors, risk for hypoglycemia, glucose variability, and long-term glycemic control.

Methods

Sixteen thousand computer simulation trials were conducted using 100 simulated adults with type 1 diabetes. Each simulated subject was used in four simulation experiments aiming to assess the impact of SMBG errors on detection of hypoglycemia (experiment 1), risk for hypoglycemia (experiment 2), glucose variability (experiment 3), and long-term average glucose control, i.e., estimated hemoglobin A1c (HbA1c)(experiment 4). Each experiment was repeated 10 times at each of four increasing levels of SMBG errors: 5, 10, 15, and 20% deviation from the true blood glucose value.

Results

When the permitted SMBG error increased from 0 to 5–10% to 15–20%-the current level allowed by International Organization for Standardization 15197–(1) the probability for missing blood glucose readings of 60 mg/dl increased from 0 to 0–1% to 3.5–10%; (2) the incidence of hypoglycemia, defined as reference blood glucose ≤70 mg/dl, changed from 0 to 0–0% to 0.1–5.5%; (3) glucose variability increased as well, as indicated by control variability grid analysis; and (4) the incidence of hypoglycemia increased from 15.0 to 15.2–18.8% to 22–25.6%. When compensating for this increase, glycemic control deteriorated with HbA1c increasing gradually from 7.00 to 7.01–7.12% to 7.26–7.40%.

Conclusions

A number of parameters of glycemic control deteriorated substantially with the increase of permitted SMBG errors, as revealed by a series of computer simulations (e.g., in silico) experiments. A threshold effect apparent between 10 and 15% permitted SMBG error for most parameters, except for HbA1c, which appeared to be increasing relatively linearly with increasing SMBG error above 10%.

Introduction

Extensive studies have shown that intensive treatment with insulin or with oral medications aimed at maintaining near-normal levels of glycemia markedly reduces chronic complications in both type 1 (T1DM)^1,2 and type 2 diabetes mellitus (T2DM).³ However, because exogenous insulin provides imperfect replacement to its natural endogenous secretion, patients under intensive insulin therapy typically face an increased risk for hypoglycemia.^4–7 Thus, hypoglycemia has been identified as the primary barrier to safe attainment of good glycemic control.^8–10 In other words, people with T1DM and T2DM face a lifelong behaviorally controlled optimization problem: to maintain strict glycemic control without increasing their risk for hypoglycemia. The key to this (as well as to any) optimization is providing accurate information about the status and dynamics of the system (in this case the patient's). The sources of information are at various stages of development and clinical acceptance: hemoglobin A1c (HbA1c) assays have been confirmed as the gold standard evaluation of glycemic control for both T1DM and T2DM,¹¹ self-monitoring of blood glucose (SMBG) is now routine practice, and continuous glucose monitoring (CGM) systems are developing rapidly and entering the clinical mainstream.

Focusing on SMBG, contemporary home blood glucose (BG) meters offer convenient means for frequent BG determi-nations. A review of standards and analytical methods used to judge SMBG device performance has been presented by Krouwer and Cembrowski.¹² The accuracy of SMBG devices has been evaluated by multiple studies,^13–16 and recommendations have been made for its improvement.^17,18 The critical question is then: to what extent do inaccuracies in SMBG information, inherent with any measurement technology, influence the glycemic control of a person?

Several studies have addressed this question, offering various viewpoints and degrees of analytical complexity. Boren and Clarke¹⁹ presented an extensive review of over 30 publications addressing the accuracy of SMBG devices. The primary conclusion of that review was because SMBG devices are prone to errors, “when examining blood glucose monitor performance in the real world, it is important to consider if an improvement in analytical accuracy would lead to improved clinical outcomes for patients.”¹⁹ Raine and colleagues²⁰ investigated the influence of miscoding meters on certain potential glycemic outcomes, such as hypoglycemia and hyperglycemia. They found that miscoding could result in significant meter bias, with a maximum deviation from reference BG of –224 mg/dl and a probability of over 10% to produce blood glucose reduction leading to hypoglycemia.²⁰ The common perception is therefore that SMBG accuracy (or errors) should be judged in the context of clinical outcomes. Clinical outcome studies of SMBG accuracy are, however, quite complex to design and difficult to execute. The reason is simple—controlled administration of meter errors in vivo is intricate and may be unethical in some cases.

A viable alternative to clinical trials testing the impact of SMBG inaccuracy was presented by the landmark studies of Boyd and Bruns,^21,22 which employed computer simulation to assess the influence of meter errors on insulin dosing. These studies reported detailed results linking meter bias and imprecision to insulin dosing errors. The second of these studies also used a model of physiologic response to changing insulin dose to assess glucose outcomes due to meter errors. Two conclusions of these studies can be considered precursors to the computer simulation “in silico” experiments presented in this article: (1) “simulation of the clinical effects of measurement error is an attractive approach for assessment of assay performance requirements” and (2) “sophisticated models that give highly accurate representations of true physiologic response of glucose to insulin … would be the ideal models to apply in simulation studies.”²² Indeed, a computer simulator of the human metabolic system has been developed by Dalla Man and colleagues^23,24 in collaboration with our research team and was employed in various in silico experiments of insulin treatment in the past 2 years.²⁵ This simulation platform has been used to assess differences in bolus calculator recommendations among four insulin pumps²⁶ and was suggested as an in silico test bed for assessment of the accuracy of hypoglycemia alarm systems in CGM.²⁷ In their 2009 work, Boyd and Bruns²² advocated the use of our simulator for assessing the impact of meter inaccuracies on clinical outcome.

Following this work, this article proposed to analyze the clinical effect of fixed standards for SMBG accuracy, i.e., what clinical gain should be expected when a standard is tightened from the current ±20% down to ±5%. To perform this analysis, we used the simulation platform cited earlier.

Methods

Continuing the work of Bruns and Boyd, we performed four in silico experiments using the University of Virginia/Padova simulation platform. These experiments were designed to test the impact of SMBG errors on detection of hypoglycemia (experiment 1), BG target achieved and risk for hypo- or hyperglycemia following a correction bolus (experiment 2); glucose variability caused by meter-induced errors in both premeal and correction boluses (experiment 3); and long-term average glucose control, i.e., estimated HbA1c calculated from simulated reference BG (experiment 4).

Subjects

One hundred simulated “adults” with T1DM were employed in computer simulation experiments. Each of these “subjects” is a complex entity, generally described by the dynamical network model of the human metabolic system proposed by Dalla Man and colleagues and identified by 26 individual parameters.^23,24 The individual parameters of the simulated subjects were selected carefully to span the interperson variability observed in vivo in T1DM,²⁵ i.e., different simulated subjects represent different people sampled representatively from the T1DM population. The “demographic” characteristics of the 100 simulated subjects have been published previously²⁵ and are presented in Table 1.

Table 1.

Key Demographic and Metabolic Parameters of 100 In Silico “Adults” Available in Simulation Environment

Parameter	Mean (SDb)	Minimum	Maximum
Weight (kg)	79.7 (12.8)	52.3	118.7
Insulin (U/day)	47.2 (15.2)	21.3	98.4
Estimated HbA1ca	7.0 (1.1)	5.4	9.7
Carbohydrate ratio (g/U)	10.5 (3.3)	4.6	21.1
Insulin effect on glucose utilization (10-2 mg/kg/min per pmol/liter)—a measure of insulin sensitivity	3.82 (1.34)	1.08	8.08

^aIn simulation, the HbA1c estimate depends on the simulated diabetes management regimen imposed on the subjects. Here, HbA1c corresponds to average glucose achieved under open-loop therapy based on each subject's optimal carbohydrate ratio and correction factor.

^bStandard deviation.

Model of SMBG Errors

Self-monitoring of blood glucose errors were modeled using independent Gaussian (normal) random variables with distribution parameters (μ, σ) depending on the error to be generated. The parameter μ, which corresponds to the mean of a normal distribution, was kept at zero during the simulations, i.e., we did not investigate the effect of meter bias, which has been studied extensively in the past.^20–22 The parameter σ, which corresponds to standard deviation, was used to tune the magnitude of the error, i.e., the imprecision of SMBG. In addition, σ was made dependent on the BG level to simulate the current International Organization for Standardization (ISO) standard, which states that “ninety-five percent of the indi-vidual glucose results shall fall within ±0.83 mmol/liter (15 mg/dl) of the results of the manufacturer's measure-ment procedure at glucose concentrations ≤4.2 mmol/liter (75 mg/dl) and within ±20% at glucose concentrations >4.2 mmol/liter (75 mg/dl).”²⁸ The symmetry implied by the standard (same margin above and below the true value) led us to the choice of normal distribution.

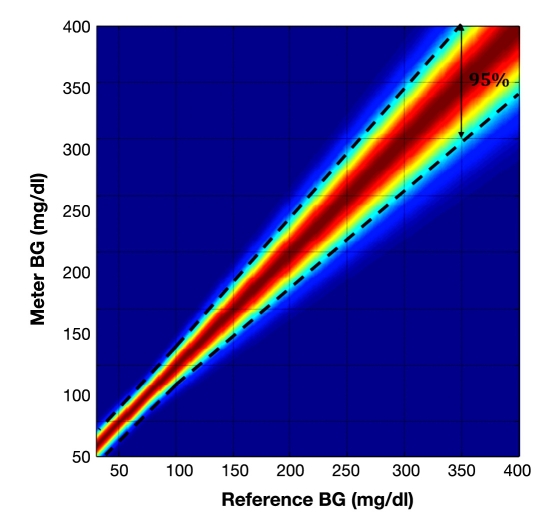
Figure 1 presents the 95th percentile of the simulated SMBG error (A) and the color-coded distribution of the error (B) at the permitted SMBG error level of 20%, i.e., at the upper limit of ISO requirements.

Figure 1.

Distribution of simulated SMBG errors at the maximum error level of 20% permitted for BG >75 mg/dl by the ISO standard. The error for BG ≤75 mg/dl is kept within ±15 mg/dl from reference. To simulate a lower degree of error, e.g., 15, 10, or 5%, this distribution is scaled by appropriate reduction in its standard deviation.

The following text refers to the ISO-permitted level of inaccuracy as 20% error. The simulation experiments scaled down the permitted SMBG error to 10 and 5%. It is important to emphasize that the permitted SMBG error does not translate into mean absolute relative deviation (MARD) of the same magnitude. Table 2 illustrates the relationship between the degree of permitted SMBG error and MARD.

Table 2.

Permitted (at 95th Percentile²⁸) SMBG Error and Corresponding MARD

Permitted SMBG error	5%	10%	15%	20%
Observed MARD of the meter	2.01%	4.02%	6.03	8.04%

It is evident that the observed MARD is ∼2.5-fold lower than the 95% percentiles permitted for meter error—a ratio that is a function of the distribution of the SMBG error described in the previous paragraph.

Procedure

As noted previously, we proposed four different simulations, each looking at four critical aspects of glucose control: (i) hypoglycemia detection, (ii) hyper-glycemia correction, (iii) meal control, and (iv) overall glucose control.

Experiment 1

Goal

Assess the deterioration of hypoglycemia detection as a function of SMBG inaccuracy levels.

Protocol

Hypoglycemia was induced with an insulin bolus and SMBG was performed at the precise time when the reference BG level reached an array of BG levels between 70 and 50 mg/dl. For each of these reference BG levels, the probability of SMBG missing the hypoglycemic episode was assessed as a function of the permitted meter error. The experiment was repeated 100 times per subject (n = 10,000).

Relevance

People with T1DM rely on SMBG measures to assess their glycemic state (hypoglycemic, euglycemic, or hyperglycemic). Because hypoglycemia requires immediate treatment, detection of hypoglycemia is a critical use of point-of-care meters.

Experiment 2

Goal

Assess the effect of SMBG inaccuracy on the capacity to treat hyperglycemia.

Protocol

Subjects were kept at reference BG of 200 mg/dl using a basal rate that was lower than nominal. An SMBG reading was “taken” at that point, with an error defined by the SMBG error model described earlier. Based on the SMBG reading, a correction insulin bolus was administered using the exact correction factor for each subject and the subject's normal basal rate was resumed, with the goal of bringing the subject to a target BG of 100 mg/dl. The degrees of deviations from target and the risk for hypoglycemia were assessed at 5, 10, 15, and 20% levels of SMBG imprecision. The experiment was repeated 10 times per subject per accuracy level (n = 1000).

Relevance

Treatment of hyperglycemia in T1DM requires a glucose measurement from which the amount on insulin to be taken is computed. Thus, improper insulin dosing can lead to failure to correct hyperglycemia or to hypoglycemia.

Experiment 3

Goal

Assess glucose variability associated with a meal at different SMBG inaccuracy levels.

Protocol

Subjects were kept fasting at 100 mg/dl. An SMBG reading was “taken” at that point, with an error defined by the SMBG error model described earlier. Based on the SMBG reading, a premeal insulin bolus was administered using the exact carbohydrate ratio for each subject, with the goal of covering approximately 60% of a meal containing 75 grams of carbohydrate, i.e., the meal was underbolused by 40% in order to necessitate a postmeal correction bolus. After observing a postprandial glucose increase, a second SMBG reading was taken, again with an error, and a correction bolus was administered as needed. Glucose variability was assessed during this up–down swing of BG as a function of meter errors. The experiment was repeated 10 times per subject per accuracy level (n = 1000).

Relevance

Glucose variability has documented negative consequences; increased variability around meals can lead to vicious cycles of overtreatment and both hyper- and hypoglycemic episodes.

Experiment 4

Goal

Estimate the deterioration of overall glucose control (HbA1c) created by increased SMBG inaccuracy.

Protocol

Long-term glucose control was assessed as follows: First, the subject's glycemic control was stabilized at a “nominal level” using their optimal carbohydrate ratio and correction parameters. The nominal glycemic control regiment carried a certain nominal risk for hypoglycemia, which was memorized for each subject. Further, subjects were “observed” for 10 days (it is understandable that a 10-day observation in vivo would not change HbA1c significantly because of the time needed to renew red blood cells; in silico, however, this effect is instantaneous) during which their control was based on SMBG with errors generated by the error model described previously. In some subjects, SMBG errors caused increased risk for hypoglycemia. We dialed this risk back to nominal levels for each subject and continued the simulation for another 10 days. Limiting the risk for hypoglycemia caused increases in the average blood glucose level of the affected subjects, simulating the detrimental effect of hypoglycemia on diabetes control observed in vivo.^9,10 We converted the increase in average BG needed to offset hypoglycemia into an increase in HbA1c using the formula recommended by the American Diabetes Association (ADA)(28.7 × A1C – 46.7 = eAG²⁹), thereby assessing in silico the relationship between SMBG errors and change in HbA1c as mediated by each subject's risk for hypoglycemia. The experiment created n = 1000 days of data.

Relevance

Hemoglobin A1c is the gold standard assess-ment of glycemic control in diabetes. Thus, it is important to assess possible deviations in HbA1c due to SMBG errors.

Data Analysis

We used frequency analysis and graphical representation of the results to present the observed relationships. The main outcome measure for each experiment is as follows.

• Experiment 1: Probability of hypoglycemia (BG <70 mg/dl) detection, as estimated by the frequency method.

• Experiment 2: Probability of a hypoglycemic event, as estimated by the frequency of hypoglycemia. Secondary outcome measures: distribution of the achieved BG value, as represented by the box plot.

• Experiment 3: Glucose variability as estimated by the A+B zone percentage of control variability grid analysis (CVGA^30–32).

• Experiment 4: Risk of hypoglycemia as estimated by the percentage of days with at least a hypoglycemic event. Secondary outcome measure: HbA1c change resulting from increase in the risk of hypoglycemia as computed by the ADA formula.²⁹

Results

Experiment 1

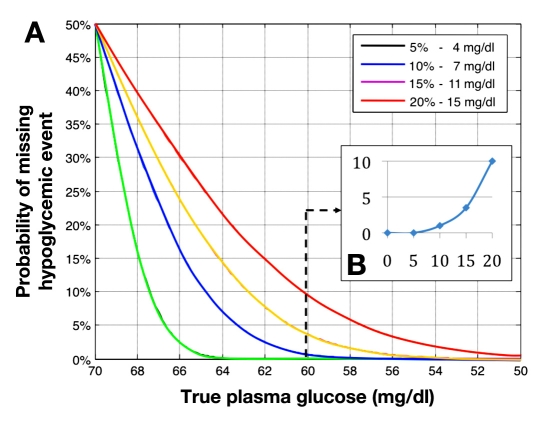
Figure 2A presents the probability for missing hypo-glycemic reference BG events as a function of reference BG and meter error. It is evident that this probability increases sharply with the increase of SMBG error. For example, a reference BG level of 60 mg/dl will be always detected at an SMBG error of 5%, but the chances of missing that event even if SMBG is performed right on time increase to 1, 3.5, and 10% for SMBG errors of 10, 15, and 20%, respectively. Thus, at the 20% error level permitted by the ISO standard,²⁸ 1 in 10 hypoglycemic episodes of 60 mg/dl would remain undetected, even if the SMBG reading is perfectly timed at the precise time of hypoglycemic event.

Figure 2.

(A) Probability of SMBG missing hypoglycemia as a function of BG level and permitted SMBG error. It is evident that even significant hypoglycemic episodes of 60 mg/dl or lower can be missed by SMBG with errors within 20% as allowed by ISO 15197. (B) Reference BG is fixed at 60 mg/dl. The probability for missing that hypoglycemic event increases, initially slowly, until the permitted SMBG error reaches a level between 10 and 15%. After that error threshold, the increase accelerates substantially.

Figure 2B presents another view of this problem, plotting the probability for missing a hypoglycemic level of 60 mg/dl as a function of the SMBG error. A certain threshold effect is evident between 10 and 15% SMBG error—the probability for missing hypoglycemia is initially relatively low (≤1%) and increases sharply thereafter.

Experiment 2

Figure 3 presents the distribution of BG levels achieved following a correction bolus administered at a reference BG level of 200 mg/dl and calculated precisely to bring the “subject” down to 100 mg/dl if there were no SMBG measurement errors. Having meter errors introduces certain dispersion of the BG level achieved. The dispersion increases with the increase of the SMBG error to the extent that SMBG errors within the permitted 20% range can cause hypoglycemia (BG ≤70 mg/dl) and hyperglycemia (BG >180 mg/dl), i.e., clinically significant over- or undercorrection.

Figure 3.

Distribution of BG levels achieved when a correction bolus was calculated precisely to bring each of the simulated subjects from 200 to 100 mg/dl. It is evident that the chances for not achieving the target increase substantially with the increase in meter error.

The incidence of hypoglycemia, defined as reference BG ≤70 mg/dl, increased from 0% at an SMBG error of 5 and 10% error to 3.5% at 15% error and 5.5% at 20% error. The incidence of overshooting the target, defined as reference BG >140 mg/dl, increased from 0% at an SMBG error of 5 and 10% to 0.1% at 15% error and 5.5% at 20% error. Again, a certain threshold effect is apparent—the probabilities for hypoglycemia and for overshooting the target are close to zero for permitted SMBG errors of up to 10% and increase faster thereafter.

Experiment 3

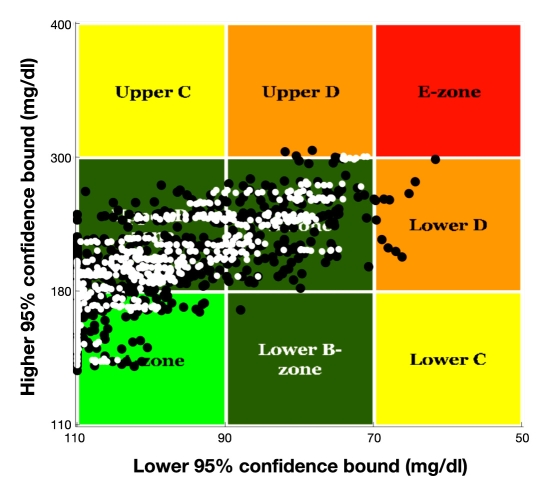
In this experiment, we simulated a sequence of two SMBG readings, premeal and postmeal at the peak of postprandial BG elevation. Figure 4 presents a CVGA plot comparing a 5% permitted meter error (white dots) vs a 20% permitted meter error identified by black dots. Each data point on the plot has two coordinates: X is the minimum BG level for each subject and Y is the maximum BG level for each subject during the experiment. The spread of data over the CVGA plot is a measure of overall variability.³² It is evident that a higher SMBG error results in a wider spread of data, indicating higher glucose variability. The percentage of points within the desired CVGA A+B zones decreases from 97% at permitted 5% error to 85% at 20% error, and percentage readings in the dangerous C, D, and E zones increase fivefold, from 3% at 5% error to 15% at 20% error.

Figure 4.

A CVGA plot comparing 5% permitted meter error (white dots) to 20% permitted meter error (black dots) in terms of glucose variability caused by SMBG inaccuracy. It is evident that the amplitude of BG fluctuations increases with increased SMBG error.

Experiment 4

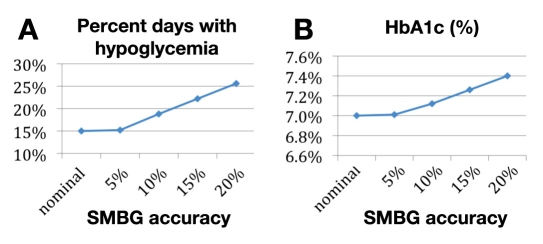
Under nominal conditions (no SMBG error and optimal control), 15% of all observed patient days had at least one hypoglycemic episode across the 100 simulated subjects. Increasing the SMBG error resulted in an increased percentage of hypoglycemic episodes to 15.2% at permitted 5% error, 18.8% at 10% error, 22% at 15% error, and 25.6% at 20% error. In order to scale back the risk for each subject to its nominal level of 15%, we needed to increase the average BG by 0.5 mg/dl at 5% error, 3.5 mg/dl at 10% error, 7.5 mg/dl at 15% error, and 11.5 mg/dl at 20% error. This corresponds to an increase in HbA1c by 0.01 at 5% error, 0.12 at 10% error, 0.26 at 15% error, and 0.40 at 20% error. Figure 5A presents the relationship between magnitude of permitted SMBG error and expected increase in incidence of hypoglycemia. Figure 5B presents the expected increase in HbA1c due to the detrimental effects of hypoglycemia on subjects' average glucose control.

Figure 5.

Relationship between the degree of permitted SMBG error and percent days with hypoglycemia during experiment 4 (A). Deterioration in HbA1c as mediated by risk for hypoglycemia (B).

It appears that while 5% SMBG error has almost no influence on HbA1c, the estimated HbA1c increases nearly linearly with a further increase in permitted SMBG errors.

Discussion

The experiments presented in this article are best explained by quoting the famous statistician George E.P. Box, who wrote: “Essentially, all models are wrong, but some are useful.”³³ Here, we relied on sophisticated models of the human metabolic system, which are capable of approximating the system response to insulin and glucose challenges. While these models are imperfect and cannot truly encompass the vast variability observed in vivo, these models are also useful. In particular, they allow for experiments that are virtually impossible (or very time-consuming and expensive) in vivo. The full control over all variables in simulated experiments and the reproducibility of in silico results are other advantages to be considered when interpreting our results.

In general, model-based computer simulation is a main-stream engineering tool, which is being used extensively for the design and the safety analysis of a number of mechanical systems, from the simplest tools to sophisticated aircraft.³⁴ In diabetes research, computer simulation has been used in the past to assess trends and treatment effects at a population level.^35,36 Assessment of the impact of permitted SMBG errors on insulin dosing and glucose control has been simulated as well.^21,22 As suggested by the Boyd and Bruns,²² the limiting step in these earlier experiments was the lack of realistic computer simulation that could mimic the reaction of human glucose control to inaccurate SMBG readings. This limitation is being overcome by newer studies, which employ simulators equipped with realistic simulated subjects. For example, Wilinska and associates³⁷ used a cohort of 18 simulated subjects to show that the incidence of severe and significant hypoglycemia was reduced 2300- and 200-fold, respectively, during simulated overnight closed loop compared to that observed during open-loop overnight clinical studies in young subjects with T1DM. In our experience, in silico studies have been extremely helpful in the development and testing of closed-loop control algorithms, cutting the development time from years needed for animal studies to only a few months.^38,39

This article used one of the most sophisticated currently available simulators of the human metabolic system developed to investigate the impact of permitted SMBG errors in four types of in silico experiments. First, we showed that SMBG errors can cause hypoglycemic episodes to be missed, with a 10-fold increase in missed BG levels of 60 mg/dl when permitted SMBG errors range from 10 to 20%, even if the timing of SMBG is perfect. Then we showed that SMBG errors can cause hypoglycemia when SMBG is used to dose insulin corrections at moderately high BG levels of 200 mg/dl and that the incidence of hypoglycemia increased progressively with the magnitude of the SMBG error. Certain threshold effects were observed in experiment 1 where the probability for missing hypoglycemia is relatively low (≤1%) for permitted SMBG errors of up to 10% and increases sharply thereafter, and in experiment 2 where the probabilities for hypoglycemia and for overshooting the target were close to zero for permitted SMBG errors of up to 10% and increase thereafter.

Further, we expanded the SMBG sequence to encompass both premeal and correction boluses. This allowed simulation of a BG swing from low to high and back to low BG levels and permitted analysis of the influence of SMBG errors on glucose variability. The CVGA plot showed that certain sequences of errors observed in one-quarter of all simulated trials can cause extreme BG excursions into both hypo- and hyperglycemic ranges. Finally, we simulated long-term patterns of glycemic control. In doing so, we speculated that an increased incidence of hypoglycemia would cause deterioration of average glucose levels, possibly through a behavioral reaction to the increased risk—an idea that is consistent with the concept of hypoglycemia being the major obstacle to optimal glycemic control.^9,10 This allowed evaluation of a relationship between increasing permitted SMBG errors and deterioration of HbA1c, showing that permitted SMBG errors of 5% have virtually no effect on HbA1c but that HbA1c increases steadily thereafter with the increase in SMBG error. A permitted SMBG error of 15% would result in a quarter point increase in HbA1c.

In this study we did not investigate the effect of SMBG errors in patients with T2DM because our simulation environment is still not ready for this task. We also deliberately omitted investigation of the effect of consistent bias in SMBG, which may occur due, for example, to miscoding of the meter, interfering substances, oxygenation of the blood, or hematocrit levels. This subject has been studied extensively in the past^20–22 and adding a separate study of SMBG bias would have overloaded this article. Our investigation was also limited to the effects of SMBG errors in T1DM. Similar in silico experiments with T2DM can be done when the simulation environment is equipped with a cohort of T2DM-simulated subjects—a development that is ongoing.

In conclusion, in silico experiments allowed establishing certain relationships between the degree of permitted SMBG errors and the risk for hypoglycemia, glucose variability, and long-term glycemic control in T1DM represented by estimated HbA1c. We need to emphasize, however, that these results should be viewed cautiously because their validity is limited by the proximity of our simulations to real-life events. Nevertheless, because our simulator has been tested extensively in the past 2 years, we can anticipate that future clinical studies would confirm our in silico findings. Until then, we can only rely on the usefulness of our models.⁴⁰

Abbreviations

ADA

American Diabetes Association

BG

blood glucose

CGM

continuous glucose monitor

CVGA

control variability grid analysis

HbA1c

hemoglobin A1c

ISO

International Organization for Standardization

MARD

mean average relative deviation

SMBG

self-monitoring of blood glucose

T1DM

type 1 diabetes mellitus

T2DM

type 2 diabetes mellitus