Simulating School Closure Strategies to Mitigate an Influenza Epidemic

Abstract

Background

There remains substantial debate over the impact of school closure as a mitigation strategy during an influenza pandemic. The ongoing 2009 H1N1 influenza pandemic has provided an unparalleled opportunity to test interventions with the most up-to-date simulations.

Methods

To assist the Allegheny County Health Department during the 2009 H1N1 influenza pandemic, the University of Pittsburgh Models of Infectious Disease Agents Study group employed an agent-based computer simulation model (ABM) of Allegheny County, Pennsylvania, to explore the effects of various school closure strategies on mitigating influenza epidemics of different reproductive rates (R₀).

Results

Entire school system closures were not more effective than individual school closures. Any type of school closure may need to be maintained throughout most of the epidemic (ie, at least 8 weeks) to have any significant effect on the overall serologic attack rate. In fact, relatively short school closures (ie, 2 weeks or less) may actually slightly increase the overall attack rate by returning susceptible students back into schools in the middle of the epidemic. Varying the illness threshold at which school closures are triggered did not seem to have substantial impact on the effectiveness of school closures, suggesting that short delays in closing schools should not cause concern.

Conclusions

School closures alone may not be able to quell an epidemic but, when maintained for at least 8 weeks, could delay the epidemic peak for up to a week, providing additional time to implement a second more effective intervention such as vaccination.

The recent and ongoing 2009 H1N1 influenza pandemic has sharpened debate over the impact of school closure in the control of an influenza epidemic. Students interacting very closely in schools transmit influenza virus to one another and then subsequently to their families and others in the community.^1,2 Closing schools will curtail these interactions in the school and therefore eliminate an important potential transmission site.

However, closing schools is not a trivial decision. Closing schools can cause significant social and economic disruption to the local community by placing additional burdens on parents, causing loss of income to school staff, and interfering with children’s education, nutritional status, and other activities.^1,3 Parents who are forced to stay at home to care for their children when schools are closed may have to sacrifice needed income or even lose their jobs, which could be disproportionately more likely among low-income families. In addition, those parents may have essential skills (such as healthcare) that are consequently temporarily lost to the system. Beyond education, schools are the sources of many vital community services, such as lunches and after-school programs. Therefore, a thorough understanding of the potential benefits and effects of school closure should accompany school closure policy-making.

School closures rose in prominence as a possible epidemic mitigation strategy after studies suggested that schools play an important role in influenza transmission. Glezen wrote in 1996 that “the fires of the epidemic are carried by healthy school-age children,” a perspective supported by extensive historical data from the 1918–19 and 1957 pandemics and the 1978 influenza season in Houston.^4–6 School classes with children in kindergarten through 12th grade have “high potential for virus transmission” according to social network analyses conducted in the United States,⁷ Germany,⁸ and Belgium.⁹

Public health and school officials face numerous decisions when preparing for a potential influenza epidemic. They need to decide whether and when to close schools, how many schools to close, and how long they should keep schools closed. An official may choose to keep schools open and simply isolate students who contract influenza, close schools in which influenza cases appear (individual school closure), shut down the entire school system as soon as enough cases appear in the community, or some combination of these various strategies. The optimal choice depends on the potential effectiveness of each strategy and any synergistic effects in mitigating an influenza epidemic. However, decision makers may not have enough available data to make effective choices between the different strategies, and prospective studies may be difficult or impossible to perform. Retrospective data may be limited and not generalizable to different situations and circumstances. Computer simulations can help decision makers explore different possible strategies and their probable consequences.

In May 2009, to assist the Allegheny County Health Department (ACHD) during the spring wave of the H1N1 influenza pandemic, the University of Pittsburgh Models of Infectious Disease Agents Study (MIDAS) group employed an agent-based computer simulation model (ABM) of Allegheny County, Pennsylvania. This model included explicit representations of the county’s population, school system, work-places/commutes, households, and communities. The model also represented individual county residents, which allowed us to simulate different influenza epidemic scenarios and the ACHD to explore the effects of various school closure strategies. Our model incorporated many methods from other previously published MIDAS simulation models.^10,11 The objectives of this study were to determine how school closures as an isolated strategy may minimize the course of an epidemic (as measured by the number of infected cases) and how these effects may vary with differing school closure durations, triggers, and types. Understanding the impact of school closure in isolation is important when other major mitigation strategies are not available or practical because the epidemic arrived unexpectedly (eg, the 2009 H1N1 pandemic when vaccines were not available and mass prophylaxis with antiviral medications was not attempted) or the infectious agent is completely novel. The model could be applied to other infectious diseases transmissible by casual contact, such as severe acute respiratory syndrome, by incorporating parameter values (eg, incubation period and transmissibility) specific to that infectious disease.

Materials and Methods

Model structure and synthetic census-based population

Our ABM represented each person in Allegheny County (a total of 1 242 755 agents living in households) with a synthetic computer agent assigned a set of characteristics and behaviors: age, sex, employment status, occupation, household location, household membership, school assignment of students and teachers, work location assignment of employed adults, work status as employed or unemployed, and disease status.¹² Construction of the agent population used a method developed by Beckman et al, US Census Bureau’s Public Use Microdata files, and Census aggregated data to first generate a synthetic US population and then extract the Allegheny County population.^13,14

Our model also represented individual households, schools, and workplaces in Allegheny County. The model included a total of 537 405 households, each containing a specific set of agents based on the US 2000 Census data.^15,16 The model also consisted of 35 333 work-place locations. Assignment of Allegheny County’s 563 874 employed adults to each workplace used the Census 2000 Special Tabulation: Census Tract of Work by Census Tract of Residence (STP 64) database.¹⁶ A fraction of the workplaces consisted of 35 hospitals in Allegheny County, which employ an estimated 25 766 persons, of which 11 672 are HCWs who see patients on a daily basis.

Assignment of the 212 315 school-aged children to each school location was based on school capacity (used a similar method detailed by grade) and distance to schools as described by Ferguson et al¹⁰ and Wheaton et al.¹⁴ There are 43 school districts in Allegheny County including the city of Pittsburgh. These represent approximately 155 000 public school students in 289 schools. The additional schools and students attend in either private or parochial schools in the region. There is tremendous variability in socioeconomic status, race, and ethnicity by school district, with the city of Pittsburgh school system being the most diverse.

At any given time, each agent is in one of four mutually exclusive states: susceptible (S), exposed (E), infectious (I), or recovered (R). All people are initially susceptible (S) to disease until infectious individuals are introduced into the model. Contact with an infectious person has an assigned probability of disease transmission from the infectious person to the susceptible person, as listed in Table 1, derived from studies by Longini et al,¹⁷ Ferguson et al,¹⁰ Germann et al,¹⁸ and Halloran et al,¹⁹ on the basis of the 1957–58 Asian influenza pandemic. For example, as the third row in Table 1 indicates, an infectious child coming into contact with a susceptible adult in a shared household has a .3 probability of transmitting the virus to the adult. By comparison, the fifth row of Table 1 indicates that an infected student who comes into contact with a susceptible student has a .0435 probability of transmitting the virus. The lower half of Table 1 delineates the frequency at which different individuals contact other individuals at different locations (eg, a student will contact 13.5 other students within his or her classroom and 15 students in the same school but other classrooms each school day). A newly infected person then moves to the exposed (E) state for the duration of the disease’s incubation period and then to the infectious state (I) in which the person may infect others. Consistent with the results of the MIDAS combined-model study, only two-thirds of infectious patients exhibit symptoms.¹¹ After the duration of the infectious period, the person proceeds to the recovered state (R) and remains immune to subsequent infections for the remainder of the simulation.

TABLE 1.

Model transmission and contact parameter values^a

Social network	Infected	Susceptible	Transmission probability
Household	Adult	Adult	.4
Household	Child	Adult	.3
Household	Adult	Child	.3
Household	Child	Child	.6
Elementary school	Student	Student	.0435
Middle school	Student	Student	.0375
High school	Student	Student	.0315
Workplace	Adult	Adult	.0575
Hospital	HCW	HCW	.0575
Hospital	HCW	Patient	.01
Hospital	Patient	HCW	.01
Community	All	Child	.00255
Community	All	Adult	.00480
	Individual	Others	Mean contacts/day
School	Student	Classmates	13.5
School	Student	Nonclassmates	15
Community (weekday)	Student	Outside of school	16.2
Community (weekend)	Student	Outside of school	24.3
Workplace	Worker	Office mates	2
Workplace	Worker	Other coworkers	8
Community	Adults	Community	32.4
Workplace	Healthcare worker (HCW)	Coworkers (in same clinic/ward)	2 2
Workplace	HCW	Other coworkers	8
Workplace	HCW	Patients	30

^aTransmission probabilities are obtained from Ferguson et al,¹⁰ Halloran et al,¹¹ and Longini et al.¹⁷

These simulations incorporated a set of assumptions describing movements and contact patterns within the county population, with each individual represented by a computer agent, and is based on research done in other MIDAS network models.^10,11,18 Each weekday (in computer time), the computer agents moved back and forth from their households to their designated workplaces (if they were employed adults) or schools (if they were school-aged children), where they interacted with other agents in close proximity based on the contact rates shown on Table 1. Each agent interacted daily with other family members who shared the same household. In schools and workplaces, each student or worker agent contacts a fixed mean number of agents per day (representing that agent’s classroom or office) and has an additional random probability of interacting with other agents within the same school or firm but in different classrooms or offices. Worker agents in firms that have only one office repeatedly contact the same people each day. Every day, all agents, including students, potentially interact with each other in the community, although with a fairly low probability of transmitting the virus. On weekends, student agents do not go to school but have community interactions with an increase of 50 percent in frequency. Our base model also assumed that 20 percent of working adult agents work on weekends.²⁰ Our base case scenario assumed that 50 percent of sick students and workers stay home with no community contacts unless they see a doctor, and 40 percent of patients with influenza symptoms visit a clinic or emergency department, values that have been used in previous studies.^{10,19,21–23} Our model also assumed that students would continue to maintain their usual community contacts during school closure, which included increasing community contacts by 50 percent during weekends.²⁴

Model calibration

Initial model calibration utilized the Ferguson et al approach with data from historical (1957–58 and 1968–69) influenza pandemics.¹⁰ Calibration targeted an epidemic with an attack rate (AR) of 33 percent as measured in the 1957–58 pandemic and established daily contact rates to satisfy the 30–70 rule developed by Ferguson et al, which posits that 70 percent of all transmission occurred outside the household (which includes 33 percent that occurred in the general community and 37 percent in schools and workplaces).¹⁰ Once this is accomplished, straight multipliers of the transmission probabilities are used to strengthen or weaken the overall infection to produce desired ARs.

Epidemic simulations

To account for the spectrum of potential influenza-transmission characteristics and dynamics, our simulation runs explored the effects of varying the basic reproductive rate (R₀), which is the expected number of secondary cases that a typical infected individual will produce in a completely susceptible population. Each simulation started with a single case (adult or child) and introduced the case into Allegheny County in a random location. The ABM was programmed in C++ and is naturally parallel with regards to statistical realizations. Simulations were performed at the Pittsburgh Supercomputing Center on Axon, an Intel Xeon-based Infiniband cluster. Each simulation run took on average 2 minutes over 100 computational cores.

School closure strategies

Different simulation runs depicted various combinations of the following school-focused strategies:

• Isolating sick students: This strategy focuses on identifying and confining symptomatic sick students to their households while leaving schools open. As a request from the previously mentioned work with the ACHD, the base case scenario supposes that parents are able to identify and keep 60 percent of symptomatic children at home. Schools then are able to identify and send home 25 percent of symptomatic students within the first 2 hours of their arrival at schools. Schools can then identify and send home 10 percent of symptomatic students on the second day of symptoms. Schools and parents thus allow five percent of all symptomatic students to remain in schools throughout the duration of their illness. Sensitivity analyses varied the percentage of influenza cases that are symptomatic and the probabilities of parents and schools detecting symptomatic cases.

• School system closure: This strategy involved shutting down the entire school system once a certain trigger, that is, a threshold number or percentage of cases, was reached. For our base scenario, school system closure occurred when the total number of influenza cases of all ages in the county exceeded 1 percent of the Allegheny County population. Sensitivity analyses ranged this threshold and the duration of school system closure.

• Individual school closure: This strategy entailed closing only those schools in which influenza cases were identified. Our base case scenario assumed school closure 1 day after a case appeared in that school. Each school remained open until at least one case was identified among its students. Sensitivity analyses varied the number of cases that can occur in a school before closing the schools and the duration of the school closure.

Results

All of the presented epidemic curves are the averages of 100 simulation runs that resulted in epidemics after seeding the population with one randomly infected individual. The continuous lines represent 4-day moving average trend lines, which smoothed out irregular patterns produced by the weekend effect (ie, students and workers having different weekend contact patterns).

Baseline runs with no mitigation

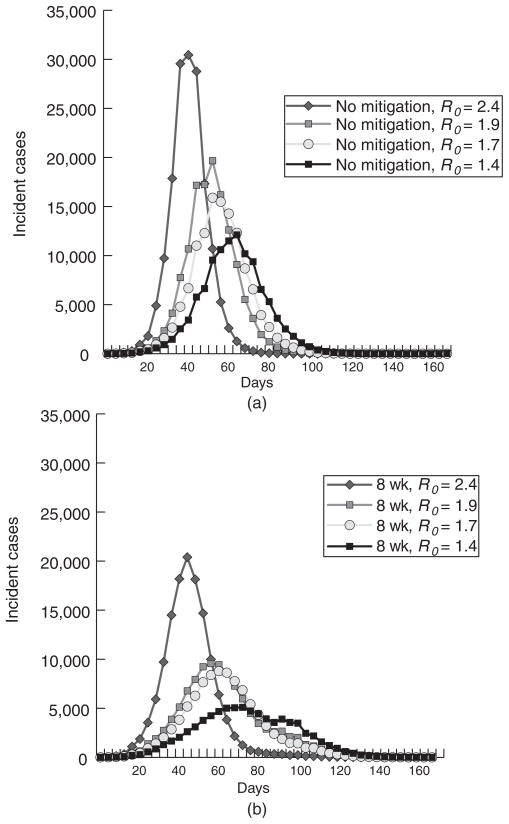
Figure 1 presents 4 baseline (no interventions) epidemic curves of increasing severity (R₀ values of 1.4, 1.7, 1.9 to 2.4). The R₀ = 1.4 baseline is of particular interest because it was used as part of the model calibration process,¹⁷ with an AR targeted at 35 percent. Our calibration of the model at R₀ = 1.4 (averaged over 100 statistical realizations) produced an AR of 35.1 percent, which corresponds to 435 745 infected persons. The AR for adults was 29.2 percent (274 342 infected adults) and students 70 percent (163 005 infected students). This higher AR for students was consistent with the other MIDAS models of R₀ = 1.4 epidemics.^17,25 Figure 1(a) shows incidence infections curves with no mitigations implemented for the various R₀ values calibrated for the research in the article, and Figure 1(b) displays incidence infection curves for the same values with systemwide school closure of a duration of 8 weeks.

FIGURE 1.

Epidemic Curve for Unmitigated Strategy vs Implementing an 8-Week Systemwide School Closure at Varying Reproductive Rates (R₀)

Identification and isolation of sick students

Isolation (identification of ill students and keeping them from attending schools) had minimal effect on the epidemic (Table 2). In our sensitivity analyses, the maximal effect showed a decrease in the overall AR to 29 percent and a delay in the peak of the epidemic by 1 week (when parents were able to identify and prevent 60 percent of symptomatic children from going to schools). When parents were able only to catch 20 percent of symptomatic children before they went to schools, this strategy had no significant effect on the epidemic. Isolation as a strategy did not prevent asymptomatic infectious students from entering schools and spreading disease. In fact, the effectiveness of isolation as a strategy was highly sensitive to the percentage of infectious children who were symptomatic: decreasing this percentage from 75 to 25 increased the overall attack mean rate for an R₀ = 1.4 epidemic from 27.4 percent to 35.4 percent.

TABLE 2.

Parents and schools identifying and isolating sick students

Scenario	Reproductive rate (R0) = 1.4
	AR, %	PD	PI	ΔPI, %
Unmitigated	34.6	68	12113	…
Varying probability of parents identifying and keeping at home sick student
Parents identify and keep at home 20% of sick students	32.6	68	10758	−11.2
…40% of sick children	31.0	76	9500	−21.6
…60% of sick children	28.9	76	8708	−28.1
Varying probability of schools identifying and sending home sick student
Schools identify and send home 10% of sick students the first day and 25% of sick students the second daya	29.4	76	8764	−27.6
…11% the first day and 4% the second day	30.0	76	9003	−25.7
…18% the first day and 18% the second day	29.2	76	8669	−28.4
…18% the first day and 7% the second day	29.6	76	8830	−27.1
…25% the first day and 10% the second day	28.9	76	8565	−29.3

Abbreviations: AR, serologic attack rate; PD, epidemic peak day; PI, epidemic peak incidence; and ΔPI, change in peak incidence compare to unmitigated scenario.

^aSome students will be detected the first day that they appear sick in schools and some will be caught the second day.

School closure duration

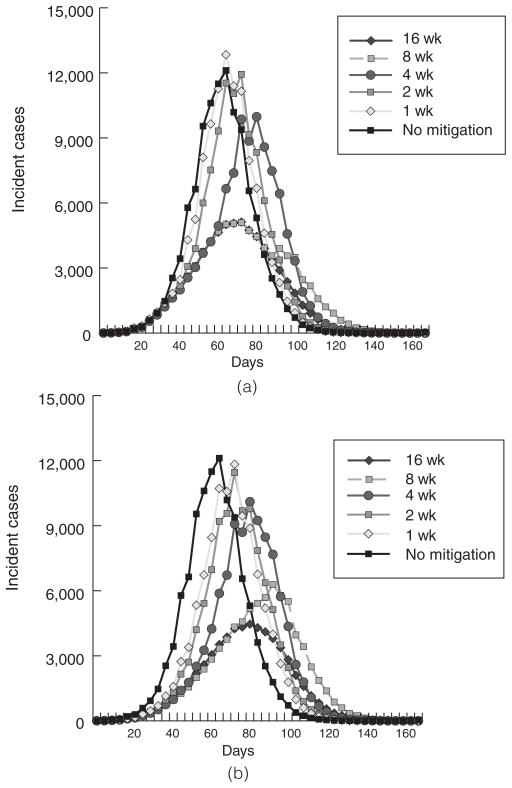
Table 3 compares the overall AR, peak incidence day of epidemic, and peak incidence of infected individuals in an unmitigated epidemic (no school closures) with school closures of entire systems or individual schools and for varying durations (1, 2, 4, 8, and 16 weeks). Whether the school closure strategy was systemwide or individual made no consistent or significant difference on these epidemic parameters. For both school closure strategies, durations of less than 8 weeks had little impact on the overall AR and durations of 2 weeks or less actually slightly increased the overall AR.

TABLE 3.

Effects of varying the length of school closure

Closure length	Reproductive rate (R0) = 1.4				R0 = 1.7				R0 = 1.9				R0 = 2.4
	AR, %	PD	PI	ΔPI, %	AR, %	PD	PI	ΔPI, %	AR, %	PD	PI	ΔPI, %	AR, %	PD	PI	ΔPI, %
Unmitigated	35.1	68	12 113	…	40.2	56	15 895	…	43.2	56	19 668	…	53	44	30 442	…
School system closure, wk
1	35.5	68	12 841	6.0	40.9	60	16 221	2.0	43.6	56	20 519	4.3	53.5	48	33 090	8.7
2	35.0	76	11 932	−1.5	40.6	68	15 643	−1.6	43.4	60	18 495	−6.0	53.3	48	34 300	12.7
4	33.2	84	9 975	−17.7	39.1	68	12 857	−19.1	41.9	68	15 799	−19.7	50.8	56	20 744	−31.9
8	25.1	76	5 099	−57.9	32.2	64	8 817	−44.7	34.2	60	9 560	−51.4	43.6	48	20 404	−33.0
16	21.9	76	5 119	−57.7	29.6	64	8 735	−45.0	29.3	64	8 645	−56.0	43.0	48	20 354	−33.1
Individual school closure
1	33.7	76	11 834	−2.3	40.6	64	15 546	−2.2	42.7	60	18 001	−8.5	52.8	48	33 234	9.2
2	33.2	76	11 458	−5.4	40.3	68	16 122	1.4	42.4	64	17 445	−11.3	52.5	48	32 315	6.2
4	31.8	84	10 106	−16.6	39.3	76	14 379	−9.5	41.4	68	15 842	−19.5	50.7	56	23 823	−21.7
8	25.3	96	6 290	−48.1	33.7	68	8 527	−46.4	35.5	68	8 851	−55.0	43.5	52	18 997	−37.6
16	19.4	84	4 460	−63.2	29.0	72	8 530	46.3	29.9	68	8 894	−54.8	42.2	52	19 031	−37.5

Abbreviations: AR, serologic attack rate; PD, epidemic peak day; PI, epidemic peak incidence; and ΔPI, change in peak incidence compare to unmitigated scenario.

For an R₀ of 1.4, 1-week systemwide school closure peak timing was similar to the unmitigated epidemic (day 68), but slightly higher levels of peak incidence compared with no school closure (12 841 vs 12 113 cases) and overall AR (35.3% vs 35.1%). A 2-week system closure also resulted in a slightly higher overall AR (35.0%) with a slightly delayed peak (between days 68 and 76). Only with a 4-week closure did the overall AR (33.2%) dip below the unmitigated level. Systemwide closures of 8 weeks or longer resulted in substantially lower ARs (25.1% for 8 weeks and 21.9% for 16 weeks), as well as a peak that was delayed by 8 days (day 76). Although the effects on overall ARs were modest, the peak incidence was substantially decreased for closures of over 4 weeks. The simulation runs showed similar results at the higher R₀ values for all systemwide closures, ARs were higher, and epidemic peaks were same as earlier. For individual school closure, variations of duration and R₀ value generated findings very similar to those observed for school system closures. Figures 2a and 2b present epidemic curves for varying lengths of school system closure and reactive school closures, respectively, for an R₀ = 1.4 influenza epidemic.

FIGURE 2.

Epidemic Curves for Individual School Closures for Varying Durations (R₀ = 1.4 and 1.9)

Thresholds for implementing school closures

Table 3 summarizes the simulations for 8-week school closures using different thresholds for implementation. For individual school closures, at the threshold the number of symptomatic cases was 1, 5, and 10. For systemwide school closures, the rate of symptomatic cases within the population was 0.10, 0.50, 1.00, or 1.50 percent. Interestingly, the overall ARs fell slightly when the thresholds were higher for both school closure strategies and all R₀ values.

Effects of changing the initial seed cases

Additional scenarios explored the effects of changing the number and timing of introducing new influenza cases to Allegheny County. Changing the initial seed from 1 to 10, 100, and 1000 cases made school closures even less effective. We also examined the effects of adding daily and weekly seeds; that is, 10 or 100 new cases are introduced every day or week. These changes did not affect the following general findings also listed above: school closure duration of less than 8 weeks had little impact on the overall AR and durations of 2 weeks or less actually slightly increased the overall AR, isolation (identification of ill students and keeping them from attending schools) had minimal effect on the epidemic, and closing schools earlier was not as important as ensuring that schools were closed until the majority of the epidemic was completed (ie, adequate herd immunity was achieved).

Discussion

The results of his modeling exercise emphasize the importance of keeping schools closed until the epidemic curve is far past its peak. Closing schools quickly was less important than keeping them closed continually throughout the epidemic once they were closed. Very early school closure at the start of the epidemic actually worsened the AR when schools were reopened in the middle of the epidemic, releasing a whole population of susceptible students to mix and be infected and extend the length of the epidemic.

While other mitigation strategies (eg, vaccination and antivirals) may accompany school closures, there are many situations in which school closures may be the only major intervention option. Epidemics or pandemics, such as the 2009 H1N1 influenza pandemic, may arrive unexpectedly, leaving little time to design, produce, and distribute an effective vaccine (eg, egg-based cultures require 4–6 months to produce influenza vaccine). Even if the infectious agent is influenza and susceptible to antiviral medications, mass continuous prophylaxis with antivirals throughout the course of an epidemic may not be practical. Moreover, our model is not limited to influenza and could apply to any infectious disease transmitted by casual contact (eg, other respiratory diseases such as severe acute respiratory syndrome or measles) as long as the relevant parameter values for the disease are available. Adequate pharmaceutical interventions may not be readily available for such diseases, especially if the infectious agent is novel.

In February 2007, the Centers for Disease Control and Prevention (CDC) published a detailed “community strategy” as the first line of defense against a novel pandemic virus.²⁶ This strategy focused on “nonpharmaceutical interventions” since vaccine would be initially unavailable and medications would likely be unavailable or in very short supply. These guidelines focused on six strategies intended to be implemented as “targeted and layered defense,” including

• closing schools,

• canceling public gatherings,

• planning for liberal work leave policies,

• tele-working strategies,

• voluntary isolation of cases, and

• voluntary quarantine of household contacts.²⁶

These strategies were developed in part on the basis of the established public health principles and supported by Markel et al² in their detailed study of the use of nonpharmaceutical interventions in 43 major US cities during the 1918–19 pandemic.² Markel et al noted that a strong association between reduced total mortality and early, sustained, and layered application of these interventions during this time period, with school closure appearing to play an important role.² A previous survey by Aledort et al²⁷ had found disagreement about using school closures during a pandemic in either its early localized phase or its advanced phase.

However, as the 2009 H1N1 influenza pandemic emerged and continues, considerable controversy persists over whether and how to close schools. In the spring of 2009, the World Health Organization recommended utilization of school closure as a potential strategy, although it noted that “class suspensions” instead of full school closures might be considered.²⁸ The CDC said that school closures should be implemented “at the discretion of local authorities based on local considerations.”²⁸ The CDC-affiliated scientists have emphasized the need to close schools early in the course of a pandemic and to do so in combination with other mitigation measures.²⁹

Our analysis implied that school closures as an isolated mitigation strategy (under the epidemic conditions explored) are not effective unless implemented and sustained for at least 8 weeks. At best, shorter school closures delayed the epidemic peak only briefly and, at worst, actually resulted in a slightly higher peak incidence. Increasing the peak incidence could tax the healthcare system especially if its daily capacity is severely limited (eg, clinics and emergency departments cannot handle an additional surge of cases on a given day). School closures were effective in reducing the overall AR only when schools remain closed throughout the bulk of the epidemic and reopened after the epidemic has subsided (or an additional effective mitigation strategy such as vaccination is implemented in the interim). Reopening schools during the epidemic simply released a population of susceptible children to be subsequently infected and may continue to fuel the epidemic. However, school closures for 4 weeks or more did have a significant impact in reducing the peak incidence, which would be of value in mitigating medical service needs during the epidemic.

In addition, our results showed no significant differences between individual reactive school closures and the more radical systemwide entire school system closure. This has several potential policy implications. First, systemwide school closures will result in more lost school days and, consequently, be much more costly than individual school closures. Second, an entire school system closure may be more difficult to coordinate and implement, depending on the location and jurisdiction, although it would certainly reduce confusion. It raises the questions of who has ultimate decision-making power and which schools in a county fall within the scope of those decisions. For example, in a given county, there may be different officials who hold authority to close public schools in various school districts and private schools. Individual schools with symptomatic students may be more willing and able to close quickly; ironically, schools may close in response to expressed parental concern or to reduce potential litigation.

There is also debate over the “illness” thresholds at which to close schools. Should schools be closed after a certain number of cases appear in schools, the community, or both? Will it make a difference if this threshold is based on the number of deaths or the severity of the observed cases? Our results suggested that the impact of school closures on overall ARs is not highly sensitive to changes in this threshold level, that is, when exactly school closure is initiated. Delays in closing schools did not have substantial effects on the epidemic. Instead, the most important factor seemed to be keeping schools closed for a long duration, that is, throughout most of the epidemic, once they are closed.

Our study also found that simply identifying and confining symptomatic cases will do little to mitigate an epidemic. Such a strategy will be effective very early in the epidemic only if it rapidly identifies and confines nearly all infectious cases before they can transmit the virus to others. This appears to be unlikely, since many infectious students will be asymptomatic and compliance among parents and schools will fall far short of 100 percent. So while this strategy may be locally beneficial, it will do little to stem the overall epidemic and essentially “chases” the epidemic without preventing asymptomatic infectious students from staying in schools and continuing to transmit the virus.

All computer models are simplifications of reality and can never account for every possible factor or interaction. Rather than make decisions, computer models provide information to decision makers about possible scenarios and relationships. An influenza pandemic and the resulting circumstances may not necessarily conform to the data and assumptions that our model drew from referenced sources or previously published models. School closures may still be effective under epidemic conditions not explored in our study (eg, R₀ <1.4 or >2.4).

This simulation did not include mortality as an epidemic parameter, which could vary with influenza viruses. Higher rates of mortality would probably influence decision makers to close schools at lower thresholds of incidence and for longer durations. We did not model the effects of hand hygiene measures because their quantitative effects on influenza transmission have not been established, although preliminary results from the CDC-funded Pittsburgh Influenza Prevention Project suggest that hand hygiene measures may have little effect on the overall epidemic curve. Our future studies may model the effects of layering additional interventions such as vaccination and antiviral medications on top of school closure.

Conclusions

Our study suggested that short-term school closures as an isolated mitigation strategy (under the conditions we explored) will do little to mitigate overall ARs during an influenza epidemic, but closures of 4 weeks or longer did have the effect of decreasing the peak incidence of illness. Schools must remain closed for at least 8 weeks, that is, throughout most of the epidemic, to have a significant impact on overall ARs. Simply, screening for ill students and keeping them from attending schools had minimal effect on the overall extent of the epidemic. Individual and systemwide school closures appeared to be equally effective so if the latter are more difficult to execute, the former can suffice. In addition, our results did not support any specific “illness” threshold level at which to close schools. In other words, short delays in school closure may not have a significant effect on the AR, timing of epidemic peak, or peak incidence. Finally, school closures may delay the epidemic peak for up to a week, which may provide more time to implement a second more effective intervention such as vaccination. The observed effect of reducing the peak incidence during an epidemic could place more importance on school closures when medical care capacity is anticipated to become strained or overloaded because of the number of patients needing care during the epidemic. This might be especially important in the setting where flu vaccine was becoming available just at the beginning of the school year. It is possible that delay of school opening for several weeks, in order to ensure that students get vaccination prior to beginning the school year, could be highly effective. As flu vaccine production becomes more efficient, this scenario becomes increasingly possible.

TABLE 4.

Effects of varying the trigger for school closure

Trigger for school closure	Reproductive rate (R0) = 1.4				R0 = 1.7				R0 = 1.9				R0 = 2.4
	AR, %	PD	PI	ΔPI, %	AR, %	PD	PI	ΔPI, %	AR, %	PD	PI	ΔPI, %	AR, %	PD	PI	ΔPI, %
Unmitigated	35.1	68	12 113	…	40.2	56	15895	…	43.3	56	19 668	…	52.3	44	30 442	…
Symptomatic cases per school
1	25.3	96	6 290	−48.1	33.7	68	8 527	−46.4	35.5	68	8 851	−55.0	43.5	52	18 997	−37.6
5	23.9	68	5 332	−56.0	30.9	64	8 782	−44.8	32.7	60	9 566	−51.4	43.1	52	20 114	−33.9
10	25.3	68	6 652	−45.1	31.5	60	9 843	−38.1	33.0	56	10 862	−44.8	43.7	4	20 524	−32.6
Symptomatic cases in population (% of overall population)
0.10	30.5	96	9 349	−22.8	36.7	84	9 591	−36.7	39.6	76	10 369	−47.3	45.7	52	19 370	−36.4
0.50	27.0	96	5 787	−52.2	33.5	68	8 606	−45.8	36.0	64	9 474	−51.8	43.9	48	20 086	−34.0
1.00	25.3	96	6 290	−48.1	32.2	64	8 817	−44.5	34.2	60	9 560	−51.4	43.6	48	20 404	−33.0
1.50	24.5	68	5 275	−56.5	31.3	64	9 932	−44.4	33.6	56	9 850	−49.9	43.5	48	20 787	−31.7

Abbreviations: AR, serologic attack rate; PD, epidemic peak day; PI; epidemic peak incidence; and ΔPI, change in peak incidence compare to unmitigated scenario.