Dissecting the THz spectrum of liquid water from first principles via correlations in time and space

Abstract

Solvation of molecules in water is at the heart of a myriad of molecular phenomena and of crucial importance to understanding such diverse issues as chemical reactivity or biomolecular function. Complementing well-established approaches, it has been shown that laser spectroscopy in the THz frequency domain offers new insights into hydration from small solutes to proteins. Upon introducing spatially-resolved analyses of the absorption cross section by simulations, the sensitivity of THz spectroscopy is traced back to characteristic distance-dependent modulations of absorption intensities for bulk water. The prominent peak at ≈200 cm^-1 is dominated by first-shell dynamics, whereas a concerted motion involving the second solvation shell contributes most significantly to the absorption at about 80 cm^-1 ≈2.4 THz. The latter can be understood in terms of an umbrella-like motion of two hydrogen-bonded tetrahedra along the connecting hydrogen bond axis. Thus, a modification of the hydrogen bond network, e.g., due to the presence of a solute, is expected to affect vibrational motion and THz absorption intensity at least on a length scale that corresponds to two layers of solvating water molecules. This result provides a molecular mechanism explaining the experimentally determined sensitivity of absorption changes in the THz domain in terms of distinct, solute-induced dynamical properties in solvation shells of (bio)molecules—even in the absence of well-defined resonances.

Water, often referred to as the “matrix of life” (1, 2), is a liquid that features many eccentricities (1, 3). As such water is the native solvent for biological processes. In recent years, however, the role of water has been revealed to be far more active than just being an inert solvent (2). Water molecules at protein/water interfaces, dubbed “hydration water” or “interfacial water,” have been shown not just to thermodynamically stabilize the native structure of biomacromolecules, but also to enhance their dynamical flexibility needed for efficient enzymatic catalysis and especially for the folding process that leads to the active structure of such molecules (4–7). Solvation was shown to be a key feature for protein function (8), with the coupling between protein and water dynamics (9) as an important ingredient to understand protein folding and binding. Hydration water has been in the focus of numerous theoretical and experimental studies (2), ranging from Raman and IR spectroscopy (10), femtosecond nonlinear spectroscopy (11), inelastic neutron scattering (12), femtosecond fluorescence spectroscopy (13), and molecular dynamics (MD) simulations (14, 15), to name but a few.

The intermolecular vibrational modes in the frequency window from 1 THz up to about 10 THz (16, 17), corresponding to ≈30–300 cm^-1, have been proven recently to be a unique tool to study the hydration dynamics around solutes (18–21). Using THz laser spectroscopy, water dynamics has been shown to be influenced within an “extended dynamical hydration shell” (20) of about 6–7 Å for small solutes like carbohydrates (18) by changes in the absolute absorption intensity as probed at 2.4 THz (i.e., ≈80 cm^-1). For proteins (20), this shell extends even up to ≈20 Å and is affected by e.g., folding state (21). The long-ranged sensitivity of THz absorption to dynamical properties of water at interfaces results from the presence of numerous processes in water occurring on picosecond time scales, e.g., hydrogen bond (HB) rearrangements and rotational relaxation. However, a full interpretation of the insights revealed by THz spectroscopy remains a daunting task.

Due to the importance of understanding the dynamics of solvation water it is thus mandatory to understand liquid water itself in the THz domain. The experimental far IR spectrum at THz frequencies (22, 23) features two pronounced maxima at approximately 200 and 650 cm^-1. Roughly speaking the 200 cm^-1 peak is related to hindered longitudinal translations of water molecules in the HB network (i.e., HB stretching vibrations) with a distinct collective character. The intermolecular vibrational modes belonging to frequencies above 300 cm^-1 stem from librational (i.e., hindered rotational) motion (24, 25). In Raman spectra, additional resonances around 60 cm^-1 are attributed to HB bending (24, 25) and contribute only weakly to the IR absorption. Based on this gross picture, the frequency range probed by the aforementioned THz experiments is therefore expected to be dominated in an intricate way by HB network motion.

In this study we have used MD simulations to address the nature of the underlying intermolecular motions. Unfortunately, the low-frequency absorption regime governed by intermolecular vibrations continues to be a challenge to force field based MD simulations (26–28). Although the IR spectrum of ambient water is qualitatively well described by force fields above ≈300 cm^-1, the significant resonance at 200 cm^-1 is either absent or emerges as a weak feature in such simulations (26–28). Polarizable force fields improve selected aspects of vibrational spectra, but also face difficulties to reproduce the prominent 200 cm^-1 peak (27, 28). In contrast, pioneering ab initio MD (AIMD) simulations of the IR spectrum of heavy water (29) were able to reproduce the 200 cm^-1 feature and assigned this to antisymmetric HB stretching modes. This discrepancy in the IR absorption cross section obtained from (polarizable) force fields versus AIMD studies has been explained (30, 31) in terms of intermolecular charge fluctuations in locally tetrahedral HB environments. These studies thus underline the collective character of low-frequency modes in conjunction with electronic polarization effects beyond single molecules (30, 31).

In the following, we introduce a consistent framework for a systematic decomposition of the IR absorption spectrum and intermolecular motion down to the THz regime in terms of correlations in time and space. In particular, analysis techniques are introduced which are able to spatially resolve the contributions of intermolecular motion and cross-correlation at given frequencies. These space-resolved methodologies in conjunction with an extensive set of AIMD trajectories of (light) liquid water allow us to assign the low-frequency modes at 2.4 THz to specific collective molecular motions that extend up to several Angstroms away from reference molecules.

Methodology: Spatial Decompositions of IR Spectra

The isotropic IR absorption coefficient per unit length is obtained as usual in linear response from

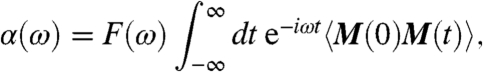[1]

which has been shown to work well for anharmonic HB systems (32). The prefactor reads F(ω) = (1/4πϵ₀)(2πβω²/3Vcn(ω)) and M(t) is the total dipole moment of the sample of volume V with refractive index n(ω) at temperature T = 1/k_Bβ. The total dipole moment can be decomposed into a sum of molecular dipole moments, , obtained from the centers of maximally localized Wannier functions (see Sec. 7.2 in ref. 33). This approach allows for the decomposition of M(0)M(t),

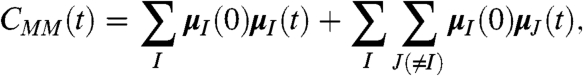[2]

in terms of self- and distinct-terms, i.e., auto- and cross-correlations of the molecular dipoles, respectively, and its generalization used to separate solute/solvent contributions (34, 35).

At variance with this established approach, we define here a smooth local dipole density

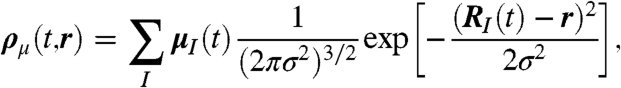[3]

where R_I(t) is the Ith center-of-mass and σ is a suitable regularization parameter. The total dipole moment, M(t) = ∫_Vdrρ_μ(t,r), can thus be decomposed smoothly in space, allowing one to introduce a spatially resolved total dipole autocorrelation function

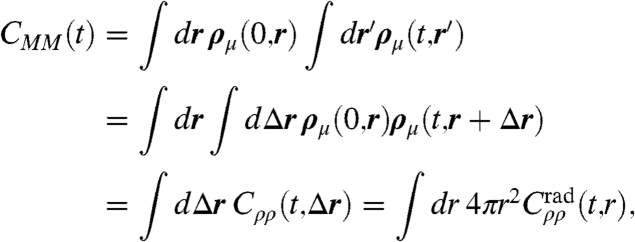[4]

which is done numerically upon introducing a spatial grid; here r^′ = r + Δr is used, and in the last step isotropy has been imposed. Based on this transformation, a spatially-resolved IR absorption coefficient α(ω,r) can be introduced

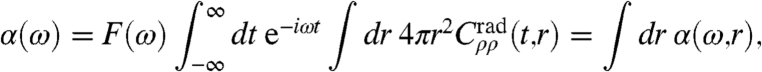[5]

which allows one to disentangle the spectra systematically at each frequency ω in terms of radially dependent contributions, r∈[0,r^max]; this continuous decomposition is similar to the discrete scheme introduced earlier (31) for analyzing the intermolecular contribution to dipole correlations only. In particular, absorption due to the self-term contributes exclusively for r → 0, whereas delocalized, collective modes will manifest themselves for r≫0 in terms of positive or negative α(ω,r) values at a fixed frequency ω, corresponding to correlated and anticorrelated motion, respectively. Furthermore, one obtains full spatial resolution α^3D(ω,r,θ,ϕ) when employing C_ρρ(t,Δr) in Eq. 5 in conjunction with a molecule-centered, moving coordinate system.

Extending this approach, the vibrational density of states I(ω) can be analyzed in space by introducing a local density ρ_v(t,r) of the mass-weighted velocities of atoms at positions r_i(t) analogous to Eq. 3 as 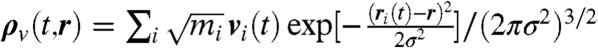. Radially and spatially resolved functions I(ω,r) and I^3D(ω,r,θ,ϕ), respectively, are defined in a similar way as introduced for the IR spectrum but without the prefactor F(ω). At variance to the IR spectrum approach, the commonly known vibrational density of states contributes only to I(ω,r ≈ 0) and I^3D(ω,r ≈ 0,θ,ϕ) because it does not include cross-correlations of particle velocities.

A complementary decomposition scheme is established by the idea of auto-correlating the dipole moment within a finite region,

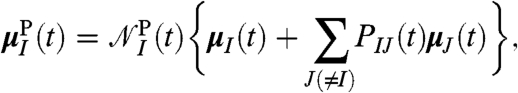[6]

around a (moving) molecule I serving as reference.

The considered region is thus a sphere, properly embedded in the bulk environment, that contains all J-molecules. Using Fermi’s cutoff function, P_IJ(t) = 1/{1 + exp[(R_IJ(t) - R₀)/D]}, allows for a continuous selection of the set of “neighboring particles” {J}, both in time and space, with R_IJ(t) = |R_I(t) - R_J(t)| being the intermolecular center-of-mass distance at time t; R₀ determines the cutoff radius, D measures the sharpness. The prefactor 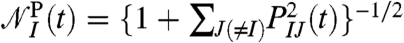normalizes with respect to the (fractional) number of contributing J-molecules. Based on this projection, a distance-dependent absorption coefficient is defined

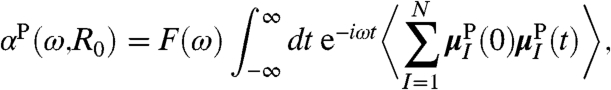[7]

after summing over all equivalent reference molecules {I}.

It is stressed that 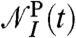is constructed as to properly take into account the growing number of contributing molecules upon increasing R₀. The meaning of the IR spectrum α^P(ω,R₀) is most easily revealed by considering two limiting cases. In the “bulk limit” all molecules are effectively taken into account, i.e., P_IJ(t) = 1 in Eq. 6, which is obtained in the analysis by increasing R₀ far beyond the average nearest-neighbor distance, 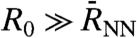, such that 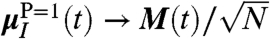in Eq. 7 and one finds 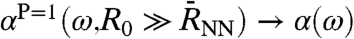as defined in Eq. 1. In contrast, the “single molecule limit,” P_IJ(t) = δ_IJ obtained via 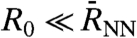, yields 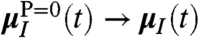in Eq. 7, i.e., 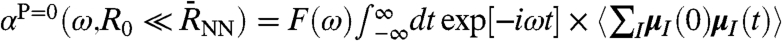, and thus only the self-term of Eq. 2 contributes. Most interesting is obviously the intermediate regime, i.e., from 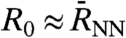up to several intermolecular distances 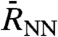, where α^P(ω,R₀) quantifies the distinct responses of successive hydration shells. Thus, monitoring changes of α^P(ω,R₀) upon increasing R₀ from small to intermediate distances might reveal how the solvation environment induces characteristic modulations of the IR absorbance around the reference molecule, starting from the individual polarized molecule via interfacial water towards bulk water at preselected frequencies ω.

A further approach draws on the phenomenon that on average, any water molecule finds itself close to four neighbors in a roughly tetrahedral arrangement subject to fluctuations and defects (3, 29–31, 36, 37). This suggests to define four symmetry-adapted internal symmetric and antisymmetric stretching (ss, as) coordinates

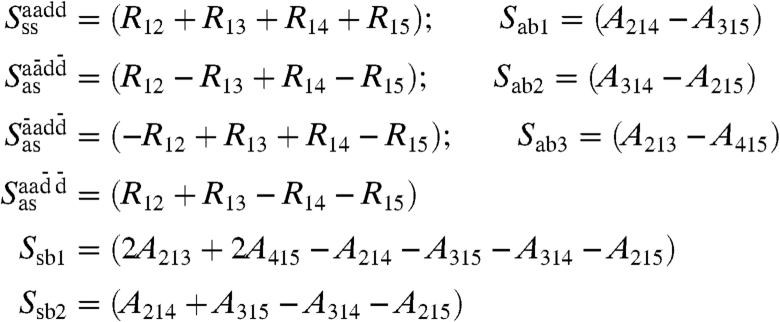[8]

as well as five such bending coordinates (sb, ab). Here R_IJ is the center-of-mass distance between I and nearest-neighbor J whereas A_JIK denotes the angle of J and K relative to the center-of-mass of the tetrahedron around I. Furthermore, in order to account for possible influences due to accepted and donated HBs the convention is introduced that waters 2 and 3 accept (a) a HB from 1 whereas 4, 5 donate (d) a HB to 1 according to the patterns encoded in the superscripts; bars denote a counterphase stretching of the corresponding HB.

In the same spirit, the second shell can be included after extending this tetrahedron by attaching a second tetrahedron via a HB to one of the corners of the former, i.e., with the additional water molecules 6, 7, and 8 being hydrogen bonded to 2. Using the introduced labeling the following intermolecular tetrahedron modes

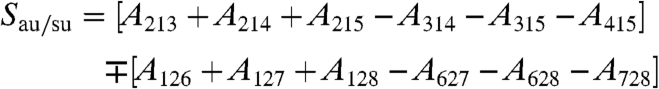[9]

are constructed which antisymmetrically/symmetrically correlate the umbrella motion (au/su) of the two tetrahedra with respect to the interconnecting HB axis. The corresponding spectral densities of these modes, 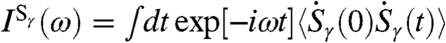, are obtained as usual from the mode velocities, 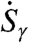. Note that these procedures are related in spirit to, but clearly different from, earlier analysis techniques (29–31).

Results and Discussion

Spatial Unfolding of Computed IR Spectra.

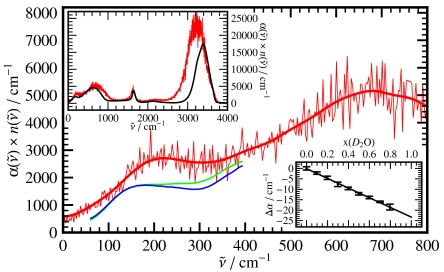
In Fig. 1 we compare the IR spectrum computed for (light) liquid water to experimental data, 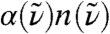, as a function of frequency in wave numbers 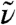. To emphasize the statistical quality of the presented results we show the raw spectrum obtained from AIMD without applying any additional smoothing or signal extraction algorithm. As expected, the overall agreement is promising on the frequency and intensity scales set by the full spectrum (upper inset), apart from the well known red-shift (30) of the intramolecular OH-stretching band at high frequencies. More importantly, the difference between measured and computed H₂O peak maximum of the 200 cm^-1 resonance and the subsequent minimum both amount to ≈40 cm^-1 (main) so that close accord is observed also at low frequencies where intermolecular motion determines the spectrum. In order to carefully assess the impact of quantum effects on liquid water in the THz frequency regime the experimental H₂O spectrum is compared to that of pure heavy water (main). The differences are rather small and mainly sharpen up the peak around 200 cm^-1 for H₂O. In addition, we explore possible influences of anomalous quantum behavior of isotopic mixtures of liquid water (38) by precise measurements of the change in THz absorption 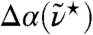of H/D isotopic mixtures as a function of D₂O concentration at a fixed frequency interval centered at 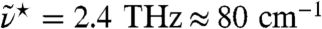(lower inset). Within our experimental accuracy the recorded absorption changes turn out to be linear with increasing D₂O mole fraction. Altogether, these experiments validate the basic approximation of using classical mechanics in conjunction with Eq. 1 in order to simulate the dynamics of liquid water for the purpose of the analyses to follow.

Fig. 1.

Absolute experimental THz absorption spectra, 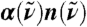, for H₂O (blue) and D₂O (green) at 20 °C from Fourier transform spectroscopy compared to the AIMD H₂O spectrum (red) obtained from Eq. 1; thick red line shows smoothened AIMD data to guide the eye. In the upper inset the full AIMD IR spectrum, 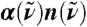, is compared to the standard experimental H₂O data (23). For mixtures of light and heavy water with increasing mole fraction of heavy water, x(D₂O), the change in absorbance with respect to pure H₂O, 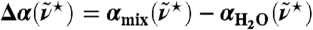, is shown in the lower inset at 20 °C; The difference of the integrated THz absorption coefficient between 2.1 and 2.8 THz (centered at 2.4 THz) was measured as a function of D₂O fraction (see Methods). 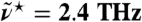≈80 cm^-1.

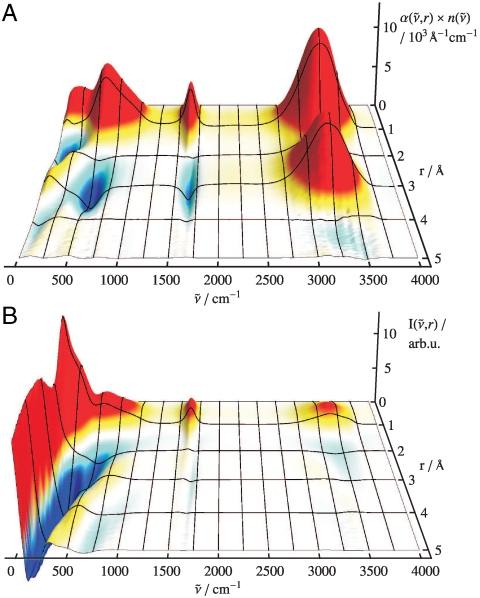
Secondly, the radially resolved spatial decomposition of 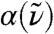, i.e., 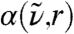as introduced in Eq. 5, reveals pronounced distance-dependent correlations and anticorrelations as a function of frequency 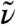according to Fig. 2A. Notably, and in accord with Eq. 5, the total IR absorption spectrum as shown in Fig. 1 is restored from Fig. 2A upon integration along the correlation distance r. In the decomposed spectrum the positive auto-correlations seen for about r < 1 Å are found to dominate the IR spectrum at all frequencies, whereas distinct frequency-dependent cross-correlations are observed beyond. Motions of the nearest-neighbors up to r ≈ 3.5 Å around a given water molecule at r = 0 Å induce dipole cross-correlations within the first solvation shell in qualitative accord with earlier observations (31). Note that the computed center-of-mass radial distribution function g_com(r) has its first intermolecular maximum and minimum at r ≈ 2.7 Å and ≈3.3 Å, respectively, and a second maximum at ≈4.4 Å. For the OH-stretching band around 3,200 cm^-1 a strong correlation peak is observed in the IR spectrum with a maximum close to ≈3 Å, followed by a faint anticorrelation around 4.5 Å. Joint analysis of the corresponding vibrational correlations in (B) can reveal its nature: the radially-resolved IR spectrum in (A) includes the electronic contributions to cross-correlations via the (fully polarizable) water dipoles obtained from Wannier analysis of the electronic degrees of freedom, whereas the radially-resolved vibrational density of states in Fig. 2B is exclusively sensitive to the underlying motion of the atom positions. This one-to-one comparison discloses that at 3,200 cm^-1 there is almost no correlated particle motion for separations exceeding about r ≈ 1 Å, whereas pronounced dipole correlations do exist in the first shell followed by weak anticorrelations in the second shell. Notably, the positive (red) and negative (blue) dipole correlations observed in Fig. 2A in the first shell, r ≈ 3 Å, at the intramolecular vibrations, i.e., at ≈3,200 and 1,650 cm^-1 respectively, vanish upon replacing the full electronic structure as embodied in the Wannier representation by classical point-charge electrostatics. This finding clearly supports that the observed dipole correlations in the first solvation shell are largely imprinted by correlated electronic polarization effects and not due to correlated particle motion at intramolecular frequencies. This result not only supports earlier findings (39, 40) concerning the OH-stretching IR band (where this mode, however, is termed delocalized or collective) but also provides the space-resolved decay of both the underlying dipole and particle correlations.

Fig. 2.

(A) Top: Radially-resolved IR absorption spectrum, 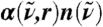, of liquid H₂O from AIMD obtained from Eq. 5. (B) Bottom: Corresponding radially-resolved vibrational correlations, 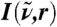, see text.

This picture changes drastically at lower frequencies, i.e., in the domain where intermolecular motion dictates the dynamics and thus the spectra. Below about 1,000 cm^-1 the very broad IR bands in Fig. 2A feature significant negative cross-correlations in the first solvation shell and possibly also in the second shell below 100 cm^-1. Even more pronounced is the spatial extent of concerted particle motions that contribute to the vibrational cross-correlations, i.e., for r > 1 Å, which can be both strongly positive and negative on the scale of several Angstroms into the bulk according to Fig. 2B. This result not only indicates a qualitative change of mechanism but clearly quantifies the collective nature and delocalized character of these low-frequency modes, which are shown here to involve systematic correlations of particle motion beyond the first solvation shell. This scenario is distinctly different from the purely intramolecular vibrational motion revealed in Fig. 2B for frequencies above 1,000 cm^-1, where the longer-ranged correlations clearly detected in the radially-resolved IR spectrum in Fig. 2A are induced by coupled fluctuations of the electrons at neighboring water molecules.

Contributions of Solvation Shells to IR Absorption.

In order to understand this qualitatively different behavior in the intramolecular vs. intermolecular frequency windows, the distance-dependent IR absorption coefficient, Eq. 7, is employed, where the dipole fluctuations of all molecules within a smooth sphere of a fixed but arbitrary radius R₀ contribute to the IR signal. This analysis therefore not only includes the self-correlations of all water dipoles around a reference molecule up to R₀ but all their cross-correlations as well. This complements the results shown in Fig. 2A, where dipole auto-correlations (r → 0) are separated from the cross-correlations (r≫0). The integral 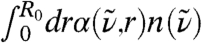of the data shown in Fig. 2A may be compared to 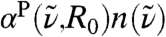, however it must be noted that in the limiting case 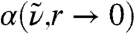describes the local dipole density spectrum of an average point in space, while 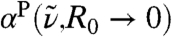describes the proper single molecule limit. Since both quantities yield the same total spectrum 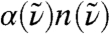for 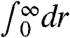and as R₀ → ∞, respectively, the approach to this limit must be different. Both spectral decompositions therefore provide rather independent information and can only be compared with care.

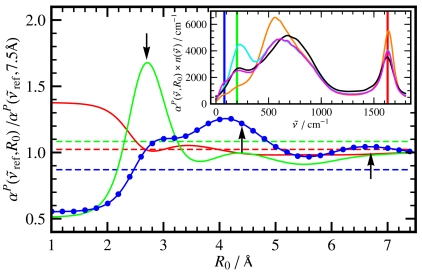
The IR spectra 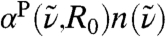feature a strong and nonmonotonic intensity modulation as a function of R₀, see inset of Fig. 3, which is found to exceed the correlations within the first solvation shell depending on frequency. In particular, the IR peak around 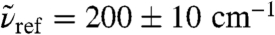displays a steep maximum at R₀ ≈ 2.7 Å corresponding to the first solvation shell according to the center-of-mass radial distribution function, g_com(r), followed by an only weakly modulated and mild increase beyond, approaching the bulk value for large R₀ as shown in the main plot of Fig. 3.

Fig. 3.

Relative intensities from distance-decomposed IR absorption spectra, 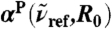of liquid H₂O from AIMD obtained from Eq. 7, as a function of R₀ at selected reference frequencies 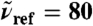(blue, dots), 200 (green), and 1,630 cm^-1 (red) integrated within a window of 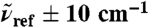. The intensities are shown relative to the distance-decomposed absorption intensity at R₀ = 7.5 Å, i.e., 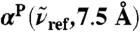, where n(80 cm^-1)α^P(80 cm^-1,7.5 Å) = 1,335 cm^-1, n(200 cm^-1)α^P(200 cm^-1,7.5 Å) = 2,654 cm^-1, n(1,630 cm^-1)α^P(1,630 cm^-1,7.5 Å) = 4,124 cm^-1. Vertical arrows mark the successive maxima of the center-of-mass radial distribution function, g_com(r), stemming from contributions due to first, second, and third solvation shell. Horizontal dashed lines mark the usual integrated intensities obtained in the bulk, i.e., 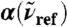obtained from Eq. 1 again relative to 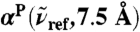, corresponding to 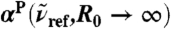for infinitely large systems. Inset: Overview 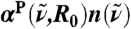spectra as a function of 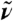at selected distances R₀: R₀ → 0 (single molecule limit, orange), R₀ = 2.7 Å (cyan), 4.1 Å (magenta), and R₀ → ∞ (bulk limit, black). The vertical bars indicate the frequency windows used in the main figure with the same color code.

The second frequency window, 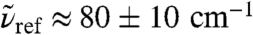, is selected based on the results of previous studies in which the absorption at 2.4 THz ≈ 80 cm^-1 revealed long-range effects in solvation dynamics of various molecules using THz laser spectroscopy (18, 20). Most interestingly, the distance-resolved IR spectra, 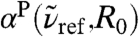, uncover a strong and long-ranged spatial modulation at 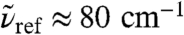where no peak can be discerned in the bulk absorption spectrum, , see Fig. 1. In stark contrast to the 200 cm^-1 resonance, the distance-dependent absorption at about 80 cm^-1 is characterized by a shoulder at the first shell whereas the most pronounced absolute absorption is observed close to the second solvation shell as heralded by a significant and broad maximum at about R₀ ≈ 4.1 Å. One can even detect the onset of another modulation of 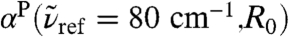around R₀ ≈ 6.7 Å which coincides with the third solvation shell according to the third maximum of the g_com(r). The intensity ratio between the maximum value found in the second shell and the bulk value, i.e., 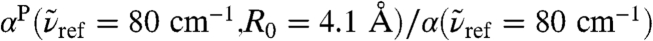, features a clear increase in the interfacial region with respect to the bulk limit. Although this result cannot be compared directly for obvious reasons, it is noted that a similar absorbance increase has been measured by THz laser spectroscopy at 2.4 THz ≈ 80 cm^-1 around solvated molecules (18, 20) and ascribed to an “extended dynamical solvation shell” (20). Overall, the long-ranged modulation of the distance-dependence in the THz frequency domain, stemming from intermolecular modes, is distinctly different from the essentially monotonous behavior as observed for intramolecular modes in the IR regime, as exemplified for the bending mode at ≈1,630 cm^-1. This confirms our statement that the THz regime requires new concepts and cannot be described by those known from the infrared.

Characterizing Intermolecular Modes in the THz Domain.

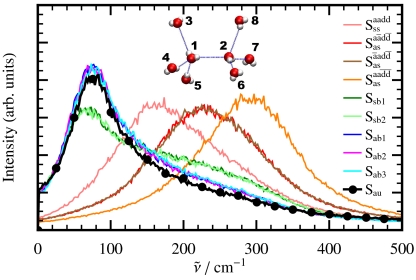
Having explicitly demonstrated that the 200 cm^-1 resonance is dominated by particle motion within the first solvation shell, the vibrational density of states corresponding to the tetrahedral S_γ coordinates as defined in Eq. 8 are used to analyze this band in Fig. 4. As expected, based on a multitude of previous analyses, this band is dominated by stretching motions of HBs. Here, we characterize these motions systematically in terms of symmetric stretching S_ss at the lowest frequency ≈160 cm^-1, antisymmetric stretching 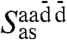due to counterphase stretching motion of the two donor vs. acceptor HBs at the highest frequency ≈290 cm^-1, and two degenerate antisymmetric stretches and 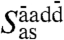at intermediate frequency around 220 cm^-1 which involve counterphase donor and acceptor motion; the two modes at ≈220 cm^-1 are estimated to contribute most to the IR activity followed by the lower-lying symmetric stretch while the highest antisymmetric mode at 290 cm^-1 appears to be essentially silent. Thus, the distinct HB donor/acceptor topologies accessible in first solvation shells due to HB fluctuations occurring on the picosecond time scale imprint their signature on the frequencies of vibrational motion involving the first nearest-neighbors and contribute to the broadness of the measured 200 cm^-1 resonance in view of their different average frequencies. In addition to the four stretches, the remaining five modes are due to HB bending motion. They all peak significantly between 75–80 cm^-1 but they also feature extended tails deep into the 200 cm^-1 resonance; permuting the donor/acceptor ordering results in similar spectra. In conjunction with the previous distance-dependent analysis of the IR absorption coefficient, see Fig. 3, we can associate the stretching modes to be responsible for the pronounced maximum at ≈2.7 Å of the 200 cm^-1 peak and the bending modes for the first-shell shoulder detected at .

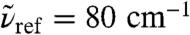Fig. 4.

Power spectra 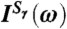of the nine tetrahedral HB stretching and bending modes and of the antisymmetric umbrella mode as defined in the text; scheme and inset define labeling in Eqs. 8, 9.

Still, the major contribution around 80 cm^-1 must come from motion involving the second solvation shell according to the 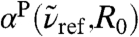analysis. The antisymmetric umbrella mode, S_au, which involves two HB tetrahedra interconnected via a HB as defined in Eq. 9 and sketched in Fig. 4, accounts for second-shell motion and features a pronounced resonance around 80 cm^-1 in the power spectrum. Note that the symmetric umbrella motion, S_su, leads to a similar resonance, which is however broader with a tail towards higher frequencies due to more pronounced couplings to stretching-like deformations. Cross-correlating the S_au mode with its local dipole demonstrates that its integrated contribution to the total IR activity is indeed very weak, which is consistent with the lack of any resonance around 80 cm^-1 in the integrated IR spectrum, see Fig. 1. Combining these findings, we assign the long-range distance-dependent modulation of the IR intensity at 80 cm^-1 ≈ 2.4 THz in Fig. 3 to be dominated by relative motion of two hydrogen-bonded water tetrahedra. This finding might explain the rich modulation of absorption intensities uncovered by THz laser spectroscopy of solvated molecules (18, 20) at this particular frequency.

Summary, Conclusions, and Outlook

THz spectroscopy of aqueous solutions has been shown of late to provide a stimulating experimental perspective on the dynamics of interfacial water molecules, for instance hydration water around biomolecules. At variance with traditional IR spectroscopy, which draws on the strength of well defined intramolecular (normal or local) modes and thus harmonic analysis, e.g., in the fingerprint region, low-frequency bands in the THz domain are typically extremely broad and void of features due to rather complex intermolecular motion dominated by anharmonicity. Based on AIMD simulations of liquid water, H₂O, we provide insights into the underlying nature of the absorption of bulk water at THz frequencies. Our results offer a firm microscopic understanding of the ability of THz spectroscopy to probe the collective dynamics of water molecules on a spatial scale spanning several solvation shells. The study also shows that the traditional IR spectra at frequencies above 1,000 cm^-1 and THz spectra are governed by distinctly different mechanisms. While the underlying vibrations of the former show no significant correlation in particle motions beyond the first solvation shell, but a pronounced coupling of electronic origin, strongly correlated particle motion dominates at THz frequencies. This peculiar behavior can point towards the significance of solvent dynamics in the THz regime for the influence on large amplitude fluctuations of proteins.

Space-resolved analyses of spectra and vibrational motion confirm at high frequencies pronounced correlations mainly within the first solvation shell that are dominated by intramolecular motion and induced electronic polarization of close-by neighbors. In stark contrast, the correlation length is shown to extend beyond nearest-neighbors in the THz domain, thus involving the second and even third solvation shell. Decomposition of particle motion in terms of symmetry-adapted coordinates inspired by a tetrahedral coordination model of water shows that the four HB stretching modes contribute to the resonance around 200 cm^-1 at three distinct frequencies depending on the particular HB donor/acceptor pattern. The remaining five tetrahedral HB bending modes all yield pronounced maxima at ≈80 cm^-1 whereas their tails extend deep into the 200 cm^-1 peak.

The introduced distance-dependent absorption cross section is found to be characterized by strong intensity modulations that depend crucially on the probe frequency. Indeed, the strongest contribution to the 200 cm^-1 peak is shown to come from the first solvation shell in agreement with the assignment to intermolecular HB stretching modes. At variance, the main contribution to the intensity around 80 cm^-1 is shown to stem from motion within the second solvation shell; the data even indicate the presence of nonnegligible third shell effects. This dynamics is well captured by umbrella-like displacements of two HB tetrahedra with respect to their interconnecting HB axis, thus involving concerted motion of second-nearest-neighbors. Most importantly, although these modes around 80 cm^-1 ≈ 2.4 THz neither lead to a peak nor to a significant shoulder in the IR spectrum and have therefore initially been underestimated in their importance, they do induce a very characteristic modulation of the absorption intensity in space, i.e., a spatial response. One is tempted to speculate that this distinct modulation could be the mechanism that allows THz spectroscopy to sensitively detect changes of the solvation behavior from small molecules to proteins undergoing folding, which is the topic of future research. The analysis approach established here for liquid water can be generalized to probe the hydration shell dynamics around solvated molecules including small biomolecules.

Methods

The AIMD simulations (33) have been carried out using the CP2k package with Born-Oppenheimer propagation generated via the Quickstep electronic structure module (41). The Perdew-Burke-Ernzerhof (PBE) functional has been employed together with dual-space norm-conserving pseudo potentials (42) in conjunction with plane waves up to 400 Rydberg and a TZV2P basis set (41) to expand density and orbitals, respectively. A sample of 128 H₂O molecules in a cubic ≈15.6 Å supercell corresponding to 1 g/cm³ has been used. The system was equilibrated at ambient conditions using massive Nosé-Hoover chain thermostatting (33) at a rescaled temperature of 400 K to approximately counterbalance the systematic underestimation (43) of temperature by about 20%–30% when using PBE. Sixteen statistically independent initial conditions were then sampled from a 90 ps canonical simulation to initialize microcanonical trajectories of 20 ps length using a time step of 0.5 fs. Every 2 fs the maximally localized Wannier functions have been computed (see Sec. 7.2.4 in ref. 33) and molecular dipole moments μ_I(t) (assigned to the center-of-mass R_I(t)) were constructed using the Wannier centers (see Sec. 7.2.6 in ref. 33). To obtain spatially-resolved IR absorption spectra and vibrational density of states, the local dipole and velocity densities according to Eq. 3 have been computed on a cubic grid with a spacing of 0.489 Å using a regularization parameter σ of 0.4 Å. The corresponding data shown in Fig. 2 have been smoothened in the frequency domain via convolution with a Gaussian filter with . The sharpness parameter was set to D = 0.25 Å in order to compute the distance-dependent absorption according to Eq. 7. All data shown have been averaged over all NVE trajectories thus yielding canonical averages.

The THz laser spectroscopy experiments have been performed as described earlier (20), whereas the Fourier transform far IR measurements have been carried out using the Bruker VERTEX 80v FTIR spectrometer with diamond window sample cells and a sample thickness of 44 μm. The data evaluation has been performed as described in detail in ref. 44; the refractive indices 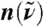of H₂O and D₂O are tabulated in ref. 22. For each H₂O/D₂O concentration, three independent samples were prepared followed by three independent measurements each at a constant temperature of (20 ± 1) °C.