Metabolic cost as a unifying principle governing neuronal biophysics

Abstract

The brain contains an astonishing diversity of neurons, each expressing only one set of ion channels out of the billions of potential channel combinations. Simple organizing principles are required for us to make sense of this abundance of possibilities and wealth of related data. We suggest that energy minimization subject to functional constraints may be one such unifying principle. We compared the energy needed to produce action potentials singly and in trains for a wide range of channel densities and kinetic parameters and examined which combinations of parameters maximized spiking function while minimizing energetic cost. We confirmed these results for sodium channels using a dynamic current clamp in neocortical fast spiking interneurons. We find further evidence supporting this hypothesis in a wide range of other neurons from several species and conclude that the ion channels in these neurons minimize energy expenditure in their normal range of spiking.

The mammalian genome contains genes encoding hundreds of types of ion channels, most of which can be produced in multiple splice variants and regulated at multiple phosphorylation sites by numerous intrinsic and extrinsic factors (1–4). Which combination of these ion channels will be expressed by any particular neuron, with any particular computational or behavioral role? Because any given electrical phenotype can be produced by many combinations of ion channels (5–8), on functional grounds alone, this question is severely underconstrained. What other constraints might govern ion channel expression? And can exploring these constraints help us understand how cells or circuits are constructed?

Energy consumption may be one such constraint. The brain is one of the most energetically demanding organs in the body (9, 10); the human brain uses more than twice as much glucose per day as the heart (10). Neuronal activity—action potential generation, input integration, and synaptic transmission—accounts for 50–80% of this energy use (11–14). Potential energy is stored in transmembrane ion gradients, which creates a cellular battery whose maintenance accounts for most of the brain's ATP consumption (11, 13, 15, 16). Action potential generation taps into these gradients and expends some of this potential energy, which needs to be actively restored. How can this energy be most efficiently used to generate activity or carry out computation?

This question has inspired a body of research on how to encode a signal, or perform a computation, using as few action potentials—and thus as little energy—as possible (17–24). Which combinations of ion channels will minimize energy cost depends both on the neuron's function, such as its typical firing rate, as well as on the detailed kinetics of the channels (25). Here, we combine biophysical modeling with dynamic-clamp electrophysiology to understand the constraints on the kinetics and density of the ion channels underlying action potential generation. We find that ion channel expression in various species, neural structures, and cell types supports the hypothesis that they may be constrained to minimize energy use, subject to functional requirements.

Basics of Action Potential Generation.

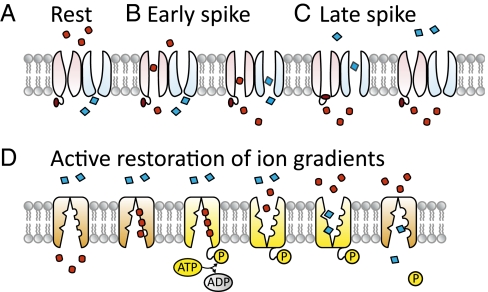
The Hodgkin–Huxley model of action potential generation uses fast voltage-gated sodium (Na⁺) channels, delayed rectifier potassium (K⁺) channels, and voltage-independent (“leak”) potassium channels. At rest (Figs. 1A and 2A-1), the cell's batteries are already charged—Na⁺ ions are more concentrated outside the cell than inside (Fig. 1, red ovals), whereas K⁺ ions (Fig. 1, blue diamonds) are more concentrated inside the cell than outside. The action potential is triggered when modest depolarization (Fig. 2A-2) causes the sodium channels’ activation/deactivation gates (“m” gates, Fig. 2B, light red) to enter the “open state” (Fig. 1B). This increases the membrane's permeability to Na⁺ ions (Fig. 1B; Fig. 2C, red), permitting Na⁺ ions to passively flow down their concentration gradient and enter the cell. This influx of positive charge (Fig. 2D, red) depolarizes the membrane, bringing the membrane potential up to the Na⁺ ions’ reversal potential, ∼50 mV (Fig. 2A-3).

Fig. 1.

(A) At rest, both sodium channels (light red) and K⁺ channels (light blue) are closed, Na⁺ ions (red ovals) are concentrated extracellularly, and K⁺ ions (blue diamonds) are concentrated intracellularly. (B) Depolarization causes Na⁺ channels to open, permitting Na⁺ ions to flow down their concentration gradients into the cell. This influx of positive charge depolarizes the neuron. (C) This depolarization causes K⁺ channels to open, letting K⁺ leave the cell, hyperpolarizing the membrane potential; at the same time, depolarization causes Na⁺ channel inactivation gates (dark red ball and chain) to close, limiting Na⁺ influx. Eventually the hyperpolarization is sufficient to close and deinactivate the Na⁺ channels and close the K⁺ channels, restoring the channel states to baseline. (D) The Na⁺ influx and K⁺ efflux are reversed by the Na⁺,K⁺ ATPase.

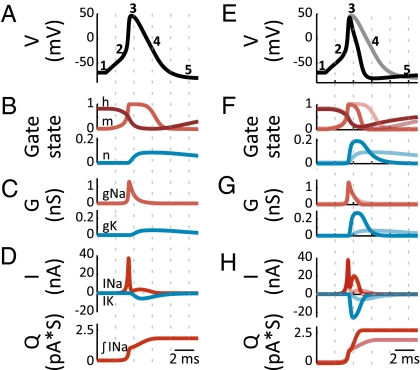
Fig. 2.

(A and E) Voltage waveforms. (B and F) Gate states. Light red, “m” (Na⁺ channel activation) gate; dark red, “h” (Na⁺ channel inactivation) gate; blue, “n” (K⁺ channel activation) gate. 1 = fully open, 0 = fully closed or inactivated. (C and G) Na⁺ (red) and K⁺ (blue) conductances. (D and H) (Upper) Na⁺ (red) and K⁺ (blue) currents; (Lower) cumulative Na⁺ current influx. (Right) The traces from the broad action potential in A–D are overlaid on the corresponding traces from a narrower action potential, generated by tripling the rate of K⁺ channel activation/deactivation.

This strong depolarization triggers the potassium channel activation/deactivation gates (“n” gates, Fig. 2B, blue) to open, increasing the membrane's permeability to K⁺ ions (Fig. 2C, blue), which lets potassium exit the cell (Fig. 2D, blue). This efflux of K⁺ ions competes with the influx of Na⁺ ions to control the membrane potential; the net effect is to hyperpolarize the neuron (Fig. 2A-4). At the same time, the sodium channels’ inactivation gates (“h” gates, Fig. 1C; Fig. 2B, dark red) begin to block the sodium channels, slowly reducing the membrane's sodium permeability. Eventually, sufficient hyperpolarization causes the m and n gates both to enter the deactivated state, (Fig. 2 A-5 and B), bringing the membrane's sodium and potassium permeability back to baseline levels.

These changes in gate states, channel conductances, and current flow were fueled by the energy stored in the cell's Na⁺ and K⁺ gradients: No ATP was expended during the generation of the action potential itself. These gradients are now partly run down and must be actively restored. The sodium-potassium pump (Na⁺,K⁺ ATPase) is primarily responsible for this restoration. It imports two K⁺ ions and extrudes three Na⁺ ions (Fig. 1D), at the cost of one ATP. There is thus a direct relationship between the number of Na⁺ ions that enter the cell during action potential generation and the energy cost of recovering from the action potential.

Spike Cost and Spike Rate.

The ionic currents underlying the action potential are plotted in Fig. 2D Upper, and the cumulative Na⁺ influx is plotted in Fig. 2D Lower. Note that action potential repolarization (between times 3 and 5), not just depolarization (between times 2 and 3), accounts for a substantial portion of this Na⁺ influx. Intuitively, this occurs because during depolarization, sodium conductance far exceeds potassium conductance. Sodium entry during depolarization is thus approximately limited to what is required to charge the cell's capacitance. But during repolarization, both sodium and potassium channels are open and sodium enters the cell at the same time that potassium exits the cell. These fluxes mostly cancel each other, so that only a small part of the charge exchanged goes into changing the cell's membrane potential.

Second, note that the duration of this repolarization, and thus the duration of the action potential itself, limits the rate at which the neuron can spike. Partial sodium channel deinactivation is required to replenish the pool of sodium channels available for action potential generation, and this deinactivation can occur only when the membrane is sufficiently hyperpolarized. Indeed, narrowing the action potential by tripling the rate of potassium channel activation (detailed in Fig. 2 E–H) does increase the rate at which the model neuron is able to spike (Fig. 3A). However, because sodium channel inactivation accumulates slowly, sodium channels are less inactivated earlier in the action potential. If potassium channels activate earlier, sodium and potassium conductances will overlap more extensively (Fig. 2G). Earlier hyperpolarization will therefore be opposed by a greater sodium current flow, increasing the total Na⁺ influx during repolarization and thus increasing the metabolic cost of the action potential (Fig. 2H). These two factors thus imply a trade-off between the energy cost of action potential generation, particularly repolarization, and neurons’ functional capacity—their ability to spike rapidly or their bandwidth.

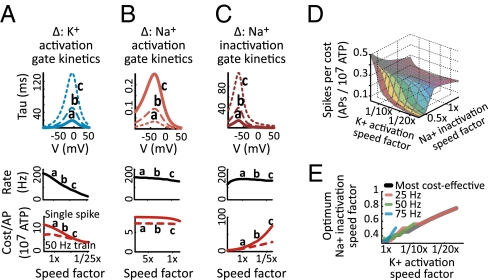
Fig. 3.

(A–C) (Top) Time constants as a function of membrane potential. Gate kinetics were systematically speeded or slowed by multiplying the time constants at all voltages by the same constant speed factor. (Middle) Maximum spike rate as a function of speed factor. (Bottom) Cost (in ATP) for a single action potential (solid line) or for an action potential in a 50-Hz train (dashed line) as a function of speed factor. (D) Maximum number of spikes per 10⁷ ATP (z axis) as a function of n-gate speed factor (x axis) and h-gate speed factor (y axis and surface color). (E) Na⁺ channel inactivation speed factor that maximizes the spikes/cost, for spikes generated as efficiently as possible (black) and for spikes generated in 25-, 50-, and 75-Hz trains (red, green, blue).

Kinetics, Rates, and Costs.

For the model shown in Fig. 3A, systematically speeding (curves and points on curves labeled “a” in Fig. 3A) or slowing (curves and points on curves labeled “c” in Fig. 3A) the time constants of potassium channel activation speeds or slows the maximum action potential rate. Both for single action potentials (solid lines in Fig. 3A) and for action potentials generated in trains (50 Hz shown, dotted lines in Fig. 3A), faster K⁺ channels increase Na⁺ influx—and thus increase energy cost—and slower K⁺ channels decrease Na⁺ influx and energy cost. In other words, although fast-activating potassium channels do give cells the ability to spike quickly, this increased bandwidth comes at a cost, and this cost must be paid every time the neuron generates any action potential. This result implies that neurons whose computational role does not require the ability to spike quickly need not pay this cost to perform their function. We thus predict that naturally slow-spiking neurons should not express fast-activating potassium channels.

Are there other strategies that cells might adopt to achieve the fast-spiking phenotype? And how metabolically expensive are they? This minimal model has two other gates, whose kinetics may be varied. Faster sodium channel activation/deactivation (i.e., faster m gates) somewhat increases the rate at which neurons can spike, with almost no effect on metabolic cost (Fig. 3B). Intuitively, this occurs because the total Na⁺ influx during the upstroke of the action potential is nearly independent of sodium channel activation speed, because during this period the sodium conductance depolarizes the cell without significant opposition. The contribution of sodium channel deactivation to Na⁺ influx during the action potential downstroke is also relatively small—by the time that the cell has hyperpolarized enough to cause m gates to reenter the closed state (deactivation), the sodium current is sufficiently inactivated (h gate) to keep the sodium current low, irrespective of how long this transition takes.

Differences in sodium channel inactivation/deinactivation (i.e., faster h gate) kinetics also have little effect on the rate at which neurons can spike, outside of the degenerate range in which inactivation occurs too quickly for the neuron to support action potential generation (Fig. 3C). However, faster sodium channel inactivation limits the degree to which sodium and potassium currents overlap during repolarization, limiting waste current; slower inactivation increases this overlap, increasing waste. These differences thus have an enormous effect on action potential cost. This implies that to minimize metabolic cost (while preserving the ability to spike quickly) sodium current inactivation must occur as fast as possible, outside of the degenerate range. This relationship between τ_n, τ_h, and metabolic efficiency (i.e., spikes per ATP) is characterized in Fig. 3D. Note that optimum inactivation rate—the point at which inactivation becomes too fast to sustain spike generation—varies with potassium channel activation speed: If potassium channels activate more slowly, the speed of sodium channel inactivation must be reduced, so that sodium-mediated depolarization still lasts long enough to activate the potassium channels. Conversely, if potassium channels activate more rapidly, then sodium channels must also inactivate rapidly to minimize waste current. The sodium inactivation speed that minimizes cost per spike is a linear function of potassium activation speed, both when action potentials are generated as fast as possible and when they are generated at a given rate (Fig. 3E). This is another prediction of the model.

Densities, Rates, and Costs.

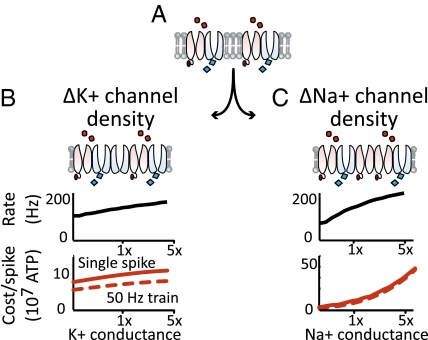
Cells can also express different densities of the same ion channels. Does changing channel density permit rapid action potential generation, and, if so, at what cost? Increasing potassium channel density, like speeding potassium channel kinetics, increases the rate at which a cell can spike by narrowing its action potential, with a roughly proportional increase in the cost per action potential (Fig. 4B). Conversely, increasing sodium conductance also increases the rate at which a cell can spike, but without narrowing action potentials (Fig. 4C). Instead, increased sodium conductance reduces the refractory period by decreasing the voltage threshold for spike generation, allowing spikes to be generated even when a smaller proportion of the total sodium conductance is available. However, the combination of wider action potentials with increased sodium flow at each stage of the action potential makes this an expensive strategy.

Fig. 4.

The default membrane Na⁺ and K⁺ channel densities (A) can be changed by adding or removing K⁺ channels (B Top), or by adding or removing Na⁺ channels (C Top). (B and C) (Middle) Maximum spike rate as a function of channel density. (B and C) (Bottom) Cost (in ATP) for a single action potential (solid line), or for an action potential in a 50-Hz train (dashed line), as a function of speed factor.

These relationships between metabolic cost, functional capabilities, and channel kinetics and density allow us to make predictions about what biophysical strategies cells with different firing properties will adopt, if their aim is to minimize metabolic cost and meet their functional requirements. But these trade-offs are derived from a greatly reduced model, whereas real neurons are morphologically complicated and contain numerous, diverse voltage-gated channels. It is therefore unclear to what extent we should expect these relationships to hold in real neurons. Two factors make this question difficult to address experimentally. First, in real neurons, individual channel or gate kinetics cannot be systematically varied, which makes parameter sweeps impossible. Further, in any given neuron, one cannot simultaneously measure the voltage response to a given current input and reverse engineer the contributions of different ionic currents to this response, which complicates estimation of energy costs.

Rate and Costs in Real Neurons.

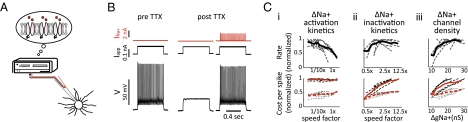
Both problems can be resolved using dynamic voltage clamping. In a dynamic clamp, a computer is reciprocally connected to a neuron through an amplifier. At each time step, the computer reads the cell's membrane potential from the amplifier, calculates how much current would be flowing through the simulated conductance at that membrane potential, commands the amplifier to apply that amount of current, and updates the state of the simulated conductance (Fig. 5A). We first blocked cells’ intrinsic voltage-gated sodium channels with tetrodotoxin (TTX) and then used a high-speed dynamic clamp to reinsert simulated sodium channels, modeled using the same equations as in our parameter sweeps above (Fig. 5). Of all of the ion channels in a cell the sodium channel has the fastest time constants, which requires a comparably fast dynamic clamp.

Fig. 5.

(A) Dynamic clamp schematic: A computer (left), simulating a voltage-gated sodium conductance is reciprocally connected to a neuron (right). The cell's voltage determines the driving force on the simulated conductance and thus the current command sent to the amplifier; at each time step, the dynamic clamp computer uses the cell's voltage to update the state of its sodium conductance model. (B) Intracellular recording of a fast-spiking interneuron showing its ability to generate fast, nonadapting trains of action potentials. TTX application (Middle) blocks action potential generation. Dynamic clamp restoration of sodium conductance (Right; command current in red) permits the neuron to generate fast, nonadapting trains of action potential-like waveforms. (C) Maximum spike rate (Upper) and spike cost (Lower) as a function of Na⁺ channel activation rate (i), inactivation rate (ii), and channel density (iii). Black traces, average of normalized values for all cells; gray traces, normalized values for each cell.

After sodium channel replacement, cells could generate action potential-like waveforms in response to depolarizing current steps. The upsweeps of these waveforms were generated by the user-defined, artificial sodium conductances—but the repolarization was mediated by the cell's own potassium channels, whose kinetics, densities, positions, and diversity were unchanged. “Sodium” influx was now measurable, simply by tracking the amount of current injected by the dynamic clamp system over time. Because the simulated sodium current had user-definable kinetics and density, it was now possible to systematically alter the kinetics of the underlying modeled gates and the density of the modeled channels. This dynamic clamp enabled parameter sweeps over sodium channel properties, in real neurons, similar to those performed in the model. We were thus able to test how similar the relationships between sodium channel properties, cellular function, and energy cost, observed in our simple model, were to the relationships among these factors found in real neurons.

We found that both modeled and real neurons displayed qualitatively similar relationships between sodium channel properties, bandwidth, and metabolic cost (Fig. 5C). Faster-activating sodium channels moderately increased the rate at which cells could fire, with little effect on action potential cost (Fig. 5C, i); faster-inactivating sodium channels had little effect on the rate at which cells could fire, but decreased spike cost (Fig. 5C, ii); and increased sodium current density increased the rate at which cells could fire, but increased spike cost (Fig. 5C, iii). We thus conclude that the trade-offs between kinetics, rates, and cost that we observed in the model are robust to variations in channel kinetics, voltage dependence, and subcellular localization and are therefore likely to hold in real neurons. We propose that if the energy cost of action potential generation is a constraint on brain volume, coding strategy, or computational capacity, then cellular ion channel expression will be optimized not merely to achieve function, but also to achieve function while minimizing metabolic cost; and that if this is the case, then ion channel expression patterns will obey the trade-offs predicted by our model and experiments.

Comparisons Across Cell Types, Structures, and Species.

We found two biophysical strategies, speeding potassium channel activation and increasing the sodium conductance density, which could strongly increase the rate at which neurons were able to fire. Both strategies also increased the energy cost of action potential generation. But the two strategies were very different in their energy efficiency: Doubling a cell's maximum spike rate from 100 to 200 Hz by speeding potassium channel activation roughly doubles the energy cost per spike, but doubling the rate by adding sodium conductance multiplies the energy cost per spike by a factor of 20. We therefore predict that cells with higher spike-rate requirements will fulfill these requirements by expressing faster potassium channels and not by expressing more sodium channels. Further, because faster potassium channels are expensive even in a cell that spikes slowly, we predict that only cells whose operation requires them to be able to spike quickly will express fast potassium channels. This is the principle of minimally acceptable bandwidth. Many brain regions contain multiple cell types with different in vivo spike rates, from which we can infer differences in their functional or bandwidth requirements. Do faster-spiking neurons achieve these spike rates through faster-activating potassium channels or through greater expression of sodium channels?

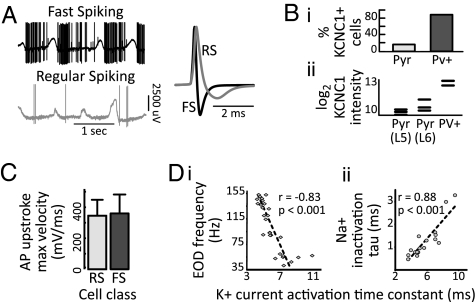
In the cerebral cortex, parvalbumin-positive (Pv+) interneurons are tonically active at comparatively high rates, whereas regular-spiking pyramidal neurons spike relatively infrequently and irregularly (Fig. 6A). The faster spiking neurons display far narrower action potentials—to the degree that Pv+ neurons are one of only a few cell types identifiable in extracellular recording. These action potentials are made narrow specifically by the expression of the fast-activating potassium channel Kv3.1/KCNC1. A far greater proportion of Pv+ interneurons, compared with pyramidal neurons, contain mRNA for KCNC1 (Fig. 6B, i) (26), and KCNC1 RNA levels are 10-fold higher in Pv+ interneurons than in regular spiking Thy1+ pyramidal neurons (Fig. 6B) (27). These neurons do not adopt the dense-sodium strategy to permit fast spiking: In vivo, maximal action potential upstroke velocities, a proxy for available sodium current, are not significantly different between fast- and regular-spiking cortical neurons (Fig. 6C) (28). A similar pattern is found in a wide variety of neural structures. In the hippocampus, neurons that spontaneously fire faster (29) have narrower action potentials (30), mediated by faster-activating potassium currents (31). Similarly, thinner-spiking neurons have higher in vivo firing rates in both the striatum (32, 33) and the amygdala (34–36). In the songbird high vocal center, thinner-spiking neurons have faster spiking rates in vivo (37). In the lateral parabrachial nucleus, central lateral neurons, compared with external lateral neurons, have briefer action potentials mediated by faster repolarization and also far less spike frequency adaptation (permitting comparatively fast sustained spiking), with no difference in rate of rise (38).

Fig. 6.

(A) Action potential rate (Left) and shape (Right) in a thin-spiking interneuron (black) and a regular-spiking neuron (gray) during up and down states in vivo. (B, i) Percentage of pyramidal neurons and PV+ interneurons identified as KCNC1-positive through single-cell PCR. (B, ii) Microarray measurements of KCNC1 RNA levels in pyramidal neurons and PV+ interneurons. (C) Maximum action potential upstroke velocity in regular spiking (RS) and fast spiking (FS) cortical neurons. (D, i) electric organ discharge (EOD) frequency in the electric organ of n = 28 different fish, vs. K⁺ current activation time constant in EOD cells of the same fish (measured at 25 mV above threshold). (D, ii) Na⁺ current inactivation time constant vs. K⁺ activation time constant in n = 17 fish. (A) Adapted from ref. 68. (B, i) Adapted from ref. 26. (B, ii) Adapted from ref. 27. (C) Adapted from ref. 28. (D) [Reproduced with permission from McAnnelly and Zakon (39) (Copyright 2000, Society for Neuroscience).]

Although faster potassium channels can endow a cell with the ability to spike quickly, this ability comes with increased energy cost. The extra cost can be kept to a minimum by speeding sodium channel inactivation, which minimizes the overlap between sodium and potassium conductance opening. But this speeding is beneficial only up to a point, and this point is proportional to potassium conductance activation speed. We thus predict that, all else being equal, cells with faster potassium channel activation kinetics will display faster sodium channel inactivation kinetics.

These comparisons are difficult to make between neurons with different action potential heights, spike thresholds, and resting potentials—i.e., between neurons with sodium channels that experience vastly different ranges of voltage before the repolarizing phase of the action potential. However, we can straightforwardly compare kinetics across neurons with similar prespike and early-spike voltages. An example of an entire family of cells with similar resting membrane potential, action potential height, and spike threshold, but with variable firing rate requirements, is found in the electric organ of weakly electric fish. The electrically active cells (electrocytes) in these fish generate the electric organ discharge (EOD). Each fish generates the EOD at a characteristic frequency, but different fish generate this discharge at different frequencies, spanning a wide range from 50 to 200 Hz, and the same fish may change its frequency with hormonal shifts. In fish with faster EOD frequencies, electrocytes contain potassium channels with faster activation kinetics (39) (Fig. 6D, i). This result can be predicted from functional considerations alone. Yet cells with faster-activating potassium channels, and thus with thinner action potentials, also contain faster-inactivating sodium channels (Fig. 6D, ii). This relationship cannot be predicted from functional constraints alone, because fast sodium inactivation is not required for thin spikes or fast action potential generation. Yet this relationship is required for cells to minimize energy costs subject to functional constraints (i.e., while preserving the ability to spike quickly). Similarly, during development, the calyx of Held develops the ability to spike progressively faster, through progressive speeding of its potassium channel kinetics (as predicted above). During the same period, sodium channel inactivation kinetics become faster (40). Again, this relationship is predicted by mixed functional and metabolic, not purely functional, considerations.

Discussion

Neural tissue is inordinately expensive. Brain ranks behind only heart and kidney in glucose used per gram (10, 41, 42), and the human brain accounts for one-fifth of the body's total energy consumption (43, 44). Much of this cost derives from the essential ongoing neural activity (14, 45, 46) that maintains the circuit context in which sensory processing, planning, decision making, and motor control can occur (46–55). Expensive functions prompt the evolution of expense-minimizing adaptations (56), and energy availability does appear to have constrained the evolution of macroscopic brain features, resulting in minimization of brain volume subject to functional requirements (44, 57–59). We propose that the same principle holds on a microscopic level. One aspect of this optimization involves the kinetics and densities of the ion channels underlying spikes, but this principle may have driven other aspects of ion channel expression. Substantial energy is expended on ion transport in nonspiking neural tissue such as retina (9, 60) and on synaptic and integrative activity in spiking neurons (15, 16, 25, 61–64). If evolution has optimized the expression of the spike- generating ion channels to minimize metabolic cost while preserving spiking bandwidth, perhaps it has also optimized expression of the ion channels involved in subthreshold input integration to minimize metabolic cost while preserving computational ability. This is an extremely general framework for interpreting neurons’ biophysical specializations.

We have not found any data to contradict the broader conclusion that evolution has honed the properties of ion channels and their densities to minimize energy consumption while ensuring sufficient bandwidth to perform necessary computation. This analysis focused on ATP consumption, the coin of the cellular realm, and should not depend on details regarding glucose consumption, such as whether activity-related glycolysis occurs in glia or neurons. The results are also independent of the fraction of energy used for action potential generation, compared with that needed to support other activity-dependent processes such as dendritic integration and vesicle recycling.

The results presented here build on a long tradition of research on optimality in neural signaling (21–23, 44, 65), including more recent studies examining the cost of single action potentials (25, 66). Consistent with prior studies, our results confirm that mismatches between Na⁺ and K⁺ kinetics are likely to be a primary contributor to the cost of action potential generation. Our results extend the previous work in several major ways. First, by using a dynamic clamp, we assessed, in actual neurons, how their diverse ensembles of hyperpolarizing currents interact with simple depolarizing conductances to control spike cost and function. Second, by using Hodgkin–Huxley-style models rather than bulk conductance models (25), we linked our models to the actual biophysical mechanisms—channel gating kinetics and voltage dependence—that could be altered in each cell type to optimize energy cost, and by using dynamic clamp to simulate changes in gating parameters, we confirmed these models’ predictions in real neurons. Third, we considered not only the cost of a single action potential, but also energetic cost in the context of broader functional requirements, such as the ability to support sustained spiking. For example, we showed that high maximum spike rates carry a high metabolic cost. This result implies that neurons that do not need to fire at high frequencies are likely to adopt different solutions to optimization of spike cost. Finally, by examining neurons’ biophysical specializations in the context of cost optimization, we combined data from functionally diverse neurons spanning brain structures and species to support the hypothesis that neurons’ biophysics are tuned to minimize metabolic cost subject to functional constraints. We propose that this principle generalizes broadly and constrains the range of solutions neurons might adopt to satisfy competing functional and energetic requirements.

Materials and Methods

Model.

Simulations were performed using a single compartment, Hodgkin–Huxley-style model (details given in SI Materials and Methods). Action potentials were required to begin and end below −50 mV and cross at least 0 mV at maximum. The cost of a single action potential was determined by finding the smallest-amplitude 1-ms current pulse that evoked an action potential, integrating the sodium current during the 20-ms poststimulus, and converting integrated sodium current to ATP required to transport the Na⁺ ions using the 3:1 stoichiometry of the Na⁺, K⁺ ATPase. Spike trains were elicited from 200-ms current pulses. The cost per spike for spikes in a train was determined by applying a 200-ms current pulse, integrating the sodium current over the pulse and the following 20 ms, and dividing by the number of spikes evoked. In Figs. 2 and 3, gate kinetics were speeded or slowed by multiplying the time constants calculated at each time step by a constant factor. In Fig. 4, maximum sodium or potassium conductances were scaled by a constant factor.

Dynamic Clamp.

Slices were prepared and neurons recorded using standard patch-clamp techniques (detailed in SI Materials and Methods). TTX (1 μM) was applied to block voltage-gated sodium currents, and sodium current block was confirmed using current pulses. To “replace” the blocked sodium current, a fast real-time dynamic clamp was implemented using an RTLDC-based dynamic clamp (67) with cycle speed of 25–35 ms. This system generated an artificial sodium conductance (kinetics described in SI Materials and Methods) that interacted with the cell's intrinsic potassium conductances to produce action potential-like waveforms (as in Fig. 5). Dynamic-clamp generated spikes were required to be at least 80% as tall as the cell's natural spikes. Single spikes were elicited from 0.2-ms current pulses. Spike trains were elicited from 500-ms current pulses. Costs were determined by integrating the dynamic clamp sodium current over the duration of the spike or train. To aggregate data from cells with different sizes and potassium channel kinetics, group data were constructed by normalizing each parameter-rate curve to have a maximum of 1 or normalizing each parameter-cost curve by the maximum cost per spike for a single spike.