Optimum b value for resolving crossing fibers: a study with standard clinical b value using 1.5-T MR

Abstract

Introduction

We sought to investigate the optimum b value for resolving crossing fiber using high-angular resolution diffusion imaging (HARDI)-based multi-tensor tractography. The study tested the standard b values that are commonly used in the routine clinical setting.

Methods

Ten normal volunteers (five men and five women) with a mean age of 26.3 years (range, 22–32 years) were scanned using a 1.5-T clinical magnetic resonance unit. Single-shot echo-planar imaging was used for diffusion-weighted imaging with a diffusion-sensitizing gradient in 32 orientations. The b values of 700, 1,400, 2,100, and 2,800 s/m² were used. Data postprocessing was performed using multi-tensor methods. The depiction of the optic nerves, optic tracts, and decussation of superior cerebellar peduncles were assessed.

Results

The depictions of the nerve fibers were independent of the b values tested.

Conclusion

The depiction of crossing fibers by HARDI-based multi-tensor tractography is not substantially influenced by b values ranging from 700 to 2,800 s/m². Thus, the optimum b value within this range may be the lowest one considering the higher signal to noise ratio.

Introduction

The fiber tracking technique is a unique and robust tool that is used to assess the locations of vital neuronal pathways throughout the brain [1]. Conventional single-tensor models, however, are limited to the depiction of only a portion of the entire tract [2, 3]. In addition, fiber tracking is difficult in brain regions where several fiber bundles are crossing. In such cases, the directions of the principal eigenvectors do not correspond to the fiber directions. The diffusion tensor in these areas may even have an oblate disk-shape form [4], and the direction of the principle vector may be undefined. In such cases, the common second-order diffusion-tensor model is no longer valid [4–8], and the single-tensor approach cannot correctly estimate the brain fibers.

Recent advances in image acquisition and postprocessing techniques allow the resolution of fibers crossing within a voxel [5, 9–13]. This is achieved by using images obtained by diffusion-sensitizing gradients in multiple orientations (typically over 30 axes) with a high b value, typically over 3,000 s/mm². These high-angular resolution diffusion imaging (HARDI) techniques tend to require an extended data acquisition time, which may hamper their use in the clinical setting. Thus, HARDI studies have so far focused only on methodological development and have not been applied to clinical practice.

In order to make this tool clinically feasible, a low b value is necessary, since this will help to maintain a high image signal to noise ratio (SNR). At low b values, however, the angular dependency of the signal profile is relatively small, and the fiber orientation density function reconstruction is noise sensitive. At high b values, on the other hand, the angular dependency is more pronounced, but the signal attenuation is so large that the noise begins to predominate. As our aim was to investigate the possibility of resolving crossing fibers in clinical setting, we tested the b values used for standard magnetic resonance (MR) imaging at 1.5 T.

We investigated the effect of b value on structures that are known to have decussation, i.e., the optic chiasm and decussation of superior cerebellar peduncle (DSCP). We chose these structures since their decussations are well documented anatomically. For example, approximately half of the fibers within the optic nerve decussate to the contralateral optic tract via the optic chiasm. Similarly, the DSCP is reconstituted by fibers from the ipsilateral superior cerebellar peduncle, which travels to the area around the contralateral red nucleus.

Materials and methods

Our study population comprised 10 healthy volunteers (five men and five women; mean age, 26.3 years; age range, 22–32 years) without any history of neurologic injury or psychiatric disease. No subjects had abnormal neurologic signs or symptoms. Informed consent was obtained from all subjects before the MR examinations.

Imaging technique

All images were obtained using a 1.5-T whole body scanner (Gyroscan Intera; Philips Medical Systems, Best, the Netherlands) with a six-channel phased-array head coil. Single-shot echo-planar imaging was used for diffusion-tensor imaging (DTI) (repetition time, 5,000 ms; echo times (TEs), 55, 65, 72, and 78 ms) with a motion-probing gradient in 32 orientations and b values of 700, 1,400, 2,100, and 2,800 s/mm². The selected TEs were the shortest possible, depending on the selected b values. We only imaged the optic chiasm, superior cerebellar peduncle, and red nucleus to minimize the scan duration. The scan durations for each b value were kept constant (3 min), since the aim of the study was to find the optimum b value to be used within a clinically feasible time frame. These 3-min DTI protocols were repeated twice, and the data were averaged after image reconstruction in order to increase the SNR.

A parallel imaging technique was used to record 128 × 37 data points, which could be reconstructed into images equivalent to 76 × 76 resolution. A total of 12 slices with a thickness of 3.0 mm each were obtained without interslice gaps. The field of view was 230 × 230 mm; thus, the size of a voxel was 3.0 × 3.0 × 3.0 mm.

Image postprocessing

The diffusion-weighted imaging (DWI) data were transferred to an offline workstation for registration, averaging, and analysis (Precision 530; Dell, Round Rock, TX, USA). PRIDE software (Philips Medical Systems, Best, the Netherlands) written in Interactive Data Language (RSI, Inc., Boulder, CO, USA) was used for image analysis. A total of 32 acquisitions using different diffusion-sensitizing gradients were performed, which were registered with respect to the b = 0 measurement using the method of Netsch et al. [14]. This was done to remove distortion and possible head motion over various slices and scans. Affine transformation was used for registration.

Modeling—multi-tensor

For the multi-tensor analysis, the data of the 32 directional apparent diffusion coefficients were fitted to a two-tensor model. This two-tensor model is best described by equation 12 presented in the paper by Frank [5]. Both the orientations of each tensor (6 degrees of freedom for each tensor) and the relative volume fractions were obtained in this manner. Thus, in the given model, there were 13 degrees of freedom.

The three diffusivities (λ ₁, λ ₂, and λ ₃) of each tensor were restricted to a range of λ _{i min} and λ _{i max}, so that they would reflect highly oriented fibers. This also limited the computation time. For our calculations, these were set to 1.2/1.8, 0.2/0.7, and 0.2/0.7 (10⁻³ mm²/s) for the three diffusivities (λ ₁, λ ₂, and λ ₃), respectively. These diffusivity values are close to those found in highly oriented white matter, such as the spinal cord and corpus callosum. Thus, in our model, we assumed that a voxel with crossing fibers consists of two individual fibers that have highly oriented diffusion patterns.

Regions of interest

To trace the optic chiasm, a pair of regions of interest (ROIs) was placed over the optic nerve and ipsi-/contralateral optic tract. To trace the DSCP, a pair of ROIs was placed over the red nucleus and contralateral superior cerebellar peduncle. The red nucleus was identified by the low signal region for the transaxial plane of the B0 image. Exclusion ROIs were also utilized when fibers with clearly wrong anatomy were depicted. The locations of these ROIs were determined by the consensus of two board-certified neuroradiologists.

Image analysis

The tractographic portrayal of fiber tracts between the two ROIs was evaluated by a consensus of two neuroradiologists. The optic nerve was graded on the axial section, and the DSCP was graded on both the axial section and the sagittal section. Grading was performed by visual assessment of the fibers. The readers were blinded to the b value used for scanning.

The scoring system used in assessing fiber tractography was as follows: grade 3 (excellent, i.e., the depicted fiber tracts were of sufficient volumes), grade 2 (moderate), grade 1 (poor, i.e., the fibers were barely depicted), and grade 0 (none, i.e., not visible) (Fig. 1). The angles formed by the optic chiasm and DSCP were also measured.

Fig. 1.

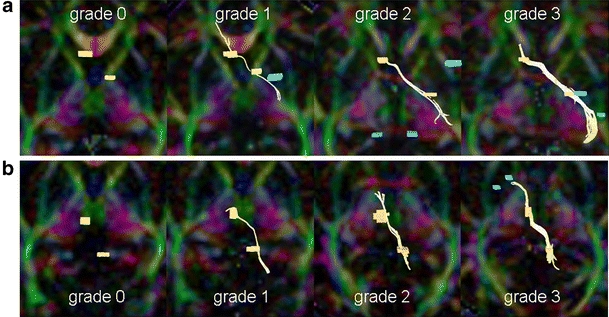
Scoring system for fiber tract depiction (grades 0 to 3). Yellow lines represent the depicted tracts. The scoring system is as follows: grade 3 (excellent), grade 2 (moderate), grade 1 (poor), and grade 0 (none). a Tractographic images of optic pathway superimposed on axial color map viewed from caudal aspect. b Tractographic images of the decussation of superior cerebellar peduncles superimposed on axial color map viewed from caudal aspect

SNR measurement

The SNR of DWI was calculated from two separate MR examinations. Calculation was performed using the following equation:

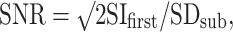where SI_first is the signal intensity of the ROI placed on the first DWI, and SD_sub is the standard deviation of the subtraction images from the first and second scans [15]. The ROIs were placed upon the brainstem at the levels of the midbrain and pons. The mean values of these measurements were used for analysis.

Statistical analysis

Scores for each tract in each subject were analyzed statistically. The Wilcoxon signed rank test was applied to examine the difference in the ability of the b value to assess the depiction of the fiber. Non-parametric Wilcoxon signed rank test was used to analyze the depiction of crossing versus non-crossing fibers. We used JMP version 6.0.0 software (SAS Campus Drive, Cary, NC, USA). For all statistical analyses, p < 0.05 was considered a significant difference.

Results

The crossing fibers of each subject were treated as separate fiber bundles for the analysis, and thus, there were 20 fibers for the optic chiasm and the DSCP, respectively. The majority of these crossing fibers were successfully depicted with at least one of the b values (80% and 95%, respectively). There were crossing fibers that were not depicted using any of the b values; these subjects were excluded from the final analysis (four subjects for the optic chiasm and one for the DSCP). The subjects’ images that were excluded from analysis appeared degraded by motion artifact or distortion due to a technical problem during data acquisition. We thus examined a total of 16 optic chiasm fiber tracts 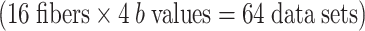and 19 DSCPs .

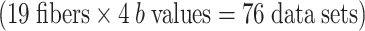Depiction of crossing fibers did not differ significantly by b value for either the optic chiasm or the DSCP (Fig. 2). When depiction of non-crossing fibers was compared with crossing fibers at the optic chiasm, there was a significantly better delineation of the non-crossing fibers (Fig. 3) as compared to the crossing fibers (p < 0.0001).

Fig. 2.

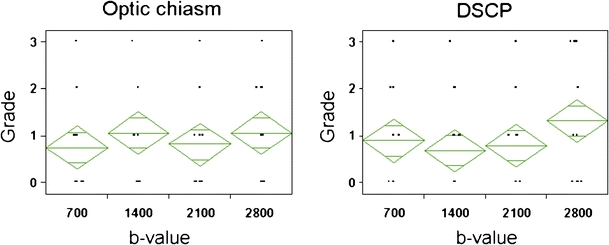
Grade of the fiber tract depiction at optic chiasm and decussation of superior cerebellar peduncle (DSCP) for each b value. Depiction of crossing fiber does not differ significantly by b values, neither at the optic chiasm nor at the DSCP. The breadth of each green rhomboid shows the number of cases in the group, the height shows the 95% confidence interval, the middle line shows the average of the group, and the horizontal lines in the upper and lower parts show the overlap marks. The overlap marks of each of the four groups are not separated in these figures, indicating that there is no significant difference between each group

Fig. 3.

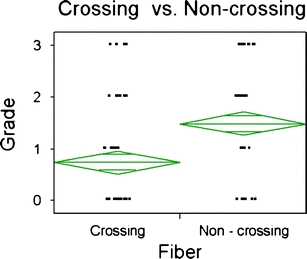
Depiction of the grade of fiber tract at tractography for crossing and non-crossing fibers of the optic chiasm. The overlap marks of the two groups are completely separated in this figure, which indicates that there is a substantial difference between the two groups (p < 0.0001)

The SNR of diffusion-weighted images were 14.0 ± 4.9, 6.8 ± 1.7, 4.1 ± 0.88, and 2.4 ± 0.6 using b values of 700, 1,400, 2,100, and 2,800 s/mm², respectively (Fig. 4). The angles formed by the fibers of the optic chiasm were 63 ± 17, and the angles formed by the fibers of the DSCP were 89 ± 14°.

Fig. 4.

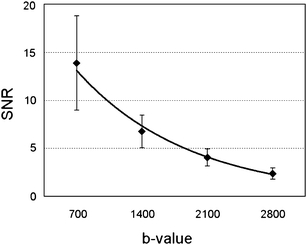
Correlation between the b value and the signal to noise ratio (SNR). Each data point and error bar represent the mean of SNR and standard deviation at each b value, respectively. The SNR deteriorates as the b value increases, and the SNR at b = 2,800 images decreases to 17% of the b = 700 images

Discussion

Previous studies have suggested that the HARDI technique can better portray crossing fibers at higher b values [16]. The trade-off, however, in using a high b value is a substantial reduction in SNR by the elongation of TE [17]. A previous study has indicated that the SNR of b = 3,000 images are reduced to 45% of the SNR achieved when using b = 1,000 [18]. The SNR measurements on our DTI data sets have also shown marked reduction. The b = 2,800 images had 17% of the SNR of b = 700 images. If one attempts to compensate for this signal loss, the excitation has to be increased by a factor of 5.

In clinical practice, scan time is always one of the most important issues. If the patient remains in the scanner for too long, the images will be degraded by motion artifact. Given that scan time is limited, our aim was to determine the optimum b value to solve the crossing fiber problem using a fixed scan time.

We have shown that resolution of crossing fibers is independent on b values in the range of 700 to 2,800 s/mm². Thus, the optimum b value within this range would be the lowest due to the higher SNR at the lowest b value. Our results are not surprising in light of a previous simulation study that suggested that the ability to portray crossing fibers is independent of b values ranging from 1,000 to 3,000 [19]. This simulation study used b values at incremental steps of 1,000 s/mm² from 1,000 to 5,000 s/mm². Using approximately similar scanning techniques to ours (i.e., SNR = 2.4–14, diffusion encoding orientations = 32), their simulation data indicated that separation of two crossing fibers is imperfect at b values between 1,000 and 2,000 s/mm². A slight improvement was found above 3,000, however. Therefore, both sets of data have shown that there is no merit in using b values smaller than 3,000.

Future development in the MR hardware, including increased magnetic field strength, gradient power, and multiple phased-array receiver coils, could allow much higher b values routinely. Then, the higher b value DTI or multi-tensor tractography would better reflect the clinical situation. When such hardware improvement becomes available for clinical use, one has to keep in mind that a b value of no less than 3,000 should be considered.

Our study has several limitations. First, some of the subjects had to be eliminated from the final analysis because their images failed to demonstrate any fibers. Image distortion and motion artifact was considered to be the source of this problem. The optic chiasm is an especially challenging location to perform DTI because of the susceptibility artifacts from the paranasal sinuses. There are areas with less susceptibility artifact, such as the corona radiata or forceps minor. These regions are, however, not ideal locations for assessing crossing fibers, as their architecture is more complex compared to the optic chiasm or DSCPs.

Second, we did not compare the results of different b values at similar SNR. It would be interesting to confirm previous simulation data by performing a study with identical SNR across different b values. This was not attempted in the present study, however, since it was thought to be clinically inapplicable to perform scans that take five times longer than the routine scan time.

Third, our study was limited to a relative narrow range of b values. Further study with higher b values (over 3,000 s/mm²) would be necessary to elucidate the positive trend of better fiber depiction with increasing b values. The results of our study, however, may suggest that a small-scale alteration of b values above 2,800 may not have substantial impact upon the depiction of crossing fiber.

Finally, this examination was performed using a 1.5-T MR scanner. Since the 3-T magnets imaging is now becoming a standard equipment of choice for neuroimaging, HARDI at 1.5-T magnets may have less impact, and thus optimization on 3-T magnets will be necessary in the future. It is our hope that the results of this study can be extrapolated to the following study using 3-T magnets.

Conclusion

We have shown that the depiction of crossing fiber by HARDI-based multi-tensor tractography is not substantially influenced by b values ranging from 700 to 2,800 s/mm². Thus, the optimum b value within this range may be the lowest one considering the advantage of higher SNR.