Abstract
Representing the 3D structures of ligands in virtual screenings via multi-conformer ensembles can be computationally intensive, especially for compounds with a large number of rotatable bonds. Thus, reducing the size of multi-conformer databases and the number of query conformers, while simultaneously reproducing the bioactive conformer with good accuracy, is of crucial interest. While clustering and RMSD filtering methods are employed in existing conformer generators, the novelty of this work is the inclusion of a clustering scheme (NMRCLUST) that does not require a user-defined cut-off value. This algorithm simultaneously optimizes the number and the average spread of the clusters. Here we describe and test four inter-dependent approaches for selecting computer-generated conformers, namely: OMEGA, NMRCLUST, RMS filtering and averaged-RMS filtering. The bioactive conformations of 65 selected ligands were extracted from the corresponding protein:ligand complexes from the Protein Data Bank, including eight ligands that adopted dissimilar bound conformations within different receptors. We show that NMRCLUST can be employed to further filter OMEGA-generated conformers while maintaining biological relevance of the ensemble. It was observed that NMRCLUST (containing on average 10 times fewer conformers per compound) performed nearly as well as OMEGA, and both outperformed RMS filtering and averaged-RMS filtering in terms of identifying the bioactive conformations with excellent and good matches (0.5 < RMSD < 1.0 Å). Furthermore, we propose thresholds for OMEGA root-mean square filtering depending on the number of rotors in a compound: 0.8, 1.0 and 1.4 for structures with low (1–4), medium (5–9) and high (10–15) numbers of rotatable bonds, respectively. The protocol employed is general and can be applied to reduce the number of conformers in multi-conformer compound collections and alleviate the complexity of downstream data processing in virtual screening experiments.
Electronic supplementary material
The online version of this article (doi:10.1007/s10822-010-9365-1) contains supplementary material, which is available to authorized users.
Keywords: Ligand-based drug design, Query conformers, 3D similarity search, Virtual screening, Conformer clustering
Introduction
Ligand-based drug design (LBDD) approaches, such as 3D-similarity searches [1, 2], pharmacophore modeling [3, 4], and 3D-QSAR development [5–7], involve predicting the bioactive conformations of drugs in the absence of a structural model for the receptor. Typically, multiple conformations of potential drug molecules are generated via random or systematic conformational searches in vacuum, distance-dependent dielectric or implicit solvent [8, 9], and employed to search for bioactive conformations. However, it has been established that flexible ligands undergo conformational changes upon binding to receptors, do not bind in their lowest energy solution- or gas-phase free states [10–12] and are more extended in the bound state [13, 14]. Therefore, the success of LBDD relies heavily on the ability of conformer generators to produce conformers whose conformational space includes the bioactive state (except in cases where methods are largely independent of the precise ligand conformation) [15]. Because of the difference between bound and unbound states, another consideration is how many unbound conformations should be employed to contain a representative of the bioactive conformation(s). The level of interest in addressing this question is reflected in the number of studies that have been undertaken either by testing existing conformer generators with different protocols [9, 11–13, 16–22] or by developing more efficient conformational search algorithms [23–26].
The contribution of internal energy to the thermodynamics of binding necessitates a good 3D representation of the conformers. For example, a 1.4-kcal/mol increase in conformational energy results in an approximately 10-fold decrease in affinity [27]. Furthermore, intramolecular hydrogen bonding (due to its directionality) and electrostatics (due to its sensitivity to distance) increase the complexity of conformational search space, among others. Therefore, the treatment of these interactions is crucial for conformer generators, some of which include CAESAR [24], OMEGA [28], ConfGen [29], CatConf [30], and stochastic proximity embedding [31, 32], to cite a few. Having generated the conformers the next step involves a judicious selection of structures to be employed in further work (ligand- or structure-based investigations). The most common strategies employed by some established conformer generators comprise RMS filtering [28, 29] and poling [30]. In addition RMS could also be used for post filtration.
Studies to determine what metrics to employ in selecting unbound conformers to represent a bioactive conformation typically include energy- and geometry-based methods. Alternatively, structural similarity and activity similarity have been used together to derive putative bound conformations [33]. Energy-based methods, on the other hand, involve comparing the internal strain energies of the global or local minima of computer-generated models with those of the bound conformer or a generated conformer that is geometrically very similar to the bound state [9–11, 16, 34]. The energies are computed employing quantum–mechanical methods or empirical force fields in different environments. The energy-based methods are outside the scope of this work; however, it suffices to note that these methods have resulted in cut-offs ranging from 0.5 [16] to 41.6 kcal/mol [10], which truly illustrates the diversity present in the energetics of ligand binding events. Thirdly, in geometric approaches [10, 13, 18, 21] root-mean-squared deviations (RMSD) are computed between the heavy atom positions of computer-generated low energy conformers of a ligand and those of its bioactive conformer. Previously, conformational differences were observed between bound and unbound structures; however, in nine out of ten cases the bound and free conformations displayed similarities in the positions of key atoms involved in ligand recognition [21]. Utilizing 100 low energy conformers per ligand, Günther et al. [18] reproduced the bound states of ligands for 70% of the entire dataset and 90% of the time for averaged-sized (5.6 rotatable bonds) molecules with a similarity threshold of 1.0 Å. At a 1.0-Å cutoff, Auer et al. identified bioactive structures in 75% of the ligands studied [13], while the RMSDs of at least 86% of the ligands investigated by Kirchmair et al. were within 2.0 Å of the bioactive conformer [12].
These RMSD and energy ranges indicate that they cannot be applied broadly, but only by simultaneously considering the number of rotatable bonds of the ligand and the functional form of the force field or energy-based method. Given that bioactive conformers span a range of internal energies it is reasonable to select conformers that cover this range, while at the same time employing a cutoff that does not result in an unmanageable number of conformers in a multi-conformer database. Quantum mechanics methods are the most rigorous; however, their computationally intensive nature prohibits their application to a multi-conformer database. Hence, the use of faster but less accurate empirical methods remains.
Our broad goal is to integrate objective ensemble clustering strategies with established conformer generators in order to select as few computer-generated conformers as possible to represent the bioactive conformer(s) in a search database, in an effort to minimize the complexity of downstream analyses of results. Ensemble clustering has been implemented before using principal component analysis to determine unique conformers from a collection of conformers [35]. Also, it was demonstrated earlier that conformational diversity could be achieved by including a poling penalty function in the search algorithm, which penalizes current conformers that are closely related to pre-existing conformers [36]. The conformer generator employed in this study, OMEGA [28], utilizes RMSD filtering to reduce conformer redundancy during the filtration step; nonetheless, the number of conformers generated can potentially be reduced. Additional downstream or on-the-fly enhancements can be employed by clustering methods that do not require user-defined cut-off values to pare down the number of conformers in large databases, for instance, the hundreds of thousands of compounds typically found in combinatorial libraries. In the current work, we employed the NMRCLUST algorithm implemented in the Chimera version 1.4.1 command line interface [37] as the extra step. NMRCLUST is non-subjective compared to other clustering schemes because it avoids the requirement for the user to specify a maximum intra-cluster RMSD cutoff that is directly linked to the number of clusters generated. In practice this is convenient since knowledge of the full conformational landscape of a compound is generally not known a priori. In this work we show that further filtering of OMEGA-generated conformers with the NMRCLUST algorithm produces a smaller number of structures that can be employed to represent the conformational space of a drug-like molecule, while at the same time maintaining biological relevance of the ensemble.
Methods
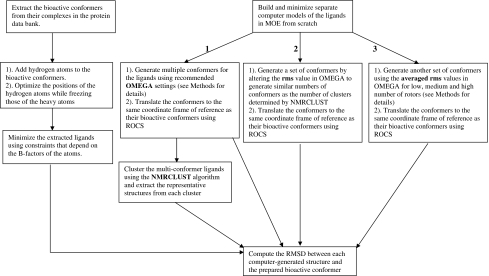
The workflow employed in this study is illustrated in Fig. 1. The bound conformations of the ligands were obtained from their co-crystallized complexes in the Protein Data Bank (PDB). These structures had been employed previously to investigate the relative energies of the bound conformations of drug-like molecules [16]. Two structures (1RO9 and 3CPA) were removed from the list, because of questionable B-factors [16]. In addition, eight pairs of identical ligands that crystallized in dissimilar conformations in different receptors were included. A subset of 65 ligands was selected to represent the entire range of rotatable bonds reported for some drug-like compounds (Tables 1, 4) [12]. Hydrogen atoms were added to the crystal structures of the ligands employing the AddH tool of Chimera version 1.4.1 [37], and each ligand inspected visually for structural consistency. The positions of hydrogen atoms were optimized, while the heavy atoms were fixed utilizing the default minimization criteria in Chimera version 1.4.1 (100 steps, stepsize 0.02 Å, update interval 10, Gasteiger charges). Finally, each structure was minimized in the Molecular Operating Environment version 2008.10 (MOE) program [38] employing heavy-atom positional constraints that are related to atomic B-factors and the temperatures at which the crystals were solved. This treatment of the dataset was performed to take into consideration high B-factors that can lead to inaccurate fitting of ligand atoms. Details of this approach have been published elsewhere [16]. Briefly, this method takes advantage of the notion that atoms with low B-factors have well-resolved electron densities, therefore, their positions are well-defined by the experimental coordinates and may not require further adjustments. However, high B-factors indicate high atomic mobility and positional uncertainties. Thus, in minimizing the bioactive structures the positional constraints are higher on atoms with well-defined atomic coordinates compared to those with poorly-defined coordinates. As a result atoms with low B-factors would be relatively stationary, while the positions of atoms with high B-factors would move presumably to their optimal positions. (In this study superposing pre- and post-minimized bioactive conformations did not lead to any significant changes in compound geometry, see the Results section and Table S1). Additional factors, such as protein environment, explicit solvent effects, etc. are not considered in this process.
Fig. 1.
The workflow employed in this study. For the goal of comparing different tools in their ability to reproduce the conformation of ligands in their bound states, conformers generated by OMEGA were subsequently clustered and the information in the smaller number of cluster centers was compared to the information contained in the original OMEGA output
Table 1.
The protein data bank IDs from which the ligands were extracted, the number of rotatable bonds, the number of conformers
| Ligand | Rotors | omega a | nmrclust b | rms c | rms_avg d | Ligand | Rotors | omega a | nmrclust b | rms c | rms_avg d |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1CIM | 1 | 8 | 4 | 4 | 4 | 1UVT | 8 | 500 | 57 | 66 | 253 |
| 1QPE | 2 | 2 | 2 | 2 | 1 | 1YDT | 8 | 500 | 44 | 52 | 121 |
| 1YDR | 2 | 25 | 7 | 11 | 12 | 2CGR | 8 | 500 | 55 | 68 | 66 |
| 2PCP | 2 | 5 | 5 | 5 | 3 | 3ERT | 8 | 500 | 92 | 102 | 8 |
| 1F4E | 3 | 26 | 6 | 6 | 5 | 1M48 | 9 | 500 | 48 | 48 | 54 |
| 1FCX | 3 | 111 | 21 | 23 | 27 | 1NHU | 9 | 500 | 47 | 54 | 104 |
| 1H1P | 3 | 378 | 47 | 50 | 44 | 1NHV | 9 | 500 | 88 | 99 | 113 |
| 1H9U | 3 | 32 | 5 | 8 | 8 | 2QWI | 9 | 500 | 35 | 35 | 15 |
| 1 JSV | 3 | 68 | 16 | 18 | 24 | 1K1 J | 10 | 500 | 57 | 64 | 142 |
| 1BR6 | 4 | 79 | 16 | 20 | 23 | 1KV2 | 10 | 500 | 72 | 72 | 44 |
| 1DLR | 4 | 109 | 16 | 17 | 19 | 1MQ6 | 10 | 500 | 62 | 66 | 76 |
| 1FCZ | 4 | 135 | 19 | 20 | 24 | 7DFR | 10 | 500 | 78 | 84 | 28 |
| 1L2S | 4 | 34 | 7 | 7 | 8 | 1EZQ | 11 | 500 | 68 | 69 | 88 |
| 2CSN | 4 | 88 | 10 | 10 | 11 | 1FKG | 11 | 500 | 78 | 84 | 92 |
| 1K7E | 5 | 75 | 19 | 23 | 10 | 1K22 | 11 | 500 | 54 | 60 | 33 |
| 1KV1 | 5 | 38 | 6 | 8 | 6 | 1QBU | 11 | 500 | 66 | 69 | 118 |
| 1QL9 | 5 | 500 | 54 | 60 | 198 | 1HFC | 12 | 500 | 54 | 59 | 50 |
| 1YDS | 5 | 319 | 22 | 22 | 11 | 1MNC | 12 | 500 | 55 | 55 | 57 |
| 5STD | 5 | 331 | 48 | 54 | 29 | 1OHR | 12 | 500 | 44 | 44 | 47 |
| 1EVE | 6 | 500 | 37 | 46 | 31 | 1UVS | 12 | 500 | 58 | 60 | 83 |
| 1F0T | 6 | 500 | 64 | 68 | 262 | 7EST | 12 | 500 | 62 | 68 | 29 |
| 1H1S | 6 | 500 | 61 | 69 | 88 | 1ELA | 13 | 500 | 39 | 45 | 25 |
| 1HDQ | 6 | 45 | 9 | 12 | 6 | 1GWX | 13 | 500 | 110 | 120 | 274 |
| 1K7F | 6 | 500 | 75 | 80 | 52 | 1HPV | 13 | 500 | 41 | 47 | 115 |
| 1A42 | 7 | 500 | 63 | 67 | 33 | 1O86 | 13 | 500 | 33 | 34 | 27 |
| 1IF7 | 7 | 500 | 70 | 82 | 179 | 1F4G | 14 | 500 | 49 | 49 | 35 |
| 1L8G | 7 | 500 | 36 | 36 | 50 | 1HTF | 15 | 500 | 58 | 59 | 149 |
| 1LQD | 7 | 500 | 60 | 65 | 182 | 1MMB | 15 | 500 | 37 | 37 | 63 |
| 966C | 7 | 500 | 52 | 56 | 45 | Average | 7.7 | 366.8 | 43.8 | 47.7 | 65.0 |
The number of conformers generally increased with the number of rotors for each method
aEnumerated with recommended settings in OMEGA
Generated by: b Clustering the OMEGA conformers employing the NMRCLUST algorithm
cAdjusting the rms parameter of OMEGA to generate similar numbers of conformers as the number of clusters identified by the NMRCLUST algorithm
dPartitioning the dataset into low, medium and large numbers of rotatable bonds, averaging the rms values in each group and using the averaged rms values
Table 4.
The PDB structures employed for ligands present in dissimilar bound conformations in different receptors
| Namea | Rotorsb | RMSD differencesc (Angstroms, Å) | RMSD pre/post-minimizationd (Angstroms, Å) | Number of conformers | Minimum RMSD (Angstroms, Å) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| omega e | nmrclust f | rms g | rms_avg h | omega e | nmrclust f | rms g | rms_avg h | ||||
| pbn_1TNI | 4 | 1.386 | 0.44 | 39 | 8 | 9 | 7 | 0.48 | 0.664 | 0.48 | 0.48 |
| pbn_1UTP | 4 | 0.312 | 39 | 8 | 9 | 7 | 0.507 | 0.63 | 0.761 | 0.761 | |
| pt1_1BR6 | 4 | 2.107 | 0.308 | 78 | 15 | 15 | 19 | 0.613 | 1.121 | 0.794 | 0.794 |
| pt1_1TX0 | 4 | 0.513 | 78 | 15 | 15 | 19 | 0.894 | 1.112 | 1.107 | 0.966 | |
| adp_13PK | 6 | 2.193 | 1.134 | 500 | 65 | 68 | 180 | 1.132 | 1.154 | 1.192 | 1.192 |
| adp_1HW8 | 6 | 0.862 | 500 | 65 | 68 | 180 | 1.435 | 1.486 | 1.441 | 1.363 | |
| kan_1KNY | 6 | 2.248 | 0.709 | 500 | 41 | 45 | 70 | 1.855 | 1.855 | 2.039 | 2.039 |
| kan_1L8T | 6 | 0.626 | 500 | 41 | 45 | 70 | 2.026 | 2.026 | 1.764 | 1.815 | |
| i84_1EKO | 8 | 1.369 | 0.519 | 500 | 62 | 69 | 50 | 1.124 | 1.149 | 1.217 | 1.609 |
| i84_1EL3 | 8 | 0.383 | 500 | 62 | 69 | 50 | 0.891 | 0.947 | 0.962 | 0.997 | |
| fad_1A8P | 13 | 2.851 | 0.656 | 500 | 40 | 48 | 500 | 1.634 | 1.746 | 2.288 | 1.634 |
| fad_1B2R | 13 | 0.605 | 500 | 40 | 48 | 500 | 2.116 | 2.363 | 2.169 | 1.574 | |
| acd_1ADL | 14 | 1.859 | 0.667 | 500 | 64 | 69 | 148 | 1.081 | 1.081 | 1.081 | 1.081 |
| acd_1CVU | 14 | 0.57 | 500 | 64 | 69 | 148 | 1.306 | 1.532 | 1.494 | 1.435 | |
| im1_1SBG | 16 | 3.306 | 0.357 | 500 | 68 | 75 | 75 | 1.576 | 1.595 | 1.76 | 1.76 |
| im1_1TCW | 16 | 0.414 | 500 | 68 | 75 | 75 | 1.732 | 1.732 | 1.665 | 1.665 | |
| L95 | 6.422 | 1.607 | 0.452 | 284.277 | 33.242 | 36.545 | 48.531 | 0.997 | 1.128 | 1.106 | 1.087 |
| Mean | 8.875 | 2.165 | 0.567 | 389.625 | 45.375 | 49.750 | 131.125 | 1.275 | 1.387 | 1.388 | 1.323 |
| U95 | 11.328 | 2.723 | 0.683 | 494.973 | 57.507 | 62.954 | 213.719 | 1.554 | 1.646 | 1.671 | 1.558 |
| Standard deviation | 4.60 | 0.67 | 0.22 | 197.70 | 22.77 | 24.78 | 155.00 | 0.52 | 0.49 | 0.53 | 0.44 |
The statistics of the data are shown in the last four rows of the table
aThe name of the ligands and protein databank IDs are represented by the first three and last four alphanumeric characters, respectively
bThe number of rotatable bonds in the ligands
cRMSDs between the bound conformations of the same ligand in the two receptors selected
dThe RMSDs between the minimized and unminimized bound ligand conformation. More details are presented in the Methods section
eEnumerated with recommended settings in OMEGA
Generated by: f Clustering the OMEGA conformers employing the NMRCLUST algorithm
gAdjusting the rms parameter of OMEGA to generate similar numbers of conformers as the number of clusters identified by the NMRCLUST algorithm
hPartitioning the dataset into low, medium and large numbers of rotatable bonds, averaging the rms values in each group and using the averaged rms values. L95 and U95 are the lower and upper 95% confidence interval of the mean, respectively
Next, the computational 3D models were built from scratch, and minimized employing the MMFF94x force field and default parameters in MOE. Four conformer sets were generated from these initial conformers. The first set of conformers (omega) was generated utilizing default OMEGA version 2.3.1 parameters except for the following: rms = 0.4; ewindow = 25.0 kcal/mol, maxconfs = 500; searchff = mmff94s_noestat. The initial number of conformers generated was 50,000, specified via the maxconfgen parameter. The rms parameter sets a lower limit for filtering similar conformers; maxconfs determines the final number of conformers to be retained from the initial ensemble requested via maxconfgen; the searchff specifies the force field employed to compute internal energies during conformer search; and ewindow sets an upper limit for retaining the generated conformers. The incomplete force field, mmff94s_noestat, was employed in order to neglect intramolecular gas-phase interactions that could lead to collapsed conformations, given that bound conformers are generally more extended than unbound conformers [13, 14]. The OMEGA parameters were employed because they have been shown to be optimal in terms of reproducing the bound conformations of ligands [12]. In addition, the maxconfs limit of 500 was set because the clustering algorithm scales as O(n2), see below. The OMEGA-generated conformers were translated to the same coordinate frame of reference as the bioactive conformer employing a rigid-body superposition with the ROCS version 2.3.1 program [39]. The second set (nmrclust) was generated by clustering the OMEGA-generated conformers of each molecule using the NMRCLUST algorithm in the Chimera command line interface, which employs the Kelley penalty function [40] to determine an optimal number of clusters. Utilizing the NMRCLUST algorithm avoids subjective inputs of pre-defined intra-cluster cut-offs or spreads, by selecting the number of clusters that minimizes a penalty function during hierarchical clustering of an RMS distance matrix, D(i, j) employing the average-linkage method. The average-linkage method performed best for this type of studies compared to single or complete linkage [40]. For each hierarchy a penalty function is determined using the number of clusters and the average spread of the clusters. The hierarchy that gives the minimum value of the penalty function is selected to represent the optimum number of clusters for the conformer ensemble. Briefly, a distance matrix consisting of heavy-atom pairwise RMSDs for an ensemble of structures is generated. Next, hierarchical clustering is performed with the matrix using the average-linkage method:
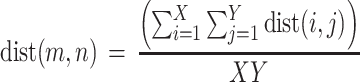 |
for clusters m and n with X and Y members, respectively, and dist(i, j) the RMS between the superimposed i and j from m and n, respectively [40].
In the course of the clustering, the average spread is determined at each stage using the spreads determined by: [40]
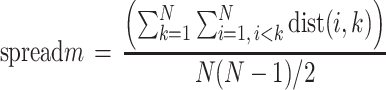 |
for cluster m containing N members, with conformers i and k; by definition, clusters that contain only one member (singletons or N = 1) are excluded in the calculation of the spread. The average spread is computed by: [40]
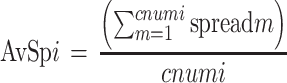 |
where i is a given hierarchy, and cnumi the number of clusters at that hierarchy. The average spreads are then normalized with values between one and (N T − 1), whereby N T is the total number of structures in the ensemble as follows: [40]
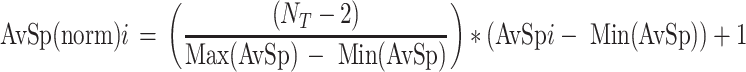 |
Max(AvSp) and Min(AvSp) denote the maximum and minimum average spreads, respectively, in the set across all the stages of the clustering. This results in equal weights in the average spreads and number of clusters in a penalty function that is computed as the sum of the normalized average spread at a given hierarchy and the corresponding number of clusters (including singletons). The penalty scores are then stored as a function of the number of clusters and the average normalized spreads: [40]
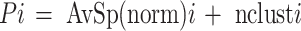 |
The number of clusters that corresponds to the minimum penalty score defines the cut-off for the ensemble. This cut-off represents the stage wherein the clusters are as highly populated as possible, while concurrently minimizing the spread. After this analysis, a structure closest to the centroid of each cluster is selected as the representative structure. The third set of structures (rms) was generated by altering the value of the rms parameter in OMEGA in order to obtain a comparable number of conformers as the number of representative structures identified by NMRCLUST. Finally, the fourth set of structures (rms_avg) was generated by partitioning the dataset in terms of number of rotors: low, having between one and four rotatable bonds; medium, possessing between five and nine rotatable bonds; and high, with ten to 15 rotatable bonds. The rms-filtering cutoffs employed in set three for the compounds in each category were averaged and employed to generate conformers for each molecule in the rms_avg set.
The RMSDs between the computer-generated structures and their bioactive conformations were computed for each multi-model file, utilizing the g_rms module of GROMACS [41], and the RMSD statistics (average, standard deviation, minimum and maximum values) were extracted (see Table 2). Perl scripts were written for the automation of the conformer generation, ROCS overlays, and RMSD analyses procedures.
Table 2.
The minimum RMSDs between the bioactive conformations and the structures from the different computer-generated datasets
| Ligand | omega a | nmrclust b | rms c | rms_avg d | Ligand | omega a | nmrclust b | rms c | rms_avg d |
|---|---|---|---|---|---|---|---|---|---|
| 1CIM | 1.199 | 1.199 | 1.199 | 1.199 | 1UVT | 1.315 | 1.329 | 1.296 | 1.315 |
| 1QPE | 0.775 | 0.775 | 0.736 | 0.775 | 1YDT | 1.104 | 1.154 | 1.154 | 1.154 |
| 1YDR | 0.932 | 0.932 | 0.932 | 0.932 | 2CGR | 1.087 | 1.087 | 1.659 | 1.613 |
| 2PCP | 1.14 | 1.14 | 1.14 | 1.14 | 3ERT | 0.384 | 0.569 | 0.472 | 0.738 |
| 1F4E | 0.787 | 0.787 | 1.019 | 0.801 | 1M48 | 1.315 | 1.41 | 1.658 | 1.678 |
| 1FCX | 0.761 | 0.81 | 0.871 | 0.81 | 1NHU | 1.267 | 1.458 | 1.458 | 1.458 |
| 1H1P | 0.493 | 0.681 | 0.708 | 0.708 | 1NHV | 1.227 | 1.227 | 1.051 | 1.051 |
| 1H9U | 0.766 | 1 | 0.772 | 0.772 | 2QWI | 1.035 | 1.114 | 1.082 | 1.106 |
| 1 JSV | 1.049 | 1.229 | 1.229 | 1.229 | 1K1 J | 1.528 | 1.528 | 1.528 | 1.528 |
| 1BR6 | 0.6 | 0.751 | 0.6 | 0.6 | 1KV2 | 2.163 | 2.118 | 2.167 | 2.143 |
| 1DLR | 0.164 | 0.164 | 0.599 | 0.599 | 1MQ6 | 0.991 | 1.177 | 1.197 | 1.23 |
| 1FCZ | 1.083 | 1.105 | 1.114 | 1.114 | 7DFR | 1.654 | 1.851 | 0.929 | 1.455 |
| 1L2S | 0.533 | 0.738 | 1.033 | 0.935 | 1EZQ | 0.871 | 0.953 | 1.054 | 1.116 |
| 2CSN | 0.267 | 0.33 | 0.267 | 0.267 | 1FKG | 1.639 | 1.66 | 1.118 | 1.413 |
| 1K7E | 0.857 | 0.977 | 0.796 | 1.113 | 1K22 | 1.02 | 1.02 | 1.224 | 1.224 |
| 1KV1 | 0.435 | 0.435 | 0.63 | 0.8 | 1QBU | 1.241 | 1.453 | 1.509 | 1.446 |
| 1QL9 | 0.836 | 1.018 | 1.064 | 0.98 | 1HFC | 1.018 | 1.306 | 1.386 | 1.047 |
| 1YDS | 0.951 | 1.058 | 1.008 | 1.065 | 1MNC | 0.572 | 1.057 | 1.152 | 1.152 |
| 5STD | 0.314 | 0.586 | 1.351 | 1.663 | 1OHR | 1.174 | 1.298 | 1.298 | 1.298 |
| 1EVE | 0.394 | 0.467 | 0.969 | 1.082 | 1UVS | 1.483 | 1.541 | 1.541 | 1.541 |
| 1F0T | 0.933 | 1.13 | 1.204 | 0.932 | 7EST | 1.25 | 1.475 | 1.371 | 1.393 |
| 1H1S | 0.839 | 0.839 | 1.153 | 1.231 | 1ELA | 0.892 | 0.892 | 0.945 | 1.108 |
| 1HDQ | 0.766 | 0.766 | 0.788 | 1.099 | 1GWX | 1.375 | 1.375 | 1.375 | 1.375 |
| 1K7F | 0.715 | 0.715 | 0.807 | 0.807 | 1HPV | 1.094 | 1.094 | 1.733 | 1.136 |
| 1A42 | 0.907 | 0.951 | 0.937 | 1.012 | 1O86 | 0.885 | 1.05 | 1.205 | 1.205 |
| 1IF7 | 0.334 | 0.534 | 0.941 | 0.657 | 1F4G | 1.266 | 1.304 | 1.367 | 1.367 |
| 1L8G | 1.44 | 1.44 | 1.361 | 1.361 | 1HTF | 1.284 | 1.395 | 1.395 | 1.256 |
| 1LQD | 0.724 | 0.992 | 1.138 | 0.726 | 1MMB | 0.915 | 0.915 | 0.915 | 0.915 |
| 966C | 1.41 | 1.525 | 1.625 | 1.625 | Average | 0.973 | 1.068 | 1.127 | 1.131 |
It can be seen that the bioactive conformer is present when a smaller ensemble size is employed
aEnumerated with recommended settings in OMEGA
Generated by: b Clustering the OMEGA conformers employing the NMRCLUST algorithm
cAdjusting the rms parameter of OMEGA to generate similar numbers of conformers as the number of clusters identified by the NMRCLUST algorithm
dPartitioning the dataset into low, medium and large numbers of rotatable bonds, averaging the rms values in each group and using the averaged rms values
Results and discussions
The metric employed to assess deviations between the computer-generated and bioactive conformers was the RMSD between each pair of computed and experimental structures. To improve the quality of the structures, the bioactive conformers were refined via energy minimizations taking into account positional uncertainties in the experimental atomic coordinates via atomic B-factors. Details are provided in the Methods section. It is conceivable that these minimizations may significantly alter the conformations of the bioactive structures, though minimizations of experimental structures in energy and structural comparisons are not uncommon [16, 22]. In this study superposing the pre- and post-minimized bioactive conformations of each compound did not reveal any significant changes, Table S1.
For the computer-generated ensembles, the first set (omega) was employed as a performance reference as well as the input file for subsequent clustering steps. It could also be seen from this output whether the number of conformers generated with our OMEGA parameters actually included the bioactive conformation in the first place. The second set (nmrclust) served to represent the conformational space of each molecule employing a smaller number of conformers by clustering, with the aim of retaining the bioactive conformation. The clustering approach employed here does not require a priori knowledge of the desired number of conformers, nor the maximum spread of distance cut-off to include structures in a cluster [40]. In the third set of structures, the rms parameter of OMEGA was adjusted for each compound to give a similar number of conformers as obtained with the clustering method. This set is intended to determine whether the clustering can be avoided by simply modifying the rms filtering value to generate the desired number of conformers per molecule. Lastly, a fourth set was constructed, named rms_avg. Structures in this set were generated to determine whether specific values could be employed during conformational sampling depending on the number of rotors in a compound. It is recognized that the last two sets of structures (rms and rms_avg) include information derived from the clustering dataset. As such it is presumed that the NMRCLUST algorithm is an efficient clustering approach.
The ligands employed in this work, the number of rotatable bonds and the initial numbers of conformers generated by OMEGA are presented in Table 1. The number of clusters identified employing the NMRCLUST algorithm, and the number of conformers generated by the rms and rms_avg filtering schemes are also shown. As expected, [42] the number of conformers generally increased with the number of rotors for each method. For instance for two rotors the average number of conformers was 10.67, 4.67, 6 and 5.33 for omega, nmrclust, rms and rms_avg, respectively, compared to 500, 47.5, 48 and 106, respectively, for fifteen rotors.
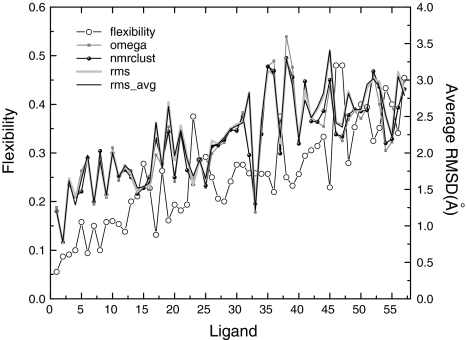
As a way to account for the molecular size, the ratio between the number of rotatable bonds and the total number of bonds between the heavy atoms for each ligand was determined. This ratio is an indication of the flexibility of the molecule. Lower values of this ratio indicate that the compound is generally less flexible, more unsaturated, with cyclic substructures that may or may not be fused. Consequently, its bioactive conformer can be determined with relative ease. The reverse is true for higher values. There was an overall increase in this ratio, visualized in Fig. 2 as the black line-open circles, reflecting some of the challenges encountered when utilizing conformer generators to obtain a conformer that closely resembles the bioactive conformation of highly flexible compounds, in agreement with previous studies [10, 12]. Also shown in Fig. 2, are the average RMSDs computed between the conformers in each computer-generated multi-conformer file and their bioactive conformer. The average RMSDs were statistically similar across all four methods, and did not provide specific details about the similarities between individual computer-generated conformers and their bioactive conformer.
Fig. 2.
Average RMSDs and flexibility for each compound for each method employed. The order of the compounds is the same as in Table 1; as the number of the compound increases the number of rotatable bonds also increases. Thus, the left- and right-most abscissa points have one and fifteen rotors, respectively. It can be seen that the average RMSD and flexibility increase with the number of rotors
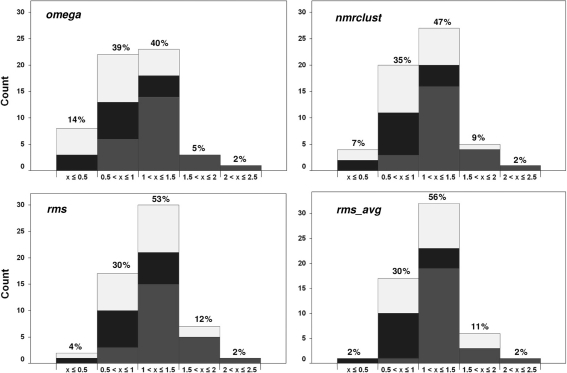
To obtain a better indication of the occurrence of the bioactive conformer among the computer-generated conformers the range of RMSD values was determined for each ligand for the different schemes. The bins and populations of the minimum RMSD values between each ligand and its bioactive conformer for the four methods employed are shown in Fig. 3. A tabular format of these data is given in supplementary material Table S2. A classification of RMSD values between computer-generated and bound conformers has been suggested before: [12] RMSD < 0.5 indicates an excellent match; 0.5 ≤ RMSD < 1.0 signifies a good match; 1.0 ≤ RMSD < 1.5 suggests an acceptable match; 1.5 ≤ RMSD < 2.0 is still acceptable; and RMSD ≥ 2.0 is unacceptable. The population distributions are color-coded with black, spotted and gray representing the low, medium and high number of rotor categories, respectively. Overall, the RMSD distributions covered the entire range from excellent to unacceptable, although the majority of the values occupied the good to acceptable limits (from 0.5 to 1.5 Å). It is worth pointing out that for ligands with high numbers of rotatable bonds (10–15) none of the datasets contained a conformer that was in excellent agreement with the bioactive conformer. This is most likely a reflection of insufficient numbers of conformers because of the difficulty in exhaustively sampling the conformational space of highly flexible molecules [42].
Fig. 3.
Distributions of the minimum RMSDs (x) between each ligand and its bioactive conformer for the four methods employed. The qualitative descriptions are as follows: x < 0.5 = excellent; 0.5 ≤ x < 1.0 = good; 1.0 ≤ x < 1.5 = acceptable; 1.5 ≤ x < 2.0 = still acceptable; x ≥ 2.0 = unacceptable. The numbers above each column represent populations within each RMSD range. The bars are color-coded to indicate the occurrence of rotor categories. Black: Low; Spotted: medium; Gray: High number of rotors
Comparing the four different sets of generated conformers in terms of getting the bound ligand structure revealed some notable trends, Fig. 3. For RMSDs ≤ 0.5 Å the rankings were as follows: omega > nmrclust > rms > rms_avg. The trend was similar for good reproduction, except that rms = rms_avg. Given the observed trends for excellent and good reproduction it is expected that the order will be reversed for acceptable and still-acceptable fits with the rankings being rms_avg > rms > nmrclust > omega and rms > rms_avg > nmrclust > omega, respectively. That the trends were reversed for the latter RMSD ranges simply indicates the greater number of compounds distributed in the “excellent” and “good” categories of the RMSD fits for omega and nmrclust, compared to rms and rms_avg. It is interesting to note that nmrclust was better than rms in terms of “excellent” and “good” fits, given that rms filtering had at least as many structures as nmrclust.
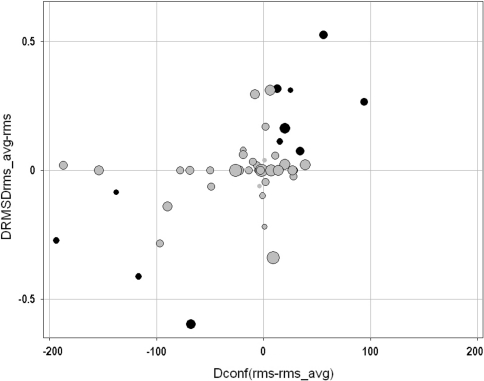
Since the rms_avg set was derived from the rms set, it is expected that the number of conformers generated in the rms_avg set would differ from the number of conformers from the rms set; in fact, only in few cases such as 1CIM and 1H9U were the number of conformers from these two sets identical (Table 1). It was hypothesized that ligands with more conformers in the rms_avg set than in the rms set would be more likely to capture the bioactive conformation, while the reversed would be true for ligands with a smaller number of conformers. The overall comparison of the number of conformers and the differences between minimum RMSDs to the bioactive conformation for the rms_avg and rms sets are shown in Fig. 4. The horizontal axis represents conformer differences (rms—rms_avg), while the vertical axis represents differences in minimum RMSD (rms_avg—rms). The quadrants depict the dataset as follows: lower-left, rms has less conformers and worse representation of the bioactive conformers; upper-left, rms has less conformers and better representation of the bioactive conformers; lower-right, rms has more conformers and worse representation of the bioactive conformers; upper-right, rms has more conformers and better representation of the bioactive conformers. It is expected that no data points populate the upper-left and lower-right quadrants of this plot. The few cases falling into these quadrants have either a small difference in the number of conformers or a small difference in the minimum RMSD (rms_avg—rms). Black circles (10 data points) represent ligands that were classified into different categories in the qualitative classification of Fig. 3. The relatively few number of these highlighted entries may explain why the rms_avg and rms filtering methods performed equally well in the classification presented in Fig. 3. Interestingly, increasing the number of conformers did not ensure better fits; in fact some cases (far left) provided at best the same performance (the difference in minimum RMSD is close to zero).
Fig. 4.
Differences in the number of conformers between the rms_avg and rms filtering with respect to RMSD differences between the same sets. The horizontal and vertical axes represent differences in the number of conformers and RMSDs, respectively. Sized by increased flexibility. Black circles indicate ligands whose RMSDs were in different ranges of the qualitative categories. The relatively small number of these bold entries may explain why rms_avg and rms filtering performed very similar in the classification made in Fig. 3
The statistics for the number of conformers and minimum RMSD values generated by each method are presented in Table 3. It is demonstrated that employing a smaller number of conformers in nmrclust, rms or rms_avg we were able to get equal overall performances (56/57 acceptable RMSDs) from these methods. However, whenever possible nmrclust would be the recommended approach given that rms_avg was derived from rms and will involve the cumbersome adjustments of individual rms cutoffs for compounds in a large database. The rms_avg values of 0.76, 1.01 and 1.39 for small, medium and large number of rotors, respectively, derived in this study may serve as guidelines in OMEGA for these categories of compounds.
Table 3.
Statistics for the number of conformers and minimum RMSD obtained by the four methods utilized
| L95 | Mean | U95 | Standard deviation | ||
|---|---|---|---|---|---|
| Rotors | 6.74 | 7.719 | 8.699 | 3.774 | |
| Number of conformers | omega | 314.67 | 366.807 | 418.944 | 200.833 |
| nmrclust | 37.136 | 43.825 | 50.514 | 25.766 | |
| rms | 40.435 | 47.684 | 54.934 | 27.925 | |
| rms_avg | 47.36 | 64.982 | 82.605 | 67.881 | |
| Minimum RMSD (Angstroms, Å) | omega | 0.871 | 0.973 | 1.074 | 0.386 |
| nmrclust | 0.971 | 1.068 | 1.166 | 0.371 | |
| rms | 1.038 | 1.127 | 1.216 | 0.338 | |
| rms_avg | 1.045 | 1.131 | 1.218 | 0.327 |
L95 and U95 Lower and upper 95% confidence interval of the mean, respectively
In addition, eight ligands adopting different bioactive conformations in different complexes were included, Table 4. The aim was to test whether the methods could sample multiple bioactive conformations for the same ligand. Generally, except for the kanamycin (KAN) and FAD ligands the omega, nmrclust, rms and rms_avg methods sampled both bioactive conformers within acceptable limits (RMSD < 2.0 Å). For the KAN case, the methods sampled the bound conformation reasonably in at least one complex. In the final case (FAD in 1A8P and 1B2R), while rms did not capture the bound conformation of the ligand, it was sampled at least once by omega, nmrclust and rms_avg filtering. It is worth pointing out that when the rms_avg value was employed in OMEGA for ligand FAD the number of conformers retained was 500, similar to the number generated by omega, Table 4. For FAD in 1A8P, rms_avg identified the same closest conformer as omega. However, for 1B2R rms_avg sampled a conformer that better reproduced the bioactive conformer compared to omega. Also worth mentioning are cases wherein a small number of conformers exhibited a better representation of the bioactive conformer, comparing omega and rms_avg. These include: ADP in 1HW8; kanamycin in 1L8T; FAD in 1B2R; IM1 in 1TCW. (See 1H1P and 2CSN in Table 2). Although small in number, these cases indicate that different conformers are being sampled and that more than 500 conformers should be considered, especially for highly flexible molecules. The overall performances of the methods were omega (88%), nmrclust (88%), rms (81%) and rms_avg (94%). The statistics of the number of conformers and minimum RMSDs indicate, once more, that a smaller number of ensembles may be utilized to capture the bioactive conformer for this set of ligands.
Employing a predictive model it has been hypothesized that for small RMSD filtering values and large numbers of rotors the number of conformers required to exhaustively cover the conformational space ranges from the hundreds to hundreds of thousands [42]. This suggests that increasing the likelihood of incorporating a bioactive conformer during the conformer generation stage in ligand-based methods could result in huge computational costs during the screening stage. It is worth noting that there are some instances wherein it has been stated [43] and demonstrated [22] that the determination of a bioactive conformation or number of query conformers employed does not improve the performance of a 3D shape-based method such as ROCS in recovering active compounds during virtual screenings. This attests to the conformer generating strengths of OMEGA, and the ability of ROCS to score the compounds correctly even though the conformation may not represent the bound state. However, in cases such as pharmacophore modeling [18] and molecular-field-based similarity analysis [35] where the description of ligand features complementary to an active site is crucial, an accurate representation of the bound conformation is still of utmost importance. Therefore, it would be computationally efficient to reduce the number of conformers per compound in a database, while still retaining the bioactive conformer.
In a previous study, 10 conformers were recommended [18] for averaged-sized molecules, while 50 conformers have also been proposed for screening databases containing several million compounds [12]. The goal of the current work was to produce the least number of computer-generated structures, while still including the bioactive conformer. Our results reflected this possibility, demonstrated by the four conformer sets exhibiting acceptable representations (RMSD < 2.0 Å) of their bound conformations in 56/57 (98%) instances.
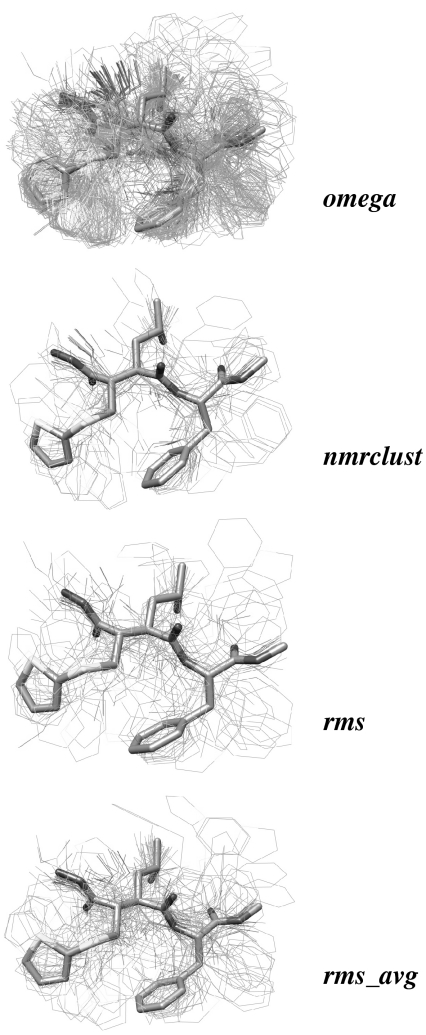
The conformational overlap between the bound ligands and the computer generated conformers is shown in Fig. 5 for the ligand with PDB ID 1MMB as an example. This representation provides a qualitative view of how the methods are performing in terms of sampling the bioactive conformer. The generation of several structures dissimilar to the bound conformer is observed. More importantly, the bioactive conformer is captured, using a smaller number of computer generated structures.
Fig. 5.
Overlays of the bioactive and computer-generated models portrayed in stick and wire representations, respectively. As described in the text, it is shown that the bioactive structure is captured with a smaller ensemble of computer-generated conformers
Conclusions
Ensemble conformer clustering implemented using the NMRCLUST algorithm has here been employed to determine the extent to which clustering of computer-generated conformers reduces ensemble size, while still retaining the bioactive conformation. This approach relies on the ability of the conformer generator, in this case OMEGA 2.3.1, to generate the bioactive conformation in the first place. Analysis of the minimum RMSD values between the bioactive and the computer-generated ligands indicated that the presence of more conformers in the ensemble increased the probability of including the bound conformation. Even though downsizing the number of generated conformers by clustering may result in a potential loss of bioactive conformers, we showed that this approach successfully reproduced acceptable bound ligand conformations 56 out of 57 of the cases. In addition, OMEGA 2.3.1 sampled satisfactorily different bound conformations for the same ligand in different receptors. In terms of “excellent” and “good” representations, ensemble clustering performed closest to the reference method (omega) compared to the two RSMD filtering methods employed here. Therefore, by using this clustering method we showed that a smaller number of conformers was sufficient to capture the bioactive conformers of the ligands. It remains to be determined how multiple conformers derived from other conformer generators will perform. For combinatorial libraries that range from hundreds of thousands to millions of compounds such an approach may be applied to reduce the number of conformers per ligand by performing on-the-fly clustering, thus allowing less intensive virtual screening campaigns.
Supporting information available
The RMSDs between pre- and post-minimized bioactive conformers and the distribution of the minimum RMSDs relative to the bioactive structures. The experimental and computer-generated coordinates of the ligands employed in this work.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
This work was supported by the State of Florida, Executive Officer of the Governor’s Office of Tourism, Trade and Economic Development and partially performed within the framework of the Dutch Top Institute Pharma, project number: D1-105 (A.B.). We thank Dr. Xavier Barril for providing both the SVL scripts and instructions on how to implement the B-factor and temperature-dependent constraints in MOE; Dr. Gerald M. Maggiora for insightful discussions; and Dr. Conrad C. Huang for the NMRCLUST algorithm. We thank the referees for helpful suggestions. Molecular graphics images were produced using the UCSF Chimera package from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (Supported by NIH P41 RR-01081). We thank OpenEye Scientific Software for providing the OMEGA, ROCS, and VIDA programs.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.Bender A, Glen RC. Org Biomol Chem. 2004;2:3204. doi: 10.1039/b409813g. [DOI] [PubMed] [Google Scholar]
- 2.Johnson MA, Maggiora GM. Concepts and applications of molecular similarity. New York: Wiley; 1990. [Google Scholar]
- 3.van Drie JH. Curr Pharm Desgn. 2003;9:1649. doi: 10.2174/1381612033454568. [DOI] [PubMed] [Google Scholar]
- 4.Alvarez J, Shoichet B. Virtual screening in drug discovery, Taylor and Francis Group. Boca Raton: LLC CRC Press; 2005. [Google Scholar]
- 5.Tong W, Welsh WJ, Shi LM, Fang H, Perkins R. Environ Toxicol Chem. 2003;22:1680. doi: 10.1897/01-198. [DOI] [PubMed] [Google Scholar]
- 6.Dixon SL, Smondyrev AM, Knoll EH, Rao SN, Shaw DE, Friesner RA. J Comput Aided Mol Des. 2006;20:647. doi: 10.1007/s10822-006-9087-6. [DOI] [PubMed] [Google Scholar]
- 7.Kubinyi H. Drug discovery today. 1997;2:457. doi: 10.1016/S1359-6446(97)01079-9. [DOI] [Google Scholar]
- 8.Leach AR, Willet VJ. An introduction to chemoinformatics. Dordrecht: Kluwer Academic Publishers; 2003. [Google Scholar]
- 9.Perola E, Charifson PS. J Med Chem. 2004;47:2499. doi: 10.1021/jm030563w. [DOI] [PubMed] [Google Scholar]
- 10.Nicklaus MC, Wang SM, Driscoll JS, Milne GWA. Bioorg Med Chem. 1995;3:411. doi: 10.1016/0968-0896(95)00031-B. [DOI] [PubMed] [Google Scholar]
- 11.Boström J, Norrby PO, Liljefors T. J Comput Aided Mol Des. 1998;12:383. doi: 10.1023/A:1008007507641. [DOI] [PubMed] [Google Scholar]
- 12.Kirchmair J, Wolber G, Laggner C, Langer T. J Chem Inf Model. 2006;46:1848. doi: 10.1021/ci060084g. [DOI] [PubMed] [Google Scholar]
- 13.Auer J, Bajorath J. J Chem Inf Model. 2008;48:1747. doi: 10.1021/ci8001793. [DOI] [PubMed] [Google Scholar]
- 14.Diller DJ, Merz KM., Jr J Comput Aided Mol Des. 2002;16:105. doi: 10.1023/A:1016320106741. [DOI] [PubMed] [Google Scholar]
- 15.Bender A, Mussa HY, Gill GS, Glen RC. J Med Chem. 2004;47:6569. doi: 10.1021/jm049611i. [DOI] [PubMed] [Google Scholar]
- 16.Butler KT, Luque FJ, Barril X. J Comput Chem. 2009;30:601. doi: 10.1002/jcc.21087. [DOI] [PubMed] [Google Scholar]
- 17.Chen IJ, Foloppe N. J Chem Inf Model. 2008;48:1773. doi: 10.1021/ci800130k. [DOI] [PubMed] [Google Scholar]
- 18.Günther S, Senger C, Michalsky E, Goede A, Preissner R (2006) BMC Bioinformatics 7 [DOI] [PMC free article] [PubMed]
- 19.Hao MH, Haq O, Muegge I. J Chem Inf Model. 2007;47:2242. doi: 10.1021/ci700189s. [DOI] [PubMed] [Google Scholar]
- 20.Kirchmair J, Laggner C, Wolber G, Langer T. J Chem Inf Model. 2005;45:422. doi: 10.1021/ci049753l. [DOI] [PubMed] [Google Scholar]
- 21.Vieth M, Hirst JD, Brooks CL., III J Comput Aided Mol Des. 1998;12:563. doi: 10.1023/A:1008055202136. [DOI] [PubMed] [Google Scholar]
- 22.Kirchmair J, Distinto S, Markt P, Schuster D, Spitzer GM, Liedl KR, Wolber G. J Chem Inf Model. 2009;49:678. doi: 10.1021/ci8004226. [DOI] [PubMed] [Google Scholar]
- 23.Dorfman RJ, Smith KM, Masek BB, Clark RD. J Comput Aided Mol Des. 2008;22:681. doi: 10.1007/s10822-007-9156-5. [DOI] [PubMed] [Google Scholar]
- 24.Li J, Ehlers T, Sutter J, Varma-O’Brien S, Kirchmair J. J Chem Inf Model. 2007;47:1923. doi: 10.1021/ci700136x. [DOI] [PubMed] [Google Scholar]
- 25.Izrailev S, Zhu FQ, Agrafiotis DK. J Comput Chem. 2006;27:1962. doi: 10.1002/jcc.20506. [DOI] [PubMed] [Google Scholar]
- 26.Pavlov T, Todorov M, Stoyanova G, Schmieder P, Aladjov H, Serafimova R, Mekenyan O. J Chem Inf Model. 2007;47:851. doi: 10.1021/ci700014h. [DOI] [PubMed] [Google Scholar]
- 27.Liljefors T, Petterson I. In: A textbook of drug design and development. Krogsgaard-Larsen P, Liljefors T, Madsen U, editors. Amsterdam: Overseas Publishers Association; 1996. pp. 60–93. [Google Scholar]
- 28.OMEGA: version 2.2.1 OpenEye Scientific Software: Santa Fe, NM, USA, www.eyesopen.com
- 29.Schrodinger, LLC, New York, NY 2008
- 30.Accelrys, Burlington, MA
- 31.Agrafiotis DK, Gibbs AC, Zhu FQ, Izrailev S, Martin E. J Chem Inf Model. 2007;47:1067. doi: 10.1021/ci6005454. [DOI] [PubMed] [Google Scholar]
- 32.Agrafiotis DK, Xu HF. Proc Natl Acad Sci USA. 2002;99:15869. doi: 10.1073/pnas.242424399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Martinez-Mayorga K, Medina-Franco JL, Giulianotti MA, Pinilla C, Dooley CT, Appel JR, Houghten RA. Bioorg Med Chem. 2008;16:5932. doi: 10.1016/j.bmc.2008.04.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tirado-Rives J, Jorgensen WL. J Med Chem. 2006;49:5880. doi: 10.1021/jm060763i. [DOI] [PubMed] [Google Scholar]
- 35.Mestres J, Rohrer DC, Maggiora GM. J Comput Aided Mol Des. 2000;14:39. doi: 10.1023/A:1008168228728. [DOI] [PubMed] [Google Scholar]
- 36.Smellie A, Teig SL, Towbin P. J Comput Chem. 1995;16:171. doi: 10.1002/jcc.540160205. [DOI] [Google Scholar]
- 37.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. J Comput Chem. 2004;25:1605. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 38.Version 2007; Chemical Computing Group Inc.: Montreal, Quebec, Canada
- 39.ROCS: version 2.3.1 OpenEye Scientific Software: Santa Fe, NM, USA, www.eyesopen.com
- 40.Kelley LA, Gardner SP, SM J (1996) Protein Eng 9:1063 [DOI] [PubMed]
- 41.Hess B, Kutzner C, van der Spoel D, Lindahl E. J Chem Theory Comput. 2008;4:435. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 42.Borodina YV, Bolton E, Fontaine F, Bryant SH. J Chem Inf Model. 2007;47:1428. doi: 10.1021/ci7000956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hawkins PCD, Skillman GA, Nicholls A. J Med Chem. 2007;50:74. doi: 10.1021/jm0603365. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.