Improved Recognition of Figures containing Fluorescence Microscope Images in Online Journal Articles using Graphical Models

Abstract

Motivation

There is extensive interest in automating the collection, organization, and analysis of biological data. Data in the form of images in online literature present special challenges for such efforts. The first steps in understanding the contents of a figure are decomposing it into panels and determining the type of each panel. In biological literature, panel types include many kinds of images collected by different techniques, such as photographs of gels or images from microscopes. We have previously described the SLIF system (http://slif.cbi.cmu.edu) that identifies panels containing fluorescence microscope images among figures in online journal articles as a prelude to further analysis of the subcellular patterns in such images. This system contains a pretrained classifier that uses image features to assign a type (class) to each separate panel. However, the types of panels in a figure are often correlated, so that we can consider the class of a panel to be dependent not only on its own features but also on the types of the other panels in a figure.

Results

In this paper, we introduce the use of a type of probabilistic graphical model, a factor graph, to represent the structured information about the images in a figure, and permit more robust and accurate inference about their types. We obtain significant improvement over results for considering panels separately.

Availability

The code and data used for the experiments described here are available from http://murphylab.web.cmu.edu/software. Contact: murphy@cmu.edu

1 INTRODUCTION

The dramatic increase in biological data in recent years, especially with respect to the sequences and structures of genes and proteins, has led to the creation of a number of biological databases. The information in these databases is largely incorporated by computer-generated links to relevant entries in other structured databases or entered manually by scientists in the relevant fields. Such structured databases are well-suited to collect, store, and deliver clearly specified information, but they usually do not typically allow uncertainty, alternative views or conflicting evidence. To capture these nuances, results of traditional biological research are most commonly communicated via journal articles in which raw data, methods, processed results and conclusions are mixed. In order to take full advantage of both paradigms, it is necessary to have approaches that can bridge between the systematic, structured information in biological databases and the idiosyncratic, unstructured information in journal articles.

The SLIF (Subcellular Location Image Finder) system was developed to illustrate the feasibility of addressing this need for information that is contained in both text and images in journal articles (Murphy et al. ^{2001, 2004}). Figures in journal articles may consist of multiple panels of many different types. The SLIF system focuses on initially identifying the type of each panel, and then doing extensive analysis on one type of images, fluorescence microscope images (FMI). FMI can capture information about the distribution of proteins and other biological macromolecules inside cells, and previous results have illustrated the value of the SLIF system for the specific task of identifying images depicting particular subcellular location patterns. More recently, other systems for figures in biomedical journal articles have been described. Rafkind et al. (2006) automatically classified general biological images in journals into five categories (gel images, graphs, images of things, mixtures, and models) using text and image features. Yu and Minsuk (2006) sought to make a connection between abstract sentences and biological images in the same article, so that the biological images can be accessed from abstract sentences. These two systems considered each figure in journal as a single object. However, a figure very often contains multiple panels which may consist of more than one type of image. Thus processing figures at the level of each panel, as is done in SLIF, can yield a more accurate reflection of figure content. In a similar vein, Shatkay et al. (2006) classified the panels in journal figures into hierarchical categories, and then used the categories as a feature vector to represent the article for document retrieval purposes.

In this paper, we focus on improving the recognition of FMI. High accuracy for this task is important for SLIF, since only panels considered to be FMI should be further processed to analyze subcellular patterns. Our starting point is to use edge and intensity histogram features with support vector machines to assign a type to each panel. Since the types of panels in a figure are often correlated, we conjectured that the performance on individual panels could be improved by considering information from more than one panel at a time. To this end, some simple voting methods can be used, such as the plurality voting method and the Borda count method, in which the type of each object is determined using information on the types of other objects. As these methods only need to calculate a function of the class probabilities of all or some objects, their computational cost is very low. However, these voting functions cannot capture the spatial relationships among the objects. Probabilistic graphical models provide a convenient and powerful way to represent uncertain information about objects and to facilitate reasoning. Therefore, in this paper, a type of probabilistic graphical model, the factor graph, is applied to capture information from all panels and collectively classify all interrelated images in a figure.

Below we will briefly introduce SLIF, explain how to construct a factor graph according to intuitions about the interaction among panels in a figure, describe the assignment of class probabilities to panels using probabilistic inference, present experimental results, and give conclusions and directions for further work.

2 SLIF

SLIF contains several modules for image and text processing, and the structured SLIF database is built by combining their results.

2.1 Figure processing

Figure processing in SLIF consists of extracting figures from articles, splitting each into panels (meaningful subfigures), identifying fluorescence microscope panels, detecting panel annotations, and classifying and analyzing subcellular patterns. The methods used for each of these steps, and evaluations of their accuracy, have been described in detail previously (Murphy et al. 2004).

Extracting figures from online journal articles

The original SLIF system used a web robot to retrieve PDF versions of online journal articles that might have relevant images. The current version processes articles in XML format, extracting matching figures and captions.

Splitting figures into panels

For figures composed of multiple panels, the individual panels must be isolated in order to interpret them appropriately. Fluorescence microscope panels usually have a dark background with light areas showing where fluorescence was detected. Based on this fact, a recursive algorithm was proposed for finding the light boundaries between micrographs even when the panels are not arranged in a symmetric pattern (Murphy et al. 2001). Journal figures contain other types of panels that are not surrounded by a boundary, and the performance of the recursive algorithm may degenerate for these types. However, it works well for separating micrographs from the remainder of the figure, so this is not a major problem for SLIF.

Identifying FMI

After the panels have been isolated, the next task is to identify what type of image they contain, the focus of this paper. The initial approach in SLIF consisted of a k-nearest neighbor classifier built on a collection of hand-labeled panels. For each panel, a histogram of pixel intensities was constructed with 64 equally-spaced bins ranging from the minimum to the maximum pixel intensity in that panel; the frequencies of the bins were used as features. These achieved a precision of 100% and recall of 90% on panels extracted from PDF files (Murphy et al, 2001). As journal articles became increasingly available in XML format with associated figure files, SLIF was modified to be able to process articles in this format. The initial FMI classifier did not perform as well for the more variable images thus obtained. Therefore, we developed an improved classifier for FMI panels (Hua et al, 2007). This uses edge features in addition to intensity histogram features. Using a support vector machine, the new classifier achieved a precision, recall, and F-measure of 85% on a randomly-chosen set of panels from a large collection of articles from the Proceedings of the National Academy of Sciences, U.S.A. (Hua et al, 2007).

Detecting panel annotations

Fluorescence micrograph panels typically may have three types of annotations contained within them. The first is a panel serial label that follows the arrangement order of panels in a figure and connects panels to information in the caption. The second is a scale bar whose length is usually defined in the caption. The third is text or symbols that are used for attracting the reader’s attentions to specific locations in the figure. All of these annotations need to be detected, analyzed, and then removed from the image before further processing (Kou et al. 2003). The current version of SLIF can automatically detect and recognize internal labels (labels that are embedded in the panels, the most common situation), with a precision of 79.1% and recall of 70.7% (Kou et al. 2003). In the FMI recognition method discussed in this paper, panel serial labels will be an important alternative source for representing the structured information among the panels in a figure.

Analyzing subcellular patterns

The steps above complete the task of finding FMI in journal articles. While SLIF then uses a number of methods for extracting appropriate subcellular location information from these FMI, those methods will not be discussed here since the focus of this paper is on FMI recognition.

2.2 Text processing

Text processing in SLIF focuses on information extraction from the captions of figures, and the resulting information is combined with image information to form an integrated SLIF database. Caption processing has three goals: identifying the “image pointers” (e.g., “(A)”) in the caption that refer to panel serial labels in the figure, dividing the caption into fragments (or “scopes”) that refer to an individual panel or the entire figure, and recognizing protein and cell names. The first of these is the only one that is required for the work described in this paper, since caption processing can aid identification of the type of panel . The list of “image pointers” obtained by interpreting the caption associated with a figure can correct possible missing or incorrect panel serial labels obtained by detecting panel annotations. Using string matching approaches to align “image pointers” and panel serial labels, the precision and recall for recognizing panel serial labels was improved to 83.2% and 74.0% respectively (Kou et a. 2003). It should be noted that in this paper we use the term “panel class label” to represent the type of a panel and “panel serial label” to represent its arrangement order in a figure.

3 FACTOR GRAPHS FOR IDENTIFYING FMI

The classification methods previously implemented in SLIF for identifying FMI classify the panels individually based on their own properties. In fact, identifying FMI from multiple panels in a figure, however, is a special classification problem that involves sets of related objects whose class labels tend to be consistent with each other. In other words, all of the panels in a figure, or sets of neighboring panels in a figure, are often of the same image class. We will consider how to “revise” the class probabilities of the panels (obtained by classifying them independently) by using potential interactions between them. Probabilistic graphical models provide a theoretical foundation and a practical tool for this task. In this paper, a factor graph is introduced to represent and process this interaction mechanism. Factor graphs (Kschischang et al. 2001) are more general than other graphical models (such as Bayesian networks and Markov random fields) in terms of their ability to express information. The advantages of factor graphs for our problem are that the interaction between panels need not be modeled as a causal entity, and cycles can be supported.

3.1 Preprocessing

Before creating the factor graph, we need to prepare the data that will be used as the inputs at each node. These steps are included in the overall SLIF pipeline described above, but are identified here as particularly needed for inference about panel types. First, the initial classification results for each panel are obtained by classifying panels independently using their image features. Various classification approaches can be used in this step, but the outputs should be the class probabilities of each panel, i.e., each panel i has a probability p(x_i = FMI) of being classified as FMI and a probability p(x_i = nonFMI) = 1 − p(x_i = FMI) of being classified as any of the other type. Second, panel serial labels are detected and recognized. This is a challenging problem because the serial label is usually a single character embedded in a complex background; we have described various strategies for improving performance (Kou et al. 2003). However, for some figures, we still do not obtain their panel serial labels for various reasons (including the possibility that the panel serial labels are outside the panels rather than within them), so that the information about the panel arrangement in a figure cannot be derived from panel serial labels. Therefore, the third type of information we compute about each panel is its position within the figure. The recursive panel splitting method used in SLIF always returns rectangular panels, so the positions of the two diagonal corners of the rectangle, or the position of the center and the side lengths of the rectangle, determine the position of a panel. In the work described here, we have explored using panel serial labels, panel positions, or both to provide information about the arrangement of panels in a figure.

3.2 Constructing the factor graph

A factor graph explicitly indicates how a joint function of many variables can be factored into a product of local functions (also called potential functions) of smaller sets of variables. The joint function is usually the joint probability distribution. A factor graph is defined as a bipartite graph with two vertex (node) types: variable vertices V_x and factor vertices _Vf of size n and m respectively such that the ith node in V_f is connected to the jth node in V_x if and only if x_j is an argument of function f_i . Let X = {x₁, x₂,…, x_n} be a set of variables. Consider a function f (X ) with factors as follows

$$f(x_1,x_2,\cdots ,x_n)=\prod _{i=1}^m{f}_i\left(C_i\right)$$ (1)

where C_i is the set of variables (a clique of vertex f_i ), which are the arguments of the local function f_i . Fig. 1b and 1c show the graph representations of

$$\begin{array}{cc}\hfill f\left(X\right)=& f_A(x_1,x_2)f_B(x_1,x_2,x_3)f_C(x_2,x_3,x_4)\hfill \\ \hfill & f_D(x_3,x_4,x_5)f_E(x_4,x_5,x_6)f_F(x_5,x_6)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill f\left(X\right)=& f_A(x_1,x_2,x_3)f_B(x_1,x_2,x_4)f_C(x_1,x_3,x_4,x_5)\hfill \\ \hfill & f_D(x_2,x_3,x_4,x_6)f_E(x_3,x_5,x_6)f_F(x_4,x_5,x_6)\hfill \end{array}$$

The variable vertices are marked as circles and the factor vertices as squares.

Fig. 1.

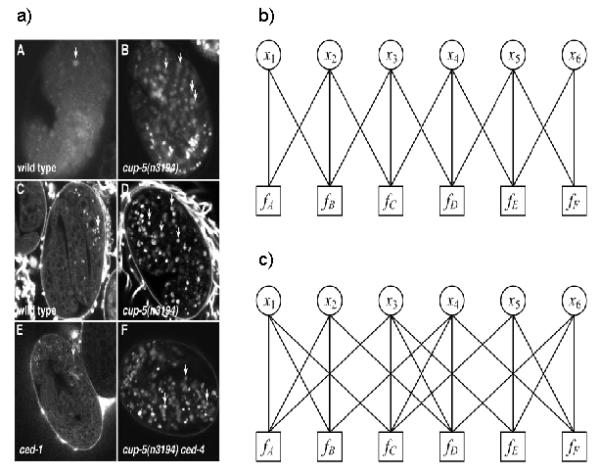
Illustration of construction of factor graphs. a) An example figure with six panels (from Hersh et al. 2002). b) A factor graph for the figure in panel (a) in which the neighbors of a panel are determined by its panel serial label. For example, the class probability of panel d is influenced by the class probabilities of panel c and panel e. c) A factor graph in which the neighbors of a panel are determined by their positions. The class probability of panel d is influenced by the class probabilities of panel b, c and f.

Many problems in recognition and learning are formulated as minimizing or maximizing a global function marginalized for a subset of its arguments. For the problem of identifying FMI from a figure, one of main contributions of this paper is a computational framework in the form of a factor graph that can factor a complex joint distribution of the class probabilities of panels in a figure into a product of their local interaction functions.

The key task of constructing a factor graph is to define the local functions that describe the interaction among the panels in a figure. These functions can be learned from examples, or directly specified from domain intuition/knowledge. In our problem, we postulate that the local functions should favor the same class label for all panels in the same clique. In this case, a common approach is to use a Potts model (Potts 1952), which penalizes assignments that do not have the same label in the clique. Since every clique of a Potts model has only two variable vertices, the local functions are simple and inference becomes efficient and fast. However, the Potts model does not perfectly capture the notion that influence on the class label of a vertex should reflect the class labels of all its neighbors. We have previously described an alternative potential function, the voting potential, which sums the contributions of each neighbor of an object into a vote which then influences that object’s classification (Chen et al, 2006a). When this model is applied to identify FMI, each variable vertex x_i represents a panel in a figure (with value equal to the class of the panel, in our case either FMI or non-FMI), and it has a corresponding factor node f_i that captures the intuition that the class probability of panel i is influenced by the class probabilities of the other panels in the same clique (these panels are also called the neighbors of panel i) i.e., the panel i tends to have a same class label as the other panels. The function f_i can be defined as

$$f_i(x_i,\mathrm{N}(x_i\left)\right)=\frac{\lambda +\sum _{x_j\in \mathrm{N}\left(x_i\right)}\delta (x_i,x_j)}{\lambda +s_i}$$ (2)

where the assignment of x_i is FMI or non-FMI. Ν(x_i) is the neighbors of panel i except itself, and s_i is the number of vertices in Ν(x_i). λ is a control parameter (the smaller λ is, the more strongly the class probability of panel i is influenced by its neighboring panels). δ is an indicator function which is 1 when the value of x_i is equal to that of x_j and 0 otherwise.

However, the above function considers that the panels in Ν(x_i) have the same impact on panel i, which is not always right in most cases. Here we extend it by proposing a weighted voting potential, in which every neighbor of one panel has its individual strength of impact on it so that they can contribute different influences. Compared with the original voting potential, the weighted voting potential may represent interactions more precisely. Therefore, a new local function can be defined as

$$f_i(x_i,\mathrm{N}(x_i\left)\right)=\frac{\lambda +\sum _{x_j\in \mathrm{N}\left(x_i\right)}{w}_{ij}\delta (x_i,x_j)}{\lambda +\sum _{x_j\in \mathrm{N}\left(x_i\right)}{w}_{ij}}$$ (3)

where w_ij is the strength of impact of panel j on panel i,

Now the remaining task is to decide the neighbors of each panel, and their corresponding strengths of impact on that one, which can be computed with their positions and serial labels in a figure. From a large number of figures in journal biological articles, we found that if two panels have the same or consecutive panel serial labels, or their positions are close to each other, they have a large interaction. Thus w_ij is defined as

$$w_{ij}=\alpha \left(\delta (l_i,l_j)+0.5\left(\delta \right(l_i,l_j+1)+\delta (l_i,l_j-1\left)\right)\right)+(1-\alpha )\left(\frac{\mathit{dist}\_\mathit{panel}(i,j)}{\mathit{size}\_\mathit{figure}}\right)$$ (4)

where l_i is the index of panel serial label of panel i, dist _ panel(i, j) is the Euclidean distance between centers of panel i and j, and size _ figure is the diagonal length of the figure. The first term in the right side of equation (4 ) represents the information derived from panel serial labels, the second term represents the information derived from panel positions, and α controls the balance between them (e.g., if the panel serial labels can not be accurately extracted, α should be 0, and the first term will be ignored). The position information is calculated as Euclidean distance between two panels normalized by the diagonal size of the figure containing them.

The neighbors of panel i are given by

$$\{\begin{array}{cc}{x}_j\in \mathrm{N}\left(x_i\right),\hfill & \text{if}{w}_{ij}\ge T,\hfill \\ x_j\notin \mathrm{N}\left(x_i\right),\hfill & \text{if}{w}_{ij}<T.\hfill \end{array}\phantom{\}}$$ (5)

This also serves to limit the size of clique to improve the computational efficiency of the factor graph.

3.3 Probabilistic inference on a factor graph

After a factor graph is constructed, the next task is to infer the class probabilities of panels by Bayesian reasoning method. The belief propagation (BP) scheme is commonly used, in which the Sum-Product algorithm can compute marginal probabilities and then compute the assignment of each variable that maximizes its individual marginal (Pearl 1988). It is based on message-passing according to a simple rule: “the message sent from a node v on an edge e is the product of the local function at v (or the unit function if v is a variable node) with all messages received at v on edges other than e, summarized for the variable associated with e.” (Kschischang et al. 2001).

In the Sum-Product algorithm, the message from the variable node x_i to the factor node f _j is defined as

$$v_{x_i\to f_j}\left(x_i\right)=\text{evidence}\left(x_i\right)\prod _{t\in \mathrm{N}\left(x_i\right)\backslash f_j}{\mu }_{t\to x_i}\left(x_i\right)$$ (6)

where evidence(x_i) is the initial class probability of panel i. Ν(x_i)is a set of factor nodes that are connected to variable node x_i by edges. The message from the factor node f_j to the variable node x_i is defined as

$${\mu }_{f_j\to x_i}(x_i=\sum _{\mathrm{N}\left(f_j\right)\backslash x_i)}\left(f\left(\mathrm{N}\right(f_j\left)\right)\prod _{x_h\in \mathrm{N}\left(f_j\right)\backslash x_i}{v}_{x_h\to f_j}\left(x_h\right)\right)$$ (7)

where Ν( f_j )is a set of variable nodes that are connected to factor node f_j by edges. After the message-passing computation is completed, the marginal probability of panel i can be calculated by

$$p(x_i\mid \text{evidence})=\text{evidence}\left(x_i\right)\prod _{t\in \mathrm{N}\left(x_i\right)}{\mu }_{t\to x_i}\left(x_i\right)$$ (8)

If the factor graph is a factor tree (cycle-free), the two messages for each edge (from variable node to factor, and from factor node to variable node) only need to be computed once, and the Sum-Product algorithms can produce exact inference results. Otherwise, if a factor graph has cycles, more complicated and approximate inference mechanisms are needed. Among them, the loopy belief propagation (LBP) is commonly used (Yedidia et al. 2000). Since the factor graphs discussed in this paper always have cycles, we chose to use the LBP-based Sum-Product algorithm. The iterative procedure of LBP is:

1. Compute all messages from variable nodes to factor nodes with equation (6 )

2. Compute all messages from factor nodes to variable nodes with equation (7 )

3. Repeat until convergence condition is satisfied.

According to equation (7 ), the computational cost of a message from a factor node to a variable node is linearly scaled to the number of arguments of the corresponding potential function, that is c^m, where c is the number of classes (here we only two class labels FMI and non-FMI, so c=2) and m is the size of the corresponding potential function. Therefore BP, and even LBP, becomes computationally intractable when the size of the cliques and the number of classes are too large. To speed up LBP, even further approximations are required. Some forms of approximations have been proposed by discarding low-likelihood states (Coughlan and Ferreira 2002), pruning edges, quantizing the potential function, or redefining the messages (Minka 2001). No matter which approximation method is used, we would like to know what effect the approximations introduced will have on the overall inference performance. Some theoretical results concerning the convergence of message approximation and its distance bound to the LBP message have been achieved (Ihler et al. 2005). They assume that there are “true” messages (as the “true” messages are usually not acquired, in practice they can be replaced with the messages of the standard LBP). If the error between approximate messages and “true” message satisfies some conditions, these approximations maybe guaranteed to converge to some regions of fixed points, as well as have bounds on the resulting error over “true” LBP. However, perhaps more important in practice, many experimental results have shown that if the difference between the approximate messages and the “true” message is relatively small, the overall solutions will not have obvious changes. This gives us freedom to construct approximate algorithms of LBP on a factor graph.

Here, we developed two message approximation methods to simplify the standard LBP Sum-Product algorithm, both based on the idea of prior updating (Chen and Murphy, 2006; Chen et al, 2006a) that considers only important and dominant messages to be updated in iterations, and furthermore uses approximations for even these remaining messages. The first approximate method only selects the messages from each factor f_i to its corresponding variable x_i to be updated, and the other messages from factor f_i to Ν( f_i ) \ x_i are ignored (all given a unit function). The reason is that the factor node f_i captures the information of panel i being influenced by its neighboring panels, so that it plays a dominant role in updating the probability of panel i. Although this approximation can speed up LBP, we still need to scan all arguments of the potential functions. Therefore, our second approximation method also approximates equation (7 ) by

$${\mu }_{f_j\to x_i}(x_i=k)=\frac{\lambda +\sum _{x_{\mathrm{h}}\in \mathrm{N}\left(f_j\right)\backslash x_i}{w}_{jh}{v}_{x_h\to f_j}(x_h=k)}{\lambda +\sum _{x_h\in \mathrm{N}\left(f_j\right)\backslash x_i}{w}_{jh}}$$ (9)

where k represents the kth class label. This equation need not scan all arguments of the potential functions. These two simplified LBP algorithms are refereed to as PULBP1 and PULBP2 respectively. The next section will demonstrate that inference results with these simplified LBP algorithms are almost the same as those with standard LBP, but that the computational cost can be greatly reduced.

4 EXPERIMENTAL RESULTS

We used two datasets for testing panel recognition performance. Both were created by choosing a random set of panels from the results of SLIF processing on a collection of articles in the Proceedings of the National Academy, U.S.A. (volumes 94-99) and categorizing each panel as FMI or non-FMI by visual inspection of the figure and caption (Hua et al., 2007).

• Dataset A: 86 figures with 570 panels, of which 287 panels are FMI. For these figures, the labels were not embedded in the panels, so the current version of SLIF cannot automatically assign them. They were therefore manually assigned.

• Dataset B: 89 figures with 525 panels, of which 371 panels are FMI. In this set, all panel serial labels were automatically obtained. An improved SVM-based FMI classifier (Hua et al, 2007) was used as the baseline for comparison to other methods, and its output was used as the evidence in the factor graph (Platt 1999). For evaluation, we measured accuracy [(TP+TN)/total], precision [TP/(TP+FP)], recall [TP/(TP+FN)], and F-measure, [2*prec*recall/(prec+recall)], where TP is True Positives, FP False Positives, TN True Negatives, FN False Negatives and positive is FMI. We chose F-measure as our primary figure of merit.

Before giving an overall evaluation of the performance of the graphical models, we will examine three typical cases and how inference results compare to manually-assigned ground truth. In these examples, the PULBP2 inference algorithm was used.

Figure 2 shows a typical figure for which graphical model inference maintained the correct initial classification results. Table 1 shows the class probabilities for each panel as given by the baseline classifier and the PULBP2 algorithm for various values of the inference parameters. In this case, the individual panels were all correctly classified by the baseline classifier. The interaction between panels in the factor graph modifies the initial class probabilities for each panel, but does not alter the correct initial result.

Fig. 2.

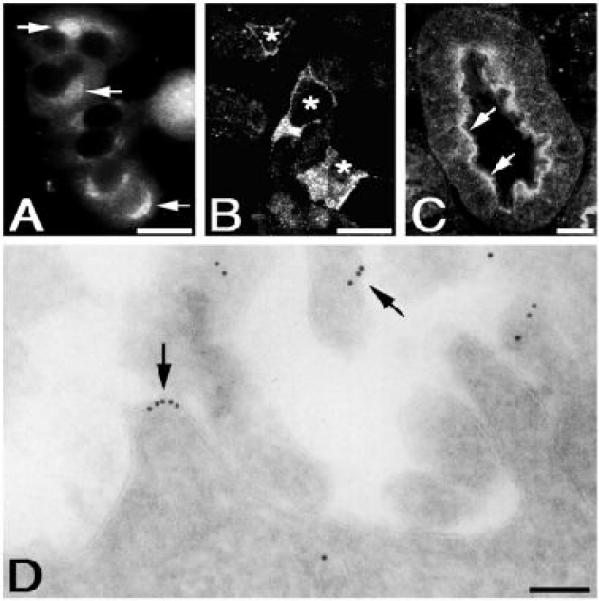
This figure (from Zheng et al. 2000) includes four panels. Panel (A-C) are FMI, and panel (D) is not.

Table 1.

Inference results for the case shown in Fig. 2. Shown are the initial label probabilities of the panels, obtained using a single panel (baseline) classifier, and the final label probabilities of the panels, obtained using a factor graph with the PULBP2 algorithm.

Actual class	Initia l F M I prob.	Final FMI probabilities ( α =0, λ = 2 )	Final FMI probabilities ( α =0.5, λ = 2 )	Final FMI probabilities ( α =1, λ = 2 )
FMI	0.740	0.838	0.882	0.883
FMI	0.704	0.809	0.835	0.863
FMI	0.695	0.800	0.762	0.742
Non	0.000	0.000	0.000	0.000

Figure 3 and Table 2 show a typical case where the correct class labels of all panels are the same (FMI), and most but not all of the panels are correctly classified by the initial classifier. Using the graphical model, the panels that were not initially correct are assigned their correct label. This is because the influence of the panels with the correct class label is stronger than that of the ones with the wrong class label and the initial probabilities of the incorrectly classified panels were not high (and were therefore easy to push above or below the recognition threshold). This example illustrates the kind of improvement that we sought to obtain.

Fig. 3.

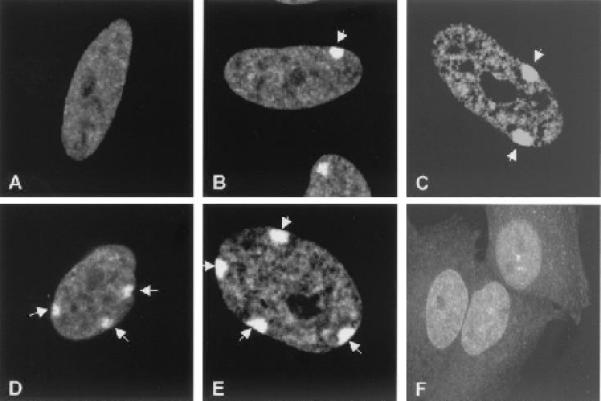
This figure (from Hong et al. 2001) includes six panels, all of which are FMI.

Table 2.

Inference results for the case shown in Fig. 3. Note that in this case the factor graph corrects the misclassification of the last panel.

Actual class	Initial FMI prob.	Final FMI probabilities ( α = 0, λ = 2 )	Final FMI probabilities ( α = 5.0, λ = 2 )	Final FMI probabilities ( α = 1, α = 2 )
FMI	0.792	0.958	0.946	0.938
FMI	0.784	0.956	0.948	0.946
FMI	0.718	0.939	0.928	0.921
FMI	0.796	0.959	0.942	0.932
FMI	0.731	0.925	0.916	0.926
FMI	0.492	0.797	0.726	0.672

Figure 4 and Table 3 show a more complex case in which more than one type of image exists and one of the FMI panels is incorrectly classified. The incorrect panel can be easily corrected to FMI even in the presence of non-FMI panels.

Fig. 4.

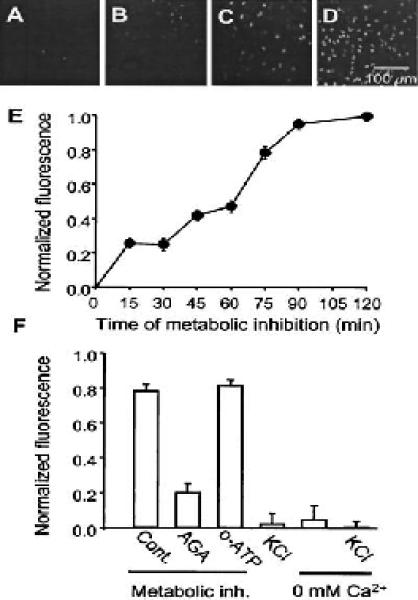
This figure (from Contreras et al. 2002) has four top FMI panels and two bottom non-FMI panels.

Table 3.

Inference results for the case shown in Fig. 4. Note that the factor graph corrects the incorrect panel even when both types are present.

Actual class	Initial label prob	Final label probabilities ( α = 0, λ = 2 )	Final label probabilities ( α = 0.5, λ = 2 )	Final label probabilities( α = 1, α = 2 )
FMI	0.877	0.947	0.955	0.972
FMI	0.869	0.940	0.953	0.974
FMI	0.810	0.905	0.917	0.940
FMI	0.491	0.664	0.667	0.675
Non	0.038	0.045	0.025	0.006
Non	0.018	0.004	0.003	0.003

The above examples illustrate the mechanism by which graphical models may be expected to improve the recognition of FMI. Encouraged by these results, we carried out a more quantitative evaluation of the performance of the graphical model methods. Figure 5 shows the F-measures for the three inference algorithms for various values of the two parameters, α and λ, in our model. λ controls the strength of the interaction between neighboring panels, so _{λ = 0, 2, and 5} represent strengths ranging from large to small. Compared with the baseline classifier, the F-measures of the three factor graph inference algorithms for various values of the parameters were improved from 1% to 4%. Table 4 shows the average performances on the two datasets for the three algorithms, which are calculated by averaging their performance measures over the parameter combination of α = 0, 0.5,1 and λ = 0, 2, 5.

Fig. 5.

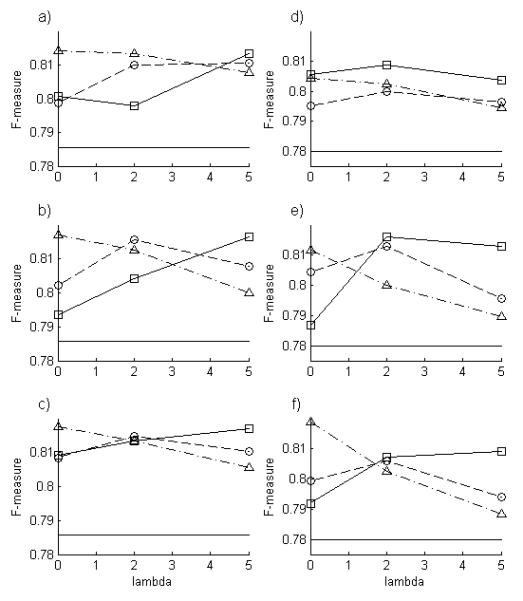
Performance of factor graph methods as a function of model parameters. The F-measures for LBP (squares), PULBP1 (circles), and PULBP2 (triangles) are shown for dataset A (left) and B (right) for various values of λ and for α 0.5 (a,d), α = 1 (b,e) and α = 1 (c,f). Note the roles of the model parameters: increasing a corresponds to a shift from inference based solely on panel position to inference based solely on panel serial label, and increasing l corresponds to decreasing influence of neighboring nodes. The F-measure for the baseline classifier is also shown ().

Table 4.

Panel classification performance of different algorithms. Values shown are averages over the parameter combination of α = 0, 0.5, 1 and λ = 0, 2, 5on dataset A (first value in each cell) or B (second value).

	Accuracy	Recall	Precision	F-measure
Baseline	79.1 / 72.4	79.8 / 69.3	77.4 / 89.2	78.6 / 78.0
LBP	81.1 / 76.0	78.8 / 70.6	82.9 / 93.5	80.7 / 80.5
PULBP1	81.1 / 75.4	79.3 / 70.2	82.5 / 93.1	80.8 / 80.0
PULBP2	81.2 / 75.4	80.4 / 70.6	81.9 / 92.7	81.1 / 80.1

Although the above experiments appear to show that recognition performance is improved using factor graphs, we wished to determine if these effects were statistically significant. We created 30 samples by randomly selecting a baseline classifier (RBF kernel SVM with argument ranging from 5 to 20), and used random α (0 to 1) and λ (0 to 5) values to analyze them with all three methods. We then tested the null hypothesis that a given performance measure (precision, recall, F-measure) for a given method was equal to that of the SVM. This was rejected at the 0.005 significance level for all three measures and all three methods).

The performance of the factor graph method can be also evaluated at the level of entire figures rather than on individual panels. That is, a figure is considered to be correctly classified only if all its panels are correctly classified. Table 5 shows the average accuracies of figure recognition for LBP, PULBP1, and PULBP2. Compared with the baseline classifier, the improvements ranged from 20% to 25%, which are much larger than the improvements of accuracy at the panel level (2% to 4%, Table 4). This phenomenon reflects the characteristics of graphical model methods. The figures that are wrongly recognized by the initial classifier can be categorized into two types in terms of the proportion of the panels with the wrong class label in a figure. The first type has a small number of panels with the wrong class label, so the influence of the panels with the correct class label is strong and the panels that were not initially correct are easily assigned their correct class label using graphical model methods. The second type of figure has a larger number of incorrect panels, so graphical model methods fail because the panels with the correct class label may not have enough strength to influence the ones with the wrong class label. Although the number of panels in the first type of figures that were corrected by graphical model methods is not large relative to the total panels with the wrong class label, the number of these figures is large relative to the total figures, which made improvement measures different at the panel and figure levels.

Table 5.

Accuracy at the figure level. A figure is considered to be correct if all of its panels are correctly classified. The average accuracy measures of each method are obtained by averaging their accuracy over the parameter combination of α = 0, 0.5, 1 and λ = 0, 2, 5.

	Baseline	LBP	PULBP1	PULBP2
Dataset A	43.0	62.3	61.2	62.4
Dataset B	39.3	66.3	65.8	65.5

Overall, the results indicate that recognition performance can be improved by the factor graph method. All three inference algorithms perform significantly better than the baseline classifier, and there are no significant differences between them in overall recognition performance. However, their running times are very different, with PULBP2 being much faster (Table 6). Both panel serial labels and positions well represent the structuring information of panels in a figure, so we can use either or both of them to improve FMI recognition. λ affects the recognition performance, but there is no general rule for determining an optimal value. Performance can be expected to be improved by the factor graph model as long as λ values are in a reasonable range.

Table 6.

Elapsed CPU times for LBP, PULBP1, and PULBP2 using an Intel Pentium 1.73G processor with 512M memory. Values shown are average CPU times (in seconds) over the inference parameter combinations of α = 0, 0.5, 1 and λ = 0, 2, 5.

	LBP	PULBP1	PULBP2
Dataset A	4846	1115	101
Dataset B	2765	812	145

For SLIF, we are often willing to sacrifice recall (number of FMI found) to obtain higher precision (fraction of predicted FMIs correct). We therefore created precision-recall curves. The panels were ranked from high to low according to value of their maximum marginal probability, and precision and recall were calculated cumulatively as the minimum acceptable marginal probability was decreased from 1 (Fig. 6). PULBP2 provides better performance than the baseline classifier and very high precisions can be obtained.

Fig. 6.

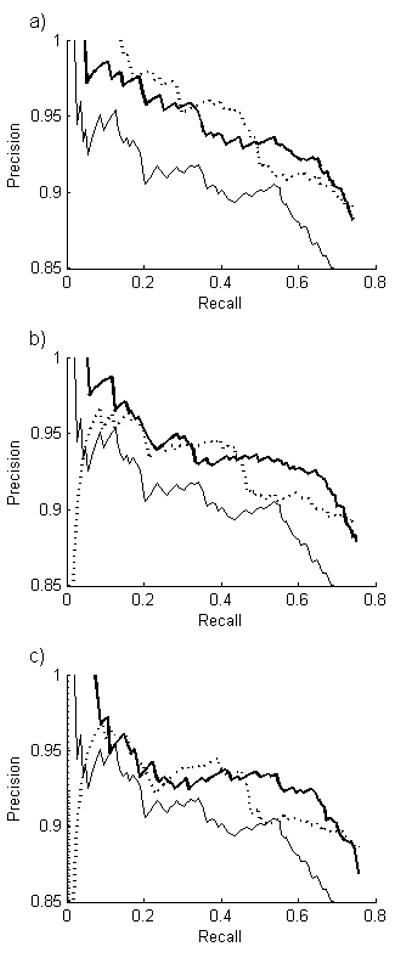
Recall-precision curves for PULBP2 for various inference parameters. A threshold on the estimated marginal probability of each panel classification was varied. Values shown are for α = 0 (left) and α = 1 (right). ( , baseline classifier: ). Values for λ = 5 were similar to λ = 2 (not shown).

The graphical model method we have presented is based on the interaction between the multiple panels in a figure. It was therefore of interest to determine how the performance is affected by the number of panels in a figure. The figures in dataset A and B were partitioned into groups by the number of panels. Then the performance measures on these groups were averaged over various values of parameters and for both datasets. Figure 7 shows PULBP2 usually produced better recognition performance than the baseline classifier whenever more than one panel was present.

Fig. 7.

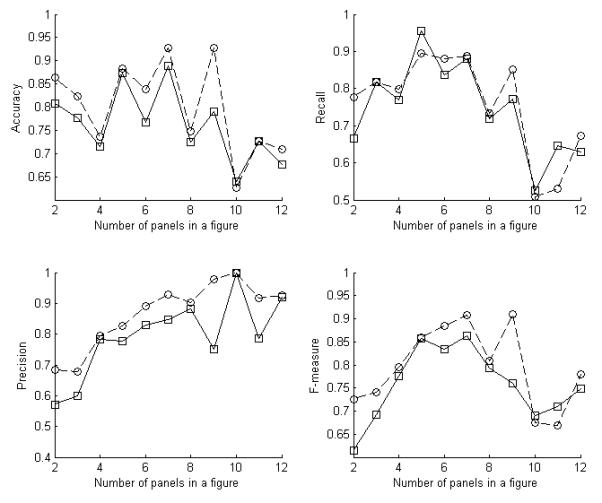
The average recognition measures of PULBP2 for the parameter combination of α = 0, 0.5, 1 and λ = 0, 2, 5 on the figures in dataset A and B with different numbers of panels. The numbers of figures with each number of panels from 2 to 12 are 13, 12, 49, 11, 25, 9, 25, 9, 5, 3, 8 respectively. (Baseline classifier: solid line, PULBP2: dashed line).