Susceptibility gradient quantization by MRI signal response mapping (SIRMA) to dephaser

Abstract

Purpose

Susceptibility effects are a very efficient source of contrast in Magnetic Resonance Imaging. However, detection is hampered by the fact the induced contrast is negative. In this work, the SIgnal Response MApping to dephaser (SIRMA) method is proposed to map susceptibility gradient to improve visualisation.

Methods

In conventional gradient echo acquisitions, the echo formation of susceptibility affected spins is shifted in k-space, the shift being proportional to the susceptibility gradient. Susceptibility gradients map can be produced by measuring this induced shifts. The SIRMA method measures these shifts from a series of dephased images collected with additional incremental dephasers. These additional dephasers correspond either to a slice refocusing gradient offset or to a reconstruction window off-centering. The signal intensity profile as a function of the additional dephaser, was determined on a pixel-by-pixel basis from the ensemble of dephased images. Susceptibility affected voxels presented a signal response profile maximum shifted compared to non-affected voxels ones. Shift magnitude and sign were measured for each pixel to determine susceptibility gradients and produce susceptibility gradient map.

Results

In vitro experiments demonstrated the ability of the method to map gradient inhomogeneities induced by a cylinder. Quantization accuracy was evaluated comparing SIRMA images and simulations performed on the well-characterized air filled cylinder model. Performances of the SIRMA method, evaluated in vitro on cylinders filled with various superparamagnetic iron oxide SPIO concentrations, showed limited influence of acquisition parameters. Robustness of the method was then assessed in vivo after an infusion of SPIO-loaded nanocapsules into the rat brain using a convection-enhanced drug delivery approach. The region of massive susceptibility gradient induced by the SPIO loaded nanocapsules was clearly delineated on SIRMA maps and images were compared to T2* weighted images, Susceptibility Gradient Map and histological Perl’s staining slice. The potential for quantitative evaluation of SPIO distribution volume was demonstrated.

Conclusions

The proposed method is a promising technique for a wide range of applications especially in molecular or cellular imaging with respect to its quantitative nature and its computational simplicity.

Introduction

Susceptibility effects are a very efficient source of contrast in Magnetic Resonance Imaging. Therefore, the ability to selectively track or quantify object-induced local susceptibility gradient is a challenge of importance with applications in numerous domains. Indeed, interventional devices tracking¹, visualization of superparamagnetic iron oxide (SPIO) contrast agents, cell trafficking assessment², BOLD imaging³, estimation of osteoporosis in spongy bones⁴ or even bubble size in alveolar products⁵ may benefit from the local susceptibility gradient quantization. Susceptibility effect appears as signal loss on the T2* weighted gradient echo images due to the induced magnetic field inhomogeneity. A fundamental drawback of negative contrast is the difficulty to discriminate susceptibility-induced hyposignal from other sources of signal voids such as tissue interface, haemorrhage, or motion artefacts. Recently, to overcome these problems, efforts have been made on converting this hyposignal into a positive contrast.

Positive contrast techniques are based, either on the local resonance frequency changes or on the shift of the echo peak in k-space. Frequency-based methods use spectrally selective RF pulses to produce off-resonance selective excitation⁶ or on-resonance selective suppression⁷. K-space shift methods aim at suppressing background signal while preserving susceptibility shifted signal via modified acquisition sequence (gradient compensation based technique⁸) or post-processing calculation (dephased MRI⁹).

However, the previously described methods require an a priori knowledge and/or optimization to reach optimal positive contrast. One way to overcome this limitation is to quantitatively map the susceptibility gradient. Several works have been performed over the past years to map the susceptibility gradient mainly to correct geometrically distorted EPI for functional MRI^10,11. However, most of the time, these magnetic field mapping techniques require extra scan time and/or use complex phase unwrapping algorithm. An alternative method which saves scan time was proposed by Dahnke et al.^12,13 where susceptibility gradient maps, or SGM, were calculated directly from conventional gradient echo acquisition.

In this work, we propose another method to map susceptibility gradients and improve SPIO visualisation. This method, based on k-space shift methods, is referred to as SIgnal Response MApping to dephaser (SIRMA).

Theory

In conventional gradient echo sequence, the k-space energy peak is located at the center of the acquisition window. As initially shown by Posse in 1992¹⁴ and then formalized by Bakker et al.⁹, the incorporation of an additional gradient G_ad corresponds to a shift $\overrightarrow{\delta k}=(\delta k_x,\delta k_y,\delta k_z)$ of the echo peak in the original k-space data. δk_x, δk_y, δk_z are called dephasers and correspond to the shift induced along x, y and z respectively. The original signal s is then modified as follows:

$$S_{G_{ad}}(k_x,k_y,k_z)=s(k_x+\delta k_x,k_y+\delta k_y,k_z+\delta k_z)$$ [1]

As susceptibility effect corresponds to an additional local gradient, G_sus, the echo formation of affected spins, is shifted away from the center in k-space in the G_sus direction. The shift is proportional to the susceptibility gradient¹³. One way to create positive contrast is to preserve the susceptibility-shifted signal by inducing a shift in k-space, opposite to the one induced by the susceptibility gradient. A dephaser can be used to induce such an opposite shift. This dephaser can either be the imaging gradients adjusted to compensate susceptibility effects (gradient compensation technique⁸ also called “white maker” technique) or an off-centering of the reduced reconstruction window of a conventional gradient echo dataset (dephased MRI⁹). One step further is to map the susceptibility gradient from the measure of the echo-shift in k-space¹⁵. The amount of shifting can be measured by SGM^12,13 or by the new SIRMA method.

Susceptibility Gradient Mapping

Dahnke et al. showed how to determine susceptibility gradient vector by post-processing regular complex gradient-echo dataset. Initially, the echo-shift vector in k-space was measured for each voxel by performing a local Fourier analysis in a small neighborhood for the three spatial directions^13,16. However, taking into account the fact that the echo shift was calculated by performing a 1D FT over a subset of n voxels, the resulting positive images had an n-fold lower spatial resolution compare to the original gradient echo dataset. Dahnke et al.¹² have recently overcome this drawback by implementing the k-space energy spectrum analysis to quantify the echo-shifting effect. This process was initially developed by Chen et al. for the correction of distortions in gradient echo EPI¹⁷. The k-space energy spectrum measured the impact of k-space truncation on the Fourier transformed image. The k-space energy spectrum for one direction of k-space corresponds to the signal intensities of a given pixel, reconstructed from partial Fourier data when the number of truncated k lines varies from 1 to the size of k-space in this direction. An abrupt change of signal intensity was observed when the peak of k-space echo signals was truncated. Analysis of the echo peak deviation from the k-space center represented the echo shift induced by the susceptibility gradient. By performing this procedure in the three spatial dimensions, the echo-shift vector was measured showing the same resolution than the gradient echo image from which it was calculated. Until now, susceptibility gradient mapping was mainly used to create positive image by assigning grey value to its magnitude^13,15,18,19.

The SIRMA method

We introduce a new method, referred to as SIgnal Response MApping to dephaser (SIRMA) to map the susceptibility effects. In gradient echo imaging, the echo peak of susceptibility-affected spins is shifted in k-space and signal loss occurs. As the shift is proportional to susceptibility gradient, susceptibility gradients map can be produced by measuring susceptibility induced shifts. For this purpose, a series of dephased images or positive contrast images are collected using incremental dephasers. Signal intensity profiles as a function of dephasers are then generated on a pixel-by-pixel basis from the ensemble of dephased image. The signal modulation corresponds to a sinc function^9,20. Susceptibility affected voxels present a signal response profile maximum shifted compared to non affected voxels one^21,22. The magnitude and sign of this shift are measured by the SIRMA method for each pixel to produce susceptibility gradient map.

The incremental dephasers to produce dephased images correspond to a slice refocusing gradient offset. A gradient table in the slice direction is integrated into a conventional 2D gradient echo to partition the slice. Indeed, susceptibility effects are often crucial in this direction because voxels are larger in this dimension. However, the SIRMA method may also be applied to any dataset of images obtained with different dephasers. Particularly, conventional 3D gradient echo data set can be used to obtain the signal response map. In this latter case, the series of dephased images is generated by shifting the reconstruction windows in the original k-space data. Each off-center position degree correspond to a dephaser magnitude. As reconstruction window may be shifted in any k-space directions, susceptibility gradient maps may then be generated not only in the slice encoding direction but also in the frequency or phase encoding directions.

Methods

MR Imaging experiments were performed on a Bruker Avance DRX system (Bruker Biospin SA, Wissembourg, France) operating on a Paravision (version 4.0) software platform (Bruker Biospin SA, Wissembourg, France). The system is equipped with a 150 mm vertical super-wide-bore magnet operating at 7 tesla, a 84 mm inner diameter shielded gradient set capable of 144 mT/m maximum gradient strength and a 64 mm diameter birdcage resonator. Post-processing was performed on a HP xw4400 workstation using Matlab software (version 2008a, Mathworks, Natick, USA).

SPIO Nanoparticle and SPIO loaded lipid nanocapsule preparation

SPIO nanoparticles

Synthesis of SPIO nanoparticles coated with HEDP (1-hydroxyethylidene-1.1-bisphosphonic acid) was previously described²³. The average size of the magnetite crystal was 4 nm and the hydrodynamic diameter of the particles was 20 nm. The average iron concentration of the native solution of SPIO nanoparticles was 1.26 g/L.

SPIO loaded lipid nanocapsules

Oleic acid-coated SPIO nanoparticles were prepared prior to encapsulation in lipid nanocapsules from an adapted protocol described by Igartua et al²⁴. The hydrodynamic diameter of the nanocapsules was 106 nm. The average iron concentration of the nanocapsule solution was 0.08 g/L.

In vitro experiments

SIRMA susceptibility mapping quantization was evaluated on the well-characterized cylinder model. A 48 mm inner diameter phantom filled with a 0.01 mM NiCl₂/MnCl₂-doped water solution containing a glass tube filled with air (6mm inner diameter) was used. The small tube axis was about perpendicular to Bo.

Three perpendicular 2D spoiled gradient echo images were acquired with a TR of 200 ms, an echo time of 20 ms, a sampling bandwidth of 100 kHz, a 1ms three-lobe sinc RF pulse, a flip angle of 20°, a slice thickness of 3 mm, a field-of-view of 37 mm and a matrix size of 128². The number of experiments (Nex) was 1. One slice was perpendicular to the air tube axis for localization purpose and the two others slices were parallel to the air tube axis at respectively 5.8 mm (slice 1) and 6.0 mm (slice 2) from the center of the air tube. For SIRMA visualization, a gradient table in the slice direction was added for the two slices parallel to the air tube with 32 phase-encoding steps and a maximum gradient value ± 111% of the slice refocusing gradient. All others parameters were identical to the reference scan.

Numerical simulation of magnetic field distortions caused by an infinitely long cylinder filled with SPIO nanoparticles perpendicular to Bo was performed according to²⁵:

$$\mathrm{\Delta }B(r)=\left[\frac{\mathrm{\Delta }\chi }{2}·\frac{a^2}{r^2}·cos(2\phi )\right]·B_0\forall r\rangle a$$ [2]

Where Δχ is the susceptibility difference inside and outside the tube, a is the radius of the tube. The position of the observation point is given in polar coordinates; r is the distance from the tube axis and φ is the polar angle in the plane defined by Bo and the tube axis. Magnetic field gradients were simulated with a magnetic field of 7 T, Δχ = −9 ppm and a = 1.5 mm by partial derivatives of equation [2].

Acquisition parameters influence was explored on a phantom made of two glass tubes (3.4mm inner diameter) filled with SPIO nanoparticles, with different iron concentration (1.26 g/L and 0.42 g/L ). Tubes were about perpendicular to Bo and inserted in a large water tube.

First, SIRMA acquisition were performed on a slice parallel to the SPIO filled tubes axis at 4 mm from the center of tubes with a TR of 200 ms, a sampling bandwidth of 100 kHz, a 1ms three-lobe sinc RF pulse, a flip angle of 20°, a slice thickness of 3 mm, a field-of-view of 55 mm, Nex =1, an echo time of 5 ms, and a matrix size of 128², 32 phaseencoding steps in the slice direction with and a maximum gradient value ± 62% of the slice refocusing gradient. Then, slice distance from the center of tube (from 3.75 to 6.5mm), echo time (from 3.5ms to 7.5ms), phase-encoding steps in the slice direction (from 8 to 64) and maximum gradient value (from 43 to 123% of the slice refocusing gradient) were varied to explore method performances.

A 3D conventional acquisition with a matrix size of 128×128×64 and a slice thickness of 12.5 mm was also acquired to calculate a set of dephased images accordingly to Bakker et al. method⁹ and generate also a SIRMA image.

In vivo experiments

The potential of SIRMA method was illustrated in an evaluation of a novel approach to directly deliver drugs into brain tissue and brain tumors called convection-enhanced drug delivery (CED). CED is based on delivering a continuous infusion of drugs via intracranial catheters, enabling convective distribution of high drug concentrations over large volumes of the target tissue while avoiding systemic toxicity. The monitoring of drug delivery using CED is crucial but difficult to evaluate. We therefore used SPIO-loaded nanocapsules as contrast probe to mimic therapeutic nanocarriers²⁶. The SIRMA method helps to quantitatively evaluate the convection extent by determining the area of modified susceptibility induced by the SPIO.

Animal care and use were in strict accordance with the regulations of the French Ministry of Agriculture. A solution of sucrose (30 %) was mixed with SPIO-loaded nanocapsules and infused (60μL) at a rate of 0.5 μL/min for a duration of 120 min into the striatum of normal Sprague-Dawley rats (female, 150–200 g) accordingly to CED protocol previously described²⁶. Imaging was performed one hour post-infusion to assess the convection extent.

A slice, located on the CED infusion plane, was acquired with a TR of 110 ms, ten echo times ranging from 3.1 ms to 31 ms, a sampling bandwidth of 64 kHz, a flip angle of 30°, a field-of-view of 45 mm×45 mm, a slice thickness of 3 mm and a matrix size of 128×96 zero-filled to 128×128 and Nex 2. For SIRMA visualization, a gradient table in the slice direction was added with 16 phase-encoding steps and a maximum compensation slice refocusing gradient offset of ± 60 % of the slice refocusing gradient leading to a total acquisition time of 5 min 37 s. A 3D conventional acquisition with a matrix size of 128×128×32 and a slice thickness of 15 mm was also acquired for SGM processing. All others parameters were identical to the previous scan.

At the end of the MR protocol, brains were removed and cut into 1mm thick slices using an acrylic brain matrix (Harvard Apparatus, Les Ullis, France) prior to an incubation in Perl’s reagent for 30 minutes to reveal SPIO²³.

Post-processing calculation

SIRMA images were generated from the set of images obtained with different dephasers. The maxima of the signal intensity profile as a function of dephasers was determined for every voxel. The echo shift sign and strength were measured in units of partition-encoding gradient steps, ΔG_x,y,z, from the zero value. The susceptibility gradient was then be estimated from the echo shift m_x,y,z via:

$${\text{G}}_{\text{sus}}\approx -{\text{m}}_{\text{x},\text{y},\text{z}}·\mathrm{\Delta }{\text{G}}_{\text{x},\text{y},\text{z}}·{\tau }_{\text{x},\text{y},\text{z}}/\text{TE}$$ [3]

where τ_x,y,z is the partition-encoding gradient duration and TE the echo time.

In case of shimming imperfections, susceptibility gradient maps were corrected for nonuniform shim. Large scale shift image was estimated from the original shift image using a morphological opening method²⁷, then subtracted from the original image and the corrected shift image was converted to susceptibility gradient map.

SGM was calculated accordingly to Dahnke et al. method¹². Susceptibility gradient magnitude and direction were then plotted in 3D field as cones.

Results

The cylinder model, well characterized²⁸ and easily applicable experimentally, was used to demonstrate the ability of the new method to quantify susceptibility gradient. Susceptibility gradient images (fig. 1b–c) were simulated according to analytical equation describing field inhomogeneities induced by a theoretically infinitely long cylinder perpendicular to Bo and susceptibility gradient profiles (fig. 2) were computed for slices parallels to the cylinder and in its vicinity as shown on figure 1a. The experimental setup to measure susceptibility gradient was performed using an air-filled tube of small diameter compared to its length placed about perpendicular to Bo. Two perpendicular imaging planes were chosen, both parallel to the air tube axis as shown on the 2D gradient-echo image (fig. 1a). The signal response curves to dephaser were plotted (fig. 3a) from the set of positive contrast images acquired with the incremental slice refocusing gradient offset sequence (fig. 3b–c) for three voxels. Two were close to the SPIO tube and therefore exposed to the larger susceptibility effect and a third one, distant from the tube and exposed to moderate susceptibility effect. The signal response curves showed sinc profiles and the shift of their maxima as a function of the dephaser intensity appeared to be dependent on the susceptibility effect experienced by voxels. Echo shift, determined for every voxel, were converted into susceptibility gradient (equation [3]) to produce SIRMA images (fig 1d–e). Then, susceptibility gradient profiles were extracted from these SIRMA images and compared to simulated ones (fig 2). Gradients present similar patterns and magnitude on simulated profiles and on SIRMA profiles.

Figure 1. Quantization of susceptibility gradient in the vicinity of an air tube perpendicular to Bo.

(a) On the 2D gradient-echo image perpendicular to tube axis, the three pixels used to plot the signal response curve to dephaser showed in figure 3 are indicated; (b–c) Simulations of magnetic gradients induced by an air tube perpendicularly to its axis (gradient in-plane direction indicated by the arrows); (d–e) SIgnal Response MAp (SIRMA) to dephaser (in mT/m), calculated from a series of images collected with incremental slice refocusing gradient offset (fig 3b–c) for slices 1(d) and 2(e) identified on fig.1a.

Figure 2. Quantization of susceptibility gradient in the vicinity of an air tube perpendicular to Bo.

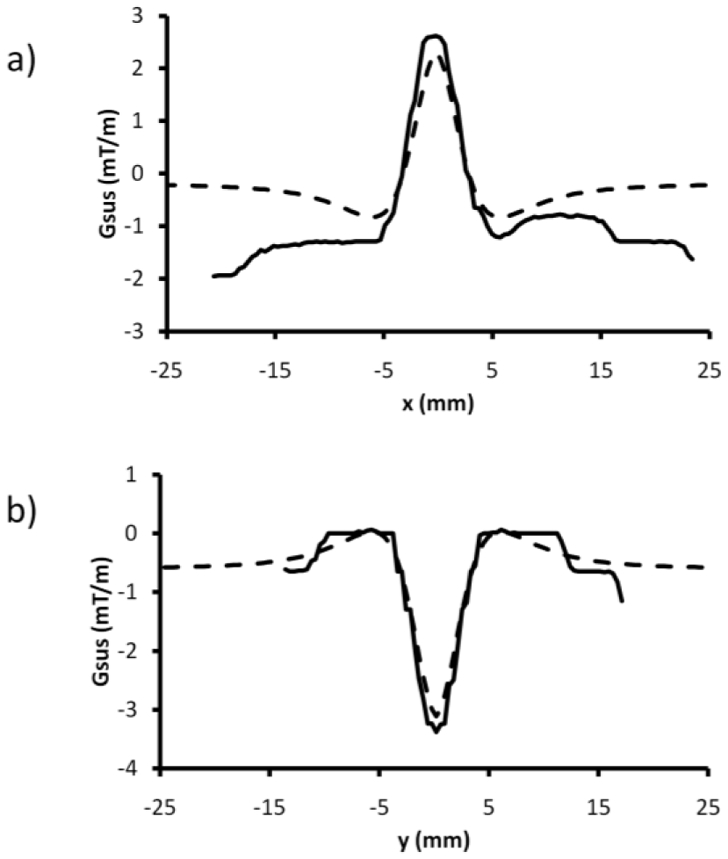
Comparison of susceptibility gradient profiles for direction parallel to the air tube axis and in its vicinity simulated (- - -) or extracted from the SIRMA images (–) for slice 1 (a) et slice 2 (b) identified on fig 1a.

Figure 3. Quantization of susceptibility gradient in the vicinity of an air tube perpendicular to Bo.

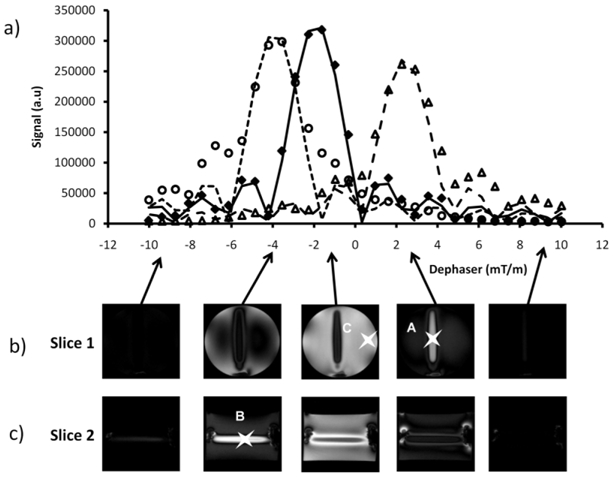
(a) Signal response curves to dephaser for the three voxels identified on fig.1a, differently affected by susceptibility plotted from positive contrast images acquired with an incremental slice refocusing gradient offset (b–c) measured experimentally [A (△), B(○) and C(◆)] or simulated [A (---), B(^···) and C(–)].

The performances of the SIRMA method with respect to echo time, slice distance from the center of tube, phase encoding steps and maximum gradient value in the slice direction are shown in figure 4 for two iron concentrations. As expected, the measured susceptibility gradient is different for the two iron concentrations and their values decrease when the slice is moved away from the tube (fig 4a). No evolution of the measured susceptibility gradient was observed with the others parameters even when their choice was suboptimal (fig 4b–c). Figure 4e displays the SIRMA image calculated from the set of positive contrast images generated with the incremental slice refocusing gradient offset sequence. A second SIRMA image (fig 4f) was also generated by post processing a conventional 3D gradient-echo dataset. The set of positive contrast images necessary to calculate the SIRMA image was generated by off-centering the reconstruction window in the slice direction at the expense of resolution. Both SIRMA images are very similar even if small discrepancies are visible, mainly due to the difficulty to match slices geometry.

Figure 4. Performances of the SIRMA method.

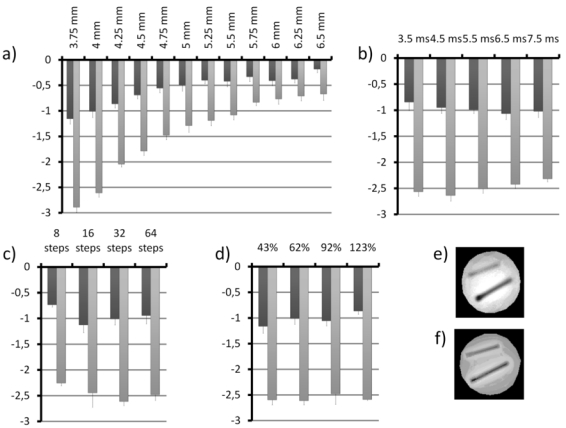
Susceptibility gradient were quantized in the vicinity of two tubes about perpendicular to Bo, filled with SPIO nanoparticles with different average iron concentration [1.26 g/L (grey bars) and 0.42 g/L (black bars)] (mean and standard deviation upon 26 pixels). The performances were evaluated with respect to slice distance from the center of tube (from 3.75 to 6.5mm) (a), echo time (from 3.5ms to 7.5ms) (b), phase encoding steps (from 8 to 64)(c) and maximum gradient value (from 43 to 123% of the slice refocusing gradient) (d) in the slice direction. Two SIRMA images of the tubes are presented, calculated from a different sets of positive contrast images either (e) acquired with the incremental slice refocusing gradient offset sequence either (f) calculated by off-centering the reconstruction window in the slice direction of a conventional 3D gradient-echo dataset.

Robustness of the SIRMA method to quantitatively map susceptibility gradient was also evaluated in vivo. On T2* weighted gradient-echo rat brain images after CED-infusion of SPIO-loaded nanocapsules, the SPIO induced signal void volume increases with T2* weighting (fig 5a) illustrating the difficulty to correctly map the convection extent in vivo. On SIRMA images obtained from different T2* weighted dataset (for TE = 3.1 ms to 31 ms) (fig. 5b) regions of massive susceptibility gradient induced by the SPIO loaded lipid nanocapsules are clearly visible. The quantitative evaluation of the convection extent was performed by measuring the thresholded area of modified susceptibility on SIRMA images obtained for different TEs (fig. 5a). Even though the susceptibility area tends to increase for the short TEs, a plateau (4.67± 0.25 mm²) is rapidly reached for TE values from 12.4 ms to 31 ms. This measure is consistent with the area estimated on the histological Perl’s staining slice (ca. 5 mm²) (fig. 5a,c). The SGM 3D coneplot (fig. 5d) also clearly delineated susceptibility gradients induced by the SPIO loaded lipid nanocapsules as well as the ear cavities. A susceptibility gradient map in the slice direction (fig 5e) was extracted for comparison purpose with SIRMA. The magnitude of susceptibility gradients measured with SIRMA and SGM are in the same range.

Figure 5. In vivo quantitative evaluation of the area infused by SPIO-loaded nanocapsules using convection-enhanced drug delivery in a rat brain.

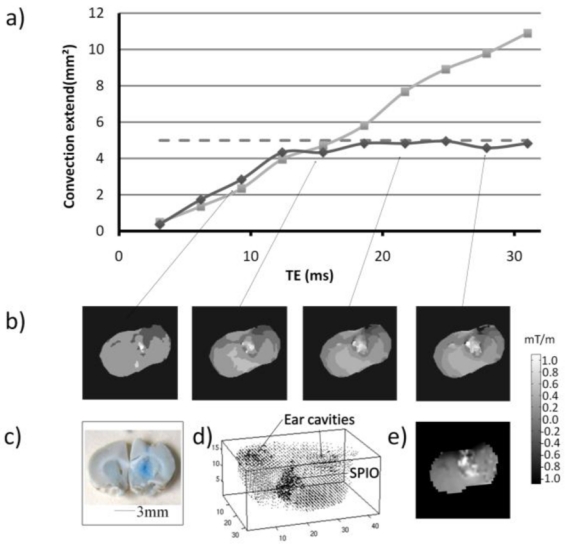
(a) The area of modified susceptibility induced by the SPIO-loaded nanocapsules on thresholded SIRMA images (–), on T2*weighted images ( - - ) of a rat brain after infusion by convection-enhanced drug delivery was measured as a function of the T2* weighting (TE = 3.1 to 31ms). Convection extent was also measured on histological post-mortem Perl’s staining image (^···). Corresponding representative SIRMA gradient maps (b), histological post-mortem Perl’s staining (c), SGM 3D coneplot (d) and SGM map in the slice direction (e) were also displayed.

Discussion

Susceptibility gradient visualization and quantization are crucial points for SPIO detection, especially in the moving field of cellular and molecular MRI but also in the estimation of bubble size in alveolar structure for instance or in osteoporosis within spongy bones. The proposed method called SIgnal Response MApping (SIRMA) aims at quantifying susceptibility gradient using a set of positive contrast images collected with different dephasers. Such set of positive contrast images can either be obtained via a specific MR acquisition with incremental slice refocusing gradient offset or from a conventional 3D-gradient echo datasets. In the first case, the acquisition pattern used is adapted from approaches proposed by Reichenbach et al.²⁹ and by Yang et al.³⁰. In both methods, three-dimensional acquisition with a gradient table in the slice direction was used to produce a two-dimensional image with reduced susceptibility artifacts along the slice-selection direction. However, these methods differ by the presence or absence of a third Fourier transform in the slice direction. The signal amongst partitions is modulated by the strength and direction of the susceptibility gradient in the absence of the third Fourier transform and by the excitation profile after the third Fourier transform. In Reichenbach et al.²⁹ approach, 3D partitions were collapsed, without Fourier transform beforehand, to produce projections across the slab thickness for each partition-encoding gradient step. Stepping through the projections allowed to highlight susceptibility gradients in known increments. For the Yang et al.³⁰ method (called Gradient-Echo Slice Excitation Profile Imaging or GESEPI), the acquired data set was reconstructed with a 3D Fourier transformation and a final 2D image with reduced susceptibility artifacts was obtained by adding the magnitude images within the excited slice. With SIRMA, the dataset is also acquired with incremental slice refocusing gradient offset. In the absence of the third Fourier transform, each increment of the slice refocusing gradient offset is then used as an individual dephaser. However, the originality of SIRMA reside in the way the dataset is processed to produce a susceptibility gradient 2D map by measuring the echo maximum shift on a pixel-by-pixel basis. Furthermore, this dataset offers the opportunity to obtain, also a susceptibility artifact free image by simply performing a Fourier Transform in the slice encoding direction and adding the magnitude images as described by Yang et al³⁰. Although it required longer acquisition time than classical T2* 2D acquisition, the SIRMA image was easily obtained without spatial resolution losses. In the second case, SIRMA images are computed from conventional 2D or 3D gradient-echo sequences. The set of positive contrast images is reconstructed by varying the degree of dephasing of the images via off-centering the reconstruction windows. In this case, no extra acquisition time is required but the SIRMA images are obtained at the expense of a loss in spatial resolution. Indeed, the reconstruction window shift was only possible if there is room to shift the reconstruction window in k-space. Obviously, SIRMA images could be obtained in any spatial encoding direction as it was straightforward to shift reconstruction window in various orientations.

The main advantage of the SIRMA method is its quantitative nature as the measured echo shift is directly proportional to the magnitude of the susceptibility effect. Indeed, once using conventional gradient compensation method or dephased MRI, the positive contrast depends on the chosen dephaser. Therefore, if multiple foci with different susceptibility gradients are present on the image, one chosen dephaser could highlight some of them and null others unless a set of compensation gradients is used to compensate for each particular level of susceptibility gradient. With SIRMA, only the maximum gradient offset and number of sampling points need to be correctly chosen to accurately sample all the susceptibility shifted echoes while keeping all of them within the acquisition window. Adequate value depends on the distribution of susceptibility gradients within an imaging slice and on the echo time and therefore can be easily transposed between similar scans. The comparison between SIRMA susceptibility gradients evaluation and simulation in vitro or SGM results in vivo has demonstrated the good ability of the new method to correctly quantify and map gradients. Furthermore, even in case of suboptimal parameters choice, the influence on susceptibility gradient determination was shown to be limited. Considering cellular and molecular imaging applications, with different iron loading²³, localization of the target and compartmentalization within the targeted cell³¹ responsible for a large panel of susceptibility-induced effects, the SIRMA method could then allow the detection of all of them in one shot as opposed to positive contrast imaging. Moreover, SIRMA also presents the advantage to discriminate relevant susceptibility gradient induced by SPIO from large scale susceptibility artefacts estimated by morphological opening calculation²⁷.

Although positive contrast images or T2* weighting images are often sufficient to localize massive contrast agent tagging area, SIRMA method offers the possibility to quantify precisely the SPIO distribution volume as shown with the in vivo evaluation of CED extent. Indeed, as opposed to T2* weighting imaging with perturbation volume dependent of echo time or to positive imaging where the enhancement is dependent on the dephaser, SIRMA volume estimation is independent of the T2* weighting except for short TEs where the volume was underestimated. This may certainly arise from the insufficient sensitization to susceptibility effect for short TE. However, the major limitation of the SIRMA method is its incapability to produce 3D susceptibility gradient map. This limitation was recently overcome by using 3D-SGM method¹² but at the expense of long and complex processing.

In summary, this study propose a new method to quantify susceptibility gradient which applicability and performances has been demonstrated in vitro through quantization of susceptibility gradient induced in a cylinder model and in vivo through the quantitative detection of SPIO distribution volume. With respect to its quantitative nature, its computational simplicity and its adaptability to different dataset, this method deserves further attention for use in a wide range of applications especially in molecular or cellular imaging.