Integrative computational models of cardiac arrhythmias -- simulating the structurally realistic heart

Abstract

Simulation of cardiac electrical function, and specifically, simulation aimed at understanding the mechanisms of cardiac rhythm disorders, represents an example of a successful integrative multiscale modeling approach, uncovering emergent behavior at the successive scales in the hierarchy of structural complexity. The goal of this article is to present a review of the integrative multiscale models of realistic ventricular structure used in the quest to understand and treat ventricular arrhythmias. It concludes with the new advances in image-based modeling of the heart and the promise it holds for the development of individualized models of ventricular function in health and disease.

Introduction

The cyclic mechanical pumping of the heart is essential for the sustenance of body function. Accordingly, cardiac disease is the leading cause of morbidity and mortality in the developed world. A large body of current basic and clinical research is devoted to the comprehensive understanding of cardiac function in health and disease. In the past decade, advanced computational modeling of cardiac electromechanical function has become an important complementary approach to experimental and clinical research by aiding hypothesis formation, integration and interpretation of data, extraction of information, and the development of new, targeted therapies. In addition, a host of relevant phenomena are not open to direct experimental manipulation or observation, and precise methods for three-dimensional assessment of the distribution of many variables reflecting electrical and mechanical processes in the heart are not yet available; modeling approaches are well-poised to fill these gaps in our knowledge.

Disturbances in cardiac rhythm, or arrhythmias, the most malignant of which lead to sudden cardiac death, have long been the focus of intense interdisciplinary research. Computational modeling of cardiac arrhythmogenesis and arrhythmia maintenance has made a significant contribution to the understanding of the mechanisms of rhythm disorders in the heart. Much computational cardiac electrophysiology research has focused on the dynamics of cellular and sub-cellular processes, such as ionic currents and calcium cycling, that give rise to the myocyte action potential [1–3]. The effects of alterations in the kinetics of gating and other state variables have been extensively explored for a number of species. Recent developments in these computational approaches have culminated with the development of Markov-chain ionic models [4]. These have been instrumental in the exploration of the role of cardiac ion channel proteins genetic defects in abnormalities in cardiac action potential and thus, in the origin of arrhythmias in patients with inherited channelopathies. However it has become increasingly clear that most common human diseases, including myocardial ischemia, heart failure, and arrhythmias, are not due to a single defective gene. As such, it has become essential to develop multiscale systems approaches to cardiac function in health and disease that go well beyond genotype–phenotype arrhythmia associations. A key strategy in integrating individual building blocks within the whole heart is to characterize the emergent properties that arise at each successive scale in the hierarchy of biological complexity. The goal of this article is to provide a review of the integrative computational models and approaches to uncovering the mechanisms underlying ventricular arrhythmias. We specifically focus on models using structurally-realistic ventricular geometry, since these models can capture the unique 3D electrophysiological behavior and wave propagation in the ventricles.

Models of ventricular arrhythmia mechanisms

Cardiac tissue and whole-heart electrophysiological computations are based on principles of reaction-diffusion systems. Numerical solutions to the governing equations are computed using finite element methods [5]. Such methods require a representation (or model) of the geometry and the fiber structure of the ventricular myocardium. In ventricular simulation studies, the canine model constructed at Auckland University [6] and the rabbit model developed at the University of California, San Diego [7] have been most widely used. The data for the canine model were obtained using a specially designed mechanical rig, while the rabbit model was constructed from digital images of histological sections.

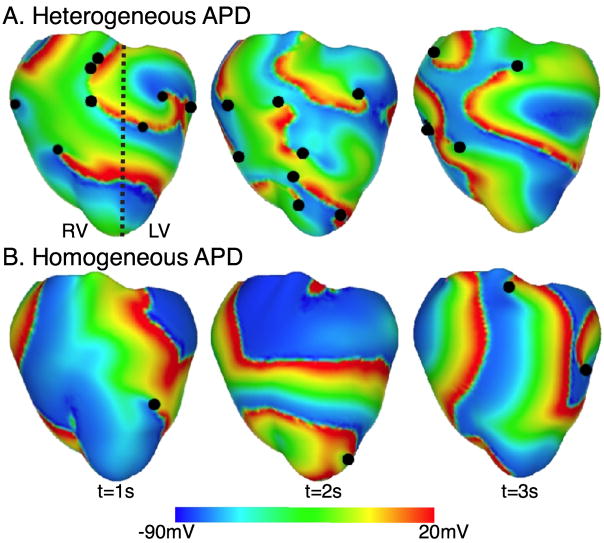
The majority of the ventricular models used in the study of arrhythmia mechanisms have focused on the rotational propagation of complex 3D electrical waves in the heart. These self-sustaining reentrant waves (termed spiral waves in 2D and scroll waves in 3D) occur in a variety of nonlinear excitable media. A seminal experimental study using fluorescence mapping of electrical activation in the heart from Jalife’s group [8] demonstrated the presence of such waves in cardiac tissue and their role in ventricular fibrillation (VF), the most malignant of all arrhythmias. Panfilov and Keener [9] were the first to construct a realistic, 3D model of scroll-wave activation in the heart using the Auckland canine geometry. The authors captured the dynamics of excitable tissue by using the 2-variable FitzHugh-Nagumo model [10] of membrane kinetics. The study demonstrated for the first time that the organizing centers (filaments) of reentrant activity in the structurally-normal heart could be maintained entirely within the myocardial wall, manifesting themselves as focal sources of activation on the cardiac surfaces. The same model was subsequently used by Jalife and co-workers [11,12] to propose that while in small hearts (mice, rabbis) a single rapidly drifting and meandering rotor could underlie VF, in large hearts including those of humans, VF could be sustained by numerous coexisting rotors. Panfilov [13] extended this concept by demonstrating, in the same ventricular model, that not only the presence of scroll waves in the heart, but also their breakup (dynamical instability) were relevant to the sustenance of VF. The role of the 3D ventricular geometry in wave fragmentation and spiral wave break-up was further explored in studies by Rogers [14] and Xie et al [15]. Additionally, in a series of studies, Clayton and co-workers [16,17] examined the scroll-wave filament dynamics in the rabbit and canine ventricles, quantifying the number of filaments and their lifetimes, and classifying their shapes. Furthermore, the behavior of the vortex filaments was found to depend on action potential duration (APD) heterogeneity in the ventricles, as determined by Arevalo et al [18]. Figure 1 shows VF in ventricles with both homogeneous and heterogeneous APD. The authors determined that heterogeneity in APD produced increased turbulence in the ventricles (Figure 1) as demonstrated by the number of filaments present (and manifested in the number of phase singularities, the points where filaments intersect the surface).

Figure 1.

Transmembrane potential distributions in VF for heterogeneous APD (i.e. left, LV, and right, RV, ventricles have different APDs) and for homogenous APD. The dashed black line denotes the border between regions characterized by a different APD. Epicardial phase singularities are marked with solid black circles. Based on figures from [18].

Realistic models of ventricular geometry were used to ascertain the mechanisms responsible for the onset of VF, and in particular, the transition from tachycardia to fibrillation. These studies focused on the development of APD alternans [19] and the role of alternans and APD restitution [20,21] in conduction block, dynamic stability in reentrant activity, and transition to VF. In order to investigate the contributions of dynamical factors and their manifestation within the ventricular geometry of the heart, these studies employed increasingly complex membrane kinetics models in which the contribution of the various ionic currents could be modified.

Finally, in recent years, significant advances have been made in the use of biophysically detailed membrane kinetics models integrated with realistic geometries to understand the mechanisms by which arrhythmias arise and are maintained in the human heart [22]. The geometrical data for the model were obtained from histological slices of an ex-vivo normal human heart. To account for the anisotropic structure of the heart, the authors mapped the fiber architecture of a canine heart onto their model. The study by ten Tussher et al [22] was the first to provide insight into VF dynamics in the human heart. Using the same model, Keldermann et al. [23] further investigated the effect of heterogeneous restitution properties in human VF by incorporating clinically-measured restitution properties. The study found that the number of filaments and the excitation periods depended on the extent of the restitution heterogeneity. Thus, restitution heterogeneity was found to play an important role in arrhythmogenesis by providing a substrate for cardiac arrhythmias.

Ventricular models of arrhythmias in the diseased heart

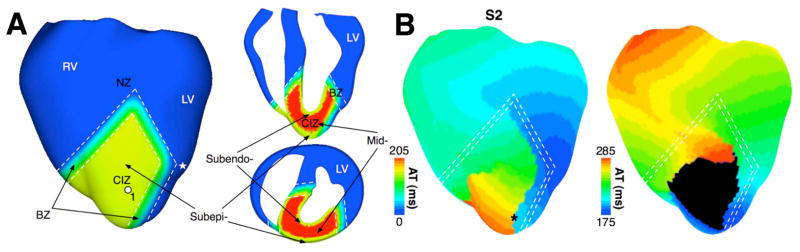
The studies reviewed above examined the mechanisms underlying arrhythmogenesis and maintenance of arrhythmia within a general nonlinear dynamics framework, but did not represent particular cardiac diseases. Computational research into arrhythmias in the setting of cardiac disease using realistic ventricular models remains in its infancy. Simulation research into regional ischemia in the ventricles and concomitant arrhythmogensis is one notable exception. The article by Tice et al [24], which used a geometrical model of a slice through the rabbit ventricles to study arrhythmias in acute regional ischemia phase 1a, revealed that both ischemic electrophysiological heterogeneity and the shape of the ventricles contribute to arrhythmia maintenance. The study by Jie et al. (Jie X, Trayanova N. Mechanisms for initiation of reentry in acute regional ischemia phase 1B, Heart Rhythm, in revision, 2009) characterized the substrate of ischemia phase 1B arrhythmia by examining how the interplay between different degrees of hyperkalemia in the surviving layers, and different degrees of cellular uncoupling between these layers and the mid-myocardium, contribute to reentrant arrhythmias. Both studies used realistic representations of the ischemic insult (hyperkalemia, acidosis, hypoxia), including its spatial distribution (a central ischemic zone and border zones). Figure 2 shows the model of regional ischemia phase 1b in the rabbit ventricles and the generation of a reentry following the slow propagation of a premature stimulus in the sub-epicardium. The results demonstrated that a wide border zone reduced the inducibility of reentry by blocking propagation in the central ischemic zone. In addition to ischemia, other notable models of arrhythmogenesis in disease include those on the pro-arrhythmic consequences of congenital mutations in the cardiac sodium channel (encoded by the SCN5A gene) [25] and in the KCNQ1 gene, which encodes the alpha-subunit of the slow potassium current [26]. While both studies used a wedge model extracted from the rabbit ventricular geometry, the novelty of these modeling studies lay in the use of transmural electrophysiological heterogeneities, as well as representations of beta-adrenergic stimulation and mechanistic descriptions of the mutations.

Figure 2.

Model of regional ischemia and induction of arrhythmia therein.

A. Views of the rabbit ventricular model showing demarcation of the normal zone (NZ), central ischemic zone (CIZ) and border zone (BZ) following occlusion of the left anterior descending coronary artery. White dashed lines outline BZ. Asterisk indicates the stimulus site. LV-left ventricle; RV-right ventricle. B. Activation maps on the anterior epicardial surface (see text for detail). Based on figures from Jie X and Trayanova N, Heart Rhythm 2009 (in revision).

Ventricular models of arrhythmia initiation with electric shocks and defibrillation

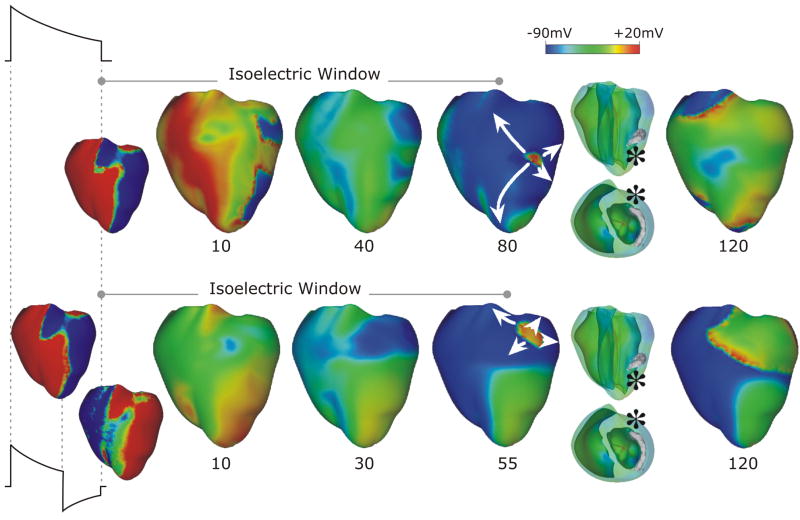
Ventricular models incorporating realistic geometry have also been used to examine the mechanisms by which a defibrillation shock induces arrhythmia and defibrillates (terminates VF in) the heart. These models are accompanied by further complexities, as they require the use of the bidomain representation of cardiac tissue, in which current flow in the extracellular space is explicitly accounted for. Studies by Trayanova’s group determined the mechanisms by which virtual electrode polarization is induced following a defibrillation shock in the ventricles with complex 3D geometry [27,28] and the mechanisms by which post-shock activations originate. In studies of arrhythmogenesis with external monophasic shocks in a 3D bidomain model of the rabbit ventricles [29], Rodriguez et al [30,31] demonstrated that shock outcome and the type of post-shock arrhythmia induced by the shock depend on the location of the intramural postshock excitable area formed by shock-induced deexcitation of previously refractory myocardium. The article by Ashihara et al [32] extended these findings and proposed a new theory of postshock propagation and shock-induced arrhythmogenesis. The authors suggested that the mechanism that underlies the quiescent period following strong shocks near the upper limit of vulnerability or defibrillation threshold (this period is termed the isoelectric window) is due to a “tunnel propagation” of a postshock activation through intramural excitable areas. Figure 3 demonstrates this concept for monophasic (top) and biphasic (bottom) shocks. Formation of virtual electrode polarization, quick re-excitation, and synchronous repolarization took place sequentially. However, a wavefront that originated deep within the wall remained submerged, giving rise to an isoelectric window, until it broke through onto the epicardium and then propagated, resulting in intramural reentry. The mechanisms underlying initiation of post-shock arrhythmias under the conditions of global ischemia have also been studied using the same ventricular model [33].

Figure 3.

Monophasic (top) and biphasic (bottom) shock episodes resulting in isoelectric window and arrhythmia initiation. Progression of activity from virtual electrode polarization through intramural activation (marked by* in transparent views) to epicardial breakthrough, followed by focal activation pattern and reentry. Shocks are external, of duration 10ms (6/4ms for the biphasic shock) and of strengths 16 (monophasic) and 12 (biphasic) V/cm. Based on figures from [32].

The Purkinje system has also been implicated in the failure of the defibrillation shock. Vigmond and co-workers have developed a unique rabbit ventricular model that incorporates the free-running His-Purkinje system [34]. Initial studies using this model demonstrated that the Purkinje fibers might be involved in maintaining VF early post-shock by providing alternative propagation pathways [35]. The presence of Purkinje fibers led to re-entry initiation at lower shock strengths, and could be the source of the rst post-shock activations, providing an alternative to the tunnel propagation hypothesis above.

Finally, a bidomain rabbit ventricular model, in combination with a 3D model of photon scattering over the same geometry, has been used to understand the role of photon scattering in optical mapping of arrhythmogenesis and defibrillation. Optical mapping is a widely used experimental technique capable of providing high spatiotemporal resolution recordings of electrical activity from the surface of the heart. However signal distortion occurs during optical mapping due to scattering of fluorescent photons from excited tissue. Simulation papers by Bishop and co-workers [36–38] have demonstrated that that distortion in the optical signal as a result of fluorescent photon scattering is truly a 3D phenomenon, and depends critically upon the geometry of the ventricles, the direction of wavefront propagation, and the specifics of the experimental setup. These studies provided important insight into characteristics of the optical signals that arise from photon scattering in the ventricles during arrhythmias and defibrillation.

Image-based models of ventricular arrhythmias

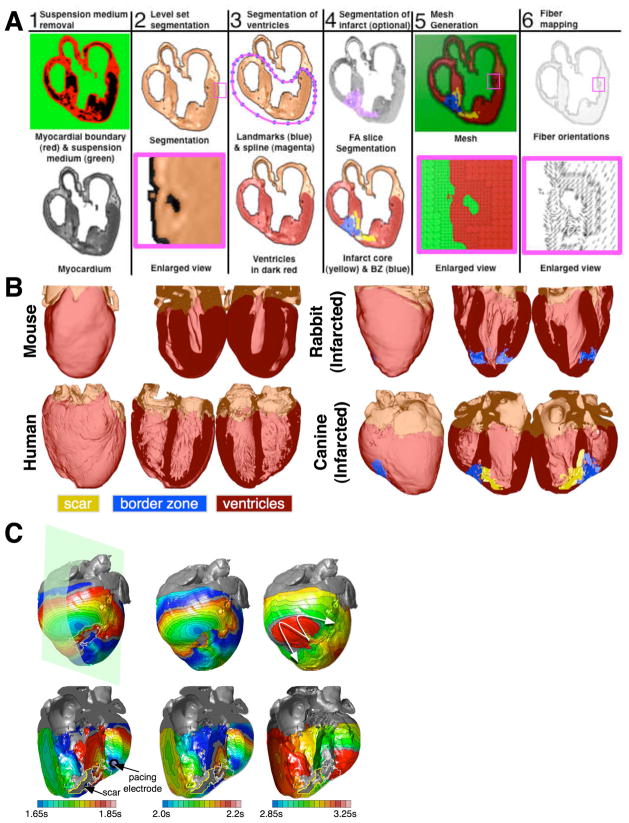
We conclude this review article with a brief description of the newest trend in computational cardiac electrophysiology and arrhythmia research. Magnetic resonance (MR) imaging technologies can now acquire the structure of the ex-vivo heart at a very high spatial resolution. Advanced diffusion tensor (DT) MR scans can additionally measure the diffusivity of water in the tissue; the primary eigenvectors of the DTs have been shown to align with the prevailing cardiomyocyte (fiber) orientations. Given these advances, and the rapid progress of high-performance computing, anatomically detailed, tomographically reconstructed models are now being developed that integrate functions from the level of ion channels to the electrophysiological interactions in the intact heart [35,39,40]. To generate models of the heart from structural and DTMR images of both normal and structurally-remodeled hearts, it is necessary to classify (or segment) the voxels (three-dimensional pixels) in the image into different groups, such as myocardium, infarct, background, etc. From the segmented image, a finite element mesh is generated, and fiber orientations are assigned to the elements based on the DTMR data. Figure 4A diagrams the pipeline used to assemble image-based models of the heart [35,39] by showing the processing of an example image slice. It is important to note that models generated in this way retain fine structural details, such as endocardial trabeculations and papillary muscles, provided that such structural details are resolved by the imaging method. Using reconstructed heart geometry from various species (Figure 4B), multiscale models of arrhythmogenesis are developed. For example, Figure 4C presents epicardial and intramural views of activation patterns during ventricular tachycardia induction from a pacing site in the canine infarcted heart [35]. The simulations demonstrate that all reentrant circuits were initiated and anchored around the zone of infarct. These results are consistent with experimental findings during electrical mapping of ventricular tachycardia in infarcted canine hearts.

Figure 4.

Image-based models of the heart. A. The pipeline for reconstructing the geometry of the heart. B. Heart models of various species. C. Epicardial (top) and intramural (bottom) activation maps during tachycardia induction. The plane indicates the transmural view. The scar is outlined in yellow. Ventricular tachycardia is induced, having an epicardial gure-of-eight reentrant morphology (last panel, arrows indicate direction of propagation). Panel A is based on figures from [35,39].

Conclusion

The models of ventricular arrhythmogenesis reviewed here underscore the importance of using integrative multiscale models of realistic cardiac structure. An exciting future awaits computational cardiac electrophysiology as it strides nowadays from image-based models of hearts from various species towards patient-specific predictive models of cardiac disease and therapeutic interventions.